Casson Fluid Saturated Non-Darcy Mixed Bio-Convective Flow over Inclined Surface with Heat Generation and Convective Effects
Abstract
1. Introduction
- How do Biot numbers influence the flow profiles of bioconvective Casson fluid through non-Darcy porous media?
- What are the comparative impacts of inclined, vertical, and horizontal surfaces on velocity, temperature, and microbial distributions?
- How do variations in mixed convection parameters affect the interplay between forced and free convection regimes in the presence of gyrotactic microorganisms?
2. Mathematical Modeling
2.1. Flow Model
- a.
- Steady Two-Dimensional Laminar Non-Darcy Flow Model: The flow is assumed to be steady and laminar, suitable for low Reynolds number conditions. The use of a non-Darcy model accounts for the inertial effects in the porous medium, making it applicable to a wider range of flow conditions beyond the linear Darcy regime.
- b.
- Boussinesq Approximation: The density variation is considered only in the buoyancy term, which is a standard assumption for free and mixed convection analysis, ensuring mathematical simplicity without significant loss of accuracy for moderate temperature differences.
- c.
- Free, Mixed, and Forced Convection in an Incompressible Casson Fluid Over an Inclined Surface: The model captures the combined effects of buoyancy (free convection), external driving forces (forced convection), and their interaction (mixed convection). Casson fluid, representing a non-Newtonian fluid with yield stress, is selected to model complex biological fluids like blood.
- d.
- Coordinate System Definition: The -axis is taken along the inclined surface, and the -axis is perpendicular to it. This coordinate system aligns with the flow direction, providing a clear understanding of the velocity and temperature distributions.
- e.
- Slip Condition at Surface: A velocity slip condition is introduced at the surface, accounting for real-world scenarios where the fluid does not perfectly adhere to the surface, enhancing the model’s flexibility.
- f.
- Non-Darcy Porous Medium Saturated with Gyrotactic Microorganisms: The porous medium is isotropic, ensuring uniform permeability, and it is populated with gyrotactic microorganisms (e.g., Chlamydomonas nivalis), which align and swim in response to external stimuli like gravity.
- g.
- Convective Boundary Conditions at Surface: Convective boundary conditions are applied, allowing the surface to exchange heat with the surrounding fluid, making the model more adaptable to practical scenarios like geothermal reservoirs or bioreactors.
- h.
- Model Validity for Low Reynolds Number: The model is particularly suitable for low Reynolds number conditions, ensuring that the flow remains laminar and avoiding complexities of turbulence.
2.2. Governing Equations and Boundary Conditions
3. Numerical Methodology
3.1. The Kafoussias–Williams Method:
- (i)
- the common finite difference method with central differencing;
- (ii)
- a tridiagonal matrix modification;
- (iii)
- a final iterative procedure to ensure convergence.
3.2. The bvp4c Technique
3.3. Validation
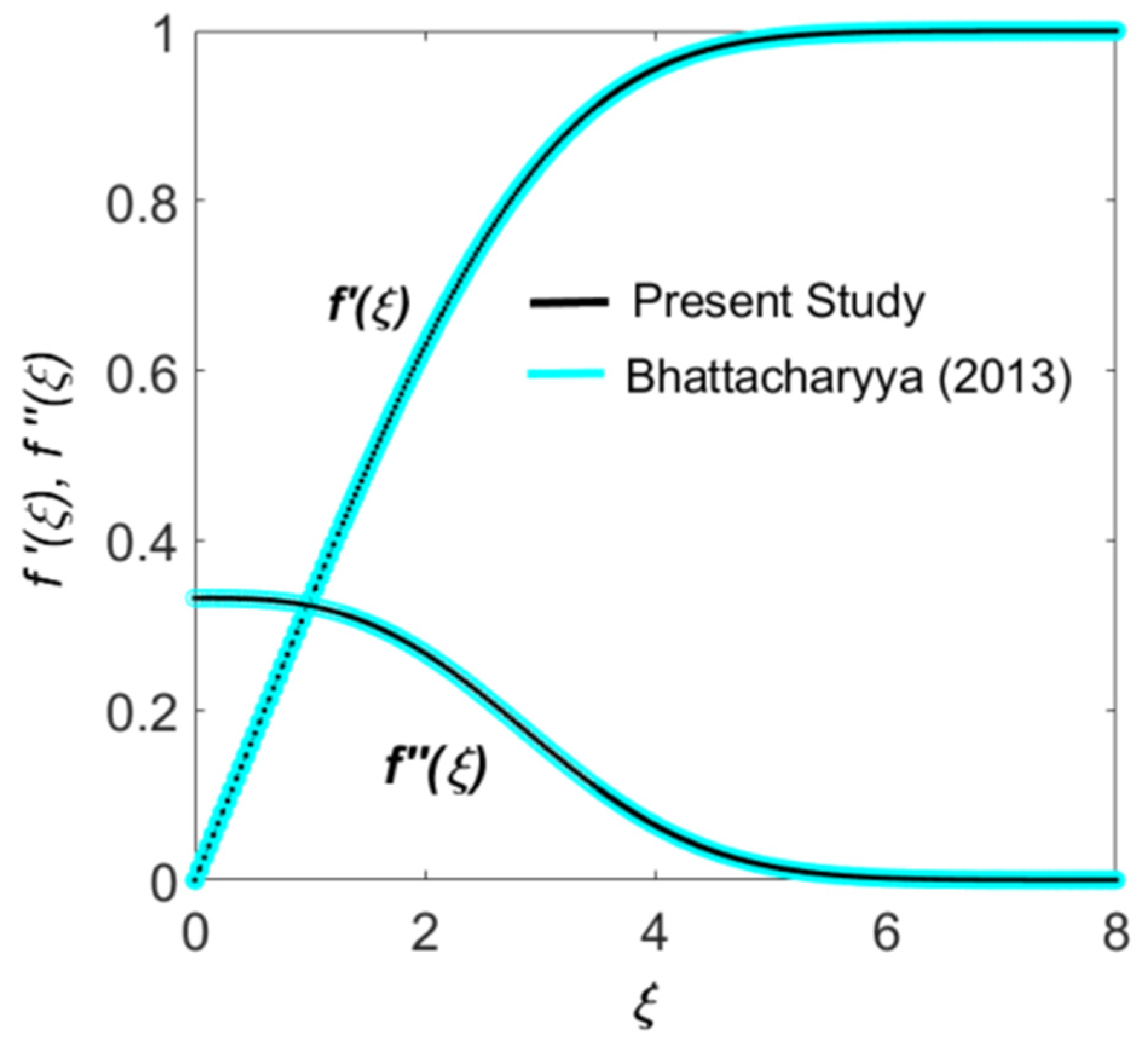
- A graphical comparison of the velocity profile and shear stress profile was made against the results reported by Bhattacharyya et al. [44] for mixed convective boundary layer slip flow. As illustrated in Figure 2, the outcomes of the present study show an excellent correlation with their published data, confirming the accuracy of the underlying mathematical and computational framework.
- Furthermore, a comparative analysis for the velocity profile , surface temperature , and heat transfer rate was conducted against the findings of Nima and Ferdows [23]. This comparison, shown in Table 7, also revealed remarkable compatibility, providing additional confidence in the model’s predictive capabilities.
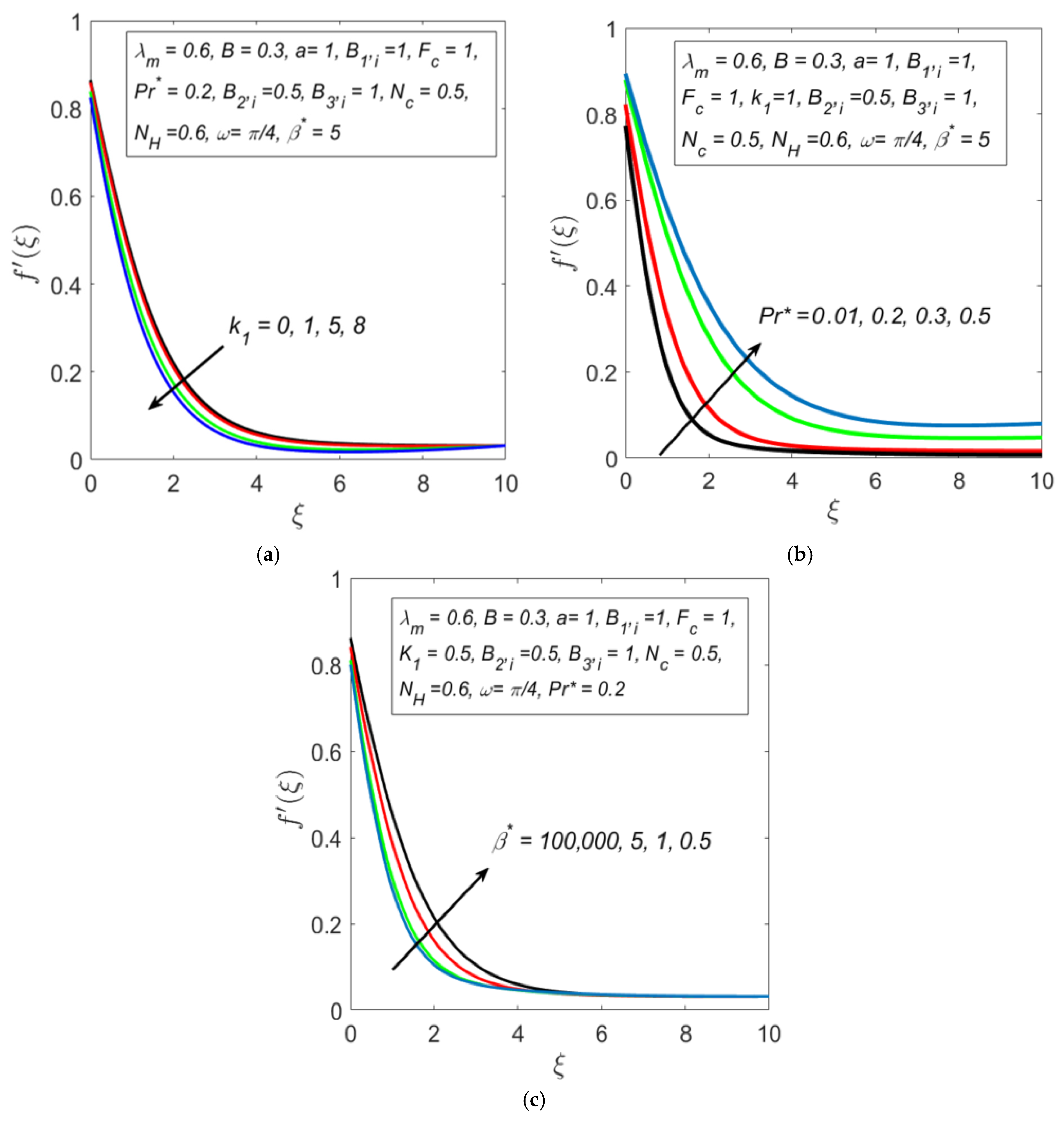
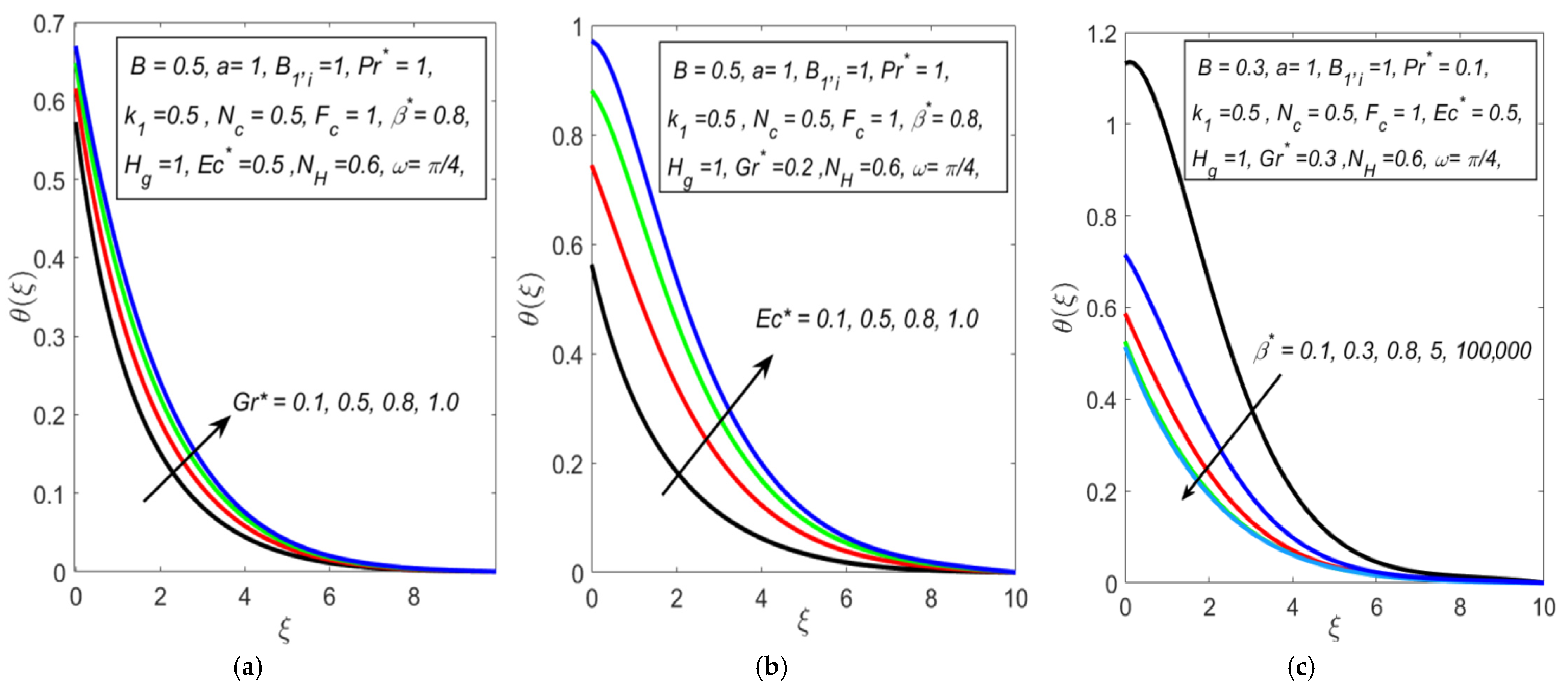
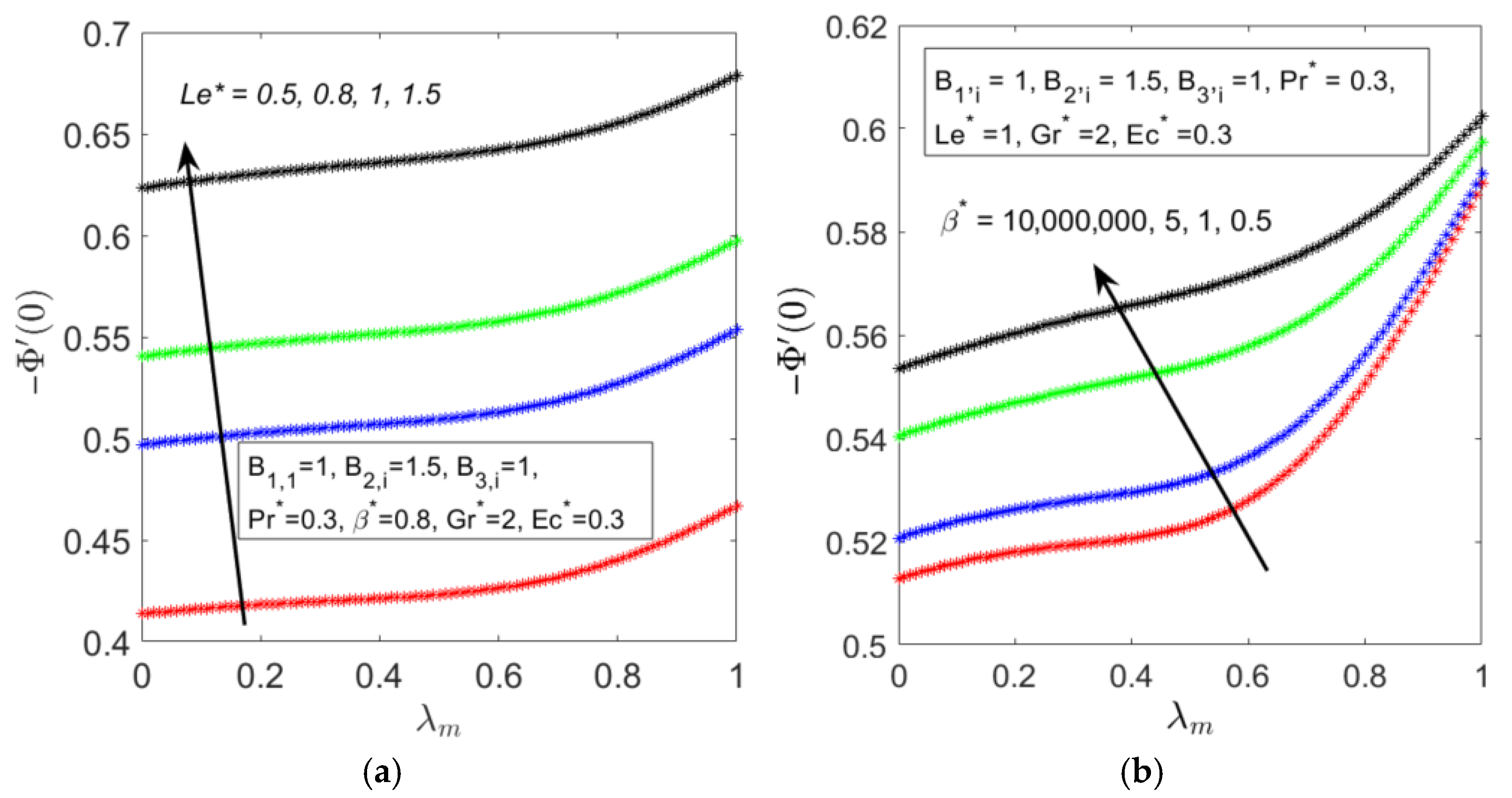
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Microorganism concentration difference parameter | |
| Slip coefficient | |
| Slip parameter | |
| Biot number of heat transfer | |
| Biot number of mass transfer | |
| Biot number of microorganism transfer | |
| Volume fraction of oxygen species | |
| Wall volume fraction of oxygen species | |
| Ambient volume fraction of oxygen species | |
| Modified Eckert number | |
| Forchheimer constant | |
| Modified Grashof number | |
| Acceleration due to gravity | |
| Heat generation parameter | |
| Permeability parameter | |
| Bioconvection Lewis number | |
| Lewis number | |
| Buoyancy ratio parameter | |
| Buoyancy ratio parameter | |
| Volume fraction of gyrotactic motile microorganisms | |
| Ambient concentration of motile microorganism | |
| Bioconvection Peclet number | |
| Prandtl number | |
| Rayleigh number for the porous medium | |
| Reynolds number | |
| Temperature | |
| Wall temperature | |
| Ambient temperature | |
| Maximum cell swimming speed | |
| Velocity components along axes | |
| Cartesian coordinates (x-axis aligned along the horizontal surface and y-axis is normal to it) | |
| Thermal diffusivity of the porous medium | |
| Buoyancy parameter due to temperature | |
| Buoyancy parameter due to concentration | |
| Buoyancy parameter due to motile microorganisms | |
| Dimensionless oxygen species concentration distribution | |
| Similarity variable | |
| Mixed convection parameter | |
| Casson fluid parameter | |
| Dimensionless temperature | |
| Dynamic viscosity of fluid | |
| Kinematic viscosity of fluid | |
| Fluid density | |
| Dimensionless density of gyrotactic motile microorganisms |
References
- Shahzad, H.; Wang, X.; Ghaffari, A.; Iqbal, K.; Hafeez, M.B.; Krawczuk, M.; Wojnicz, W. Fluid structure interaction study of non-Newtonian Casson fluid in a bifurcated channel having stenosis with elastic walls. Sci. Rep. 2022, 12, 12219. [Google Scholar] [CrossRef] [PubMed]
- Tawalbeh, M.; Shomope, I.; Al-Othman, A. Comprehensive Review on Non-Newtonian Nanofluids, Preparation, Characterization, and Applications. Int. J. Thermofluids 2024, 22, 100705. [Google Scholar] [CrossRef]
- Ali, A.; Farooq, H.; Abbas, Z.; Bukhari, Z.; Fatima, A. Impact of Lorentz force on the pulsatile flow of a non-Newtonian Casson fluid in a constricted channel using Darcy’s law: A numerical study. Sci. Rep. 2020, 10, 10629. [Google Scholar] [CrossRef] [PubMed]
- Israel-Cookey, C.; Davies, O.A.; Ngeri, A.P. Magnetohydrodynamic forced convection and heat transfer of a Casson fluid flow in an anisotropic porous channel with Isoflux boundaries. World J. Adv. Res. Rev. 2023, 18, 1332–1347. [Google Scholar] [CrossRef]
- Yadav, D.; Nair, S.B.; Awasthi, M.K.; Ragoju, R.; Bhattacharyya, K. Linear and nonlinear investigations of the impact of chemical reaction on the thermohaline convection in a permeable layer saturated with Casson fluid. Phys. Fluids 2024, 36, 014106. [Google Scholar] [CrossRef]
- Yadav, D.; Awasthi, M.K.; Singh, A.K.; Ravi, R.; Bhattacharyya, K.; Mahabaleshwar, U.S. Thermal boundary conditions and rotation effects on the onset of casson fluid convection in a permeable layer produced by purely interior heating. Numer. Heat Transf. Part B Fundam. 2024, 1–15. [Google Scholar] [CrossRef]
- Hussain, M.; Shoaib, M.A.; Ranjha, Q.; Shoaib Anwar, M.; Ahmad, Z.; Inc, M. Numerical solution to flow of Casson fluid via stretched permeable wedge with chemical reaction and mass transfer effects. Mod. Phys. Lett. B 2024, 38, 2341008. [Google Scholar] [CrossRef]
- Elsanoose, A. Non-Darcy Flow Through Synthetic Porous Media and Development of Non-Darcy Coefficient Correlations. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2023. [Google Scholar]
- Menni, Y.; Chamkha, A.J.; Azzi, A. Nanofluid transport in porous media: A review. Spec. Top. Rev. Porous Media Int. J. 2019, 10, 49–64. [Google Scholar] [CrossRef]
- Lopez-Hernandez, H.D. Experimental Analysis and Macroscopic and Pore-Level Flow Simulations to Compare Non-Darcy Flow Models in Porous Media. Master’s Thesis, Colorado School of Mines, Golden, CO, USA, 2007. [Google Scholar]
- Hemalatha, R.; Kameswaran, P.K.; Murthy, P.V.S.N. Effect of nanoparticle shape on the mixed convective transport over a vertical cylinder in a non-Darcy porous medium. Int. Commun. Heat Mass Transf. 2022, 133, 105962. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Buonomo, B.; Manca, O.; Sheremet, M.A. Heat transfer of chemically reacting mixed convection fluid using convective surface condition: Non-Darcy model. Therm. Sci. Eng. Prog. 2021, 25, 101044. [Google Scholar] [CrossRef]
- Bejawada, S.G.; Reddy, Y.D.; Jamshed, W.; Eid, M.R.; Safdar, R.; Nisar, K.S.; Isa, S.S.P.M.; Alam, M.M.; Parvin, S. 2D mixed convection non-Darcy model with radiation effect in a nanofluid over an inclined wavy surface. Alex. Eng. J. 2022, 61, 9965–9976. [Google Scholar] [CrossRef]
- Seth, G.S.; Tripathi, R.; Mishra, M.K. Hydromagnetic thin film flow of Casson fluid in non-Darcy porous medium with Joule dissipation and Navier’s partial slip. Appl. Math. Mech. 2017, 38, 1613–1626. [Google Scholar] [CrossRef]
- Jat, K.; Sharma, K.; Choudhary, P.; Soni, P.; Ali, R.; Ganesh, M. Significance of Darcy–ForchheimerCasson fluid flow past a non-permeable curved stretching sheet with the impacts of heat and mass transfer. Case Stud. Therm. Eng. 2024, 61, 104907. [Google Scholar] [CrossRef]
- Chen, X.; Wu, Y.; Zeng, L. Migration of gyrotactic micro-organisms in water. Water 2018, 10, 1455. [Google Scholar] [CrossRef]
- Ahmad, S.; Younis, J.; Ali, K.; Rizwan, M.; Ashraf, M.; Abd El Salam, M.A. Impact of swimming gyrotactic microorganisms and viscous dissipation on nanoparticles flow through a permeable medium: A numerical assessment. J. Nanomater. 2022, 2022, 4888128. [Google Scholar] [CrossRef]
- Li, Y.; Leng, Y.; Baazaoui, N.; Arain, M.B.; Ijaz, N.; Hassan, A.M. Exploring the dynamics of active swimmers microorganisms with electromagnetically conducting stretching through endothermic heat generation/assimilation flow: Observational and computational study. Case Stud. Therm. Eng. 2023, 51, 103560. [Google Scholar] [CrossRef]
- Gangadhar, K.; SujanaSree, T.; Wakif, A. Generalized slip impact of Cassonnanofluid through cylinder implanted in swimming gyrotactic microorganisms. Int. J. Mod. Phys. B 2024, 38, 2450380. [Google Scholar] [CrossRef]
- Usman, A. Examinations of viscous dissipation, magnetic field and thermal radiation on the systematic flow of Casson fluid with gyrotactic microorganisms. ITM Web Conf. 2024, 67, 01049. [Google Scholar] [CrossRef]
- Sarma, A.K.; Sarma, D. Unsteady magnetohydrodynamic bioconvection Casson fluid flow in presence of gyrotactic microorganisms over a vertically stretched sheet. Numer. Heat Transf. Part A Appl. 2024, 1–24. [Google Scholar] [CrossRef]
- Elhag, S.H. Numerical Study on 3D MHD Darcy-Forchheimer Flow Caused by Gyrotactic Microorganisms of the Bio-Convective CassonNanofluid across a Stretched Sheet. Front. Heat Mass Transf. 2024, 22, 377–395. [Google Scholar] [CrossRef]
- Nima, N.I.; Ferdows, M. A sustainable computational modeling on gyrotactic free forced bioconvective flow with various slip effects. J. Interdiscip. Math. 2022, 25, 1989–1997. [Google Scholar] [CrossRef]
- Faghri, A.; Zhang, Y.; Howell, J.R. Advanced Heat and Mass Transfer; Global Digital Press: Kanpur, India, 2010. [Google Scholar]
- Miralles, V.; Huerre, A.; Malloggi, F.; Jullien, M.C. A review of heating and temperature control in microfluidic systems: Techniques and applications. Diagnostics 2013, 3, 33–67. [Google Scholar] [CrossRef] [PubMed]
- Kotha, G.; Kolipaula, V.R.; VenkataSubba Rao, M.; Penki, S.; Chamkha, A.J. Internal heat generation on bioconvection of an MHD nanofluid flow due to gyrotactic microorganisms. Eur. Phys. J. Plus 2020, 135, 600. [Google Scholar] [CrossRef]
- Jamuna, B.; Balla, C.S. Bioconvection in a porous square cavity containing gyrotactic microorganisms under the effects of heat generation/absorption. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 1534–1544. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.; Asker, H.G.; Nagy, B. The effects of heat generation absorption on boundary layer flow of a nanofluid containing gyrotactic microorganisms over an inclined stretching cylinder. Ain Shams Eng. J. 2022, 13, 101690. [Google Scholar] [CrossRef]
- Nagendramma, V.; Raju, C.S.K.; Mallikarjuna, B.; Shehzad, S.A.; Leelarathnam, A. 3D Cassonnanofluid flow over slendering surface in a suspension of gyrotactic microorganisms with Cattaneo-Christov heat flux. Appl. Math. Mech. 2018, 39, 623–638. [Google Scholar] [CrossRef]
- Makanda, G.; Shaw, S.; Sibanda, P. Effects of radiation on MHD free convection of a Casson fluid from a horizontal circular cylinder with partial slip in non-Darcy porous medium with viscous dissipation. Bound. Value Probl. 2015, 2015, 75. [Google Scholar] [CrossRef]
- Baitharu, A.P.; Sahoo, S.; Dash, G.C. Numerical approach to non-Darcy mixed convective flow of non-Newtonian fluid on a vertical surface with varying surface temperature and heat source. Karbala Int. J. Mod. Sci. 2020, 6, 332–343. [Google Scholar] [CrossRef]
- Ashraf, S.; Mushtaq, M.; Jabeen, K.; Farid, S.; Muntazir, R.M.A. Heat and mass transfer of unsteady mixed convection flow of Casson fluid within the porous media under the influence of magnetic field over a nonlinear stretching sheet. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 20–38. [Google Scholar] [CrossRef]
- Prasad, D.K.; Chaitanya, G.K.; Raju, R.S. Double diffusive effects on mixed convection Casson fluid flow past a wavy inclined plate in presence of Darcian porous medium. Results Eng. 2019, 3, 100019. [Google Scholar] [CrossRef]
- Animasaun, I.L. Effects of thermophoresis, variable viscosity and thermal conductivity on free convective heat and mass transfer of non-darcian MHD dissipative Casson fluid flow with suction and nth order of chemical reaction. J. Niger. Math. Soc. 2015, 34, 11–31. [Google Scholar] [CrossRef]
- Humane, P.P.; Patil, V.S.; Shamshuddin, M.D.; Rajput, G.R.; Patil, A.B. Role of bioconvection on the dynamics of chemically active Cassonnanofluid flowing via an inclined porous stretching sheet with convective conditions. Int. J. Model. Simul. 2024, 44, 232–251. [Google Scholar] [CrossRef]
- Qawasmeh, B.R.; Alrbai, M.; Al-Dahidi, S. Forced convection heat transfer of Casson fluid in non-Darcy porous media. Adv. Mech. Eng. 2019, 11, 1687814018819906. [Google Scholar] [CrossRef]
- Farooq, U.; Hussain, M.; Ijaz, M.A.; Khan, W.A.; Farooq, F.B. Impact of non-similar modeling on Darcy-Forchheimer-Brinkman model for forced convection of Cassonnano-fluid in non-Darcy porous media. Int. Commun. Heat Mass Transf. 2021, 125, 105312. [Google Scholar] [CrossRef]
- Saha, K.C.; Saha, G.; Alhazmi, H.; Mohammed, N.A.; Khan, W.A.; Aljohani, A.F.; Khan, I. Finite difference simulations for Darcy–Forchheimer–Brinkman model of MHD Oldroyd B fluid flow past a permeable sheet containing microorganisms. ZAMM-J. Appl. Math. Mech. Z. Mech. 2024, e202300945. [Google Scholar] [CrossRef]
- Sadeghi, M.; Sontti, S.G.; Zheng, E.; Zhang, X. Computational fluid dynamics (CFD) simulation of three–phase non–Newtonian slurry flows in industrial horizontal pipelines. Chem. Eng. Sci. 2023, 270, 118513. [Google Scholar] [CrossRef]
- Jithin, M.; Siddharth, S.; Das, M.K.; De, A. Simulation of coupled heat and mass transport with reaction in PEM fuel cell cathode using lattice Boltzmann method. Therm. Sci. Eng. Prog. 2017, 4, 85–96. [Google Scholar] [CrossRef]
- Saeed, R.; Gul, T. Bioconvection Casson nanofluid flow together with Darcy–Forchheimer due to a rotating disk with thermal radiation and Arrhenius activation energy. SN Appl. Sci. 2021, 3, 77. [Google Scholar] [CrossRef]
- Ferdows, M.; Alshuraiaan, B.; Nima, N.I. Effects of non-Darcy mixed convection over a horizontal cone with different convective boundary conditions incorporating gyrotactic microorganisms on dispersion. Sci. Rep. 2022, 12, 16581. [Google Scholar] [CrossRef] [PubMed]
- Kafoussias, N.G.; Williams, E.W. An improved approximation technique to obtain numerical solutionof a class of two-point boundary value similarity problems in fluid mechanics. Int. J. Numer. Methods Fluids 1993, 17, 145–162. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C. Similarity solution of mixed convective boundary layer slip flow over a vertical plate. Ain Shams Eng. J. 2013, 4, 299–305. [Google Scholar] [CrossRef]


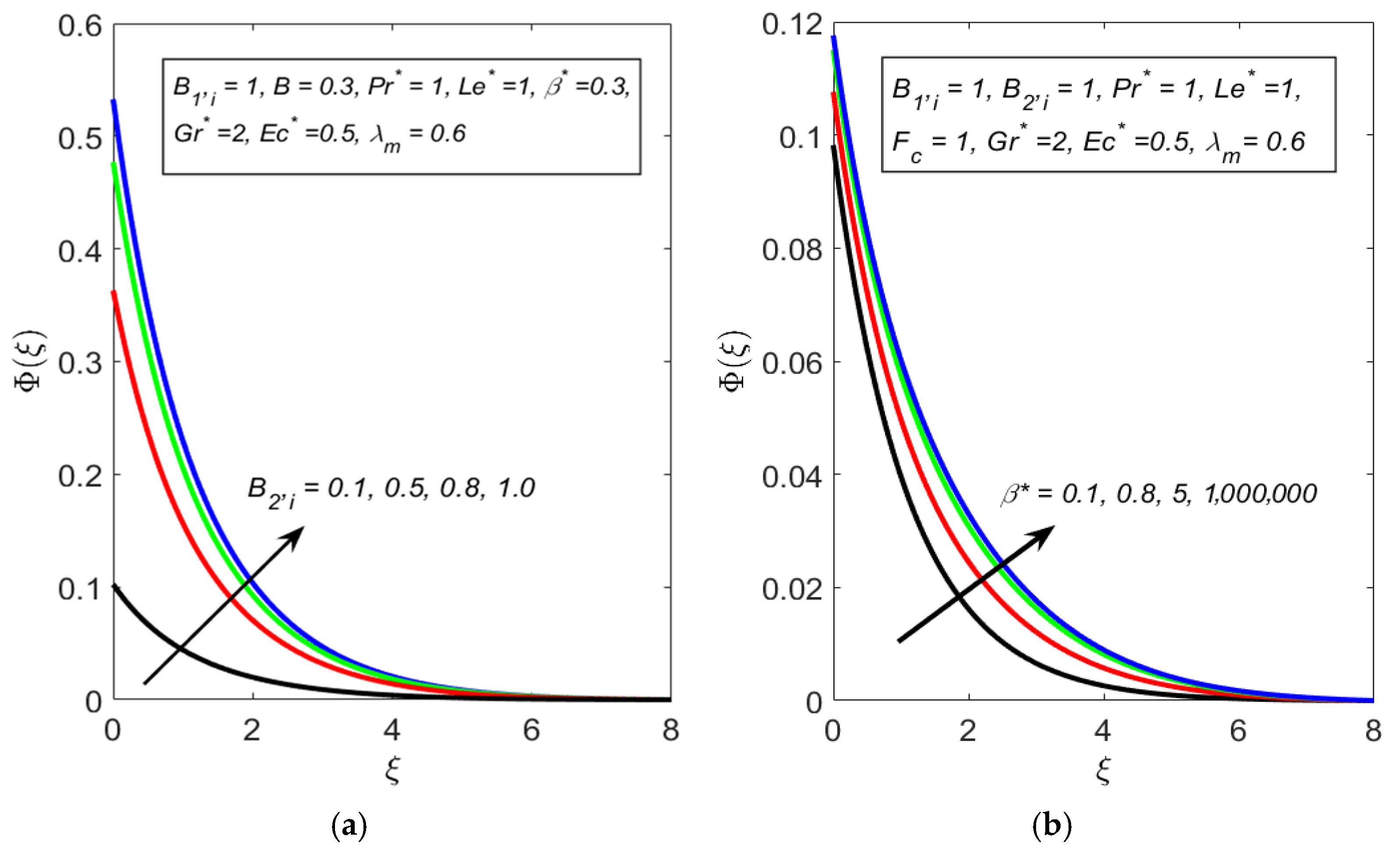

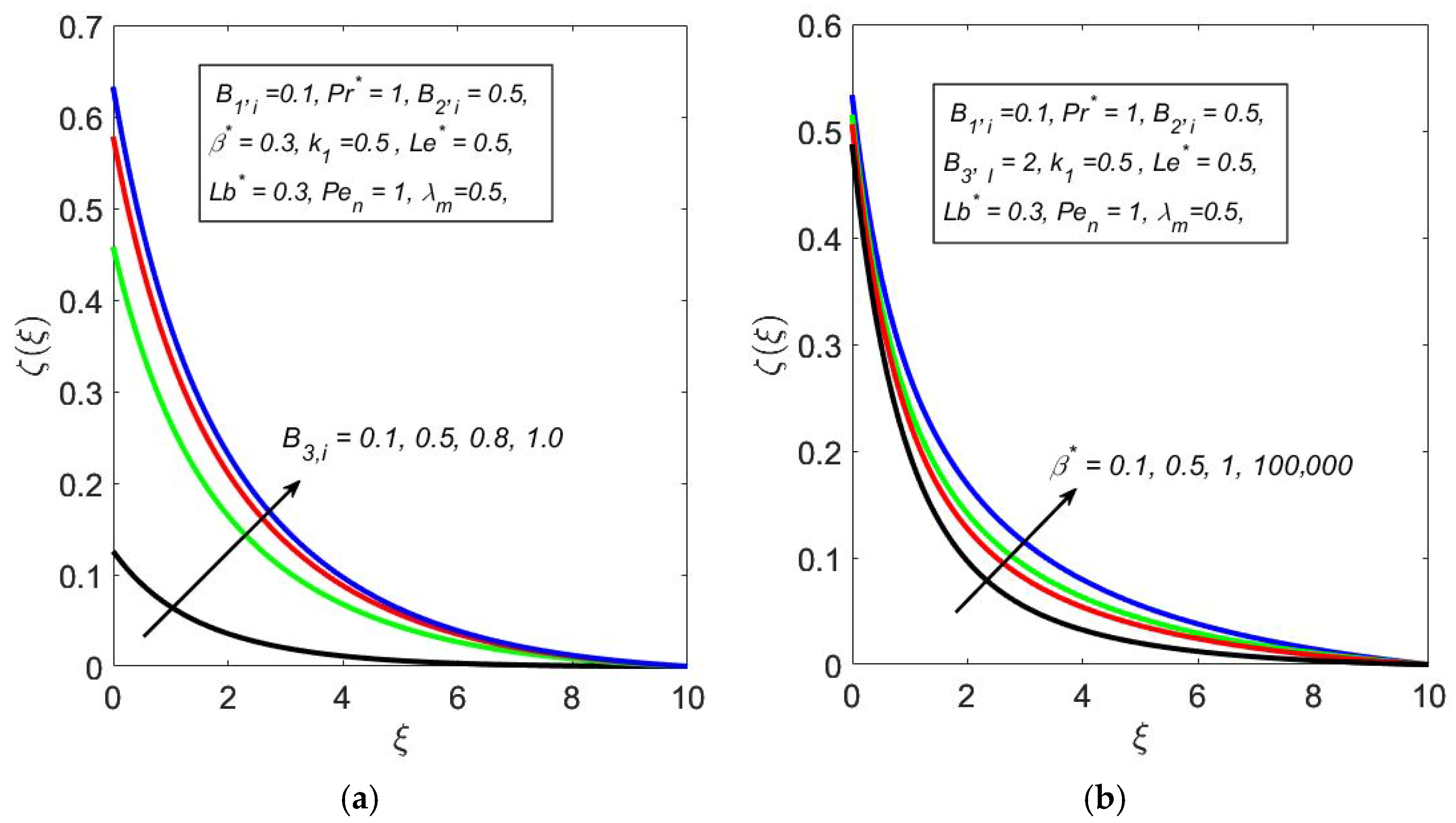
| Study | Surface Orientation | Fluid and Microbial Type | Non-Darcy Term Treatment | Convection Mechanisms | Remarks |
|---|---|---|---|---|---|
| Yadav et al. [5] | _ | Casson fluid (no microorganism) | Darcy model | Thermohaline convection | Does not consider bioconvection or non-Darcy effects. |
| Hemalatha et al. [11] | Vertical cylinder | Nanofluid (no microorganisms) | Non-Darcy model | Mixed convection | Limited to vertical orientation and nanofluids; no microbial dynamics. |
| Gangadhar et al. [19] | Stretching surface | Casson fluid with gyrotactic microorganisms | _ | Bioconvection | Does not incorporate non-Darcy porous media effects. |
| Usman [20] | _ | Casson fluid with gyrotactic microorganisms | _ | Bioconvection | Lacks analysis of porous media or mixed convection regimes. |
| Bejawada et al. [13] | Inclined wavy Surface | Nanofluid (no microorganism) | Non-Darcy model | Mixed convection | Focuses on nanofluids; does not include gyrotactic microorganisms. |
| Jat et al. [15] | Curved surface | Casson fluid (no microorganisms) | Darcy–Forchheimer model | _ | Does not consider microbial effects. |
| Nima and Ferdows [23] | Vertical | Gyrotactic microorganism | Darcy model | Free forced convection | Limited to Darcy flow and a single surface orientation (vertical). |
| Current study | Inclined, vertical, and horizontal | Casson fluid with gyrotactic microorganism | Non-Darcy model | Free, mixed, and forced convection | Integrates multiple physical phenomena across varied surface inclinations and all convection regimes. |
Finite Difference Scheme | Bvp4c Scheme | |||||
|---|---|---|---|---|---|---|
| 0.2 | −0.4588 | −0.3471 | −0.2191 | −0.4590 | −0.3476 | −0.2192 |
| 0.3 | −0.4953 | −0.3819 | −0.2298 | −0.4959 | −0.3824 | −0.2297 |
| 0.5 | −0.5458 | −0.4313 | −0.2398 | −0.5464 | −0.4301 | −0.2422 |
| 0.6 | −0.5641 | −0.4467 | −0.2461 | −0.5646 | −0.4474 | −0.2460 |
| 0.8 | −0.5921 | −0.4733 | −0.2511 | −0.5927 | −0.4738 | −0.2512 |
| 1.0 | −0.6470 | −0.5252 | −0.2585 | −0.6477 | −0.5252 | −0.2585 |
Finite Difference Scheme | Bvp4c Scheme | |||||
| 0.2 | 0.2479 | 0.2479 | 0.2479 | 0.2481 | 0.2481 | 0.2481 |
| 0.3 | 0.2511 | 0.2511 | 0.2511 | 0.2512 | 0.2512 | 0.2512 |
| 0.5 | 0.2509 | 0.2509 | 0.2509 | 0.2509 | 0.2509 | 0.2509 |
| 0.6 | 0.2500 | 0.2500 | 0.2500 | 0.2501 | 0.2501 | 0.2501 |
| 0.8 | 0.2488 | 0.2488 | 0.2488 | 0.2482 | 0.2482 | 0.2482 |
| 1.0 | 0.2463 | 0.2463 | 0.2463 | 0.2464 | 0.2464 | 0.2464 |
Finite Difference Scheme | Bvp4c Scheme | |||||
|---|---|---|---|---|---|---|
| 0.0 | −0.5156 | −0.4515 | −0.2511 | −0.5157 | −0.4515 | −0.2512 |
| 0.8 | −0.6331 | −0.4866 | −0.2512 | −0.6332 | −0.4867 | −0.2512 |
| 1.0 | −0.6579 | −0.4951 | −0.2512 | −0.6581 | −0.4951 | −0.2512 |
| 1.5 | −0.7139 | −0.5155 | −0.2513 | −0.7141 | −0.5154 | −0.2512 |
Finite Difference Scheme | Bvp4c Scheme | |||||
|---|---|---|---|---|---|---|
| 0.0 | 0.2673 | 0.2967 | 0.3190 | 0.2673 | 0.2967 | 0.3191 |
| 0.8 | 0.2360 | 0.2925 | 0.3191 | 0.2359 | 0.2924 | 0.3191 |
| 1.0 | 0.2371 | 0.2914 | 0.3191 | 0.2273 | 0.2914 | 0.3191 |
| 1.5 | 0.2048 | 0.2883 | 0.3192 | 0.2048 | 0.2888 | 0.3191 |
| Step Size | CPU Time | |||||
|---|---|---|---|---|---|---|
| 0.04 | −0.9556 | 0.0015 | −0.9555 | 0.02725 | 0.226 s | |
| 0.08 | −0.9113 | 0.00287 | −0.9112 | 0.05221 | ||
| 0.04 | −0.9551 | 0.00148 | −0.9550 | 0.02745 | 0.117 s | |
| 0.08 | −0.9104 | 0.00283 | −0.9104 | 0.05257 | ||
| 0.04 | −0.9543 | 0.00144 | −0.9542 | 0.02788 | 0.098 s | |
| 0.08 | −0.9086 | 0.00277 | −0.9086 | 0.05333 | ||
| Present Study | 0.098066 | 1.01000 | 0.621745 |
| Nima and Ferdows [23] | 0.098166 | 1.00000 | 0.623746 |
| 0.1 | −0.7391 | −0.5729 | −0.2439 | −1.4783 | −1.1458 | −0.4878 |
| 0.3 | −0.6135 | −0.4914 | −0.2096 | −1.2271 | −0.9829 | −0.4192 |
| 0.5 | −0.5274 | −0.4321 | −0.1839 | −1.0548 | −0.8642 | −0.3678 |
| 0.8 | −0.4382 | −0.3676 | −0.1555 | −0.8765 | −0.7353 | −0.3110 |
| 1.0 | −0.3948 | −0.3351 | −0.1410 | −0.7896 | −0.6702 | −0.2820 |
| 0 | −0.3948 | −0.3323 | −0.0808 | −0.7896 | −0.6647 | −0.1617 |
| −0.3948 | −0.3336 | −0.1077 | −0.7896 | −0.6672 | −0.2155 | |
| −0.3948 | −0.3351 | −0.1410 | −0.7896 | −0.6702 | −0.2820 | |
| −0.3948 | −0.3370 | −0.1872 | −0.7896 | −0.6741 | −0.3745 | |
| −0.3948 | −0.3418 | −0.3240 | −0.7896 | −0.6837 | −0.6480 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nima, N.I.; Hannan, M.A.; Alam, J.; Rouf, R.A. Casson Fluid Saturated Non-Darcy Mixed Bio-Convective Flow over Inclined Surface with Heat Generation and Convective Effects. Processes 2025, 13, 2295. https://doi.org/10.3390/pr13072295
Nima NI, Hannan MA, Alam J, Rouf RA. Casson Fluid Saturated Non-Darcy Mixed Bio-Convective Flow over Inclined Surface with Heat Generation and Convective Effects. Processes. 2025; 13(7):2295. https://doi.org/10.3390/pr13072295
Chicago/Turabian StyleNima, Nayema Islam, Mohammed Abdul Hannan, Jahangir Alam, and Rifat Ara Rouf. 2025. "Casson Fluid Saturated Non-Darcy Mixed Bio-Convective Flow over Inclined Surface with Heat Generation and Convective Effects" Processes 13, no. 7: 2295. https://doi.org/10.3390/pr13072295
APA StyleNima, N. I., Hannan, M. A., Alam, J., & Rouf, R. A. (2025). Casson Fluid Saturated Non-Darcy Mixed Bio-Convective Flow over Inclined Surface with Heat Generation and Convective Effects. Processes, 13(7), 2295. https://doi.org/10.3390/pr13072295








