Digital Twin for Upstream and Downstream Integration of Virus-like Particle Manufacturing
Abstract
1. Introduction
2. Materials and Methods
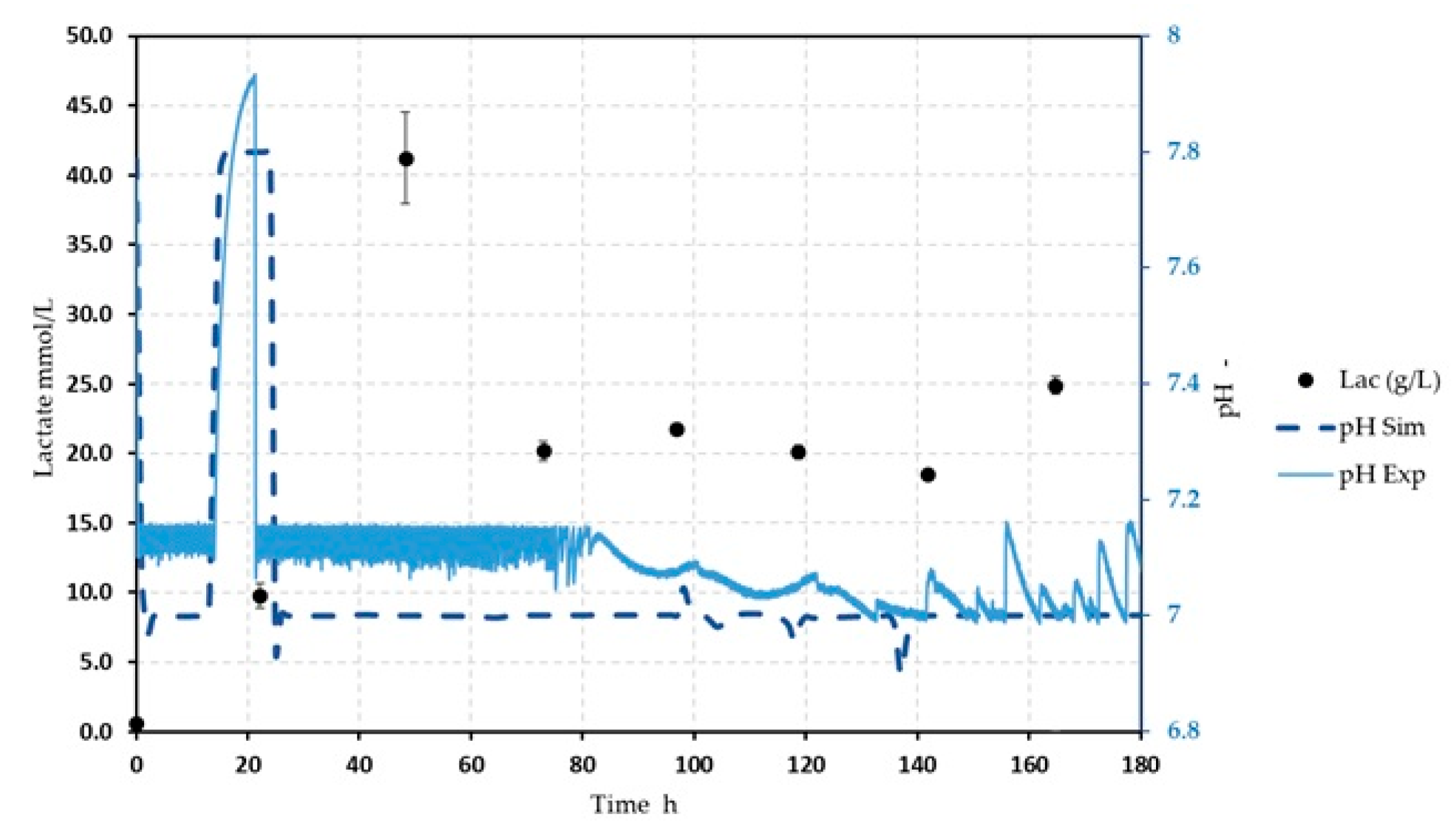
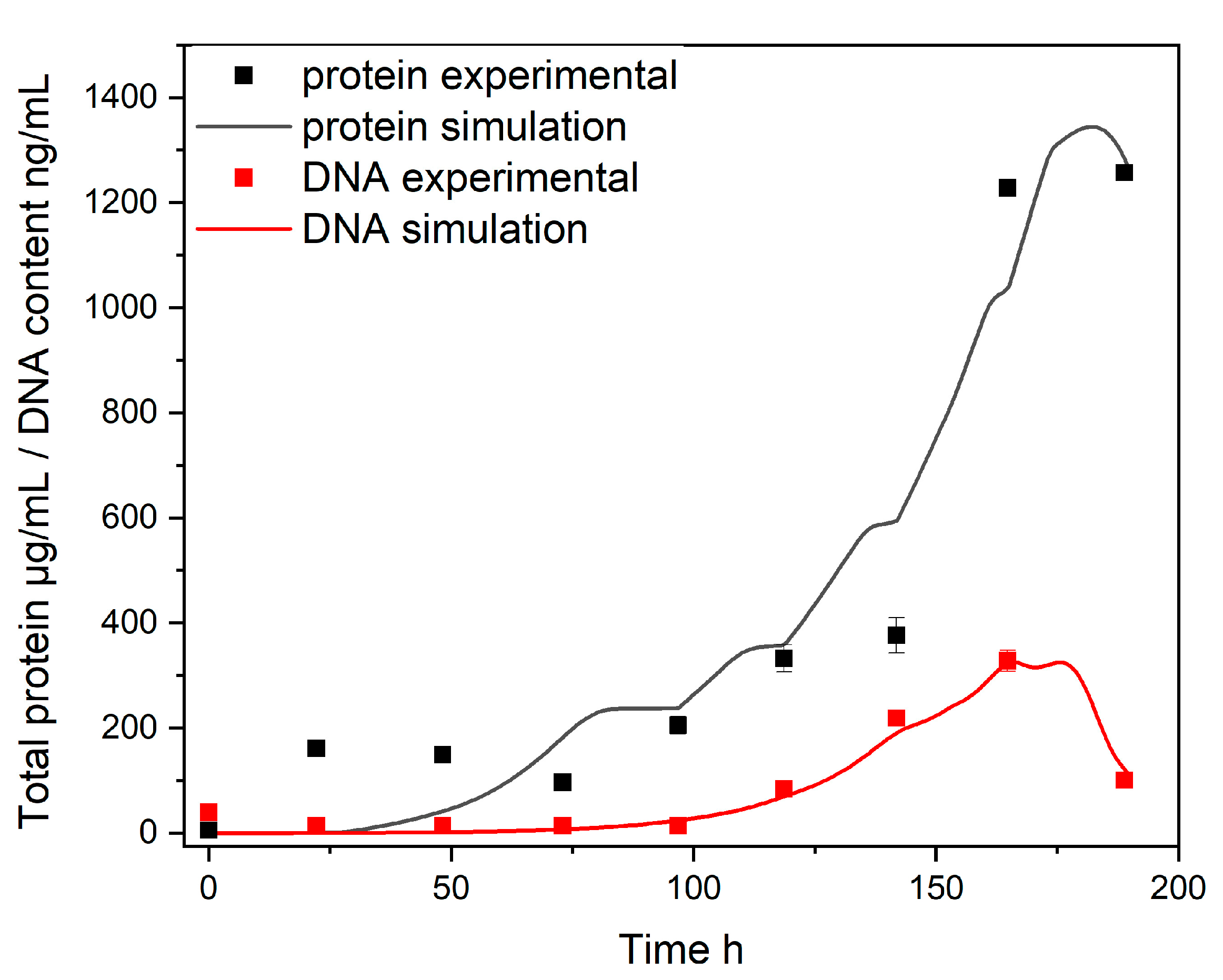
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kushnir, N.; Streatfield, S.J.; Yusibov, V. Virus-like Particles as a Highly Efficient Vaccine Platform: Diversity of Targets and Production Systems and Advances in Clinical Development. Vaccine 2012, 31, 58–83. [Google Scholar] [CrossRef] [PubMed]
- Hadj Hassine, I.; Ben M’hadheb, M.; Almalki, M.A.; Gharbi, J. Virus-like Particles as Powerful Vaccination Strategy against Human Viruses. Rev. Med. Virol. 2024, 34, e2498. [Google Scholar] [CrossRef] [PubMed]
- González-Domínguez, I.; Lorenzo, E.; Bernier, A.; Cervera, L.; Gòdia, F.; Kamen, A. A Four-Step Purification Process for Gag VLPs: From Culture Supernatant to High-Purity Lyophilized Particles. Vaccines 2021, 9, 1154. [Google Scholar] [CrossRef]
- Chackerian, B. Virus-like particles: Flexible Platforms for Vaccine Development. Expert Rev. Vaccines 2007, 6, 381–390. [Google Scholar] [CrossRef]
- Von Elling-Tammen, M.S.; Taft, F.; Thom, V.; Stitz, J.; Barbe, S.; Krause, A. Optimizing Nuclease Treatment to Enhance Anion Exchange Chromatography of HIV-Derived Virus-like Particles. J. Chromatogr. B 2025, 1256, 124539. [Google Scholar] [CrossRef]
- Deng, F. Advances and Challenges in Enveloped Virus-like Particle (VLP)-Based Vaccines. J. Immunol. Sci. 2018, 2, 36–41. [Google Scholar] [CrossRef]
- Petiot, E. Influence of HEK293 Metabolism on the Production of Viral Vectors and Vaccine. Vaccine 2015, 33, 5974–5981. [Google Scholar] [CrossRef]
- Rosengarten, J.F.; Schatz, S.; Wolf, T.; Barbe, S.; Stitz, J. Components of a HIV-1 Vaccine Mediate Virus-like Particle (VLP)-Formation and Display of Envelope Proteins Exposing Broadly Neutralizing Epitopes. Virology 2022, 568, 41–48. [Google Scholar] [CrossRef] [PubMed]
- Yusa, K.; Zhou, L.; Li, M.A.; Bradley, A.; Craig, N.L. A Hyperactive piggyBac Transposase for Mammalian Applications. Proc. Natl. Acad. Sci. USA 2011, 108, 1531–1536. [Google Scholar] [CrossRef]
- Bire, S.; Gosset, D.; Jégot, G.; Midoux, P.; Pichon, C.; Rouleux-Bonnin, F. Exogenous mRNA Delivery and Bioavailability in Gene Transfer Mediated by piggyBac Transposition. BMC Biotechnol. 2013, 13, 75. [Google Scholar] [CrossRef]
- Tschorn, N.; Van Heuvel, Y.; Stitz, J. Transgene Expression and Transposition Efficiency of Two-Component Sleeping Beauty Transposon Vector Systems Utilizing Plasmid or mRNA Encoding the Transposase. Mol. Biotechnol. 2023, 65, 1327–1335. [Google Scholar] [CrossRef] [PubMed]
- Baukmann, S.; Hengelbrock, A.; Katsoutas, K.; Stitz, J.; Schmidt, A.; Strube, J. Platform Process for an Autonomous Production of Virus-like Particles. ACS Omega 2025, 10, 3917–3929. [Google Scholar] [CrossRef] [PubMed]
- Cervera, L.; Gòdia, F.; Tarrés-Freixas, F.; Aguilar-Gurrieri, C.; Carrillo, J.; Blanco, J.; Gutiérrez-Granados, S. Production of HIV-1-based virus-like particles for vaccination: Achievements and limits. Appl. Microbiol. Biotechnol. 2019, 103, 7367–7384. [Google Scholar] [CrossRef] [PubMed]
- Bandeira, V.; Peixoto, C.; Rodrigues, A.F.; Cruz, P.E.; Alves, P.M.; Coroadinha, A.S.; Carrondo, M.J.T. Downstream Processing of Lentiviral Vectors: Releasing Bottlenecks. Hum. Gene Ther. Methods 2012, 23, 255–263. [Google Scholar] [CrossRef]
- Schmidt, A.; Helgers, H.; Vetter, F.L.; Zobel-Roos, S.; Hengelbrock, A.; Strube, J. Process Automation and Control Strategy by Quality-by-Design in Total Continuous mRNA Manufacturing Platforms. Processes 2022, 10, 1783. [Google Scholar] [CrossRef]
- Yu, L.X.; Amidon, G.; Khan, M.A.; Hoag, S.W.; Polli, J.; Raju, G.K.; Woodcock, J. Understanding Pharmaceutical Quality by Design. AAPS J. 2014, 16, 771–783. [Google Scholar] [CrossRef]
- Hogwood, C.E.; Bracewell, D.G.; Smales, C.M. Measurement and Control of Host Cell Proteins (HCPs) in CHO Cell Bioprocesses. Curr. Opin. Biotechnol. 2014, 30, 153–160. [Google Scholar] [CrossRef]
- Capito, F.; Skudas, R.; Stanislawski, B.; Kolmar, H. Matrix Effects during Monitoring of Antibody and Host Cell Proteins Using Attenuated Total Reflection Spectroscopy. Biotechnol. Prog. 2013, 29, 265–274. [Google Scholar] [CrossRef]
- Yatipanthalawa, B.S.; Gras, S.L. Predictive Models for Upstream Mammalian Cell Culture Development—A Review. Digit. Chem. Eng. 2024, 10, 100137. [Google Scholar] [CrossRef]
- Zehetner, L.; Széliová, D.; Kraus, B.; Graninger, M.; Zanghellini, J.; Hernandez Bort, J.A. Optimizing VLP Production in Gene Therapy: Opportunities and Challenges for in Silico Modeling. Biotechnol. J. 2023, 18, 2200636. [Google Scholar] [CrossRef]
- Bayer, B.; Duerkop, M.; Pörtner, R.; Möller, J. Comparison of Mechanistic and Hybrid Modeling Approaches for Characterization of a CHO Cultivation Process: Requirements, Pitfalls and Solution Paths. Biotechnol. J. 2023, 18, 2200381. [Google Scholar] [CrossRef] [PubMed]
- Ben Yahia, B.; Malphettes, L.; Heinzle, E. Macroscopic Modeling of Mammalian Cell Growth and Metabolism. Appl. Microbiol. Biotechnol. 2015, 99, 7009–7024. [Google Scholar] [CrossRef]
- Pimentel, G.A.; Dewasme, L.; Santos-Navarro, F.N.; Boes, A.; Côte, F.; Filée, P.; Wouwer, A.V. Macroscopic Dynamic Modeling of Metabolic Shift to Lactate Consumption of Mammalian Cell Batch Cultures. In Proceedings of the 2023 9th International Conference on Control, Decision and Information Technologies (CoDIT), IEEE, Rome, Italy, 3–6 July 2023; pp. 1–6. [Google Scholar]
- Martínez-Monge, I.; Albiol, J.; Lecina, M.; Liste-Calleja, L.; Miret, J.; Solà, C.; Cairó, J.J. Metabolic Flux Balance Analysis during Lactate and Glucose Concomitant Consumption in HEK293 Cell Cultures. Biotechnol. Bioeng. 2019, 116, 388–404. [Google Scholar] [CrossRef]
- Nolan, R.P. Dynamic Model of CHO Cell Metabolism. Metab. Eng. 2011, 13, 108–124. [Google Scholar] [CrossRef]
- Van Rosmalen, R.P.; Smith, R.W.; Martins Dos Santos, V.A.P.; Fleck, C.; Suarez-Diez, M. Model Reduction of Genome-Scale Metabolic Models as a Basis for Targeted Kinetic Models. Metab. Eng. 2021, 64, 74–84. [Google Scholar] [CrossRef] [PubMed]
- Hengelbrock, A.; Helgers, H.; Schmidt, A.; Vetter, F.L.; Juckers, A.; Rosengarten, J.F.; Stitz, J.; Strube, J. Digital Twin for HIV-Gag VLP Production in HEK293 Cells. Processes 2022, 10, 866. [Google Scholar] [CrossRef]
- Cloutier, M.; Perrier, M.; Jolicoeur, M. Dynamic Flux Cartography of Hairy Roots Primary Metabolism. Phytochemistry 2007, 68, 2393–2404. [Google Scholar] [CrossRef] [PubMed]
- Robitaille, J.; Chen, J.; Jolicoeur, M. A Single Dynamic Metabolic Model Can Describe mAb Producing CHO Cell Batch and Fed-Batch Cultures on Different Culture Media. PLoS ONE 2015, 10, e0136815. [Google Scholar] [CrossRef]
- Hengelbrock, A.; Probst, F.; Baukmann, S.; Uhl, A.; Tschorn, N.; Stitz, J.; Schmidt, A.; Strube, J. Digital Twin for Continuous Production of Virus-like Particles toward Autonomous Operation. ACS Omega 2024, 9, 34990–35013. [Google Scholar] [CrossRef]
- Helgers, H.; Hengelbrock, A.; Rosengarten, J.F.; Stitz, J.; Schmidt, A.; Strube, J. Towards Autonomous Process Control—Digital Twin for HIV-Gag VLP Production in HEK293 Cells Using a Dynamic Metabolic Model. Processes 2022, 10, 2015. [Google Scholar] [CrossRef]
- Sidoli, F.R.; Mantalaris, A.; Asprey, S.P. Modelling of Mammalian Cells and Cell Culture Processes. Cytotechnology 2004, 44, 27–46. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Vijayasankaran, N.; Shen, A.; Kiss, R.; Amanullah, A. Cell Culture Processes for Monoclonal Antibody Production. mAbs 2010, 2, 466–479. [Google Scholar] [CrossRef]
- Radhakrishnan, D.; Wells, E.A.; Robinson, A.S. Strategies to Enhance Productivity and Modify Product Quality in Therapeutic Proteins. Curr. Opin. Chem. Eng. 2018, 22, 81–88. [Google Scholar] [CrossRef]
- Brunner, V.; Siegl, M.; Geier, D.; Becker, T. Challenges in the Development of Soft Sensors for Bioprocesses: A Critical Review. Front. Bioeng. Biotechnol. 2021, 9, 722202. [Google Scholar] [CrossRef] [PubMed]
- Bayer, B.; Von Stosch, M.; Melcher, M.; Duerkop, M.; Striedner, G. Soft Sensor Based on 2D-fluorescence and Process Data Enabling Real-time Estimation of Biomass in Escherichia coli Cultivations. Eng. Life Sci. 2020, 20, 26–35. [Google Scholar] [CrossRef]
- Alhuthali, S.; Kontoravdi, C. Population Balance Modelling Captures Host Cell Protein Dynamics in CHO Cell Cultures. PLoS ONE 2022, 17, e0265886. [Google Scholar] [CrossRef]
- Bianconi, E.; Piovesan, A.; Facchin, F.; Beraudi, A.; Casadei, R.; Frabetti, F.; Vitale, L.; Pelleri, M.C.; Tassani, S.; Piva, F.; et al. An Estimation of the Number of Cells in the Human Body. Ann. Hum. Biol. 2013, 40, 463–471. [Google Scholar] [CrossRef]
- Russo, J.; Russo, I.H. Techniques and Methodological Approaches in Breast Cancer Research; Springer: New York, NY, USA, 2014; ISBN 978-1-4939-0717-5. [Google Scholar]
- Amaral Silva, D.; Al-Gousous, J.; Davies, N.M.; Bou Chacra, N.; Webster, G.K.; Lipka, E.; Amidon, G.; Löbenberg, R. Simulated, Biorelevant, Clinically Relevant or Physiologically Relevant Dissolution Media: The Hidden Role of Bicarbonate Buffer. Eur. J. Pharm. Biopharm. 2019, 142, 8–19. [Google Scholar] [CrossRef]
- Gear, C.W. Numerical Initial Value Problems in Ordinary Differential Equations; Prentice-Hall Series in Automatic Computation; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971; ISBN 978-0-13-626606-8. [Google Scholar]
- Dennis, J.E.; Gay, D.M.; Walsh, R.E. An Adaptive Nonlinear Least-Squares Algorithm. ACM Trans. Math. Softw. 1981, 7, 348–368. [Google Scholar] [CrossRef]
- Helgers, H.; Schmidt, A.; Lohmann, L.J.; Vetter, F.L.; Juckers, A.; Jensch, C.; Mouellef, M.; Zobel-Roos, S.; Strube, J. Towards Autonomous Operation by Advanced Process Control—Process Analytical Technology for Continuous Biologics Antibody Manufacturing. Processes 2021, 9, 172. [Google Scholar] [CrossRef]
- Provost, A.; Bastin, G.; Agathos, S.N.; Schneider, Y.-J. Metabolic Design of Macroscopic Bioreaction Models: Application to Chinese Hamster Ovary Cells. Bioprocess Biosyst. Eng. 2006, 29, 349–366. [Google Scholar] [CrossRef]
- Dorka, P.; Fischer, C.; Budman, H.; Scharer, J.M. Metabolic Flux-Based Modeling of mAb Production during Batch and Fed-Batch Operations. Bioprocess Biosyst. Eng. 2009, 32, 183–196. [Google Scholar] [CrossRef]
- Liste-Calleja, L.; Lecina, M.; Lopez-Repullo, J.; Albiol, J.; Solà, C.; Cairó, J.J. Lactate and Glucose Concomitant Consumption as a Self-Regulated pH Detoxification Mechanism in HEK293 Cell Cultures. Appl. Microbiol. Biotechnol. 2015, 99, 9951–9960. [Google Scholar] [CrossRef] [PubMed]
- Trummer, E.; Fauland, K.; Seidinger, S.; Schriebl, K.; Lattenmayer, C.; Kunert, R.; Vorauer-Uhl, K.; Weik, R.; Borth, N.; Katinger, H.; et al. Process Parameter Shifting: Part I. Effect of DOT, pH, and Temperature on the Performance of Epo-Fc Expressing CHO Cells Cultivated in Controlled Batch Bioreactors. Biotechnol. Bioeng. 2006, 94, 1033–1044. [Google Scholar] [CrossRef] [PubMed]
- Großeholz, R.; Koh, C.-C.; Veith, N.; Fiedler, T.; Strauss, M.; Olivier, B.; Collins, B.C.; Schubert, O.T.; Bergmann, F.; Kreikemeyer, B.; et al. Integrating Highly Quantitative Proteomics and Genome-Scale Metabolic Modeling to Study pH Adaptation in the Human Pathogen Enterococcus faecalis. NPJ Syst. Biol. Appl. 2016, 2, 16017. [Google Scholar] [CrossRef] [PubMed]
- Geng, S.-L.; Zhao, X.-J.; Zhang, X.; Zhang, J.-H.; Mi, C.-L.; Wang, T.-Y. Recombinant Therapeutic Proteins Degradation and Overcoming Strategies in CHO Cells. Appl. Microbiol. Biotechnol. 2024, 108, 182. [Google Scholar] [CrossRef]
- O’Connor, T.F.; Chatterjee, S.; Lam, J.; De La Ossa, D.H.P.; Martinez-Peyrat, L.; Hoefnagel, M.H.N.; Fisher, A.C. An Examination of Process Models and Model Risk Frameworks for Pharmaceutical Manufacturing. Int. J. Pharm. X 2024, 8, 100274. [Google Scholar] [CrossRef]
- Costa, M.H.G.; Costa, M.S.; Painho, B.; Sousa, C.D.; Carrondo, I.; Oltra, E.; Pelacho, B.; Prosper, F.; Isidro, I.A.; Alves, P.; et al. Enhanced Bioprocess Control to Advance the Manufacture of Mesenchymal Stromal Cell-derived Extracellular Vesicles in Stirred-tank Bioreactors. Biotechnol. Bioeng. 2023, 120, 2725–2741. [Google Scholar] [CrossRef]
- Santos, R.M.; Kessler, J.; Salou, P.; Menezes, J.C.; Peinado, A. Monitoring mAb Cultivations with In-situ Raman Spectroscopy: The Influence of Spectral Selectivity on Calibration Models and Industrial Use as Reliable PAT Tool. Biotechnol. Prog. 2018, 34, 659–670. [Google Scholar] [CrossRef]
- Krampe, B.; Al-Rubeai, M. Cell Death in Mammalian Cell Culture: Molecular Mechanisms and Cell Line Engineering Strategies. Cytotechnology 2010, 62, 175–188. [Google Scholar] [CrossRef]
- Schmidt, A.; Helgers, H.; Vetter, F.L.; Juckers, A.; Strube, J. Fast and Flexible mRNA Vaccine Manufacturing as a Solution to Pandemic Situations by Adopting Chemical Engineering Good Practice—Continuous Autonomous Operation in Stainless Steel Equipment Concepts. Processes 2021, 9, 1874. [Google Scholar] [CrossRef]


| Parameter | Sleeping Beauty to PiggyBac [%] | Parameter | Sleeping Beauty to PiggyBac [%] |
|---|---|---|---|
| αAMP/ATP | 62 | vG6PDH max | 125 |
| βAMP/ATP | 321 | vGlnT fmax | 21 |
| KA AMP/ATP | 48 | vGlnT rmax | 58 |
| KD G6P | 100 | vgrowth max | 40 |
| Kgrowth dLAC | 125 | vHK max | 31 |
| Kgrowth dNH4 | 100 | vLDH fmax | 804 |
| KM ADP/ATP | 25 | vLDH rmax | 501 |
| KM ATP | 39 | vleak max | 30 |
| KM G6P | 789 | vPC max | 100 |
| KM NADH | 46 | vPDH max | 125 |
| KM PYR | 40 | vPFK max | 84 |
| vAAtoSuc max | 100 | vPGI fmax | 22 |
| vAK fmax | 81 | vPGI rmax | 217 |
| vAK rmax | 140 | vPGK max | 246 |
| vAlaTA fmax | 262 | vPK max | 60 |
| vAlaTA rmax | 889 | vPPRibP max | 125 |
| vASTA max | 15 | vresp max | 82 |
| vATPase max | 242 | vSDH max | 3 |
| vCITS max | 64 | vSDHH fmax | 216 |
| vCS max | 80 | vSDHH rmax | 113 |
| vEP max | 80 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baukmann, S.; Hengelbrock, A.; Katsoutas, K.; Stitz, J.; Schmidt, A.; Strube, J. Digital Twin for Upstream and Downstream Integration of Virus-like Particle Manufacturing. Processes 2025, 13, 2101. https://doi.org/10.3390/pr13072101
Baukmann S, Hengelbrock A, Katsoutas K, Stitz J, Schmidt A, Strube J. Digital Twin for Upstream and Downstream Integration of Virus-like Particle Manufacturing. Processes. 2025; 13(7):2101. https://doi.org/10.3390/pr13072101
Chicago/Turabian StyleBaukmann, Simon, Alina Hengelbrock, Kristina Katsoutas, Jörn Stitz, Axel Schmidt, and Jochen Strube. 2025. "Digital Twin for Upstream and Downstream Integration of Virus-like Particle Manufacturing" Processes 13, no. 7: 2101. https://doi.org/10.3390/pr13072101
APA StyleBaukmann, S., Hengelbrock, A., Katsoutas, K., Stitz, J., Schmidt, A., & Strube, J. (2025). Digital Twin for Upstream and Downstream Integration of Virus-like Particle Manufacturing. Processes, 13(7), 2101. https://doi.org/10.3390/pr13072101








