An Operating Condition Diagnosis Method for Electric Submersible Screw Pumps Based on CNN-ResNet-RF
Abstract
1. Introduction
2. Electric Submersible Progressive Cavity Pump: Fault Characteristics and Data Processing
2.1. ESPCP Working Condition Analysis
2.2. Data Preprocessing
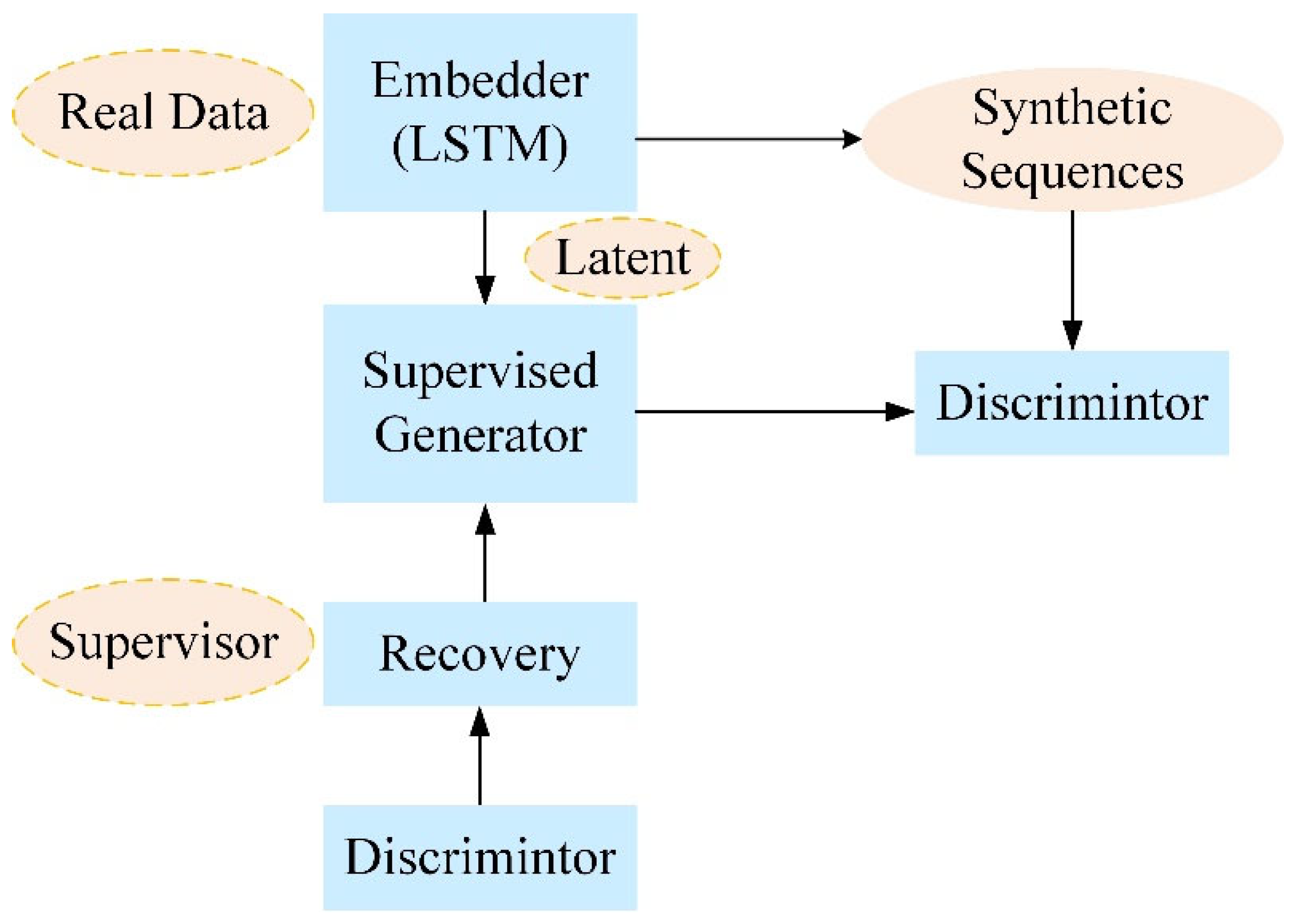
2.3. Synthetic-Data Augmentation with TimeGAN
3. Research Method
3.1. CNN Algorithm
3.1.1. Convolutional Layer
3.1.2. Pooling Layer
3.1.3. Fully Connected Layer
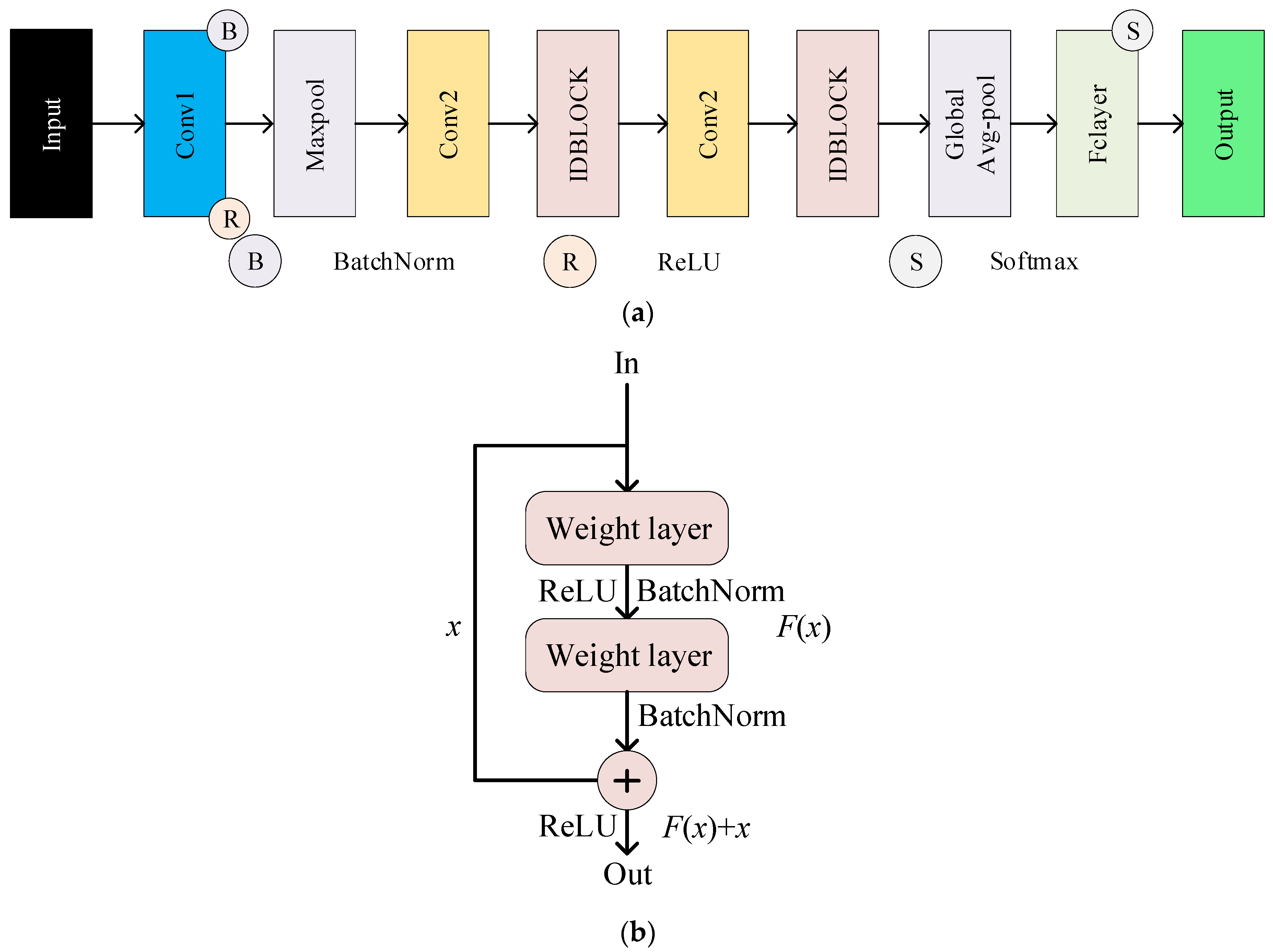
3.2. ResNet Network
- The Conv Block employs extra convolution operations to adjust input–output dimensions and accommodate deeper networks.
- The second-layer convolution plus BatchNorm yields F(x).
- Summing x and F(x) and then applying another ReLU activation produces the final output, y = F(x) + x.
3.3. Random Forest
3.4. Hybrid Model and Discriminative Value Analysis
3.5. Brief Comparison of the Five Models
4. Experimentation and Analysis
4.1. Sample Selection and Processing
4.2. TimeGAN–LSTM Cross-Validation
4.2.1. Validation and Network Setup
4.2.2. Convergence Behavior
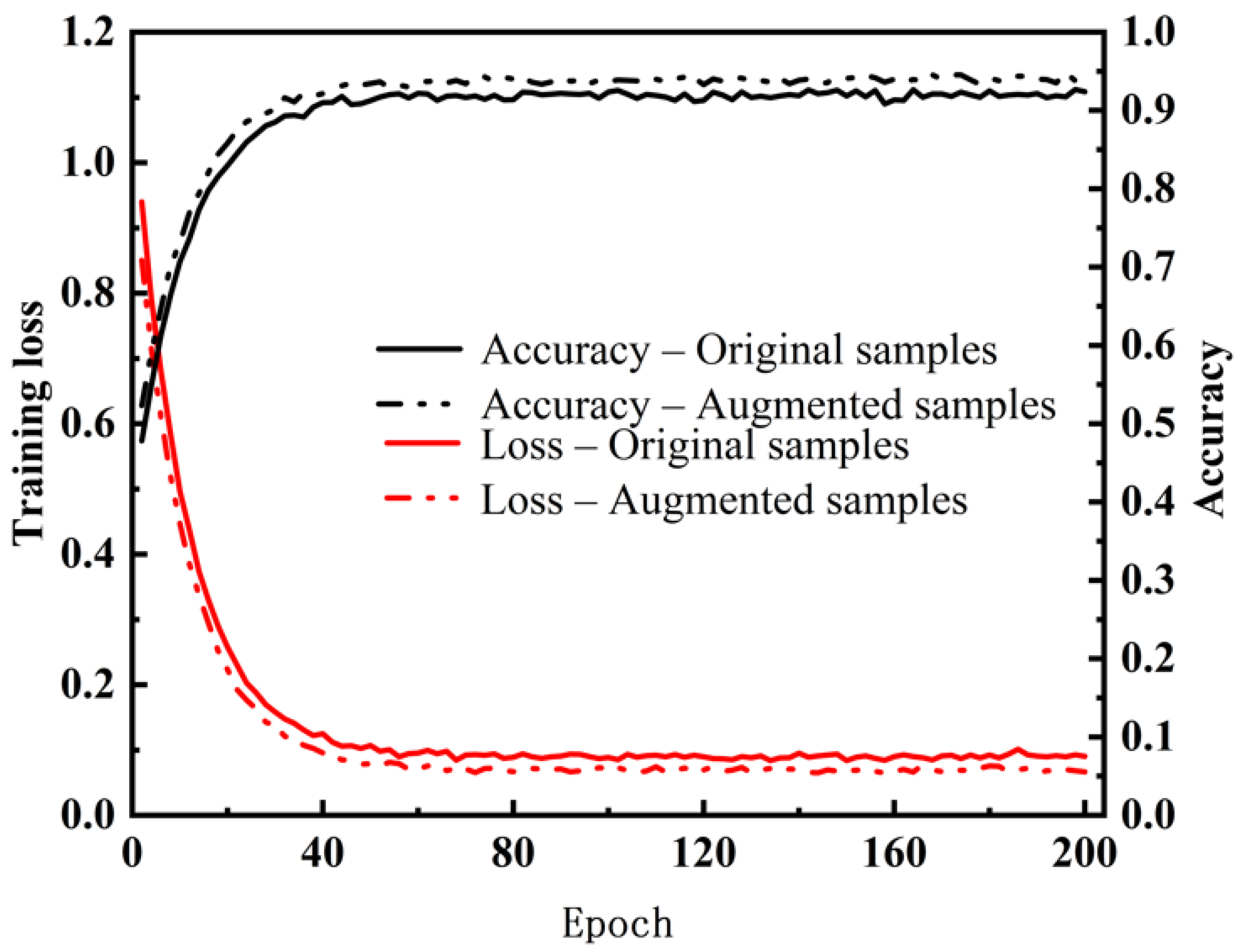
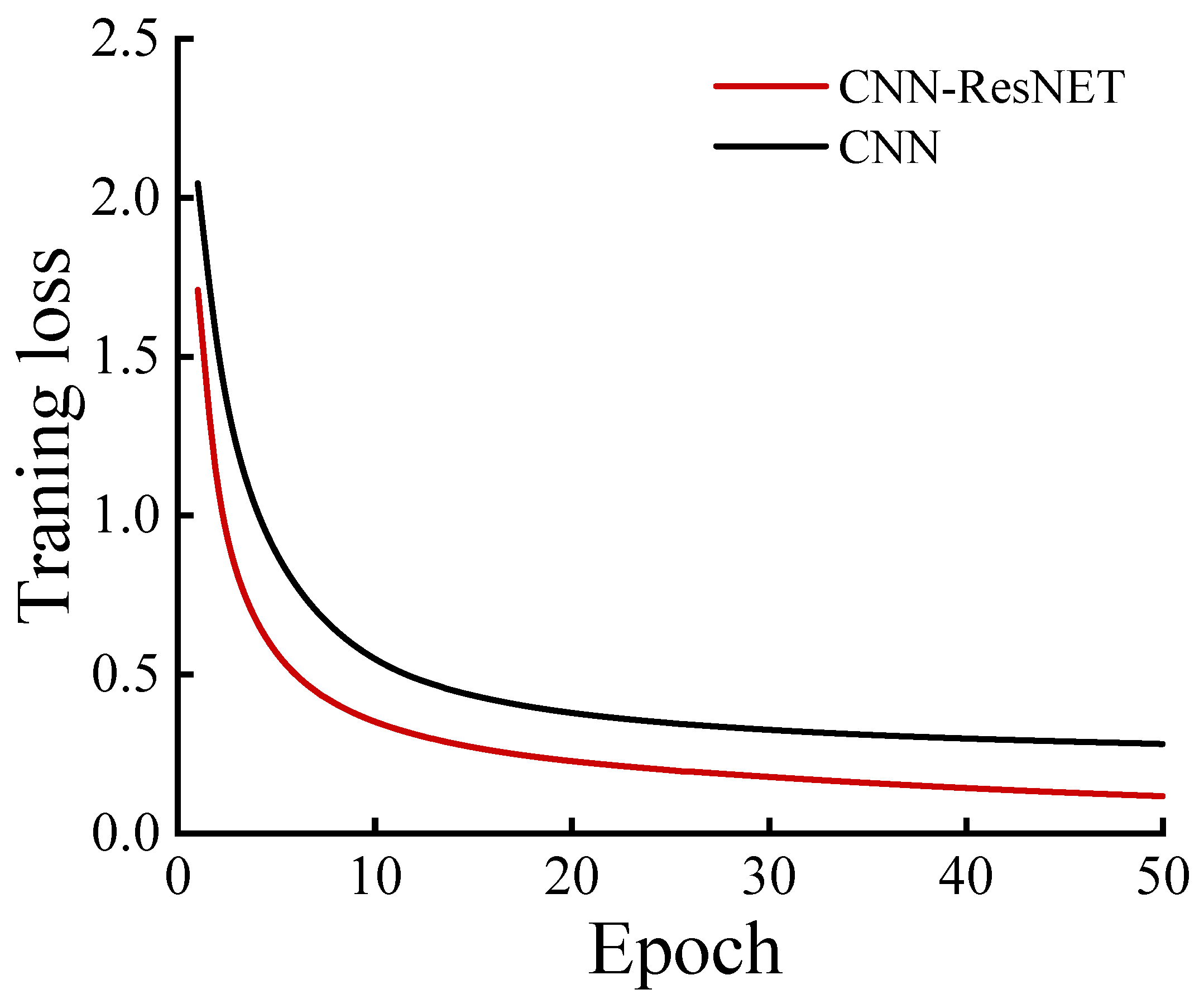
4.3. CNN and CNN-ResNet Training Convergence Characteristics
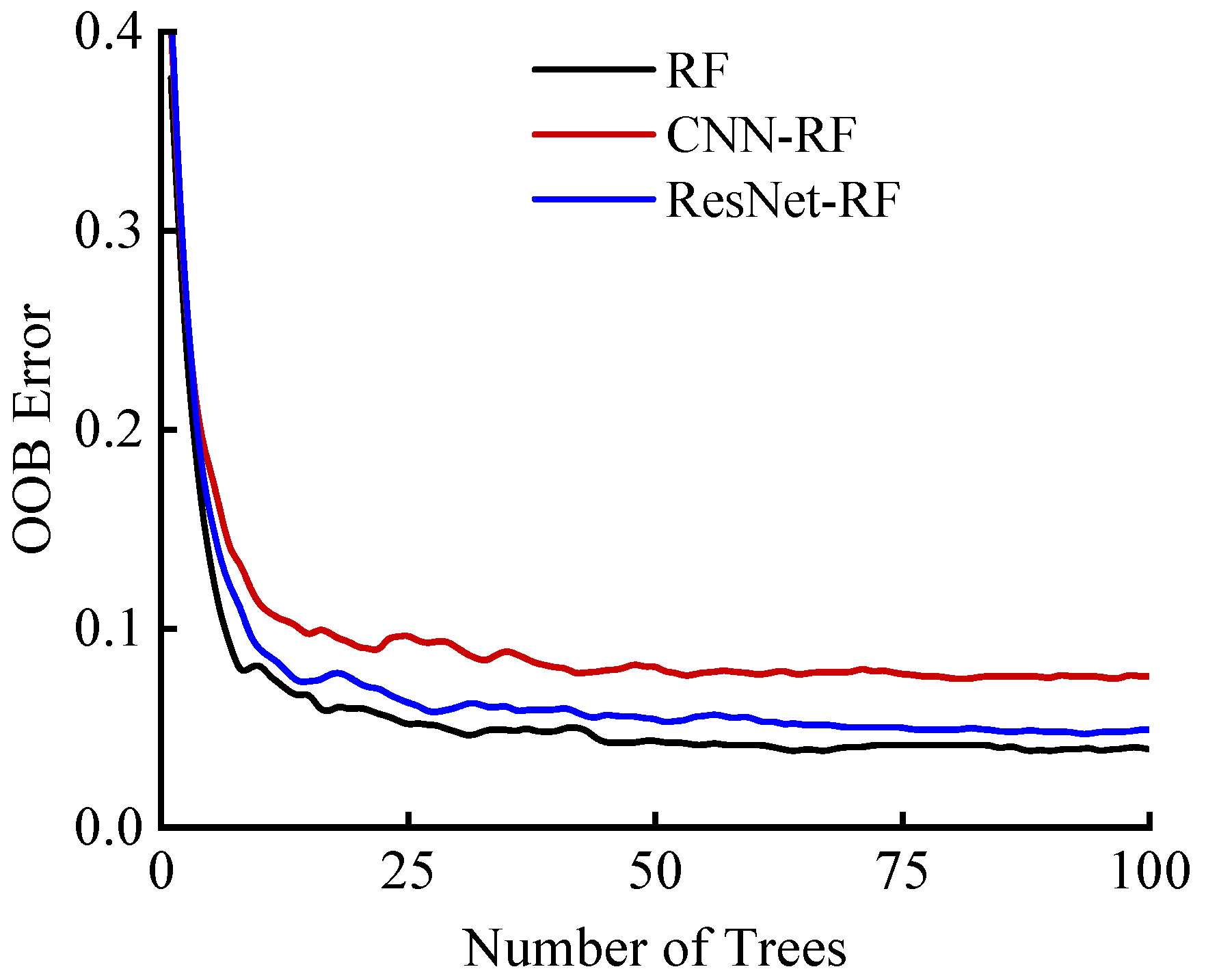
4.4. Random Forest Section and OOBError Analysis
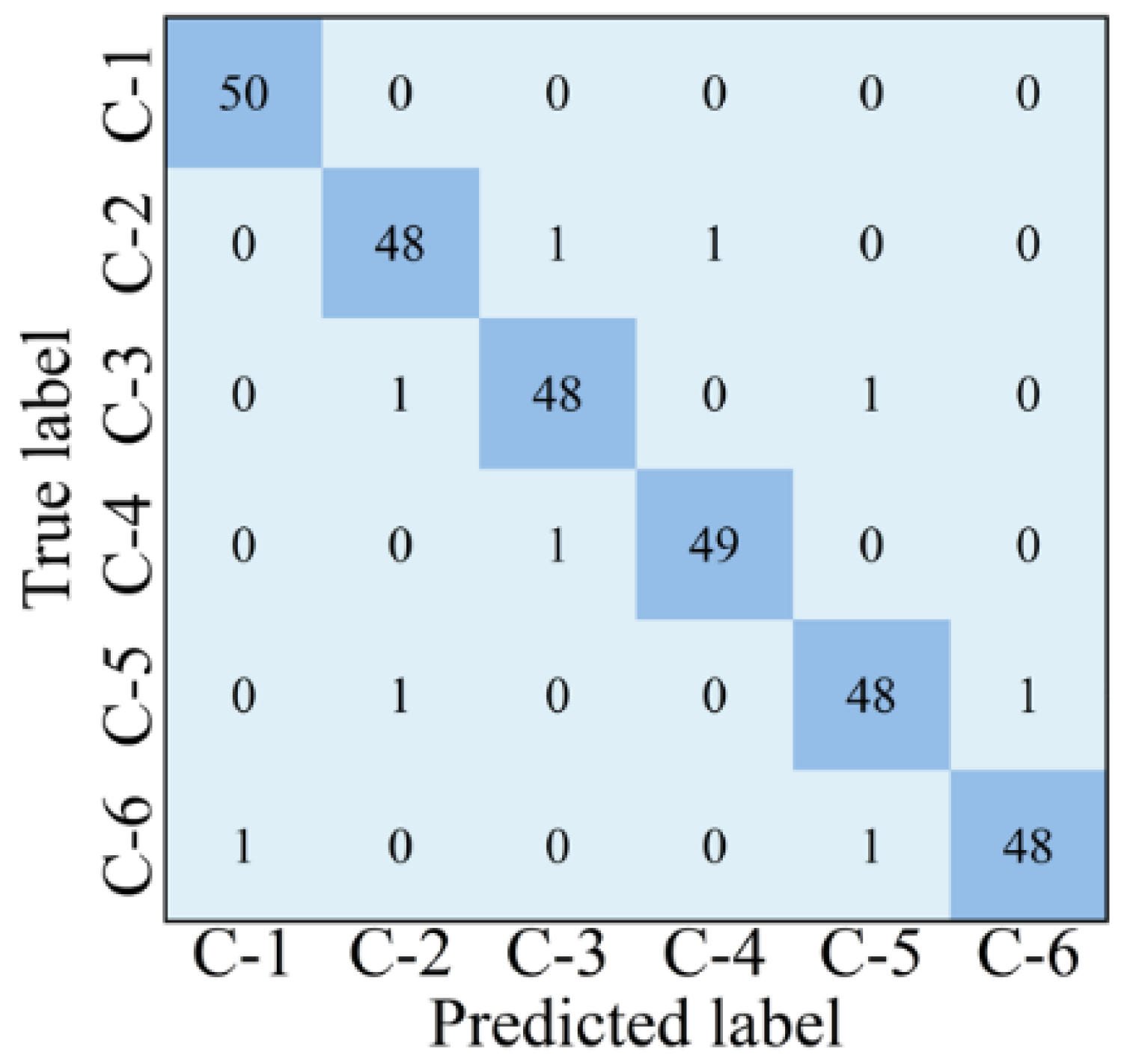
4.5. Model Comparison and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hao, Z.X.; Zhu, S.J.; Pei, X.H.; Huang, P.; Tong, Z.; Wang, B.Y.; Li, D.Y. Submersible direct-drive progressing cavity pump rodless lifting technology. Pet. Explor. Dev. 2019, 46, 621–628. [Google Scholar] [CrossRef]
- Liu, L.; Liu, W.H.; Ma, G.M.; Gen, H.Y. Field Practice of the Submersible Electric Screw Pump Production System. Oil Drill. Prod. Technol. 2003, 25 (Suppl. S1), 30–32+91–92. [Google Scholar] [CrossRef]
- Yang, P.H.; Chen, J.R.; Zhang, H.R.; Li, S. A Fault Identification Method for Electric Submersible Pumps Based on DAE-SVM. Shock. Vib. 2022, 2022, 5868630. [Google Scholar] [CrossRef]
- Jiang, M.Z.; Cheng, T.C.; Dong, K.X.; Xu, S.F.; Geng, Y.L. Fault diagnosis method of submersible screw pump based on random forest. PLoS ONE 2020, 15, e0242458. [Google Scholar] [CrossRef]
- Nolte, K.; Gerharz, A.; Jaitner, T.; Alt, T. Finding the needle in the haystack of isokinetic knee data: Random Forest modelling improves information about ACLR-related deficiencies. J. Sports Sci. 2025, 43, 173–181. [Google Scholar] [CrossRef]
- Liu, Y.C.; Li, Z.Y. Key technology and application of intelligent connected patrol vehicles for security scenario. Telecommun. Sci. 2020, 36, 53–60. [Google Scholar] [CrossRef]
- Liu, D.J.; Feng, G.Q.; Feng, G.Y.; Xie, L.J. Hybrid Long Short-Term Memory and Convolutional Neural Network Architecture for Electric Submersible Pump Condition Prediction and Diagnosis. SPE J. 2024, 29, 2130–2147. [Google Scholar] [CrossRef]
- Hu, Y.; Soltoggio, A.; Lock, R.; Cater, S. A fully convolutional two-stream fusion network for interactive image segmentation. Neural Netw. 2019, 109, 31–42. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Alguliyev, R.; Imamverdiyev, Y.; Sukhostat, L. Intelligent diagnosis of petroleum equipment faults using a deep hybrid model. SN Appl. Sci. 2020, 2, 924. [Google Scholar] [CrossRef]
- Guo, Z.; Hao, Y.; Shi, H.; Wu, Z.; Wu, Y.; Sun, X. A Fault Diagnosis Algorithm for the Dedicated Equipment Based on the CNN-LSTM Mechanism. Energies 2023, 16, 5230. [Google Scholar] [CrossRef]
- He, W.; Chen, J.; Zhou, Y.; Liu, X.; Chen, B.; Guo, B. An Intelligent Machinery Fault Diagnosis Method Based on GAN and Transfer Learning under Variable Working Conditions. Sensors 2022, 22, 9175. [Google Scholar] [CrossRef]
- Chen, M.; Wu, J.J.; Liu, L.Z.; Zhao, W.H.; Tian, F.; Shen, Q.; Zhao, B.Y.; Du, R.H. DR-Net: An improved network for building extraction from high resolution remote sensing image. Remote Sens. 2021, 13, 294. [Google Scholar] [CrossRef]
- Chai, Y.J.; Ma, J.; Liu, H. Deep Graph Attention Convolution Network for Point Cloud Semantic Segmentation. Laser Optoelectron. Prog. 2021, 58, 208–215. [Google Scholar] [CrossRef]
- Esteban, C.; Hyland, S.L.; Rätsch, G. Real-valued (medical) time series generation with recurrent conditional gans. arXiv 2017, arXiv:1706.02633. [Google Scholar] [CrossRef]
- Yoon, J.; Jarrett, D.; Van der Schaar, M. Time-series generative adversarial networks. Adv. Neural Inf. Process. Syst. 2019, 32, 5508–5518. [Google Scholar] [CrossRef]
- Gao, X.; Deng, F.; Yue, X. Data augmentation in fault diagnosis based on the Wasserstein generative adversarial network with gradient penalty. Neurocomputing 2020, 396, 487–494. [Google Scholar] [CrossRef]
- Yu, S.; Li, Z.; Gu, J.; Wang, R.; Liu, X.; Li, L.; Guo, F.; Ren, Y. CWMS-GAN: A small-sample bearing fault diagnosis method based on continuous wavelet transform and multi-size kernel attention mechanism. PLoS ONE 2025, 20, e0319202. [Google Scholar] [CrossRef]
- Bonella, V.B.; Ribeiro, M.P.; Mello, L.H.S.; Oliveira-Santos, T.; Rodrigues, A.L.; Varejão, F.M. Deep learning intelligent fault diagnosis of electrical submersible pump based on raw time domain vibration signals. In Proceedings of the IEEE 31st International Symposium on Industrial Electronics (ISIE), Anchorage, AK, USA, 1–3 June 2022; IEEE: New York, NY, USA, 2022; pp. 156–163. [Google Scholar] [CrossRef]
- Liu, L.Y.; Li, X.Y.; Lan, T.; Cheng, Y.K.; Chen, W.; Li, Z.X.; Cao, S.; Han, W.L.; Zhang, X.S.; Chai, H.F. A Survey on Anti-Money Laundering Techniques in Blockchain Systems. Strateg. Study CAE 2020, 27, 287–303. [Google Scholar] [CrossRef]
- Jiang, G.X.; Zhang, N.; Wang, W.J. Cluster Distribution-guided Label Noise Detection and Cleaning. J. Chin. Comput. Syst. 2024, 50, 154–168. Available online: http://kns.cnki.net/kcms/detail/21.1106.tp.20250311.1815.024.html (accessed on 20 March 2025).
- Liu, J.H.; Zhou, M.L.; Shao, W.W. Spatio-Temporal Characteristics and Influencing Factors Analysis of Groundwater Storage Variations in the Yellow River Basin. Yellow River 2024, 46, 67–73. [Google Scholar] [CrossRef]
- Zhang, D.U.; Jiang, H.Y.; Tian, X.; Yuan, S.B.; Zhao, L.M. Principle and design of automatic pressure release device fordownhole drive pump. Min. Process. Equip. 2016, 44, 66–70. [Google Scholar] [CrossRef]
- Xie, J.Y.; Cheng, H.; Chu, Y.J.; Lu, L.M.; Zhang, J.W. Failure Model and Intelligent Diagnosis Method of Process Control of EPCP. China Pet. Mach. 2023, 51, 116–121. [Google Scholar] [CrossRef]
- Qu, W.T.; Yan, H.; Sun, Y.P.; Shi, C.Y.; Yang, B. Fault Diagnosis Method of Surface Driven Screw Pump Well. Mach. Des. Res. 2021, 37, 159–162. [Google Scholar] [CrossRef]
- Nie, F.P.; Ma, Y.; Zhang, X.M.; Li, L.H.; Chen, W. A new method for behavior diagnose of progressive cavity pump wells. Fault-Block Oil Gas Field 2007, 14, 76–77+94. [Google Scholar] [CrossRef]
- Yu, D.L.; Li, Y.M.; Ding, B.; Ren, Y.L.; Qi, W.G. Failure Diagnosis Method for Electric Submersible Plunger Pump Based on Mind Evolutionary Algorithm and Back Propagation Neural Network. Inf. Control 2017, 46, 698–705. [Google Scholar] [CrossRef]
- Lin, J.F. Fault Analysis and Treatment Method and Maintenance Management Practice of Double Submersible Electric Pump Well. Petro Chem. Equip. 2021, 24, 80–83. [Google Scholar] [CrossRef]
- Liu, Y.; Pu, H.; Sun, D.W. Efficient extraction of deep image features using convolutional neural network (CNN) for applications in detecting and analysing complex food matrices. Trends Food Sci. Technol. 2021, 113, 193–204. [Google Scholar] [CrossRef]
- Barbhuiya, A.A.; Karsh, R.K.; Jain, R. CNN based feature extraction and classification for sign language. Multimed. Tools Appl. 2021, 80, 3051–3069. [Google Scholar] [CrossRef]
- Zhou, F.Y.; Jin, L.P.; Dong, J. Review of Convolutional Neural Network. Chin. J. Comput. 2017, 40, 1229–1251. [Google Scholar] [CrossRef]
- Wang, Y.C.; Li, M.T.; Pan, Z.C.; Zheng, J.H. Pulsar candidate classification with deep convolutional neural networks. Res. Astron. Astrophys. 2019, 19, 133. [Google Scholar] [CrossRef]
- Gao, J. Network intrusion detection method combining CNN and BiLSTM in cloud computing environment. Comput. Intell. Neurosci. 2022, 2022, 7272479. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.H.; Yan, X.P.; Liu, S.K.; Li, P.; Hao, X.H. Radar emitter multi-label recognition based on residual network. Def. Technol. 2022, 18, 410–417. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Hong, W.C. Application of variational mode decomposition and chaotic grey wolf optimizer with support vector regression for forecasting electric loads. Knowl.-Based Syst. 2021, 228, 107297. [Google Scholar] [CrossRef]
- Li, B.; He, Y. An improved ResNet based on the adjustable shortcut connections. IEEE Access 2018, 6, 18967–18974. [Google Scholar] [CrossRef]
- Guo, X.; Chen, Y.P.; Tang, R.X.; Huang, R.Z.; Qing, Y.B. Predicate Head Identification Based on Boundary Regression. Comput. Eng. Appl. 2023, 59, 144–150. [Google Scholar] [CrossRef]
- Liu, H.L.; Cao, S.J.; Xu, J.Y.; Chen, S.Y. Anti-fraud Research Advances on Digital Credit Payment. J. Front. Comput. Sci. Technol. 2023, 17, 2300–2324. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Liu, X.F.; Cao, Y.F.; Ou, Y.T.B. Fault Prediction Method for Electric Submersible Pumps Based on LSTM-PNN Neural Network. Mach. Tool Hydraul. 2024, 52, 209–215. [Google Scholar] [CrossRef]
- Wang, H.R.Q.; Wu, H.R.; Feng, S.; Liu, Z.C.; Xu, T.Y. Classification Technology of Rice Questions in Question Answer System Based on Attention_DenseCNN. Trans. Chin. Soc. Agric. Mach. 2021, 52, 237–243. [Google Scholar] [CrossRef]
- Lin, Z.X.; Wang, L.K. Network situation prediction method based on deep feature and Seq2Seq model. J. Comput. Appl. 2020, 40, 2241–2247. [Google Scholar] [CrossRef]
- Yuan, J.; Tian, Y. An Intelligent Fault Diagnosis Method Using GRU Neural Network towards Sequential Data in Dynamic Processes. Processes 2019, 7, 152. [Google Scholar] [CrossRef]
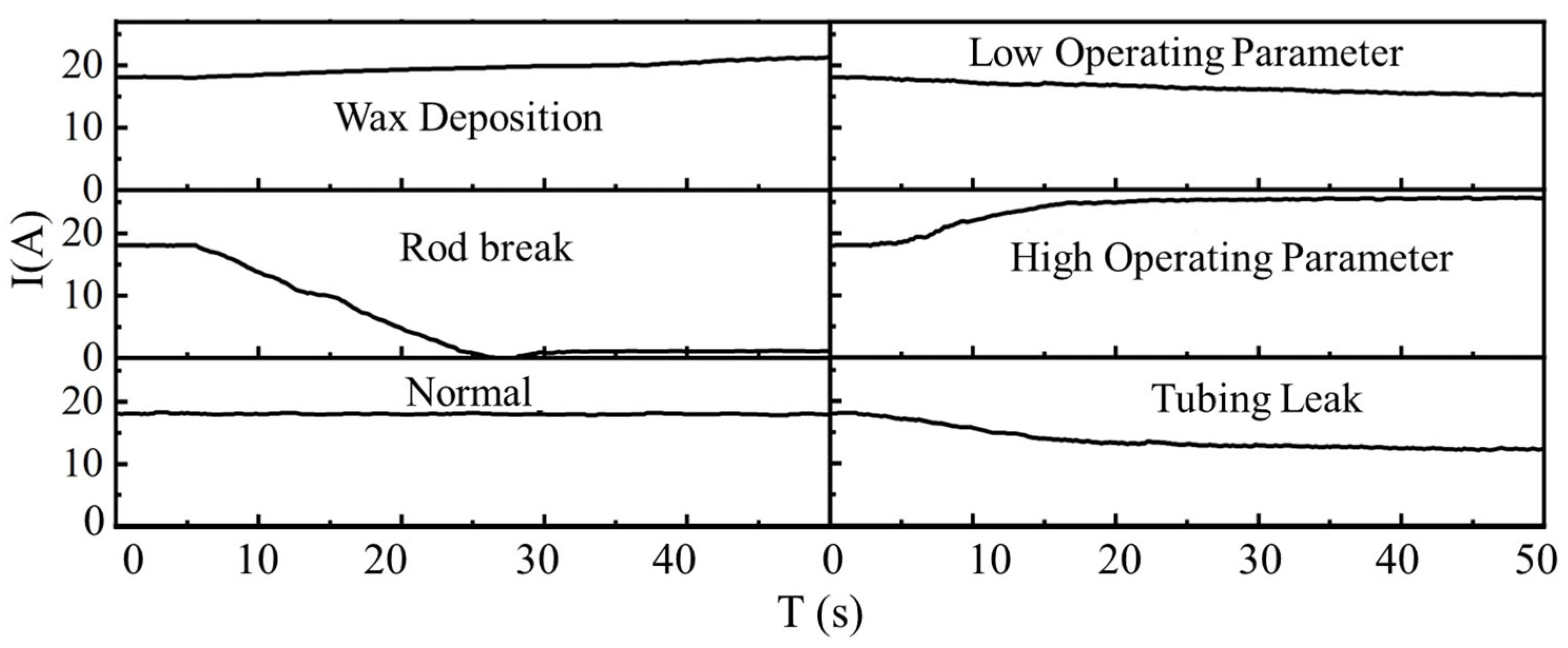




| Operating Condition | Variation in Current Signal |
|---|---|
| Normal | The current remains stable, fluctuating slightly around a fixed value. |
| Rod break | The current drops sharply at the moment of rod failure, rapidly approaching zero from its normal level. It then stays at an extremely low value or triggers device shutdown, causing the pump to enter an unloaded state. |
| Tubing leak | The current gradually decreases as fluid leakage reduces the load, ultimately stabilizing at a lower-value region. |
| Wax deposition | The current slowly rises, accompanied by a gradual increase in load, showing a smooth transition into a higher range with no abrupt changes or surges. |
| High operating parameter | The current surges steeply over a short period into a high-value region, exhibiting larger fluctuations at that high level. |
| Low operating parameter | The current gently declines over a relatively longer duration, eventually settling in a low-value range with slight oscillations. |
| Operating Condition | Status Number | Expected Output |
|---|---|---|
| Normal | C-1 | (1,0,0,0,0,0) |
| Rod Break | C-2 | (0,1,0,0,0,0) |
| Tubing Leak | C-3 | (0,0,1,0,0,0) |
| Wax Deposition | C-4 | (0,0,0,1,0,0) |
| High Operating Parameter | C-5 | (0,0,0,0,1,0) |
| Low Operating Parameter | C-6 | (0,0,0,0,0,1) |
| Model | C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | Overall |
|---|---|---|---|---|---|---|---|
| CNN | 95.6 | 86.2 | 61.9 | 90.6 | 78.1 | 48.9 | 82.6 |
| CNN-ResNET | 97.5 | 89.7 | 76.2 | 92.5 | 81.3 | 72.3 | 88.9 |
| RF | 97.5 | 92.9 | 83.3 | 88.7 | 87.5 | 82.6 | 91.4 |
| CNN-RF | 96.2 | 93.1 | 85.7 | 92.5 | 93.8 | 91.3 | 93.3 |
| CNN-ResNET-RF | 97.5 | 96.6 | 95.2 | 90.6 | 96.9 | 97.8 | 96.1 |
| Oil Well Labelling | Current | Diagnosis | Field Fault |
|---|---|---|---|
| J033 | Slow rise | Wax Deposition | Wax Deposition |
| J420 | Plummeting to zero | Rod break | Rod break |
| J172 | Gradually decline to a stable range | Tubing Leak | Tubing Leak |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Shan, J.; Liu, C.; Zhang, S.; Zhang, D.; Hao, Z.; Huang, S. An Operating Condition Diagnosis Method for Electric Submersible Screw Pumps Based on CNN-ResNet-RF. Processes 2025, 13, 2043. https://doi.org/10.3390/pr13072043
Liu X, Shan J, Liu C, Zhang S, Zhang D, Hao Z, Huang S. An Operating Condition Diagnosis Method for Electric Submersible Screw Pumps Based on CNN-ResNet-RF. Processes. 2025; 13(7):2043. https://doi.org/10.3390/pr13072043
Chicago/Turabian StyleLiu, Xinfu, Jinpeng Shan, Chunhua Liu, Shousen Zhang, Di Zhang, Zhongxian Hao, and Shouzhi Huang. 2025. "An Operating Condition Diagnosis Method for Electric Submersible Screw Pumps Based on CNN-ResNet-RF" Processes 13, no. 7: 2043. https://doi.org/10.3390/pr13072043
APA StyleLiu, X., Shan, J., Liu, C., Zhang, S., Zhang, D., Hao, Z., & Huang, S. (2025). An Operating Condition Diagnosis Method for Electric Submersible Screw Pumps Based on CNN-ResNet-RF. Processes, 13(7), 2043. https://doi.org/10.3390/pr13072043






