Improved African Vulture Optimization Algorithm for Optimizing Nonlinear Regression in Wind-Tunnel-Test Temperature Prediction
Abstract
1. Introduction
2. Basic Theory
2.1. Kernel Principal Component Analysis
2.2. Support Vector Regression
2.3. African Vulture Optimization Algorithm
- (1)
- Population grouping and selection of the leading vulture
- (2)
- Calculate the hunger level of vultures
- (3)
- Exploration Stage
- (4)
- Pre-mining stage
- (5)
- Stage 5: The later stage of mining
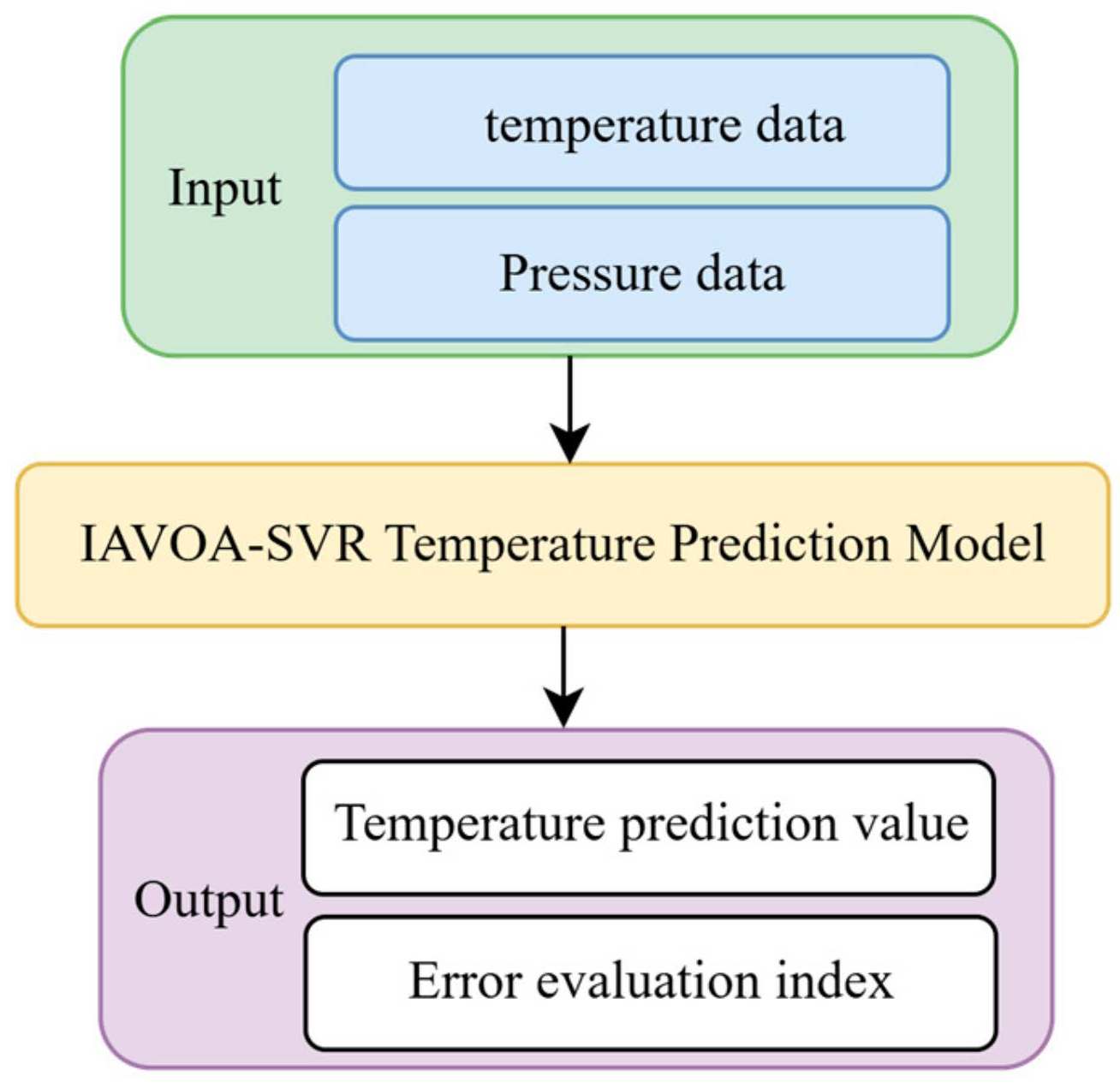
3. Optimized Model for Wind-Tunnel Thermal Prediction
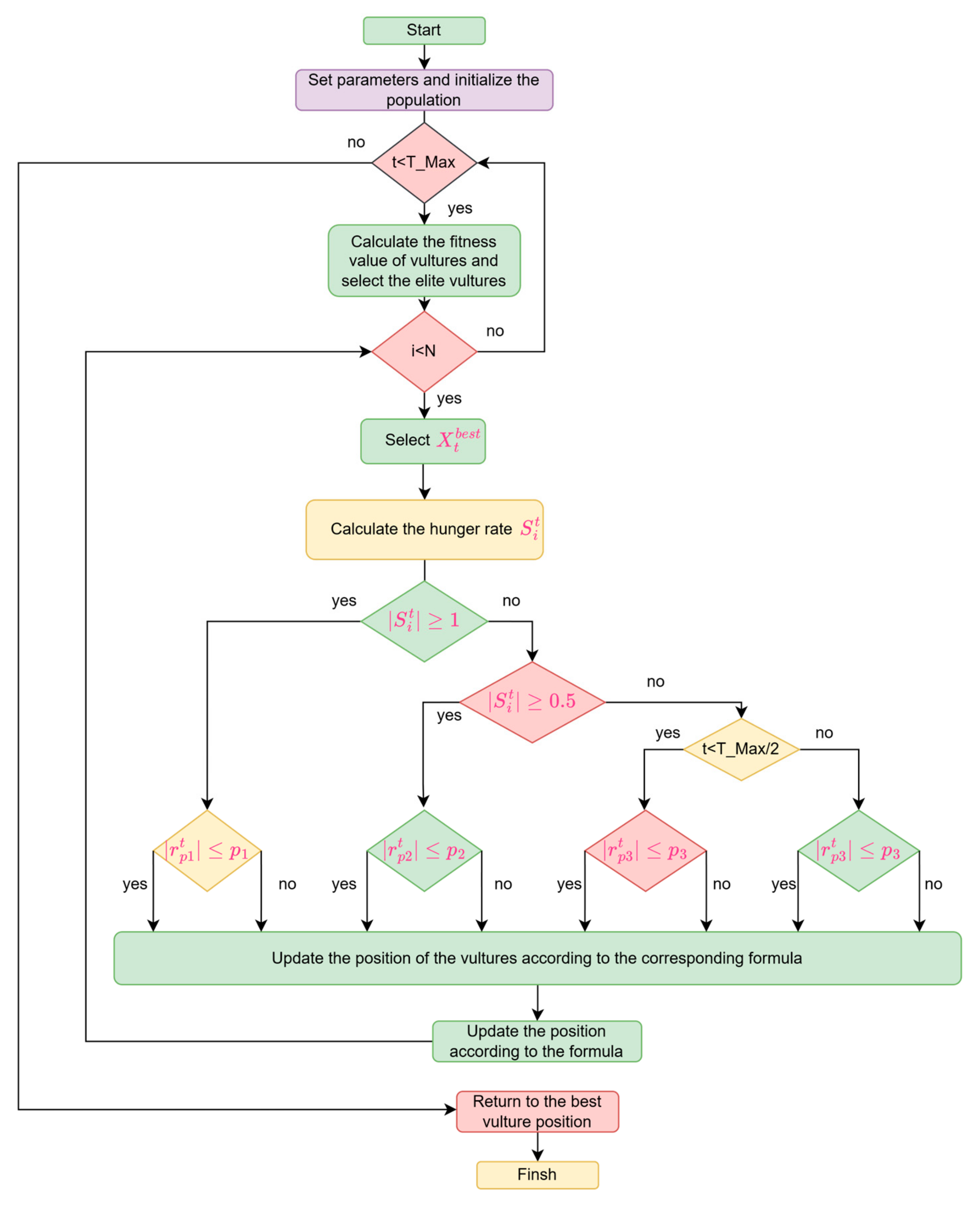
3.1. Improved African Vulture Optimization Algorithm (IAVOA)
- (1)
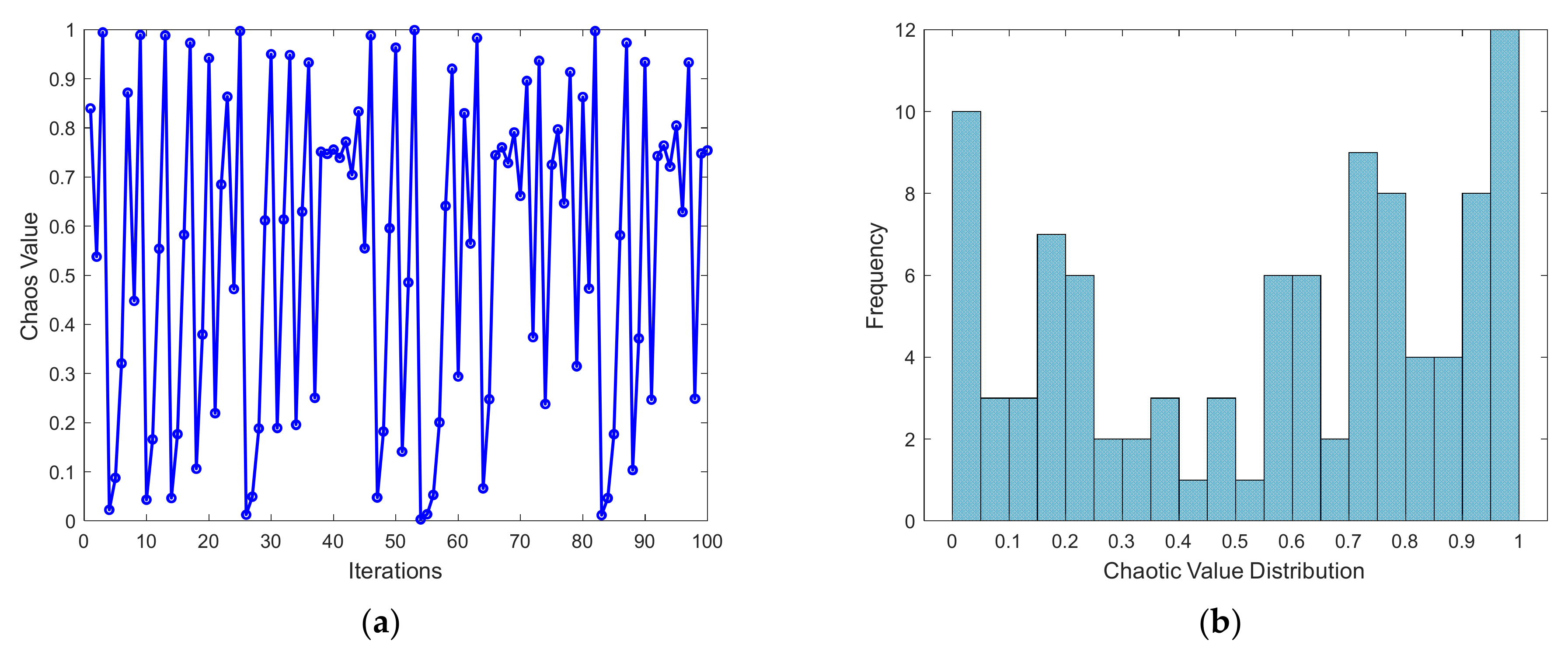
- Adaptive chaotic mapping
- (2)
- Local search enhancement
| Algorithm 1 Improves of the African Vulture Optimization Algorithm |
Input: Population size of vultures and the maximum number of iterations T_Max Output: The position and fitness value of the vulture 1: Set parameters and initialize the population 2: While (t < T_Max) do 3: Calculate the fitness of vultures, select elite vultures, and store the data 4: Set as the vulture position (the first best position) 5: Set as the vulture position (the second best position) 6: for (each vaulture) do 7: Select 8: Calculate the hunger rate 9: if () then 10: if () then 11: Update the position of the vultures 12: else 13: Update the position of the vultures 14: end if 15: else 16: if () then 17: if () then 18: if () then 19: Update the position of the vultures 20: else 21: Update the position of the vultures 22: end if 23: else 24: if () then 25: Update the position of the vultures 26: else 27: Update the position of the vultures 28: end if 29: end if 30: end if 31: Update the position of the vulture according to the formula 32: t = t + 1 33: if (t > T_Max/2) then 34: if () then 35: Update the positions of the vultures 36: else 37: Update the positions of the vultures 38: end if 39: end if 40: end while 41: Return |
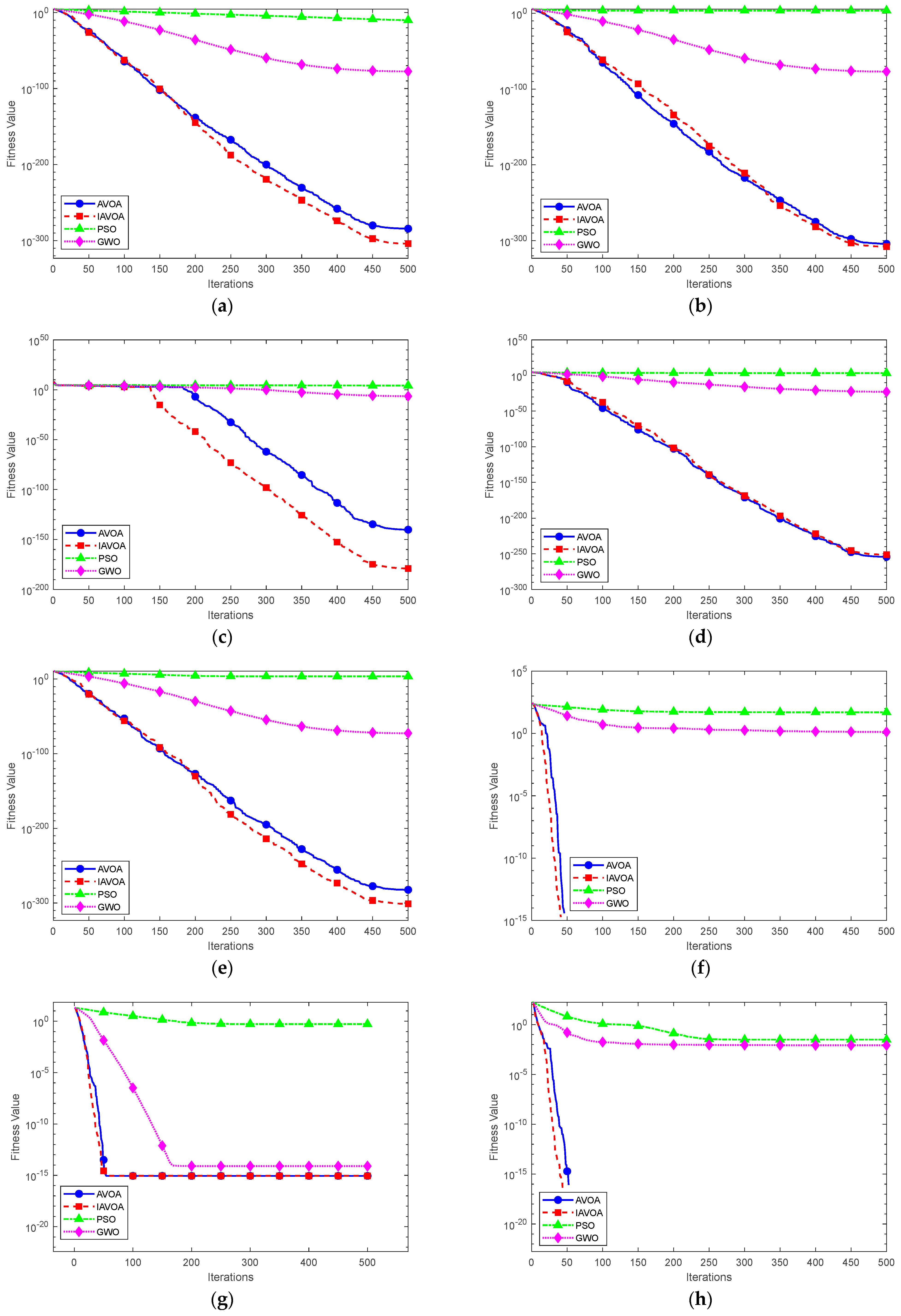
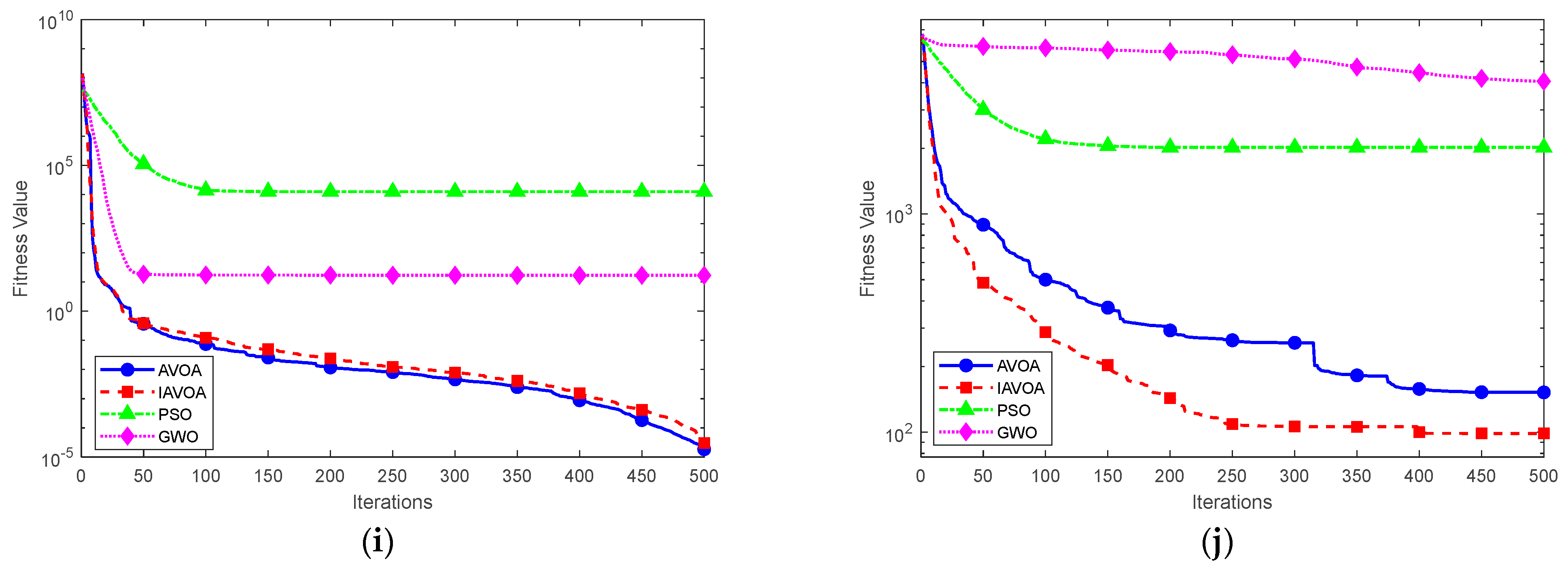
3.2. Benchmark Test Function
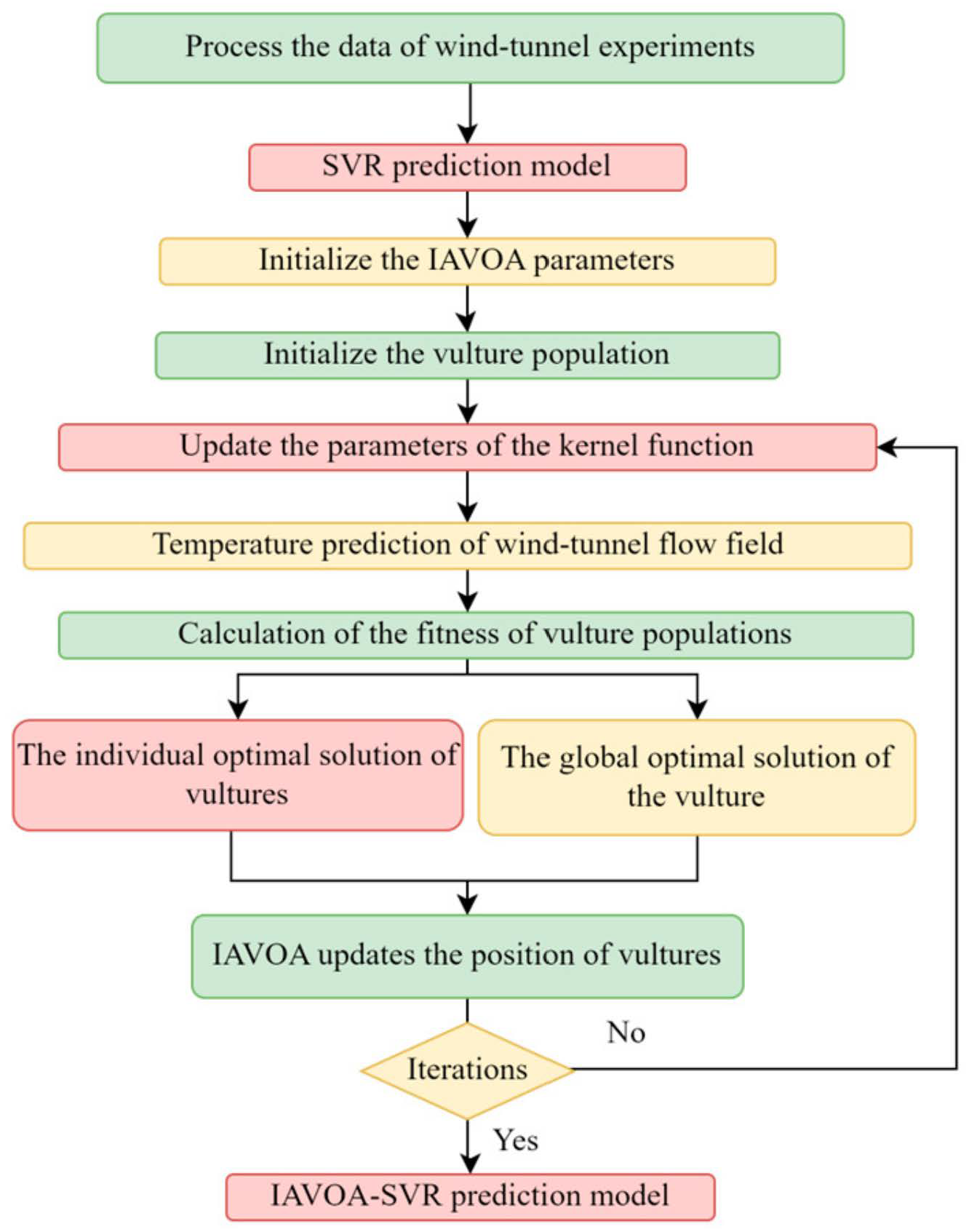
3.3. Improved AVOA-Optimized SVR
4. Experimental Results and Analysis
4.1. Data Introduction
4.2. Data Preprocessing
4.3. Error-Evaluation Index
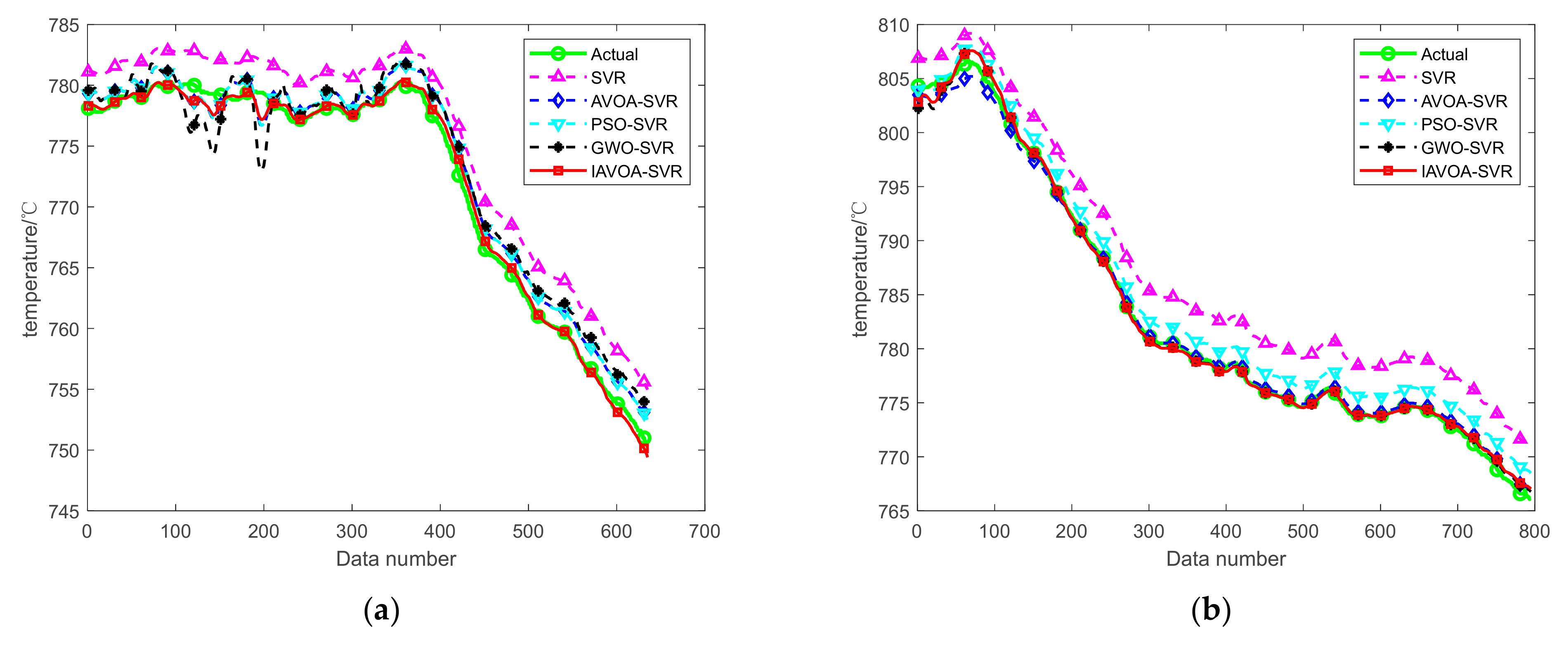
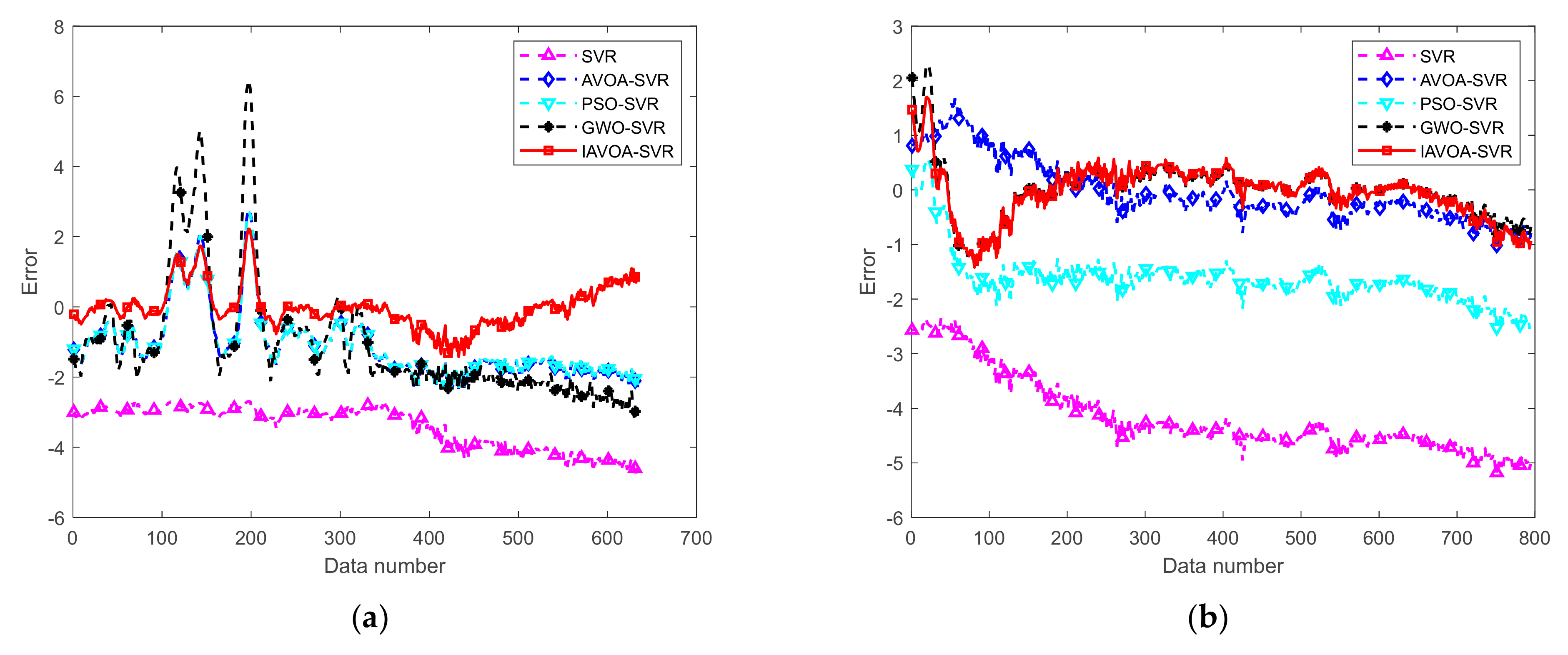
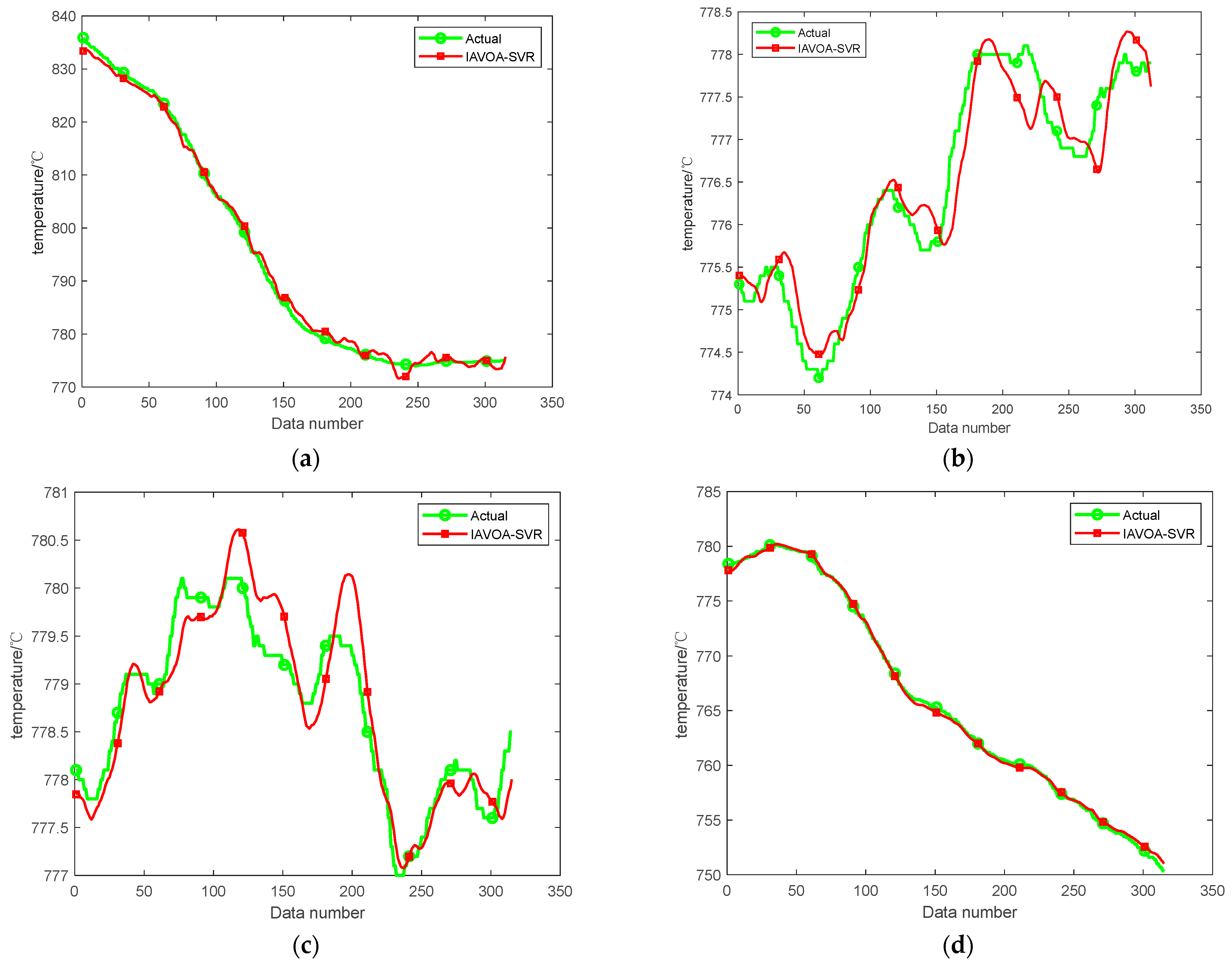
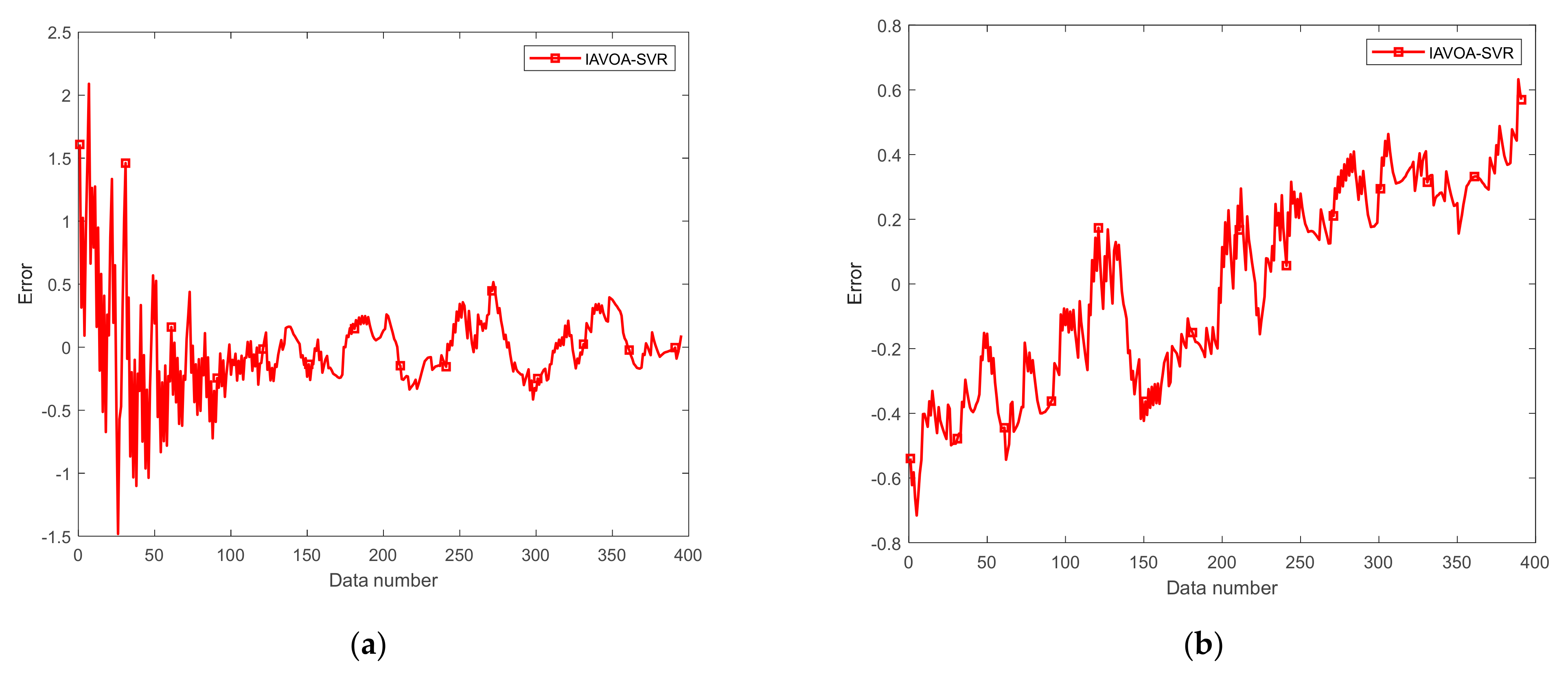
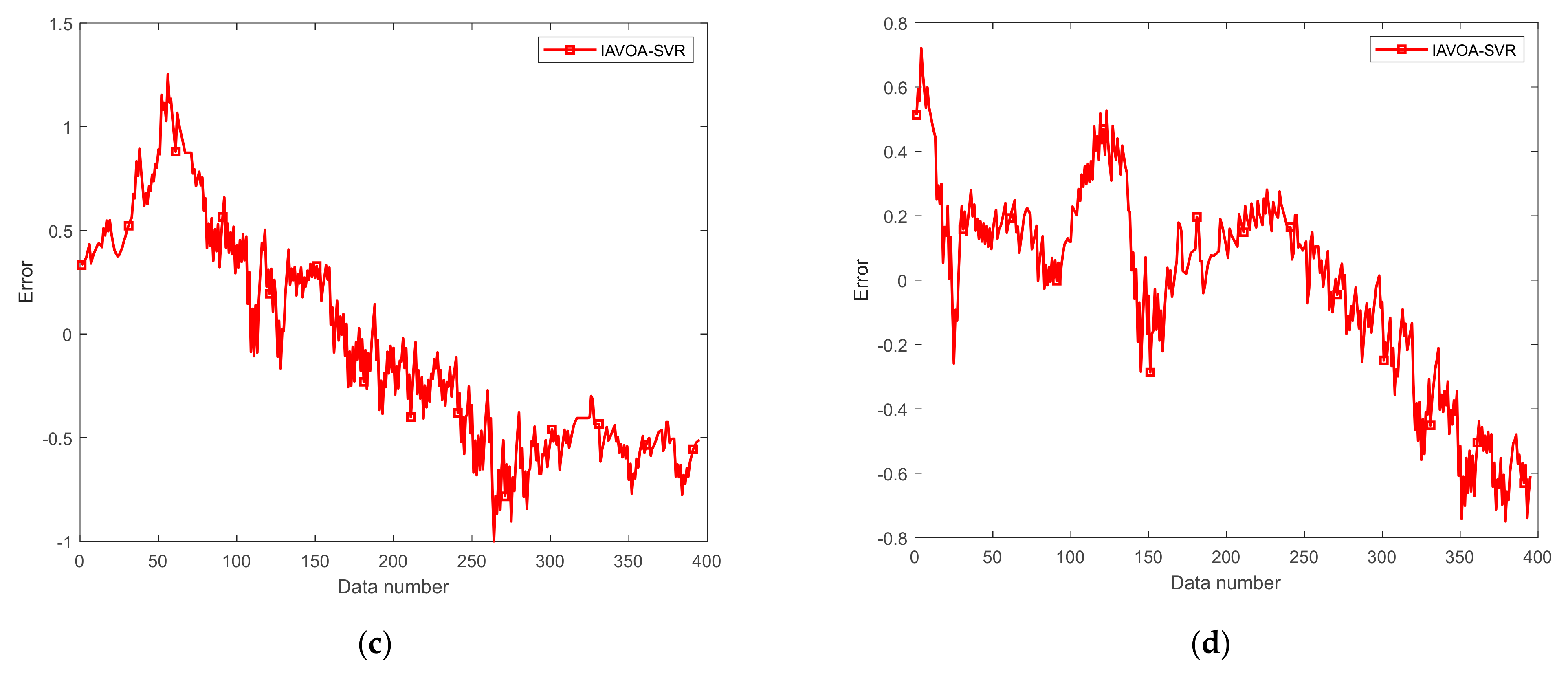
4.4. Actual Wind-Tunnel Data Analysis
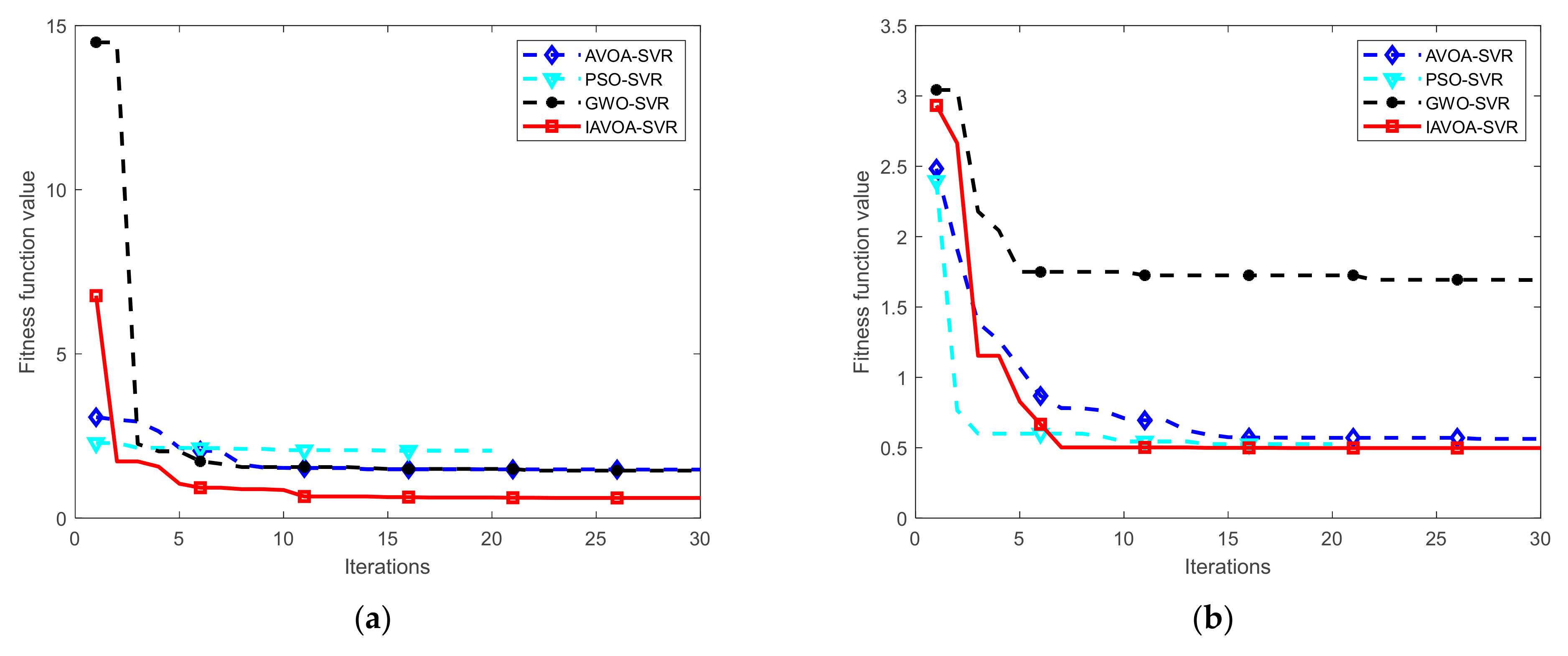
4.5. Validation of the IAVOA-SVR Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yule, G.U. On a Method of Investigating Periodicities in Distributed Series, with special reference to Wolfer’s Sunspot Numbers. Phil. Trans. R. Soc. Lond. A 1927, 226, 267–298. [Google Scholar]
- Winters, P.R. Forecasting sales by exponentially weighted moving averages. Manag. Sci. 1960, 6, 324–342. [Google Scholar]
- Tsay, R.S. Testing and modeling threshold autoregressive processes. J. Am. Stat. Assoc. 1989, 84, 231–240. [Google Scholar]
- Jones, S.; Poongodi, S.; Binu, L. Stabilizing controller using backstepping for steady mass flow in a wind tunnel. In Proceedings of the IEEE Recent Advances in Intelligent Computational Systems, Trivandrum, India, 22–24 September 2011; pp. 735–740. [Google Scholar]
- Castán-Lascorz, M.A.; Jiménez-Herrera, P.; Troncoso, A.; Asencio-Cortés, G. A new hybrid method for predicting univariate and multivariate time series based on pattern forecasting. Inf. Sci. 2022, 586, 611–627. [Google Scholar]
- Zhang, X.; Zhang, P.; Peng, B.; Xian, Y. Prediction of icing wind tunnel temperature field with machine learning. J. Exp. Fluid Mech. 2022, 36, 8–15. [Google Scholar]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm-A literature review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing, Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar]
- Price, K.V. Differential evolution. In Handbook of Optimization: From Classical to Modern Approach; Springer: Berlin/Heidelberg, Germany, 2013; pp. 187–214. [Google Scholar]
- Hansen, N.; Arnold, D.V.; Auger, A. Evolution strategies. In Springer Handbook of Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2015; pp. 871–898. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant colony optimization: Overview and recent advances. In Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 311–351. [Google Scholar]
- Jain, N.K.; Nangia, U.; Jain, J. A review of particle swarm optimization. J. Inst. Eng. Ser. B 2018, 99, 407–411. [Google Scholar] [CrossRef]
- Kıran, M.S.; Fındık, O. A directed artificial bee colony algorithm. Appl. Soft Comput. 2015, 26, 454–462. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhu, M.; Cui, Q.; Wang, J.; Gu, Z. Research on Partial Discharge Pattern Recognition of Transformer Bushings Based on KPCA and GTO-SVM Algorithm. In Proceedings of the 6th International Conference on Power and Energy Technology, Beijing, China, 12–15 July 2024. [Google Scholar]
- Li, W.; Yue, H.; Valle-Cervantes, S.; Qin, S.J. Recursive PCA for adaptive process monitoring. J. Process Control 2000, 10, 471–486. [Google Scholar] [CrossRef]
- Yuan, G.; Ma, Y.; Tan, F.; Zhang, Z. Research on Transformer Fault Diagnosis Based on Improved INGO Optimization LSSVM. In Proceedings of the International Conference on Electrical Engineering and Control Science, Hangzhou, China, 29–31 December 2023. [Google Scholar]
- Zhou, Z. Machine Learning; Tsinghua University Press: Beijing, China, 2016; pp. 125–128. [Google Scholar]
- Vapnik, V.N. Pattern recognition using generalized portrait method. Autom. Remote Control 1963, 24, 774–780. [Google Scholar]
- Mousaei, A.; Naderi, Y.; Bayram, I.S. Advancing State of Charge Management in Electric Vehicles with Machine Learning: A Technological Review. IEEE Access 2024, 12, 43255–43283. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 58, 107–408. [Google Scholar] [CrossRef]
- Kumar, C.; Mary, D.M. Parameter estimation of three diode solar photovoltaic model using an Improved African Vultures optimization algorithm with Newton-Raphson method. J. Comput. Electron. 2021, 20, 2563–2593. [Google Scholar] [CrossRef]
- Kuang, X.; Hou, J.; Liu, X.; Lin, C.; Wang, Z.; Wang, T. Improved African Vulture Optimization Algorithm Based on Random Opposition-Based Learning Strategy. Electronics 2024, 13, 3329. [Google Scholar] [CrossRef]
- Nebro, A.J.; Durillo, J.; Garcia-Nieto, J.; Coello Coello, C.A.; Luna, F.; Alba, E. SMPSO: Anew PSO-Based Metaheuristic for Multi-Objective Optimization. In Proceedings of the IEEE Symposium on Computational Intelligence in Multicriteria Decision Making, Nashville, TN, USA, 30 March–2 April 2009; pp. 66–73. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mousaei, A.; Naderi, Y. Predicting Optimal Placement of Electric Vehicle Charge Stations Using Machine Learning: A Case Study in Glasgow. In Proceedings of the Iranian Conference on Renewable Energies and Distributed Generation, Qom, Iran, 26 February 2025; Volume 14, pp. 1–7. [Google Scholar]
- Gao, C.; Ji, W.; Wang, J.; Zhu, X.; Liu, C.; Yin, Z.; Huang, P.; Yu, L. Real-Time prediction of pool fire burning rates under complex heat transfer effects influenced by ullage height: A comparative study of BPNN and SVR. Therm. Sci. Eng. Prog. 2024, 56, 103060. [Google Scholar] [CrossRef]
- Chen, Z.; Mu, H.; Liao, X.; Ouyang, H.; Huang, D.; Lu, J.; Chen, D. Multiobjective Optimization of the Difficult-to-Machine Material TC18 Based on AVOA-SVR and MOAVOA. JOM 2025, 77, 1727–1745. [Google Scholar] [CrossRef]
- Zhou, H.; Zhu, J.; Liu, Y. Transformer oil temperature prediction based on PSO-SVR. In Proceedings of the IEEE International Conference on Civil Aviation Safety and Information Technology, Hangzhou, China, 23–25 October 2024; pp. 1286–1290. [Google Scholar]
- Jin, H.; Hu, Y.; Ge, H.; Hao, Z.; Zeng, Z.; Tang, Z. Remaining useful life prediction for lithium-ion batteries based on an improved GWO–SVR algorithm. Chin. J. Eng. 2024, 46, 514–524. [Google Scholar]




| Test Function | Dimensionality | Search Range | Optimum Value |
|---|---|---|---|
| 20 | [−100,100] | 0 | |
| 20 | [−100,100] | 0 | |
| 20 | [−10,10] | 0 | |
| 20 | [−100,100] | 0 | |
| 20 | [−100,100] | 0 | |
| 20 | [−5.2,5.2] | 0 | |
| 20 | [−32,32] | 0 | |
| 20 | [−600,600] | 0 | |
| 20 | [−30,30] | 0 | |
| 20 | [−500,500] | 0 |
| Basic Function | Algorithm | Mean Value | Standard | Maximum | Minimum |
|---|---|---|---|---|---|
| AVOA [21] | 2.27 × 10−28 | 0.00 | 0.00 | 2.37 × 10−31 | |
| GWO [25] | 1.17 × 10−7 | 4.06 × 10−7 | 1.40 × 10−8 | 2.12 × 10−7 | |
| PSO [24] | 4.87 × 10−1 | 6.18 × 10−1 | 1.88 × 10−1 | 3.16 × 10−1 | |
| IAVOA | 2.09 × 10−30 | 0.00 | 0.00 | 1.74 × 10−31 | |
| AVOA [21] | 2.16 × 10−29 | 0.00 | 0.00 | 6.48 × 10−29 | |
| GWO [25] | 4.75 × 10−7 | 9.67 × 10−7 | 6.30 × 10−8 | 3.75 × 10−7 | |
| PSO [24] | 2.66 × 100 | 8.27 × 100 | 3.22 × 10−1 | 4.00 × 100 | |
| IAVOA | 1.45 × 10−31 | 0.00 | 0.00 | 4.36 × 10−30 | |
| AVOA [21] | 2.80 × 10−16 | 0.00 | 3.83 × 10−27 | 8.41 × 10−16 | |
| GWO [25] | 1.97 × 10−1 | 9.49 × 10−9 | 3.06 × 10−21 | 5.21 × 10−8 | |
| PSO [24] | 1.72 × 100 | 9.79 × 103 | 1.89 × 103 | 4.69 × 104 | |
| IAVOA | 1.38 × 10−19 | 0.00 | 3.47 × 10−26 | 4.15 × 10−18 | |
| AVOA [21] | 1.53 × 10−23 | 0.00 | 4.94 × 10−32 | 4.60 × 10−23 | |
| GWO [25] | 2.69 × 10−2 | 1.44 × 10−21 | 6.91 × 10−3 | 7.93 × 10−2 | |
| PSO [24] | 2.01 × 1030 | 2.80 × 103 | 9.71 × 10−1 | 1.01 × 104 | |
| IAVOA | 5.18 × 10−24 | 0.00 | 5.17 × 10−31 | 1.54 × 10−24 | |
| AVOA [21] | 3.49 × 10−30 | 0.00 | 0.00 | 1.04 × 10−30 | |
| GWO [25] | 2.92 × 10−7 | 6.84 × 10−73 | 1.33 × 10−77 | 3.10 × 10−7 | |
| PSO [24] | 4.00 × 103 | 4.98 × 103 | 2.75 × 10−6 | 1.00 × 104 | |
| IAVOA | 1.62 × 10−28 | 0.00 | 0.00 | 4.87 × 10−28 | |
| AVOA [21] | 0.00 | 0.00 | 0.00 | 0.00 | |
| GWO [25] | 9.99 × 10−1 | 1.78 × 10 | 0.00 | 5.94 × 100 | |
| PSO [24] | 5.39 × 101 | 3.65 × 101 | 2.38 × 101 | 2.22 × 102 | |
| IAVOA | 0.00 | 0.00 | 0.00 | 0.00 | |
| AVOA [21] | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 8.88 × 10−16 | |
| GWO [25] | 2.06 × 101 | 9.89 × 10−2 | 2.04 × 101 | 2.08 × 101 | |
| PSO [24] | 2.00 × 101 | 8.96 × 10−2 | 2.00 × 101 | 2.04 × 101 | |
| IAVOA | 6.88 × 10−16 | 0.00 | 8.88 × 10−16 | 8.88 × 10−16 | |
| AVOA [21] | 0.00 | 0.00 | 0.00 | 0.000 | |
| GWO [25] | 4.71 × 10−3 | 1.11 × 10−2 | 0.00 | 5.15 × 10−2 | |
| PSO [24] | 2.14 × 10−2 | 1.83 × 10−2 | 4.62 × 10−13 | 6.14 × 10−2 | |
| IAVOA | 0.00 | 0.00 | 0.00 | 0.00 | |
| AVOA [21] | 1.15 × 10−5 | 9.55 × 10−6 | 5.60 × 10−7 | 3.67 × 10−5 | |
| GWO [25] | 1.70 × 101 | 4.90 × 10−1 | 1.61 × 101 | 1.80 × 101 | |
| PSO [24] | 3.63 × 103 | 1.63 × 104 | 3.61 × 100 | 9.00 × 104 | |
| IAVOA | 2.10 × 10−5 | 1.76 × 10−5 | 1.63 × 10−6 | 6.08 × 10−5 | |
| AVOA [21] | 3.04 × 102 | 4.81 × 102 | 2.54 × 10−4 | 1.81 × 103 | |
| GWO [25] | 4.05 × 103 | 5.65 × 102 | 3.28 × 103 | 5.53 × 103 | |
| PSO [24] | 2.14 × 103 | 4.96 × 102 | 8.30 × 102 | 3.01 × 103 | |
| IAVOA | 1.02 × 102 | 2.84 × 102 | 2.54 × 10−4 | 1.42 × 103 |
| Step | Steps of the IAVOA-SVR Algorithm |
|---|---|
| Step1 | Carry out the kernel principal component analysis and phase-space reconstruction processing on the wind-tunnel test data |
| Step2 | Construct the SVR temperature prediction model and take the parameters of SVR to be optimized as the input of IAVOA |
| Step3 | Initialize parameters such as the population size and the number of iterations of IAVOA |
| Step4 | Establish the optimization objective function and take the SVR temperature-training model error as the IAVOA fitness function |
| Step5 | Update the SVR parameters as the number of iterations increases |
| Step6 | Update the record of the optimal-fitness function and the optimal-parameter combination |
| Step7 | Determine whether the end condition (maximum number of iterations) is met. If it is not completed, return to the fifth step |
| Step8 | Output the optimal fitness result and the optimal parameter combination |
| Data 1 | SVR [27] | AVOA-SVR [28] | PSO-SVR [29] | GWO-SVR [30] | IAVOA-SVR |
|---|---|---|---|---|---|
| 3.4530 | 0.7040 | 1.8180 | 1.4427 | 0.5305 | |
| 4.40 × 10−3 | 7.99 × 10−4 | 0.0016 | 0.0017 | 5.91 × 10−4 | |
| 0.3716 | 0.0758 | 0.1956 | 0.1553 | 0.0571 | |
| 3.4027 | 0.6139 | 1.259 | 1.3386 | 0.4542 | |
| 0.8618 | 0.9747 | 0.9512 | 0.9757 | 0.9956 |
| Data 2 | SVR [27] | AVOA-SVR [28] | PSO-SVR [29] | GWO-SVR [30] | IAVOA-SVR |
|---|---|---|---|---|---|
| 4.2189 | 0.8093 | 2.3603 | 0.6417 | 0.5061 | |
| 0.0053 | 8.63 × 10−4 | 0.0030 | 6.15 × 10−4 | 4.53 × 10−4 | |
| 0.3522 | 0.0676 | 0.1970 | 0.0536 | 0.0422 | |
| 4.1594 | 0.6793 | 2.3247 | 0.4835 | 0.3575 | |
| 0.8759 | 0.9877 | 0.9781 | 0.9800 | 0.9983 |
| Data 1 | Group 1 | Group 2 | Group 3 | Group 4 |
|---|---|---|---|---|
| 1.2778 | 0.3222 | 0.2706 | 0.9739 | |
| 1.30 × 10−3 | 3.25 × 10−4 | 2.77 × 10−4 | 9.74 × 10−4 | |
| 0.0587 | 0.2624 | 0.3092 | 0.1018 | |
| 1.0557 | 0.2527 | 2.16 × 10−1 | 0.7425 |
| Data 2 | Group 1 | Group 2 | Group 3 | Group 4 |
|---|---|---|---|---|
| 0.3764 | 0.1676 | 0.5475 | 0.1535 | |
| 3.02 × 10−4 | 1.76 × 10−4 | 6.07 × 10−4 | 1.55 × 10−4 | |
| 0.0344 | 0.0662 | 0.0543 | 0.0519 | |
| 0.2437 | 1.41 × 10−1 | 0.4811 | 0.1200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, L.; Cui, X.; Wang, B.; Li, Q.; Guo, J. Improved African Vulture Optimization Algorithm for Optimizing Nonlinear Regression in Wind-Tunnel-Test Temperature Prediction. Processes 2025, 13, 1956. https://doi.org/10.3390/pr13071956
Shen L, Cui X, Wang B, Li Q, Guo J. Improved African Vulture Optimization Algorithm for Optimizing Nonlinear Regression in Wind-Tunnel-Test Temperature Prediction. Processes. 2025; 13(7):1956. https://doi.org/10.3390/pr13071956
Chicago/Turabian StyleShen, Lihua, Xu Cui, Biling Wang, Qiang Li, and Jin Guo. 2025. "Improved African Vulture Optimization Algorithm for Optimizing Nonlinear Regression in Wind-Tunnel-Test Temperature Prediction" Processes 13, no. 7: 1956. https://doi.org/10.3390/pr13071956
APA StyleShen, L., Cui, X., Wang, B., Li, Q., & Guo, J. (2025). Improved African Vulture Optimization Algorithm for Optimizing Nonlinear Regression in Wind-Tunnel-Test Temperature Prediction. Processes, 13(7), 1956. https://doi.org/10.3390/pr13071956






