Enhancing Electrokinetic Remediation of Cu- and Pb-Contaminated Loess Using Irregular Electrode Configurations: A Numerical Investigation of Transport and Remediation Mechanisms
Abstract
1. Introduction
2. Overview of Experimental Research
2.1. Experimental Materials
2.2. Experimental Reactor
2.3. Experimental Procedure
3. Modelling Approach
3.1. Governing Equations
Transport Phenomena
3.2. Chemical Reactions
3.3. Model Implementation
3.4. Model Validation
3.5. Irregular Electrode Configurations
4. Results and Discussion
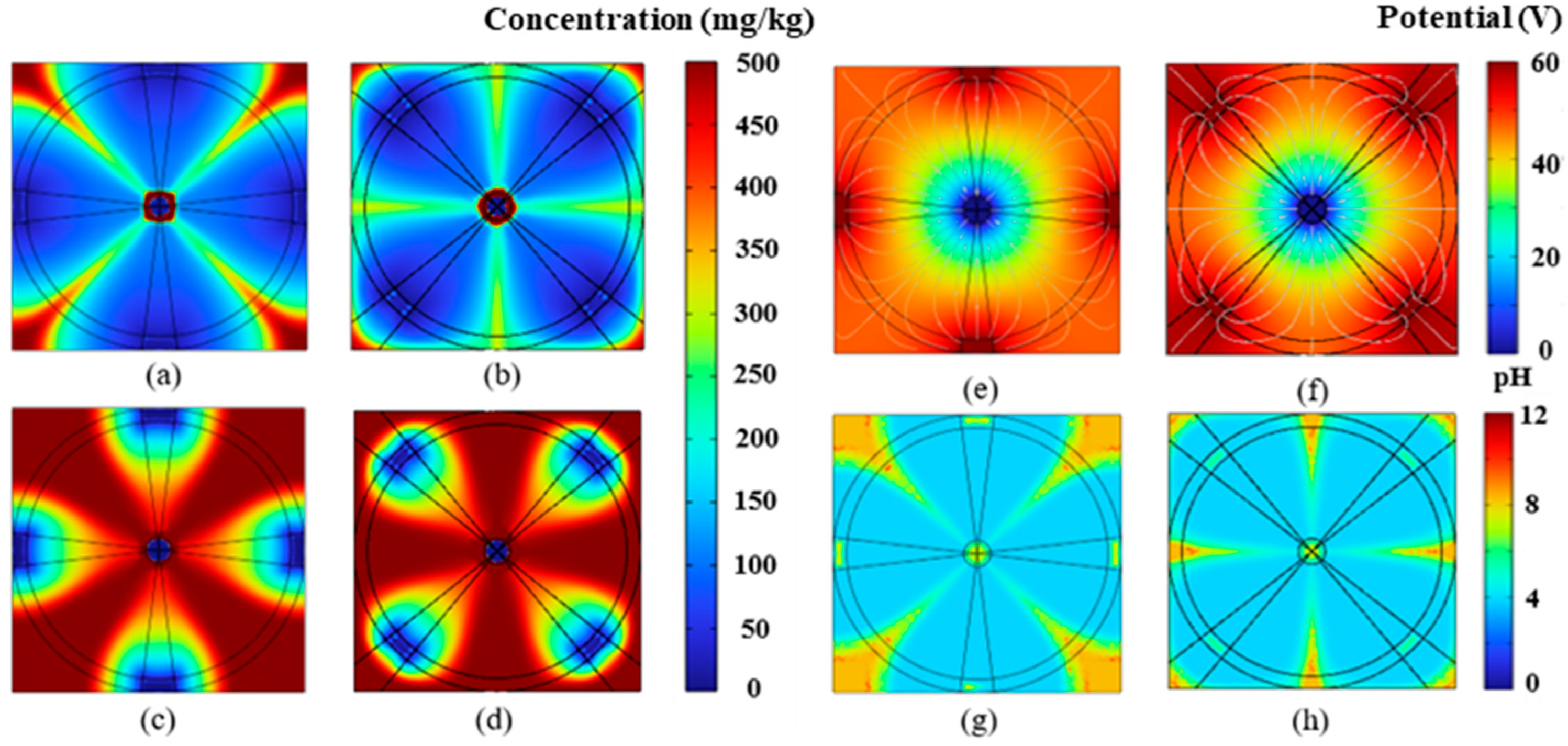
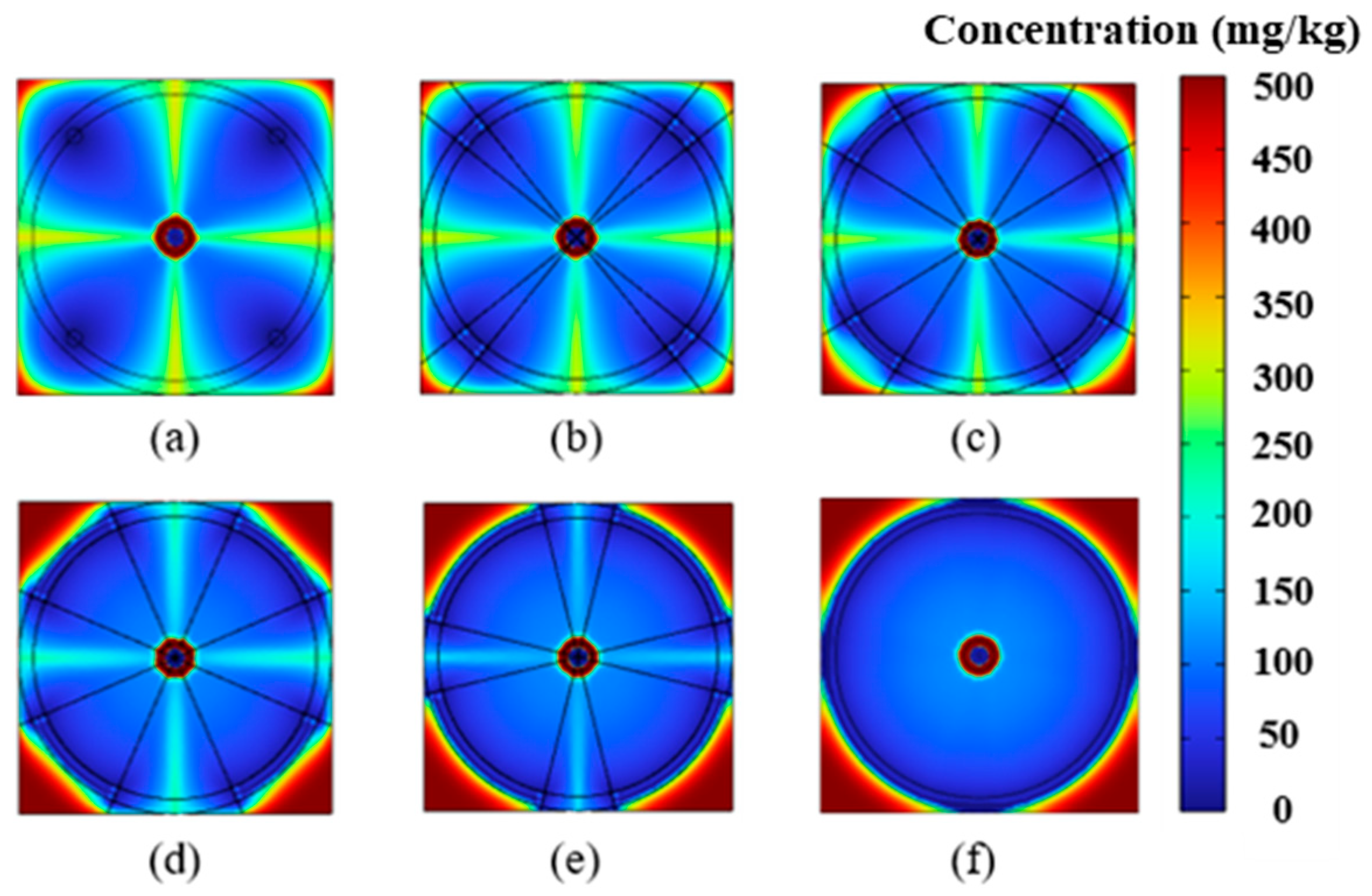
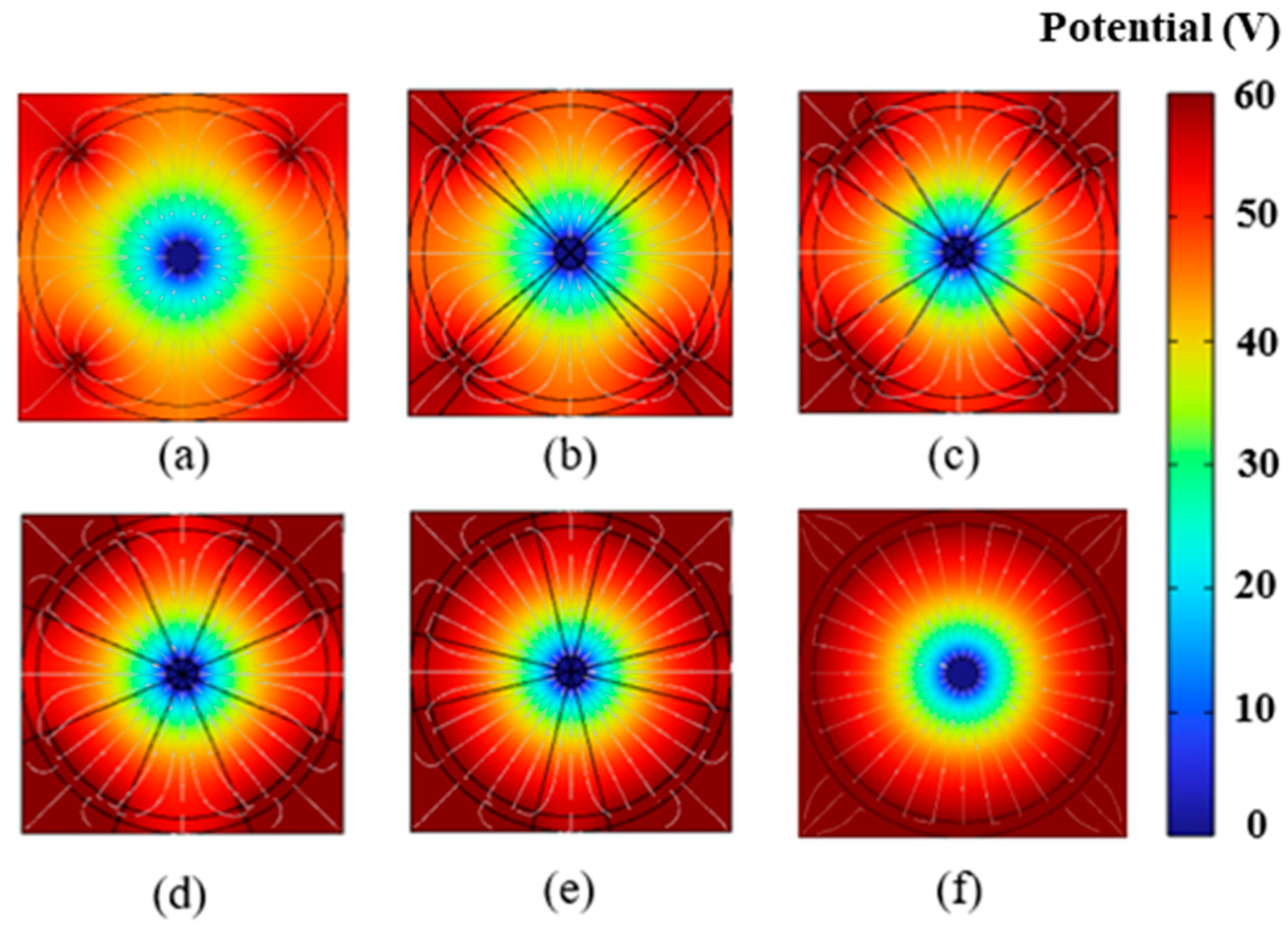
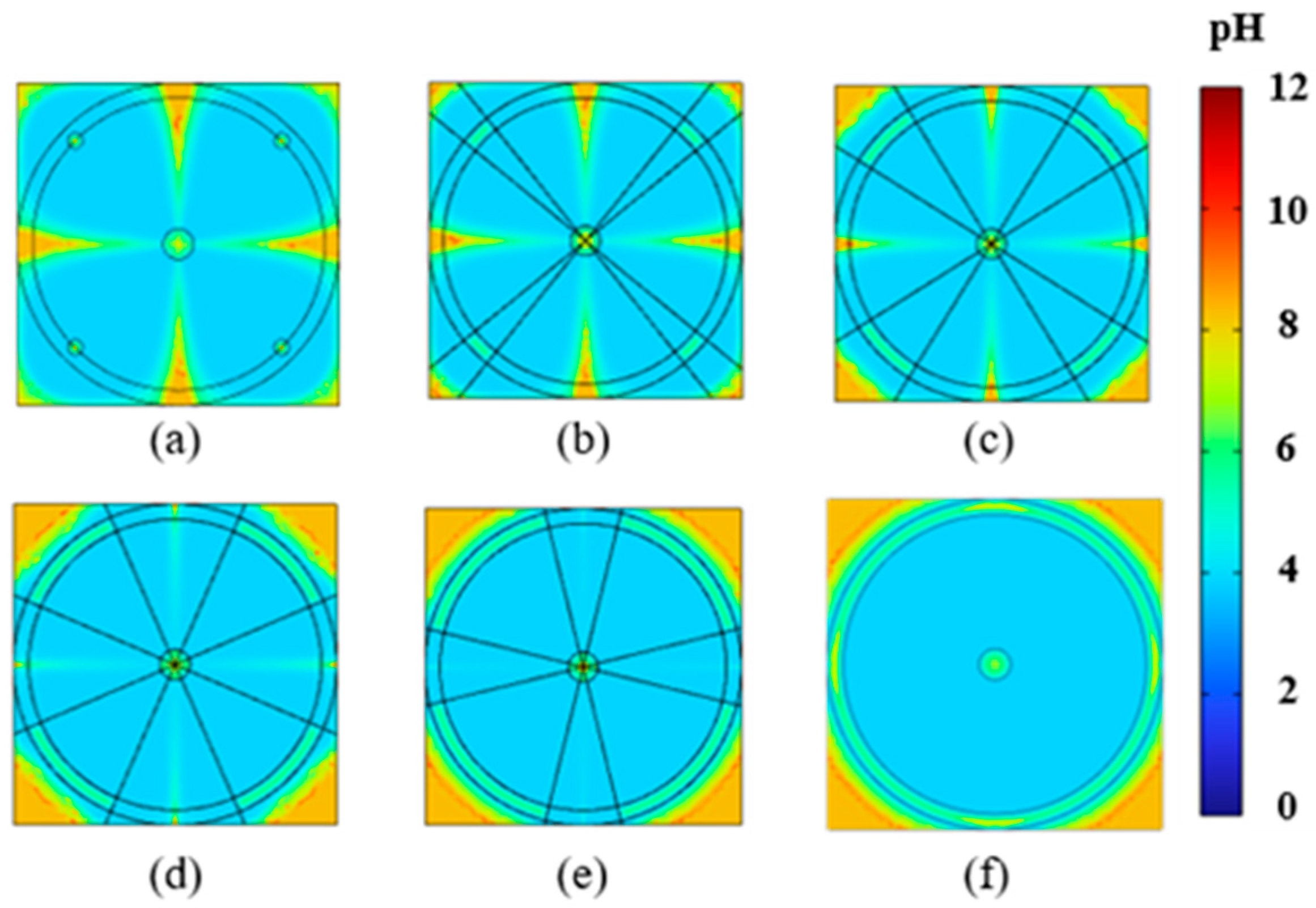
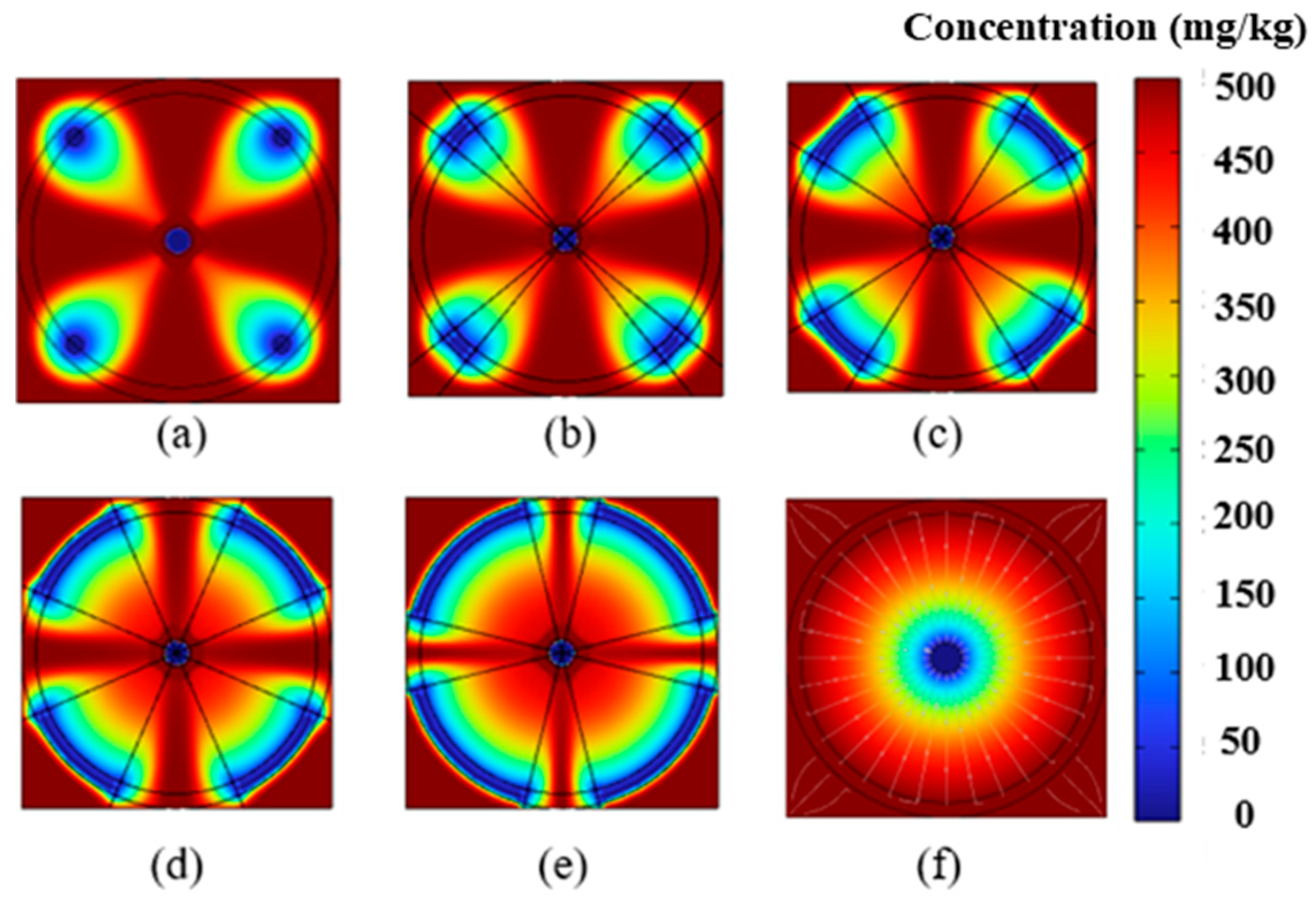
4.1. Impact of Electrode Placement on EK Remediation
4.2. Impact of Electrode Size on EK Remediation
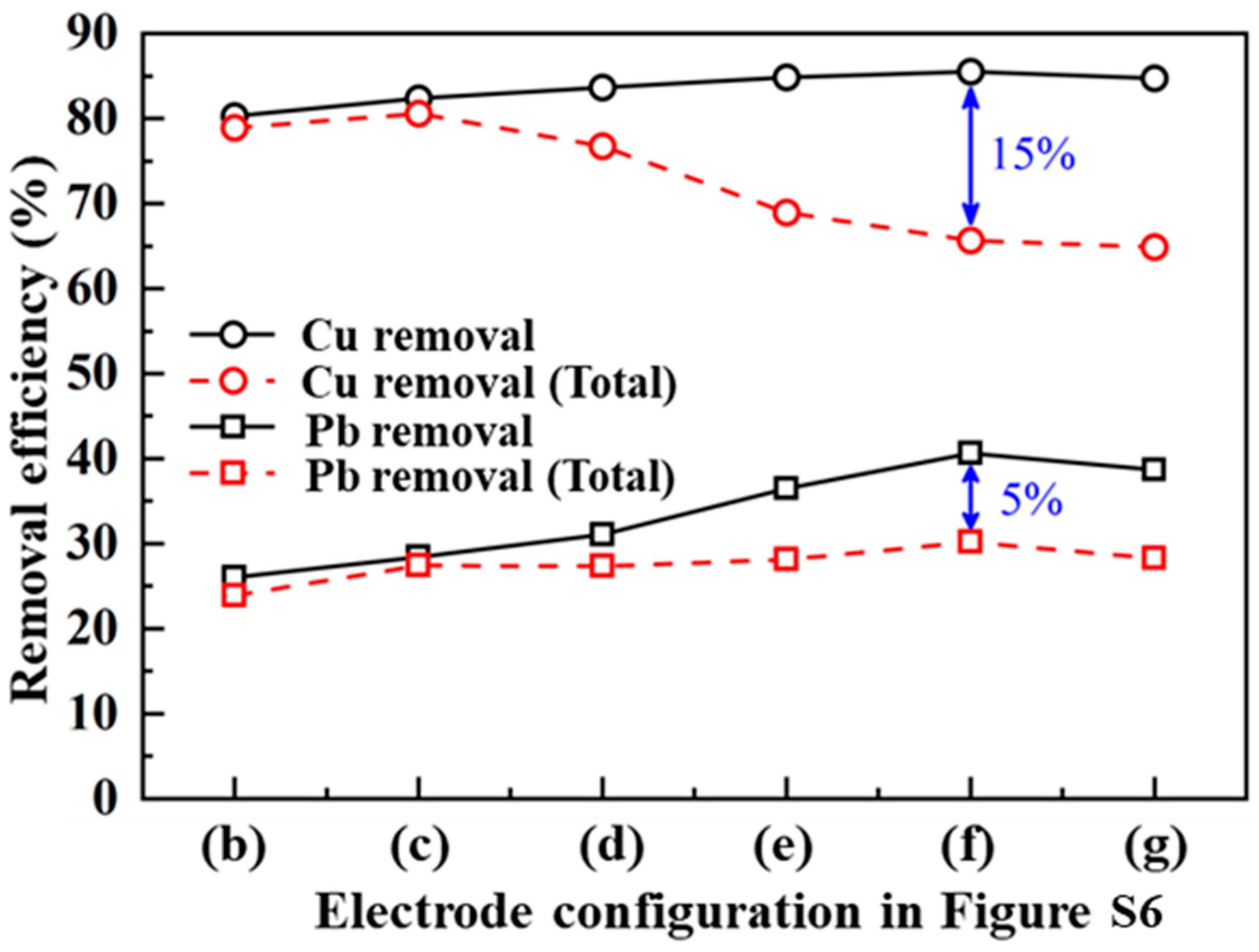
4.3. Removal Efficiency Analysis
4.4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alshawabkeh, A.N.; Acar, Y.B. Removal of contaminants from soils by electrokinetics: A theoretical treatise. J. Environ. Sci. Health Part A Environ. Sci. Eng. Toxicol. 1992, 27, 1835–1861. [Google Scholar] [CrossRef]
- Bala, R.P.; Srivastava, R.K.; Mohan, D. Electrokinetic removal of mixed heavy metals from a contaminated low permeable soil by surfactant and chelants. Environ. Earth Sci. 2015, 73, 1191–1204. [Google Scholar]
- Hu, W.L.; Cheng, W.C.; Wen, S.J. Investigating the effect of degree of compaction, initial water content, and electric field intensity on electrokinetic remediation of an artificially Cu- and Pb-contaminated loess. Acta Geotech. 2023, 18, 937–949. [Google Scholar] [CrossRef]
- Hu, W.L.; Cheng, W.C.; Wang, Y.H.; Wen, S.J.; Xue, Z.F. Applying a nanocomposite hydrogel electrode to migrate electrochemical polarization and focusing effect in electrokinetic remediation of a Cu- and Pb-contaminated loess. Environ. Pollut. 2023, 333, 122039. [Google Scholar] [CrossRef]
- Li, H.; Tian, Y.; Liu, W.; Long, Y.; Ye, J.; Li, B.; Li, N.; Yan, M.; Zhu, C. Impact of electrokinetic remediation of heavy metal contamination on antibiotic resistance in soil. Chem. Eng. J. 2020, 400, 125866. [Google Scholar] [CrossRef]
- Ren, Y.; Li, F.C.; Zhai, L.W.; Dong, D.X.; Han, R.F.; Qi, X.Y.; Zhang, X.; Li, L.; Jiang, W.Q.; Chen, X. Tween 80 assisted washing ciprofloxacin-contaminated soil, and recycled it using active chlorines. Environ. Pollut. 2023, 330, 121735. [Google Scholar] [CrossRef]
- Sharma, J.K.; Kumar, N.; Singh, N.P.; Santal, A.R. Phytoremediation technologies and their mechanism for removal of heavy metal from contaminated soil: An approach for a sustainable environment. Front. Plant Sci. 2023, 14, 1076876. [Google Scholar] [CrossRef]
- Sarker, A.; Al, M.M.A.; Deepo, D.M.; Das, K.; Nandi, R.; Ansary, M.W.R.; Islam, A.M.T.; Islam, T. Biological and green remediation of heavy metal contaminated water and soils: A state-of-the-art review. Chemosphere 2023, 332, 138861. [Google Scholar] [CrossRef]
- Liu, X.; Lan, C.R.; Yang, Z.H.; Zhuang, X.J.; Feng, H.P.; Wang, H.B.; Chen, W.; Wu, Y.F.; Tang, J. Enhanced electrokinetic remediation of cadmium contaminated soil by calcium phosphate-modified zeolite as permeable reactive barriers. Electrochim. Acta 2025, 524, 146057. [Google Scholar] [CrossRef]
- Hu, W.L.; Cheng, W.C.; Wen, S.J.; Kang, N.B. Revealing underlying mechanisms affecting electrokinetic remediation of an artificially Cu- and Pb-contaminated loess using the external regulatory system with adsorbent. Front. Mater. 2022, 9, 967871. [Google Scholar] [CrossRef]
- Hu, W.L.; Cheng, W.C.; Wang, Y.H.; Wen, S.J. Feasibility study of applying a graphene oxide-alginate composite hydrogel to electrokinetic remediation of Cu(Ⅱ)-contaminated loess as electrodes. Sep. Purif. Technol. 2023, 322, 124361. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zhao, M.M.; Chen, L.; Gong, Z.Y.; Hu, J.J.; Ma, D.G. Electrokinetic remediation for the removal of heavy metals in soil: Limitations, solutions and prospection. Sci. Total Environ. 2023, 903, 165970. [Google Scholar] [CrossRef] [PubMed]
- Song, P.P.; Xu, D.; Yue, J.Y.; Ma, Y.C.; Dong, S.J.; Feng, J. Recent advances in soil remediation technology for heavy metal contaminated sites: A critical review. Sci. Total Environ. 2022, 838, 156417. [Google Scholar] [CrossRef]
- Wang, Y.C.; Li, A.; Cui, C.W. Remediation of heavy metal-contaminated soils by electrokinetic technology: Mechanisms and applicability. Chemosphere 2021, 265, 129071. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.C.; Han, Z.J.; Li, A.; Cui, C.W. Enhanced electrokinetic remediation of heavy metals contaminated soil by biodegradable complexing agents. Environ. Pollut. 2021, 283, 117111. [Google Scholar] [CrossRef]
- Kim, G.H. Modeling study on the electrokinetic extraction of contaminants from soils. J. Korean Soc. Civ. Eng. 1998, 18, 503. [Google Scholar]
- Wang, L.; Cheng, W.C.; Xue, Z.F.; Xie, Y.X.; Lv, X.J. Feasibility study of applying electrokinetic technology coupled with enzyme-induced carbonate precipitation treatment to Cu- and Pb-contaminated loess remediation. J. Clean. Prod. 2023, 401, 136734. [Google Scholar] [CrossRef]
- Purkis, J.M.; Warwick, P.E.; Graham, J.; Hemming, S.D.; Cundy, A.B. Towards the application of electrokinetic remediation for nuclear site decommissioning. J. Hazard. Mater. 2021, 413, 125274. [Google Scholar] [CrossRef]
- Wen, D.D.; Fu, R.B.; Li, Q. Removal of inorganic contaminants in soil by electrokinetic remediation technologies: A review. J. Hazard. Mater. 2021, 401, 123345. [Google Scholar] [CrossRef]
- Gallo, A.; Sprocati, R.; Islam, K.T.; Rolle, M. Combined effects of porosity, tortuosity and pore water composition on electrokinetic transport dynamics in porous media. Electrochim. Acta 2025, 524, 145969. [Google Scholar] [CrossRef]
- Ferrucci, A.; Vocciante, M.; Bagatin, R.; Ferro, S. Electrokinetic remediation of soils contaminated with potentially toxic metals: Dedicated analytical tools for assessing the contamination baseline in a complex scenario. J. Environ. Manag. 2017, 203, 1163–1168. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Li, X.Z.; Ding, W.; Shuai, K.W.; Zhen, Q.; She, D. Enhanced removal of cadmium from aqueous environments and soil during electrokinetic remediation using Si-Mg modified sawdust-based biochar as an adsorbent and permeable reactive barrier material. Chem. Eng. J. 2025, 508, 161178. [Google Scholar] [CrossRef]
- Peng, C.S.; Almeira, J.O.; Gu, Q.B. Effect of electrode configuration on pH distribution and heavy metal ions migration during soil electrokinetic remediation. Environ. Earth Sci. 2013, 69, 257–265. [Google Scholar] [CrossRef]
- Segall, B.A.; Bruell, C.J. Electroosmotic contaminant-removal processes. J. Environ. Eng. 1992, 118, 84–100. [Google Scholar] [CrossRef]
- Penn, M.L.M. Electrokinetic Soil Remediation: Effects of pH, Temperature and Chemical Reactions; University of Cambridge: Cambridge, UK, 1997. [Google Scholar]
- Kim, S.O.; Jeong, J.Y.; Lee, W.C.; Yun, S.T.; Jo, H.Y. Electrokinetic remediation of heavy metal-contaminated soils: Performance comparison between one- and two-dimensional electrode configurations. J. Soils Sediments 2021, 21, 2755–2769. [Google Scholar] [CrossRef]
- Yan, I.D. HCET: A Finite Element Model for Solute Transport Driven by Hydraulic, Chemical, Electrical, and Thermal Gradients; Colorado State University: Fort Collins, CO, USA, 2000. [Google Scholar]
- Mattson, B.; Robert, S. Electrokinetic ion transport through unsaturated soil: 2. Application to a heterogeneous field site. J. Contam. Hydrol. 2002, 54, 99–120. [Google Scholar] [CrossRef]
- Xie, N.; Chen, Z.; Wang, H.M.; You, C.F. Activated carbon coupled with citric acid in enhancing the remediation of Pb-Contaminated soil by electrokinetic method. J. Clean. Prod. 2021, 308, 127433. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Ministry of Water Resources of the People’s Republic of China, 2019. Standard for Geotechnical Test Methods. China Planning Press: Beijing, China, 2019.
- ASTM. Standard Classification of Soils for Engineering Purposes (Unified Soil Classification System); ASTM: West Conshohocken, PA, USA, 2006. [Google Scholar]
- Tessier, A.P.; Campbell, P.G.C.; Bisson, M.X. Sequential extraction procedure for the speciation of particulate trace metals. Anal. Chem. 1979, 51, 844–851. [Google Scholar] [CrossRef]
- Masi, M.; Ceccarini, A.; Iannelli, R. Multispecies reactive transport modelling of electrokinetic remediation of harbour sediments. J. Hazard. Mater. 2017, 326, 187–196. [Google Scholar] [CrossRef]
- Masi, M.; Manuel, P.G.J.; Cesar, G.L.; Maria, V.G.; Alessio, C.; Renato, I. Modeling of electrokinetic remediation combining local chemical equilibrium and chemical reaction kinetics. J. Hazard. Mater. 2019, 371, 728–733. [Google Scholar] [CrossRef]
- Milad, R.; Gholamreza, A.; Cesar, G.L.; Maria, V.G.; Manuel, P.G.J. Modeling of electrokinetic remediation of Cd- and Pb-contaminated kaolinite. J. Hazard. Mater. 2019, 366, 630–635. [Google Scholar]
- Carlos, V.A.; Jose, M.R.M.; Rafael, A.G.D.; Cesar, G.L.; Franciso, G.H. Two-dimensional model for soil electrokinetic remediation of heavy metals: Application to a copper spiked kaolin. Chemosphere 2004, 54, 895–903. [Google Scholar]
- Yeung, A.T.; Menon, R.M. Electrokinetic remediation. II: Theoretical model. J. Geotech. Geoenviron. Eng. 1997, 123, 1078. [Google Scholar] [CrossRef]
- Muazu, N.D.; Essa, M.H. Comparative performance evaluation of anodic materials for electro-kinetic removal of Lead (II) from contaminated clay soil. Soil Sediment Contam. 2020, 29, 69–95. [Google Scholar] [CrossRef]
- Torabi, M.S.; Asadollahfardi, G.; Rezaee, M.; Panah, N.B. Electrokinetic Removal of Cd and Cu from Mine Tailing: EDTA Enhancement and Voltage Intensity Effects. J. Hazard. Toxic Radioact. Waste 2021, 25, 05020007. [Google Scholar] [CrossRef]
- Xie, N.; Wang, H.M.; You, C.F. On the electrokinetic remediation of Pb-contaminated soil: A coupled electro-transport-reaction modelling study based on chemical reaction kinetics. Chemosphere 2024, 355, 141661. [Google Scholar] [CrossRef]
- Zulfiqar, W.; Iabal, M.A.; Butt, M.K. Pb2+ ions mobility perturbation by iron particles during electrokinetic remediation of contaminated soil. Chemosphere 2017, 169, 257–261. [Google Scholar] [CrossRef]
| Parameter | Code | Value | Description | Data Source |
|---|---|---|---|---|
| Loess | n | 0.499 | Porosity | Experimental measurement |
| Rhob | 1350 kg/m3 | Dry density | Experimental measurement | |
| pH | 8.3 | Initial pH value | Experimental measurement | |
| KLcu | 11.52 m3/mol | Langmuir constant | [11] | |
| CPcu | 1.7 mol/kg | Langmuir constant | [11] | |
| KLPb | 12.43 m3/mol | Langmuir constant | [11] | |
| CPPb | 1.23 mol/kg | Langmuir constant | [11] | |
| Zeta | −10.8 mV | Zeta potential | [3] | |
| τ | 1.28 | Tortuosity | [1] | |
| R | 4.57 µm | Average pore diameter | [1] | |
| GOCH electrodes | n2 | 0.312 | Porosity | Experimental measurement |
| σ | 49.92 mS/cm | Conductivity | Experimental measurement | |
| Ecd | 0.53–5.3 A/m2 | Exchange current density | ||
| E1 | 1.229 V | Oxidation potential | ||
| E2 | 0.828 V | Reduction potential | ||
| KL2cu | 0.608 m3/mol | Langmuir constant | [11] | |
| CP2cu | 7.06 mol/kg | Langmuir constant | [11] | |
| KL2Pb | 2.49 m3/mol | Langmuir constant | [11] | |
| CP2Pb | 2.22 mol/kg | Langmuir constant | [11] | |
| Mass transfer | Ccu | 500 mg/kg | Copper Concentration | |
| Cpb | 500 mg/kg | Lead Concentration | ||
| Dcu | 7.14 × 10−10 | Diffusion coefficient of Cu2+ | ||
| Dpb | 2.50 × 10−10 | Diffusion coefficient of Pb+ | ||
| DH | 9.31 × 10−10 | Diffusion coefficient of H+ | ||
| DOH | 5.27 × 10−10 | Diffusion coefficient of OH− | ||
| Pore fluid and electrolyte | µ | 10−1 Pa·s | Dynamic viscosity | |
| σ | 0.3 S/m | Conductivity | ||
| eps | 78.3 F | Dielectric constant |
| Contaminant | Initial Concentration (mg/Kg) | Treatment Time (h) | Electric Field Intensity (V/cm) | Soil Type | Average Remediation Efficiency | References |
|---|---|---|---|---|---|---|
| Cu and Pb | 500 (Cu) and 500 (Pb) | 48 | 1.0 | Loess | 0–19% (Cu) and 0–8% (Pb) | Hu et al. [3] |
| Cu and Pb | 500 (Cu) and 500 (Pb) | 72 | 1.5 | Loess | 24.92% (Cu) and 3.45% (Pb) | Hu et al. [10] |
| Pb | 103.5 | 120 | 1.0 | Loam | 18.49% | Zulfiqar et al. [41] |
| Pb | 120 ± 5.5 | 168 | 1.08 | Clay | 14.15% | Muazu et al. [38] |
| Cu and Zn | 250–1000 (Cu), 1000–3000 (Zn) | 24, 48, and 120 | 0.4–0.8 | / | 8–18.6% (Cu) 4.3–6.8% (Zn) | Li et al. [5] |
| Pb | 833 | 480 | 1.35 | Clay | 4.1% | Xie et al. [29] |
| Cu and Pb | 500 (Cu) and 500 (Pb) | 72 | 1.5 | Loess | 42.87% (Cu) and 5.19% (Pb) | Hu et al. [10] |
| Cu and Cd | 248.4 (Cu) and 82 (Pb) | 240 | 1.0 | Mine tailing | 4.59% (Cu) and 30.65% (Cd) | Torabi et al. [39] |
| Cu and Pb | 500 (Cu) and 500 (Pb) | 72 | 1.5 | Loess | 47.25% (Cu) and 16.93% (Pb) | Hu et al. [11] |
| Cu and Pb | 500 (Cu) and 500 (Pb) | 72 | 1.5 | Loess | 80% (Cu) and 40% (Pb) | Present study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Hu, W. Enhancing Electrokinetic Remediation of Cu- and Pb-Contaminated Loess Using Irregular Electrode Configurations: A Numerical Investigation of Transport and Remediation Mechanisms. Processes 2025, 13, 1948. https://doi.org/10.3390/pr13071948
Wang X, Hu W. Enhancing Electrokinetic Remediation of Cu- and Pb-Contaminated Loess Using Irregular Electrode Configurations: A Numerical Investigation of Transport and Remediation Mechanisms. Processes. 2025; 13(7):1948. https://doi.org/10.3390/pr13071948
Chicago/Turabian StyleWang, Xinwen, and Wenle Hu. 2025. "Enhancing Electrokinetic Remediation of Cu- and Pb-Contaminated Loess Using Irregular Electrode Configurations: A Numerical Investigation of Transport and Remediation Mechanisms" Processes 13, no. 7: 1948. https://doi.org/10.3390/pr13071948
APA StyleWang, X., & Hu, W. (2025). Enhancing Electrokinetic Remediation of Cu- and Pb-Contaminated Loess Using Irregular Electrode Configurations: A Numerical Investigation of Transport and Remediation Mechanisms. Processes, 13(7), 1948. https://doi.org/10.3390/pr13071948







