Simulation of Absorption and Flash Evaporation for Natural Gas Desulfurization
Abstract
1. Introduction
2. Model Development
2.1. Thermodynamics and Chemical Equilibrium
2.1.1. Thermodynamic Properties
2.1.2. Chemical Equilibrium Process
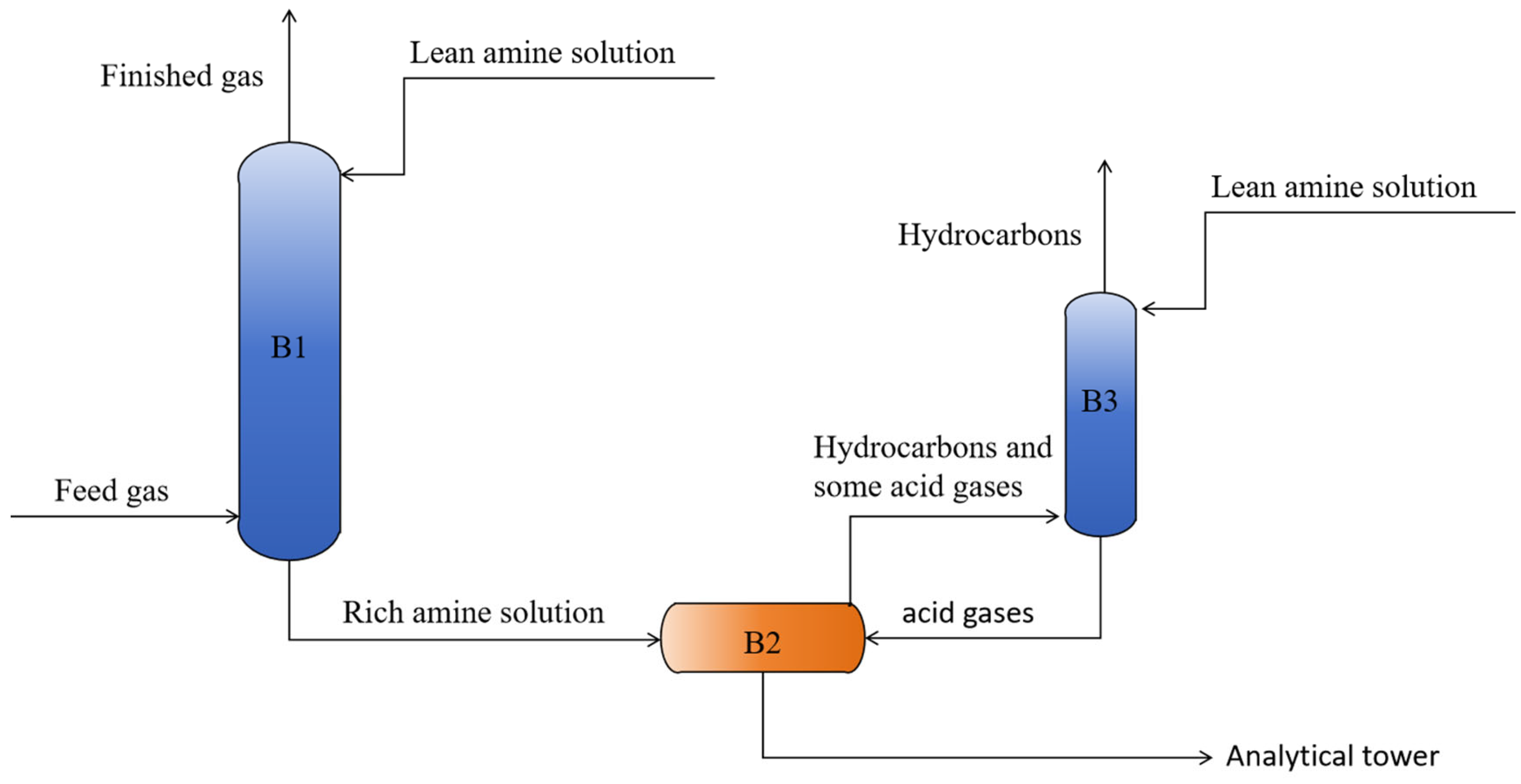
2.2. Process Modeling
- (i)
- Both physical absorption and chemical absorption are considered, with reactions occurring only in the liquid phase.
- (ii)
- The absorption column operates adiabatically.
- (iii)
- Heat transfer resistance in the liquid phase is neglected, the interfacial temperature is equal to the bulk fluid temperature, and no temperature gradient exists.
- (iv)
- Axial flow is treated as one-dimensional, with radial temperature and concentration variations neglected.
- (v)
- Countercurrent flow is assumed, and both vapor and liquid phases are perfectly mixed.
2.2.1. Material and Energy Balances
- ①
- Material Balance Equations (M-equations)
- ②
- Energy Balance Equations (H-equations)
- ③
- Summation Equations (S-equations)
- ④
- Phase Equilibrium Relations (K-equations)
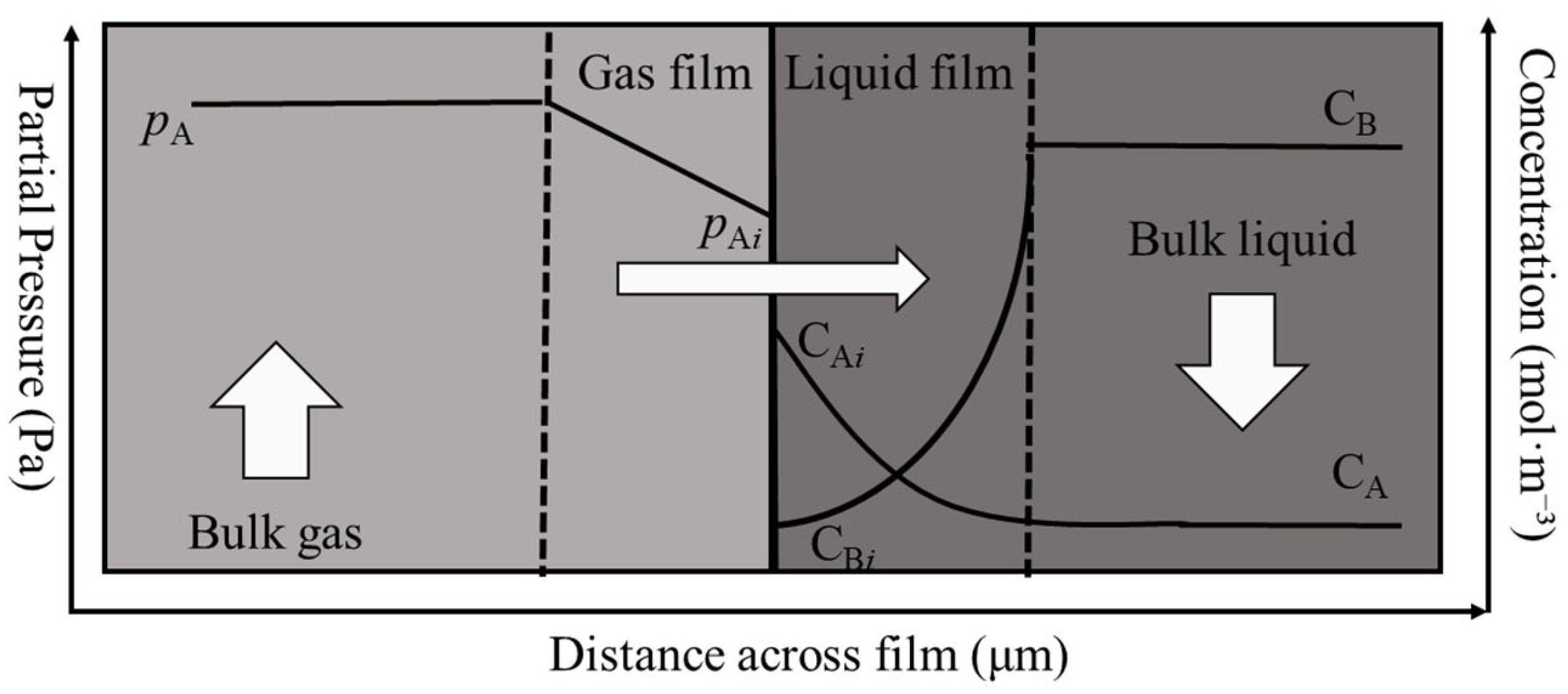
2.2.2. Mass Transfer and Enhancement Factor
2.3. Solution Procedure
- (i)
- With the feed gas and lean-liquid compositions of the absorbed species and the gas-to-liquid (G/L) ratio given, postulate component-wise overall removal fractions to initialize the calculation and thereby estimate the liquid compositions on the bottom (last) tray.
- (ii)
- Starting from the bottom tray, perform stage calculations upward: for each tray, use the inlet vapor and liquid compositions to compute phase transfer/equilibrium and obtain the outlet compositions, which then serve as the inlet to the tray above.
- (iii)
- Continue tray by tray to the column top to obtain the overhead gas compositions, from which the actual overall removal of each species across the column is determined.
- (iv)
- Compare the computed overall removals with the initial assumptions. If the maximum deviation exceeds 1.0 × 10−4, update the assumptions and iterate until the convergence criterion is satisfied.
3. Modeling Results
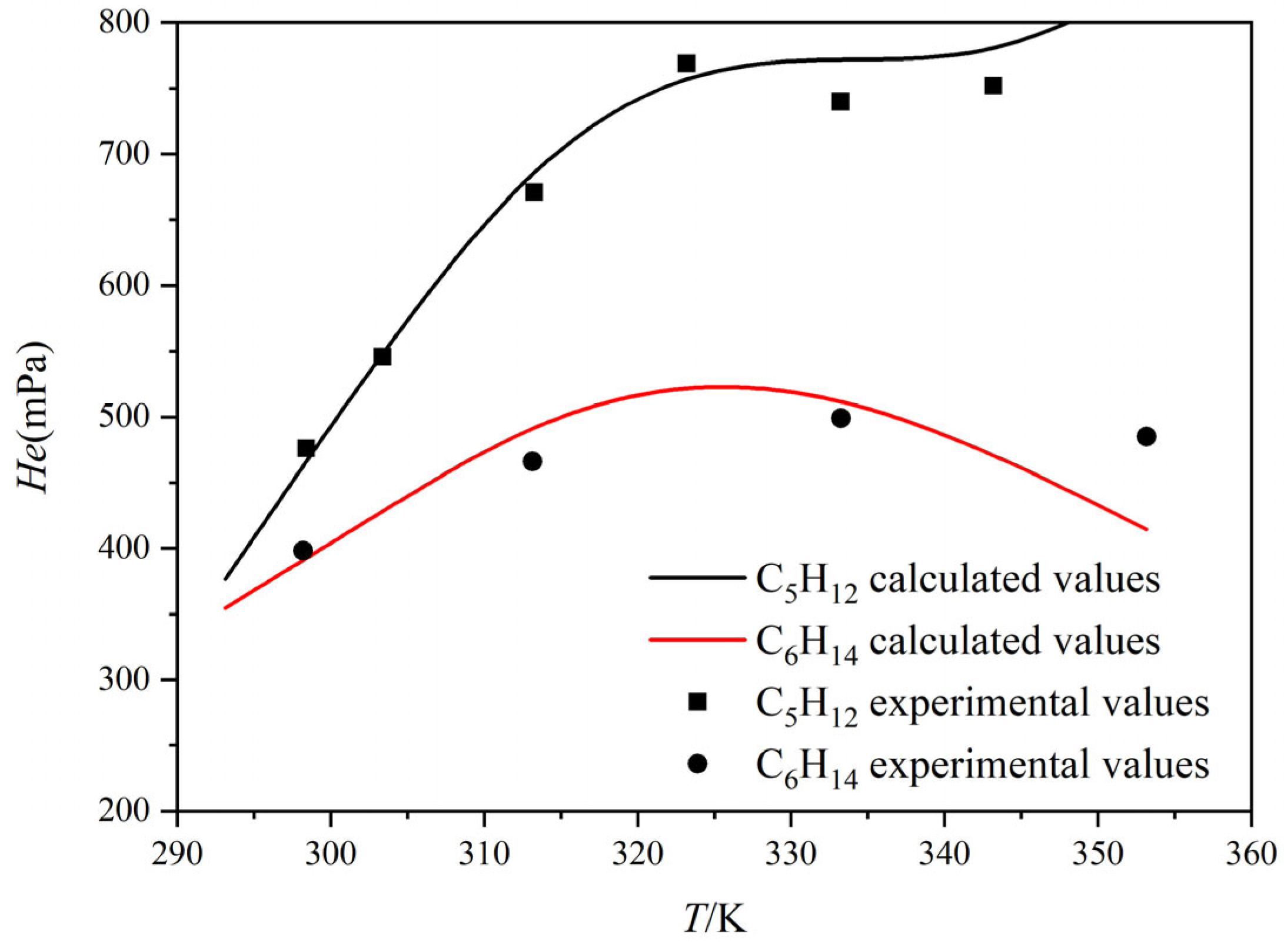
3.1. Verification of Henry’s Constants for C5H12 and C6H14
3.2. Model Validation
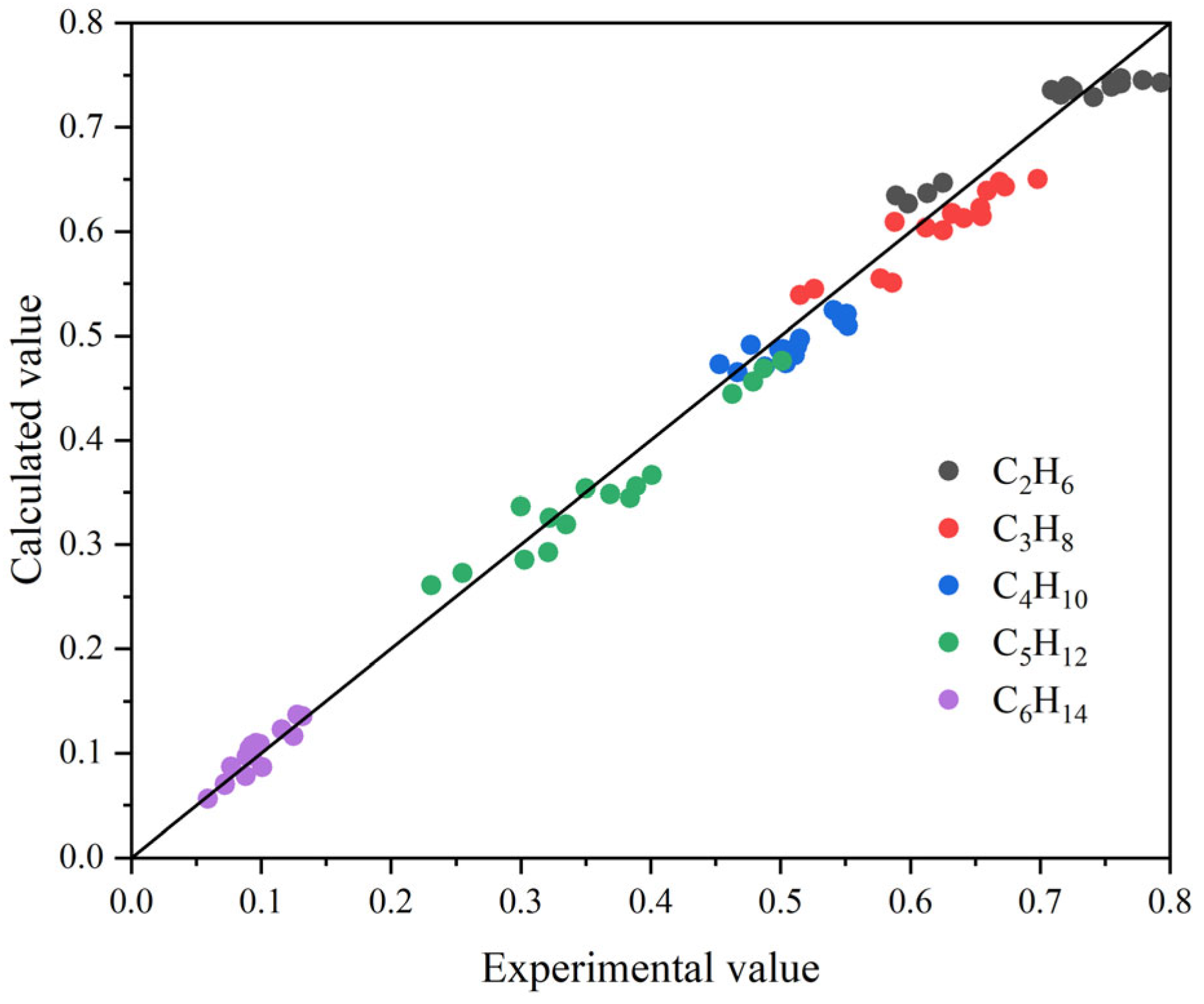
3.2.1. Absorption Model
3.2.2. Flash Model
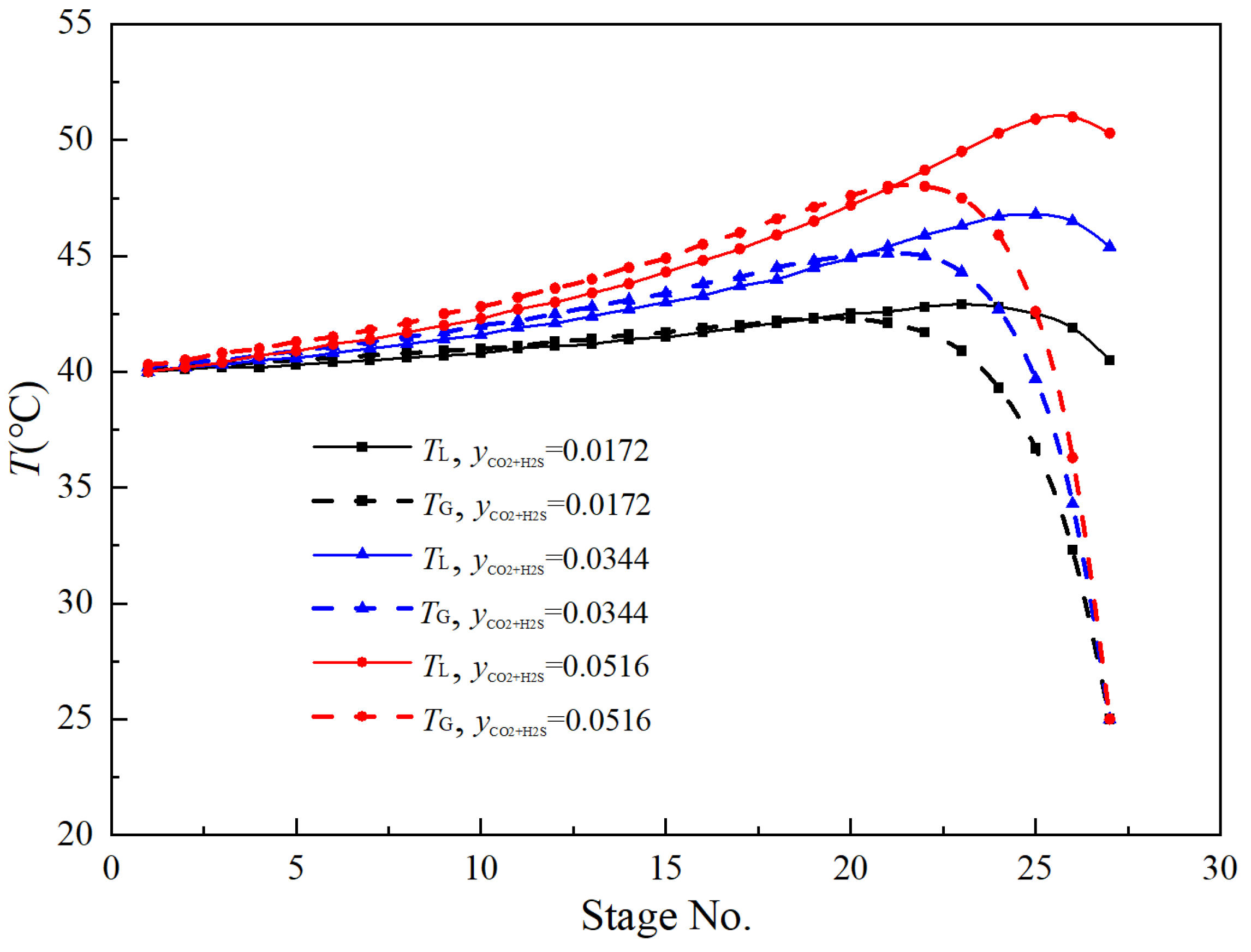
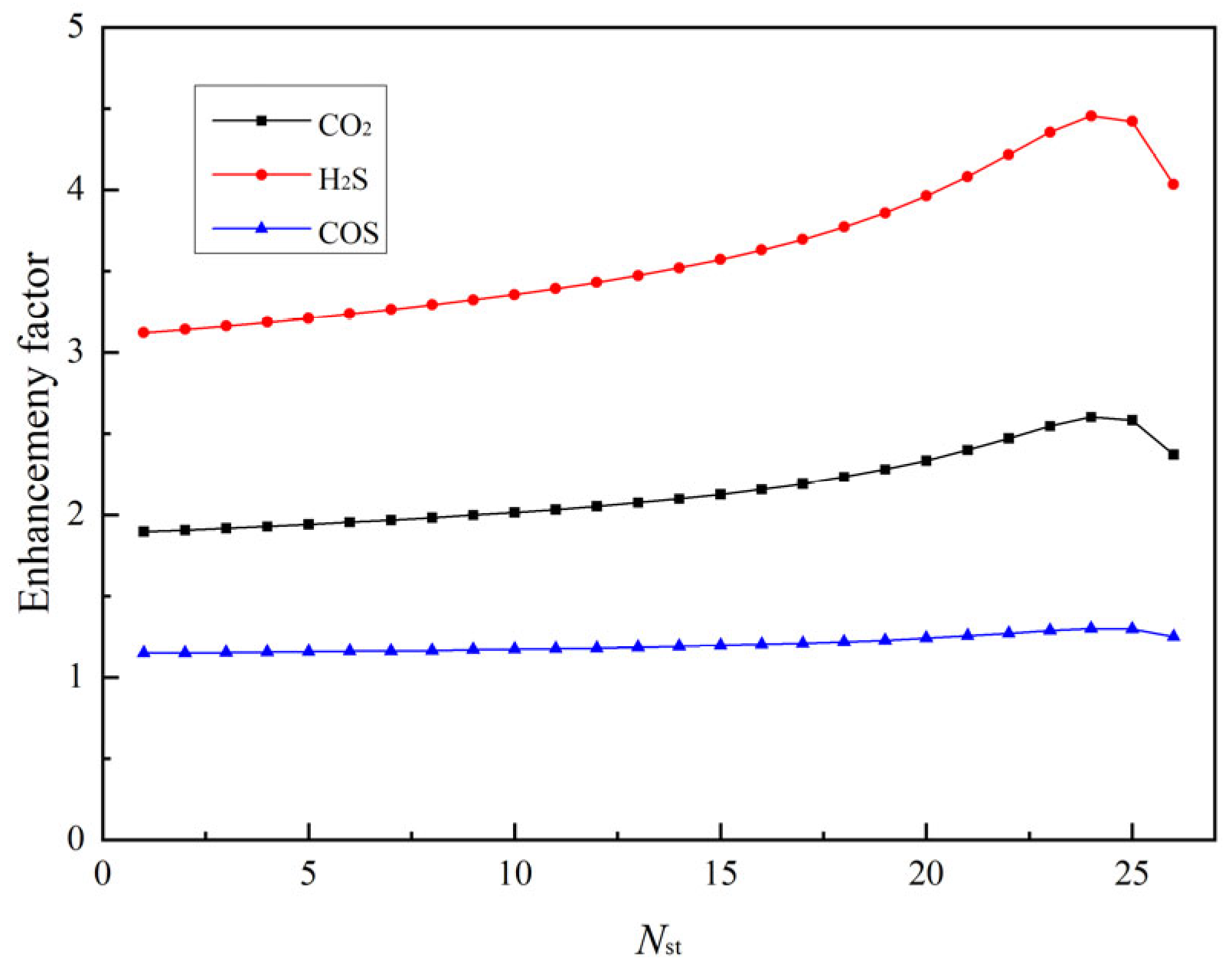
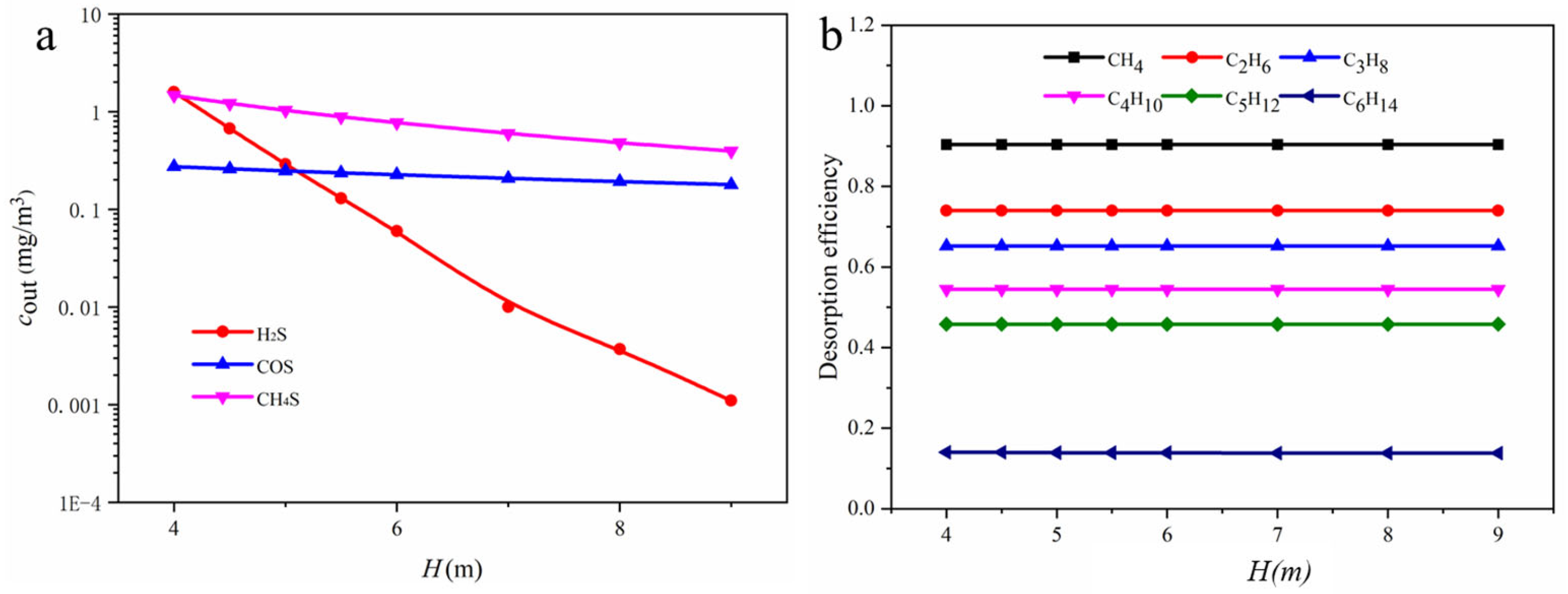
3.3. Rate-Based Absorption Model Calculations
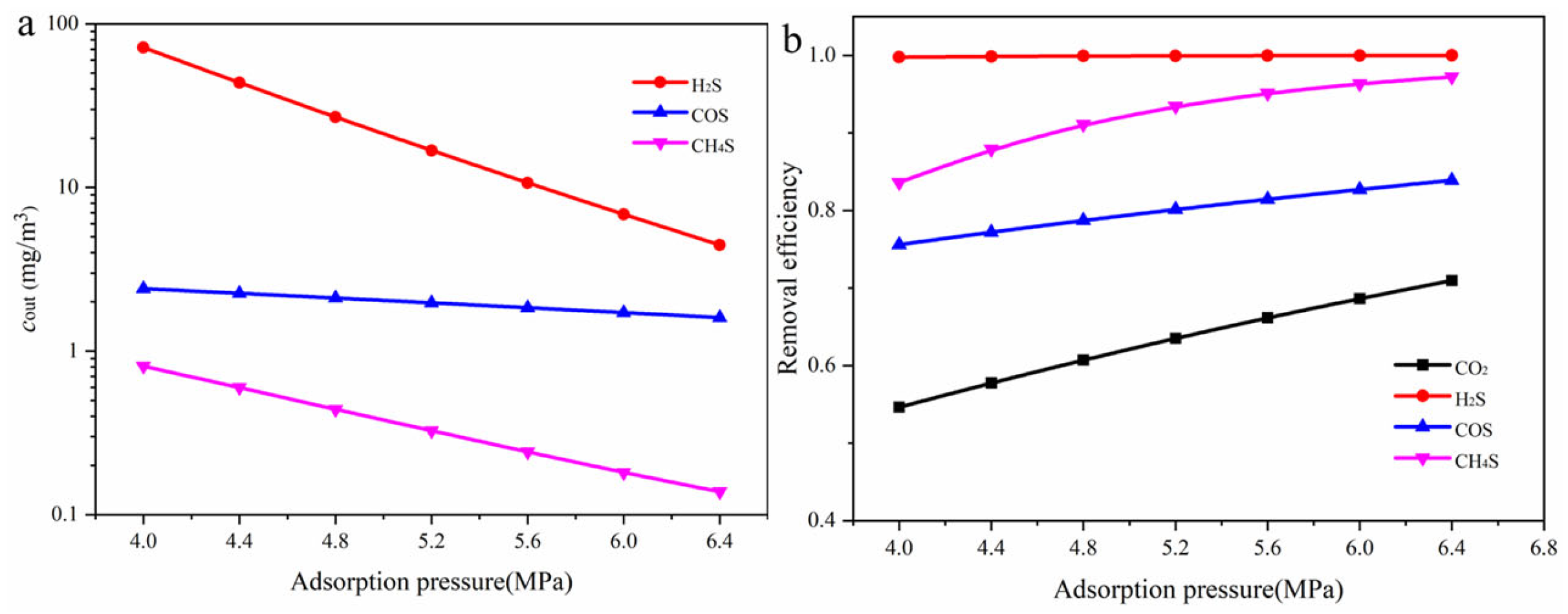
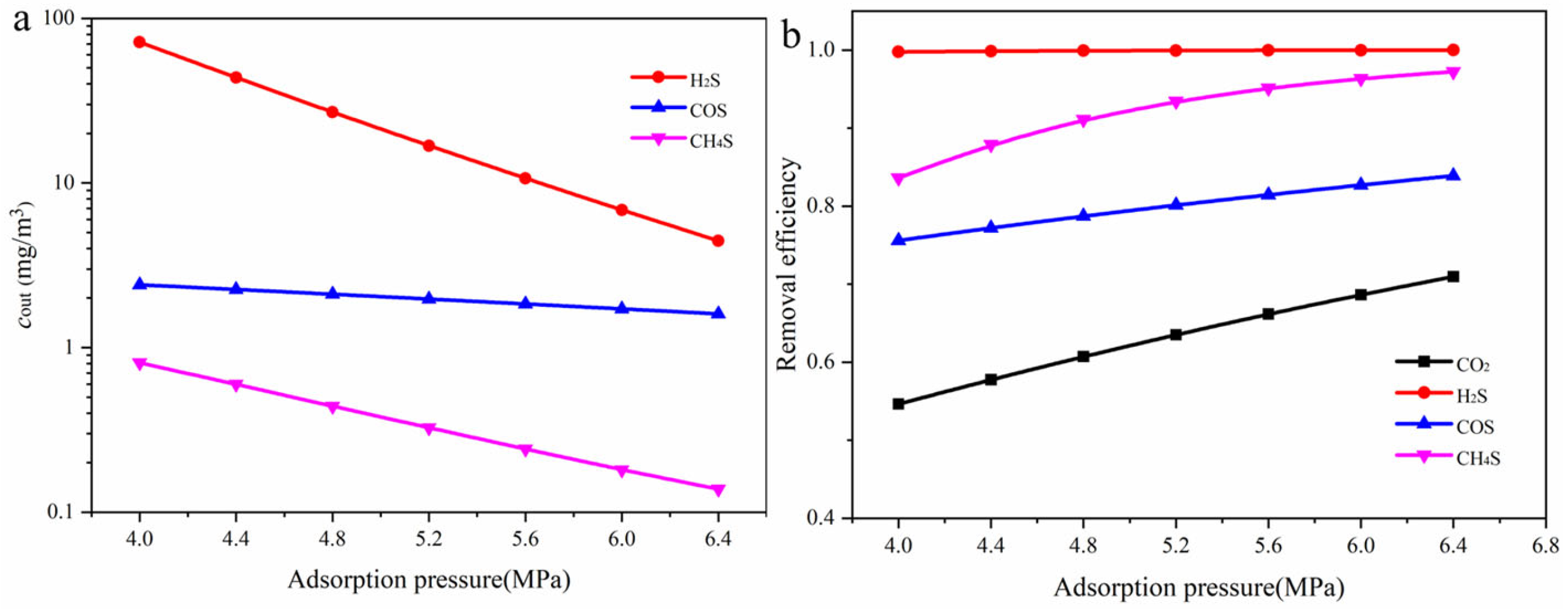
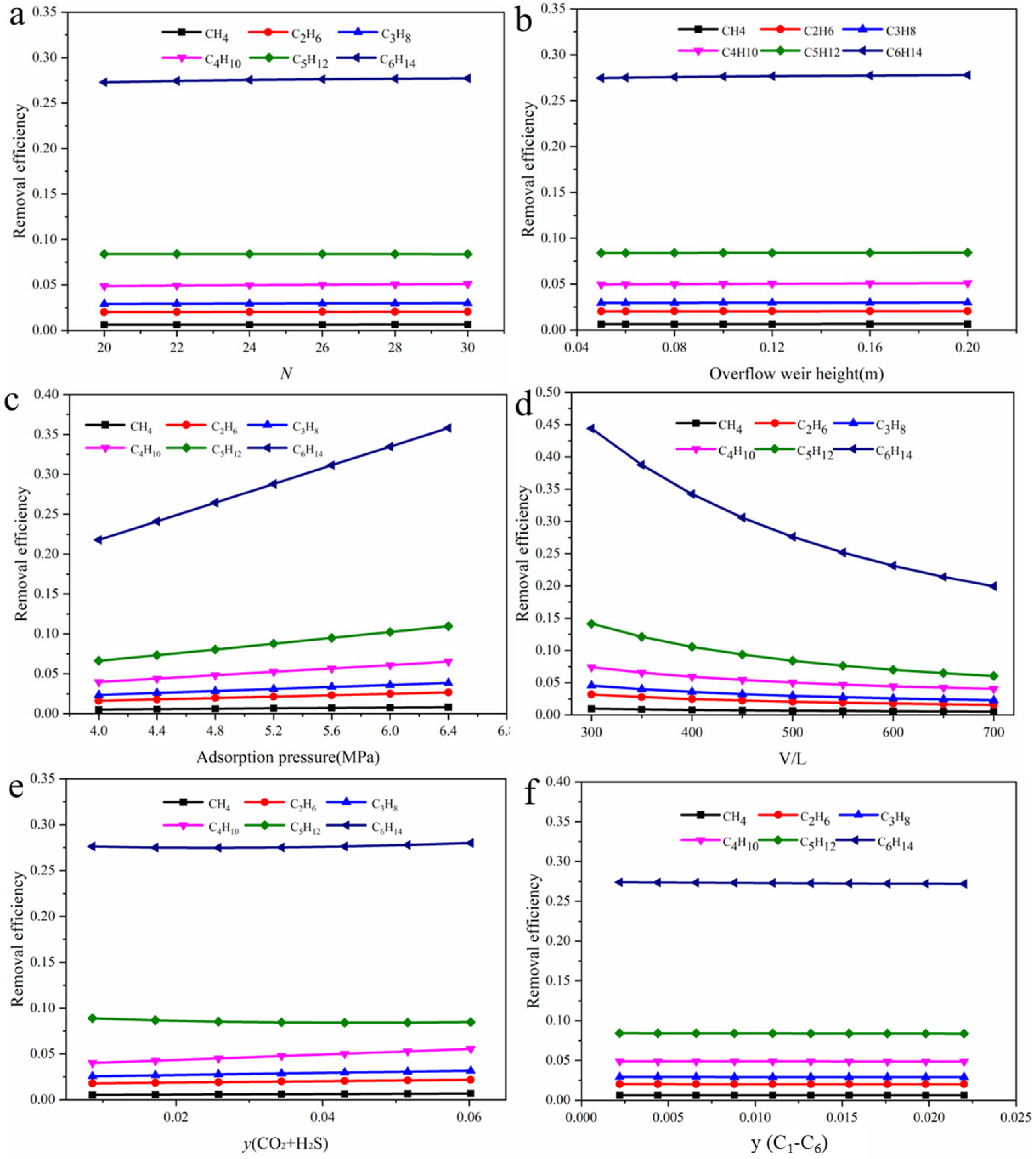
3.4. Influence of Operating Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NG | Natural gas | |
| MDEA | Methyldiethanolamine | |
| TMS | Tetramethylene sulfone | |
| G/L | Gas–liquid ratio | |
| MEA | Monoethanolamine | |
| DEA | Diethanolamine | |
| ILs | Ionic liquids | |
| DES | Deep eutectic solvents | |
| RMSE | Root mean square error | |
| MAE | Mean absolute error | |
| R2 | Coefficient of determination | |
| Symbol | Definition | Unit |
| Hi | Henry’s constant of component i | Pa |
| KG,i | Overall gas-phase mass transfer coefficient of component i | mol·m−2·s−1·Pa−1 |
| KL,i | Overall liquid-phase mass transfer coefficient of component i | mol·m−2·s−1 |
| Ei | Enhancement factor | |
| Ha | Hatta number | |
| γi | Activity coefficient of component i | |
| ϕi | Fugacity coefficient of component i | |
| ai | Activity of component i | |
| xi | Mole fraction of component i in liquid phase | |
| yi | Mole fraction of component i in vapor phase | |
| f | Unreacted MDEA ratio | |
| R | Universal gas constant | J·mol−1·K−1 |
| ΔH | Heat of absorption/desorption | kJ·mol−1 |
References
- Mubashir, M.; Ashena, R.; Bokhari, A.; Mukhtar, A.; Saqib, S.; Ali, A.; Saidur, R.; Khoo, K.S.; Ng, H.S.; Karimi, F.; et al. Effect of process parameters over carbon-based ZIF-62 nano-rooted membrane for environmental pollutants separation. Chemosphere 2022, 291, 133006. [Google Scholar] [CrossRef] [PubMed]
- Tawfik, A.; Nasr, M.; Galal, A.; El-Qelish, M.; Yu, Z.; Hassan, M.A.; Salah, H.A.; Hasanin, M.S.; Meng, F.; Bokhari, A.; et al. Fermentation-based nanoparticle systems for sustainable conversion of black-liquor into biohydrogen. J. Clean. Prod. 2021, 309, 127349. [Google Scholar] [CrossRef]
- Wainaina, S.; Awasthi, M.K.; Horváth, I.S.; Taherzadeh, M.J. Anaerobic digestion of food waste to volatile fatty acids and hydrogen at high organic loading rates in immersed membrane bioreactors. Renew. Energy 2020, 152, 1140–1148. [Google Scholar] [CrossRef]
- Asif, S.; Ahmad, M.; Bokhari, A.; Chuah, L.F.; Klemeš, J.J.; Akbar, M.M.; Sultana, S.; Yusup, S. Methyl ester synthesis of Pistacia khinjuk seed oil by ultrasonic-assisted cavitation system. Ind. Crops Prod. 2017, 108, 336–347. [Google Scholar] [CrossRef]
- Shirazizadeh, H.A.; Haghtalab, A. Simultaneous solubility measurement of (ethyl mercaptan + carbon dioxide) into the aqueous solutions of (N-methyl diethanolamine + sulfolane + water). J. Chem. Thermodyn. 2019, 133, 111–122. [Google Scholar] [CrossRef]
- Amararene, F.; Bouallou, C. Kinetics of Carbonyl Sulfide (COS) Absorption with Aqueous Solutions of Diethanolamine and Methyldiethanolamine. Ind. Eng. Chem. Res. 2004, 43, 6136–6141. [Google Scholar] [CrossRef]
- Huttenhuis, P.J.G.; Agrawal, N.J.; Versteeg, G.F. Solubility of Carbon Dioxide and Hydrogen Sulfide in Aqueous N-Methyldiethanolamine Solutions. Ind. Eng. Chem. Res. 2009, 48, 4051–4059. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.-W.; Otto, F.D.; Mather, A.E. The physicochemical properties of the mixed solvent of 2-piperidineethanol, sulfolane and water. J. Chem. Technol. Biotechnol. 1993, 56, 309–316. [Google Scholar] [CrossRef]
- Olajire, A.A. CO2 capture and separation technologies for end-of-pipe applications—A review. Energy 2010, 35, 2610–2628. [Google Scholar] [CrossRef]
- Tagliabue, M.; Farrusseng, D.; Valencia, S.; Aguado, S.; Ravon, U.; Rizzo, C.; Corma, A.; Mirodatos, C. Natural gas treating by selective adsorption: Material science and chemical engineering interplay. Chem. Eng. J. 2009, 155, 553–566. [Google Scholar] [CrossRef]
- Sifat, N.S.; Haseli, Y. A Critical Review of CO2 Capture Technologies and Prospects for Clean Power Generation. Energies 2019, 12, 4143. [Google Scholar] [CrossRef]
- Salvinder, K.M.S.; Zabiri, H.; Isa, F.; Taqvi, S.A.; Roslan, M.A.H.; Shariff, A.M. Dynamic modelling, simulation and basic control of CO2 absorption based on high pressure pilot plant for natural gas treatment. Int. J. Greenh. Gas Control 2018, 70, 164–177. [Google Scholar] [CrossRef]
- Asif, K.; Lock, S.S.M.; Taqvi, S.A.A.; Jusoh, N.; Yiin, C.L.; Chin, B.L.F.; Loy, A.C.M. A Molecular Simulation Study of Silica/Polysulfone Mixed Matrix Membrane for Mixed Gas Separation. Polymers 2021, 13, 2199. [Google Scholar] [CrossRef] [PubMed]
- Kazmi, B.; Haider, J.; Ammar Taqvi, S.A.; Qyyum, M.A.; Ali, S.I.; Hussain Awan, Z.U.; Lim, H.; Naqvi, M.; Naqvi, S.R. Thermodynamic and economic assessment of cyano functionalized anion based ionic liquid for CO2 removal from natural gas integrated with, single mixed refrigerant liquefaction process for clean energy. Energy 2022, 239, 122425. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.-C. Thermodynamic Modeling for CO2 Absorption in Aqueous MDEA Solution with Electrolyte NRTL Model. Ind. Eng. Chem. Res. 2011, 50, 163–175. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.-C. Modeling Gas Solubilities in the Aqueous Solution of Methyldiethanolamine. Ind. Eng. Chem. Res. 2011, 50, 6436–6446. [Google Scholar] [CrossRef]
- Austgen, D.M.; Rochelle, G.T.; Peng, X.; Chen, C.C. Model of vapor-liquid equilibria for aqueous acid gas-alkanolamine systems using the electrolyte-NRTL equation. Ind. Eng. Chem. Res. 1989, 28, 1060–1073. [Google Scholar] [CrossRef]
- Xuezhong, H.; Izumi, K.; Magne, H. Conceptual Process Design and Simulation of Membrane Systems for Integrated Natural Gas Dehydration and Sweetening. Sep. Purif. Technol. 2020, 247, 116993. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Amooghin, A.E.; Montazer-Rahmati, M.M.; Ismail, A.F.; Matsuura, T. State-of-the-art membrane based CO2 separation using mixed matrix membranes (MMMs): An overview on current status and future directions. Prog. Polym. Sci. 2014, 39, 817–861. [Google Scholar] [CrossRef]
- Han, Y.; Rezakazemi, M.; Zhang, W.; Liu, X.; Chen, C. Membranes for acid gas enrichment: A techno-economic study. J. Membr. Sci. 2025, 714, 122035. [Google Scholar] [CrossRef]
- Farooqi, A.S.; Ramli, R.M.; Lock, S.S.M.; Farooqi, A.S.; Shahid, M.Z.; Hasnain, S.M.W.U.; Hira, N.; Abdullah, B. Removal of carbon dioxide and hydrogen sulfide from natural gas using a hybrid solvent of monoethanolamine and N-methyl 2-pyrrolidone. ACS Omega 2024, 9, 25704–25714. [Google Scholar] [CrossRef]
- Ellaf, A.; Taqvi, S.A.A.; Zaeem, D.; Siddiqui, F.U.H.; Kazmi, B.; Idris, A.; Alshgari, R.A.; Mushab, M.S.S. Energy, exergy, economic, environment, exergo-environment based assessment of amine-based hybrid solvents for natural gas sweetening. Chemosphere 2023, 313, 137426. [Google Scholar] [CrossRef]
- Lei, Y.; Du, L.; Liu, X.; Yu, H.; Liang, X.; Kontogeorgis, G.M.; Chen, Y. Natural gas sweetening using tailored ionic liquid–methanol mixed solvent with selective removal of H2S and CO2. Chem. Eng. J. 2023, 464, 142514. [Google Scholar] [CrossRef]
- Shi, M.; Li, G.; Wu, H.; Ning, H.; Chen, X.; Wang, Y.; Zhang, Y.; Zhao, J.; Dai, S. Efficient hydrogen sulfide separation from carbon dioxide achieved by carbonyl-functionalized ionic liquids for natural gas upgrading. Angew. Chem. Int. Ed. 2025, 64, e202503498. [Google Scholar] [CrossRef] [PubMed]
- Kazmi, B.; Haider, J.; Taqvi, S.A.A.; Ali, S.I.; Qyyum, M.A.; Nagulapati, V.M.; Lim, H. Tetracyanoborate anion–based ionic liquid for natural gas sweetening and DMR-LNG process: Energy, exergy, environment, exergo-environment, and economic perspectives. Sep. Purif. Technol. 2022, 303, 122242. [Google Scholar] [CrossRef]
- Kumar, S.; Cho, J.H.; Moon, I. Ionic liquid-amine blends and CO2BOLs: Prospective solvents for natural gas sweetening and CO2 capture technology—A review. Int. J. Greenh. Gas Control 2014, 20, 87–116. [Google Scholar] [CrossRef]
- Blauwhoff, P.M.M.; Versteeg, G.F.; Van Swaaij, W.P.M. A study on the reaction between CO2 and alkanolamines in aqueous solutions. Chem. Eng. Sci. 1984, 39, 207–225. [Google Scholar] [CrossRef]
- Versteeg, G.F.; van Swaaij, W.P.M. On the kinetics between CO2 and alkanol amines both in aqueous and non-aqueous solutions—II. Tertiary amines. Chem. Eng. Sci. 1988, 43, 587–591. [Google Scholar] [CrossRef]
- Mokraoui, S.; Coquelet, C.; Valtz, A.; Hegel, P.E.; Richon, D. New Solubility Data of Hydrocarbons in Water and Modeling Concerning Vapor-Liquid-Liquid Binary Systems. Ind. Eng. Chem. Res. 2007, 46, 9257–9262. [Google Scholar] [CrossRef]
- Mokraoui, S.; Hadj-Kali, M.K.; Valtz, A.; Richon, D. New Vapor−Liquid−Liquid Equilibrium Solubility Data for iso-Butane, n-Butane, n-Pentane, and n-Hexane in Alkanolamine Aqueous Solutions. J. Chem. Eng. Data 2014, 59, 1673–1684. [Google Scholar] [CrossRef]
- Jou, F.-Y.; Deshmukh, R.D.; Otto, F.D.; Mather, A.E. Solubility of H2S, CO2, CH4 and C2H6 in Sulfolane at Elevated Pressures. Fluid Phase Equilibria 1990, 56, 313–324. [Google Scholar] [CrossRef]
- Xue, J.; Yang, C.; Fu, J.; He, J.; Li, J. Research and Performance Evaluation on Selective Absorption of H2S from Gas Mixtures by Using Secondary Alkanolamines. Processes 2022, 10, 1795. [Google Scholar] [CrossRef]
- Austgen, D.M.; Rochelle, G.T.; Chen, C.C. Model of vapor-liquid equilibria for aqueous acid gas-alkanolamine systems. 2. Representation of hydrogen sulfide and carbon dioxide solubility in aqueous MDEA and carbon dioxide solubility in aqueous mixtures of MDEA with MEA or DEA. Ind. Eng. Chem. Res. 1991, 30, 542–555. [Google Scholar] [CrossRef]
- Pacheco, M.A.; Rochelle, G.T. Rate-based modeling of reactive absorption of CO2 and H2S into aqueous methyldiethanolamine. Ind. Eng. Chem. Res. 1998, 37, 4107–4117. [Google Scholar] [CrossRef]
- Al-Ghawas, H.A.; Ruiz-Ibanez, G.; Sandall, O.C. Absorption of carbonyl sulfide in aqueous methyldiethanolamine. Chem. Eng. Sci. 1989, 44, 631–639. [Google Scholar] [CrossRef]
- Carroll, J.J.; Maddocks, J.; Mather, A.E. The Solubility of Hydrocarbons in Amine Solutions. In Laurance Reid Gas Conditioning Conference Proceedings; University of Oklahoma: Norman, OK, USA, 1998. [Google Scholar]
- Huttenhuis, P.J.G.; Agrawal, N.J.; Hogendoorn, J.A.; Versteeg, G.F. Gas Solubility of H2S and CO2 in Aqueous Solutions of N-Methyldiethanolamine. J. Pet. Sci. Eng. 2007, 55, 122–134. [Google Scholar] [CrossRef]
- Jou, F.Y.; Carroll, J.J.; Mather, A.E.; Otto, F.D. Phase Equilibria in the System Water–Methyldiethanolamine–Propane. AIChE J. 1992, 38, 511–520. [Google Scholar] [CrossRef]







| System | ln (H/pa) = a + b/T + c × ln(T) | Source | |||
|---|---|---|---|---|---|
| a | b | c | |||
| H2O | CH4 | 188.53 | −8720.4 | −24.07 | [28] |
| H2O | C2H6 | 247.81 | −11,988.3 | −32.59 | |
| H2O | C3H8 | 350.88 | −17,129 | −47.64 | |
| H2O | C4H10 | 898.95 | −44,053.7 | −127.99 | |
| H2O | C5H12 | −14.51 | 0.36 | 6.53 | [16] |
| H2O | C6H14 | 361.56 | −17,990.73 | −48.83 | |
| MDEA | CH4 | −19.59 | 2401 | 5.77 | [28] |
| MDEA | C2H6 | −23.91 | 2435.5 | 6.11 | |
| MDEA | C3H8 | −216.86 | 12,221.1 | 34.17 | |
| MDEA | C4H10 | −345.52 | 20,003.5 | 52.06 | |
| MDEA | C5H12 | 1027.12 | −47,124.34 | −149.46 | In this work |
| MDEA | C6H14 | 302.53 | −11,947.25 | −43.23 | |
| TMS | CH4 | 19.00 | 85.21 | 0 | [29] |
| TMS | C2H6 | 20.21 | −728.61 | 0 | |
| TMS | C3H8 | 20.44 | −1070.82 | 0 | [30] |
| TMS | C4H10 | −108.15 | 6708.6 | 17.89 | In this work |
| TMS | C5H12 | 1264.49 | −60,419.33 | −183.64 | |
| TMS | C6H14 | 539.90 | −25,242.16 | −77.41 | |
| Reaction | A | B/T | C | D/K−1 | T Range/K | Source |
|---|---|---|---|---|---|---|
| 6 | 819.80 | −37,655.90 | −124.50 | 0 | 273–498 | [31] |
| 7 | −553.40 | 28,412.70 | 77.70 | 0 | 273–423 | |
| 8 | −9.42 | −42,334.98 | 0 | 0 | 298–333 | |
| 9 | −32.00 | −3338.00 | 0 | 0 | 287–343 | |
| 10 | 216.05 | −12,431.70 | −35.48 | 0 | 273–498 | |
| 11 | 132.90 | −13,445.90 | −22.48 | 0 | 273–498 |
| Type | Substance | RMSE | MAE | R2 |
|---|---|---|---|---|
| Absorption tower | CO2 | 0.0290 | 0.0233 | 0.6251 |
| COS | 0.0258 | 0.0203 | 0.9206 | |
| MSH | 0.0216 | 0.0173 | 0.6560 | |
| Flash Tank | C2H6 | 0.0256 | 0.0229 | 0.8466 |
| C3H8 | 0.0269 | 0.0251 | 0.7100 | |
| C4H10 | 0.0236 | 0.0217 | 0.3011 | |
| C5H12 | 0.0251 | 0.0229 | 0.9002 | |
| C6H14 | 0.0093 | 0.0082 | 0.7921 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Xue, J.; Jia, Y.; Liu, K.; Zhang, C.; Liu, Z. Simulation of Absorption and Flash Evaporation for Natural Gas Desulfurization. Processes 2025, 13, 3504. https://doi.org/10.3390/pr13113504
Yang C, Xue J, Jia Y, Liu K, Zhang C, Liu Z. Simulation of Absorption and Flash Evaporation for Natural Gas Desulfurization. Processes. 2025; 13(11):3504. https://doi.org/10.3390/pr13113504
Chicago/Turabian StyleYang, Chaoyue, Jingwen Xue, Yong Jia, Ke Liu, Chunyang Zhang, and Zongshe Liu. 2025. "Simulation of Absorption and Flash Evaporation for Natural Gas Desulfurization" Processes 13, no. 11: 3504. https://doi.org/10.3390/pr13113504
APA StyleYang, C., Xue, J., Jia, Y., Liu, K., Zhang, C., & Liu, Z. (2025). Simulation of Absorption and Flash Evaporation for Natural Gas Desulfurization. Processes, 13(11), 3504. https://doi.org/10.3390/pr13113504





