Study on the Fracture Characteristics and Mechanisms of Iron Ore Under Dynamic Loading

Abstract

The dynamic fracture process of iron ore under blast loading is an important manifestation of ore fragmentation. To investigate the dynamic fracturing process of iron ore, Hopkinson bar experiments were conducted under different impact loads. The results indicate that under low strain rates, the dynamic stress–strain curve of iron ore exhibits compaction, elastic, and failure stages. However, as the strain rate increases, the compaction stage becomes less distinct, while the elastic modulus decreases and the failure strength increases, indicating the material toughness was enhanced at high strain rate. Moreover, under high strain rates, a significant increase in shear strain promotes the formation of tensile–shear cracks in the ore. In addition, based on the fragmentation of iron ore at different impact pressure, there exists a certain impact pressure, at which the proportion of large fragments decreases only slightly, while the amount of small fragments increases markedly. These findings provide important insights for optimizing fragmentation and improving blasting effectiveness.

1. Introduction

Iron ore, a fundamental raw material for modern industry, serves an indispensable position in the national economy [1,2]. At present, blasting techniques have become a main excavation method in open-pit iron mining. However, due to the transiency of rock blasting, unpredicted rock fragmentation and high percentage of oversized fragments are frequently encountered. Excessively coarse fragmentation not only increases explosive consumption but also increases the time of subsequent iron processing steps, including secondary crushing and grinding operations [3], and finally raising both the mining and ore processing costs [4]. Therefore, controlling the size of rock fragmentation is of great significance for improving the overall economic efficiency of mining enterprises.

Relevant research shows that the more explosive per borehole, the stronger the dynamic loading added onto the rock, resulting in a higher degree of rock fragmentation. Therefore, studying the mechanism of how dynamic loading drives rock mass failure is a key factor in controlling rock fragmentation size. As the Split Hopkinson Pressure Bar (SHPB) is capable for precisely controlling the incident energy under impact loading, the SHPB is widely used to study the relationship between impact loading and rock fragmentation [5,6,7]. Utilizing the SHPB experimental system, Gong [8] found that the energy consumption of granite fragmentation under dynamic loads correlates linearly with the strain rate, and its dynamic compressive strength increases with the increase in strain rates. Zhou [9] analyzed the constitutive relationship of rock at different strain rates, and proposed 3D scatter-gram method to represent the constitutive relationships of rate-dependent rock. Song [10] studied the mechanical property of lignite and found that the dynamic compressive strength significantly increased with the increase in strain rate.

In addition, the fracture mechanism of rock under dynamic loads was also investigated by many researchers. Xu [11] investigated the fracture process of inclined cylinder specimens and found that shear stress was apparently generated under impact loading. Furthermore, Cai [12] further studied the failure behavior of single-flawed rocks. Li [13] further investigated the dynamic fracturing process of marble containing multiple flaws and found that shear cracks generally initiated near the flaw tips, which govern the macroscopic failure, and significantly influence the energy consumption of marble.

As for the ore blasting in mining, some scholars focused on the rock fragmentation efficiency and energy consumption mechanisms of rock under dynamic loading. Zhang [14] analyzed the main factors, including the explosive, initiator, rock type, etc., that influence the rock fragmentation. Nikkhah [3] studied the influence of blasting parameters on ore fragmentation. However, due to the complexity of the iron failure under impact loading, the dynamic fracturing process of iron ore and its failure mechanism are still unclear. Therefore, in this study, the SHPB was carried out to further study the dynamic fragmentation of iron ore under different impact loading, and utilizing the digital image correlation (DIC) method, the distribution characteristics of the strain field were analyzed, and the failure patterns of iron under impact loading were discussed. The results provide valuable insights for optimizing the fragmentation of iron ore under dynamic loading.

2. Materials and Methods

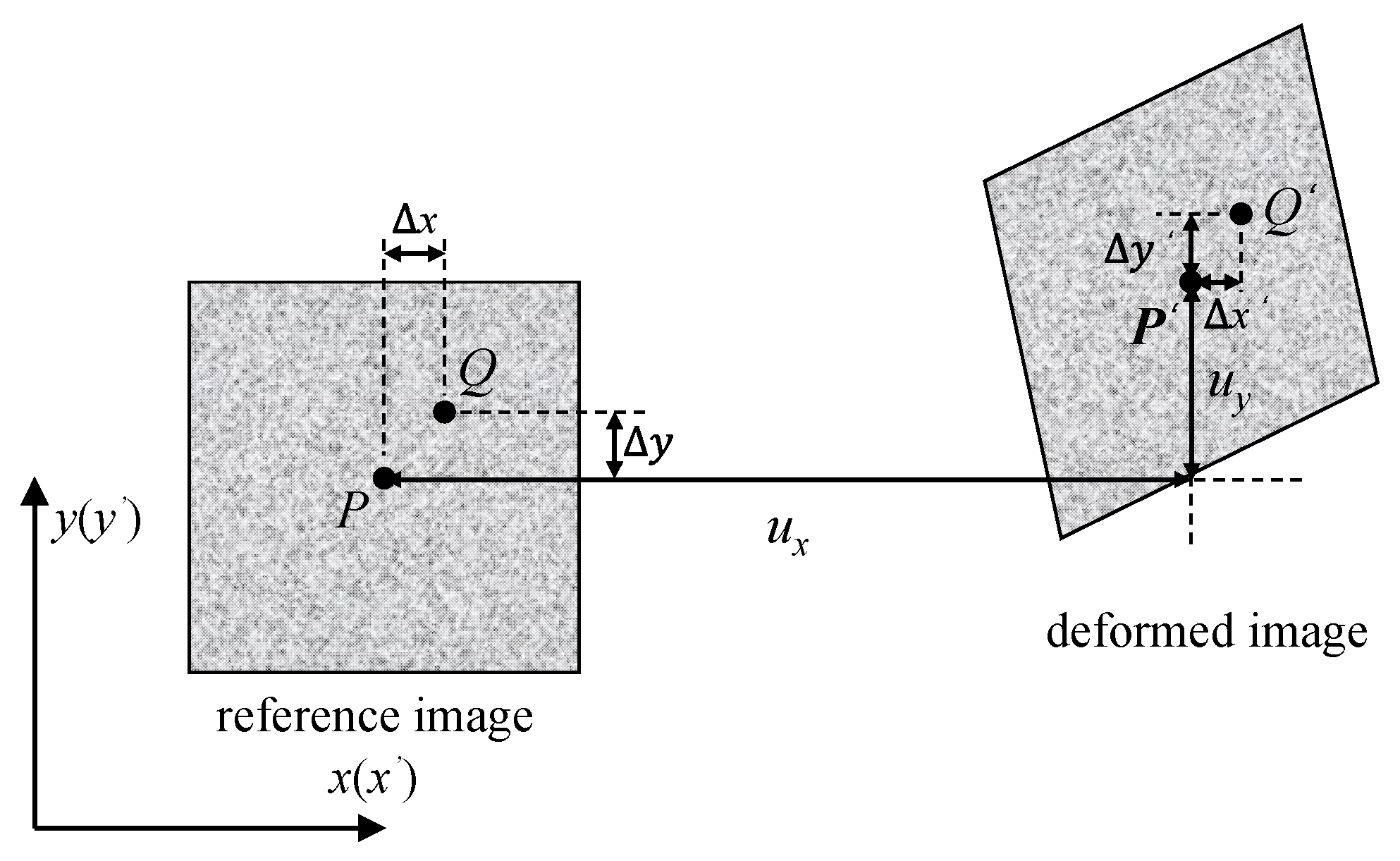
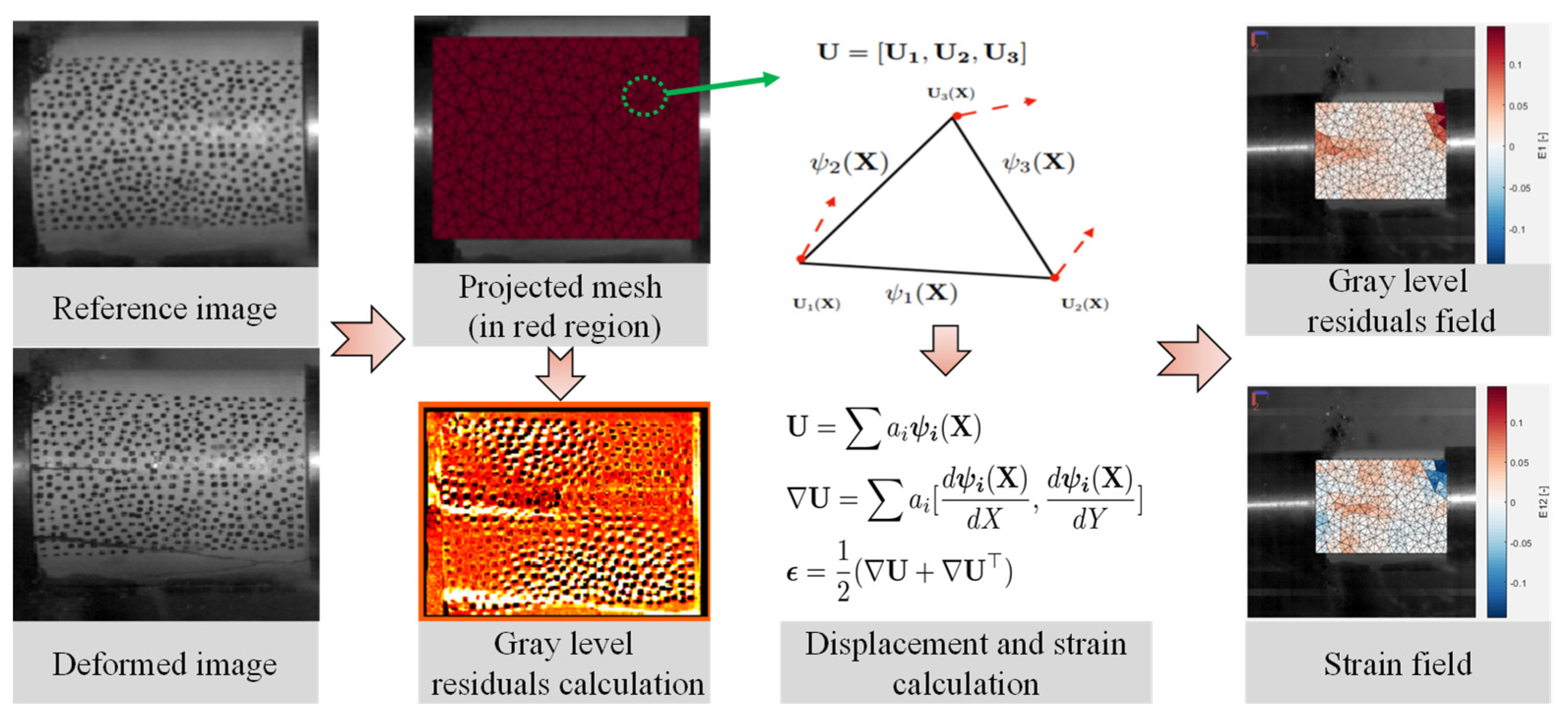
2.1. Experimental Setup and Fundamental Principles

The Split Hopkinson Pressure Bar (SHPB) experimental system used in the tests is illustrated in Figure 1. The system primarily consists of a power control system, a bar system, a data acquisition system, and a digital image monitoring system. The bar system includes an incident bar and a transmission bar, both made of 60Si2Mn steel with a diameter of 50 mm and a length of 1800 mm. The elastic modulus (E_e) of the bars is 206 GPa, and the longitudinal wave speed (C_e) is 5106 m/s. During the experiment, two strain gauges were attached to each bar. The strain gauges on each bar were arranged symmetrically along the radial direction, a half-bridge circuit configuration was applied in the experiment, and a bridge excitation voltage of 4 V to measure the strain signals in the bars. To satisfy the assumption of uniform deformation in the SHPB test and to reduce friction at the interfaces between the specimen and the bars, Vaseline lubrication was adopted at the contact surfaces between the incident bar, transmission bar, and the specimen.

During the test, the data acquisition system recorded the strain data from the incident and transmission bars. The stress, strain, and strain rate of the specimen were subsequently calculated using the following expressions:

$$\left\{\begin{array}{l}{\sigma }_s={\displaystyle \frac{E_e{A}_e}{2A_s}}\left[{\epsilon }_i(\mathrm{t})+{\epsilon }_r(\mathrm{t})+{\epsilon }_{\mathrm{t}}(\mathrm{t})\right]\\ {\epsilon }_s(\mathrm{t})={\displaystyle \frac{C_p}{L_s}}{\displaystyle {\int }_0^{\tau }\left[{\epsilon }_i(\mathrm{t})-{\epsilon }_r(\mathrm{t})-{\epsilon }_{\mathrm{t}}(\mathrm{t})\right]}\mathrm{d}t\\ {\stackrel{•}{\epsilon }}_s(\mathrm{t})={\displaystyle \frac{C_p}{L_s}}\left[{\epsilon }_i(\mathrm{t})-{\epsilon }_r(\mathrm{t})-{\epsilon }_t(\mathrm{t})\right]\end{array}\right.$$

where εᵢ, εᵣ, and εₜ represent the incident strain, reflected strain, and transmitted strain measured in the bars, respectively; A_b is the cross-sectional area of the bars; and L_s and A_s are the length and cross-sectional area of the specimen, respectively.

To analyze the deformation characteristics of the specimen under impact loading, a digital image monitoring system was employed to record the deformation process. This system comprises a high-speed camera, a lighting system, a synchronization control system, and a computer. A Phantom V2012 high-speed camera was used to record the testing process, set at a capture speed of 180,000 frames per second (fps) and an image resolution of 256 pixels × 256 pixels. This setup enabled the complete recording of the entire impact process of the specimen.

2.2. Specimen Preparation

The specimens used in the test were prepared from iron ore sourced from the same area of the open-pit mine at the Sijiaying Iron Mine, and the physical and mechanical parameters of iron were obtained by conducting series of experiments, and are shown in

Table 1. The physical and mechanical parameters of iron.

Density (kg/m3)	Longitudinal Wave Velocity (m/s)	Shear Wave Velocity (m/s)	Uniaxial Compressive Strength (MPa)	Elastic Modulus (GPa)	Poisson’s Ratio
3460	3846	1923	96.14	47.64	0.22

.

The iron ore was processed through cutting, coring, and grinding to fabricate standard specimens satisfying the experimental requirements. The end faces of the cylindrical specimen have a parallelism tolerance within ±0.02 mm. The specimens were cylindrical with a diameter of 50 mm and a height of 50 mm. To monitor the deformation process of the specimen, a stochastic black speckle pattern was painted on the surface of specimen by using white matte paint and a black marker pen, as shown in Figure 2. To study the influence of impact loading on iron failure, four different impact pressures, including 0.32 MPa, 0.34 MPa, 0.36 MPa, and 0.38 MPa, are set in our experiment; to ensure the repeatability of the results, three specimens are prepared for each impact pressure, making a total of 12 specimens.

The digital image correlation (DIC) method has been widely used to measure the displacement by many researchers [15,16,17] and was employed in our test. By using the high-speed camera, the displacement of these black speckles was recorded, and then, the strain field can be calculated by comparing the variation in the speckle patterns during the experiment. The schematic diagram of the DIC is presented in Figure 3.

The displacement of each point P(x′, y′) in the deformed images can be expressed as

$$\left\{\begin{array}{l}{x}^{\prime }=x+u_x+{\displaystyle \frac{\partial u_x}{\partial x}}\Delta x+{\displaystyle \frac{\partial u_x}{\partial y}}\Delta y\\ y^{\prime }=y+u_y+{\displaystyle \frac{\partial u_y}{\partial x}}\Delta x+{\displaystyle \frac{\partial u_y}{\partial y}}\Delta y\end{array}\right.$$

where the (x, y) is the coordinate of the point P in the reference images; u_x and u_y are the displacement of point P in the horizontal and vertical direction; $\Delta x$ and $\Delta y$ are the displacement component between point P and Q in the subset region.

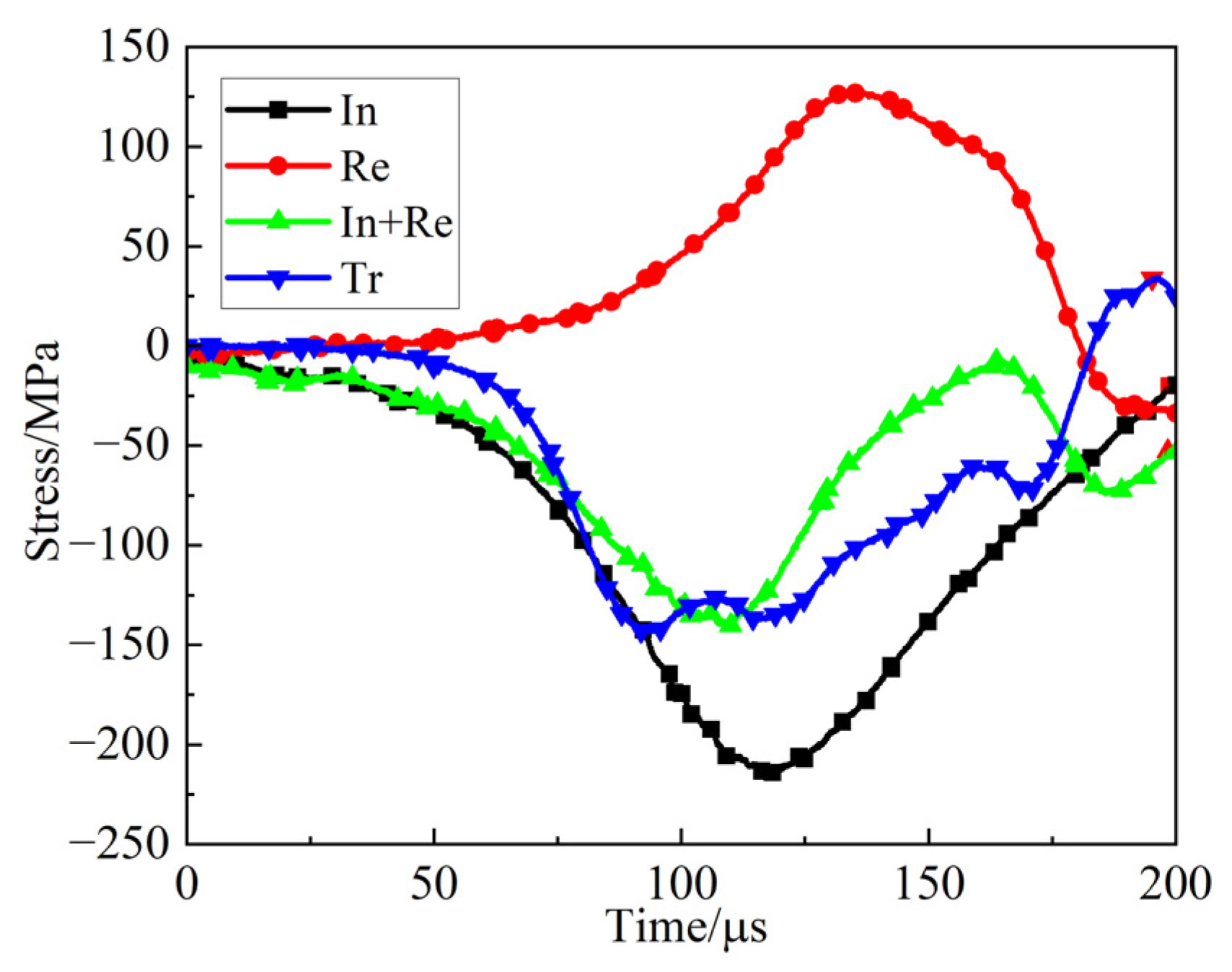
2.3. Verification of Dynamic Stress Equilibrium

The SHPB experiment requires the satisfaction of the assumption of strain (stress) uniformity within the specimen, which necessitates that the stresses at both ends of the specimen remain in dynamic equilibrium. Utilizing the incident, reflected, and transmitted waves measured from the incident and transmission bars, the stresses at both ends of the specimen were determined, as shown in Figure 4. The blank curve represents the incident wave (In) impact on the specimen, and once the incident wave arrived at the specimen, the reflected wave (Re) and transmitted wave (Tr) were generated, shown by the red curve and blue curve in Figure 3, respectively. The green curve is the algebraic sum of the incident wave and reflected wave (In + Re). It can be seen that the curve of (In + Re) closely coincides with the transmitted stress curve during the loading phase of the specimen. This indicates that the stresses at the two sides of the specimen were in a dynamic equilibrium state throughout the impact loading process, thereby fulfilling the fundamental assumption required for the validity of the experiment.

3. Results

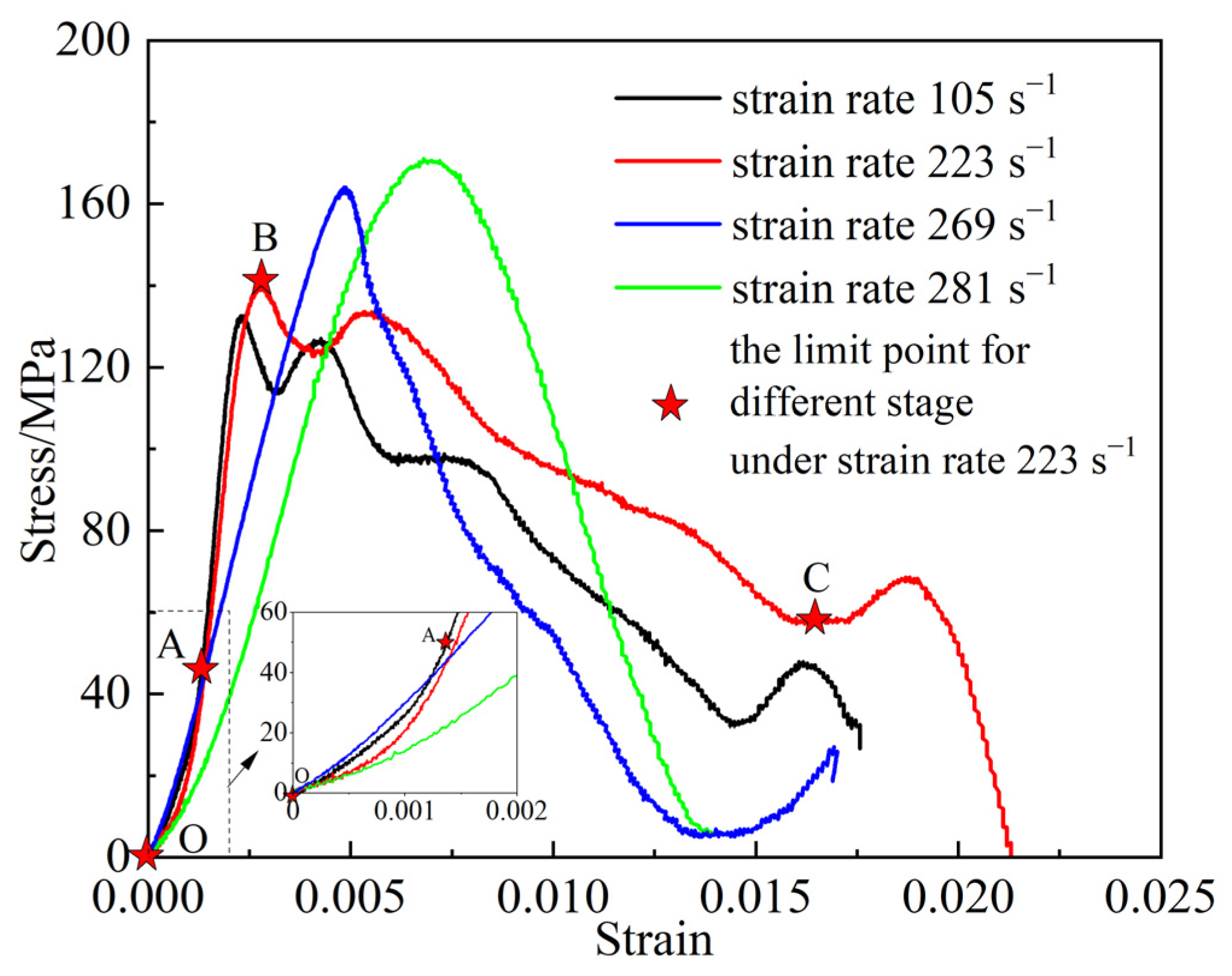
3.1. Dynamic Constitutive Relationship of Iron Ore

Figure 5 shows the dynamic stress–strain curves of iron ore under different strain rates. It can be observed from the figure that as the impact loading increases, the strain rate of the iron ore continuously increases, and its dynamic stress–strain curves also exhibit certain differences. At low strain rates (in this study, strain rate ≤ 223 s⁻¹), the dynamic stress–strain curve of iron ore can be divided into three stages. Take the stress-strain curve of iron ore under the strain rate of 223 s⁻¹ for example, those three stages are compaction stage (OA region), the elastic stage (AB region), respectively. The detailed characteristics of dynamic stress-strain curve are shown in

Table 2. The characteristics of dynamic stress–strain curve under low strain rates.

Stages	Characteristics	Reason
Compaction Stage	The stress increases slowly with the increase in strain	The internal defects of the specimen, such as pores and voids, rapidly closed under impact loading
Elastic Stage	The stress increases approximately linearly with the increase in strain	Micro-cracks began to initiate, and rock damage accumulated gradually
Failure Stage	The stress dropped rapidly with the increase in strain	Macroscopic cracks generated, leading to the production of iron ore fragment

.

At high strain rates (in this study, strain rate > 223 s⁻¹), the dynamic stress–strain curves of the iron ore exhibit significant differences. On one hand, during the initial phase of high-speed impact loading, the iron ore shows no distinct compaction stage. This may be due to the rapid closure of internal defects under high strain rates; a similar phenomenon was also observed by other researchers [18,19]. On the other hand, it is found that the elastic modulus, which represents the slope of the stress–strain curve in the elastic stage (AB region), decreased gradually with the increase in strain rate, and both the maximum compressive strength and the corresponding strain increase with increasing strain rate. This indicates that under high strain rate, more energy consumption is needed in order to fragment the iron ore, thus leading the toughness of the iron ore to increase significantly. This may plausibly be due to the existence of the defect in iron ore, which may induce multiple micro-cracks initiated simultaneously from the defect at high strain rates, resulting in a rapid increase in iron deformation, and leading the elastic modulus to decrease gradually with the increase in strain rate.

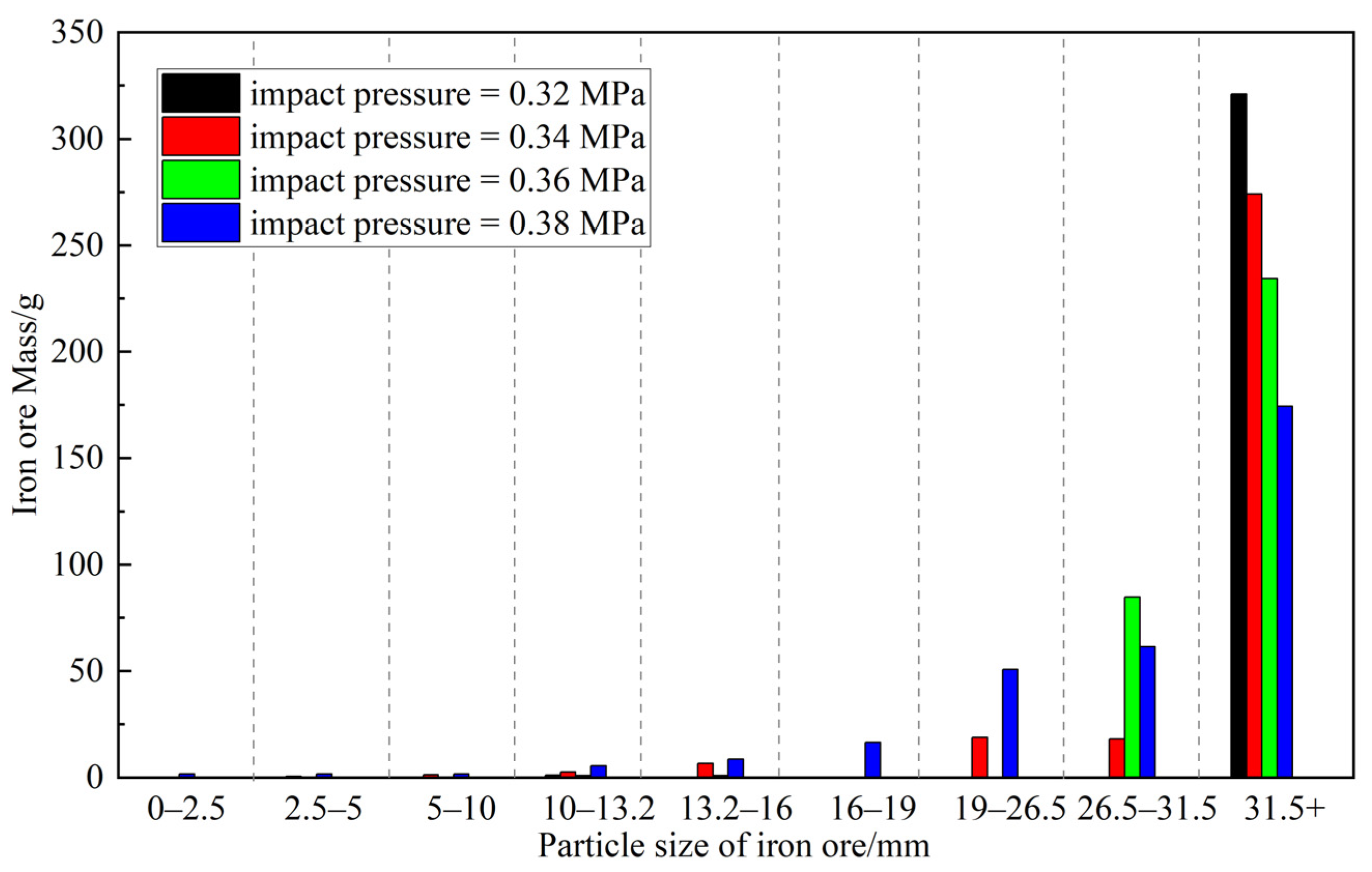
3.2. Analysis of Ore Fragmentation Characteristics

Figure 6 shows the crack propagation patterns and calculated residual results of iron specimens after failure under different impact pressures. It can be observed that the computed gray level residuals of the specimens can effectively describe the propagation behavior of surface cracks, providing a valuable tool for in-depth analysis of the iron ore fracture process [17]. At an impact gas pressure of 0.32 MPa, the ore develops a penetrating tensile crack along the loading direction, fragmenting the specimen into two large pieces. As the impact velocity increases, the degree of fragmentation gradually increases, and the resulting fragment size decreases. When the gas pressure increased to 0.34 MPa, a shear crack forms at an angle to the loading direction, breaking the specimen into three pieces with reduced largest fragment size. When the pressure increases to 0.36 MPa, the ore is crushed into multiple fragments, and the proportion of large fragments decreases significantly. With further increase in impact gas pressure, more internal cracks develop, reducing the overall fragment size.

The mass of different-sized iron fragments at different impact pressures are presented in Figure 7. It can be seen that with the impact pressure increases, the amount of large-sized iron ores decreased, while that of small-sized iron ores increased. However, when the impact pressure reached 0.38 MPa, the mass of iron fragments (26.5~31.5 mm) decreased relative to that at the impact pressure of 0.36 MPa, whereas the mass of iron fragments (below to 26.5 mm) increased significantly. This indicates that there exists an optimal impact pressure (0.36 MPa in our study), beyond which the iron ore tends to produce smaller fragments without a significant further reduction in the larger fragments. Therefore, for the practical blasting engineering, an extremely high explosive may cause more blast energy to be consumed in over-fragmenting the iron ore, resulting in high percentage of small iron fragments. Therefore, selecting an appropriate explosive consumption to optimize the size distribution of iron fragments is crucial for improving the economic efficiency in blasting.

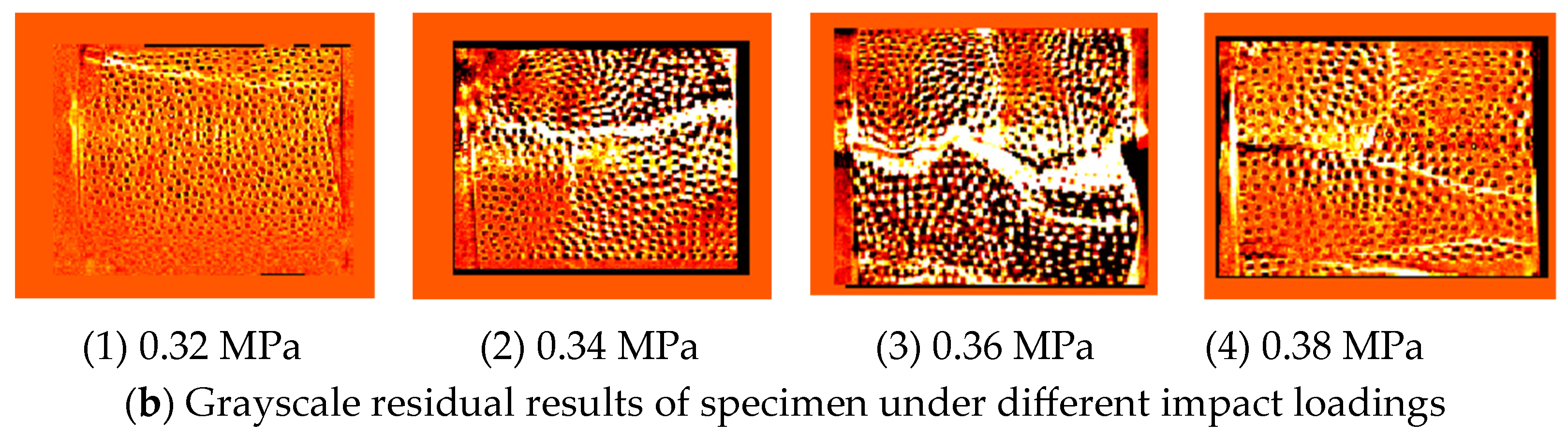
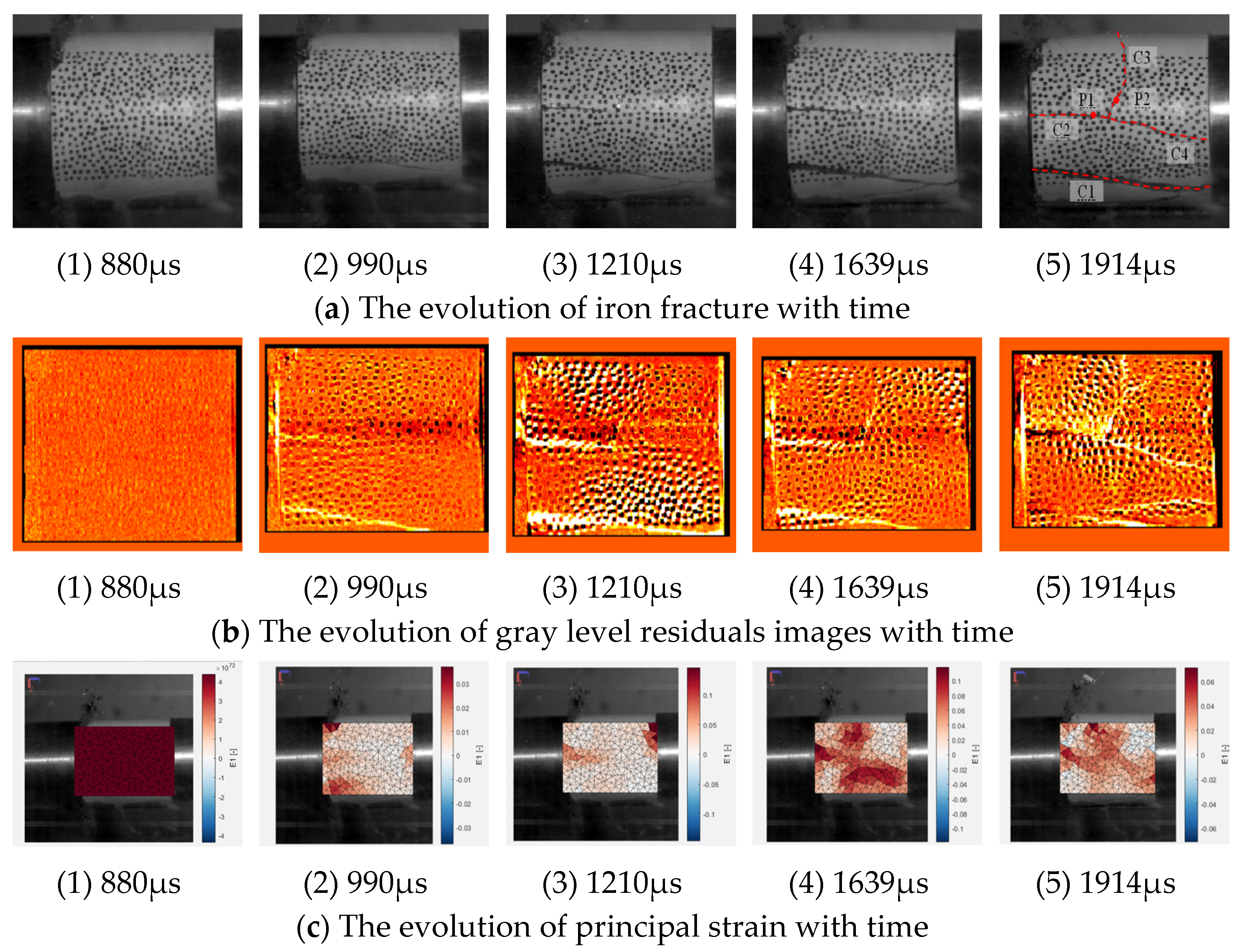
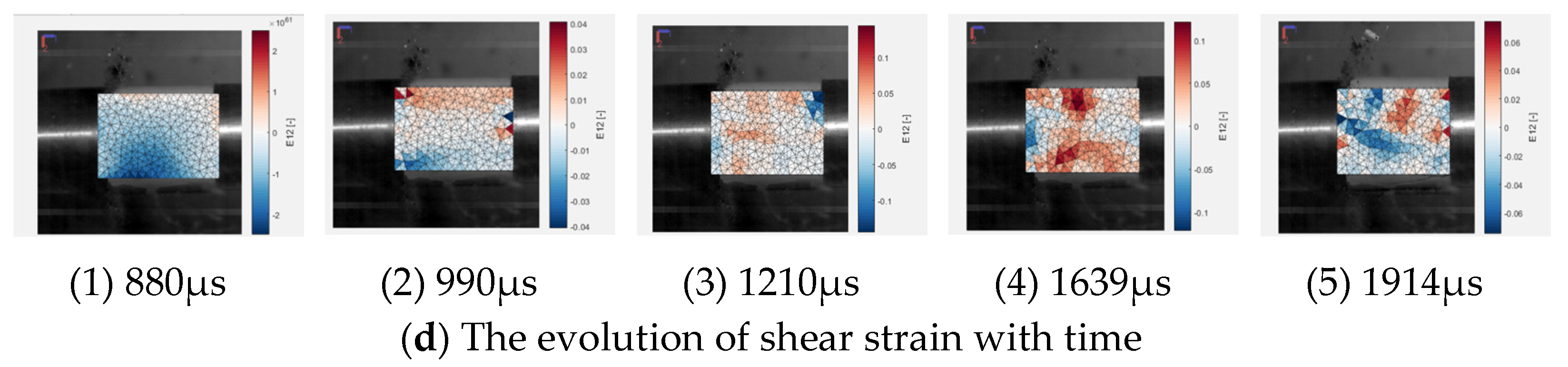
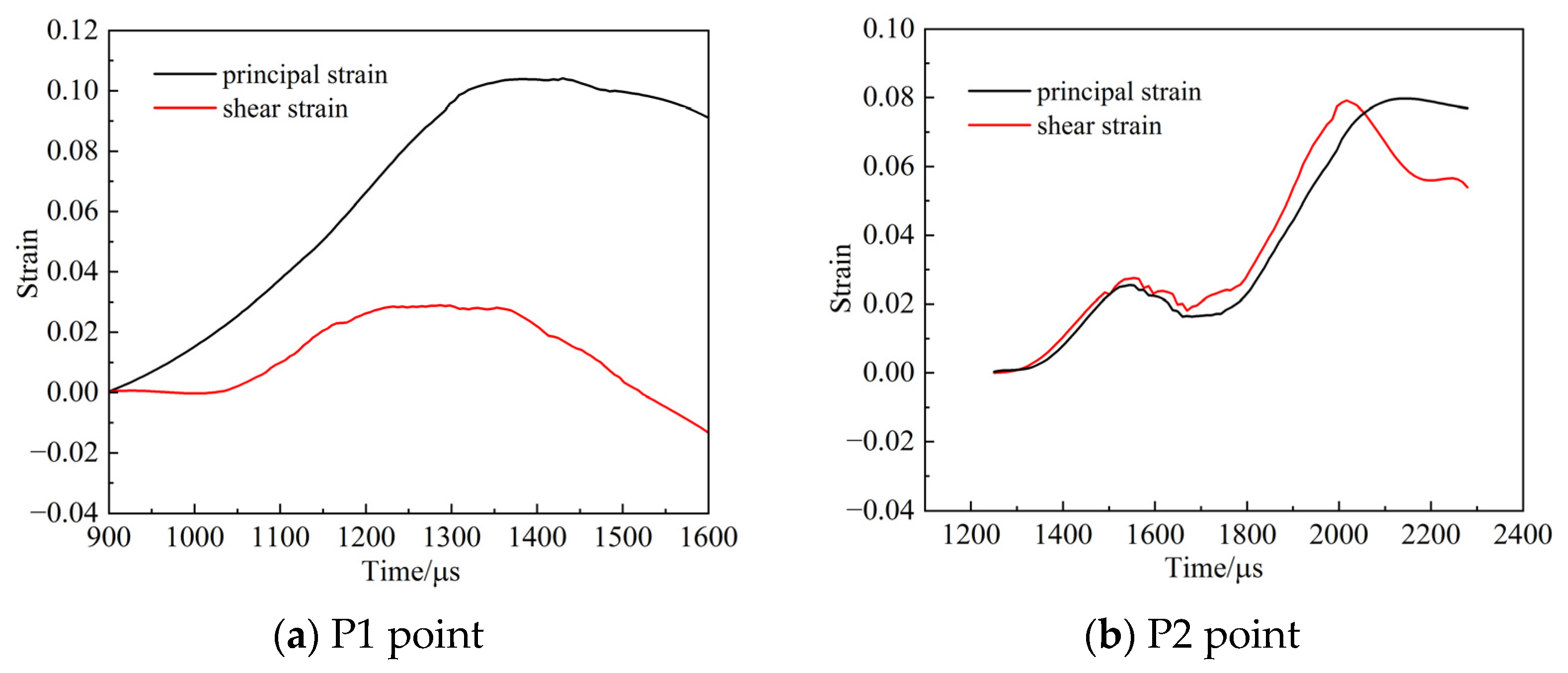
3.3. Analysis of the Specimen Fracture Process

To further analyze the fracture process and mechanism of iron ore under impact loading, the failure process and strain field evolution for a specimen tested at a gas pressure of 0.36 MPa are examined in detail, as shown in Figure 8. The moment when the specimen begins to experience impact load is defined as 0 μs. By applying the self-developed software Correli3.2 to compare the gray level correlation between the reference image and the deformed image [20], the gray level residual, displacement, and strain fields within the specimen were obtained, and the detailed methodology of the software Correli3.2 is described in reference [21].

Figure 9 shows the evolution of crack propagation and corresponding strain field subjected to an impact pressure of 0.38 MPa. It can be seen that at 990 μs, horizontal penetrating cracks C1 and C2, primarily tensile, first initiate and propagate along the loading direction. At the time of 1210 μs, the shear strain field in the central part of the specimen increases significantly, causing the horizontally propagating crack C2 to arrest and prompting the initiation of inclined micro-cracks. At 1639 μs, under the combined action of principal and shear stresses, crack C2 branches, generating a deflected inclined crack C3 and a horizontally crack C4. subsequently, the crack C3 bifurcates at the time of 1914 μs. And finally, the interconnection of horizontal and vertical cracks divides the specimen into multiple fragments.

Two monitoring points, P1 and P2, were selected on the paths of cracks C2 and C3, respectively, and the evolution curves of the maximum principal strain and shear strain at these points were extracted, as shown in Figure 10. It can be observed that the maximum principal strain at point P1 increases rapidly over time, reaching its maximum value at 1300 μs, while the shear strain at this point remains very small. This indicates that the initial propagation of crack C2 is primarily driven by tensile strain, resulting in tensile fracture. However, with the crack propagates, both the principal and shear strains at point P2 began to increase after 1300 μs, and presented double-peak evolution characteristics: the first peak value is at 1550 μs, followed by a slight drop and a subsequent rise to a second peak value at 2000 μs. Combined with the crack propagation behavior, it can be found that the first peak value coincides with the initiation of micro-cracks from the tip of C2, and the strain reached its second peak value when the micro-cracks gradually developed into a macroscopic crack C3. It is the increase in the shear strain field at point P2 that causes the stress state at the crack tip to transition from a tensile field to a tensile–shear field, slowing down the crack propagation speed, and forming tensile–shear cracks.

From Figure 9 and Figure 10, it can be seen that since the tensile strength of the ore is generally much lower than the compressive and shear strengths, tensile failure occurs first under impact loading. However, as the gas pressure increases, the increase in the internal shear strain field during the fracture process becomes the main factor causing crack deflection and branching, ultimately leading to the fragmentation of the ore into multiple pieces.

4. Conclusions

In this study, the fracture characteristics and mechanisms of iron ore under dynamic loading are studied using SHPB experiment, and some main conclusions are as follows:

(1)

Under low strain rates, the dynamic stress–strain curve of iron ore sequentially exhibits compaction, elastic, and failure stages during loading. However, as the strain rate increases, the compaction stage gradually diminishes.

(2)

With an increase in impact air pressure, the strain rate of iron ore gradually rises, the elastic modulus decreases, and the failure strength increases, resulting in enhanced toughness of the ore and greater resistance to failure.

(3)

As the impact loading increases, the failure of iron ore increased gradually. However, there exists a critical impact load, beyond which the amount of small fragments visibly increases, whereas the proportion of large fragments decreases only marginally.

(4)

Under impact loading, tensile cracks initially develop and propagate along the loading direction in the ore. However, as the impact air pressure increases, the shear strain field within the ore gradually expands, leading to an increase in tensile–shear failures. This causes the specimen to break into multiple fragments, progressively increasing the degree of ore fragmentation.