Discrete Heating and Outlet Ports’ Influences on Thermal Convection in Lid-Driven Vented Cavity System with Thermal Dispersion and LTNE Effects
Abstract
1. Introduction
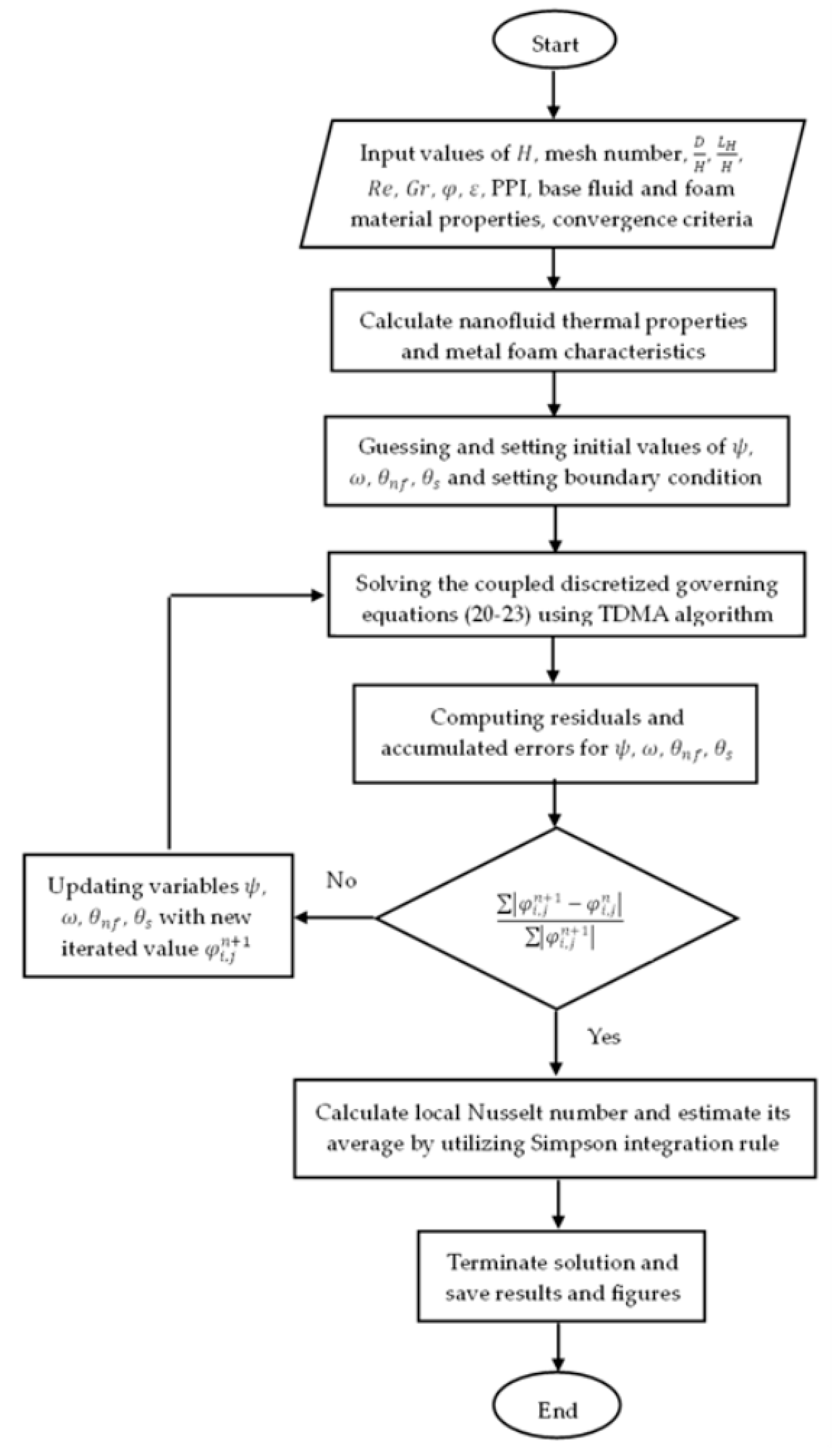
2. Computational Method
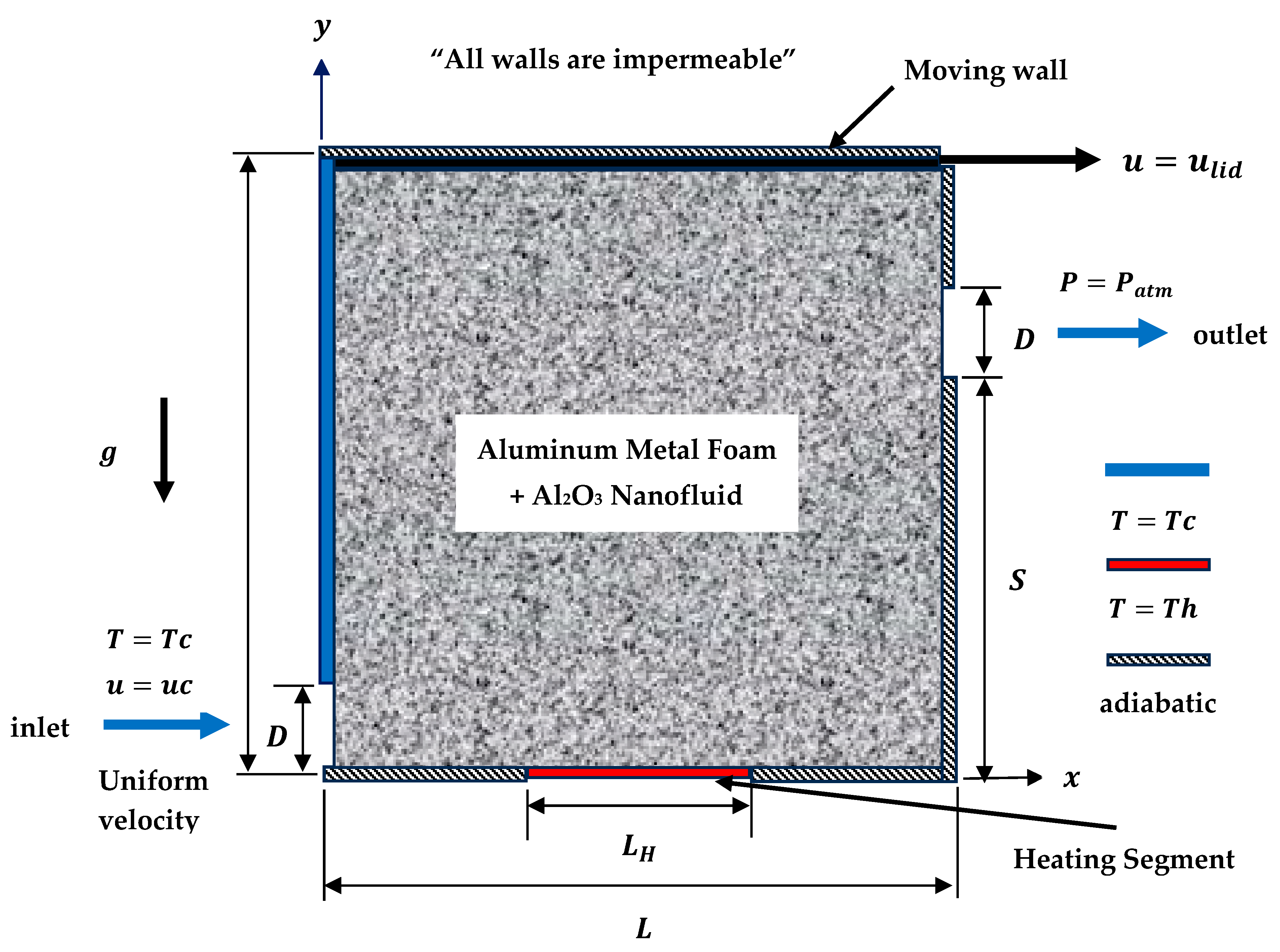
2.1. Problem Statement and Boundary Conditions
2.2. Mathematical Formulation and Assumptions
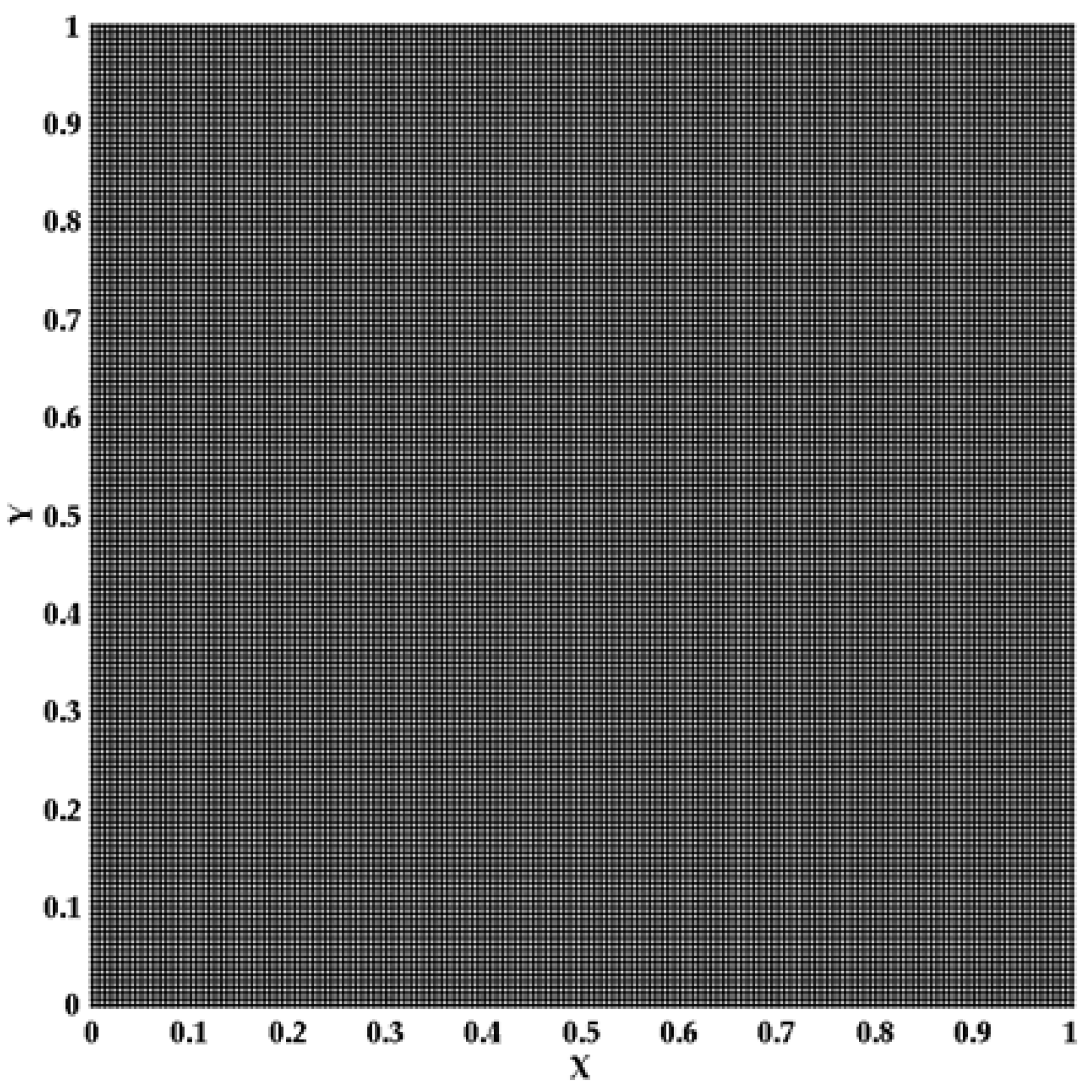
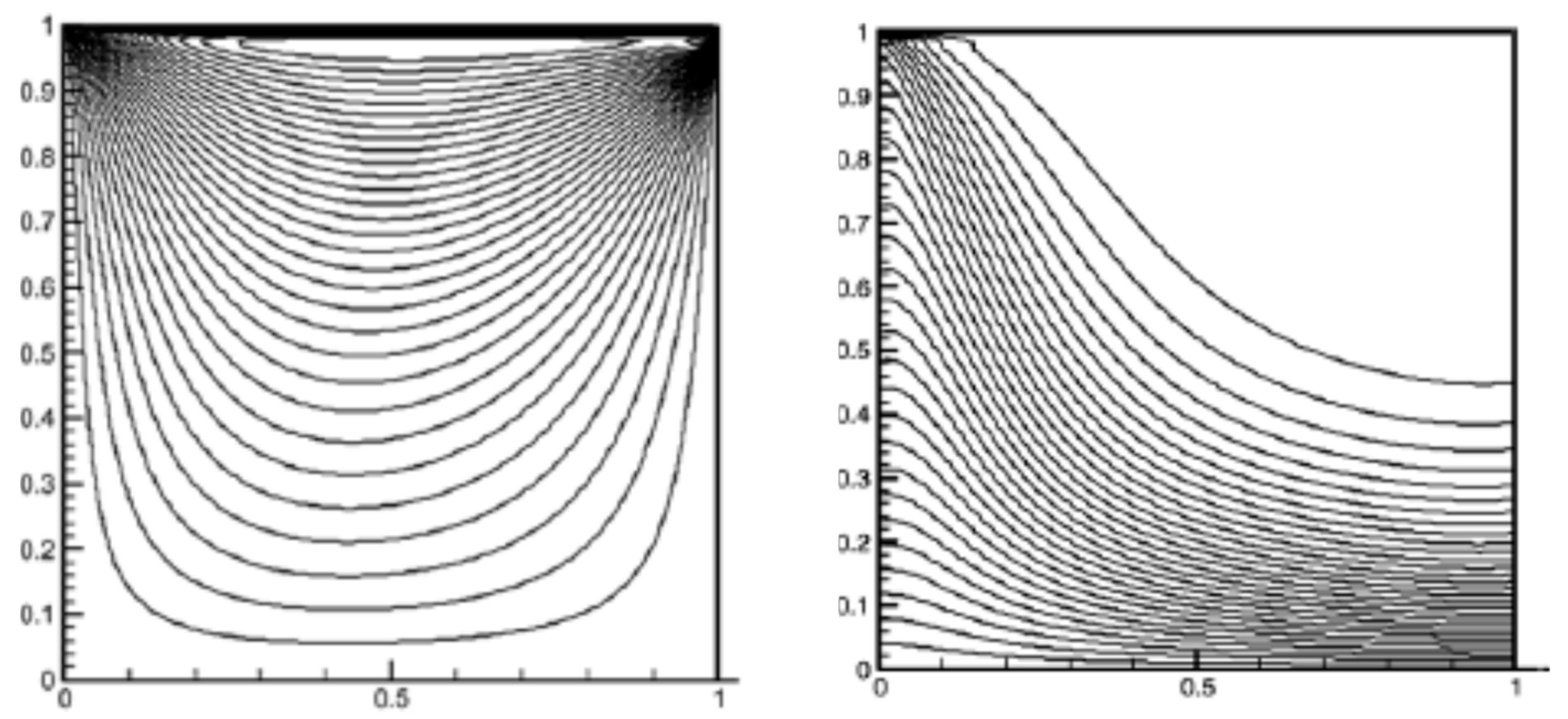
3. Grid Independence and Code Validation
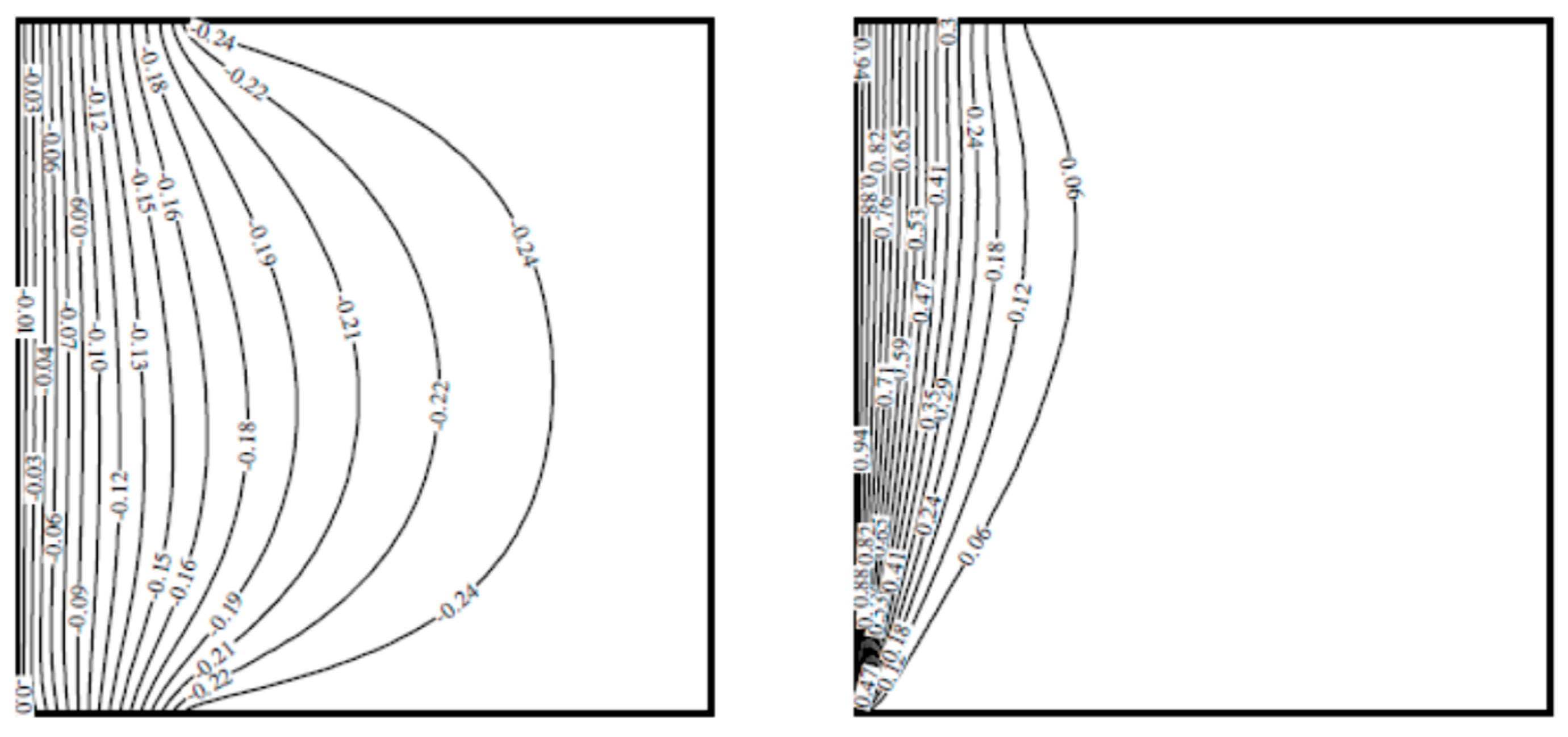
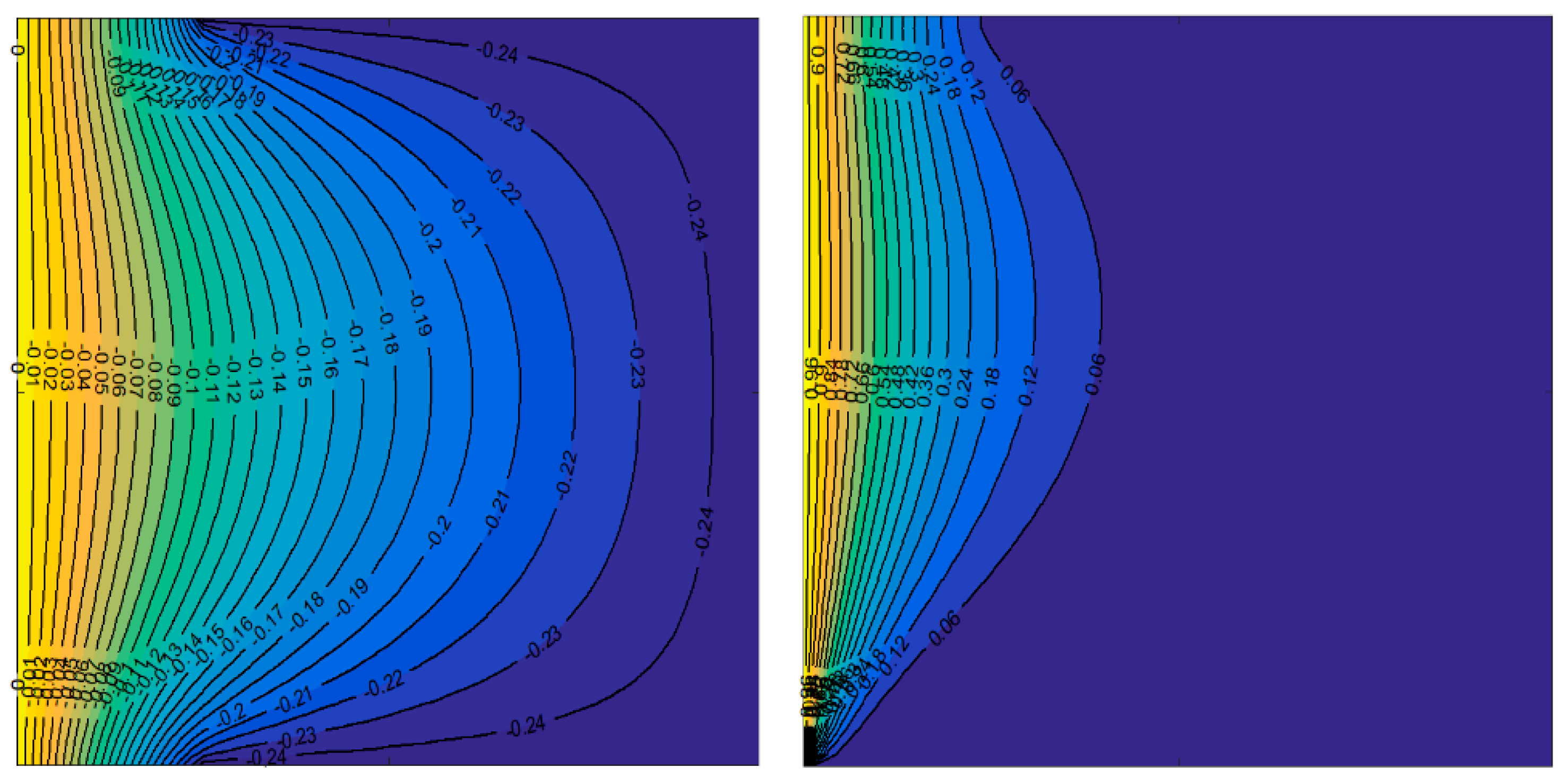
4. Results and Discussions
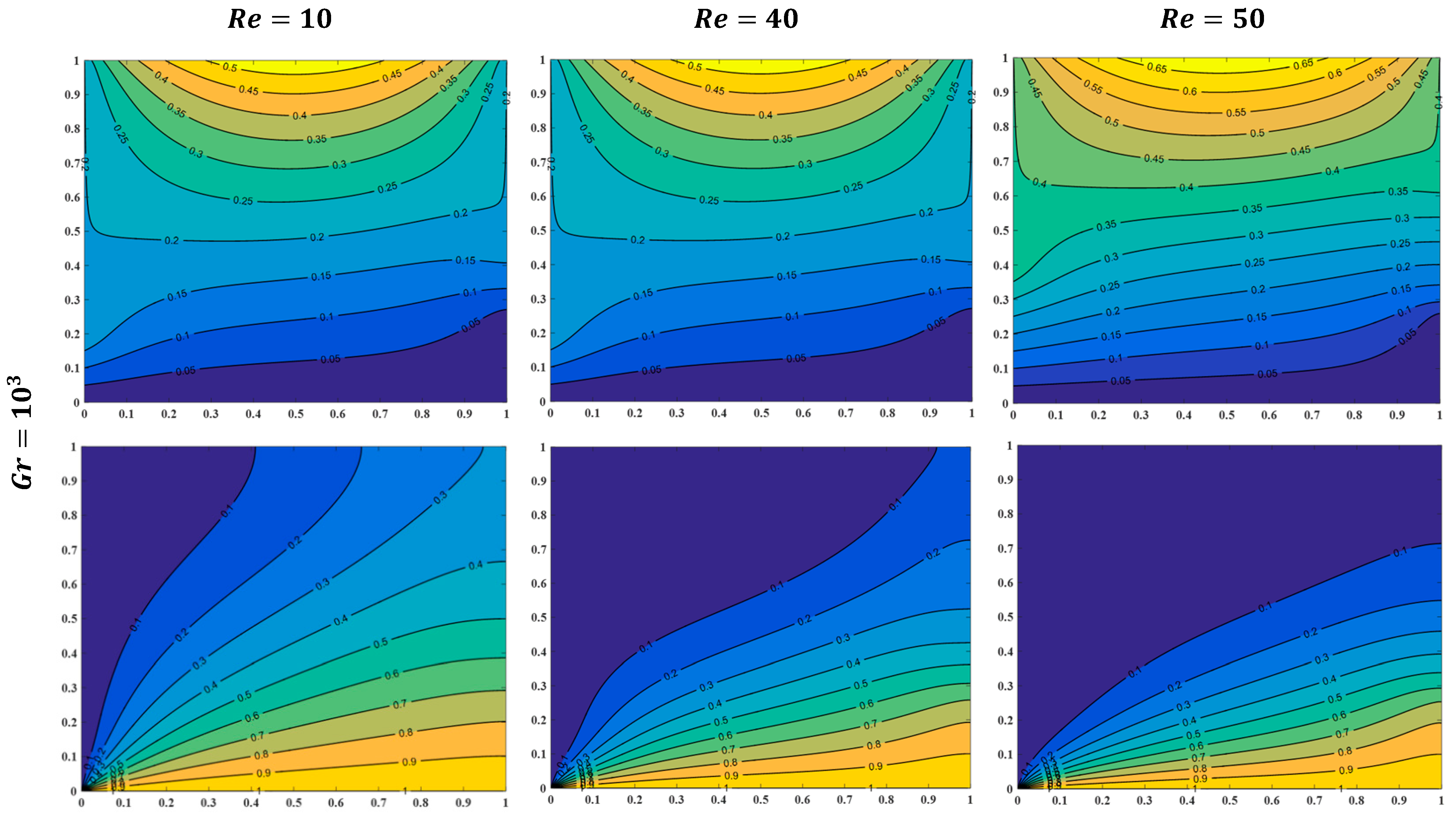
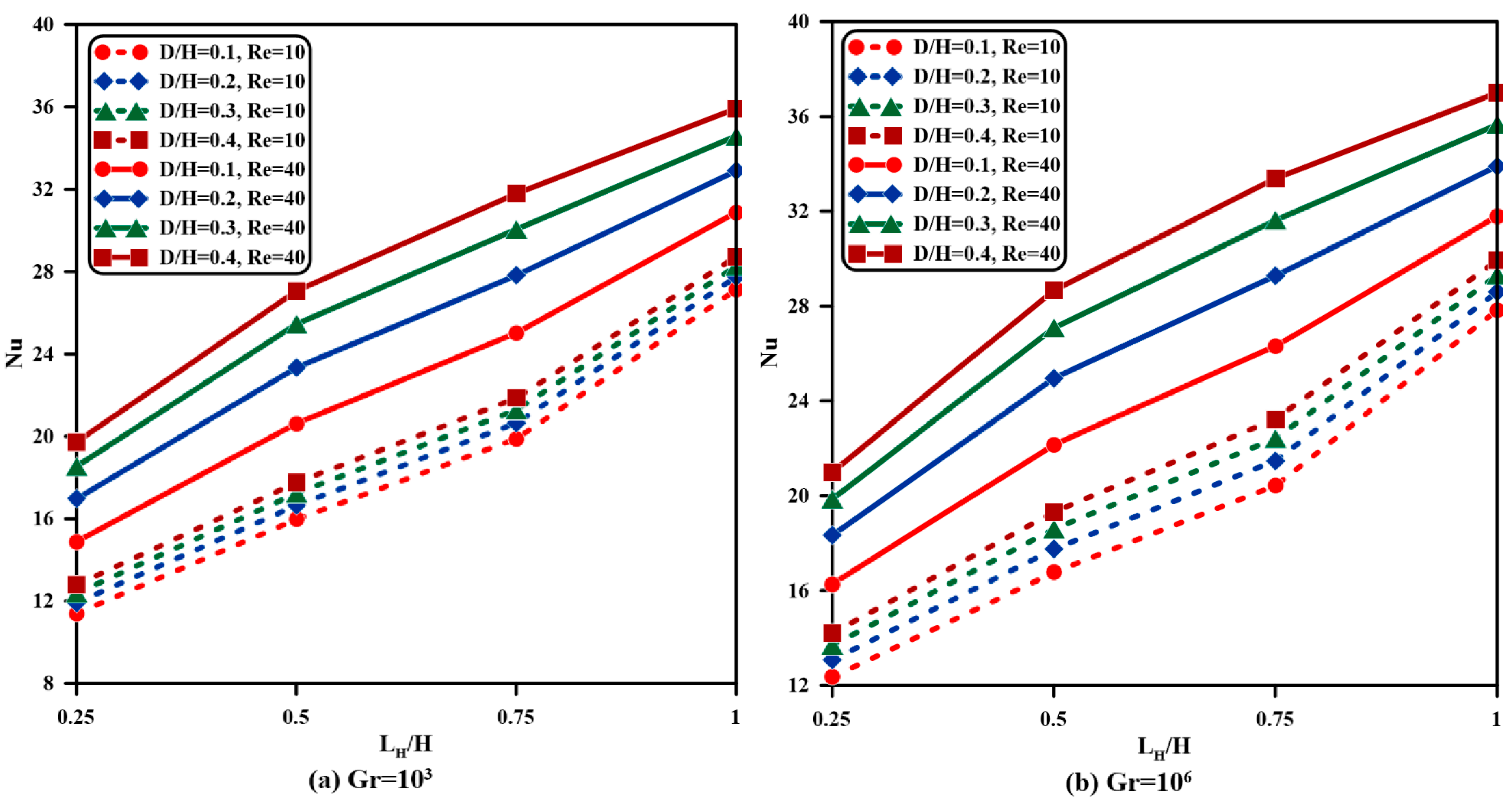
4.1. Effect of Inlet and Outlet Vents Aspect Ratio, Grashof Number, and Reynolds Number
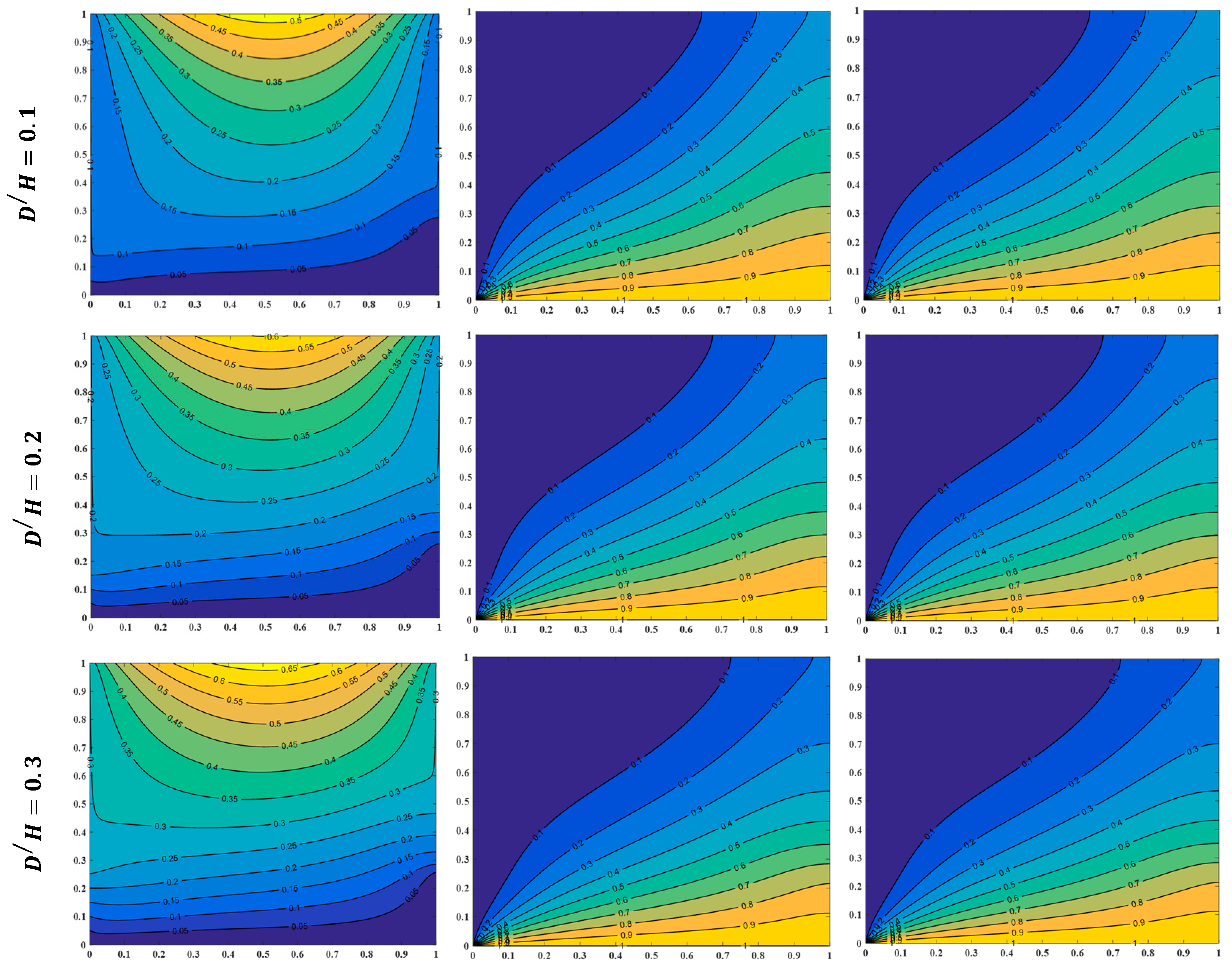
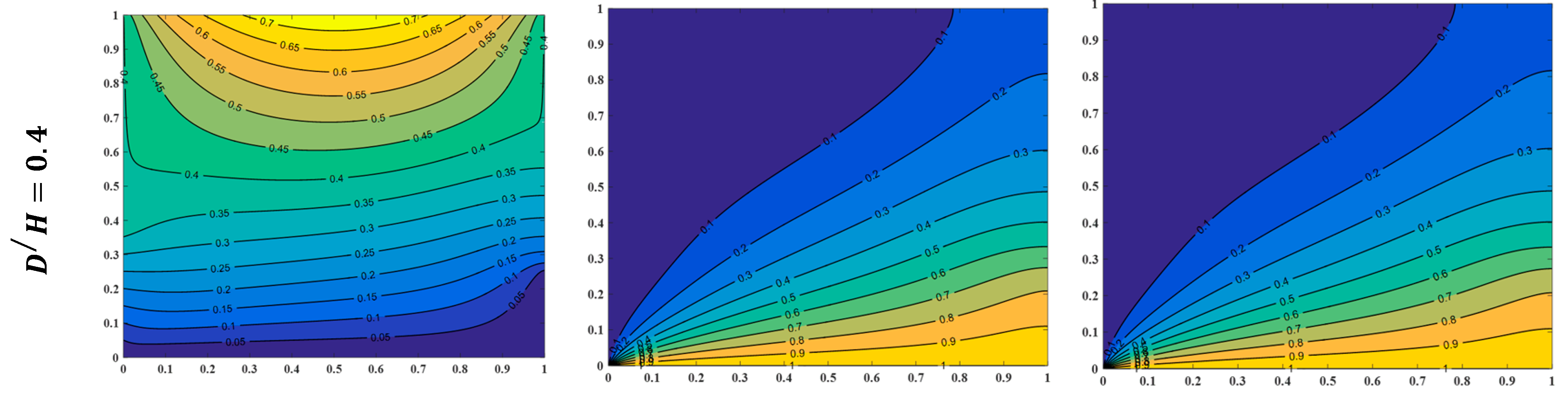
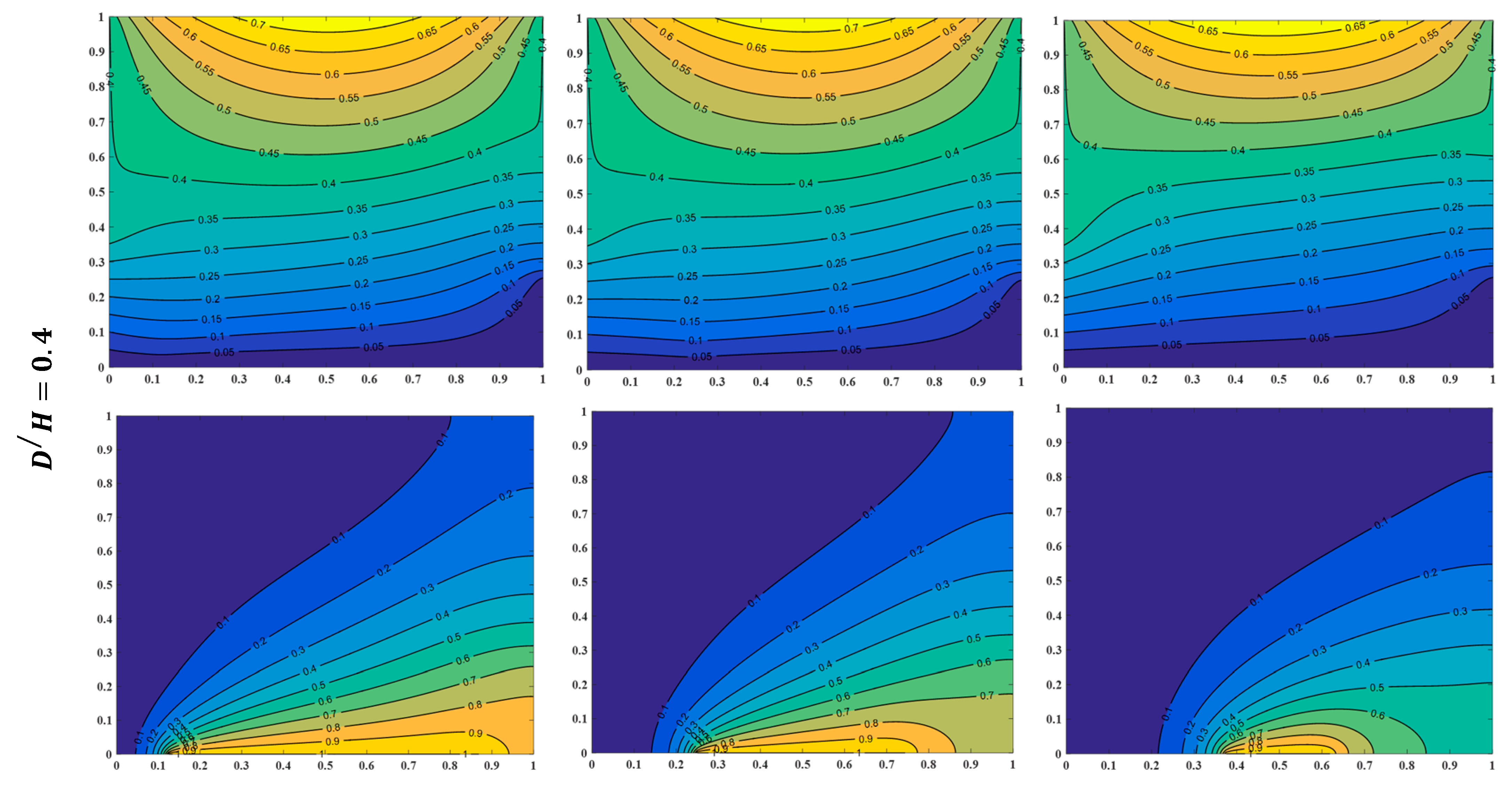
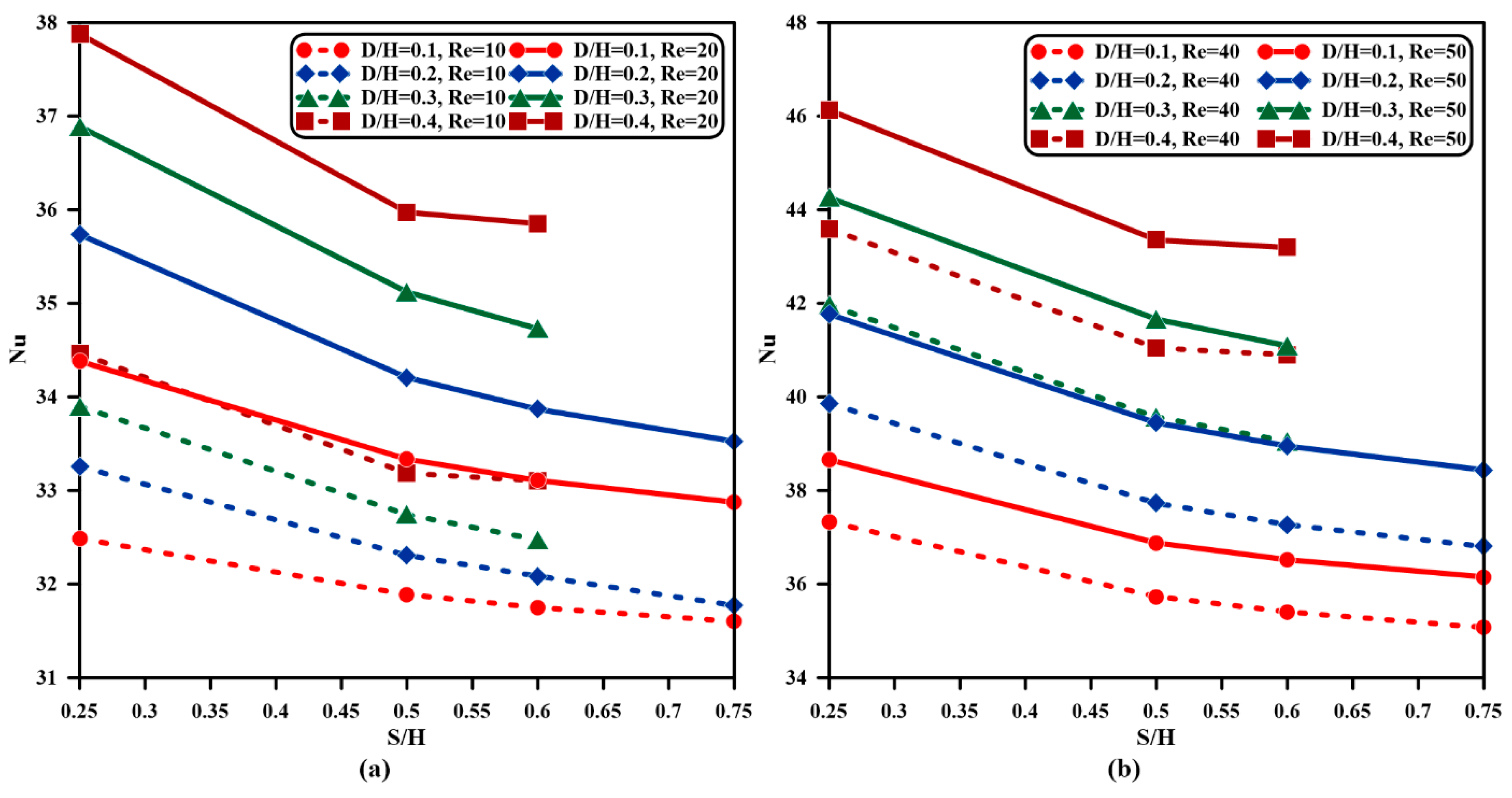
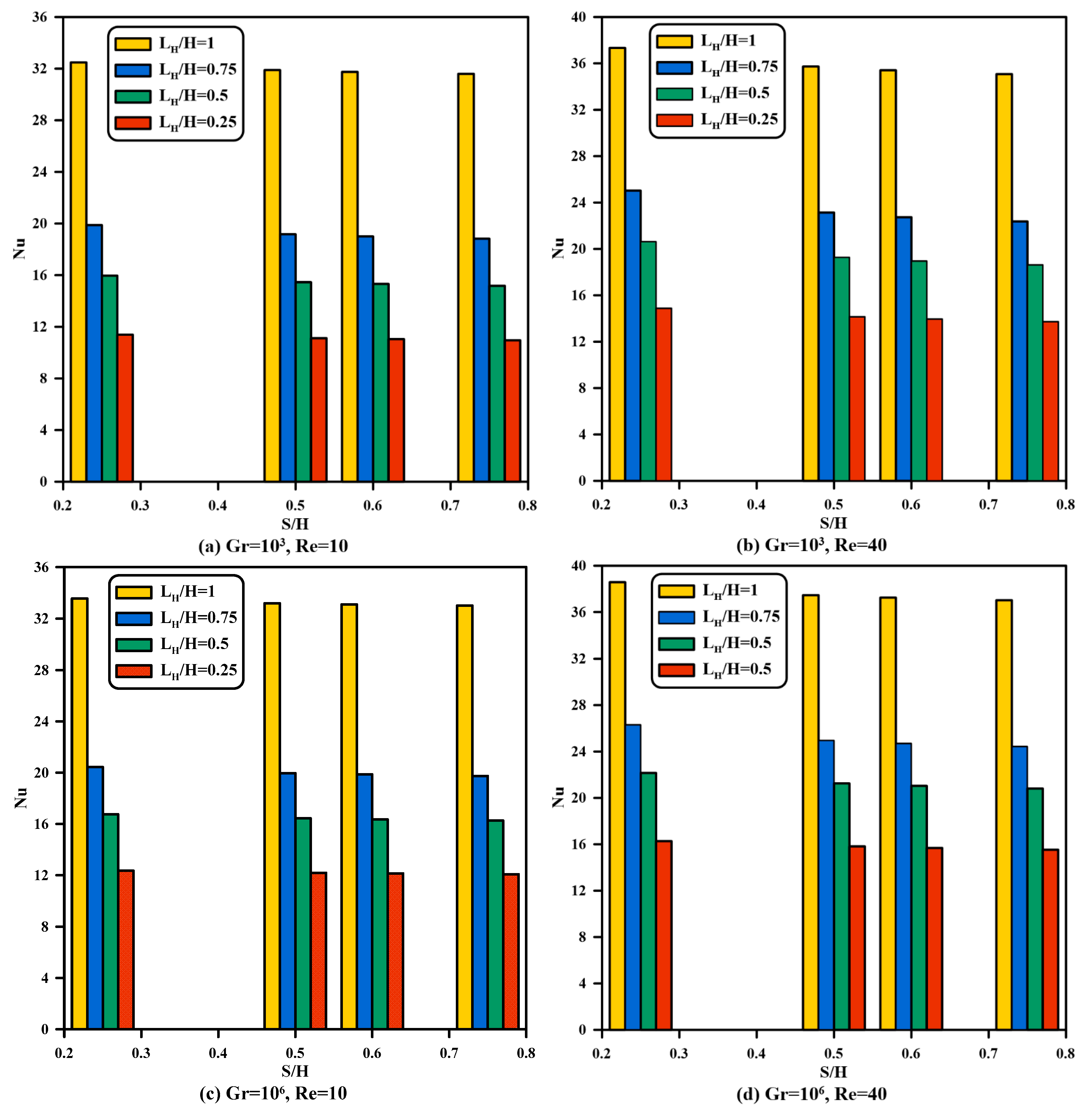
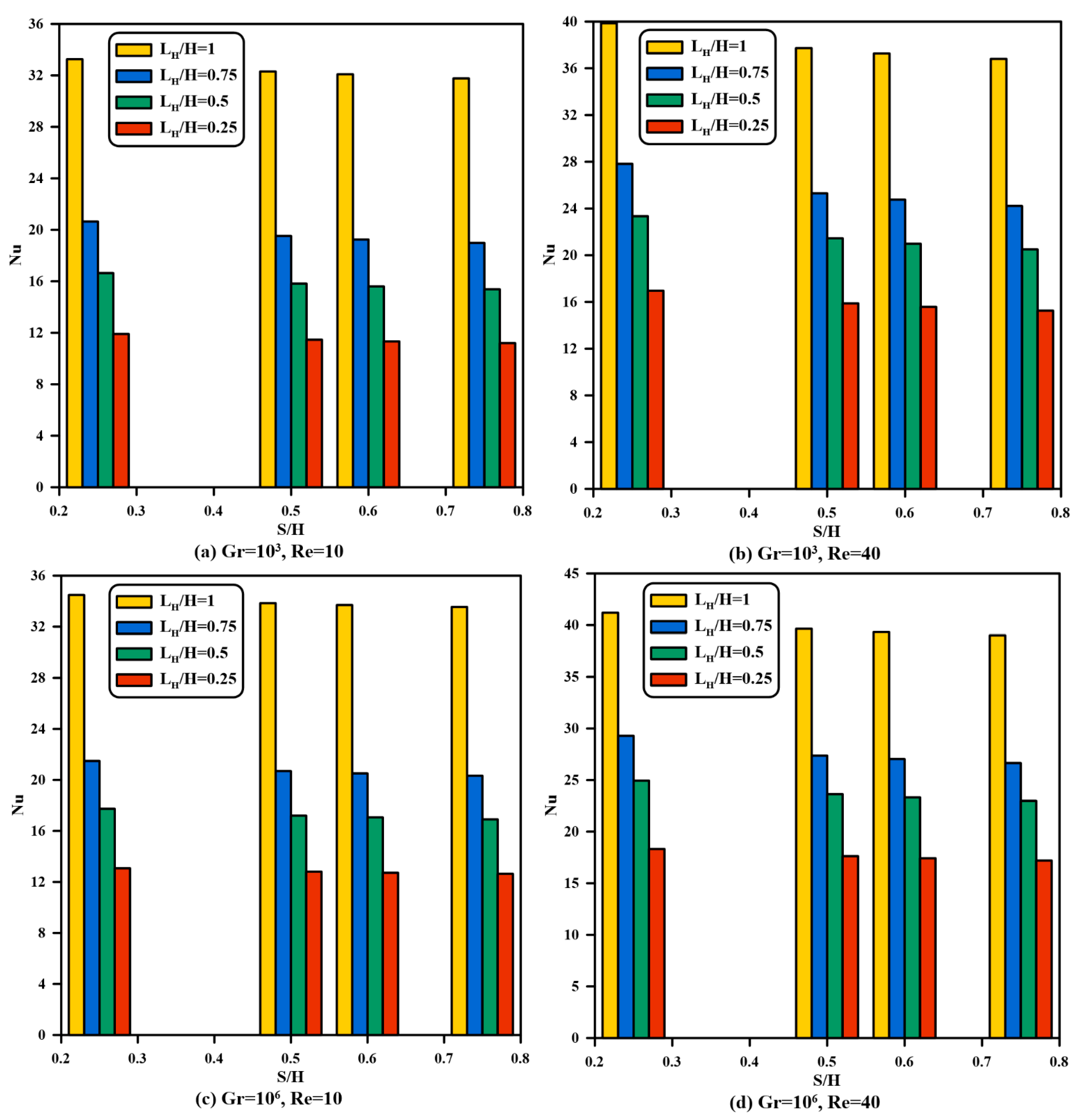
4.2. Effect of Partial Heating Length
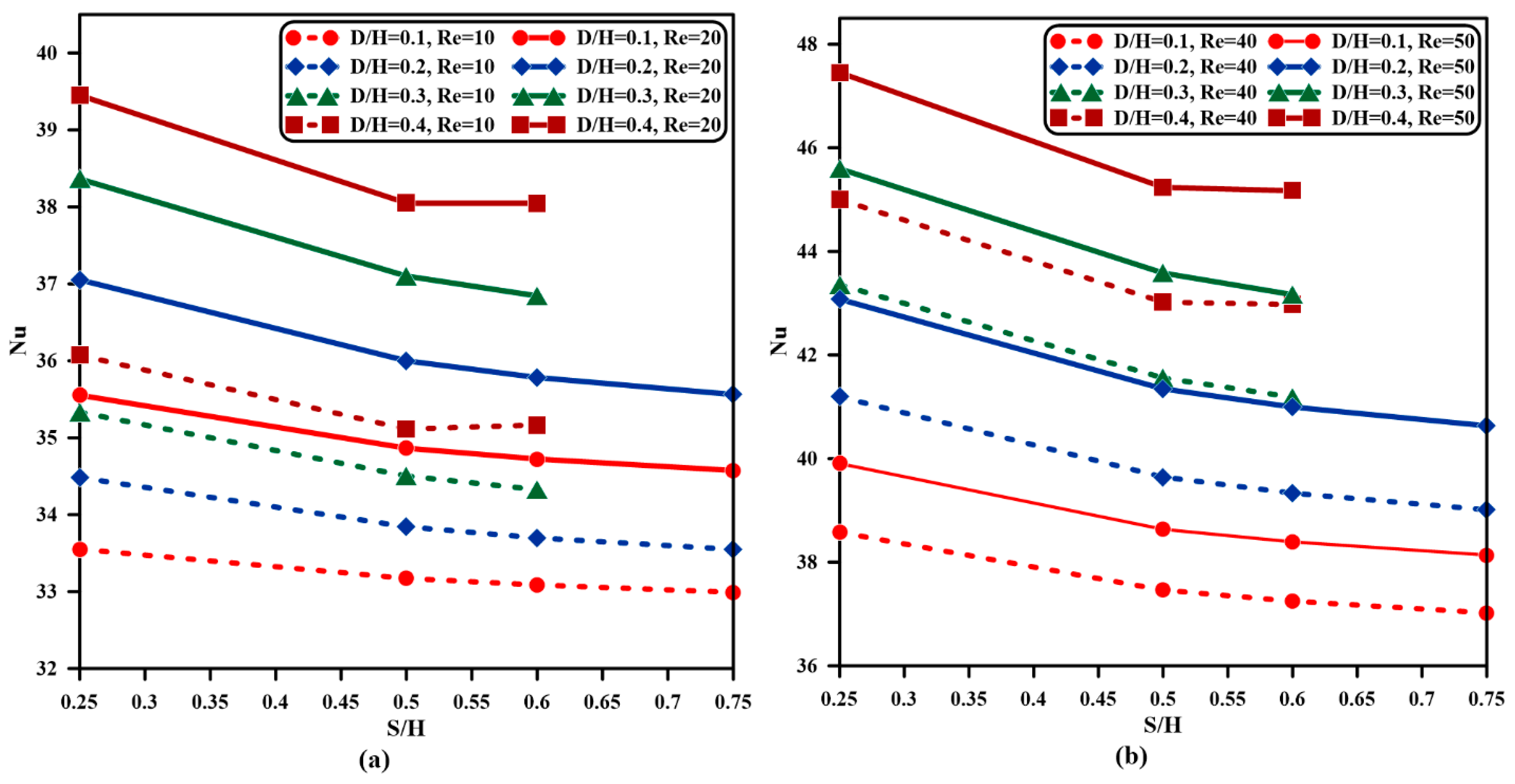
4.3. Effect of Outlet Vent Opening Location
5. Conclusions
- Increasing the inflow–outflow opening port aspect proportion creates a greater intensity in the streamline values, which implies higher forced convection currents and creates considerable distinctions in the temperature and flow fields.
- For a value of Grashof number , augmenting the Reynolds number from to does not alter the streamline and isotherms field either quantitively or qualitatively, but when the is taken as , it is observed that the streamline values increase monotonically. Whereas, when , the opposite behavior for fluid and heat transfer fields is specified, and a reduction in temperature as is amplified.
- Increasing from to leads to an adequate augment of the streamline and temperature fields for initiating higher inertia force and thus growing in fluid velocity corresponding to other heating length ratios.
- Isotherm and streamlines are intensified, and the thermal boundary layer becomes more distinct. Thus, there is a higher temperature distribution inside the cavity when the outlet port location is moved upward.
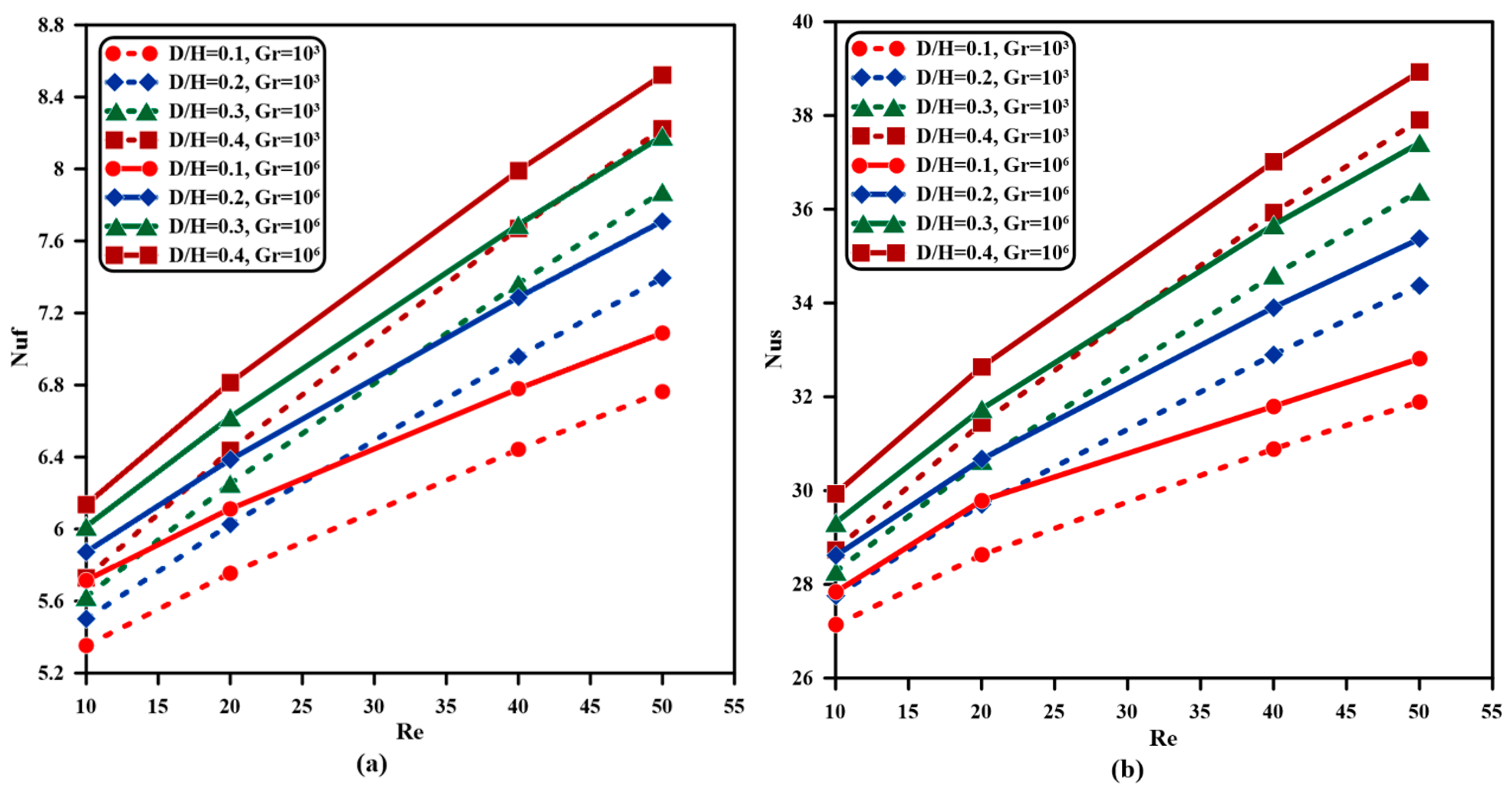
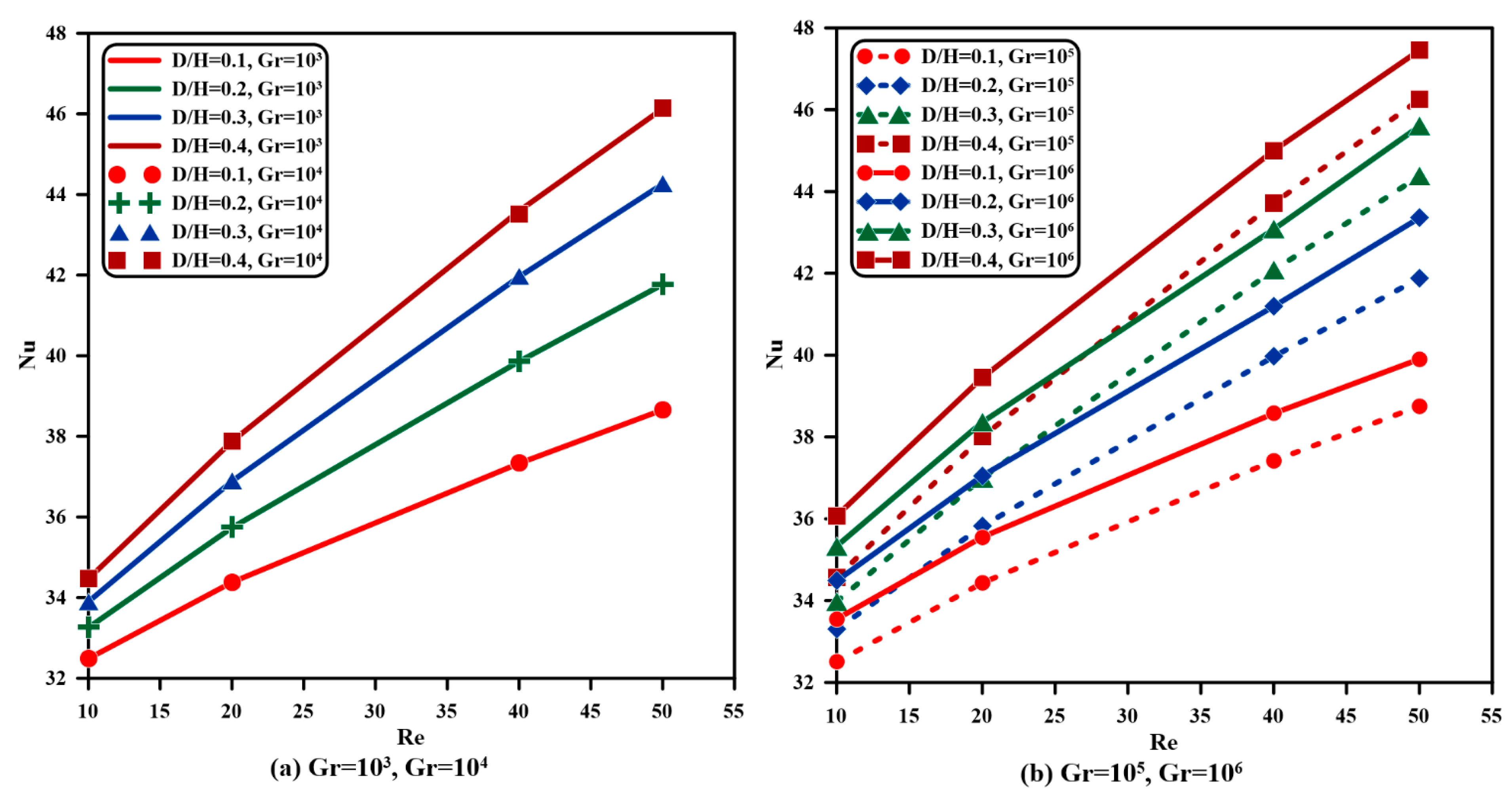
- Fluid and solid Nusselt numbers rise as the Grashof and Reynolds numbers and vent aspect ratio is augmented. Raising the from to at and creates a rise of in fluid-phase and in solid-phase Nusselt numbers, and they increase by and , respectively, as grows from to when and .
- The levitation inflow to outflow ports aspect proportion increase from to at and results in a growth of in fluid-phase and in solid-phase Nusselt numbers.
- Quantitively, the increase in the average Nusselt number as a sum of fluid- and solid-phase Nusselt numbers is almost the same as the increase in each phase individually.
- Nusselt number values do not change as the Grashof number increases from to , while raising the Grashof number from to enhances the Nusselt number.
- Raising from to intensifies with a smaller proportion, whereas raising from to increases with a higher percentage than from to ; when , , and , increases by , , and as , increases by , , and once is amplified from to , to , and to respectively.
- The average Nusselt number decreases as the outflow vent location is shifted towards the upper cavity right wall; at and , decreases by , , , and as , , , and , respectively, when is shifted from position to , while at and , reduces by , , , and when , , , and , respectively.
- For all heating length ratios, the Nusselt number decreases as the outlet vent location ratio increases, and this reduction is higher when ; as , , , and , diminishes by once is raised from to , while when , the reduction becomes , and when , the decreasing percentages are and respectively.
- The presented numerical model and constructed in-home computer code were verified and validated in contrast to accessible published numerical results, confirming their consistency within the studied relevant parameters range. Even though experimental results for the particular problem configuration are not reachable, this constraint is accepted, and experimental work for this problem will be focused on in the future.
6. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PPI | Pores Per Inch |
References
- Selimefendigil, F.; Oztop, H.F. Convection and Phase Change in a Lid-Driven Trapezoidal Vented Cavity with Encapsulated PCM under Non-Uniform Magnetic Field by Using Ternary Nanofluid. Therm. Sci. Eng. Prog. 2024, 48, 102424. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer Science & Business Media: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Abdulwahed, A.S.; Ali, L.F. Numerical Investigation of Natural Convection in a Square Enclosure Partially Filled with Horizontal Layers of a Porous Medium. Heat Transf. 2023, 52, 874–889. [Google Scholar] [CrossRef]
- Zachi, F.J.; Ali, L.F. Experimental Study of Natural Convection Heat Transfer on an Enclosure Partially Filled Porous Medium Heated from below by Constant Heat Flux. AIP Conf. Proc. 2023, 2651, 050002. [Google Scholar] [CrossRef]
- Alkinani, I.H.; Ali, L.F. 2022 Natural Convection in Annulus between Two Concentric Cylinders Partially Filled with Metal Foam Distributed with New Suggested Design. In IOP Conference Series: Earth and Environmental Science; IOP Publishing Ltd.: Bristol, UK, 2024. [Google Scholar] [CrossRef]
- Ali, L.F.; Humaidi, A.J. Offset Temperature and Amplitude–Frequency Effect on Convection Heat Transfer in Partially Gradient Porous Cavity with Different Outlet Port Locations. Processes 2025, 13, 2279. [Google Scholar] [CrossRef]
- Ali, L.F.; Togun, H.; Sadeq, A.M. Effect of Heated Wall Corrugation on Thermal Performance in an L-Shaped Vented Cavity Crossed by Metal Foam Saturated with Copper-Water Nanofluid. Computation 2025, 13, 218. [Google Scholar] [CrossRef]
- Ali, L.F.; AL-Samarraie, S.A.; Humaidi, A.J. Performance of Double Pipe Heat Exchanger—Partially Occupied by Metal Foam—Is Better Enhanced Using Robust Adaptive Barrier Function-Based Sliding Mode Control. Energies 2025, 18, 4671. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 1995. [Google Scholar]
- Daungthongsuk, W.; Wongwises, S. A Critical Review of Convective Heat Transfer of Nanofluids. Renew. Sustain. Energy Rev. 2007, 11, 797–817. [Google Scholar] [CrossRef]
- Mahmoudi, Y.; Hooman, K.; Vafai, K. Convective Heat Transfer in Porous Media; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Tien, H.-C.; Chiang, K.-S. Non-Darcy Flow and Heat Transfer in a Porous Insulation with Infiltration and Natural Convection. J. Mar. Sci. Technol. 1999, 7, 8. [Google Scholar]
- Ghazanfarian, J.; Abbassi, A. Mixed Convection in a Square Cavity Filled with a Porous Medium and Different Exit Port Position. J. Porous Media 2007, 10, 701–718. [Google Scholar] [CrossRef]
- Bhuiyan, A.A.; Banna, M.H.; Barna, S.F.; Amin, M.R.; Sadrul Islam, A.K.M. Numerical Modelling of Thermal Characteristics in a Microstructure Filled Porous Cavity with Mixed Convection. Int. J. Heat Mass Transf. 2016, 93, 464–476. [Google Scholar] [CrossRef]
- Mahmud, S.; Pop, I. Mixed Convection in a Square Vented Enclosure Filled with a Porous Medium. Int. J. Heat Mass Transf. 2006, 49, 2190–2206. [Google Scholar] [CrossRef]
- Krishna Murthy, S.V.S.S.N.; Kumar, B.V.R. Non-Darcy Mixed Convection in a Porous Square Enclosure under Suction/Injection Effects with a Non-Isothermal Vertical Wall. Numer. Heat Transf. A Appl. 2010, 57, 580–602. [Google Scholar] [CrossRef]
- Rathish Kumar, B.V.; Krishna Murthy, S.V.S.S.N.V.G. Mixed Convection in a Non-Darcian Fluid Saturated Square Porous Enclosure under Multiple Suction Effect. Int. J. Heat Mass Transf. 2010, 53, 5764–5773. [Google Scholar] [CrossRef]
- Krishna Murthy, S.V.S.S.N.; Kumar, B.V.R. Darcy Mixed Convection in a Fluid Saturated Square Porous Enclosure under Multiple Suction Effect. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 602–617. [Google Scholar] [CrossRef]
- Behzadi, T.; Shirvan, K.M.; Mirzakhanlari, S.; Sheikhrobat, A.A. Numerical Simulation on Effect of Porous Medium on Mixed Convection Heat Transfer in a Ventilated Square Cavity. Procedia Eng. 2015, 127, 221–228. [Google Scholar] [CrossRef][Green Version]
- Ali, L.F. Natural and Mixed Convection in Square Vented Enclosure Filled with Metal Foam. J. Eng. 2015, 21, 60–79. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Roşca, N.C.; Roşca, A.V.; Pop, I. Mixed Convection Heat Transfer in a Square Porous Cavity Filled with a Nanofluid with Suction/Injection Effect. Comput. Math. Appl. 2018, 76, 2665–2677. [Google Scholar] [CrossRef]
- Ataei-Dadavi, I.; Chakkingal, M.; Kenjeres, S.; Kleijn, C.R.; Tummers, M.J. Experiments on Mixed Convection in a Vented Differentially Side-Heated Cavity Filled with a Coarse Porous Medium. Int. J. Heat Mass Transf. 2020, 149, 119238. [Google Scholar] [CrossRef]
- Ahmed, S.E. Caputo Fractional Convective Flow in an Inclined Wavy Vented Cavity Filled with a Porous Medium Using Al2O3—Cu Hybrid Nanofluids. Int. Commun. Heat Mass Transf. 2020, 116, 104690. [Google Scholar] [CrossRef]
- Ullah, N.; Nadeem, S.; Saleem, A. Finite Element Analysis of Convective Nanofluid Equipped in Enclosure Having Both Inlet and Outlet Zones. J. Taiwan Inst. Chem. Eng. 2020, 113, 428–441. [Google Scholar] [CrossRef]
- Alawee, W.H.; Al-Sumaily, G.F.; Dhahad, H.A.; Thompson, M.C. Numerical Analysis of Non-Darcian Mixed Convection Flows in a Ventilated Enclosure Filled with a Fluid-Saturated Porous Medium. Therm. Sci. Eng. Prog. 2021, 24, 100922. [Google Scholar] [CrossRef]
- Hazra, C.; Biswas, N.; Manna, N.K. Thermal Magneto-Hydrodynamics in a Ventilated Porous Enclosure. Sādhanā 2020, 45, 224. [Google Scholar] [CrossRef]
- Hussain, S.; Öztop, H.F.; Alsharif, A.M.; Ertam, F. Mixed Bioconvection of Nanofluid of Oxytactic Bacteria through a Porous Cavity with Inlet and Outlet under Periodic Magnetic Field Using Artificial Intelligence Based on LightGBM Algorithm. Therm. Sci. Eng. Prog. 2024, 50, 102589. [Google Scholar] [CrossRef]
- Khanafer, K.M.; Chamkhaa, A.J. Mixed Convection in a Lid-Driven Enclosure Filled with a Fluid-Saturated Porous Medium. PERGAMON Int. J. Heat Mass Transf. 1999, 42, 2465–2481. [Google Scholar] [CrossRef]
- Al-Amiri, A.M. Analysis of momentum and energy transfer in a lid-driven cavity filled with a porous medium. Int. J. Heat Mass Transf. 2000, 43, 3513–3527. [Google Scholar] [CrossRef]
- Oztop, H.F. Combined Convection Heat Transfer in a Porous Lid-Driven Enclosure Due to Heater with Finite Length. Int. Commun. Heat Mass Transf. 2006, 33, 772–779. [Google Scholar] [CrossRef]
- Kandaswamy, P.; Muthtamilselvan, M.; Lee, J. Prandtl Number Effects on Mixed Convection in a Lid-Driven Porous Cavity. J. Porous Media 2008, 11, 791–801. [Google Scholar] [CrossRef]
- Jeng, T.M.; Tzeng, S.C. Heat Transfer in a Lid-Driven Enclosure Filled with Water-Saturated Aluminum Foams. Numer. Heat Transf. A Appl. 2008, 54, 178–196. [Google Scholar] [CrossRef]
- Basak, T.; Roy, S.; Singh, S.K.; Pop, I. Analysis of Mixed Convection in a Lid-Driven Porous Square Cavity with Linearly Heated Side Wall(s). Int. J. Heat Mass Transf. 2010, 53, 1819–1840. [Google Scholar] [CrossRef]
- Basak, T.; Krishna Pradeep, P.V.; Roy, S.; Pop, I. Finite Element Based Heatline Approach to Study Mixed Convection in a Porous Square Cavity with Various Wall Thermal Boundary Conditions. Int. J. Heat Mass Transf. 2011, 54, 1706–1727. [Google Scholar] [CrossRef]
- Ramakrishna, D.; Basak, T.; Roy, S.; Pop, I. Numerical Study of Mixed Convection within Porous Square Cavities Using Bejan’s Heatlines: Effects of Thermal Aspect Ratio and Thermal Boundary Conditions. Int. J. Heat Mass Transf. 2012, 55, 5436–5448. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Pan, K.L. Numerical Simulation on Mixed Convection in a Porous Lid-Driven Cavity with Nonuniform Heating on Both Side Walls. Numer. Heat Transf. A Appl. 2012, 61, 101–121. [Google Scholar] [CrossRef]
- Basak, T.; Roy, S.; Chamkha, A.J. A Peclet Number Based Analysis of Mixed Convection for Lid-Driven Porous Square Cavities with Various Heating of Bottom Wall. Int. Commun. Heat Mass Transf. 2012, 39, 657–664. [Google Scholar] [CrossRef]
- Rahman, M.M.; Oztop, H.F.; Saidur, R.; Mekhilef, S.; Al-Salem, K. Unsteady Mixed Convection in a Porous Media Filled Lid-Driven Cavity Heated by a Semi-Circular Heaters. Therm. Sci. 2015, 19, 1761–1768. [Google Scholar] [CrossRef]
- Muthtamilselvan, M.; Sureshkumar, S. Convective Heat Transfer in a Porous Enclosure Saturated by Nanofluid with Different Heat Sources. Nonlinear Eng. 2018, 7, 1–16. [Google Scholar] [CrossRef]
- Hussain, S.; Mehmood, K.; Sagheer, M.; Yamin, M. Numerical Simulation of Double Diffusive Mixed Convective Nanofluid Flow and Entropy Generation in a Square Porous Enclosure. Int. J. Heat Mass Transf. 2018, 122, 1283–1297. [Google Scholar] [CrossRef]
- Muthukumar, S.; Sureshkumar, S.; Chamkha, A.J.; Muthtamilselvan, M.; Prem, E. Combined MHD Convection and Thermal Radiation of Nanofluid in a Lid-Driven Porous Enclosure with Irregular Thermal Source on Vertical Sidewalls. J. Therm. Anal. Calorim. 2019, 138, 583–596. [Google Scholar] [CrossRef]
- Marzougui, S.; Mebarek-Oudina, F.; Magherbi, M.; Mchirgui, A. Entropy Generation and Heat Transport of Cu–Water Nanoliquid in Porous Lid-Driven Cavity through Magnetic Field. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 2047–2069. [Google Scholar] [CrossRef]
- Laidoudi, H.; Abderrahmane, A.; Saeed, A.M.; Guedri, K.; Weera, W.; Younis, O.; Mourad, A.; Marzouki, R. Irreversibility Interpretation and MHD Mixed Convection of Hybrid Nanofluids in a 3D Heated Lid-Driven Chamber. Nanomaterials 2022, 12, 1747. [Google Scholar] [CrossRef]
- Maneengam, A.; Bouzennada, T.; Abderrahmane, A.; Guedri, K.; Weera, W.; Younis, O.; Bouallegue, B. Numerical Study of Lid-Driven Hybrid Nanofluid Flow in a Corrugated Porous Cavity in the Presence of Magnetic Field. Nanomaterials 2022, 12, 2390. [Google Scholar] [CrossRef]
- Yaseen, D.T.; Salih, S.M.; Ismael, M.A. Effect of the Lid-Driven on Mixed Convection in an Open Flexible Wall Cavity with a Partially Heated Bottom Wall. Int. J. Therm. Sci. 2023, 188, 108213. [Google Scholar] [CrossRef]
- Yaseen, D.T.; Ismael, M.A.; Salih, S.M. Discrete Heating of Turbulent FSI in a Vented Lid-Driven Enclosure. Int. Commun. Heat Mass Transf. 2024, 158, 107910. [Google Scholar] [CrossRef]
- Ghashim, S.L. A Mathematical Analysis of Nanoparticles on Heat Transfer in a Circular Pipe. Case Stud. Therm. Eng. 2021, 28, 101524. [Google Scholar] [CrossRef]
- Al-Farhany, K.; Abdulsahib, A.D. Study of Mixed Convection in Two Layers of Saturated Porous Medium and Nanofluid with Rotating Circular Cylinder. Prog. Nucl. Energy 2021, 135, 103723. [Google Scholar] [CrossRef]
- Messaoud, H.; Adel, S.; Ouerdia, O. Mixed Convection Heat Transfer of a Nanofluid in a Square Ventilated Cavity Separated Horizontally by a Porous Layer and Discrete Heat Source. Arch. Thermodyn. 2023, 44, 87–114. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Chamkha, A.J.; Saleh, H.; Hashim, I. Natural Convection Flow of a Nanofluid in an Inclined Square Enclosure Partially Filled with a Porous Medium. Sci. Rep. 2017, 7, 2357. [Google Scholar] [CrossRef] [PubMed]
- Balla, C.S.; Kishan, N.; Gorla, R.S.R.; Gireesha, B.J. MHD Boundary Layer Flow and Heat Transfer in an Inclined Porous Square Cavity Filled with Nanofluids. Ain Shams Eng. J. 2017, 8, 237–254. [Google Scholar] [CrossRef]
- Xu, H.; Gong, L.; Huang, S.; Xu, M. Flow and Heat Transfer Characteristics of Nanofluid Flowing through Metal Foams. Int. J. Heat Mass Transf. 2015, 83, 399–407. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. Forced Convection in High Porosity Metal Foams. J. Heat Transf. 2000, 122, 557–565. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Taylor & Francis Publishers: New York, NY, USA, 1980. [Google Scholar] [CrossRef]



| Property | |||||
|---|---|---|---|---|---|
| Water | |||||
| Al2O3 | - |
| No. of Elements | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Relevant Parameter | Range of Parameter | Selected Case | Minimum–Maximum Nusselt Number | Percentage Variation |
|---|---|---|---|---|
| Reynolds number, | , | |||
| Grashof number, | , , | |||
| Inflow and outflow ports ratio, | , , , | |||
| Outflow aperture port position ratio, | , , , | |||
| Discrete partial heating length ratio, | , , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, L.F.; AL-Samarraie, S.A.; Humaidi, A.J. Discrete Heating and Outlet Ports’ Influences on Thermal Convection in Lid-Driven Vented Cavity System with Thermal Dispersion and LTNE Effects. Processes 2025, 13, 3429. https://doi.org/10.3390/pr13113429
Ali LF, AL-Samarraie SA, Humaidi AJ. Discrete Heating and Outlet Ports’ Influences on Thermal Convection in Lid-Driven Vented Cavity System with Thermal Dispersion and LTNE Effects. Processes. 2025; 13(11):3429. https://doi.org/10.3390/pr13113429
Chicago/Turabian StyleAli, Luma F., Shibly A. AL-Samarraie, and Amjad J. Humaidi. 2025. "Discrete Heating and Outlet Ports’ Influences on Thermal Convection in Lid-Driven Vented Cavity System with Thermal Dispersion and LTNE Effects" Processes 13, no. 11: 3429. https://doi.org/10.3390/pr13113429
APA StyleAli, L. F., AL-Samarraie, S. A., & Humaidi, A. J. (2025). Discrete Heating and Outlet Ports’ Influences on Thermal Convection in Lid-Driven Vented Cavity System with Thermal Dispersion and LTNE Effects. Processes, 13(11), 3429. https://doi.org/10.3390/pr13113429







