1. Introduction
To manufacture a product, effective and efficient utilization of technical personnel, physical resources, and information is crucial [
1,
2]. The responsibility for this crucial task is generally assigned to engineering management [
3]. Engineering management is a diverse field that combines the principles of engineering, business administration, and management to plan, design, organize, supervise, and lead technical projects, teams, and organizations. It applies engineering and management principles to ensure that engineering projects are completed on time, within budget, and to the required quality standards. The responsibilities of an engineering manager include coordinating and collaborating with different stakeholders involved in a project, such as engineers, clients, vendors, and regulatory bodies while managing people, resources, and risk. Engineering management encompasses a broad range of topics, including technology management, quality control, project management, cost analysis, design, procurement, construction, commissioning, project control, quality assurance/quality control, project service, and more. Ultimately, engineering management aims to effectively and efficiently utilize technical personnel, physical resources, and information to produce products or services that meet an organization’s goals and objectives [
3,
4,
5,
6].
The resource allocation, decision-making processes, and the overall organizational strategy are handled by manufacturing management to ensure effective operations [
1,
7,
8,
9]. In this regard, manufacturing management can significantly impact engineering management [
10].
Based on the provided definition, manufacturing management refers to the planning, coordination, and control of the production process to ensure that goods are produced efficiently, on time, and to the required quality standards. It involves managing the resources and activities involved in the manufacturing process, including people, materials, equipment, and information [
11].
Inefficient manufacturing management can lead to the suboptimal use of resources, delays in production schedules, and reduced productivity, negatively impacting engineering management. On the other hand, by implementing effective manufacturing management systems, organizations can optimize resource allocation and streamline the decision-making processes. This can result in improved production processes and increased efficiency in utilizing technical personnel and physical resources [
8,
12,
13].
Often, manufacturing environments may experience various rapid and sudden changes, uncertainty, unforeseen risks, unpredictable events, and/or uncontrollable fluctuations [
14]. Considering that manufacturing management assumes the role of overseeing resource allocation, decision-making processes, and the overarching organizational strategy, it is crucial that the manufacturing management is capable of identifying, analyzing, and mitigating potential risks that may arise during the production process. This includes risks related to equipment failure, supply chain disruptions, safety hazards, quality issues, and other factors that may impact the production process or product quality [
15].
The poor design of manufacturing processes can significantly contribute to the occurrence and propagation of operational risks [
16,
17,
18]. A poorly designed manufacturing process architecture lacks an alignment with good design principles, leading to complexity, low modularity, inefficient resource allocation, and limited flexibility. This deficiency increases the risk of errors, defects, and safety hazards while hindering adaptation to evolving requirements and unforeseen challenges. Inefficient processes drive up production costs, waste materials, and introduce more errors. They also impede problem identification and resolution, resulting in delays and complications. Poor process design also limits visibility and hampers process improvement over time [
16]. On the other hand, A well-designed manufacturing process architecture offers benefits to manufacturing and engineering management. It facilitates bottleneck detection and improvement identification, supported by comprehensive documentation and efficient communication channels. Real-time monitoring enables prompt issue detection and resolution, enhancing overall efficiency [
19]. Effective design is crucial in minimizing the likelihood of operational risks and their potential impact on manufacturing processes [
14].
The design of manufacturing processes has a cascading effect on engineering management in addition to manufacturing management. In fact, the design and management of manufacturing processes have a significant impact on engineering management. Engineering teams bear the responsibility of designing, implementing, and improving these processes, which necessitates specific skills and expertise aligned with the complexity and level of automation employed. Furthermore, the effectiveness of engineering management systems, including quality control and continuous improvement programs, relies on the underlying architecture of manufacturing. Therefore, the design of manufacturing process architecture falls within the scope of engineering management responsibilities, offering an opportunity for them to make a substantial impact.
Achieving a well-designed architecture for manufacturing processes is crucial, and manufacturing management plays a pivotal role in contributing to engineering management. One of the most effective and critical ways in which manufacturing management can make this contribution is by actively participating in the design phase of a product. By involving manufacturing experts from the outset, potential production and assembly challenges can be identified and addressed proactively, resulting in an optimized manufacturing process. This collaborative approach ensures the development of an efficient and streamlined process, ultimately leading to the creation of high-quality products.
2. Design of Robust Architecture for Manufacturing Processes
When it comes to manufacturing processes, particularly in the face of environmental disturbances, the significance of robustness cannot be overstated. A robust design for manufacturing processes is key to ensuring that a manufacturing process can withstand, adapt to, and recover from any unforeseen disruptions that may arise.
Al-Refaie [
20] contributed to the understanding and modeling of robustness, highlighting the need for comprehensive methodologies that consider the various factors influencing performance. Koc et al. [
21] conducted a study on process parameter variation in worm hydroforming, aiming to optimize quality, robustness, and capability. They employed response surface analysis with a Box–Behnken design to optimize parameters and evaluate process capability using univariate indices, such as Cp and Cpk. However, the study did not consider the interrelationships among response variables and noise variables, indicating the need to account for these factors in robustness assessments. The challenges associated with noise variables in robustness studies were highlighted by Mevik et al. [
22] and Robinson et al. [
23]. Their work emphasized the limitations of certain designs, such as BBD, in effectively accounting for noise variables, which are crucial for studying robustness.
Scholz-Reiter et al. [
24] suggested improving robustness by enhancing production capacities through resource utilization optimization. They explore how optimizing resource utilization can contribute to robustness in production systems. Karimi and Djokoto [
25] also discussed the topic of robust stability analysis, further emphasizing the importance of accounting for uncertainties and disturbances in manufacturing processes. Kusumoto et al. [
26] also discuss robust management in manufacturing systems, focusing on product and process robustness. They emphasize the importance of state-space analysis and structured analysis tools in achieving robustness. Alem and Morabito [
27] implement a robust optimization scheduling approach in furniture manufacturing. Their study surpasses deterministic worst-case methods in most situations, demonstrating the effectiveness of robust optimization techniques in improving robustness in manufacturing processes. Meyer et al. [
28] conducted research to analyze the influence of capacity adjustments on the performance robustness of different operational key figures in manufacturing systems. Their study investigated the trade-off between the robustness of operational performance and cost efficiency, emphasizing the importance of systems being able to withstand fluctuations and disturbances to maintain high performance and profitability. Mondal et al. [
29] focused on the measurement and modeling of robustness in serial multi-stage manufacturing processes. They employed sensitivity analysis and sensitivity matrices to evaluate and measure the robustness of these processes. The authors highlighted the complexities and interactions present in multi-stage processes, emphasizing the need for a comprehensive understanding of robustness measurement. However, they acknowledged that their methods were more suitable for large batch production scenarios and may not be effective in situations such as one-kilogram production. Additionally, Mondal et al. [
30] introduced a modeling approach that incorporated input-output and in-process parameters to assess and model process robustness in manufacturing systems. They demonstrated the application of their approach through a numerical example involving a two-stage worm gear manufacturing process. Malmström et al. [
31] explored the relationship between resource constraints and robustness in smaller companies. Their findings contribute to understanding the challenges faced by these companies in achieving and maintaining high levels of robustness. Montgomery [
32] emphasized the importance of interaction effects and noise variables in achieving robustness in design and manufacturing. He highlighted the need to understand their impact and efficiently incorporate them in experiments. Montgomery also discussed the relationship between process capability and robustness, emphasizing the need for further modeling and understanding. These insights contribute to the understanding of robust design and process robustness. Xiong et al. [
33] conducted research on evaluating the robustness of production systems. They introduced indicators related to material variances, free capacity, and the overlap between slack periods and machine failure. Their studies explored the system’s ability to handle disruptions and maintain smooth operations. Additionally, they focused on evaluating robustness in a flexible job shop problem using the concept of float time. Their research provided valuable insights into the impact of machine and tool breakdowns on the robustness of production systems. Becker et al. [
34] defined MS robustness as the ratio of feasible operations with disruptions of a specific machine to the total feasible operations without disruptions. Sharda and Banerjee [
35] presented a mathematical optimization model for designing a robust manufacturing system (MS). Their model incorporated factors such as processing times, equipment failure and repairs, and product demand to improve performance in the face of uncertainties. The model aimed to minimize the makespan, the mean work-in-progress (WIP) time, and the number of machines, considering these uncertainties during the design process. Stricker and Lanza (2014) [
36] conducted research that supports the importance of robustness in production systems. They utilized the Value-at-Risk (VaR) measure as an indicator of robustness and explored its implications in uncertain environments. Their work contributes to the understanding of robustness and its role in the success of production systems. Beber and Becker (2014) focused on exploring the relationship between topological characteristics and dynamic behavior in manufacturing networks. They highlighted the importance of the network’s static structure, represented by its topology, and the material flow within the network in influencing factors such as performance and robustness [
37]. Varas et al. (2014) contributed to the field of robust optimization by demonstrating its benefits in reducing variability and uncertainty in production schedules. Their work specifically focused on a sawmill scenario, highlighting the effectiveness of robust optimization strategies [
38]. Benderbal et al. [
39] emphasized the significance of technical disruptions in production systems. They analyzed the impact of these disruptions on system robustness and focused on optimizing schedules and designs. Benderbal et al. [
39] explored robustness in a reconfigurable production system using an average-based measure that quantified potential delays from machine failure. Their study highlighted various approaches to measuring robustness, including time span, float time, and average-based measures, providing insights into the system’s ability to handle variations and disruptions. Tian et al. [
40] introduced sensitivity analysis to analyze the effects of machining parameters in the electrical discharge machining process. Their research focused on understanding the sensitivity of these parameters and their impact on the overall process. Putnik et al. [
41] studied the impact of system size and network structure on the robustness of production networks under changing demand. They defined robustness as the ratio of production rate with perturbations to production rate without perturbations, exploring the relationship between system characteristics and robustness. Their research assessed robustness in manufacturing systems without specifying the approach or measure used. Stricker et al. [
42], their work reinforces the notion that high robustness is associated with costs. They provide insights into the trade-off between robustness and cost considerations in manufacturing systems. Giannetti and Ransing [
43] improved output quality in the steel foundry industry using tolerance synthesis to assess process robustness. Their robustness indicator, a likelihood ratio, compared the likelihood of achieving the expected output using modified input parameter regions. Validation of their methodology demonstrated its potential to improve output quality. Zhao et al. [
44] investigated the performance evaluation of the axial ventilator in the turbofan engine lubrication system. Their study aimed to assess the sensitivity of the ventilator’s performance to different factors. Meyer [
45] examined the role of redundancy in achieving robustness in manufacturing system performance. The study derived specific definitions of robustness and redundancy for the manufacturing context and explored indicators such as nestedness and elementary flux modes. Analysis of different manufacturing system configurations revealed a significant correlation between redundancy and robustness. These findings emphasized the potential of incorporating robustness in the design of manufacturing systems. Boorla and Howard [
46] contribute to the discussion of robust management in manufacturing systems. They highlight the significance of robustness measures and analysis in ensuring the resilience of products and manufacturing processes. Sakhaii et al. [
47] further contribute to the topic of technical disruptions in production systems. Their research explores the optimization of system characteristics and the impact of these disruptions. Moslemi et al. [
48] focus on modeling robustness in multistage manufacturing systems, introducing process capability as a surrogate measure of robustness. They utilize response surfaces and a robust coefficient estimation method to analyze quality characteristics. The results demonstrate the superiority of the robust multistage process and highlight the relationship between robustness and capability in multistage manufacturing. This research contributes to understanding robustness in multistage processes and the use of robustness indices as surrogates. Zeng and Yen [
49], their work focuses on the impact of global value chains on production systems. They highlight how optimizing costs in these chains can increase vulnerability to factors like geo-political disputes and transportation issues, further emphasizing the need for robustness.
Zhang et al. [
50], their research primarily focuses on ensuring robustness in manufacturing systems through technology control. They address the importance of technological advancements and control mechanisms in achieving robustness. Himmiche et al. [
51] conducted a study on the impact of disturbances and uncertainties on meeting deadlines in a production system. They evaluated various machine capacity plans and assessed the likelihood of meeting deadlines under these conditions. Additionally, their research focused on addressing technical disruptions, such as machine and tool breakdowns, and optimizing system characteristics to enhance robustness. Efthymiou et al. [
52] explore robustness in the aerospace domain, applying their metric in a supplier flow workshop. Their approach quantifies capability and enhances controllability across scenarios using likelihood-based indicators. The case study showcases the practical application of their approach, providing valuable insights into production system robustness in the aerospace industry. Pagone et al. [
53] focused on the association between high robustness and costs. They contribute to the understanding of the economic implications of achieving and maintaining robustness in manufacturing operations.
Frederico et al. [
54] addressed the challenges posed by digitization in production systems. They highlight the need for rapid adaptation to new technologies, business models, and competitors, underscoring the importance of robustness in these dynamic environments. Martín et al. [
55] illustrated the benefits of a robust optimization approach in achieving high robustness at lower costs in an automotive supplier context. Their study compared the performance of the robust optimization approach with heuristic planning approaches for production schedules, emphasizing the cost-effectiveness of the robust optimization strategy.
Hyder et al. [
56] tackled uncertainty and sustainability in cloud manufacturing, exploring tools and proposing a Collaborative Cloud Service Platform (CCSP) to enhance supplier-customer-manufacturer relations while considering robustness and sustainability in service composition. Stockmann et al. [
57] emphasized a holistic approach to assess robustness in production systems, considering tradeoffs between performance, resource requirements, and output. Their methodology evaluated robustness from an input-throughput-output perspective, connecting it with adjacent capabilities for a comprehensive understanding of production system robustness. Liang and Li [
58] explored cooperation uncertainty’s impact on robustness in manufacturing service systems (MSS). They proposed a methodology treating MSS as a network of service subsystems to identify critical paths and standardize cooperation mechanisms for enhanced robustness.
Table 1 presents a comprehensive overview of the significant aspects of the present study in comparison to the relevant studies found in the literature. The table showcases the diverse range of studies in the literature, which primarily concentrate on various aspects such as developing mathematical/statistical methods, presenting informative process capability indices, incorporating robust design principles, introducing useful robustness measures, and considering the complexity of interrelationships among manufacturing processes to tackle the issue of robustness in manufacturing process structure. Additionally, a select few of these studies also approach the problem from systems engineering perspective, specifically addressing the concept of system architecture. To achieve such robustness, a system engineering approach is adopted in the present study. This approach recognizes that all activities involved in forming the manufacturing process should be viewed as an integrated system, working together harmoniously to enhance its robustness. It is worth noting that within this category of studies, only a limited number of works propose modularization as an effective approach for achieving robustness in manufacturing processes.
Table 1 provides an overview of studies that utilize the Axiomatic Design (AD) theory to modularize the system architecture and contribute to the design of robust manufacturing processes. However, the literature review reveals that the focus has mainly been on the allocated architecture of the system, neglecting the significance of the process architecture in system robustness. According to the AD theory [
59], the physical components of the system, which are part of the physical architecture, are influenced by a set of process variables (such as men, machines, methods, and materials) belonging to the process architecture. Therefore, this study emphasizes the importance of considering modularity in the process architecture, as it indirectly supports modularity in the allocated architecture. In other words, examining the modularity of the process domain architecture is crucial for the effective allocation of components within the physical system. The literature currently lacks a clear understanding of how modularization of manufacturing process architecture can effectively enhance the robustness of the system architecture while minimizing system complexity. This gap emphasizes the need for a mathematical model that elucidates the relationship between manufacturing process architecture robustness and system architecture modularization. Such a model would provide valuable support to systems engineers in designing robust manufacturing process architecture.
The purpose of this study is to address this significant gap in the literature and develop a mathematical model that precisely defines the proposed approach. By clarifying the relationship between manufacturing process architecture and system architecture through modularization, the model aims to facilitate the creation of a robust characteristic in the manufacturing process architecture while ensuring controlled system complexity.
To modularize the system architecture and consider the identified modules more effectively, this study employs the DSM methodology.
This paper is organized as follows: the introduction provides an overview of the study;
Section 2 discusses the robust architecture for manufacturing processes, including a literature review and identification of research gaps;
Section 3 presents the background materials related to the topic;
Section 4 describes the research method and mathematical model development, specifically focusing on the relationship between “modularity” and the property of “robustness of manufacturing processes”. In this section, we present a case study and apply the robustness analysis method to the manufacturing processes of Barez Industrial Group, an Iranian company;
Section 5 concludes the paper by discussing the conclusions drawn from the robustness analysis method and providing practical recommendations.
3. Background Material
3.1. Robustness
There is a wide variety of definitions of robustness. According to Carlson and Doyle [
60], robustness is “the maintenance of some desired system characteristic despite fluctuations in the behavior of its component parts or its environment”. Fricke and Schulz [
61] define robustness as “a system’s ability to be insensitive towards changing environments. Robust systems deliver their intended functionality under varying operating conditions without being changed”. We use the definition by Barber and Salido [
62]: robustness is the ability of a system to withstand stress, pressure, perturbations, unpredictable changes, or variability in its operating environment without loss of functionality.
3.2. Axiomatic Design (AD) Theory
The Axiomatic Design (AD) Theory is a coherent framework rooted in techniques and logical thought processes aimed at conducting design activities in a systematic and scientific manner [
59]. The primary elements employed within AD encompass ‘Domains’, ‘Mapping and Zigzagging’, the ‘Independence (First) Axiom’, and the ‘Information (Second) Axiom’.
The Axiomatic Design (AD) method is a well-structured approach established to guide design activities across four distinct design domains: the ‘Customer Domain’, the ‘Functional Requirements (FRs) Domain’, the ‘Physical or Design Parameters (DPs) Domain’, and the ‘Process Variables (PVs) Domain’ (as depicted in
Figure 1). The customer domain encapsulates customer attributes (CAs). These attributes’ elements need to be transformed into functional requirements (FRs) and constraints (Cs) within the functional domain. To fulfill these FRs, design parameters (DPs) are established within the physical domain. Ultimately, to bring the system into production, process variables (PVs) are defined within the process domain. The design process operates as a dynamic interplay between two adjacent domains, cascading in a top-to-bottom manner, commencing at the system level and progressively delving into sublevels of finer detail until a comprehensive representation of the system of interest emerges. The linkage between two contiguous domains is aptly named the ‘zigzagging’ process, achieved by methodically breaking down the system into smaller design components (as illustrated in
Figure 1).
The AD theory offers two design axioms for gauging the quality of solutions and provides guidance on how to assess and choose from various alternatives [
59].
In allocation between functional and physical domains, the informational complexity of a design with a single FR and DP can be expressed as the logarithm of the reciprocal of the probability of the system success in fulfilling the FR (
P, Equation (1)), as follows:
where ‘
I’ denotes the information content, measured in bits (logarithm to base 2), and signifies the extent of effort needed to accomplish the given FR.
With the assumption of a uniform probability density function (pdf), the information content ‘
I’ can be formulated as depicted in the following Equation (2) (
Figure 2):
The system range’s extent is represented as SR, calculated from the probability density function of the FR. In essence, the SR of a particular FR signifies the performance range, PR, linked with the FR in question. The shared range’s size, CR, constitutes the segment of the earlier mentioned area within the design range, DR, as illustrated in
Figure 2. The DR defines the admissible scope linked to the relevant FR.
In the context of an uncoupled design involving n FRs (DPs), the aggregate information is formulated according to the following Equation (3):
where ‘
Pi’ represents the probability of FRi (DP
i) being fulfilled by DPi (PVi).
3.3. Design Structure Matrix (DSM) Methodology
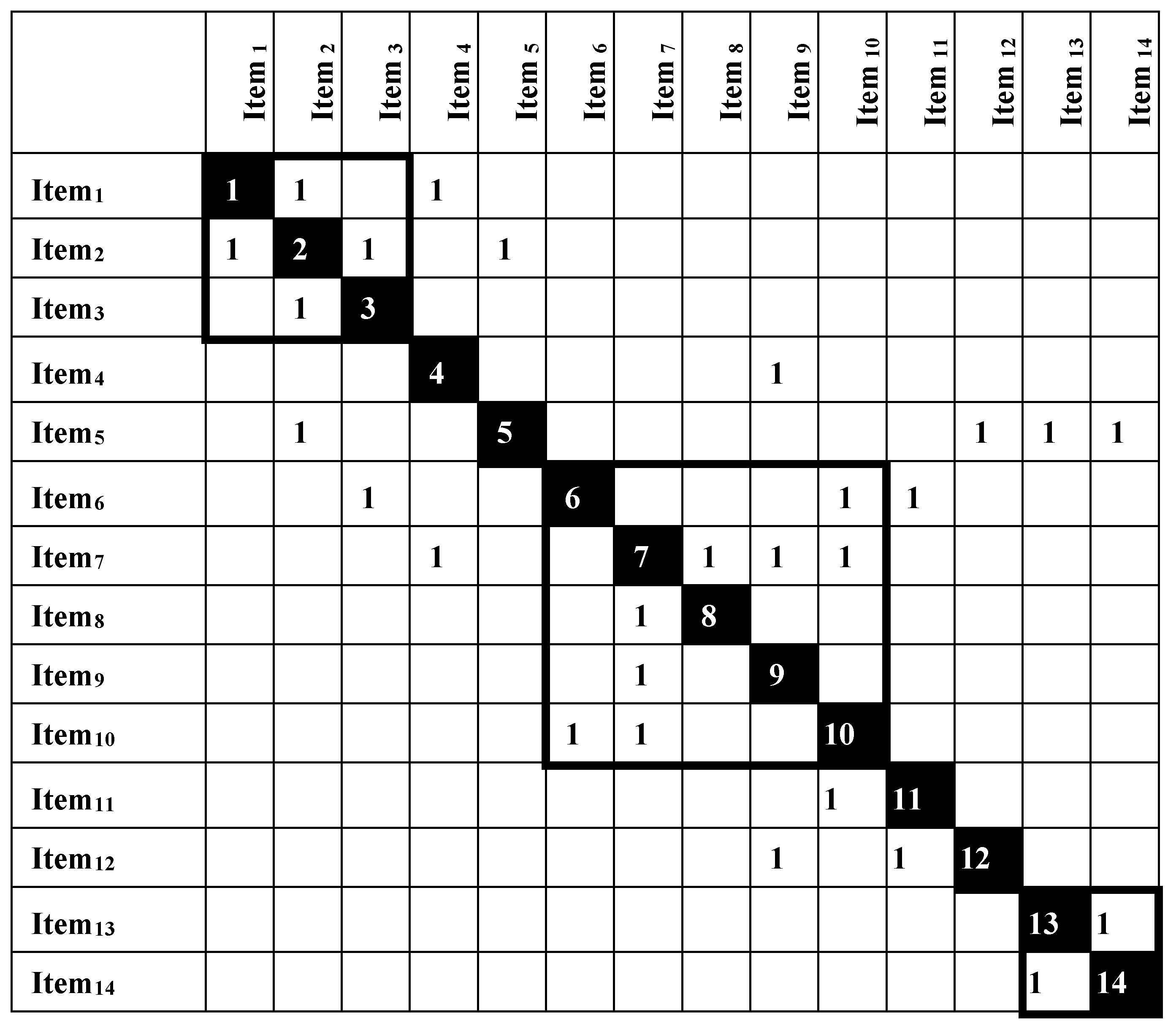
A Design Structure Matrix (DSM) stands as a potent method for illustrating intricate interdependencies among components within a system. Serving as a versatile and straightforward modeling tool, the DSM aids in the design, depiction, and management of systems. The DSM encapsulates a system’s architecture by denoting interactions and dependencies among its elements. Forming a binary square matrix with m columns and rows, along with n non-zero elements, where m symbolizes the nodes and n signifies the directed connections linking them, the DSM captures the intrinsic structure. Within a set of m elements within a system, the corresponding DSM takes shape as an m×m matrix, wherein the system elements occupy row and column headings, following the same order. Precedence relationships manifest in the matrix’s off-diagonal entries. In a binary DSM, the value of entry ij (column i, row j) is one (or marked by “X” or “●”) when element j depends on element i (i.e., i feeds j), while otherwise, it remains zero (or left vacant). Sequentially aligning the elements as they appear in the DSM, marks below the diagonal denote forward information from element i to j, and those above the diagonal embody feedback information from element j to i.
Central to the DSM analysis is the aspiration to minimize feedback loops, achieved by orchestrating the sequencing of processes/elements, thereby facilitating a lower-triangular DSM formation. The marks above the diagonal signify feedback couplings, contrasting with the sub-diagonal marks denoting feed-forward couplings. The above-diagonal markings connote iterative interactions, which should ideally be reduced as much as feasible. However, when feedback marks cannot be eliminated, the implicated elements can be categorized into iterative sub-cycles. In
Figure 3, for example, items (1, 2, 3) and items (6, 7, 8, 9, 10) fall into two such iterative sub-cycles.
Typically, the realization of this objective necessitates a two-step approach: partitioning and tearing hold promise for achieving optimal results [
14,
63,
64].
3.4. Modularity in System Architecture
Definition 1. The literature review underscores the wide array of definitions associated with the term ‘Modularity’ [65,66]. Generally, the definition of modularity emanates from the characterization of the constituent modules within a system. In essence, these definitions can primarily be categorized into two groups: ‘Structural’ definitions (These pertain to the relationships and interactions among the system components [67]. ‘Architectural’ definitions (These address the connections between system components and the functions established at a specific abstraction level within the functional domain [68] or through the relationships between models of physical and/or logical representations of systems [69,70]. Regarding the notion of modularization within each of these classes, a comprehensive elucidation has been provided by Efatmaneshnik et al. [71]. In general, the process of modularization aims to maximize the dependency within modules while minimizing relations or interactions between modules [65,72].
3.5. Measures of Modularity for an Individual Architecture (Functional/Physical/Process Architecture)
Various modularity indices assess system architecture. Jung and Simpson [
73], Bonvoisin et al. [
74] reviewed many. Tools like modularity matrix [
75], heuristics [
68], DSM [
76], axiomatic design [
59], etc., identify modules. This study chooses DSM for module identification, considering its benefits.
To gauge modularity using the Design Structure Matrix (DSM) methodology, the literature offers a range of metrics [
77]; Hölttä-Otto and de Weck [
78]; Hölttä-Otto et al. [
79]. The research emphasizes studying important interactions between element pairs. Among various modularity measures, the focus is on those developed from interactions among the elements. Notably, five key metrics stand out: ‘Grouping Capability Index (
GCI)’, ‘Grouping Efficacy’, ‘Grouping Efficiency’, ‘Utilization Rate (
U)’, and ‘Modularization Function’ [
80,
81], which have been frequently utilized [
82].
Before proceeding to the measures, establishing the notation is beneficial. Let N1 be the count of 1 s in diagonal blocks, N2 be the count of 0 s in diagonal blocks, N3 be the count of 0 s in off-diagonal blocks, and N4 be the count of 1 s in off-diagonal blocks. Moreover, N1 + N2 indicates the total number of elements (0 s and 1 s) in diagonal blocks, and N3 + N4 represents the total number of elements (0 s and 1 s) in off-diagonal blocks. The following section provides a detailed outline of the measures.
The Grouping Capability Index (
GCI) signifies the capacity of a collection of interdependent entities to establish a module (Equation (4)).
- 2.
Grouping efficacy
Grouping efficacy, denoted as
τ, quantifies the ability of a module or group to perform a task. It is contingent on the successful clustering of elements within a group. (Equation (5)).
- 3.
Grouping efficiency
Grouping efficiency, represented as
η, serves as a measure of the fit quality for a modular solution within a module. A higher
η value indicates a more suitable modular arrangement.
η (Equation (6)) symbolizes the relative capacity of components to form a module or group, as well as the compactness of a module.
and
are expressed by Equations (7) and (8), respectively.
where,
q is a weighting factor (0 <
q < 1);
- 4.
Utilization rate
Utilization rate, denoted as
U, indicates the extent to which components within a given system are dedicated to forming modules and how effectively they contribute to building modular systems (Equation (9)).
- 5.
Modularization Function
The Modularization Function, denoted as
M(u), was initially developed by Mikkola and Gassmann [
81], and subsequently refined by Mikkola [
80].
where ‘
u’ signifies the count of distinctive elements/components encompassed within an architecture; “
N” denotes the total number of standard and unique components, calculated as
N = nSTD + u;
δ represents the average intensity of coupling among elements/components and modules; “
s” indicates the substitutability factor of unique elements/components within other systems. Additionally, there exists a relationship between
δ (coupling intensity) and “
k” (number of interfaces in a module), expressed as
δ ∼ (
k/
n), where “
n” represents the count of components in a module.
3.6. Measure of Modularity Between Two Adjacent Domains
It is possible to determine a quantitative measure of independence for a given design matrix. Suh [
59] proposes two metrics of independence: reangularity,
R, and semangularity,
S. Reangularity evaluates the orthogonality between DPs and serves as a measure of interdependence.
The angle between the DP axes is denoted by
θ (Equation (11)). To provide additional clarity on the concept of reangularity, let us examine a two-dimensional case.
where
represents the entry (
i, j) of the DM and relates
DPj to
FRi (
i, j = 1, 2). Equation (12) can be rewritten as
where
For the nth dimensional case, reangularity is
The metric
S quantifies the angular relationship between the axes of DPs and FRs, evaluating the correlation between a given FR and any pair of DPs. In terms of coupling,
S represents the magnitude of the diagonal elements in a normalized DM. In the case of an nth-dimensional scenario,
Both R and S have a maximum value of 1, corresponding to an uncoupled (ideal) design. As the degree of coupling increases, both reangularity and semangularity decrease. In particular, when R or S is equal to 0, the design is considered fully coupled.
3.7. Metrics for System Robustness
System robustness reflects the degree of system coupling. According to the mathematical equations for
R and
S, it is clear that, as both R and S belong to the interval [0, 1], the larger
R and
S are, the greater
R × S is. Concerning the information content of a system, I, the smaller the information content is, the smaller is the variability of the system where (
R × S)/I becomes larger and can be employed to quantify the robustness of a system [
83].
3.8. Robustness Analysis Method
The robustness analysis method looks at the relationship among system elements and evaluates alternative sequences. Managers can then choose the best organization of elements to improve modularization and overall system robustness. The steps of the method are described in the following and presented schematically in
Figure 4:
Step 1: Consider manufacturing processes as an integrated system;
Steps 2 and 3: Develop functional and physical architecture of the system;
Step 4: Design manufacturing process architecture for robustness;
Steps 5, 6, and 7: Use DSM to modularize the physical architecture of the system;
Step 8: Map the physical to the functional architecture of the system;
Steps 9 and 10: Calculate the system architecture’s information content and robustness;
Steps 11, 12, and 13: Use the AD theory to modularize the mapping between the new physical architecture and the functional architecture;
Step 14 and 15: Recompute the system architecture’s information content and robustness;
Step 16: Compute the overall robustness of the system.
3.9. Contribution of the Study: Modularity and Robustness
Once robustness is analyzed, mapping between a system’s functional and physical architectures needs to be done, and the determination of how well the physical elements satisfy the functional elements needs to be evaluated. A literature review of design robustness has indicated that both physical component redundancy and limiting the degradation of physical components have been mentioned by several authors [
84,
85]. In the present study, the focus is on avoiding propagation of failure/disruption/ disturbance, i.e., suppression of disturbances and redundancy in some of physical component in the physical architecture. To avoid propagation failures in a system, the functional and physical components should not be coupled, and the physical components should be independent. Robustness is achieved by having a significant level of modularity that avoids propagation of noise from an affected/impaired module or element to other modules. Following is a mathematical investigation that demonstrates that modularity suppresses disturbances in the physical architecture as shown in
Figure 5, where better modularity leads to better contact elements, and ultimately, greater project success. The mathematical analysis underpins the use of AD Theory and DSM in the robustness analysis method.
3.10. Modularity and System Variance
System robustness can be improved by minimizing variance [
86,
87]. In a multi-FR design, the prerequisite for minimizing variance is the satisfaction of the independence axiom. To mathematically consider the relationship for coupling, i.e., the absence of modularity and system variance, consider an n dimensional case as in the following:
where
(
i = 1, 2, …,
n) represents the
i-th module in FRs domain,
(i = 1, 2, …, n) represents the i-th module in DPs domain,
represents a DM which associates DP-based modules with FR-based modules, and
(i = 1, 2, …, n and j = 1, 2, ..., n) are DM submatrices that have one or more dimensions where (j = 1, 2, …, n) is allocated to the (i = 1, 2, …, n).
In addition,
represents the transposition of the matrix as in the following:
is expressed as
where
represents the domain of FR-based modules (the functional domain), and
represents the domain of DP-based modules (the physical domain).
The random variability of
, i.e.,
can be expressed as
where
represents random variability of
. It is clear that
and
are
where
represents the random variability in
(I = 1, 2, …, m), and
represents the random variability in
(j = 1, 2, …, m).
The transposition of Equation (20) is
Therefore, the variance of the
is
where
E expresses the mathematical expectation. Hence, the variance of
,
, is
where
Represents the variance-covariance matrix for
.Assume that the DP-based modules, , are statistically independent of each other.
Hence,
where
represents the variance or variance-covariance matrix of module
and (
i = 1, 2, …, m) when the module is one dimensional or multi-dimensional. Then,
Moreover, the system variance,
The larger the off-diagonal entries become, the higher is the system variance, i.e., a higher system variance indicates a more coupled system design. The development of a simple, well-defined equation to clarify the relationship between reangularity/semangularity and the lack of modularity may not be easy. However, the behavior of semangularity and reangularity with respect to the magnitude of off-diagonal entries of the
DM are relatively similar. To demonstrate the degree of coupling, i.e., the lack of system modularity, for
DMs with higher dimensions, computer simulation was used for four square
DMs with sizes of 2 × 2, 3 × 3, 5 × 5, and 10 × 10 that were randomly generated 1000 times. The magnitude of the off-diagonal elements gradually increased as the number of runs increased, which showed the effect of coupling on semangularity/reangularity and system variance.
Figure 6a–d show reangularity versus lack of modularity where reangularity becomes smaller as the size of off-diagonal elements increases.
Figure 6e–h shows the system variance versus lack of modularity, where system variance becomes larger as the size of off-diagonal elements increases. This underlines the need to reduce the coupling among system elements, as done in the robustness analysis method.
3.11. Modularization of the Allocated Architecture (Mapping Between Two Adjacent Domains)
The allocated architecture of a system refers to the organization of physical elements that yields a design solution which satisfies the functional requirements of a system [
88]. Therefore, modularity of the allocated architecture is essential to achieving a robust system. Sometimes, due to possible disruptions in an operational environment, redundant elements are used to increase a system’s reliability to have a better chance of system success. When creating modules, it is important to determine whether there is any element or module that is redundant since the use of redundant elements may result in a loss of system modularity.
Concerning the improvement of system reliability, the present study adopts the notion of redundancy from AD theory, where in redundant designs, there are more
DPs than FRs to satisfy the
FRs (Suh, 2001 [
59]). For instance, a system objective may be described by a few components in such a way that if the most appropriate component is not able to satisfy the objective, other associated component, as redundant elements, can be used to meet the objective. Nevertheless, system modularity must be ensured. The following two subsections provide more detail about the modularization of the allocated architecture in the absence and presence of redundant physical modules.
3.12. Modularization of the Allocated Architecture in the Absence of Redundant Physical Modules
To map between DP-based and FR-based domains, consider a multi-
FR design
where
represents the ith module in the functional domain (
i = 1, 2, ..., n), and
represents the ith module in the physical domain
(i = 1, 2, ..., n).
Note that
or
can be a module which can encompass only one element or several fully/partially coupled elements. Using Equation (34), the derivative of
, i.e.,
Or
where,
represents the derivation of
. If
or
is a module of only one element, Equation (36) can be utilized straightforwardly. However, when
or
is a vector which includes several fully/partially coupled elements, Equation (36) needs to be expressed as the following. Let
and
(i = 1, 2, …, n) be a vector that includes a specific subset of
FRs and
DPs, respectively. Then,
and
It is assumed that
FRs are independent of each other whereas the associated
DPs are partially/fully coupled to each other. Therefore,
can be expressed as
where
represents the jth module in the physical domain with k
1 DP elements,
represents the pth member of jth module (p = 1, 2, …, k1),
represents the qth member of the jth module (q = 1, 2, …, k1), and
represents the entry (p,q) in matrix X and signifies the degree of dependency between and (p = 1, 2, …, k1; q = 1, 2, …, k1).
Matrix X in which all diagonal elements are zero is employed to express that every element of
is coupled with the remaining elements. Then,
In addition, assume that
A is the design matrix (
which allocates
DPs into
FRs that belong to the module
. Therefore,
Incorporating Equation (40) into Equation (41)
Using Equation (44), the derivative of
, i.e.,
(i = 1, 2, …, n), is
where
In order to compute
, consider
. Now,
is
Hence,
and
or
where (
.
must be within the required tolerance; thus,
where
is the desired change in
due to a change in
, and
is the required tolerance.
In an uncoupled design, must be equal to . The deviation from this ideal condition, , is given by or where or is a module of only one element (case I) or a vector (case II) that includes several fully/partially coupled elements. For an uncoupled system, the required tolerance, must be ≥ or ≥ in case I or II.
For case I,
and for case II,
Specifically, for case I, consider
, then,
or,
Specifically, for case II, consider
, then,
or,
Equation (61) provides a criterion for determining when the off-diagonal elements of a basic matrix can be disregarded.
3.13. Independence and Tolerance Theorem
An independence and tolerance theorem can be formulated as follows: In case I, a design is considered uncoupled when the specified tolerance,
, exceeds...
Therefore, the non-diagonal elements of the design matrix can be disregarded. If the
(
k = 1, 2, ..., n), which represents the stiffnesses relating changes of
to the changes of
, are constant, then...
If , then, the design is uncoupled.
3.14. Modularization of the Allocated Architecture in Presence of Redundant Physical Modules
In this case, there are more
than
, resulting in random variability (or noise) introduced by the excess
that can affect the variability of
. It is crucial for the variability to remain within the design range to ensure proper functionality. Therefore,
The random variability in is denoted as , and the variability of is represented by .
In an ideal one- design, only a single is necessary, as any additional introduce the possibility of random variability. The first term on the right-hand side (RHS) of Equation (65) accounts for the compensation effect of the primary , which is selected to vary , while the second term represents the cumulative random variability or noise introduced by any extra . To ensure proper functionality, it is crucial to adjust the error term in two possible ways to achieve .
Setting the coefficient () that corresponds to any additional to zero involves eliminating all random variability from every , which is not practical given the variability that arises during manufacturing and assembly.
To address the issue of random variability in , it is necessary to set all values of except for the chosen to be fixed during operations, allowing that specific to vary . This step is equivalent to setting the second term on the RHS of Equation (65) as a constant. Once this adjustment is made, the next step involves adjusting to compensate for any accumulated errors by setting the first and second terms on the RHS equal to one another. Then,
This approach eliminates the random fluctuations that may arise from additional units used during operations, while ensuring that the tolerance range specified in the design is met for . The primary unit must be capable of compensating for any random variations resulting from the use of extra units.
3.15. Multi- Design
In a multi-
design where the number of
units exceeds that of
units, the design becomes redundant and each
unit may be affected by multiple
units. Consequently,
Let us consider the following scenario: {
} represents the
selected to fulfill the vector {
}, with the number of
in {
} being equal to the number of
in {
}. The vector {
}
Extra, which appears as the second term on the right-hand side of Equation (67), contains redundant
that remain after {
} satisfies {
}, but these extra
may not be explicitly known. The square matrix [Square DM] represents the relationship between {
} and {
}, while [Extra Matrix] describes how the extra
affect the
. To ensure compliance with the independence axiom, [Square DM] should be either diagonal or triangular. On the other hand, [Extra Matrix] can take any form, including a full matrix, and still satisfy the independence axiom as long as [Square DM] is diagonal or triangular. Specifically, let’s look at a special case of Equation (67) where we are dealing with a multi-
design consisting of k
and numerous
.
where
represents the ith (
i = 1, 2, …, k) module in the functional domain,
represents the jth (j = 1, 2, …, n) module in the physical domain,
represents the pth member of jth module in the physical domain for (p = 1, 2, …, k1), and represents the sub-design matrix within DM and relates DPs of to the associated FRs of to satisfy them.
The first term on the right-hand side (RHS) of Equation (68) represents an uncoupled design, while the second term depicts a fully coupled design. However, even with the presence of the second term, this design can still be treated as an uncoupled design if we establish a fixed value for
through
. We can then use
,
, … and
to ensure the independence of
,
, … and
. In such cases, the design range of
would be:
When the diagonal design matrix of the first term on the right-hand side (RHS) of Equation (68) is substituted with a triangular matrix in Equation (71), the resultant design can be treated as a decoupled design
Random variability in
through
can be counteracted by using fixed values for
,
, …, and
, provided that any extra terms are fixed first and remain the same across all locations where they are used. In this manner, the design range
may be achieved using
(j = 1, 2, …, k), which is:
is the primary controller for . are secondary controllers chosen to satisfy , with a secondary effect on due to off-diagonal elements. is not a primary controller and is the source of random variability. (j = 1, 2, …, k) should be set first according to the sequence defined by the triangular matrix to control the corresponding (j = 1, 2, …, k). The variability caused by the extra terms can be fixed by eliminating (j = k, k + 1, …, n) through fixing . Finally, can be controlled using . If Square DM, the first term on the right-hand side of Equation (73), is a full matrix, the design is coupled, which violates the independence axiom. In this case, it is not possible to satisfy the independence of each when unknown introduce random variability.
The previous discussion holds significant implications for designing a robust system that satisfies multiple
simultaneously. In a multi-
design, the selection of
,
, and
must meet the same set of conditions. However, in a decoupled multi-
design, we must also satisfy an additional condition for the elements of a triangular design matrix.
If Equation (74) is not satisfied, it indicates an unacceptable design resulting from choosing the wrong . For instance, consider a scenario where diagonal elements have a smaller magnitude than off-diagonal elements. This implies that and , selected to control and , respectively, have a greater impact on than has on . In extreme cases, when one of the diagonal elements is significantly smaller than the off-diagonal elements, the design becomes coupled because one can influence more than two . Additionally, if the number of is less than the number of due to one or more diagonal elements being zero, the design becomes coupled due to an insufficient number of .
4. Application
This study focuses on verifying the proposed methodology for analyzing the robustness of manufacturing processes in the Iranian tire industry, specifically within ‘Barez Industrial Group’, an enterprise based in Tehran, Iran, specializing in Tire Manufacturing since its establishment in 1984.
The manufacturing processes under investigation are the ‘system of interest’ (SOI), and their architecture is analyzed in this study. Considering the dynamic nature of manufacturing environments, the study emphasizes the system’s ability to cope with rapid changes. The existing architecture is examined from the perspective of robustness, aiming to identify any shortcomings or limitations. If significant weaknesses are detected, the study proposes a new architecture design based on the engineering design methodology presented in this research, ensuring the system’s capability for robustness. By addressing the critical point of verifying the proposed methodology and emphasizing the importance of robustness in tmanufacturing processes, this study contributes valuable insights to the field of tire manufacturing and engineering design practices within ‘Barez Industrial Group’.
4.1. Functional Architecture of the SOI
In step 2 of the research method, the functional architecture of the system of interest (SOI) is addressed and its constituent elements are studied. Applying the Axiomatic Design (AD) theory, the elements of the SOI within the functional domain of the system are identified, considering the elements as ‘Functional Requirements’ and tagging them with FRs.
Table 2 presents and describes these FRs of the SOI.
4.2. Originate the Functional Architecture of the SOI in DSM Representation
Following steps 3–6 of the method, the DSM tool portrays the functional architecture of the system of interest (SOI).
Figure 7 shows the original architecture design. Positive values above the diagonal in the original DSM signify substantial coupling, suggesting changes in one element affect others. To curtail change propagation, a beneficial solution called ‘modularization’ is suggested.
4.3. Significance of Each System Element Within the Functional Architecture of the SOI
4.3.1. Initial Significance of Each System Element
Each SOI element’s significance is assessed by ‘C1’ (system architecture dependency) and ‘C2’ (element’s info dependency on architecture). ‘C1’ gauges system’s reliance on an element, while ‘C2’ measures element’s info contribution and input from the system.
For insights into element significance, percentage average dependencies are calculated from the original Numerical Design Structure Matrix (NDSM) of the architecture.
Table 3 and
Table 4 display this, providing a comprehensive view of individual element importance and role in the SOI.
Furthermore,
Figure 10 offers a comparison between the ‘percentage of information feed that each system element can provide’ and the ‘percentage of information inputs that each system element receives’ for/from the entire SOI.
In the figures provided, criteria C1 and C2 vary for each system element. For example, ‘FR113,10’, ‘FR113,11’, and ‘FR113,12’ show maximal information feed (C1) and receive the highest information inputs (C2) from the entire system. However, it is crucial to evaluate each process based on both criteria simultaneously to avoid misinterpretation. To address this, the study introduces the ‘compound measure’ weighting method, explained further in the following section.
4.3.2. Compound Weights of Each System Element
To assign weights to each element, two criteria, ‘C
1’ and ‘C
2’, are introduced with equal values (
WC1 = 0.5, WC2 = 0.5). Subsequently, two Multi-Criteria Decision Making (MCDM) methods, ‘SAW’ and ‘TOPSIS,’ are employed. The resulting weights obtained from these methods are collectively referred to as ‘Compound Weights’ in this study.
Table 5 displays the final compound weights of each element within the SOI, based on the outcomes from the SAW and TOPSIS methods.
Figure 11 compares compound weights of each element from the TOPSIS and SAW methods with the originally computed weights (from C
1 and C
2 only).
The figure shows significant disparities between original weights and those from MCDM methods. However, the weights from SAW and TOPSIS are similar and more reasonable.
Due to the substantial similarity between SAW and TOPSIS results, and to maintain simplicity and generality, weights from the TOPSIS method are used for further analysis.
Table 6 displays the updated prioritization of elements based on these compound weights.
Consequently, the updated prioritization of the elements can be of significant assistance to managers, enabling them to identify the most and least crucial elements with greater reliability (
Figure 12). This, in turn, offers valuable practical insights for making decisions that prioritize robustness.
4.4. Modularization of the Functional Architecture of the SOI
As highlighted in the preceding section, reducing the coupling identified within the functional architecture of the SOI is crucial. According to the principles of DSM methodology, the existence of coupling is inferred from positive values of upper-diagonal entries in the original DSM. However, it is important to note that not all positive values necessarily indicate a significant strength between the involved elements. In certain cases, some interactions between two elements may be negligible, and as a result, the associated values for those entries can be replaced by zero instead. This approach allows us to focus on the more substantial interactions while mitigating the impact of the insignificant ones.
Based on the aforementioned logic, elite members of the SOI were interviewed to determine a set of candidate cut-off points for ignoring the strength of interaction between a given pair of elements. The cut-off point refers to a specific value below which the interactions can be disregarded. As a result, the values ‘0.10’, ‘0.11’, ‘0.11’, ‘0.12’, ‘0.13’, ‘0.14’, and ‘0.15’—each reflecting the strength of interaction between system elements—are introduced as acceptable candidates for identifying an appropriate cut-off point.
For each candidate, the associated NDSM representation of the functional architecture of interest is presented in
Appendix A (
Figure A1,
Figure A2,
Figure A3,
Figure A4,
Figure A5 and
Figure A6). To diminish the coupling, the partitioning technique is applied for each of the resulted architecture.
Figure 13,
Figure 14,
Figure 15,
Figure 16,
Figure 17 and
Figure 18 display the outcomes.
Table 7 presents all the fundamental information (i.e.,
N1–N4) necessary for computing the criteria, introduced in
Section 3.5, used to measure the architecture modularity.
Using the information provided in
Table 8,
Figure 19a–d compares the modularity of all six presented designs (i.e., Designs I–VI). Based on the applied criteria, it is concluded that ‘Design VI’, for the functional architecture of the SOI, exhibits the highest modularity. Therefore, in terms of modularity, this specific design is considered the most optimal for the architecture. Notably, ‘Design VI’ introduces a new sequence to enhance the architecture while effectively removing significant coupling.
Figure 19a–d displays the scores of each design concerning the modularity measures utilized in
Table 8.
Using the modularity measure of the ‘modularization function’, the thirty-eight hierarchical sub-systems are compared based on the strength of coupling within the involved modules (
Table 9). The modules included in this analysis are referred to as the unique components of the modularization function.
Based on
Table 9, the SOI in the best design for the physical architecture is optimally organized into thirty-eight hierarchical subsystems. The achieved modularity for the functional architecture of the SOI is considered acceptable.
Regarding the optimal design VI, it is crucial to mention that among all developed subsystems (i.e., sub-systems1–38), sub-system2, sub-system32, and sub-system14 are particularly susceptible to any adjustments due to the presence of coupled elements. For these subsystems, additional techniques like the ‘tearing technique’ may prove more helpful if all the necessary information for making required assumptions is available.
4.5. Optimal Modularized Design Properties for SOI Functional Architecture and Its Robust Contribution
Through the development of the optimal modular design for the functional architecture of the SOI, the following properties have been achieved:
The information flow in the optimal design for the functional architecture follows a top-down approach, where elements placed at a higher priority require little to no information from other elements, while elements at a lower priority may require more information.
The information flow in the optimal design is optimally organized into thirty-eight hierarchical sub-systems, ensuring that all necessary information to fulfill the architecture and adapt to new situations is readily available.
The information flow in the optimal design is now clearer, simpler, more agile, and more traceable.
The achieved modularity in the architecture provides numerous possibilities for robustness. Among the presented subsystems (i.e., sub-systems1–38), many places can be easily identified and adjusted to enhance the architecture’s robustness in response to new situations.
The optimal design highlights places in the architecture where modifications are challenging due to the presence of coupled elements. These places are susceptible to any change or modification, and as a result, they remain unchanged in all possible architectures achieved through adaptation operations. These places are referred to as common platforms.
4.6. Investigating Functional Architecture Robustness and Optimal Design Selection
According to steps 7–10 of the proposed methodology, a simulation study aimed at assessing the robustness of the modularized architecture is conducted, encompassing Designs I to VI. This analysis entails evaluating the capacity of each design to withstand varying levels of complexity, which is indicative of the information content that can be accommodated by each architectural element. The outcomes of this evaluation are outlined in
Table 10 and
Figure 20.
Table 10 provides an in-depth examination of the functional integration within the System of Interest (SOI), yielding insights into the cohesive functioning of its constituent components. This analysis facilitates the comprehension of the restorative or adaptive effort necessitated in response to damage or modifications. This observation holds true for both the inherent design and the novel modular configurations embraced by the SOI. Of particular interest is the comparative evaluation illuminated by
Figure 20. This comparison underscores a discernible dissimilarity between the exigencies of the original design and the alternative modular constructs. A quantitative assessment, quantified in temporal and resource-intensive terms (Bits), reveals a pronounced differential in the demands imposed by the original versus modular design paradigms. This divergence is further elucidated in
Figure 20, a visual representation that vividly accentuates these variances. Notably, Design VI emerges as a salient exemplar within this analysis, distinctly showcasing its heightened robustness relative to the original design.
Figure 20 supplements this discernment by delineating the correlation between system resilience and complexity. The graph emphasizes a positive link between simple design and effective problem-solving and robustness. In short, avoiding excessive complexity boosts the system’s ability to adeptly handle challenges.
Upon close examination of
Figure 20, Design VI emerges as the optimal candidate among the array of six distinct modular designs. Notably, Design VI exhibits a pronounced proclivity for effectively navigating challenging scenarios. This proclivity underscores its pre-eminence within the spectrum of designs under scrutiny, particularly in comparison to the original design.
Analogous to a formidable sentinel within the realm of design configurations, Design VI assumes the role of an architectural vanguard. Its singular aptitude lies in the augmentation of the System of Interest’s (SOI) structural robustness and stability. Evidently, this revelation signifies Design VI’s unique potential to substantially elevate the quality of the SOI’s system architecture, thereby endowing it with a heightened capacity to navigate exigent circumstances.
Figure 20 provides empirical support for this observation, wherein the comparative assessment of robustness operations across all six modular designs showcases Design VI as being intrinsically associated with the most modest complexities. This distinct trait bestows upon modularized Design VI a superior capability in effectuating robustness operations within the broader system architecture of the SOI. This assertion holds particularly true when juxtaposed against the original SOI design, further validating Design VI’s exceptional competence in orchestrating structural fortitude amidst deviations from anticipated circumstances.
5. Conclusions and Discussion
In this study, we addressed the challenges faced by manufacturing processes in dynamic environments characterized by rapid changes, uncertainties, risks, and uncontrollable fluctuations. Our objective was to enhance the overall robustness of manufacturing processes through an innovative approach that integrates engineering management principles and modular design. By adopting a systems engineering perspective, we treated all manufacturing process activities as interrelated elements of an integrated system, aiming to prevent the spread of risks and disruptions among various processes.
Our research revealed a profound relationship between manufacturing management and engineering management. Manufacturing management plays a pivotal role in overseeing resource allocation, decision-making processes, and the overall organizational strategy for effective operations. Inefficient manufacturing management can lead to suboptimal use of resources, delays in production schedules, and reduced productivity, negatively impacting engineering management. On the other hand, effective manufacturing management systems can optimize resource allocation, streamline decision-making processes, and result in improved production processes and increased efficiency in utilizing technical personnel and physical resources.
Engineering management, in turn, is responsible for overseeing the design, development, and improvement of manufacturing processes. The effectiveness of engineering management systems, including quality control and continuous improvement programs, relies on the underlying architecture of manufacturing. A well-designed manufacturing process architecture is crucial in minimizing the likelihood of operational risks and their potential impact on manufacturing processes.
Our findings showcased a significant improvement in modularization, leading to enhanced overall robustness in manufacturing processes. This highlights the importance of engineering management’s proactive involvement in the design phase of manufacturing processes. By engaging manufacturing experts from the outset, potential production and assembly challenges can be addressed proactively, resulting in an optimized and robust manufacturing process.
Furthermore, our research underscores the significance of modularity within manufacturing process architecture. Taking modularity into account in the process domain architecture indirectly supports modularity in the allocated architecture, fostering a comprehensive approach that optimizes component allocation within the physical system. It is crucial to note that, from a system engineering perspective, certain environmental changes, such as market dynamics, geopolitical shifts, or technological advancements, are perceived as dynamic requirements that must be considered during system redesign. Modular architecture plays a pivotal role in enabling the adaptation of manufacturing processes to these changes. Specifically, the intentional integration of modularity into manufacturing process architecture enhances the feasibility and effectiveness of implementing modifications within specific modules while minimizing the overall impact on manufacturing processes. Additionally, the inherent flexibility of modular architecture enables the seamless integration or removal of modules, thereby facilitating responses to emerging changes within the environment or external influences.
Additionally, we highlighted the significance of redundancy in certain system elements, as it enhances system reliability while preserving modularity. Engineering management’s consideration of redundancy offers another avenue to enhance the overall robustness of manufacturing processes.
Therefore, in summary, in the present study, we have meticulously compared our proposed approach with relevant studies in the literature, as illustrated in
Table 1, showcasing the diverse methodologies and strategies utilized in prior research, including mathematical/statistical methods, process capability indices, and robust design principles. However, what distinguishes our study is our adoption of a system engineering perspective, which underscores the importance of considering manufacturing processes as integrated systems to enhance robustness. While some studies have touched upon this perspective, our emphasis on modularization within manufacturing process architecture is unique. We identified a gap in the literature that predominantly focuses on the allocated architecture of the system, overlooking the pivotal role of process architecture in system robustness. By emphasizing the significance of modularity in the process architecture and employing the Axiomatic Design (AD) theory and Design Structure Matrix (DSM) methodology, our study aims to develop a precise mathematical model that elucidates the relationship between manufacturing process architecture robustness and system architecture modularization. We focus on avoiding the propagation of failure/disruption/disturbance by ensuring modularity and independence among physical components in the physical architecture. Our approach seeks to provide invaluable support to systems engineers in designing robust manufacturing process architecture while managing system complexity, thus facilitating the creation of a resilient characteristic in manufacturing process architecture, a distinction from previous research efforts. Through mathematical investigation and analysis, we demonstrate how modularity suppresses disturbances in the physical architecture, underpinning the effectiveness of our approach in enhancing robustness.
The successful integration of engineering management principles with modular design strategies heralds new opportunities for bolstering the robustness and efficiency of manufacturing processes. Through proactive engagement of engineering management during the design phase and the application of our modularization approach, manufacturing organizations stand poised to fortify their overall system robustness and enhance their responsiveness to dynamic circumstances effectively.
Looking ahead, our research beckons further exploration into the intricate interplay between manufacturing management and engineering management. A nuanced understanding of this relationship promises to empower organizations in optimizing resource allocation, refining decision-making processes, and nurturing a culture of collaboration and knowledge exchange between engineering and manufacturing teams.
Moreover, our study illuminates avenues for future research aimed at developing comprehensive strategies that encompass various dimensions of manufacturing processes. Delving into areas such as process legality, reliability, adaptability, and recoverability will contribute to a more holistic comprehension of resilient manufacturing processes. Proposing the development of a resilience framework for manufacturing processes, our research advocates for a paradigm shift that not only prioritizes robustness but also encompasses flexibility, adaptability, and recoverability. Such a framework holds promise in providing decision-makers with a comprehensive tool to enhance overall system resilience effectively.
Despite these promising prospects, it is essential to acknowledge certain limitations inherent in our study. While we underscore the significance of modular design and engineering management principles in bolstering manufacturing process robustness, the real-world implementation challenges and adoption barriers merit further investigation. Additionally, our focus on the relationship between manufacturing and engineering management may inadvertently overlook other organizational factors influencing process robustness. Moreover, while our research underscores the importance of redundancy in system elements, determining the optimal level of redundancy and its cost-effectiveness across diverse manufacturing contexts warrants empirical validation and refinement.
On a managerial front, our study furnishes several key insights aimed at enhancing the robustness and efficiency of manufacturing processes amidst dynamic environments. Prioritizing effective resource allocation and decision-making processes emerges as a cornerstone for manufacturing management, offering a pathway to mitigate risks and uncertainties while improving production schedules and resource utilization. Equally crucial is the focus on engineering management’s role in designing and developing manufacturing processes, ensuring a well-structured architecture that minimizes operational risks. By emphasizing the importance of modularity within the manufacturing process architecture and considering redundancy in system elements, engineering management can further bolster system reliability without compromising modularity. Looking ahead, future research endeavors should delve deeper into exploring the symbiotic relationship between manufacturing and engineering management to optimize resource allocation and decision-making processes. Moreover, the development of a resilience framework encompassing robustness, flexibility, adaptability, and recoverability holds immense potential in guiding decision-makers towards enhancing overall system resilience in manufacturing processes.