Computational Fluid Dynamics (CFD) Investigation of NREL Phase VI Wind Turbine Performance Using Various Turbulence Models
Abstract
1. Introduction
2. Turbulence Models
2.1. k-ω Shear-Stress Transport (SST) Model
2.2. k-ε Model
2.3. k-ω Model
2.4. Gaussian Model
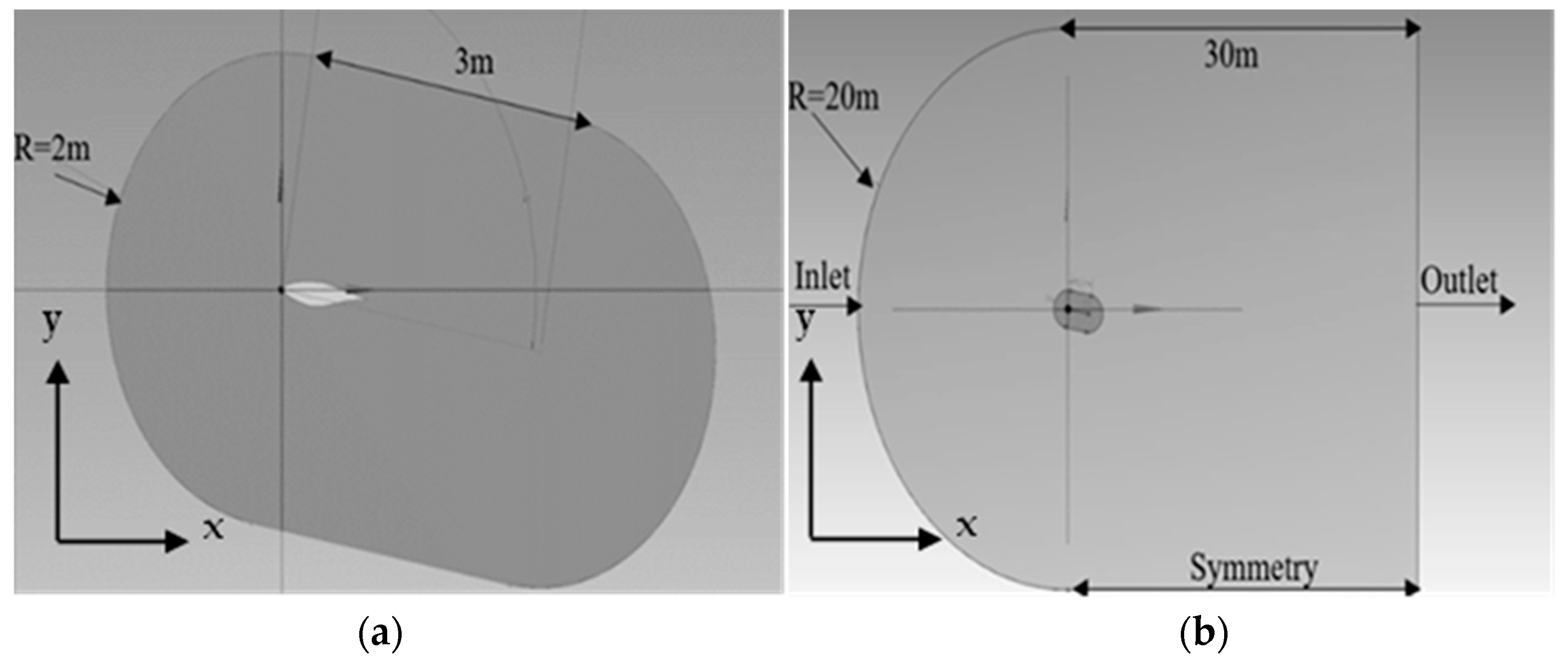
3. Design and Method
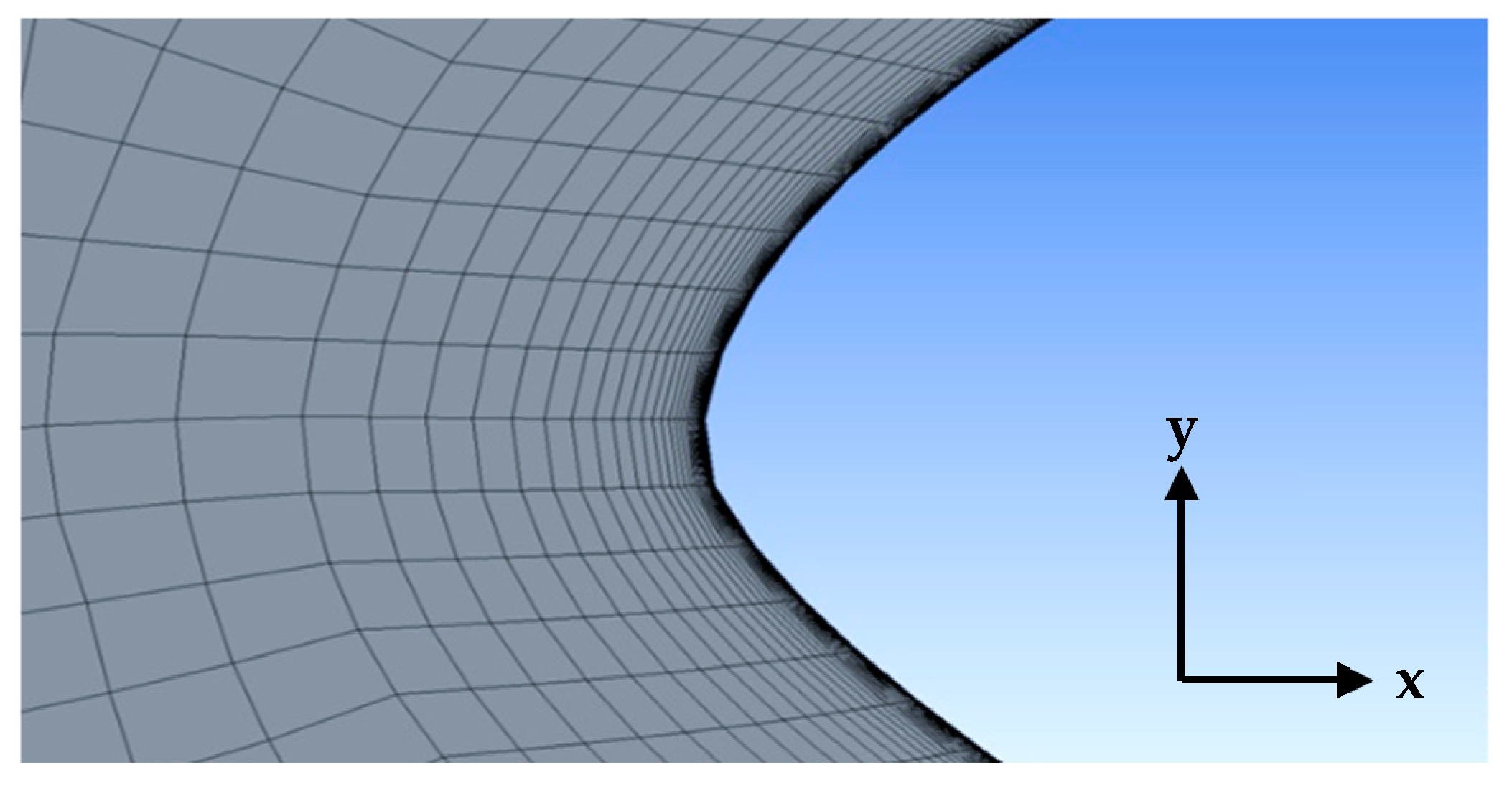
3.1. Mesh Parameters and Sizing
3.2. Mesh Topological Tolerence
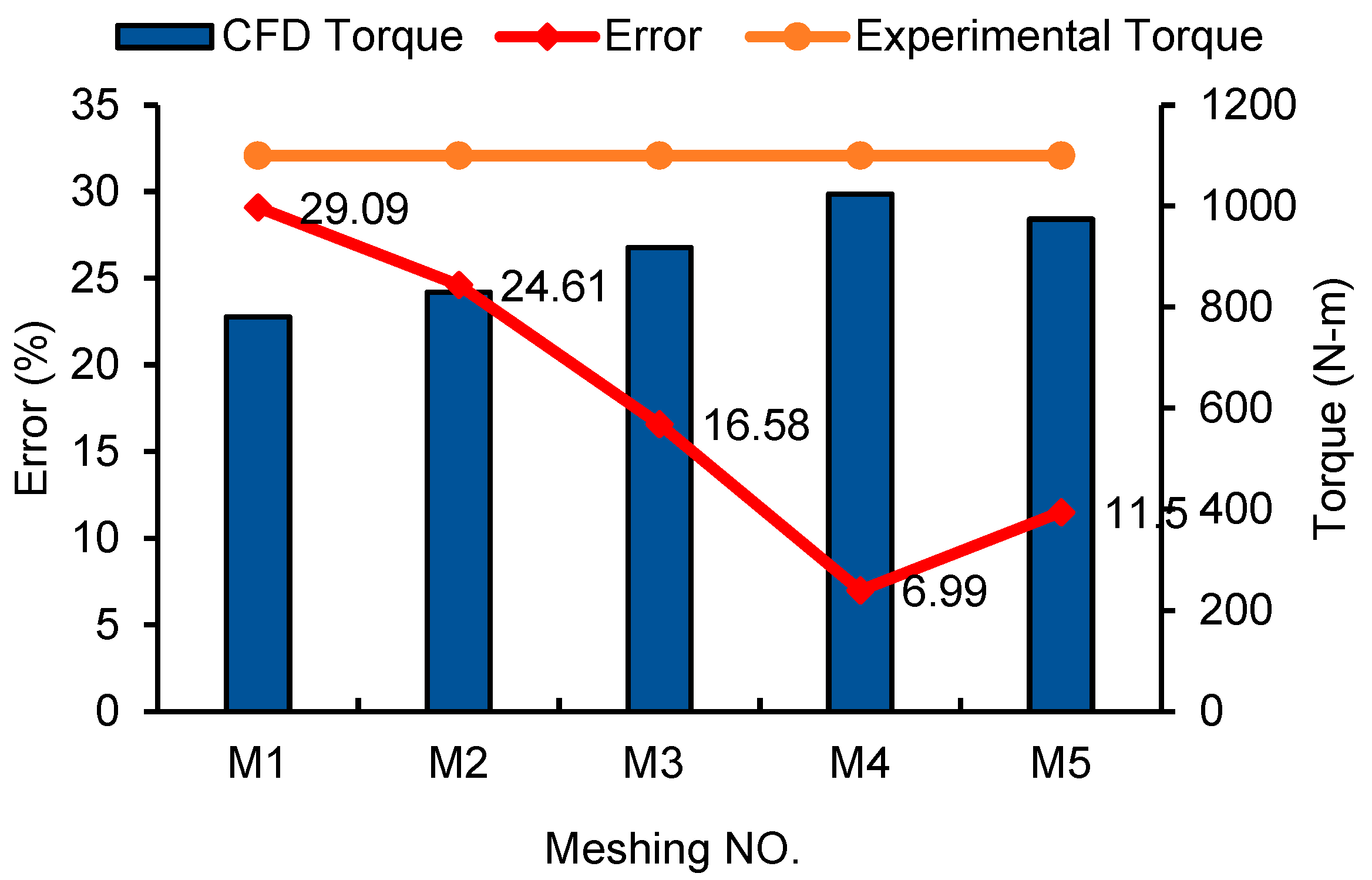
3.3. Mesh Independence Study
4. Results and Discussion
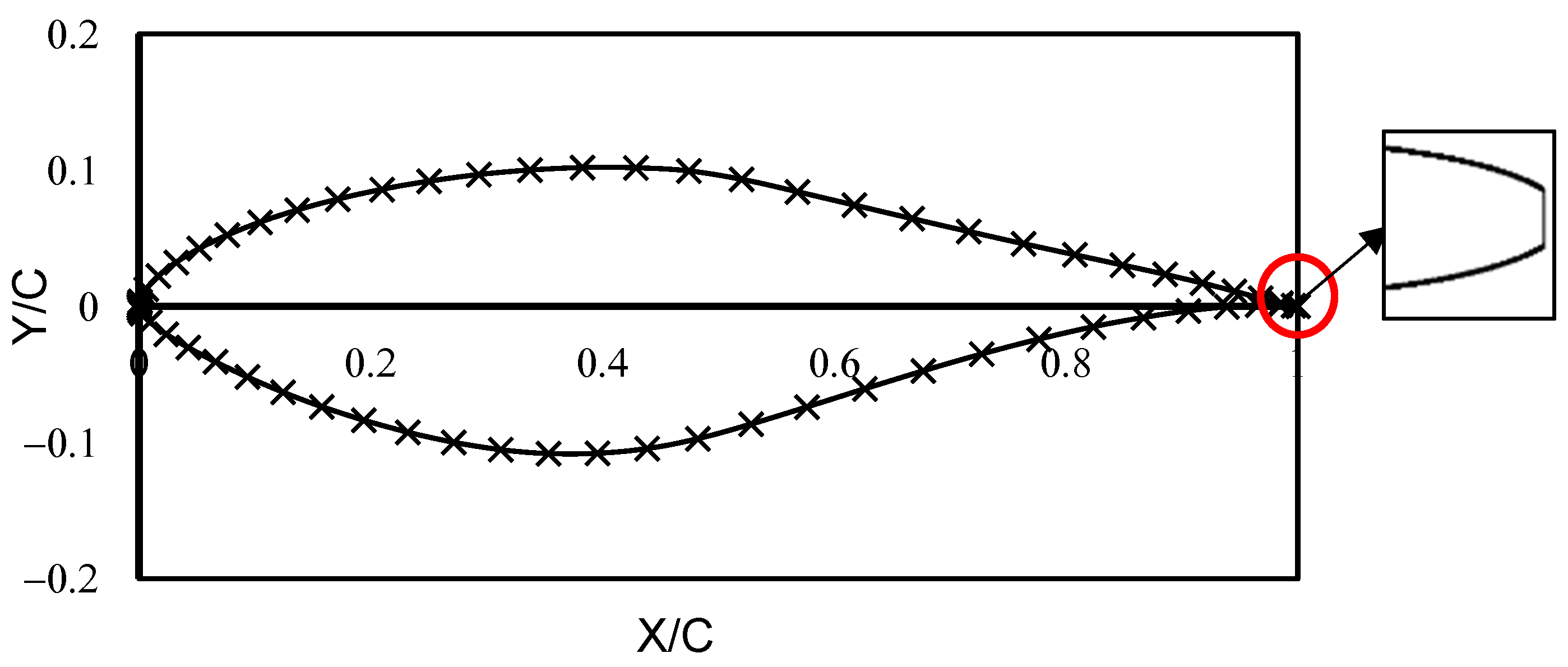
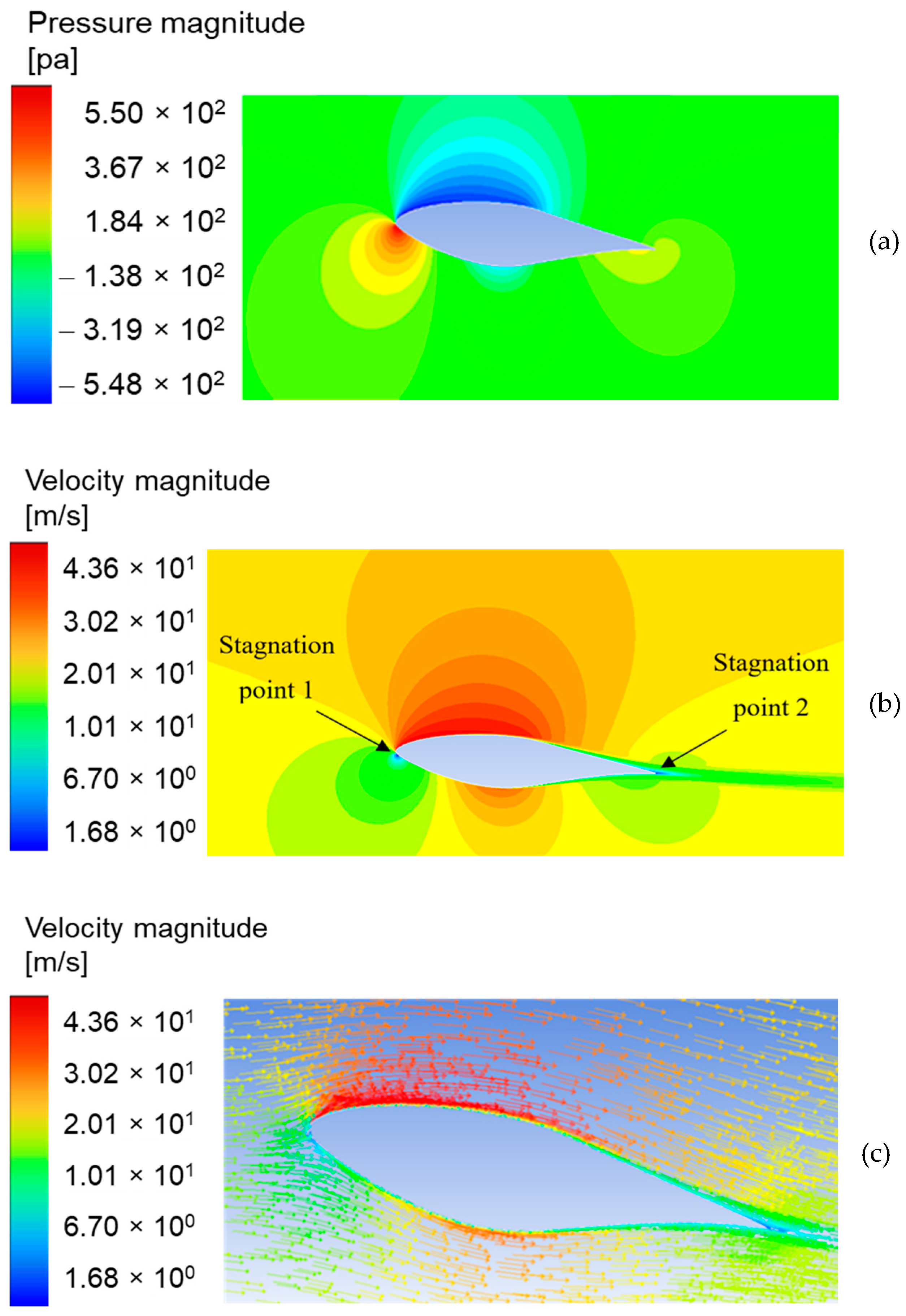
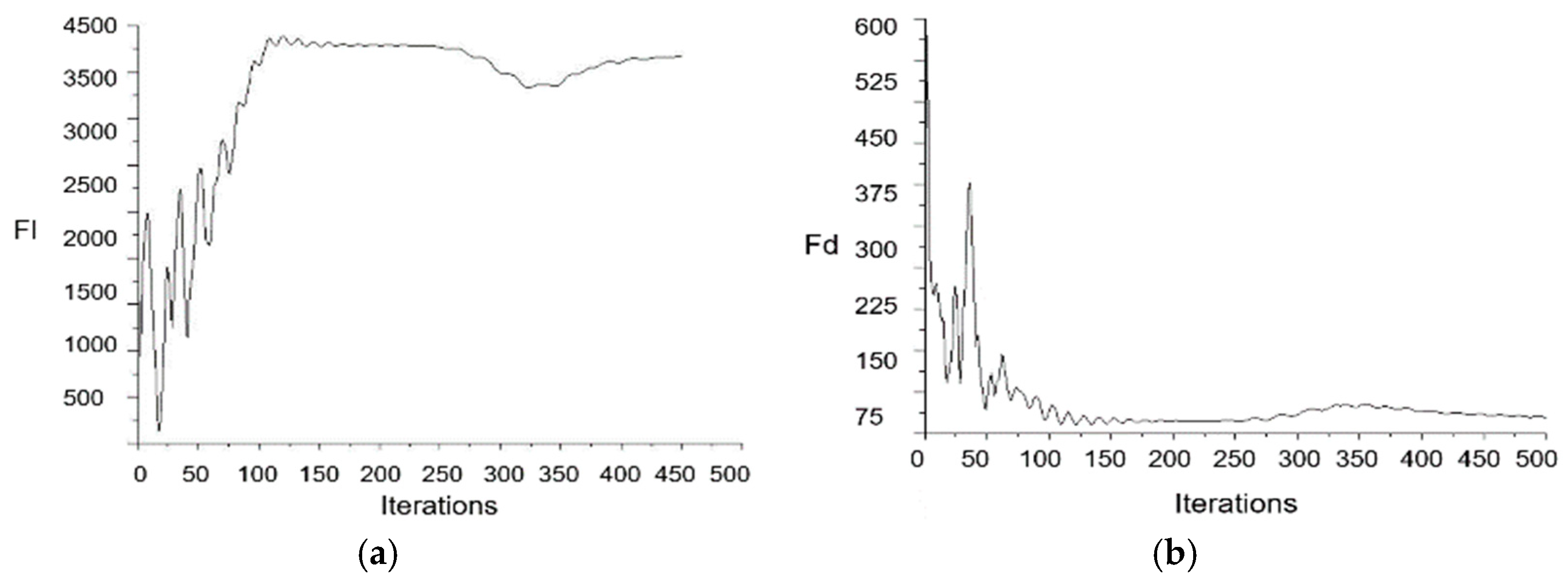
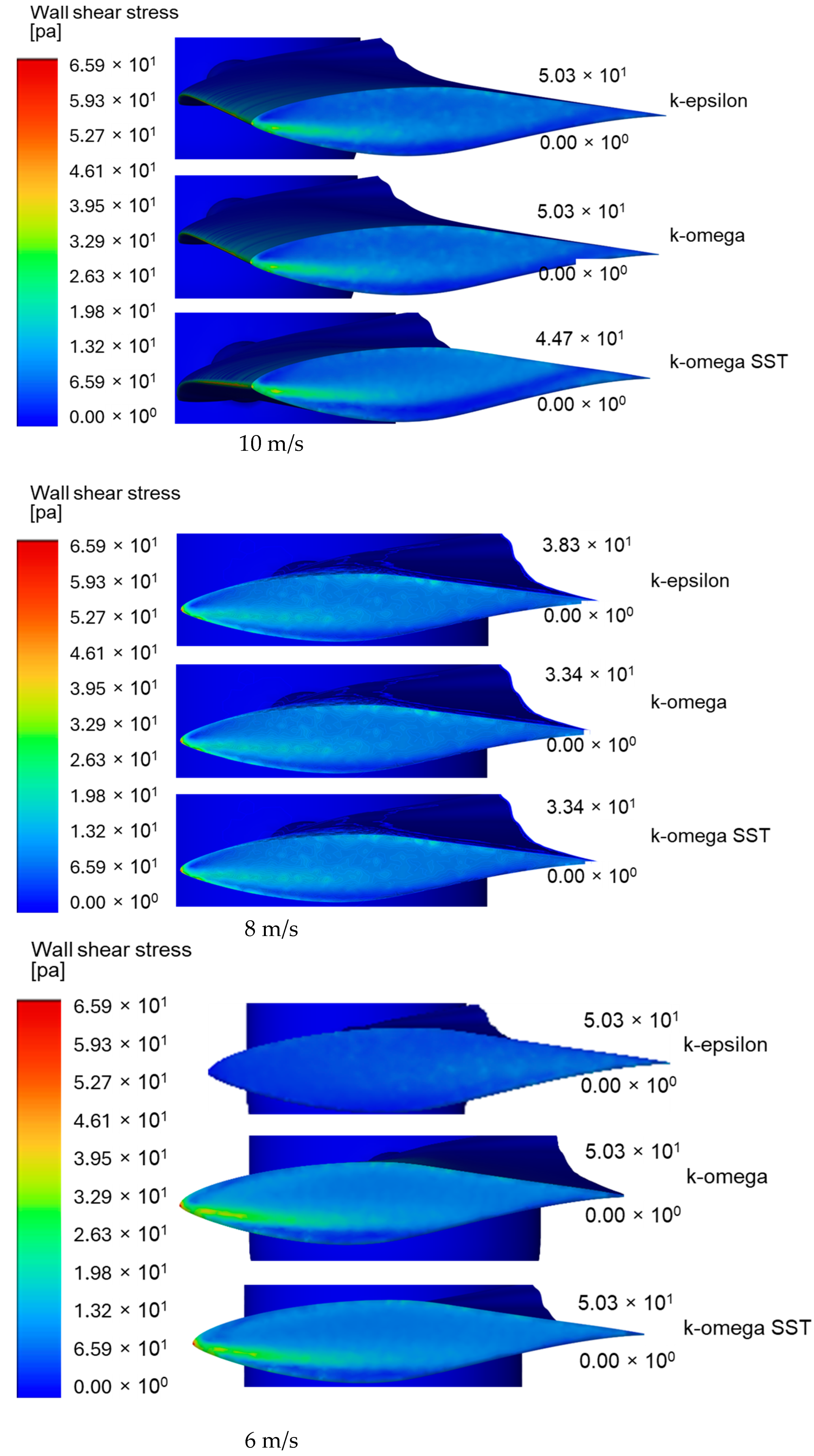
4.1. Two-Dimensional Analysis of S809 Airfoil
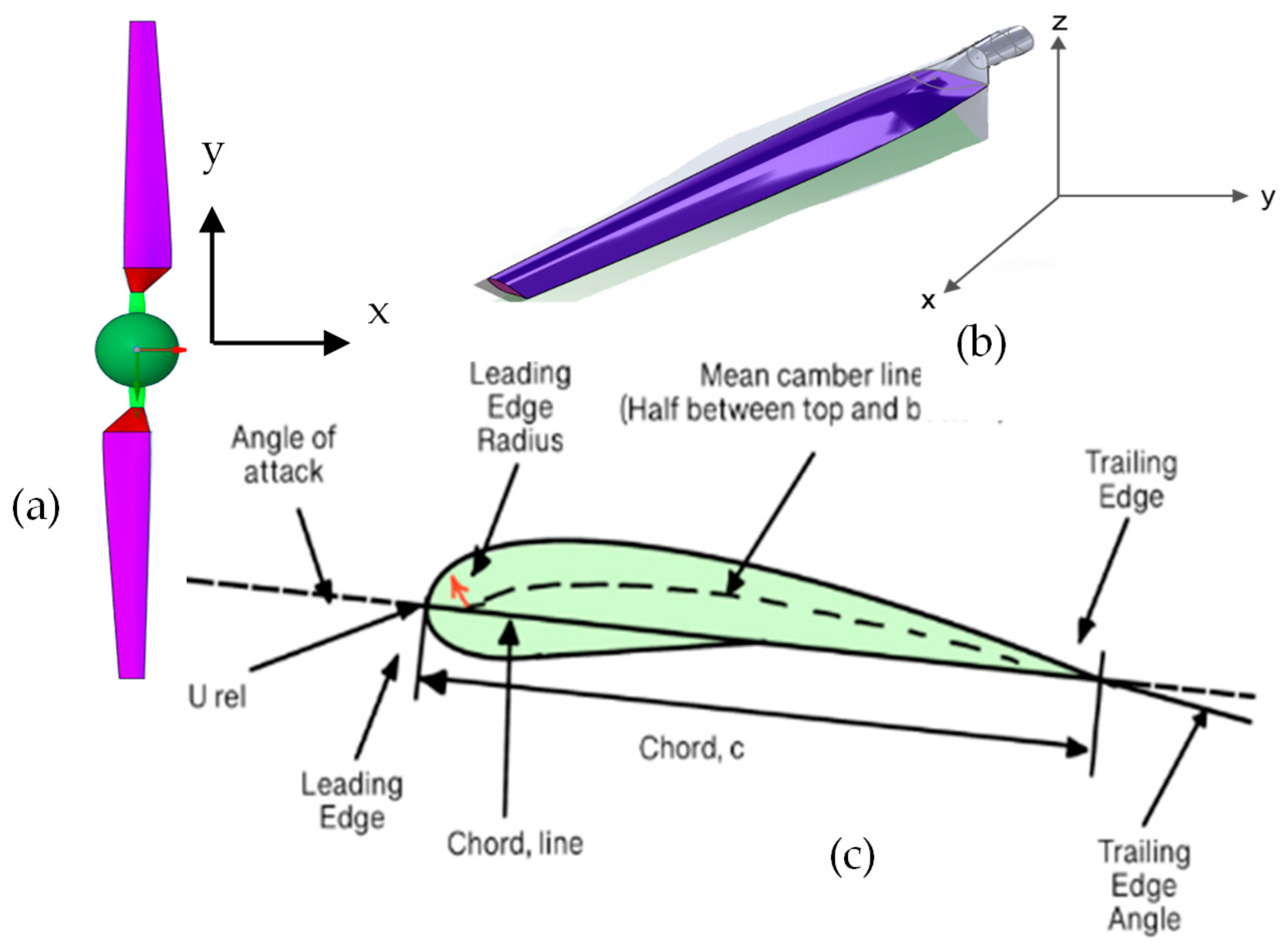
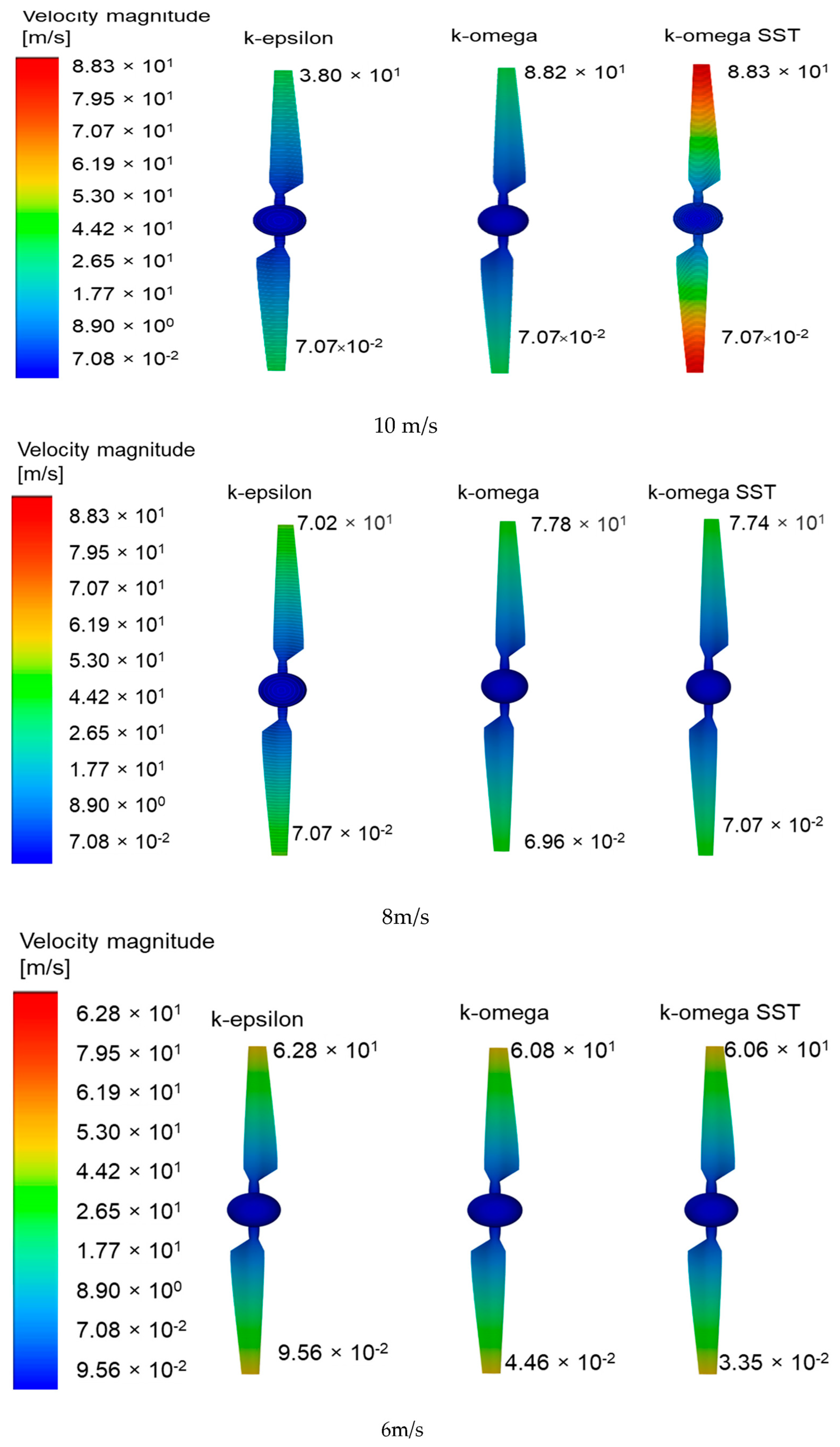
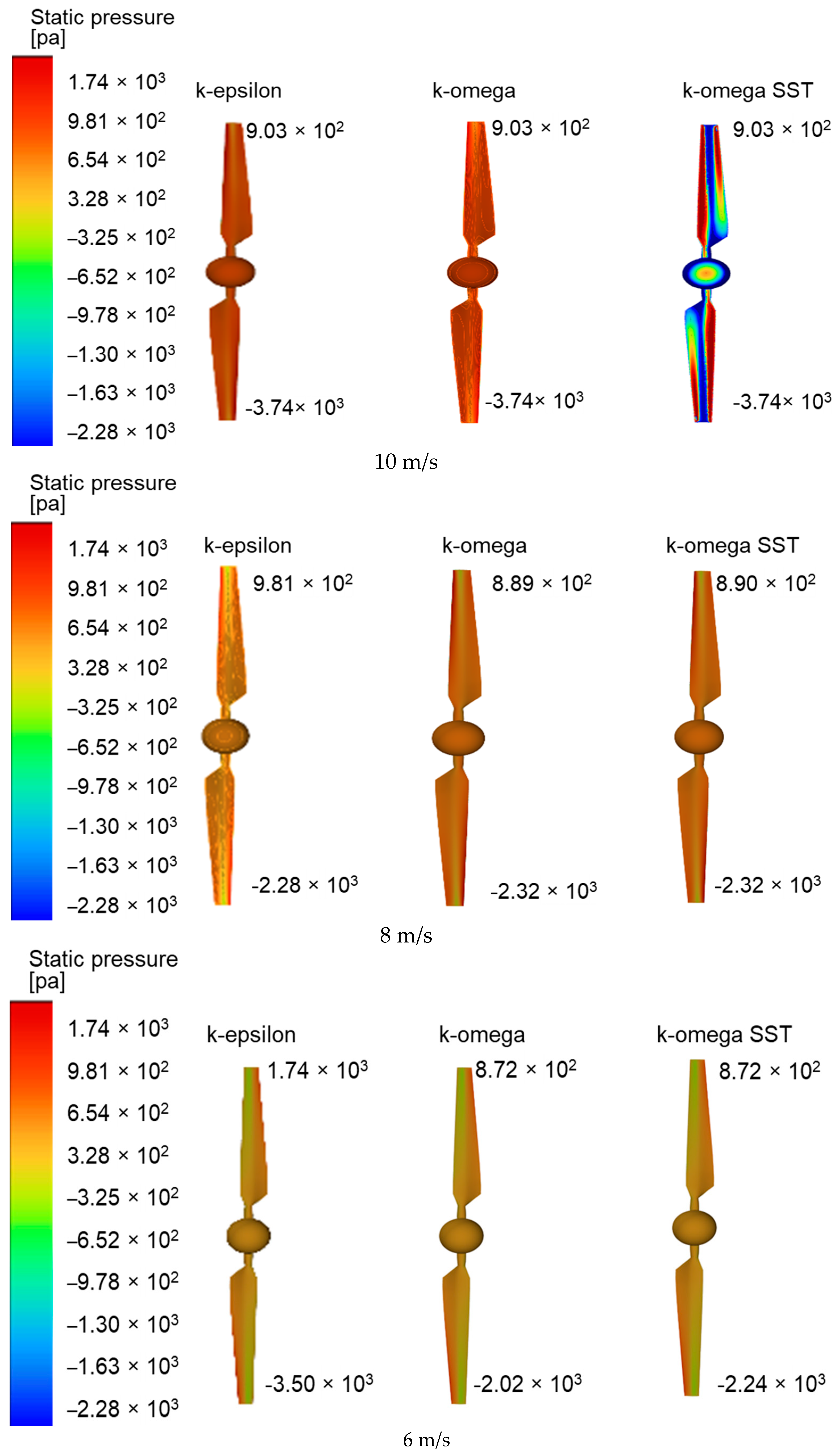
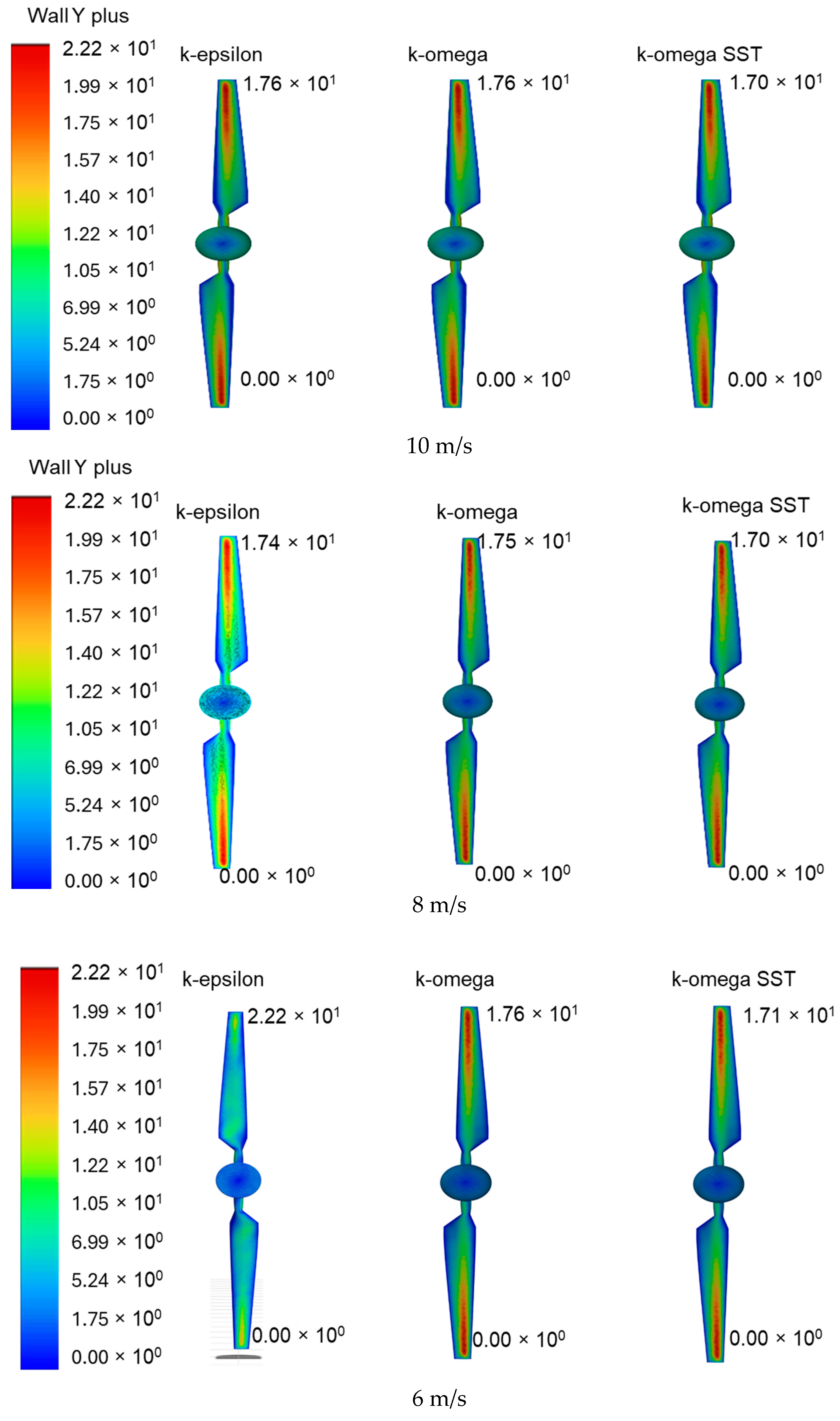
4.2. Three-Dimensional Analysis of NREL Phase VI Wind Turbine and Validation
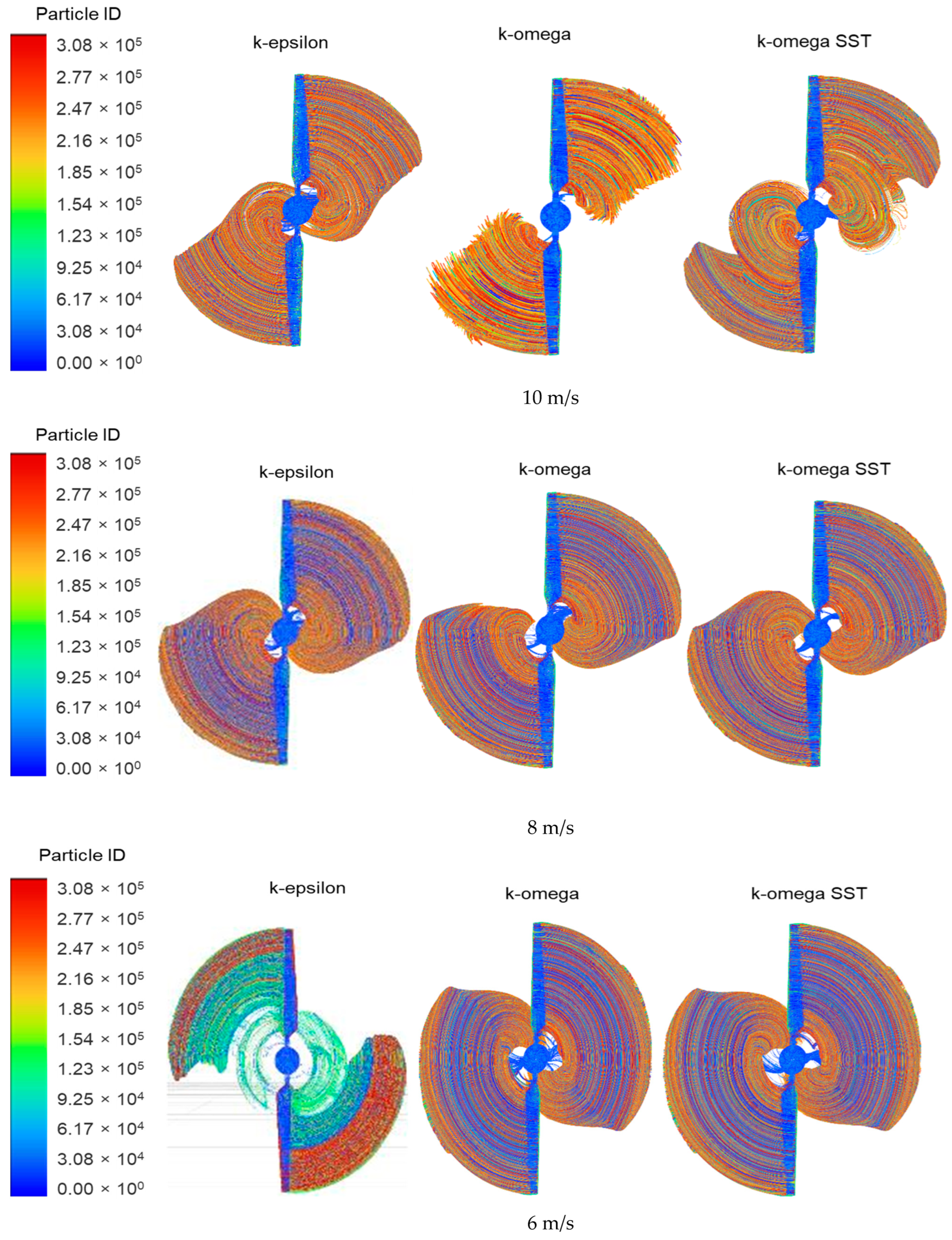
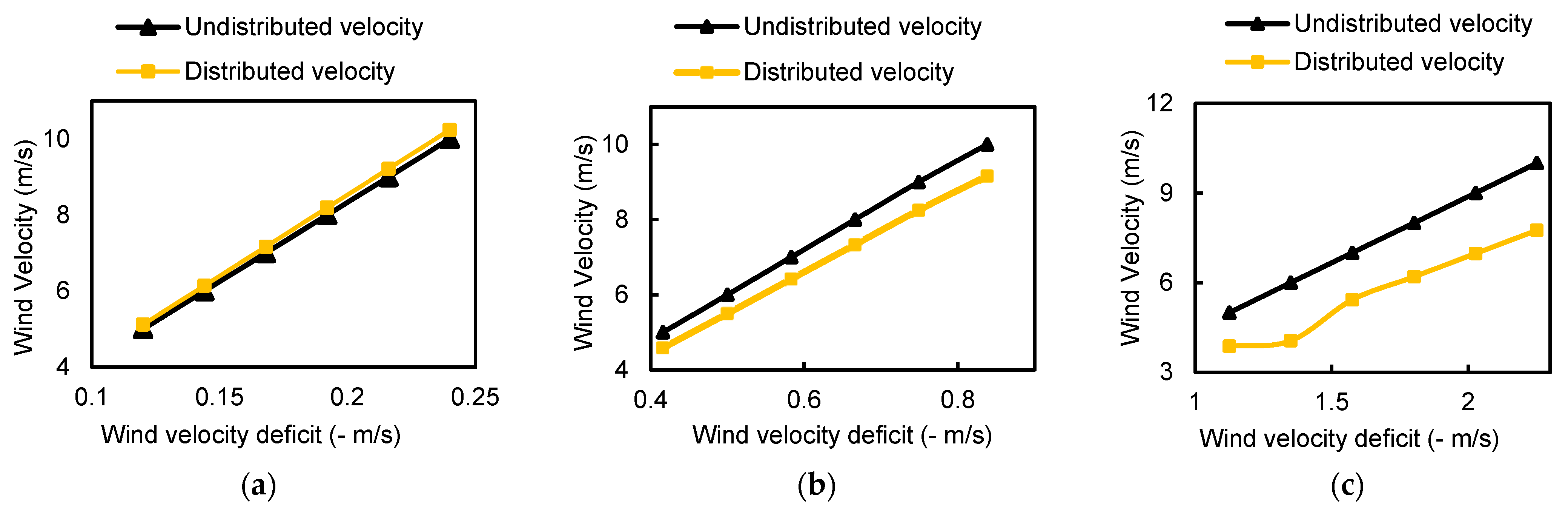
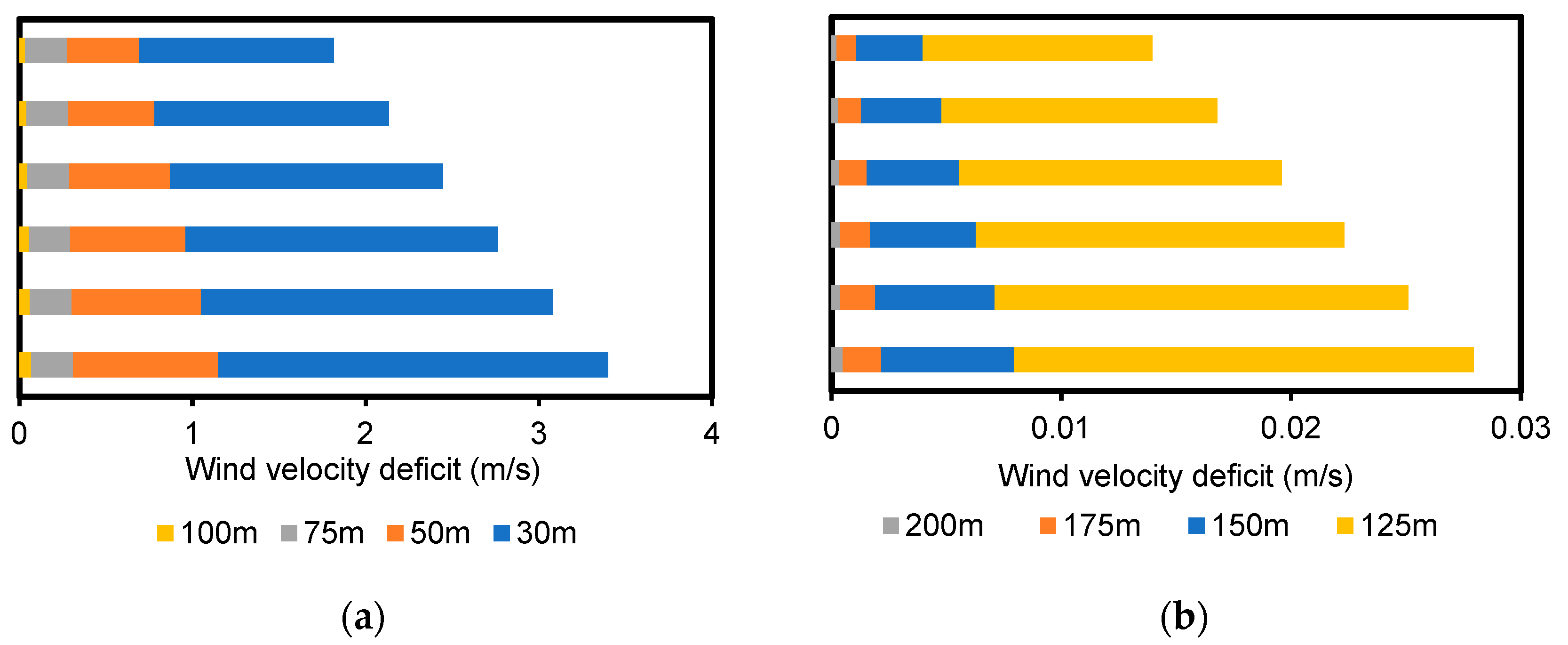
4.3. Local Wake Analysis Using the Gaussian Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CFD | Computational fluid dynamics | - |
| NREL | National Renewable Energy Laboratory | - |
| LES | Large eddy simulation | - |
| k | Turbulence kinetic energy | m2/s2 |
| ε | Turbulence dissipation rate | m2/s3 |
| ω | Specific dissipation rate | 1/s |
| U | Wind velocity at distance x | m/s |
| U0 | Free-stream wind velocity | m/s |
| D | Rotor diameter | m |
| Air density | kg/m3 | |
| μ | Dynamic viscosity | Pa·s |
| μT | Eddy viscosity | Pa·s |
| σ | Closure coefficient | - |
| τ | Reynolds stress tensor | Pa |
| Y+ | Wall distance | - |
| k-epsilon | Standard k-ε turbulence model | - |
| k-omega | Standard k-ω turbulence model | - |
| k-omega SST | Shear stress transport k-ω turbulence model | - |
| T | Torque | N·m |
| P | Power | W |
| Cp | Power coefficient | - |
| CT | Thrust coefficient | - |
| Skewness | Meshing quality metric | - |
| Orthogonal Quality | Meshing quality metric | - |
| α\alphaα | Closure coefficient for turbulence models | - |
| Wake decay constant | - | |
| ∅ | Flow angle or the angle of attack | Degrees/Rad |
References
- Ahmad, U.; Khan, M.A. Energy Demand in Pakistan: A Disaggregate Analysis Energy Demand in Pakistan: A Disaggregate Analysis. Pak. Dev. Rev. 2015, 47, 437–455. [Google Scholar] [CrossRef]
- Conti-Ramsden, J.; Dyer, K. Materials innovations for more efficient wind turbines. Renew. Energy Focus 2015, 16, 132–133. [Google Scholar] [CrossRef]
- Irfan, M.N.; Rosly, N. The Significant of Efficient Wind Turbines Arrangement in Mersing. Prog. Aerosp. Aviat. Technol. 2022, 2, 65–71. [Google Scholar] [CrossRef]
- Samsudin, M.I.S.; Mohd, S. Development of A Small-Scale Vortex-Induced Wind Turbine. Prog. Aerosp. Aviat. Technol. 2022, 2, 10–18. [Google Scholar] [CrossRef]
- Azam, S.R.S.; Malaysia, U.T.H.O.; Abidin, S.F.Z.; Ishak, I.A.; Khalid, A.; Mustaffa, N.; Taib, I.; Sukiman, S.L.; Darlis, N. Flow Analysis of Intake Manifold Using Computational Fluid Dynamics. Int. J. Integr. Eng. 2023, 15, 88–95. [Google Scholar] [CrossRef]
- Kumar, B.; Srivastav, V.K.; Jain, A.; Paul, A.R. Study of numerical schemes for the CFD simulation of human airways. Int. J. Integr. Eng. 2019, 11, 32–40. [Google Scholar] [CrossRef]
- Jamaludin, N.F.; Yusop, F.M.; Saji, N. Study Usage of Computational Fluid Dynamics (CFD) for Indoor Simulation. Prog. Eng. Appl. Technol. 2021, 2, 453–463. Available online: https://publisher.uthm.edu.my/periodicals/index.php/peat/article/view/799 (accessed on 28 September 2023).
- Cleve, J.; Greiner, M.; Enevoldsen, P.; Birkemose, B.; Jensen, L. Model-based analysis of wake-flow data in the Nysted offshore wind farm. Wind Energy 2009, 12, 125–135. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W.Z. Numerical modeling of wind turbine wakes. J. Fluids Eng. Trans. ASME 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Neiva, A.; Guedes, V.; Massa, C.L.S.; Davy, D. Bello de Freitas a Review of Wind Turbine Wake Models for Wind Park Optimization; Brazilian Association of Mechanical Engineering and Sciences: Rio de Janeiro, Brazil, 2019; Available online: https://www.researchgate.net/publication/334330334 (accessed on 28 September 2023).
- Tian, L.; Zhu, W.; Shen, W.; Zhao, N.; Shen, Z. Development and validation of a new two-dimensional wake model for wind turbine wakes. J. Wind Eng. Ind. Aerodyn. 2015, 137, 90–99. [Google Scholar] [CrossRef]
- Kontou, M.G.; Asouti, V.G.; Giannakoglou, K.C. DNN surrogates for turbulence closure in CFD-based shape optimization. Appl. Soft Comput. 2023, Volume 134, 110013. [Google Scholar] [CrossRef]
- Shakoor, R.; Hassan, M.Y.; Raheem, A.; Wu, Y.K. Wake effect modeling: A review of wind farm layout optimization using Jensen’s model. Renew. Sustain. Energy Rev. 2016, 58, 1048–1059. [Google Scholar] [CrossRef]
- Katic, I.; Højstrup, J.; Jensen, N.O. A Simple Model for Cluster Efficiency Publication Date. In Proceedings of the European Wind Energy Association Conference and Exhibition, Rome, Italy, 7–9 October 1986; Volume 1, pp. 407–410. Available online: https://backend.orbit.dtu.dk/ws/portalfiles/portal/106427419/A_Simple_Model_for_Cluster_Efficiency_EWEC_86_.pdf (accessed on 6 October 2023).
- Tian, L.; Zhu, W.; Shen, W.; Song, Y.; Zhao, N. Prediction of multi-wake problems using an improved Jensen wake model. Renew. Energy 2017, 102, 457–469. [Google Scholar] [CrossRef]
- Jensen, N.O. A Simple Model for Cluster Efficiency; European Wind Energy Association: Etterbeek, Belgium, 1983. [Google Scholar]
- Jensen, N.O. A Note on Wind Generator Interaction; Riso National Laboratory: Roskilde, Denmark, 1987; Volume 1. [Google Scholar]
- Göçmen, T.; Van Der Laan, P.; Réthoré, P.E.; Diaz, A.P.; Larsen, G.C.; Ott, S. Wind turbine wake models developed at the technical university of Denmark: A review. Renew. Sustain. Energy Rev. 2016, 60, 752–769. [Google Scholar] [CrossRef]
- Larsen, G.C. A Simple Wake Calculation Procedure; Risø-M, No. 2760; Risø National Laboratory: Roskilde, Denmark, 1988; p. 58. Available online: http://orbit.dtu.dk/ws/files/55567186/ris_m_2760.pdf (accessed on 28 September 2023).
- Farndsen, S. Analytical modelling of wind speed deficit in large offshore wind farms. Wiley Intersci. 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- Ghaisas, N.S.; Archer, C.L. Geometry-based models for studying the effects of wind farm layout. J. Atmos. Ocean Technol. 2016, 33, 481–501. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers Large eddy simulation study of fully developed wind-turbine array. AIP Phys. Fluid 2013, 22, 015110. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Pryor, S.C.; Frandsen, S.T.; Hansen, K.S.; Schepers, J.G.; Rados, K.; Schlez, W.; Neubert, A.; Jensen, L.E.; Neckelmann, S. Quantifying the impact of wind turbine wakes on power output at offshore wind farms. J. Atmos Ocean Technol. 2010, 27, 1302–1317. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Frandsen, S.T.; Rathmann, O.; Hansen, K.S.; Politis, E.; Prospathopoulos, J.; Schepers, J.G.; Rados, K.; Cabezón, D.; Schlez, W.; et al. Flow and Wakes in Large Wind Farms: Final Report for UPWIND WP8; no. Risø-R-1765 (EN); Danmarks Tekniske Universitet, Risø National Laboratory Roskilde: Lyngby, Denmark, 2011. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model Turbulence heat and mass transfer. Turbul. Heat Mass Transf. 2003, 4, 625–632. Available online: https://www.researchgate.net/publication/228742295 (accessed on 28 September 2023).
- Andias, R.; Mohd, S.; Zulkafli, F.; Didane, D.H. Simulation study of wind turbine system for electric powered vehicle. Int. J. Integr. Eng. 2020, 12, 76–81. [Google Scholar] [CrossRef]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1973, 5, 413–418. [Google Scholar] [CrossRef]
- Launder, B.E.; Sharma, B.I. Application of The Energy-Dissipation Model of Turbulence of the Calculation of Flow Near a Spinning Disc. Lett. Heat Mass Transf. 1974, 1, 131–138. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modelling for CFD 3rd Edition. 2006. Available online: http://www.dcwindustries.com (accessed on 12 June 2023).
- Reynolds, W.C. Computation of Turbulent Flow; Department of Mechanical Engineering, Stanford University: Stanford, CA, USA, 1989. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the k-ω turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics; Pearson: London, UK, 2007; Volume 10. [Google Scholar]
- Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2001; pp. 27–28. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained. Theory, Design and Application; WILEY: Hoboken, NJ, USA, 2009. [Google Scholar]



| Parameter | Value/Type |
|---|---|
| Angle of attack | |
| Kinematic viscosity | |
| Angle of attack | |
| Kinematic viscosity | |
| Number of Iterations | 500 |
| Solution method | Second order upwind |
| Length | 1 m |
| Solver type | Pressure-based |
| Density of fluid | |
| Viscous model | k-epsilon |
| Operating pressure | 0 gauge (1 atm) |
| Operating temperature | 288.16 K |
| Velocity flow | 30 m/s |
| Time | Steady |
| Skewness | Orthogonal Quality | ||
|---|---|---|---|
| Growth Rate | Meshing Metrics | Growth Rate | Meshing Metrics |
| 1.05 | 0.43 | 1.05 | 0.67 |
| 1.04 | 0.38 | 1.04 | 0.71 |
| 1.03 | 0.31 | 1.03 | 0.78 |
| 1.02 | 0.24 | 1.02 | 0.86 |
| Skewness | |||||
|---|---|---|---|---|---|
| Excellent | Very Good | Good | Acceptable | Bad | Unacceptable |
| 0–0.25 | 0.25–0.50 | 0.50–0.80 | 0.80–0.94 | 0.94–0.97 | 0.97–1.00 |
| Orthogonal Quality | |||||
| Unacceptable | Bad | Acceptable | Good | Very Good | Excellent |
| 0–0.001 | 0.001–0.14 | 0.14–0.20 | 0.20–0.64 | 0.64–0.95 | 0.95–1.00 |
| Input Parameter | Value/Type |
|---|---|
| Angle of attack | |
| Kinematic viscosity | |
| Solution method | Second order upwind |
| Length | 1 m |
| Solver type | Pressure-based |
| Turbulent intensity | 5% |
| Input parameter | Magnitude |
| Density of fluid | 1.225 |
| Viscous model | k-omega SST |
| Operating pressure | 0 gauge (1 atm) |
| Operating temperature | 288.16 K |
| Velocity flow | 5–10 m/s |
| Time | Steady |
| Turbulent viscosity ratio | 10 |
| Mesh No. | No. Cells (Millions) | Torque (N-m) | Error (%) |
|---|---|---|---|
| M1 | 11.010 | 780.25 | 29.09 |
| M2 | 11.280 | 829.30 | 24.61 |
| M3 | 11.985 | 917.60 | 16.58 |
| M4 | 13.027 | 1023.15 | 6.99 |
| M5 | 12.662 | 973.80 | 11.50 |
| Exp. [35] | ــــــــــــــــــ | 1100 | ــــــــــــ |
| Turbulence Model | Wind Speed (m/s) | CFD Torque (N-m) | Exp. Torque (N-m) [35] | Error (%) |
|---|---|---|---|---|
| k-epsilon | 10 | 1481.67 | 1340 | −10.57 |
| k-omega | 846.83 | 36.80 | ||
| k-omega (SST) | 996.66 | 25.62 | ||
| k-epsilon | 9 | 1192.33 | 1390 | 14.22 |
| k-omega | 866.87 | 37.63 | ||
| k-omega (SST) | 991.80 | 28.64 | ||
| k-epsilon | 8 | 989.10 | 1100 | 10.08 |
| k-omega | 824.73 | 25.02 | ||
| k-omega (SST) | 1023.15 | 6.986 | ||
| k-epsilon | 7 | 638.70 | 800 | 20.16 |
| k-omega | 584.00 | 27.00 | ||
| k-omega (SST) | 520.38 | 34.95 | ||
| k-epsilon | 6 | 431.80 | 478 | 9.665 |
| k-omega | 387.01 | 19.03 | ||
| k-omega (SST) | 344.44 | 27.94 |
| CFD Simulation | |||||
|---|---|---|---|---|---|
| Rot. Speed | Wind Speed | Torque | Power | Cp | Error |
| rad/s | (m/s) | (n-m) | (m/s) | unitless | (%) |
| 7.54 | 5 | 266 | 2006 | 0.329 | 7.54 |
| 7.54 | 6 | 387 | 2917 | 0.278 | 18.87 |
| 7.54 | 7 | 581 | 4380 | 0.262 | 27.38 |
| 7.54 | 8 | 915 | 6899 | 0.277 | 16.82 |
| 7.54 | 9 | 1017 | 7668 | 0.216 | 26.83 |
| 7.54 | 10 | 1108 | 8354 | 0.172 | 17.31 |
| Experimental [35] | |||||
| 7.54 | 5 | 300 | 2262 | 0.371 | - |
| 7.54 | 6 | 477 | 3596 | 0.342 | - |
| 7.54 | 7 | 800 | 6032 | 0.361 | - |
| 7.54 | 8 | 1100 | 8294 | 0.333 | - |
| 7.54 | 9 | 1390 | 10,480 | 0.300 | - |
| 7.54 | 10 | 1340 | 10,103 | 0.210 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ttowi, A.; Mohammed, A.N.; Al-Alimi, S.; Zhou, W.; Saif, Y.; Ismail, I.F. Computational Fluid Dynamics (CFD) Investigation of NREL Phase VI Wind Turbine Performance Using Various Turbulence Models. Processes 2024, 12, 1994. https://doi.org/10.3390/pr12091994
Al-Ttowi A, Mohammed AN, Al-Alimi S, Zhou W, Saif Y, Ismail IF. Computational Fluid Dynamics (CFD) Investigation of NREL Phase VI Wind Turbine Performance Using Various Turbulence Models. Processes. 2024; 12(9):1994. https://doi.org/10.3390/pr12091994
Chicago/Turabian StyleAl-Ttowi, Abobakr, Akmal Nizam Mohammed, Sami Al-Alimi, Wenbin Zhou, Yazid Saif, and Iman Fitri Ismail. 2024. "Computational Fluid Dynamics (CFD) Investigation of NREL Phase VI Wind Turbine Performance Using Various Turbulence Models" Processes 12, no. 9: 1994. https://doi.org/10.3390/pr12091994
APA StyleAl-Ttowi, A., Mohammed, A. N., Al-Alimi, S., Zhou, W., Saif, Y., & Ismail, I. F. (2024). Computational Fluid Dynamics (CFD) Investigation of NREL Phase VI Wind Turbine Performance Using Various Turbulence Models. Processes, 12(9), 1994. https://doi.org/10.3390/pr12091994







