Identification of Flow Pressure-Driven Leakage Zones Using Improved EDNN-PP-LCNetV2 with Deep Learning Framework in Water Distribution System

Abstract

This study introduces a novel deep learning framework for detecting leakage in water distribution systems (WDSs). The key innovation lies in a two-step process: First, the WDS is partitioned using a K-means clustering algorithm based on pressure sensitivity analysis. Then, an encoder–decoder neural network (EDNN) model is employed to extract and process the pressure and flow sensitivities. The core of the framework is the PP-LCNetV2 architecture that ensures the model’s lightweight, which is optimized for CPU devices. This combination ensures rapid, accurate leakage detection. Three cases are employed to evaluate the method. By applying data augmentation techniques, including the demand and measurement noises, the framework demonstrates robustness across different noise levels. Compared with other methods, the results show this method can efficiently detect over 90% of leakage across different operating conditions while maintaining a higher recognition of the magnitude of leakages. This research offers a significant improvement in computational efficiency and detection accuracy over existing approaches.

1. Introduction

Water loss in water distribution systems (WDSs) due to leakage leads to significant problems around the world. Currently, non-revenue water containing leakages, breaks, and other factors before reaching consumers is estimated to constitute approximately 32–35% of the total water in developing countries and about 25% in developed countries [1,2]. For instance, South Africa has a significant water loss with an estimated 38% of its water classified as non-revenue water, with 25.4% attributed to physical leakages in its WDSs [3]. Similarly, in Harare, Zimbabwe, water loss ranges from 29% to 43%, with over 70% of this loss attributed to leakage [4]. The total water loss in Ethiopia reaches 33.32% and 27.96% [5]. In Lithuania, the water loss percentage ranges from 17% to 52%, with an average of 24% [6]. In Europe, water loss due to leakage in urban WDSs is estimated to reach as high as 30% [7]. This problem extends to almost all countries, where water loss poses significant challenges to the sustainability of water resources.

Early leakage identifications are crucial to reduce water losses, costs, and risks. Traditionally, leak detection relies on acoustic logging [8], ground-penetrating radar inspections [9], and visual inspections [10], with each having their respective challenges. Acoustic logging is effective for pinpointing leakage in small-scale WDSs but becomes less effective for large-scale networks. Ground-penetrating radar, on the other hand, is more suited for identifying subsurface leakage but requires expensive equipment and specialized training. Visual inspections, though the most straightforward, can only detect visible leakage, often after significant water loss has already occurred. Meanwhile, these methods require substantial manpower and equipment mobilization to cover large areas. Inspections and tests are time and labor-intensive and may disrupt water service. As a result, many utilities use reactive approaches that detect only evident leakage based on surface observations, customer complaints, or unusual water usage [11].

Advanced sensing, data analytics, and machine learning techniques provide new opportunities for efficient leakage detection. By monitoring WDSs with sensors and analyzing these data using algorithms, especially the pressure and flow analysis method, leakage can be detected earlier based on subtler pressure and water flow changes [12]. Sensitivity analysis represents the pressure and flow changes at every node and link to account for varying water demand and quantifies how leakage events impact pressure across a WDS. The absolute pressure and flow differences between normal and abnormal conditions could be solved at specific locations by an extended period simulation (EPS) process [13]. Several researchers have explored sensitivity analysis using machine learning models for leakage detection in WDSs. For instance, Ponce et al. focused on leakage detection in the hydraulic calculation process using an extended-horizon analysis model with a flow and pressure sensitivity matrix [14]. Wu et al. applied a pressure-driven model for detecting leakage based on EPSs within a pressure sensitivity analysis [15,16]. Santos-Ruiz et al. investigated the use of classifiers with inlet flows for leakage localization [17]. However, these methods might show a reduced computational efficiency and significantly increase the solution search difficulty, especially when handling large nodes and links within fast computing for real-time identifying leakage.

Segmenting WDS into district metered areas (DMAs) is a crucial strategy for city water departments to facilitate leakage identification. Zheng et al. demonstrated how DMAs can optimize water system management and protect against contamination by localizing control [18]. Similarly, Di Nardo et al. highlighted the redundancy features in WDSs, showing that partitioning into DMAs improves operational reliability and helps localize leakage quickly [19]. Deuerlein explored how network graph partitioning can enhance leak detection efficiency by isolating sections of the system, allowing for targeted and quicker interventions. Both studies highlight the critical role DMAs play in improving the operational management and reliability of WDS [20]. DMAs could be established by adjusting opening degrees of specific boundary pipes, thereby forming distinct zones for respective management. Several approaches have been researched for the DMA partitioning problem. Nardo et al. evaluated various clustering methods using social network community detection and graph partitioning algorithms to assess the effectiveness of system division [21]. Rajeswaran et al. applied the graph partitioning model for leakage identification in WDSs and tested it on large-scale networks via pressure sensitivity analysis [22]. Zhang et al. developed a framework for identifying leakage zones using a support vector machine (SVM). This framework segments the network into zones based on pressure sensitivity clustering. The SVM classifier model was trained on leakage simulation data to predict leakage events from nodal pressure sensitivity analysis, proving effective in a real-world case study [11]. Although these methods offer an effective integration to WDS partitioning and leakage detection, they often depend on manual intervention to select the optimal model hyperparameters and to re-adjust the model when the network topology updates as the time changes.

Deep learning methods have shown promise for infrastructure monitoring applications [16], which can model complex nonlinear relationships in the spatial and temporal series data of sensors for anomaly detection. For instance, Fan et al. applied an autoencoder neural network for leakage detection with pressure data under leakage or normal conditions [23]. Mohamed et al. used Convolutional Neural Networks (CNNs) for vision-based surface water leakage detection through the use of infrared sensors [24]. Basnet et al. evaluated the effectiveness of supervised machine learning models, such as multilayer perceptions and CNNs for detecting leakages in WDS nodes. The study highlighted these models’ ability to handle leakage complexities without relying on labor-intensive hyperparameter optimization [25]. However, the high configuration and cost of GPU requirements prevented the installation of computing devices. The PP-LCNetV2 achieves a 4–5 times faster speedup compared to standard CNN models with similar leakage detection accuracy [26,27,28], filling the heart with hope. The efficient PP-LCNetV2 model enables low-latency leakage detection directly on infrastructure devices that can be deployed for safety-critical monitoring applications under resource constraints.

Leakage detection is hindered by several challenges, including the presence of noise in pressure and flow data, which can obscure leakage signals [29]. Demand variations and measurement noise in sensors further complicate the ability to accurately identify leakage. Additionally, large-scale WDSs require scalable solutions that can handle vast amounts of data in real time, without sacrificing detection performance. Overcoming these challenges is critical for ensuring that leakage detection methods are both reliable and practical for widespread use.

Therefore, the main objective of this research is to develop a robust, efficient, and scalable deep learning framework for the leakage detection in WDSs. The goal is to address the challenge of balancing high detection accuracy and computational efficiency in CPU operations under noisy conditions. This framework is designed to be practical for small-scale and large-scale WDS applications, ensuring that the solution is both effective and adaptable to various deployment environments.

Our contributions include the following: (1) the study presents a novel partitioning strategy, utilizing K-means clustering based on pressure sensitivity analysis, which improves the efficiency and precision of leakage detection; (2) a CPU inference deep learning framework with a hydraulic model is applied to improve the speed of computing in WDSs; (3) the framework incorporates noise robustness through data augmentation techniques, ensuring that it performs reliably even in the presence of demand and measurement noise.

The remainder of this paper is structured as follows: Section 2 describes the methodology of the leakage detection model, while Section 3 presents case studies and compares the results with other models. Section 4 discusses the advantages and limitations of this method. Finally, Section 5 provides the conclusion.

2. Methodology

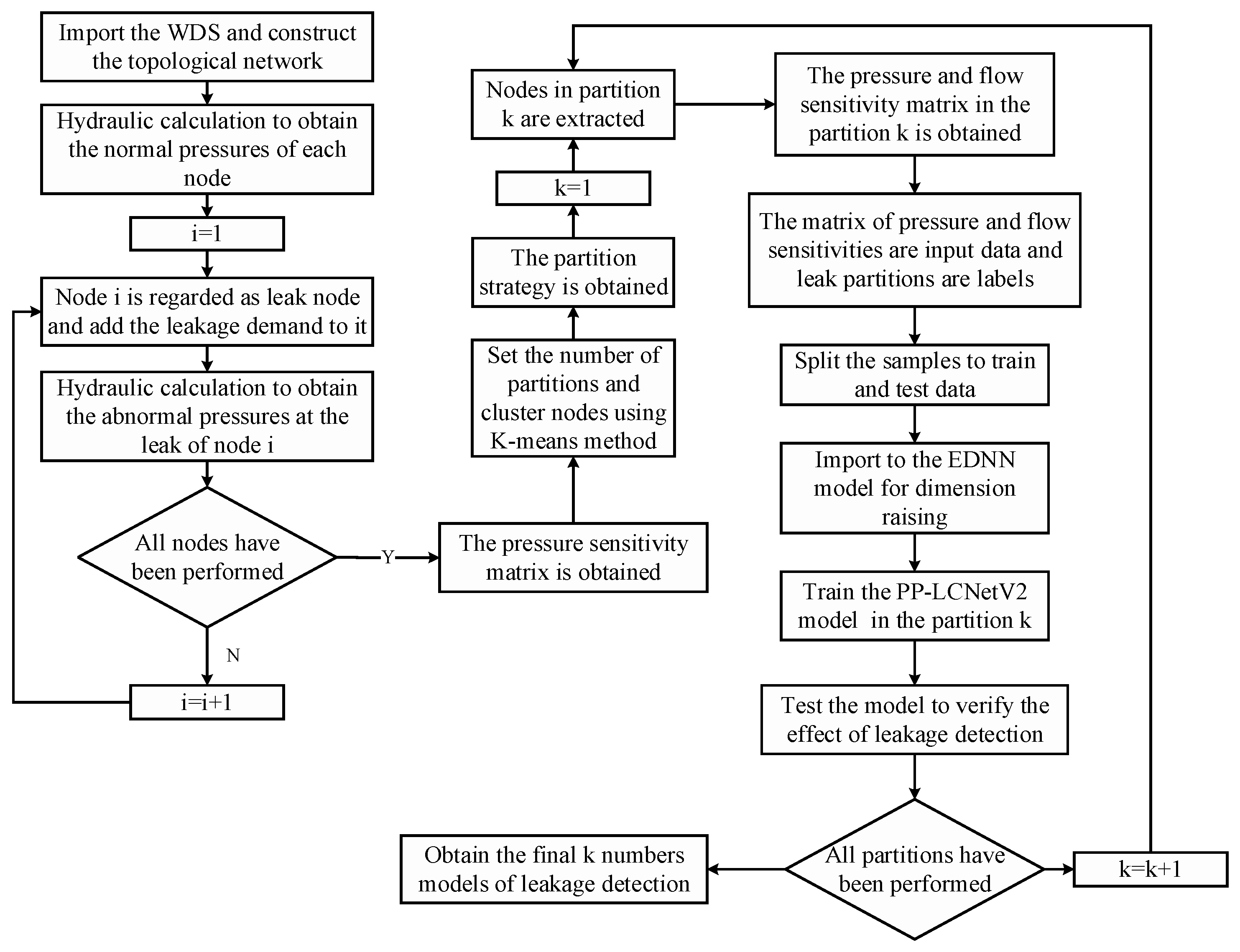
2.1. General Framework

The K-means model is utilized to systematically partition a WDS into distinct DMAs, facilitating enhanced leakage detection by clustering nodes based on pressure sensitivity and optimizing the spatial arrangement of the network. Then, the PP-LCNetV2 combines the depthwise (DW) separable convolutions [30] and attention modules [31] to build a lightweight CNN feature extractor optimized for CPU inference to satisfy the fast computing of sensors in WDSs. We explore and improve the PP-LCNetV2 [28] with an encoder and decoder neural network (EDNN) for efficient and accurate of leakage detection. Therefore, an EDNN-PP-LCNetV2 leakage detection model is presented enhanced by PP-LCNetV2 as the core feature learning component. The comprehensive framework of the method is depicted in Figure 1, providing a visual representation of the process.

2.2. Network Partition

In WDSs, effective management and operation are significantly enhanced by partitioning the network to DMAs. This strategy could facilitate precise leakage detection and minimizes response times and bolsters system reliability by isolating issues to prevent widespread impacts. The significant variations in water demands across different nodes result in pressure sensitivities that can vary widely, sometimes by orders of magnitude [2]. However, leakage events are relatively rare, making it difficult to collect a sufficient amount of data for effective partitioning. To overcome this limitation, pressure sensitivity analysis as a key component is applied, where allows to simulate leakage events in various nodes within the WDS by calculating the pressure deviations that would occur in the presence of a leakage. This process enables us to account for a wide range of potential leakage situations when applied to real-world conditions.

By leveraging a combination of pressure sensitivity matrices and clustering algorithm, the framework can create various scenarios such as pipe bursts or leaks and capture detailed trends regarding their effects on the network. The pressure sensitivity can be represented by Equation (1).

$$∆P_i^j=|P_i^j-P_i|$$

(1)

where $∆P_i^j$ is the absolute value of pressure difference between $P_i^j$ and $P_i$ at the ith node, as the leakage appeared at the jth node; $P_i^j$ is abnormal pressure at the ith node, as the leakage appeared at the jth node; $p_i$ is normal pressure at the ith node.

Subsequently, standardization should be applied [32]. This involves adjusting the mean of the pressure differences to zero and scaling the standard deviation to one, as described in Equations (2) and (3). Finally, calculating all the nodes using Equations (1)–(3), a pressure sensitivity matrix is obtained, expressed as Equation (4).

$$∆{P^{\prime }}_i^j={\displaystyle \frac{∆P_i^j-∆{\overline{P}}^j}{S_j}}$$

(2)

$$∆{P^{″}}_i^j={\displaystyle \frac{∆{P^{\prime }}_i^j-\max \left(\mathsf{\Delta }{P^{\prime }}^j\right)}{\max \left(\mathsf{\Delta }{P^{\prime }}^j\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(\mathsf{\Delta }{P^{\prime }}^j\right)}}$$

(3)

$$\left[\begin{array}{ccc}\begin{array}{c}\begin{array}{cc}∆{P^{\prime }}_1^1& ∆{P^{\prime }}_2^1\end{array}\\ \begin{array}{cc}∆{P^{\prime }}_1^2& ∆{P^{\prime }}_2^2\end{array}\end{array}& \cdots & \begin{array}{c}∆{P^{\prime }}_N^1\\ ∆{P^{\prime }}_N^2\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}∆{P^{\prime }}_1^N& ∆{P^{\prime }}_2^N\end{array}& \cdots & ∆{P^{\prime }}_N^N\end{array}\right]$$

(4)

where $∆{P^{\prime }}_i^j$ is the standardization pressure difference at the ith node as the leakage appeared at the jth node; $∆{P^{″}}_i^j$ is the normalization pressure difference in node i as the leakage is at node j; $∆{\overline{P}}^j$ is the mean of pressure difference, as the jth node is considered as a leakage node; The $\max \left(\right)\mathrm{and}\min \left(\right)$ are the maximum and minimum values, respectively; $S_j$ is the standard deviation of pressure difference in all nodes as the jth node is a leakage node; $N$ is the total number of nodes.

After that, the K-means model is employed to divide nodes into K clusters using Equation (4), with each node belonging to the cluster whose mean value is closest [11]. This method allows for more efficient and scalable leak detection in complex networks. Initially, cluster centers are selected randomly. Subsequently, nodes are allocated to the nearest cluster center by computing the Euclidean distance, as outlined in Equation (5). After all nodes are assigned, the center of each cluster is recalculated. The iterative recalculation process continues until the cluster centers converge and stabilize, thereby ensuring that the network is effectively divided into distinct partitions.

$$d={\sum }_{i=1}^N\sqrt{{\left(∆P_i^{″}-∆P_j^{″}\right)}^2}$$

(5)

where $d$ is the distance between the ith node and jth node.

2.3. Dimension Raising

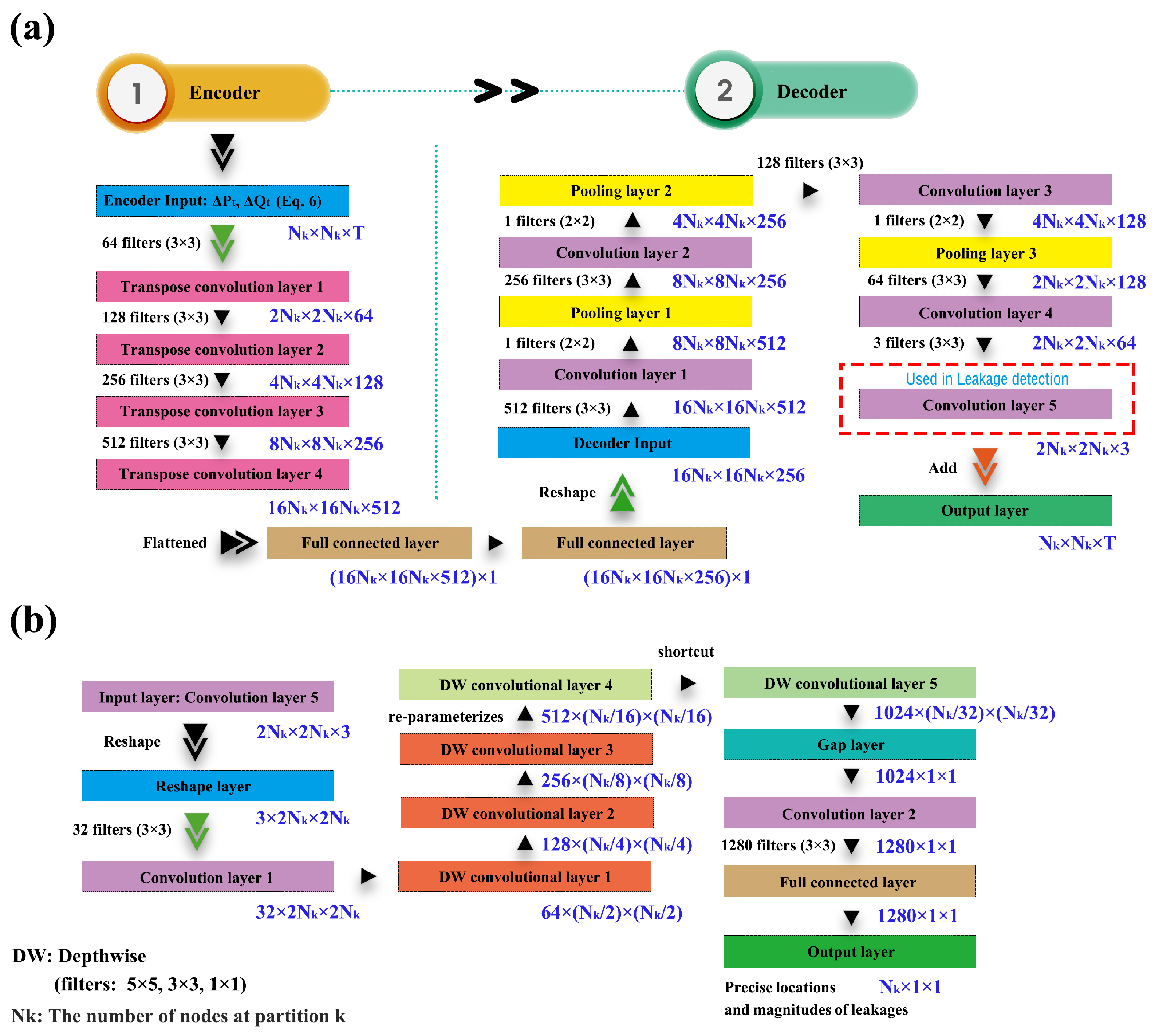
After network partition, high-dimensional pattern input should be obtained in each partition with a time series of pressure and inlet flow sensitivities for effectively detecting leakage. Thus, an encoder–decoder neural network (EDNN) is commonly used. The EDNN framework serves as the backbone of the dimension raising model for fitting the leakage detection, where an asymmetric encoder–decoder structure, in which the encoder compresses the low-dimensional input data (pressure and flow) into a higher dimensional latent representation, is utilized, and the decoder reconstructs and reduces this data dimension to fit the leakage detection. This framework allows the model to learn both spatial and temporal patterns in the data, making it well-suited for detecting small leaks that might otherwise go unnoticed.

The encoder component generally consists of a convolutional neural network (CNN) that extracts hierarchical features from the input data using a series of transposed convolutional layers, progressively capturing intricate patterns and spatial hierarchies. The backbone of the EDNN could be expressed in Figure 2a.

In Figure 2a, the input layer of encoder applies a three-dimensional matrix containing rows, columns, and pages to represent the time series of hydraulic calculation results from the EPS process, combined with pressure sensitivity analysis as a novel contribution in $k$th partition, is expressed as Equation (6).

$${\left[∆P,∆Q\right]}_k={\left[∆P_1,∆Q_1,∆P_2,∆Q_2,\dots ,∆P_T,∆Q_T\right]}_k$$

(6)

where $T$ is the total time of the EPS process and $k$ is the label of $k$th partition.

The rows and columns of the input layer contain all the nodes’ features in $k$th partition, where pressures and flows differences from abnormal to normal are considered, which can be expressed as Equations (7) and (8).

$$∆P_t=\left[\begin{array}{ccc}\begin{array}{c}\begin{array}{cc}∆P_{t,1}^1& ∆P_{t,2}^1\end{array}\\ \begin{array}{cc}∆P_{t,1}^2& ∆P_{t,2}^2\end{array}\end{array}& \cdots & \begin{array}{c}∆P_{t,N_k}^1\\ ∆P_{t,N_k}^2\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}∆P_{t,1}^{N_k}& ∆P_{t,2}^{N_k}\end{array}& \cdots & ∆P_{t,N_k}^{N_k}\end{array}\right]$$

(7)

$$∆Q_t=\left[\begin{array}{ccc}\begin{array}{c}\begin{array}{cc}∆Q_{t,1}^1& ∆Q_{t,2}^1\end{array}\\ \begin{array}{cc}∆Q_{t,1}^2& ∆Q_{t,2}^2\end{array}\end{array}& \cdots & \begin{array}{c}∆Q_{t,N_k}^1\\ ∆Q_{t,N_k}^2\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}∆Q_{t,1}^{N_k}& ∆Q_{t,2}^{N_k}\end{array}& \cdots & ∆Q_{t,N_k}^{N_k}\end{array}\right]$$

(8)

where $∆P_t$ and $∆Q_t$ represent the absolute differences in pressures and inlet flows between abnormal and normal conditions at nodes at time t, called pressure and flow sensitivities; $N_k$ is the number of nodes at partition $k$; $∆P_{t,i}^j$ and $∆Q_{t,i}^j$ represents the absolute difference between abnormal and normal pressures and flows at the ith node at time t, as the jth node is a leakage point, expressed as Equations (9) and (10).

$$∆P_{t,i}^j={|P}_{t,i}^j-P_{t,i}|$$

(9)

$$∆Q_{t,i}^j={|Q}_{t,i}^j-Q_{t,i}|$$

(10)

Then, standardization must be applied, which involves adjusting the mean of the pressure and flow differences to zero and scaling the standard deviation to one, as described in Equations (2) and (3).

As the input determined, transpose convolutional layers could be added next to the input layer using convolution and upsampling operations in the encoder process, as shown in Figure 2a. The details of these layers are as follows: The input layer is the size of $N_k$×$N_k$× T at partition $k$. Transpose convolutional layer 1 contains 64 filters. The kernel size is 3 × 3. The stride is set to 2; transpose convolutional layer 2 contains 128 filters, 3 × 3 kernels, and 2 strides; transpose convolutional layer 3 contains 256 filters, 3 × 3 kernels, and 2 strides; transpose convolutional layer 4 contains 512 filters, 3 × 3 kernels size, and 2 strides. The padding method used is SAME, ensuring that the output feature map maintains the same spatial dimensions as the input feature map. Finally, two fully connected layer are added, which flattens convolutional feature maps to shape (16$N_k$ × 16$N_k$ × 512) × 1, and then to (16$N_k$ × 16$N_k$ × 256) × 1.

Then, the decoder part upsamples the encoder output to produce a full-resolution segmentation mask. The decoder uses convolution and downsampling operations to gradually increase the spatial dimensions of the encoder’s outputs. The objective of the output layer in the decoder process is to reconstruct the information from the input layer for each node, encompassing both pressure and flow sensitivity data.

The details of layers are as follows: The first layer receives an encoded vector shaped as 16$N_k$ × 16$N_k$ × 256; convolution layer 1 contains 512 filters, 3 × 3 kernels, and 1 stride; pooling layer 1 contains 1 filter, a 2 × 2 kernel, and 1 stride; convolution layer 2 contains 256 filters, 3 × 3 kernels, and 1 stride; pooling layer 2 contains 1 filter, a 2 × 2 kernel, and 1 stride; convolution layer 3 contains 128 filters, 3 × 3 kernels, and 1 stride; pooling layer 3 contains 1 filter, a 2 × 2 kernel, and 1 stride; convolution layer 4 contains 64 filters, 3 × 3 kernels, and 1 stride. Pooling layer 4 contains 1 filter, a 2 × 2 kernel, and 1 stride; the way of padding is SAME in convolution layers. Convolution layer 5 is a convolutional layer with 3 filters, 3 × 3 kernels, 1 stride, and SAME padding to reconstruct the matrix of input. The output layer of the decoder is designed to have the same dimensions as the input layer, ensuring a consistent representation of the data.

The convolution layer 5 in the decoder is selected as an output of the EDNN as it extracts high-dimensional features from the input layer and reduces spatial dimensions. Consequently, this layer is used as the input for the PP-LCNetV2 model to identify the position of leakages.

The Mean Squared Error (MSE) serves as an effective loss function for encoder–decoder problems, quantifying the average squared difference between the predicted and actual values to optimize model accuracy. The MSE ensures that the encoder effectively extracts the most pertinent features from the input data, while the decoder accurately reconstructs the compressed representation back to the original input space. Consequently, MSE is utilized as the loss function during the backpropagation process to optimize model performance.

Finally, all partitions should be processed by the EDNN model.

2.4. EDNN-PP-LCNetV2

Pressure sensitivity analysis can be utilized to identify areas with leakage nodes by collecting the pressures and inlet flows from the sensors at a fixed time interval. The time-series data across all nodes in a partition is formatted as multi-channel input maps by EDNN and fed into the PP-LCNetV2 model. The backbone of the PP-LCNetV2 is expressed in Figure 2b.

The overall architecture of PP-LCNetV2 follows a standard CNN in the first hidden layer with H-swish used as an activation function that is a variant of the swish function [33], which avoids computing the expensive sigmoid operation. Then, four DepthSepConv (DW separable convolution) blocks are applied to extract the information of leakage. The H-swish activation function is defined as Equation (11).

$$Hswish\left(x\right)={\displaystyle \frac{xReL{U}_6\left(x+3\right)}{6}}$$

(11)

$$ReL{U}_6\left(x\right)=\min \left\{max\right(0,x),6\}$$

(12)

In these blocks, a DW separable convolution is first used as the basic building block to construct the feature extraction backbone [26]. The kernel sizes used for DW convolution are 3 × 3 or 5 × 5 with strides of 1 or 2, where separate filters are applied to each input channel independently without combining across channels. A pointwise (PW) convolution comes after each DW convolution within a block where the kernel size is 1 × 1. The 1 × 1 pointwise kernel projects each spatial location of the input channels to a multiple-dimension vector with strides of 1 or 2. A Squeeze-and-Excitation (SE) component is added at last [26].

After that, PP-LCNetV2 re-parameterizes DW convolutions with varying kernel sizes (5 × 5, 3 × 3, 1 × 1) into a single fused layer, which allows the network to extract multi-scale spatial patterns from the input feature map without increasing computational cost, shown in Figure S1. The different kernel sizes are combined through factorizing the convolution parameters. If $K_1$, $K_2$, and $K_3$ are convolution kernels of sizes 5 × 5, 3 × 3, and 1 × 1, respectively, then the re-parameterized kernel $K$ can be expressed as Equation (13).

$$K={\beta }_1{K}_1+{\beta }_2{K}_2+{\beta }_3{K}_3$$

(13)

where ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$ are learnable scalar coefficients.

Then, another DepthSepConv layer with a residual structure is used. The input and output data are added together with an element-wise addition, which enables the gradient to directly backpropagate from later layers to initial layers during training, helping with vanishing gradients in deep networks.

After that, a global average pooling layer is used for more storage of the model with little increase in inference time. A standard CNN (1 × 1) layer and a full connection layer are applied to solve the output layer, which could be converted into predicted location probabilities via the Softmax function.

The choice of objective functions for the assessment of training and validation errors is contingent upon the intrinsic nature of the problem at hand. In the context of leakage detection, the goal is to simultaneously ascertain both the precise locations (node index) and magnitudes of leakages (such as normal, leakage, and pipe blast). Therefore, the cross-entropy loss function is applied due to its widespread use in classification tasks, as it quantifies the dissimilarity between predicted probability distributions and actual class labels, effectively guiding the optimization process. Throughout the training phase, our paramount objective is to minimize the loss function, which is succinctly expressed as Equation (14). Finally, the model’s weights are updated through backpropagation with gradient descent to minimize the loss.

$$L\left(x,y\right)=-{\sum }_{i=1}^C{y}_{i}log{p}_i$$

(14)

where $y_i$ represents the ith element of the real data and $p_i$ is the probability that the model predicts that $y$ belongs to the ith class.

2.5. Leakage Detection

The network is trained to classify normal operating conditions against various single and multiple leakage scenarios using EDNN-PP-LCNetV2 model. By utilizing the lightweight PP-LCNetV2 architecture, we ensure that the system remains computationally efficient and scalable, even in large networks. The pressure changes from the simulation become input features to train the model. The nodes are labeled into three statuses: normal, leakage, and pipe blast. The label values are 0, 1, and 2, respectively.

The Monte Carlo (MC) technique is utilized to randomly generate leakage events by artificially increasing the demand at selected nodes to simulate potential leakage scenarios [11]. The events are simulated through the EPS process. In the specific steps, the MC method randomly selects one or two nodes within a partition k and assigns random leakage demands to them. Following this, the hydraulic model is executed to determine the pressure and flow variations under both normal and abnormal conditions at each node for every leakage event, as calculated during the EPS time using Equations (1)–(3). This process is repeated for successive leakage events using the Monte Carlo approach until all potential leakage scenarios have been simulated. The total leakage events are $C_{N_k}^2+C_{N_k}^1$, where $N_k$ is the total nodes in the partition $k$. The training data are combined, and these samples are provided as Equation (15). The flows and pressures exhibit significant fluctuations throughout the hours or days. Finally, the standardization should be processed for the matrix of input data, expressed as Equations (2) and (3).

$${\left[X,Y\right]}_k={\left[∆P,∆Q,Y\right]}_k$$

(15)

where $X$ is a matrix of input data, which is the same as Equation (1), and $Y$ is output data containing leakage node index and magnitudes of leakages, where the output data size is the total nodes of the partition $k$.

To better distinguish between the inherent variability in pressure and flow under usual circumstances and the irregular deviations from potential leakages, a pressure threshold value should be assigned to each node for data cleaning. The pressure precision is set to 0.1 m, and flows are set to the value of 0.5 m²/h in this study. If a sample value is less than the measurement precisions, the sample is removed.

In the training process, pressures and flows are collected from the nodes in the partition $k$. These pressures and flow differences in the partition $k$ are fed as inputs to the EDNN-PP-LCNetV2 model. The labels of leakage node index and magnitudes of leakages enable supervised learning to discriminate between leakage locations and different leakage types.

Finally, the EDNN-PP-LCNetV2 model is trained in all the partitions. If the network comprises K partitions in the network, then K distinct leakage detection models can be developed, each specifically tailored to address the unique characteristics and dynamics of its respective partition.

2.6. Data Augmentation

To ensure the robustness of the proposed framework, data augmentation is employed by simulating demand and measurement noise during model training. This step allows the EDNN to learn to differentiate between actual leakages and noise-induced anomalies, improving the model’s performance in real-world conditions.

In this process, different types of noise are added into the nodes for simulating the leakage events as follows:

(1) Demand noise: to account for potential inaccuracies in demand values in the hydraulic model, Gaussian noise [34] characterized by a standard deviation of either 10%, or 20% of the mean demand is introduced into the demand parameters during the EPS process to account for variability. This adjustment is applied before conducting hydraulic simulations, enhancing the robustness of the model. This level of noise was chosen based on an analysis of typical demand uncertainty in municipal systems. The resulting simulated pressures and flows will contain some extent of leakages due to the perturbed demands.

(2) Measurement noise: After hydraulic simulation, Gaussian noise with a zero mean and standard deviation equal to 10%, or 20% of the true value is directly added to the simulated pressure and flow at the leakage and no leakage scenarios. This accounts for anticipated measurement imprecision of pressure and flow sensors in real systems.

The type and level of noise as the data augmentation added are selected based on analysis of anticipated real-world conditions and reasonable estimates of model and measurement uncertainties. The application for leakage detection with specific noise types introduces new insights into improving model robustness.

3. Case Studies

Three cases are employed to verify the effectiveness of this method. The Open Water Analytics toolbox (OWA) is applied to the EPS hydraulic calculations within the MATLAB 2023b environment developed by the KIOS Research Center for Intelligent Systems and Networks [28]. The system is as follows: CPU is i7-12700K; RAM is DDR4-32 G; ROM is ssd-2048 G; OS is Windows 11 and MATLAB-2023b.

3.1. Network A

Network A, depicted in Figure S2, comprises 92 junctions, 117 pipes, two pumps, two reservoirs, and three tanks [35]. The network supports an average water demand of 2450.03 m³/h. The hydraulic calculations are conducted using the EPANET OWA toolbox, with the time interval set to one hour throughout the EPS process. The maximum simulation duration is configured for 24 h to capture the dynamics of the system over a full day.

Initially, the K-means model is employed to cluster the nodes into distinct partitions, optimizing the spatial distribution and enhancing the manageability of the network. The number of partitions is set to five. The result of the partition is illustrated in Figure 3. The total junctions in each partition are [12, 14, 8, 39, 19].

After that, the leakages are introduced at junctions within each partition where the pressure and flow measurements are free of noise, ensuring an accurate assessment of the system’s response to leaks. The EPS is conducted to calculate the normal pressure and inlet flow of each node. A total of ${5(C}_{92}^2+C_{92}^1)$ = 21,390 leakage scenarios are generated, where the $‘3’$ represents the types of noises. In each scenario, one or two nodes in a partition are regarded as leakage nodes, where leakage discharge 1–3% (leakage) to 4–5% (pipe blast) of the average demand (24.50–73.50 m³/h and 98.00–122.50 m³/h for leakage and pipe blast, respectively) is randomly added by the MC method. Subsequently, the pressure and flow variations in each node under both normal and abnormal values are determined for every leakage event during the EPS time, as specified by Equations (7) and (8).

After that, Gaussian noise with a standard deviation equal to 10% and 20% of the mean demand is added to the node as demand noise that simulated inaccuracies in real-world demand values. With the EPS process, the normal pressures and inlet flows taken demand noise are obtained.

Then, the measurement noise dataset is generated to verify the stability and reliability with minimal fluctuation to predict leakage scenarios under different datasets. This noise, also Gaussian with a zero mean and a 10% or 20% standard deviation, reflected the potential imprecision of pressure and flow sensors in practical settings.

Once the three types of datasets are added, the EDNN model is employed to enhance the dimension of the input data, ensuring compatibility with the input requirements of the PP-LCNetV2 model. The effectiveness of the EDNN could be found in

Table 1. The relative errors of inputs and outputs in EDNN model of network A.

Sensitivities	RE for Pressures %	RE for Flows %	RE for Average %
1	98.67	99.12	98.90
2	98.52	98.87	98.70
3	98.56	98.71	98.64
4	99.81	99.62	99.72
5	99.64	99.53	99.59
Average	99.04	99.17	99.10

, where the loss degree of pressure and flow sensitivities are explored by comparing the consistency of the input and output of the EDNN. The relative errors (RE) of the inputs and outputs for partitions are 98.90%, 98.70%, 98.64%, 99.72%, and 99.59%. These REs suggest that the model performs consistently across all partitions. Meanwhile, all REs in different partitions are up to the 98%, and the average of the RE is 99.10%. Thus, it demonstrates that the EDNN model effectively captures and retains the critical information from the input data with minimal deviation.

Then, the PP-LCNetV2 model is used for each partition to detect the leakages. The dataset is divided into a training set, a validation set, and a testing set in each partition. The proportion of the three sets is 3:1:1. The results of three datasets are obtained in each partition. Finally, the recall, F1-score, and precision metrics are computed, expressed as Equations (16)–(18). The leakage locations for the three test datasets within partition 1 are detailed in

Table 2. The leakage detection for the partition 1 in the network A.

Times	Precision %	Recall %	F1-Score %
1	96.98	94.94	95.95
2	97.79	97.43	97.61
3	96.68	96.32	96.50
Average	97.15	96.23	96.69

, providing a comprehensive overview of the model’s performance across different scenarios. The other partitions could be found in Tables S1–S4.

$$P={\displaystyle \frac{TP}{TP+FP}}$$

(16)

$$R={\displaystyle \frac{TP}{TP+FN}}$$

(17)

$$F={\displaystyle \frac{2\times P\times R}{P+R}}$$

(18)

where P, R, and F are the precision, recall, and F1-score of leakage detection, respectively; TP represents instances where the model correctly identifies leakage; TN indicates the accurate identification of normal conditions; FP refers to cases where the model incorrectly identifies a leakage; and FN denotes situations where the model fails to detect an actual leakage.

The results demonstrate that the lightweight architectures can meet the needs of leakage detection. A high level of performance by the EDNN-PP-LCNetV2 to identify leakage scenarios with an average precision of all partitions of 97.80%. The average recall is also high, at 97.24%, slightly lower than the precision. The average F1-score is also up to 97.52%. Therefore, the leakage in the network A could be effective for detection.

The predicted result of magnitudes of leakage (normal, leakage, and pipe blast) are also obtained. The accuracy of the magnitudes of leakages could be solved as Equation (19).

$$AC={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(19)

where AC is the accuracy of the magnitudes of leakages.

The result of partition 1 is illustrated in

Table 3. The magnitudes of leakages result for the partition 1 in the network A.

Times	Accuracy %
1	91.67
2	91.67
3	83.33
Average	88.89

. The results of other partitions could be found in Tables S1–S4. The accuracy results across all five partitions demonstrate consistently high performance, with values ranging from 87.71% to 100%, suggesting a potentially superior model. Partition 3 has the top performer, maintaining an impressive average accuracy of 100% in all tests. While the lowest average accuracy is still up to 84.21% at time 2 in partition 5, it exhibits the most consistent results across its tests, indicating a very stable model. The overall range of accuracy larger than 85% indicating all groups perform excellently. Therefore, the magnitudes of leakages in network A could be effective in recognizing leakages.

To assess the impact of noise on model performance, the precision, recall, F1-score, and accuracy were calculated under various noise conditions. As shown in

Table 4. The quantitative analysis of different types of noises in network A.

Noise Type	Precision %	Recall %	F1-Score %	Accuracy %
Free of Noise	98.05	97.52	97.08	90.12
10% Demand Noise	97.32	96.11	96.82	88.29
20% Demand Noise	96.57	95.45	95.54	87.56
10% Measurement Noise	97.81	96.79	97.14	88.91
20% Measurement Noise	96.01	95.29	96.89	89.58

, the model’s performance metrics slightly decreased as the noise levels increased, indicating a decline in robustness. Even under the highest noise levels, 20% demand and measurement noise, the model’s precision remains above 96%, and the recall never falls below 95%. This shows that the model could identify leakages accurately despite the introduction of noise. Additionally, the F1-score remains consistently high, staying above 95% in all scenarios, which reflects the model’s balanced ability to maintain both precision and recall even as noises are present. While the accuracy experiences a small drop, moving from 90.12% under noise-free conditions to 87.56% under 20% demand noise, this reduction is modest and demonstrates that the model is highly resilient.

Overall, the table suggests that while noise does have a minimal effect, the impact could be overcome, and the model continues to perform effectively across various noise levels.

3.2. Network B

Network B, depicted in Figure S3, consists of 126 junctions, 168 pipes, two pumps, one reservoir, and two tanks [36]. It has an average water demand of 211.81 m³/h with the maximum duration of the EPS set to 24 h to effectively analyze the system.

Firstly, the K-means model is applied to cluster the nodes to different partitions. The number of partitions is set to four. The result of partition is shown in Figure 4. The number of junctions in each partition are [24, 28, 59, 15].

After that, the leakages are added to the junctions where the pressure and flow measurements are free of noise, demand noise, and measurement noise and where Gaussian noise with a standard deviation equal to 10% of the mean demand is added. The pressures and flows in normal status are computed via the EPS process. The number of ${3(C}_{126}^2+C_{126}^1)$ = 24,003 leakage scenarios are generated for all partitions, where leakage discharge 1–3% (leakage) to 4–5% (pipe blast) of the average demand (2.12–6.35 m³/h and 8.47–10.59 m³/h for leakage and pipe blast, respectively) is randomly added by the Monte Carlo method. Upon completion of the EPS process, the pressure and flow sensitivities are obtained by Equations (1)–(3). The normal pressures and inlet flows taken demand noise are obtained.

Then, the three types of datasets are imported to the EDNN model to raise the dimension of the dataset fitting the input data of the PP-LCNetV2 model in each partition.

The effectiveness of the EDNN could be found in

Table 5. The relative errors of inputs and outputs in EDNN model of network B.

Sensitivities	RE for Pressures %	RE for Flows %	RE for Average %
1	99.17	98.39	98.78
2	99.23	98.58	98.91
3	99.87	98.71	99.29
4	99.22	98.94	99.08
Average	99.37	98.66	99.01

. The RE for pressures sensitivities across all sensitivities is consistently high, ranging from 99.17% to 99.87%. The average RE for pressure sensitivity is 99.37%, demonstrating that the EDNN model retains nearly all the pressure sensitivity data during dimensionality enhancement, but is still quite high, indicating strong retention of flow sensitivities. The RE for flows shows slightly more variability compared to pressure, with values ranging from 98.39% to 98.94%. The average RE for flows is 98.66%, showing the model performs effectively in retaining flow data as well. Thus, the EDNN model performance is robust in different partitions.

During the training process, the dataset is partitioned into a training set, validation set, and testing set, following a 3:1:1 ratio, to ensure effective model training, validation, and performance evaluation. The result of the location’s average values of precision, recall, and F1-score of partition 1 is calculated, as shown in

Table 6. The leakage detection results for the partition 1 in network B.

Times	Precision %	Recall %	F1-Score %
1	97.84	97.01	97.42
2	98.77	97.17	97.96
3	97.60	97.27	97.44
Average	98.07	97.15	97.61

. The results of other partitions can be found in Tables S5–S7. The results reveal a consistently high performance across all partitions, with values ranging from 96.42% to 98.84%. Partition 1 emerges as the top performer, exhibiting the highest score in precision. The precision, recall, F1-score are 98.07%, 97,15%, 97.61% on average, while partition 3 shows the lowest, yet still impressive, metrics (precision: 96.94%, recall: 96.51%, F1-score: 96.72%, accuracy: 97.28% on average). Partition 2 maintains a middle effectiveness of the metrics. Meanwhile, all partitions demonstrate low variability within their metrics, indicating stable performance across three tests. The results demonstrate that the model has a superior performance on predicting leakages.

The predicted results of magnitudes of leakages are illustrated in

Table 7. The magnitudes of leakages result for the partition 1 in network B.

Times	Accuracy %
1	91.67
2	87.50
3	95.83
Average	91.67

and Table S5–S7. The accuracy results of the four partitions demonstrate a high performance, with values ranging from 85.71% to 96.61%. Partition 3 has the top performer and the average accuracy of 94.92% in all tests, while the lowest average accuracy is still up to 85.71% at times 1 and 3 in partition 2. All four partitions represent high-quality models that performs well in network B. Therefore, the magnitudes of leakage in network B could also be effective in recognizing.

The impact of different types and levels of noise on model performance in terms of precision, recall, F1-score, and accuracy are shown in

Table 8. The quantitative analysis of different types of noises in network B.

Noise Type	Precision %	Recall %	F1-Score %	Accuracy %
Free of Noise	98.2	97.49	98.21	92.86
10% Demand Noise	97.85	97.22	97.56	91.54
20% Demand Noise	98.52	97.77	97.94	91.48
10% Measurement Noise	98.14	96.89	97.14	91.55
20% Measurement Noise	97.62	96.4	97.22	90.94

.

The results show that the model is highly resilient to both demand and measurement noise across all metrics. The slight reduction in precision, recall, and accuracy under measurement noise suggests that the model is less sensitive to the fluctuations in demand. Precision remains consistently high, ranging from 97.62% to 98.52%, and recalls range from 96.40% to 97.77%, suggesting that the model is slightly affected by measurement noise, though the impact is minimal. F1-scores, which balance precision and recall, remain above 97.14% across all noise levels, demonstrating the model’s overall effectiveness in identifying true leakages. The accuracy shows the most noticeable drop under 20% measurement noise, from 92.86% to 90.94%, but still indicates strong performance. Overall, the model’s high metrics across all scenarios suggest it is highly resilient to both demand and measurement noise, indicating its robustness and reliability in handling noisy data, making it suitable for practical use in noisy environments.

3.3. Network C

Network C, a large-scale network, is used to identify the effectiveness of the method in Figure S4, which consists of 12,523 junctions, 14,822 pipes, four pumps, two reservoir, and two tanks [36]. The average water demand of network C is 3833.22 m³/h. The EPS is set to 48 h.

The K-means model is applied to cluster the nodes to different partitions. The number of partitions is set to 10. The result of partition is shown in Figure 5. The number of junctions in each partition are [20, 2207, 502, 235, 1392, 391, 597, 906, 2147, 4126].

The leakages are added to the junctions where the pressure and flow measurements are free of noise, demand noise, and measurement noise and a standard deviation equal to 10% of the mean demand is added, where a leakage discharge that is 1–3% (leakage) to 4–5% (pipe blast) of the average demand is randomly added by the Monte Carlo method. The pressure and flow sensitivities are obtained after EPS process. Then, these datasets are imported to the EDNN model to fit the input data of the PP-LCNetV2 model in each partition.

The effectiveness of the EDNN could be found in

Table 9. The relative errors of inputs and outputs in EDNN model of network C.

Sensitivities	RE for Pressures %	RE for Flows %	RE for Average %
1	99.15	98.92	99.04
2	99.30	98.65	98.97
3	99.25	98.80	99.03
4	99.10	98.85	98.98
5	99.35	98.70	99.02
6	99.20	98.90	99.05
7	99.28	98.85	99.07
8	99.32	98.70	99.01
9	99.22	98.72	98.97
10	99.25	98.78	99.01
Average	99.24	98.79	99.02

. The results shown that the EDNN model demonstrates consistent performance in reconstructing pressure and flow sensitivities in network C. With RE values ranging from 99.10% to 99.35% for pressures sensitivities and 98.65% to 98.92% for flow sensitivities, the model captures nearly all critical information, maintaining an overall average RE of 99.02%. This high accuracy across both pressure and flow sensitivities indicates that the model is highly reliable in reconstructing dataset. The minimal variation between partitions suggests robustness and scalability, allowing the model to perform effectively across different partitions of the WDS. Therefore, the results highlight the model’s ability to effectively reconstruct the pressure and flow sensitivity matrix.

Then, the dataset is divided into a training set, validation set, and testing set, following a 3:1:1 ratio, to ensure effective model training, validation, and performance evaluation. The result of the location average values of precision, recall, and F1-score of partition 1 is calculated, as shown in

Table 10. The leakage detection results for the partition 1 in network C.

Times	Precision %	Recall %	F1-Score %
1	98.07	97.15	97.61
2	97.84	97.31	97.57
3	98.10	97.48	97.79
Average	98.00	97.31	97.66

. Other partitions can be found in Table S8.

The precision, recall, and F1-scores for partition 1 are all above 97% in Table 10, demonstrating a balanced and high-performing model in terms of both recall and precision in identifying leakages. It shows that the model is highly effective in distinguishing leakage events from normal conditions, with very few false identifications. The consistency across the metrics suggests that the model is good for leakage detection, offering reliable performance even under varying conditions. Other partitions (2–10) extend this analysis in Table S8, where precision, recall, and F1-scores remain consistently high, generally ranging from 96% to 98%. The slight variations across the different partitions reflect the inherent complexities of the network but still demonstrate adaptability and robustness. In the large-scale networks, the model maintains high performance, ensuring reliable leakage detection across the entire network.

The predicted results of magnitudes of leakages are illustrated in

Table 11. The magnitudes of leakages result for the partition 1 in network C.

Times	Accuracy %
1	92.71
2	93.12
3	91.50
Average	92.44

and Table S8. The average accuracy is similarly high, ranging from 92.44% to 98.17%. The accuracy results of ten partitions demonstrate that the model not only identifies the location of the leakage but also estimates the size of the leakages with considerable accuracy. All partitions represent high-quality models that perform well in network C. Therefore, the magnitudes of leakage in large-scale networks could also be effective in recognizing leakages.

The impact of different types and levels of noise on model performance in terms of precision, recall, F1-score, and accuracy are shown in

Table 12. The quantitative analysis of different types of noises in network C.

Noise Type	Precision %	Recall %	F1-Score %	Accuracy %
Free of Noise	98.20	97.49	98.21	92.86
10% Demand Noise	97.85	97.22	97.56	91.54
20% Demand Noise	97.62	96.90	97.26	90.48
10% Measurement Noise	98.00	97.40	97.70	91.95
20% Measurement Noise	98.20	97.49	98.21	92.86

. The results show the impact of various noise levels. In no-noise conditions, the model performs well, achieving a precision of 98.20%, recall of 97.49%, F1-score of 98.21%, and accuracy of 92.86%. As demand noise is added, the performance begins to decline slightly. With 10% demand noise, the precision drops to 97.85%, recall to 97.22%, F1-score to 97.56%, and accuracy to 91.54%. The decline continues with 20% demand noise, with precision, recall, F1-score, and accuracy dropping to 97.62%, 96.90%, 97.26%, and 90.48%, respectively. This suggests that demand noise has a noticeable effect on the model’s ability to accurately detect leaks, but still performs relatively well under these conditions. In measurement noise, the model shows a similar pattern of degradation but retains a slightly higher performance compared to demand noise. With 10% measurement noise, the precision, recall, F1-score, and accuracy are 98.00%, 97.40%, 97.70%, and 91.95%, respectively, demonstrating a smaller impact than demand noise. At 20% measurement noise, the values decline further, with precision at 97.50%, recall at 96.85%, F1-score at 97.17%, and accuracy at 90.75%.

Above all, the model maintains a high level with all performance metrics staying above 90%, indicating its robustness and reliability in large-scale networks where noise is inevitable.

The overall analysis underscores the capability to effectively manage leakage detection and prediction tasks, making it a strong candidate for deployment in large-scale networks.

3.4. Comparison

To assess and confirm the effectiveness of the EDNN-PP-LCNetV2 method for leakage detection, two established methods are compared: support vector machine (SVM) and back-propagation (BP) [11]. Meanwhile, traditional CNN frameworks, such as AlexNet and VGG-16 of the CPU version [37,38], are selected to replace EDNN-PP-LCNetV2 and demonstrate not only the enhanced leakage detection capabilities in this study but also its efficiency and suitability for deployment in fast computing scenarios characteristic of WDSs. By utilizing pressure and flow sensitivities as input data, the EDNN-PP-LCNetV2 method accurately identifies leakage locations and quantifies leakage magnitudes. The average values for all partitions of precision, recall, F1-score, accuracy of magnitudes of leakages, and computing time are shown in Tables S9 and S10. The proposed model achieved a higher precision across all networks over traditional CNN models and other methods show higher metrics in location precision, recall, F1-score, and accuracy of leakage magnitudes for cases (97.42%, 97.42%, 97.90%, 92.39% in network A; and 97.8%, 97.21%, 97.51%, 91.95% in network B; and 97.90%, 97.35%, 97.62%, 91.05% in network C).

Particularly in large-scale network C, it achieved a precision of 97.90% for the proposed model, higher than SVM, BP, VGG-16, and Alexnet (95.80%, 95.25%, 96.85% and 96.45%, respectively). It demonstrates the ability of the model to correctly identify true positives (correctly identifying leakage) in various sizes of networks, thereby reducing false positive rates (normal state but identifying as leakage). The recall presents the model’s ability to capture actual leakages. The model achieved a recall of 97.35% in network C, which is higher than SVM and BP and comparable to VGG-16 and Alexnet. This shows the framework’s efficacy in detecting leakages, even in large-scale networks. The F1-score balances precision and recall, further confirming the performance of the model. In all networks, the model consistently achieved the highest F1-score, which is crucial for minimizing false positive rates and true negative rates (leakage detection errors). Thus, the proposed model facilitates more effective leakage management.

The accuracies of networks A, B, and C in Table S10 show that proposed model consistently higher than other models across all networks. In network A, the model achieves an accuracy of 92.39%, surpassing the accuracy of SVM (85.57%), BP (79.74%), Alexnet (85.74%), and VGG-16 (87.28%). A similar trend is observed in network B, where the model has an accuracy of 91.95%, compared to SVM (83.46%), BP (83.19%), Alexnet (85.22%), and VGG-16 (89.39%). In network C, the accuracy shows that the model achieves the highest accuracy at 91.05%, which outperforms other models such as SVM (85.20%), BP (83.75%), Alexnet (86.24%), and VGG-16 (88.92%). While the deep learning models like Alexnet and VGG-16 demonstrate relatively high accuracy, the model still surpasses them. This improvement in accuracy indicates that our method is better suited to handle the complexities and variations present in network C. Overall, the model maintains a high accuracy while also achieving a more balanced performance across the network, demonstrating its robustness in handling complex detection tasks.

In addition, the computational efficiency, as shown in Table S10, the model demonstrates significant improvements compared to other models across all networks. For network A, SVM and BP exhibit computing times of 1.28 s and 1.54 s, respectively, while Alexnet and VGG-16 show higher times of 3.62 s and 4.87 s. In comparison, the proposed model achieves a much faster computation time of 1.47 s, highlighting its efficiency. For network B, the computing times of SVM and BP are 1.31 s and 1.49 s, while Alexnet and VGG-16 further increase to 3.44 s and 4.92 s. The proposed model again outperforms these, with a computation time of 1.66 s. In network C, where the computational demands are generally higher, SVM and BP exhibit computing times of 2.35 s and 2.53 s, and Alexnet and VGG-16 require 6.58 s and 6.82 s, respectively. Our model, however, maintains a more efficient time of 2.51 s. Thus, it proves a critical advantage in computational efficiency in CPU computing scenarios.

Overall, the EDNN-PP-LCNetV2 demonstrates significant advancements over traditional CNN models and other research.

4. Discussion

The thorough analysis of the proposed method employed in WDS reveals that the integration of EDNN-PP-LCNetV2 with K-means represents a significant advancement in tackling the complexities associated with leakage detection. This novel approach offers substantial improvements in precision and efficiency, addressing the multifaceted challenges inherent in managing water resources. By examining both its progress and its challenges, we can better understand how this approach might affect the field overall.

Several advantages can be realized:

(1)

Not only pressure sensitivity but flow sensitivity is considered as inputs, which shows that this improves the model’s performance versus single input data.

(2)

Both the leakage location and magnitudes are predicted simultaneously. Acquiring leakage size provides useful information for utilities.

(3)

Model uncertainties are considered by adding noise to the simulated data, which makes the dataset more realistic.

However, the method also faces some limitations:

(1)

The data applied to train and test the method is simulated in EPANET, not real-world data. Using simulated data may not fully capture the complexities of leakage detection in actual WDSs.

(2)

The dimension raising might lose some information on pressure and flow variations, which could not be considered.

(3)

It does not adequately test real-time application in resource-constrained environments, particularly under high-load or multitasking conditions using real IoT-based devices.

Therefore, this method is a great improvement in finding leakages, but its problems need to be fixed before it can be used widely and work well in many different WDSs.

5. Conclusions

This paper presents a novel way to detect leakage locations and magnitudes in WDSs using a combination of pressure and inlet flow sensitivity analysis processed through the EPS model. The proposed method applies an EDNN model to elevate the dimensionality of the sensitivity analysis matrix, followed by the application of the PP-LCNetV2 model for training the dataset. The effectiveness of leakage detection is evaluated using three real cases, with datasets generated under free noise, demand noise, and measurement noise conditions.

The results demonstrate that the EDNN-PP-LCNetV2 exhibits a high precision, recall, F1-score of leakage locations, and impressive accuracy in predicting leakage magnitudes. The average precision, recall, and F1-score of leakage detection went up to 97% in all cases. Additionally, the accuracy of the leakage magnitude went up to 91%. Compared with other methods, our approach not only improves detection performance but also offers significant computational efficiency, making it well suited for fast computing environments and real-time applications. According to the real cases, the results from these highlight the robustness and adaptability of the model across various network topologies and noise scenarios. This indicates the practical utility of the method in real-world networks, ensuring that water utilities can efficiently manage and reduce water loss.

However, some limitations exist. Future studies should focus on integrating this method into edge computing environments to further explore its real-time capabilities under resource-constrained and high-load conditions. Additionally, incorporating a broader set of variables into the dimension-raising process, such as location information, could enhance the model’s adaptability and optimization for real-time leakage detection. It will help further improve the model’s applicability, making it more effective for smart water supply and IoT-based water management systems.

Above all, this method provides a new perspective on enhancing water resource management through more reliable and scalable leakage detection techniques.