Reinforcement Learning-Based Vibration Control for Half-Car Active Suspension Considering Unknown Dynamics and Preset Convergence Rate
Abstract
1. Introduction
- A heuristic reinforcement learning algorithm based on PI is proposed, which rapidly computes the optimal control solution of the system without requiring model parameters.
- In controller design, the preset convergence performance is considered, and by adjusting the preset convergence rate, a balance between control energy consumption and other performance indicators was achieved.
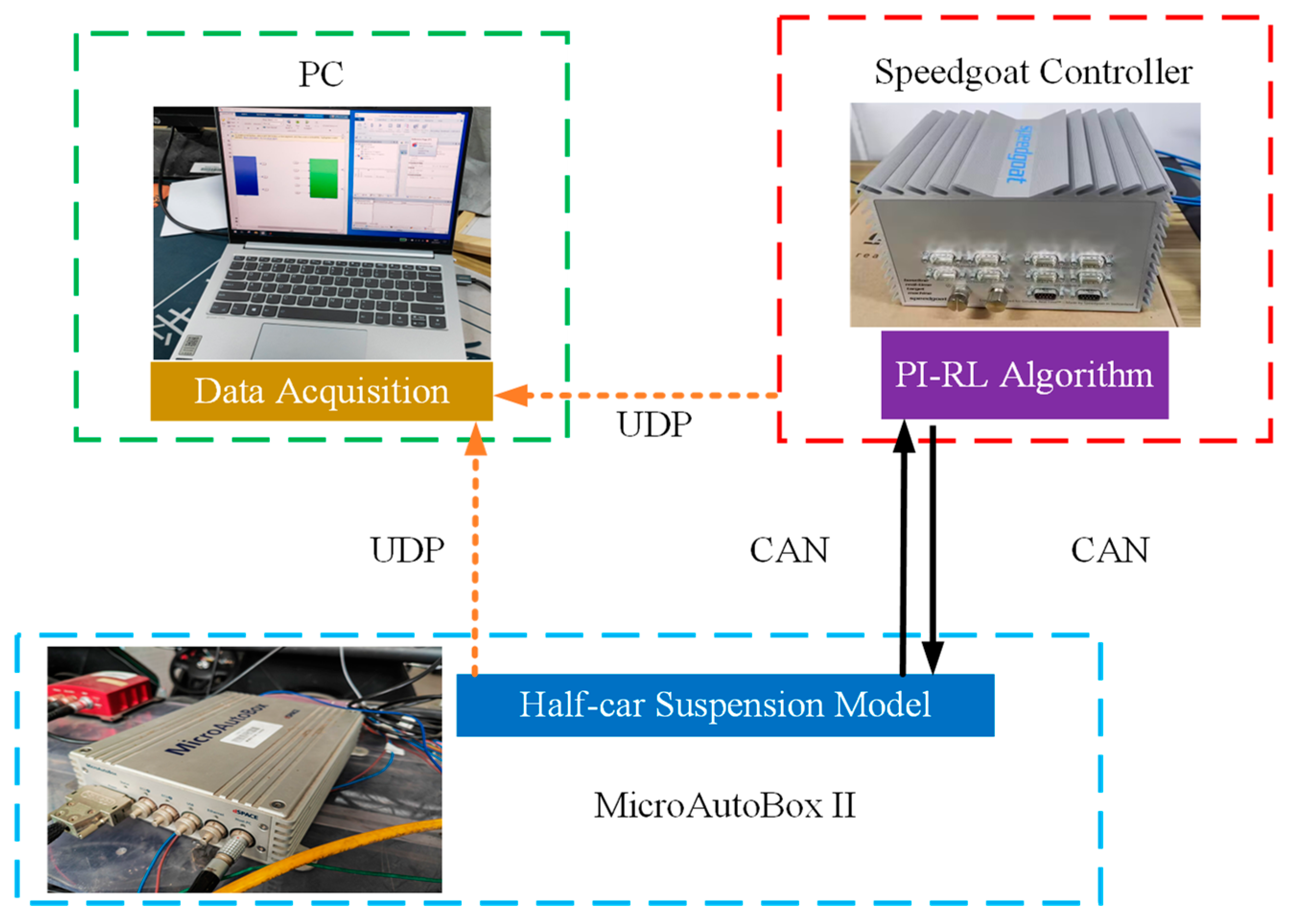
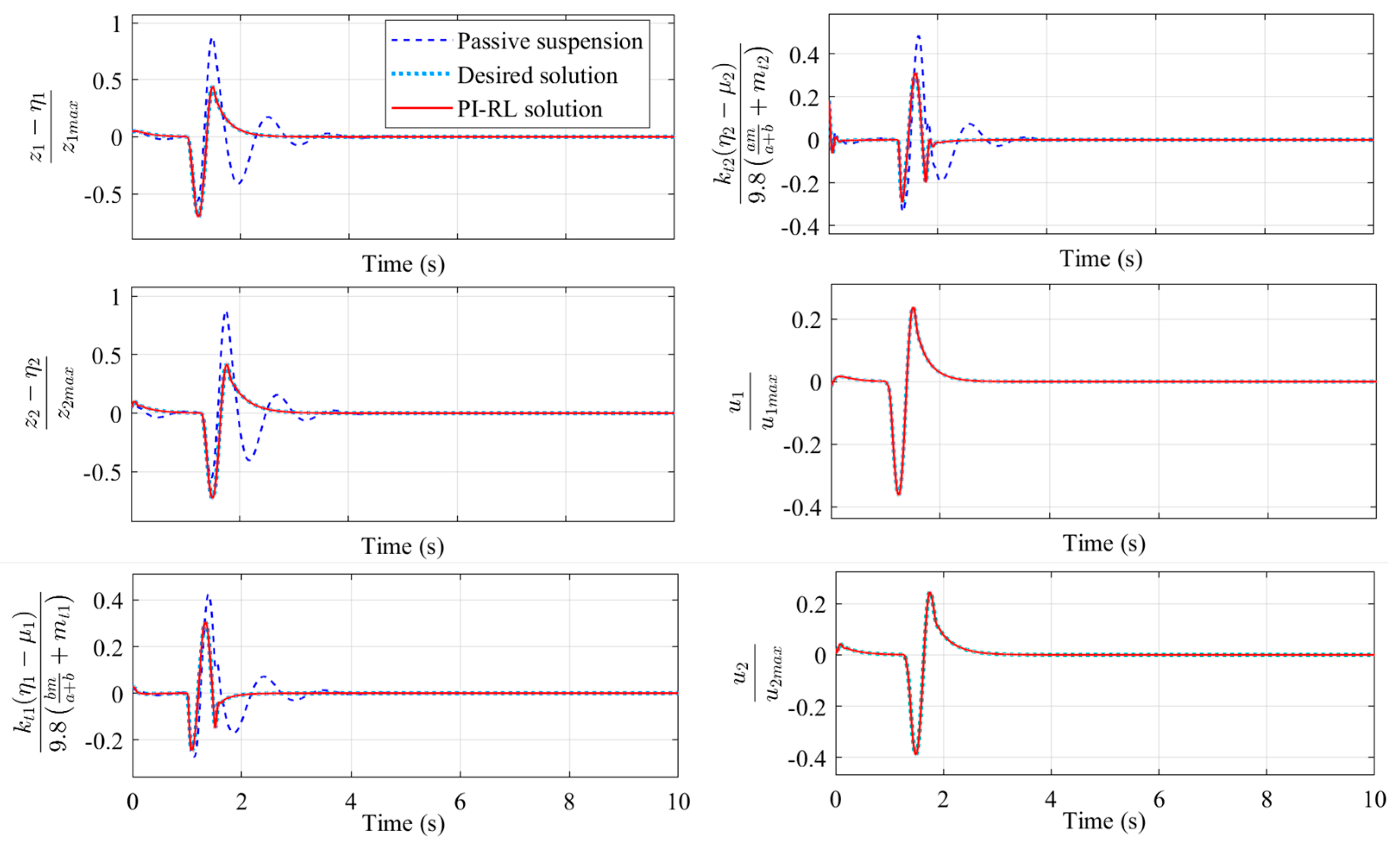
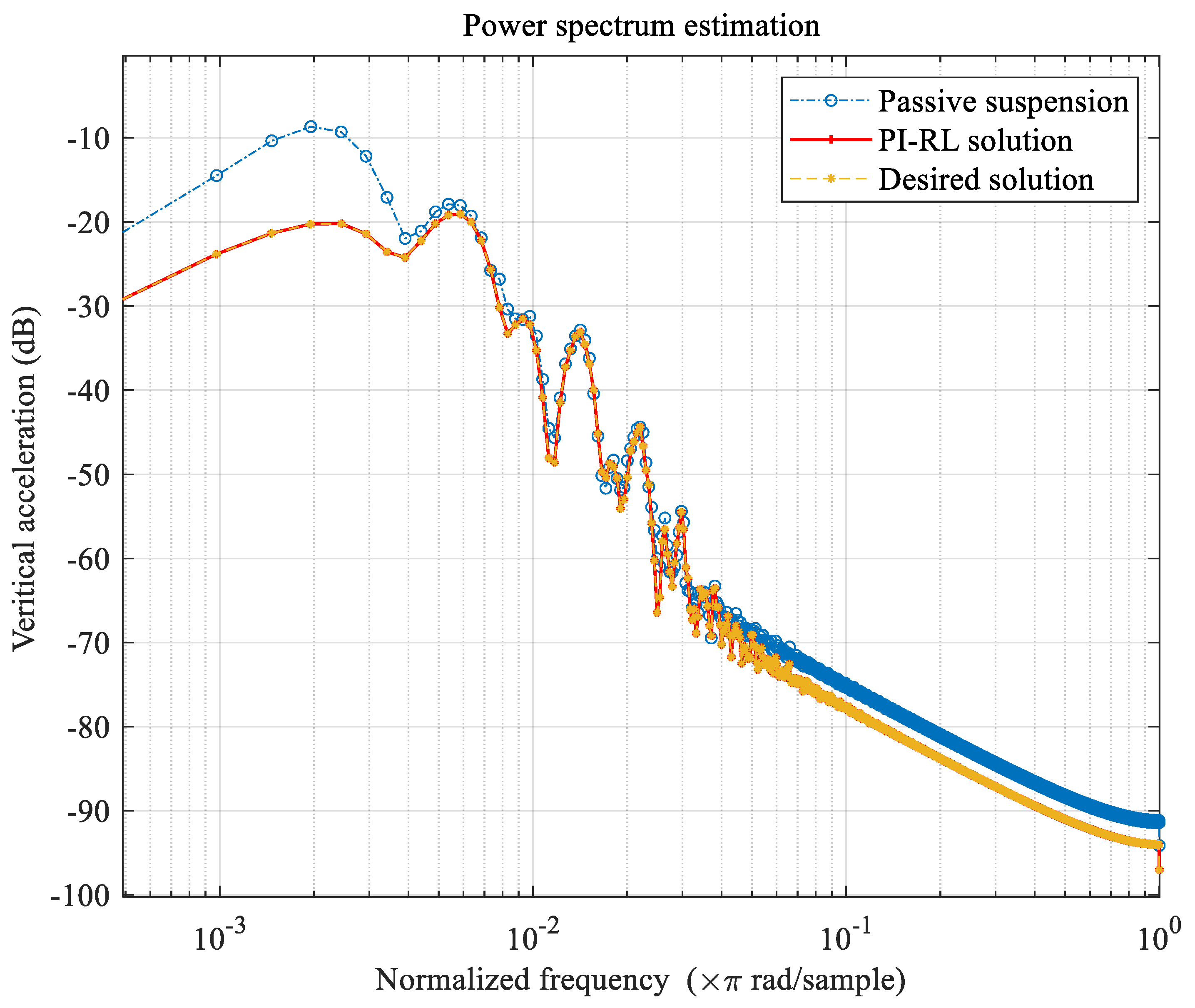
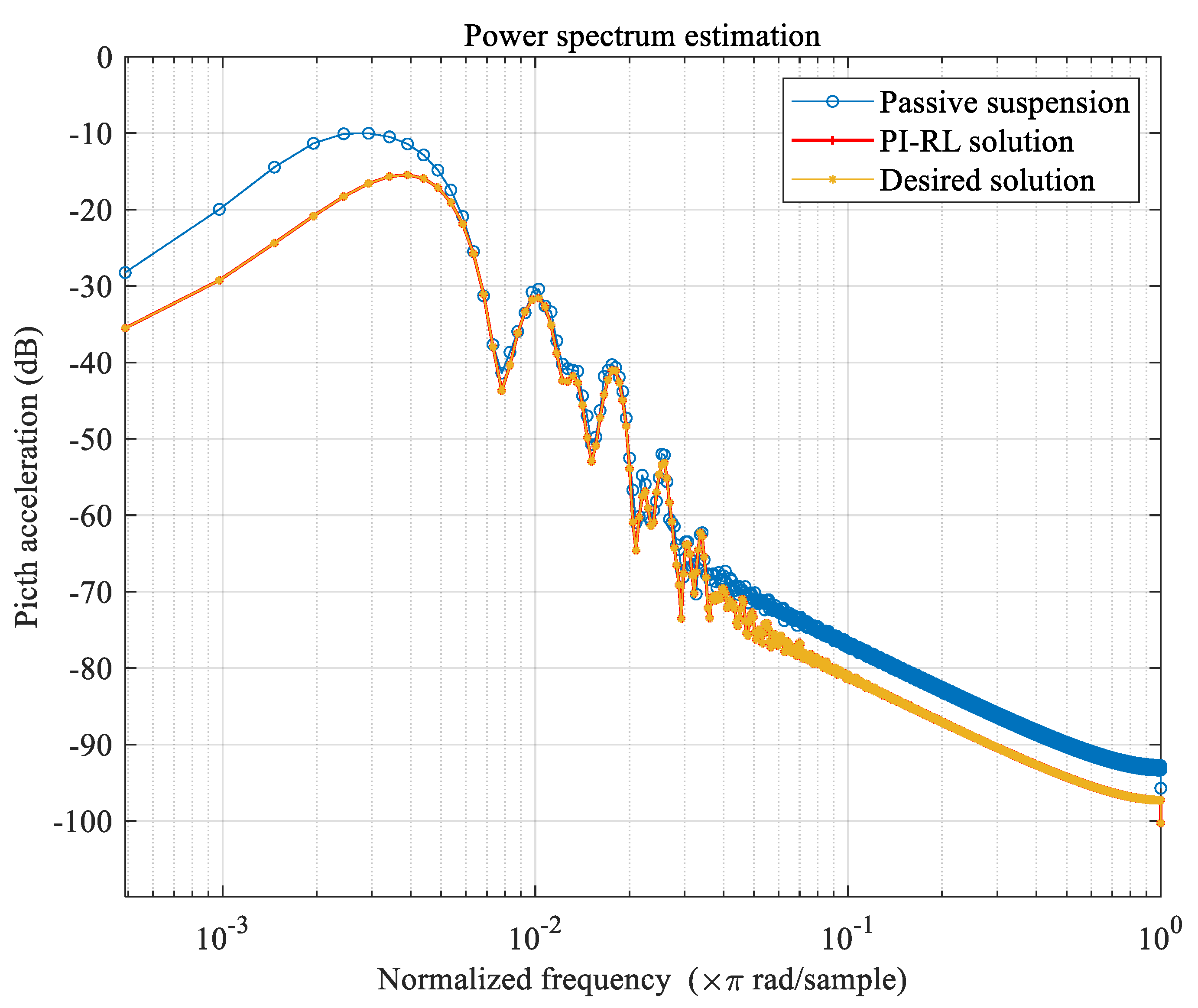
- Finally, a rapid prototyping control simulation platform was established to evaluate the energy consumption and dynamic performance of the active suspension through bumped road tests and frequency domain analysis.
2. Half-Car Control Model for Electromagnetic Active Suspension
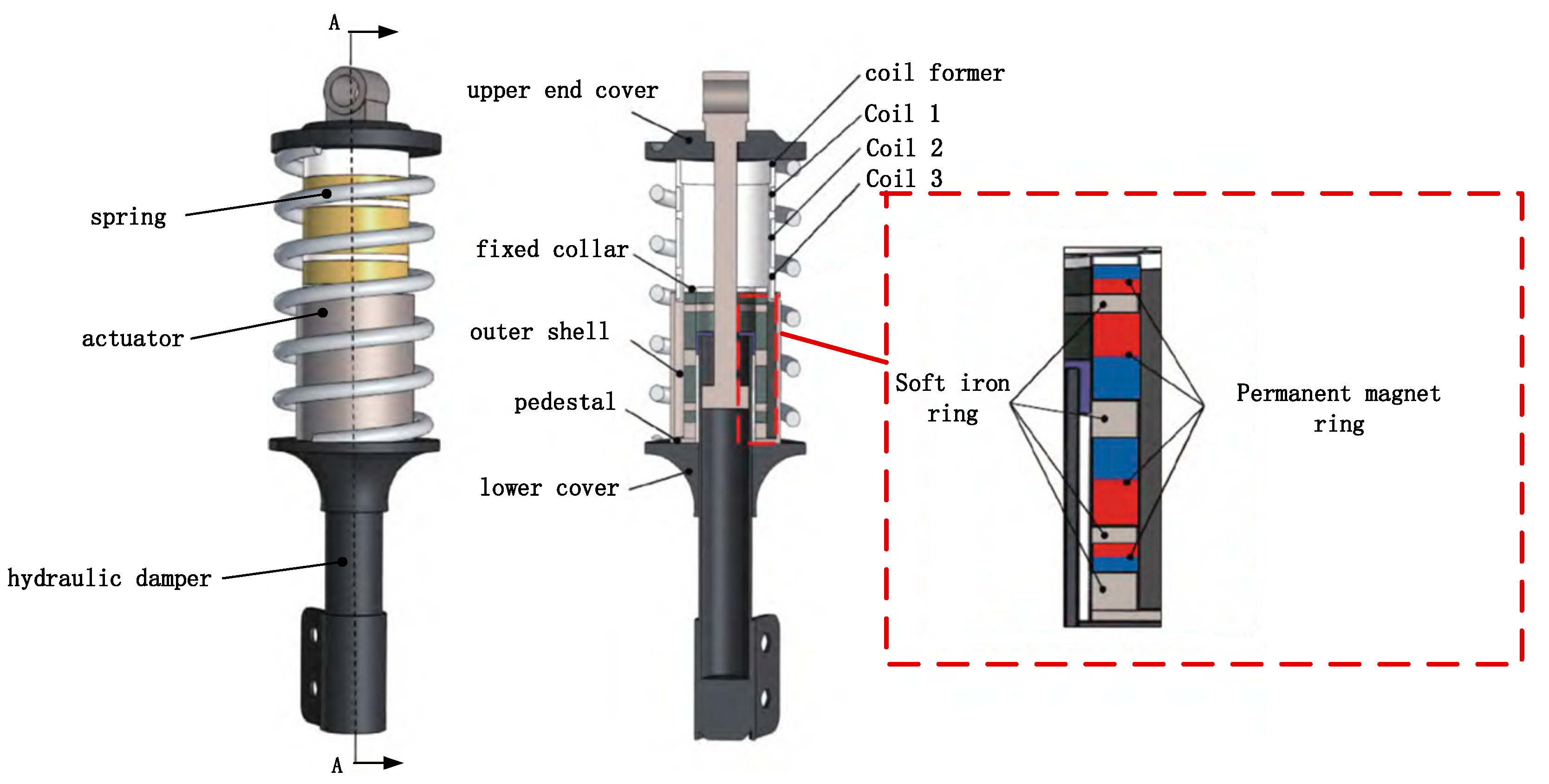
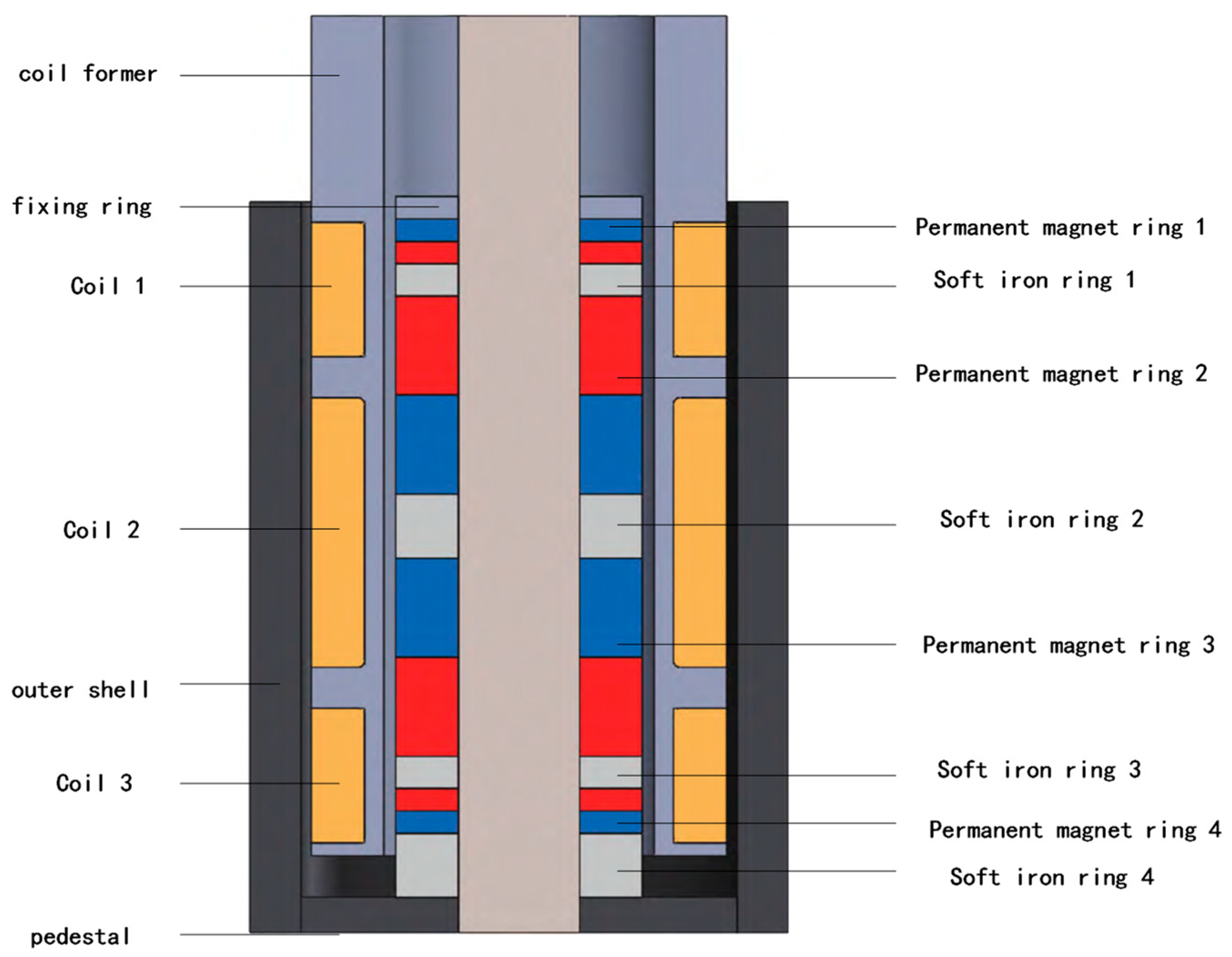
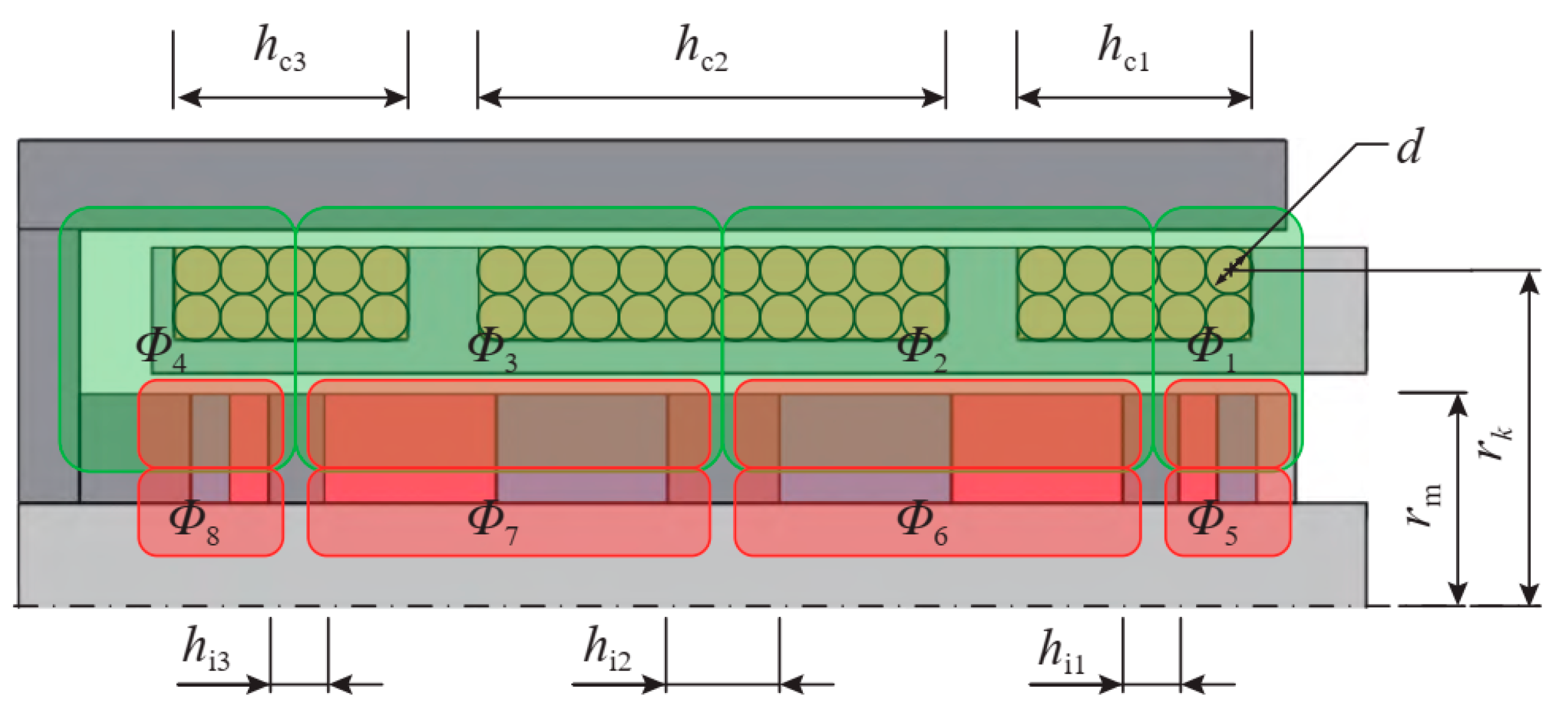
2.1. Electromagnetic Actuator Mechanical Model
2.2. Half-Car Active Suspension Dynamics Modeling
2.3. Control Problem Formulation
3. Reinforcement Learning-Based Vibration Control Strategy
3.1. Optimal Control Considering Preset Convergence Rate
3.2. PI-Based Online Reinforcement Learning Algorithm
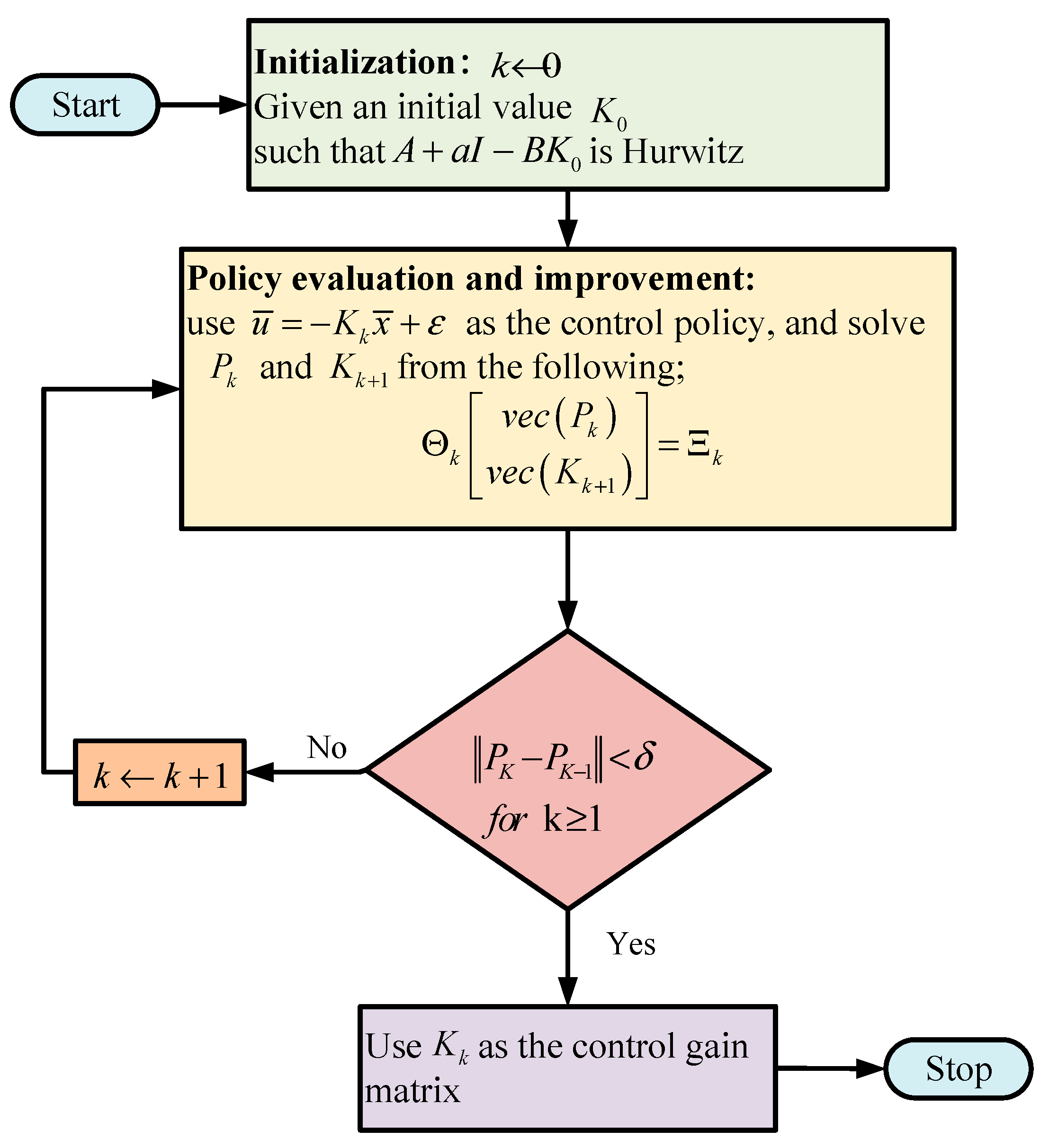
3.3. Heuristic Algorithm
| Algorithm 1: Heuristic Algorithm |
| Step 1: Set , , and execute the algorithm as shown in Figure 6 to obtain the optimal ; |
| Step 2: Set , where is a positive parameter. Execute the algorithm as shown in Figure 6. If a solution is found, output the optimal ; otherwise, adjust and and repeat Step 2. |
4. Rapid Prototyping Control Simulation
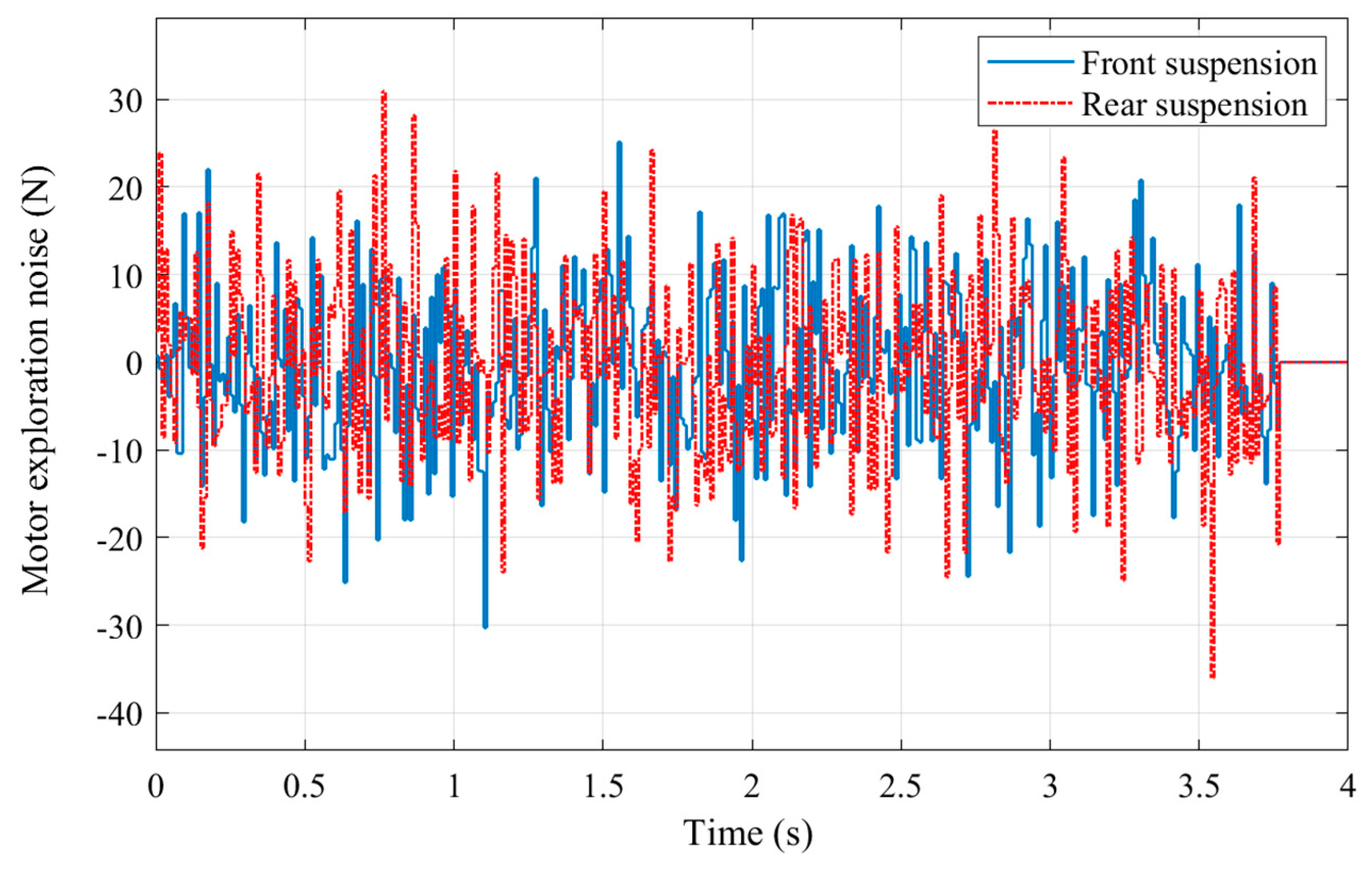
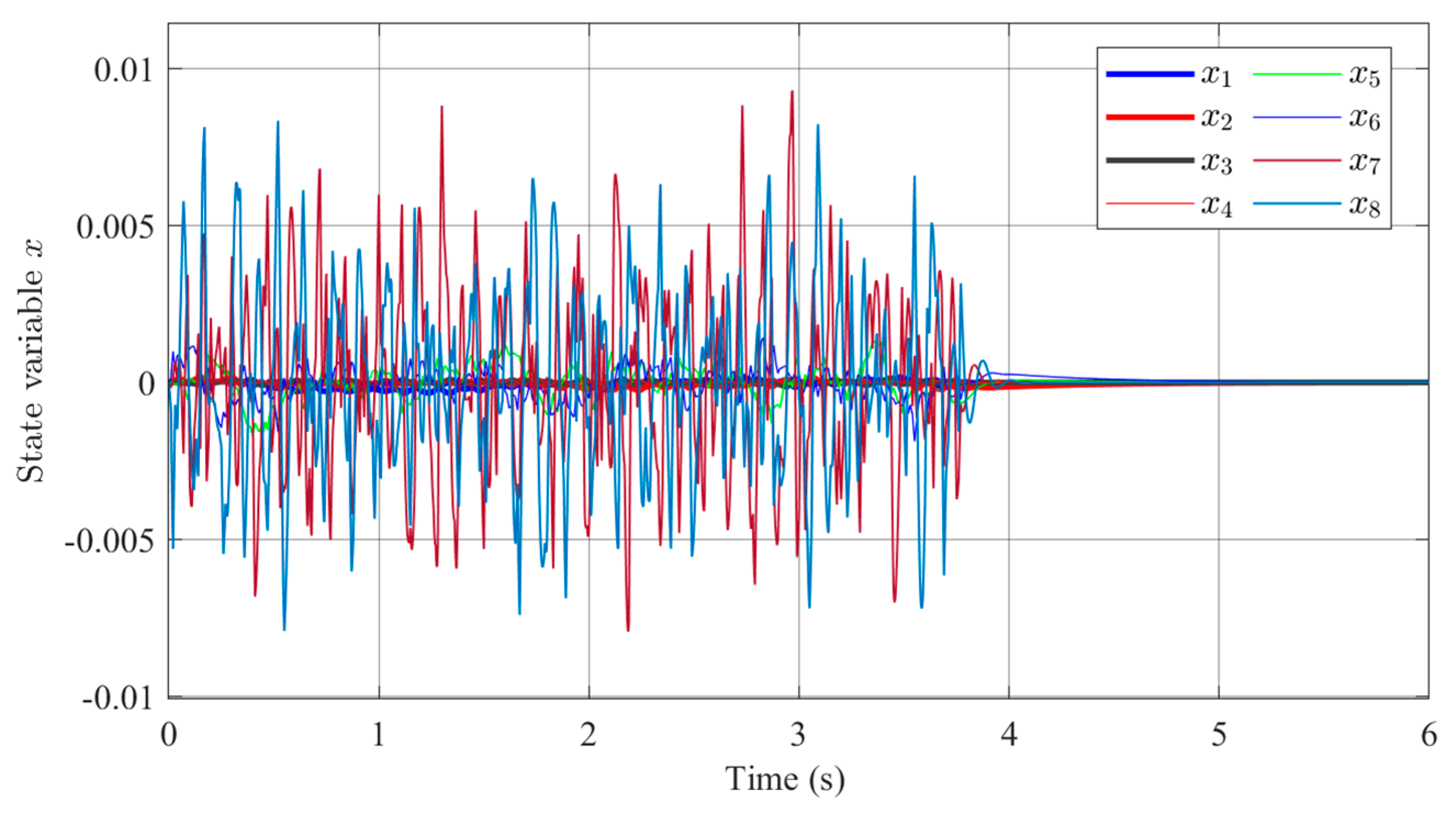
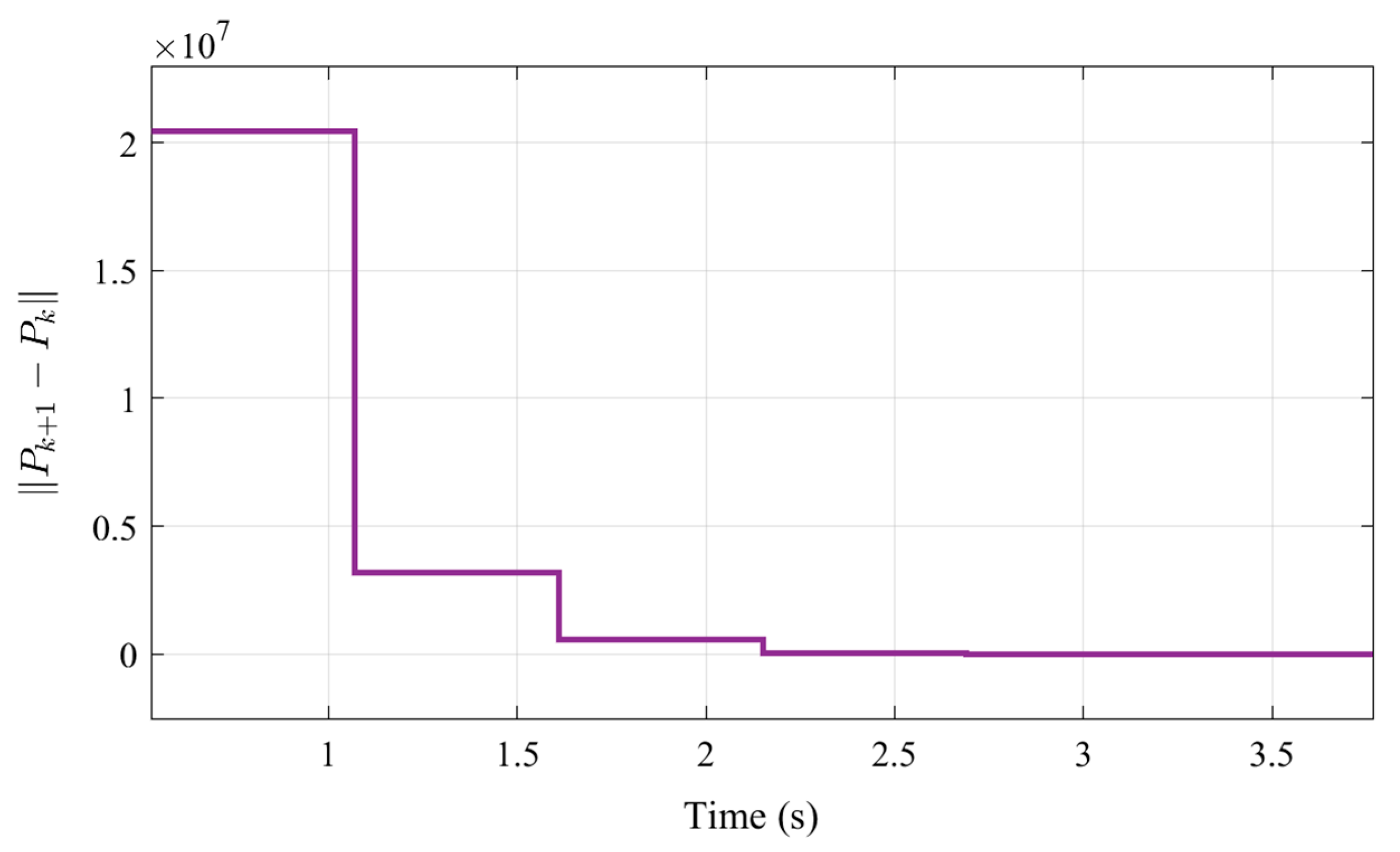
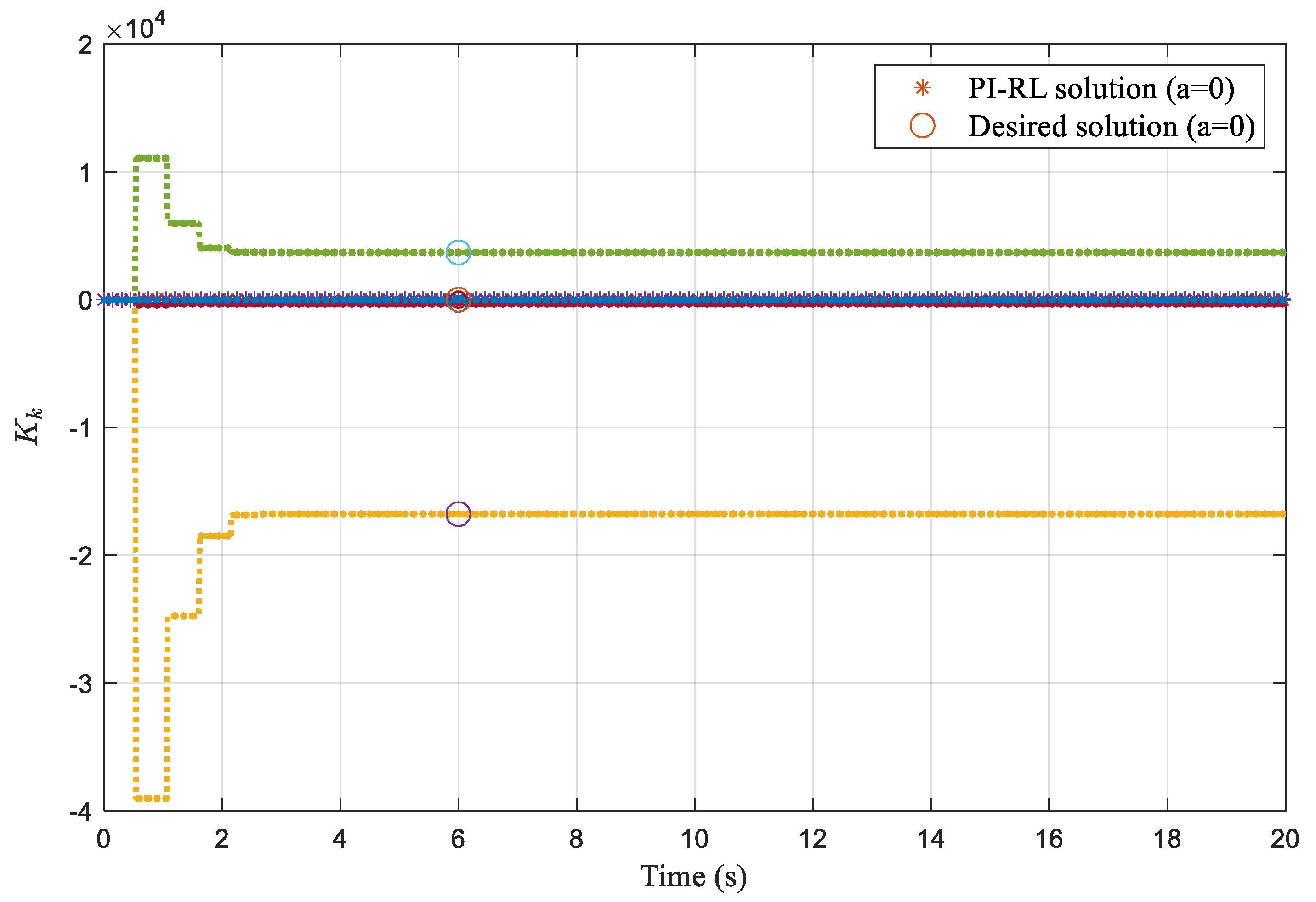
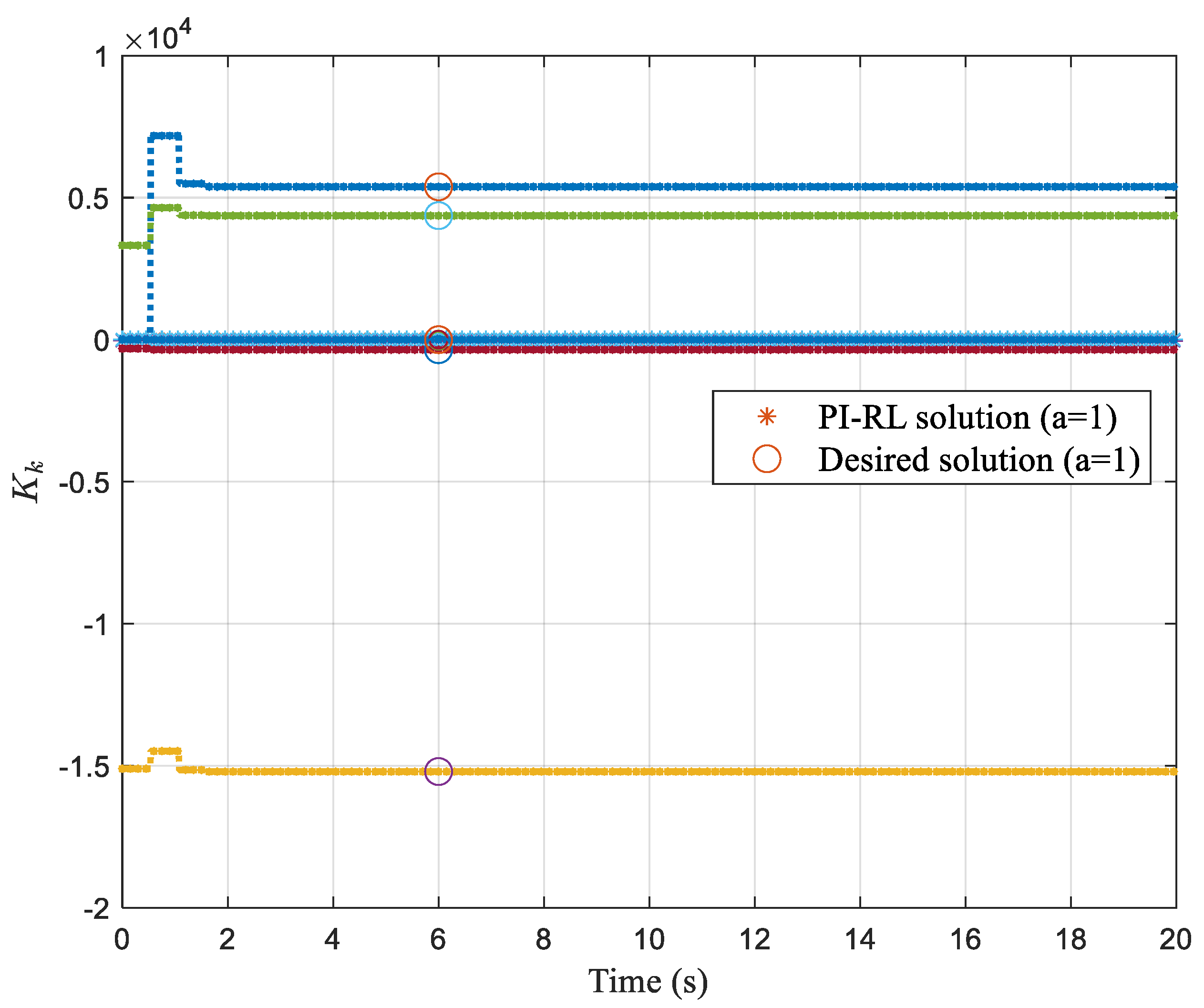
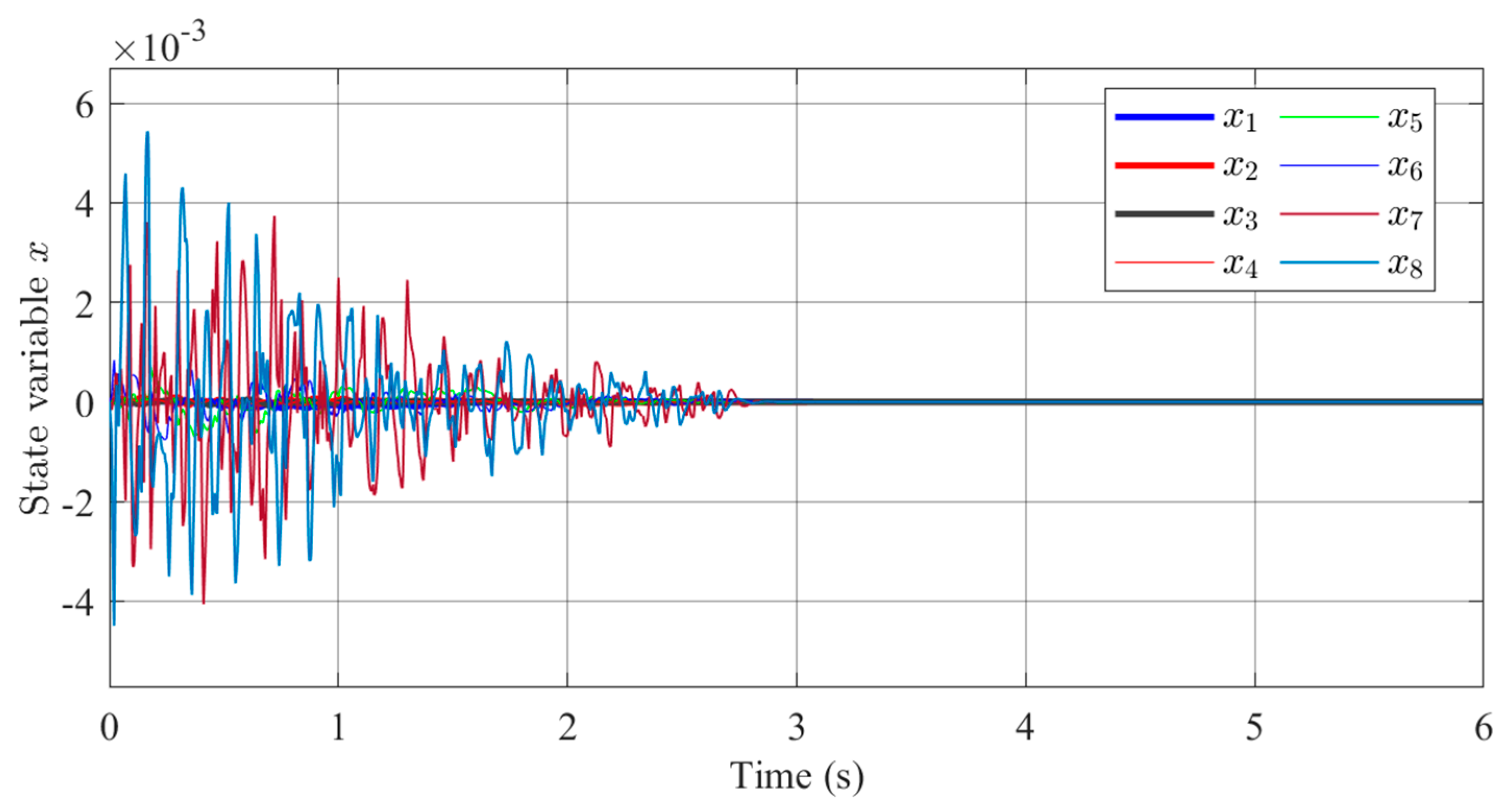
4.1. Online Learning and Optimization of Control Parameters
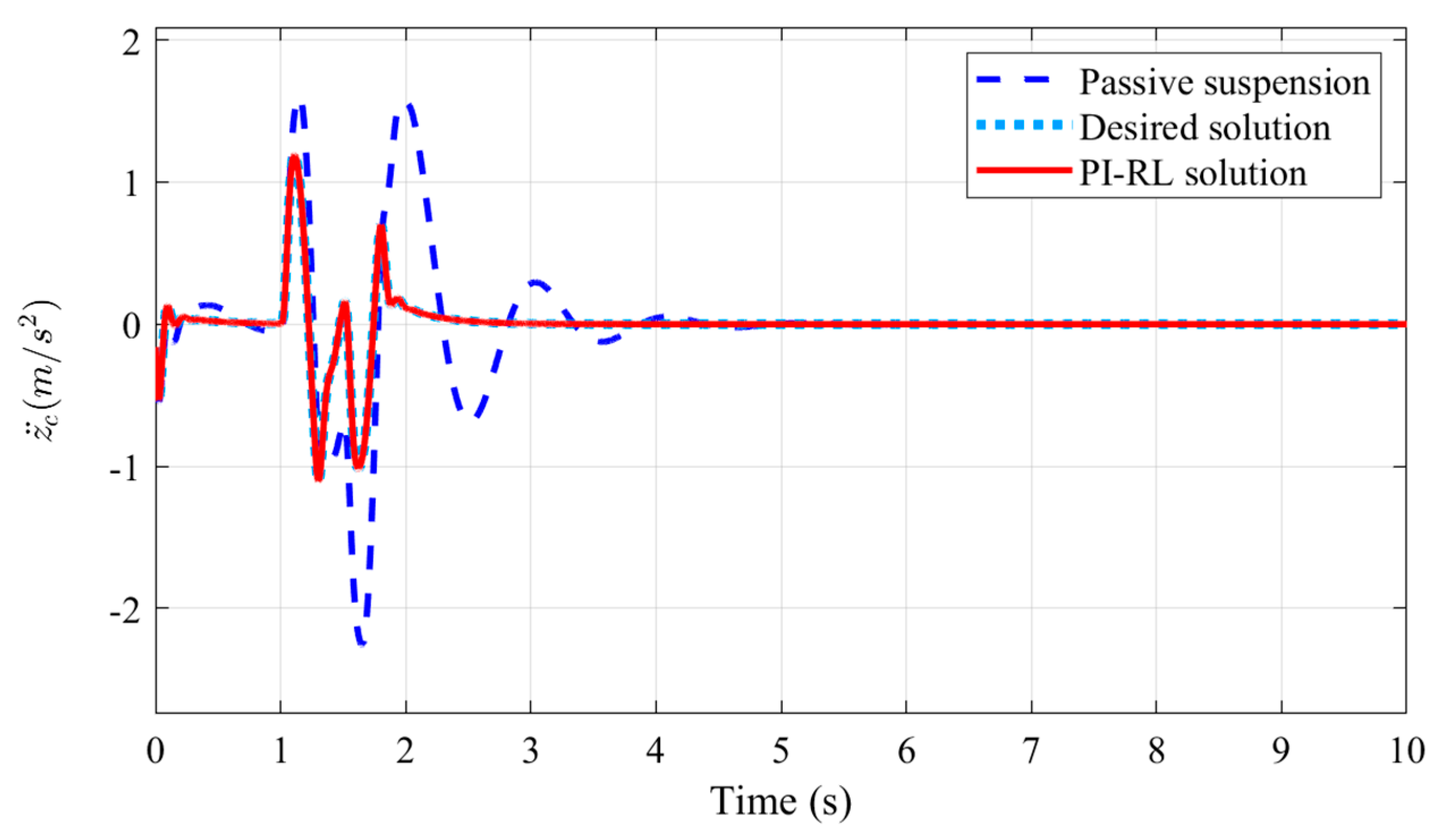
4.2. Control Implementation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sprung mass | |
| Pitch moment of inertia | |
| Unsprung mass | |
| Distance from front axle to center of mass | |
| Distance from rear axle to center of mass | |
| Tire stiffness | |
| Suspension spring stiffness | |
| Suspension hydraulic damping | |
| Motor control force | |
| Vertical displacement of the center of mass | |
| Pitch angle | |
| Vertical displacement of unsprung mass | |
| Road disturbance |
References
- Yu, M.; Evangelou, S.A.; Dini, D. Advances in Active Suspension Systems for Road Vehicles. Engineering 2024, 33, 160–177. [Google Scholar] [CrossRef]
- Zhao, W.; Gu, L. Adaptive PID Controller for Active Suspension Using Radial Basis Function Neural Networks. Actuators 2023, 12, 437. [Google Scholar] [CrossRef]
- Ding, R.; Wang, R.; Meng, X.; Chen, L. Energy consumption sensitivity analysis and energy-reduction control of hybrid electromagnetic active suspension. Mech. Syst. Signal Process. 2019, 134, 106301. [Google Scholar] [CrossRef]
- Su, X.; Yang, X.; Shi, P.; Wu, L. Fuzzy control of nonlinear electromagnetic suspension systems. Mechatronics 2014, 24, 328–335. [Google Scholar] [CrossRef]
- Liu, L.; Li, X.; Liu, Y.-J.; Tong, S. Neural network based adaptive event trigger control for a class of electromagnetic suspension systems. Control. Eng. Pract. 2021, 106, 104675. [Google Scholar] [CrossRef]
- Pang, H.; Wang, M.; Wang, L.; Luo, J. A composite vibration control strategy for active suspension system based on dynamic event triggering and long and short-term memory neural network. IEEE Trans. Transp. Electrif. 2023, 1. [Google Scholar] [CrossRef]
- Wong, P.K.; Li, W.; Ma, X.; Yang, Z.; Wang, X.; Zhao, J. Adaptive event-triggered dynamic output feedback control for nonlinear active suspension systems based on interval type-2 fuzzy method. Mech. Syst. Signal Process. 2024, 212, 111280. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, M.; Liu, H.; Jing, X. Fixed-Time Safe-by-Design Control for Uncertain Active Vehicle Suspension Systems With Nonlinear Reference Dynamics. IEEE/ASME Trans. Mechatron. 2023, 1–12. [Google Scholar] [CrossRef]
- Huang, T.; Wang, J.; Pan, H. Adaptive bioinspired preview suspension control with constrained velocity planning for autonomous vehicles. IEEE Trans. Intell. Veh. 2023, 8, 3925–3935. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Yin, H.; Zhang, B.; Jing, X. Bio-inspired structure reference model oriented robust full vehicle active suspension system control via constraint-following. Mech. Syst. Signal Process. 2022, 179, 109368. [Google Scholar] [CrossRef]
- Qin, Z.C.; Xin, Y. Data-driven H∞ vibration control design and verification for an active suspension system with unknown pseudo-drift dynamics. Commun. Nonlinear Sci. Numer. Simul. 2023, 125, 107397. [Google Scholar] [CrossRef]
- Liu, Z.; Si, Y.; Sun, W. Ride comfort oriented integrated design of preview active suspension control and longitudinal velocity planning. Mech. Syst. Signal Process. 2024, 208, 110992. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, J.; Sun, W. Robust saturated fault-tolerant control for active suspension system via partial measurement information. Mech. Syst. Signal Process. 2023, 191, 110116. [Google Scholar] [CrossRef]
- Wang, W.; Liu, S.; Zhao, D.; Zhang, C. Approximation-free output feedback control for hydraulic active suspensions with prescribed performance. Nonlinear Dyn. 2023, 111, 21673–21689. [Google Scholar] [CrossRef]
- Jeong, Y.; Yim, S. Design of active suspension controller for ride comfort enhancement and motion sickness mitigation. Machines 2024, 12, 254. [Google Scholar] [CrossRef]
- Liu, L.; Sun, M.; Wang, R.; Zhu, C.; Zeng, Q. Finite-Time Neural Control of Stochastic Active Electromagnetic Suspension System With Actuator Failure. IEEE Trans. Intell. Veh. 2024, 1–12. [Google Scholar] [CrossRef]
- Shaqarin, T.; Noack, B.R. Enhancing Mechanical Safety in Suspension Systems: Harnessing Control Lyapunov and Barrier Functions for Nonlinear Quarter Car Model via Quadratic Programs. Appl. Sci. 2024, 14, 3140. [Google Scholar] [CrossRef]
- Afshar, K.K.; Korzeniowski, R.; Konieczny, J. Evaluation of Ride Performance of Active Inerter-Based Vehicle Suspension System with Parameter Uncertainties and Input Constraint via Robust H∞ Control. Energies 2023, 16, 4099. [Google Scholar] [CrossRef]
- Arumugam, K.; Chen, B.-S. Finite-time based fault-tolerant control for half-car active suspension system with cyber-attacks: A memory event-triggered approach. IEEE Trans. Veh. Technol. 2024, 1–13. [Google Scholar] [CrossRef]
- Huang, T.; Wang, J.; Pan, H. Approximation-Free Prespecified Time Bionic Reliable Control for Vehicle Suspension. IEEE Trans. Autom. Sci. Eng. 2023, 1–11. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, C.; Sun, W. Fault-Tolerant Multiplayer Tracking Control for Autonomous Vehicle via Model-Free Adaptive Dynamic Programming. IEEE Trans. Reliab. 2022, 72, 1395–1406. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Z.; Song, H.; Dong, Y. Model Predictive Control for Speed-Dependent Active Suspension System with Road Preview Information. Sensors 2024, 24, 2255. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Li, K.; Liu, S.; Jing, H. Model-Free H∞ Output Feedback Control of Road Sensing in Vehicle Active Suspension Based on Reinforcement Learning. J. Dyn. Syst. Meas. Control 2023, 145, 061003. [Google Scholar] [CrossRef]
- Kim, J.; Yim, S. Design of Static Output Feedback Suspension Controllers for Ride Comfort Improvement and Motion Sickness Reduction. Processes 2024, 12, 968. [Google Scholar] [CrossRef]
- Li, P.; Lam, J.; Cheung, K.C. Multi-objective control for active vehicle suspension with wheelbase preview. J. Sound Vib. 2014, 333, 5269–5282. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, K.; Wu, J.; Zhang, C.; Xue, W.; Chai, T.; Lewis, F.L. H∞-based minimal energy adaptive control with preset convergence rate. IEEE Trans. Cybern. 2021, 52, 10078–10088. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, Z.-P. Computational adaptive optimal control for continuous-time linear systems with completely unknown dynamics. Automatica 2012, 48, 2699–2704. [Google Scholar] [CrossRef]
- Esmaeili, J.S.; Akbari, A.; Farnam, A.; Azad, N.L.; Crevecoeur, G. Adaptive Neuro-Fuzzy Control of Active Vehicle Suspension Based on H2 and H∞ Synthesis. Machines 2023, 11, 1022. [Google Scholar] [CrossRef]
- Dridi, I.; Hamza, A.; Ben Yahia, N. A new approach to controlling an active suspension system based on reinforcement learning. Adv. Mech. Eng. 2023, 15, 16878132231180480. [Google Scholar] [CrossRef]
- Li, H.; Liu, D.; Wang, D. Integral reinforcement learning for linear continuous-time zero-sum games with completely unknown dynamics. IEEE Trans. Autom. Sci. Eng. 2014, 11, 706–714. [Google Scholar] [CrossRef]
- Li, C.; Ding, J.; Lewis, F.L.; Chai, T. Model-free Q-learning for the tracking problem of linear discrete-time systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 3191–3201. [Google Scholar] [CrossRef] [PubMed]
- Valadbeigi, A.P.; Sedigh, A.K.; Lewis, F.L. H∞ Static Output-Feedback Control Design for Discrete-Time Systems Using Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 396–406. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wan, Y.; Zhu, J.; Lewis, F.L. H∞ tracking control for linear discrete-time systems: Model-free Q-learning designs. IEEE Control. Syst. Lett. 2020, 5, 175–180. [Google Scholar] [CrossRef]
- Lian, B.; Donge, V.S.; Lewis, F.L.; Chai, T.; Davoudi, A. Data-driven inverse reinforcement learning control for linear multiplayer games. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 2028–2041. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Gao, N.; Liu, D.; Li, J.; Lewis, F.L. Recent progress in reinforcement learning and adaptive dynamic programming for advanced control applications. IEEE/CAA J. Autom. Sin. 2023, 11, 18–36. [Google Scholar] [CrossRef]
- Wei, W.; Li, Q.; Xu, F.; Zhang, X.; Jin, J.; Jin, J.; Sun, F. Research on an electromagnetic actuator for vibration suppression and energy regeneration. Actuators 2020, 9, 42. [Google Scholar] [CrossRef]




| Symbol | Value | Unit |
|---|---|---|
| 20 | mm | |
| 40 | mm | |
| 5 | mm | |
| 10 | mm | |
| 22.6 | mm | |
| 32.1 | mm |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| M (kg) | 500 | 1.25 | |
| J (kg·m2) | 910 | 1.45 | |
| mt1 (kg) | 30 | 10,000 | |
| mt2 (kg) | 40 | 10,000 | |
| kt1 (N/m) | 100,000 | 2000 | |
| kt2 (N/m) | 100,000 | 2000 | |
| 1000 | 1000 | ||
| z1max (m) | 0.1 | kf (N/A) | 40 |
| z2max (m) | 0.1 | r (Ω) | 25.3 |
| 23.12 | 1262 |
| Method | (W) | (W) | ||
|---|---|---|---|---|
| Passive suspension | 0.4531 | 0.4799 | —— | —— |
| PI-RL (a = 0) | 0.1818 | 0.2265 | 1133 | 1378 |
| PI-RL (a = 0.3) | 0.1858 | 0.2324 | 1087 | 1299 |
| PI-RL (a = 0.6) | 0.1914 | 0.2406 | 1034 | 1210 |
| PI-RL (a = 1) | 0.201 | 0.2551 | 958.6 | 1086 |
| PI-RL (a = 1.2) | 0.2067 | 0.2638 | 922.6 | 1026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Deng, J.; Zhou, T.; Liu, S. Reinforcement Learning-Based Vibration Control for Half-Car Active Suspension Considering Unknown Dynamics and Preset Convergence Rate. Processes 2024, 12, 1591. https://doi.org/10.3390/pr12081591
Wang G, Deng J, Zhou T, Liu S. Reinforcement Learning-Based Vibration Control for Half-Car Active Suspension Considering Unknown Dynamics and Preset Convergence Rate. Processes. 2024; 12(8):1591. https://doi.org/10.3390/pr12081591
Chicago/Turabian StyleWang, Gang, Jiafan Deng, Tingting Zhou, and Suqi Liu. 2024. "Reinforcement Learning-Based Vibration Control for Half-Car Active Suspension Considering Unknown Dynamics and Preset Convergence Rate" Processes 12, no. 8: 1591. https://doi.org/10.3390/pr12081591
APA StyleWang, G., Deng, J., Zhou, T., & Liu, S. (2024). Reinforcement Learning-Based Vibration Control for Half-Car Active Suspension Considering Unknown Dynamics and Preset Convergence Rate. Processes, 12(8), 1591. https://doi.org/10.3390/pr12081591






