Research on Accurate Detection Algorithm for the Cross-Section of Shale Gas Casing Deformation Pipe String Based on Laser Ranging
Abstract
1. Introduction
2. Test Method
- (1)
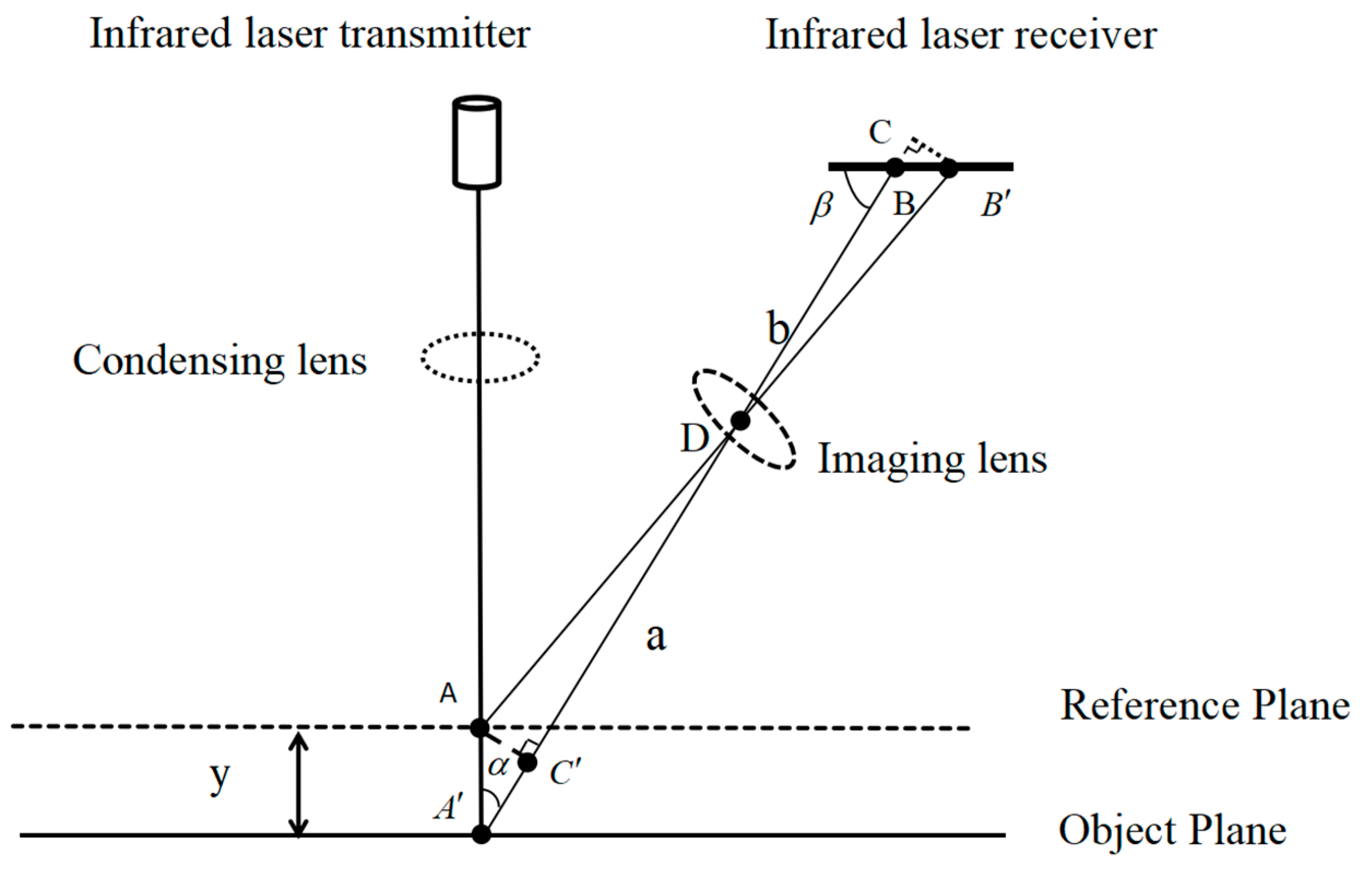
- The detection principle of laser sensors
- (2)
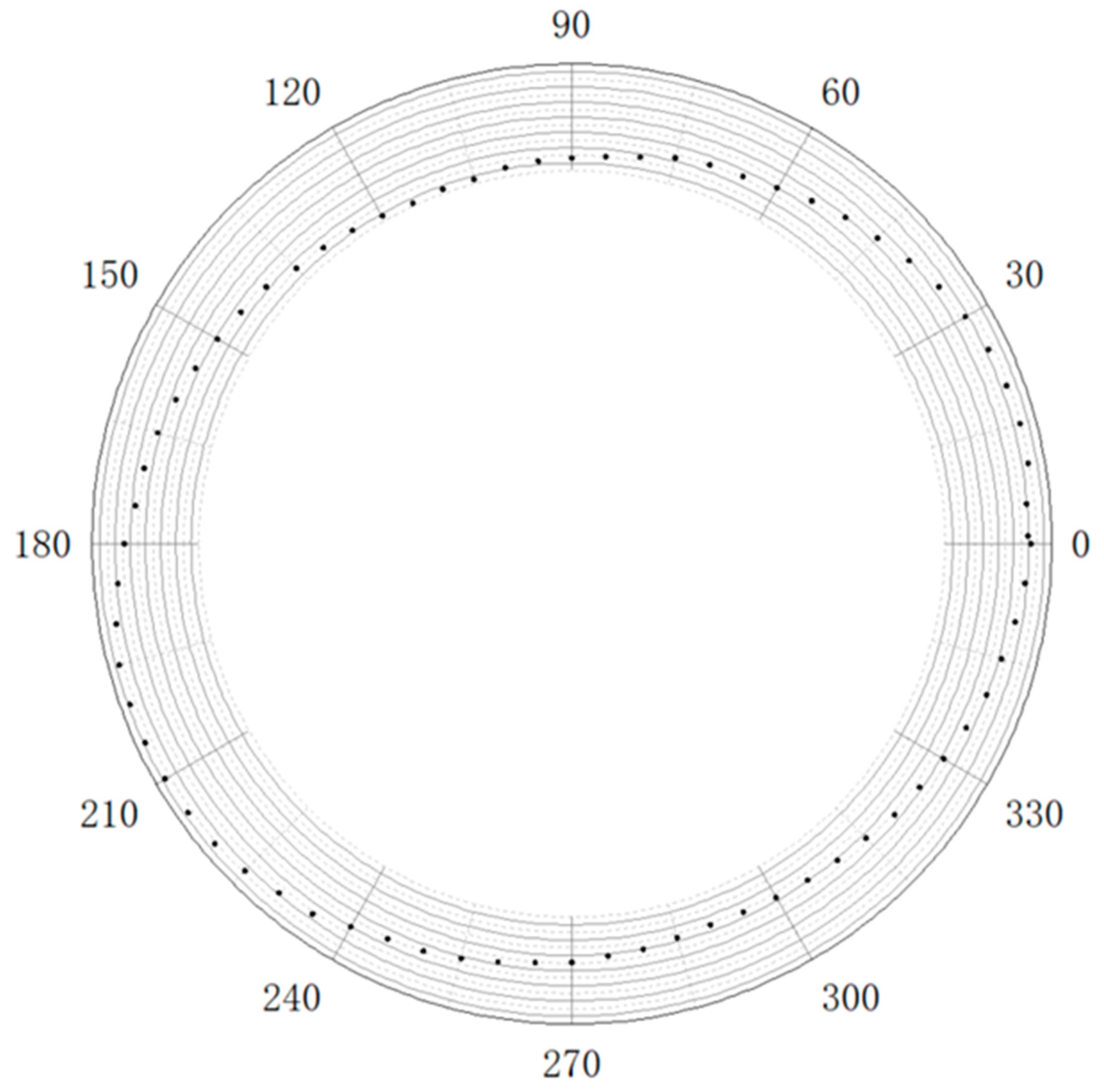
- Circular traversal detection method for inner diameter of casing
- L—Measurement step size;
- N—Total number of points collected through circular traversal, .
3. Experimental Casing Morphology and Detection Device
- (1)
- Deformation morphology of shale gas casing
- (2)
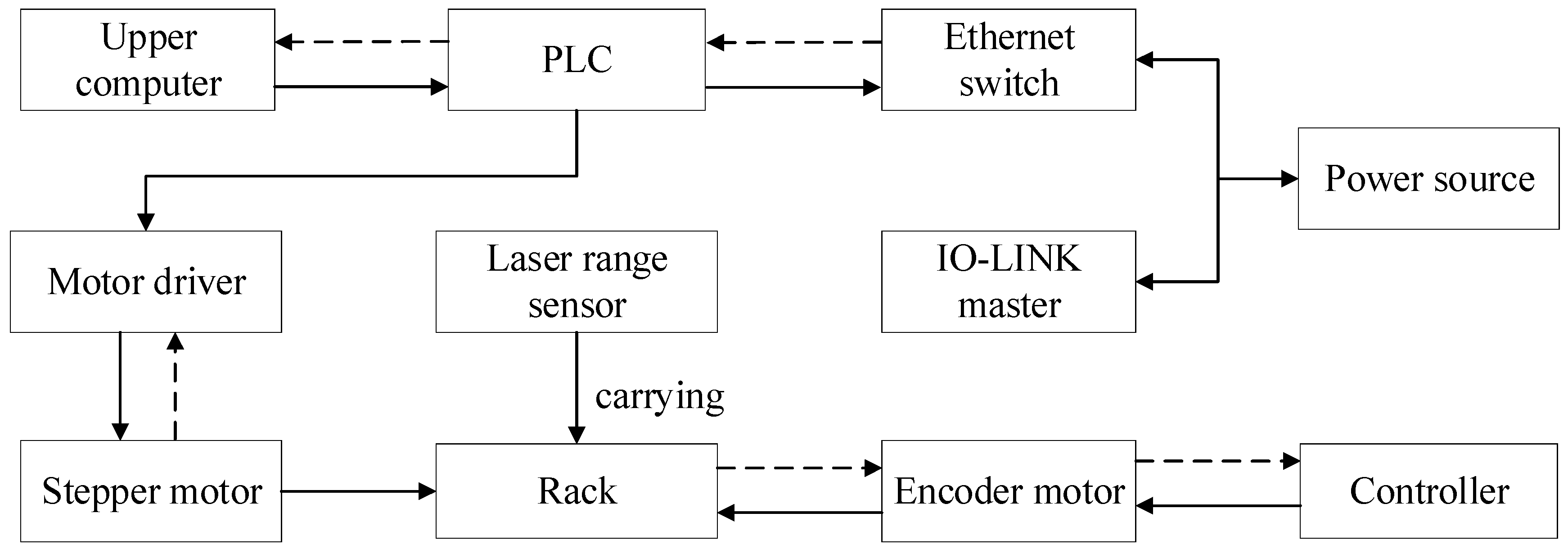
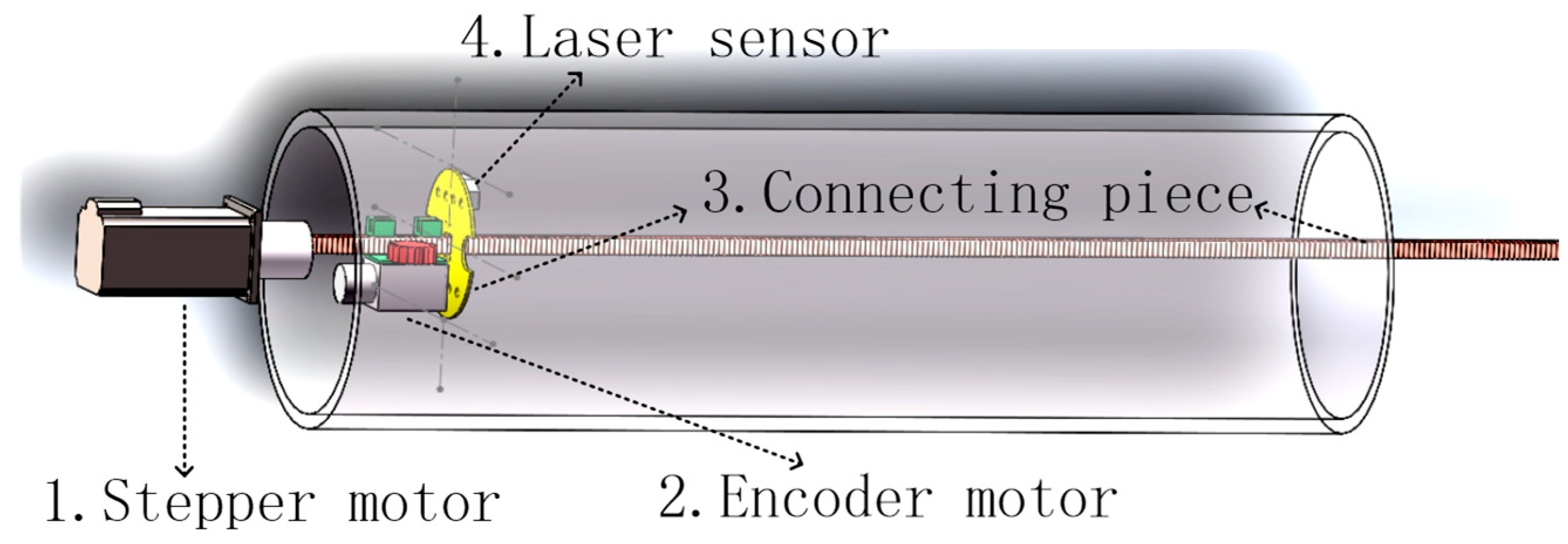
- Design of detection device
- (1)
- Selecting laser sensors with a small volume and high accuracy of short-distance measurements as measurement components;
- (2)
- Minimizing the mechanical devices that fix and drive sensor movement as much as possible;
- (3)
- The detection device needs to be able to move forward, backward, and perform circumferential measurements inside the casing.
- (1)
- The sensor can travel to the designated position inside the casing;
- (2)
- Comparison between measurement data and reference values is possible;
- (3)
- Extreme values of the measured data set are displayed inside the casing;
- (4)
- The curve graph displays a section of data inside the casing.
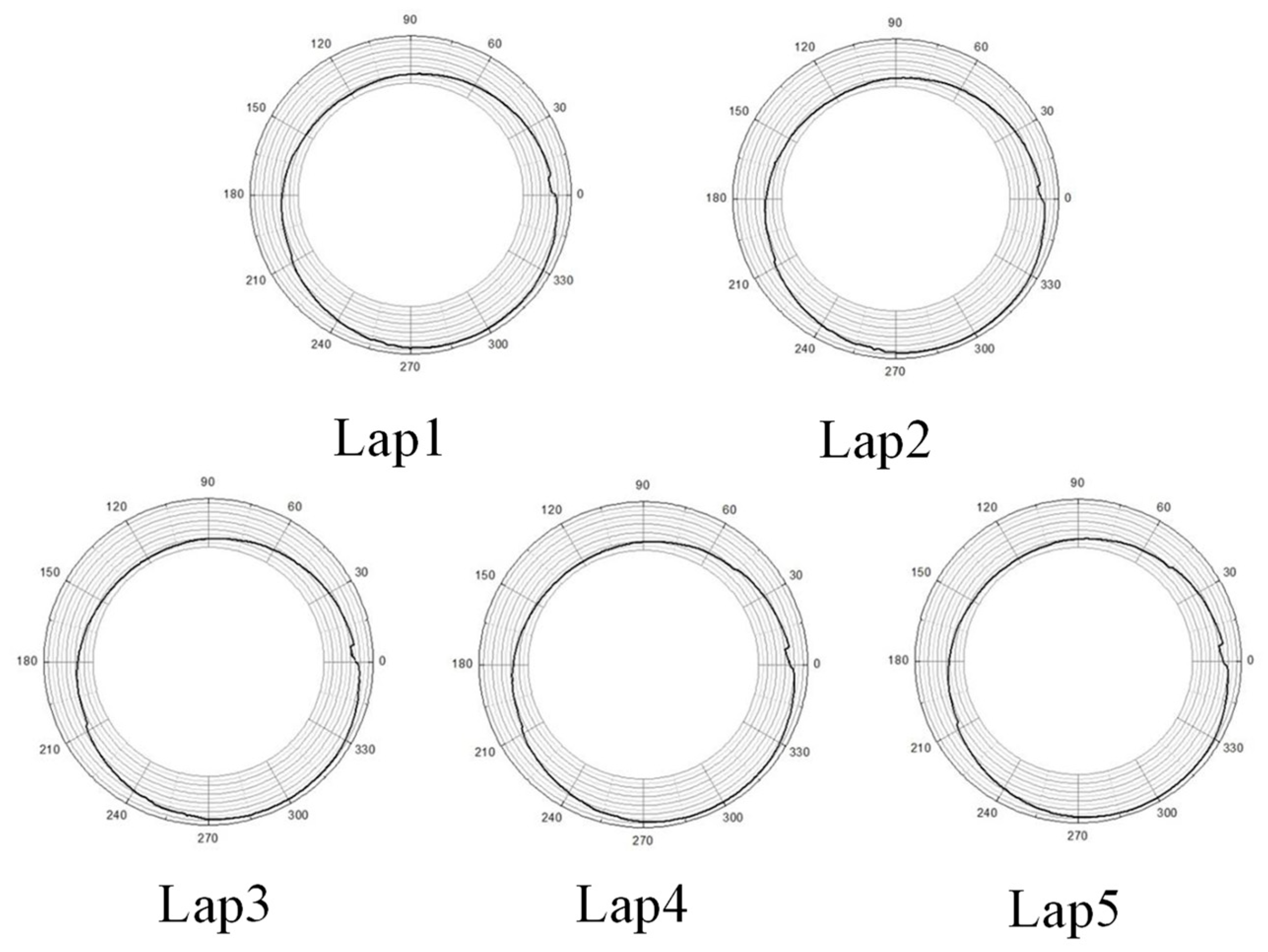
4. Methods for Eliminating Eccentricity Errors and Smoothing Curves
- (1)
- Eccentricity error elimination
- (2)
- Curve smoothing processing
| X | X0····X1·····X2 ··· ··· Xn−1·····Xn |
| Y | Y0····Y1·····Y2 ··· ··· Yn−1·····Yn |
5. Algorithm Testing
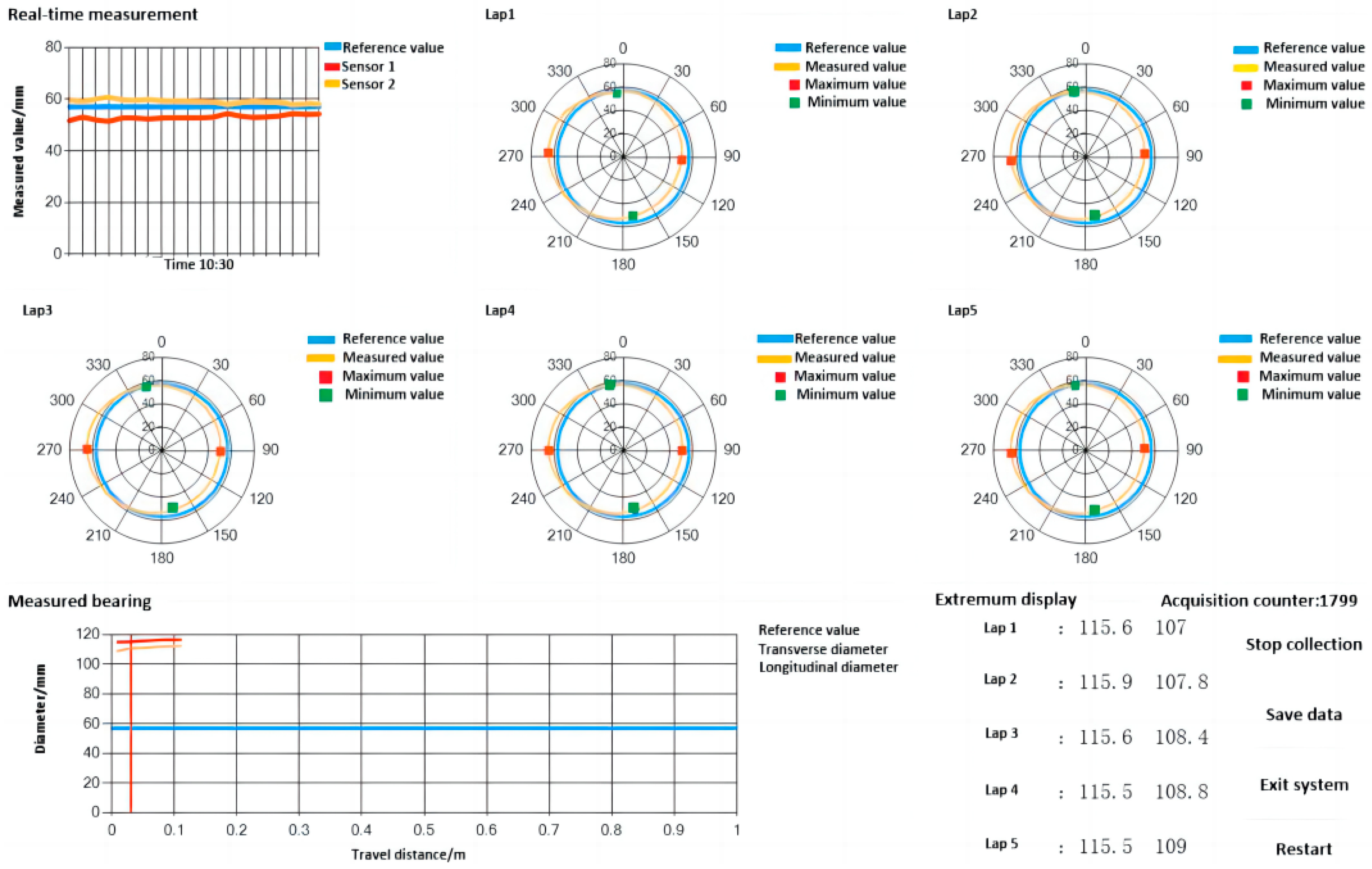
5.1. The Inner Diameter of the 114.3 mm Casing
- (1)
- Data acquisition
- (2)
- Data processing
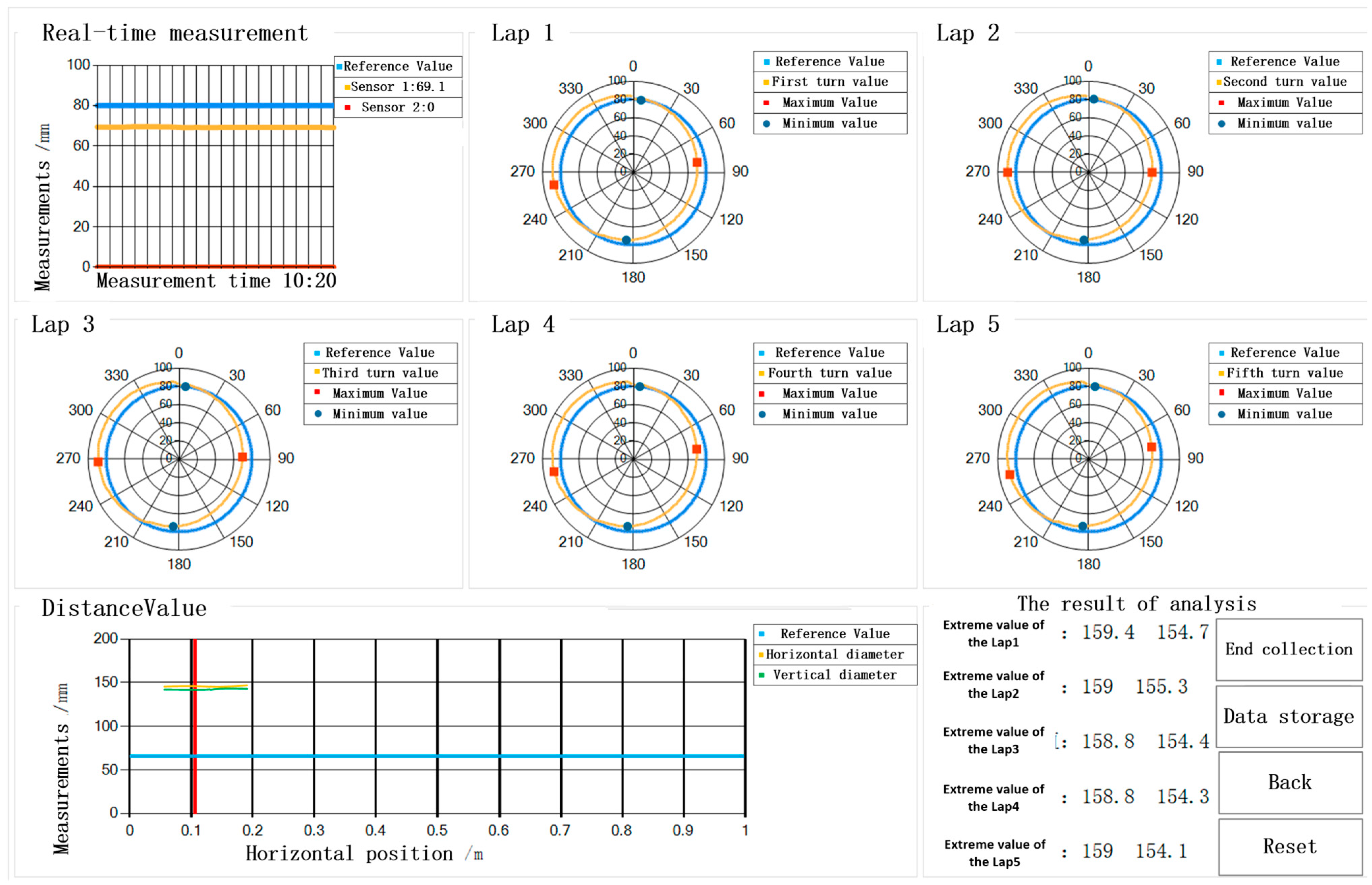
5.2. The Inner Diameter of the Casing Is 157.08 mm
- (1)
- Data collection
- (2)
- Data processing
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rui, S.; Fei, L.; Zhao, Y.; Li, G.; Yu, W. Analysis of Influential factors of multi-cluster fracturing casing stress in shale gas wells. China Pet. Mach. 2023, 51, 148–156. [Google Scholar]
- Xi, Y.; Li, J.; Liu, G.; Zeng, Y.; Li, J. Overview of casing deformation in multistage fracturing of shale gas horizontal wells. Spec. Oil Gas Reserv. 2019, 26, 1–6. [Google Scholar]
- Chen, Z.; Shi, L.; Xiang, D. Mechanism of casing deformation in the Changning–Weiyuan national shale gas demonstration area and countermeasures. Nat. Gas Ind. B 2017, 4, 1–6. [Google Scholar] [CrossRef]
- Yan, W.; Zou, L.; Li, H.; Deng, J.; Ge, H.; Wang, H. Investigation of casing deformation during hydraulic fracturing in high geo-stress shale gas play. J. Pet. Sci. Eng. 2017, 150, 22–29. [Google Scholar] [CrossRef]
- Han, L.; Li, X.; Liu, Z.; Duan, G.; Wan, Y.; Guo, X.; Cuo, W.; Cui, Y. Influencing factors and prevention measures of casing deformation in deep shale gas wells in Luzhou block, southern Sichuan Basin, SW China. Pet. Explor. Dev. 2023, 50, 979–988. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, Z.; Guo, J.; He, L.; Li, Y.; Zeng, J.; Ren, S. Hydraulic fracturing induced casing shear deformation and a prediction model of casing deformation. Pet. Explor. Dev. 2021, 48, 460–468. [Google Scholar] [CrossRef]
- Salimov, F.L.; Plugin, S.; Kramer, H. Successful application of through casing logging technology toincrease oil production in a brown field well. In Proceedings of the SPE Russian Oil and Gas Exploration and Production Technical Conference and Exhibition, Moscow, Russia, 14–16 October 2014. [Google Scholar]
- Hughes, M.A.; Kramer, H.; Ramli, M.N.; Abdul Razak, R.; Valouiski, K. Successful application of through casing saturation technology to increase oil production in an Offsgore mature well. In Proceedings of the International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 10–12 December 2014. [Google Scholar]
- Yin, F.; Han, L.; Yang, S.; Deng, Y.; He, Y.; Wu, X. Casing deformation from fracture slip in hydraulic fracturing. J. Pet. Sci. Eng. 2018, 166, 235–241. [Google Scholar] [CrossRef]
- Bingyin, J.; Fu, Y.; Meng, L.; Sun, J.; Sun, J. Full-scale test and new mechanism on collapsing strength of shale gas casing under nonuniform load. China Pet. Mach. 2023, 51, 148–154. [Google Scholar]
- Dong, Z.; Tang, S. Numerical study of near-wellbore hydraulic fracture propagation. Theor. Appl. Fract. Mech. 2019, 103, 102274. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Zhang, H.; Wang, D.; Li, T.; Liu, H. Influence of fault slip on casing shear deformation and its prevention and control measures. Fault-Block Oil Gas Field 2023, 30, 734–742. [Google Scholar]
- Huang, X.; Shen, H.; Sun, J.; Lv, K.; Liu, J.; Dong, X.; Luo, S. Nanoscale Laponite as a Potential Shale Inhibitor in Water-Based Drilling Fluid for Stabilization of Wellbore Stability and Mechanism Study. ACS Appl. Mater. Interfaces 2018, 10, 33252–33259. [Google Scholar] [CrossRef] [PubMed]
- Hui, L. Application of Multiarm Diameter and Electromagnetic Thickness Measurement TOOL Combination Logging of Casing Inspection in Changqing Oil field. Pet. Tubul. Goods Instrum. 2022, 8, 81–84. [Google Scholar]
- Xin, J.; Chen, J.; Li, X.; Wang, C.; Zhang, X.; Zhu, H. Advances in Oil and Gas Pipeline Internal Inspection Technology. China Pet. Mach. 2022, 50, 119–126. [Google Scholar]
- Dai, L.; Zhang, S.; Zhu, X.; Zhang, W.; Wang, D. Research progress of oil and gas pipeline diameter detector technology. Oil Gas Storage Transp. 2012, 31, 808–813. [Google Scholar]
- Chen, J.; Wang, J.; Ma, Y.; He, R.; Jin, Y. Internal inspection technology of pipeline cathodic protection based on current measurement. Nondestruct. Test. 2018, 40, 9–11, 31. [Google Scholar]
- Min, X.; Yang, L.; Wang, G.; Rao, X.; Liu, B. Weak Magnetism Stress Internal Testing Technology of the Long Distance Oil-gas Pipeline. J. Mech. Eng. 2017, 53, 19–27. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, H.; Tao, A.H.; Li, Y.J.; Shi, Y.B. Local defect detection of ferromagnetic metal casing based on pulsed eddy current testing. IEEE Trans. Instrum. Meas. 2022, 71, 6003109. [Google Scholar] [CrossRef]
- Xu, F.; Huang, H.; Luo, Q. Quantitative Evaluation Method of Eddy Current Detection Data for Deformation Defects in Oil and Gas Well Casing. Log. Tech. 2021, 45, 584–591. [Google Scholar]
- Xie, M.; Tian, Z. A review on pipeline integrity management utilizing in-line inspection data. Eng. Fail. Anal. 2018, 92, 222–239. [Google Scholar] [CrossRef]
- Ege, Y.; Coramik, M. A new measurement system using magnetic flux leakage method in pipeline inspection. Measurement 2018, 123, 163–174. [Google Scholar] [CrossRef]
- Khodayari-Rostamabad, A.; Reilly, J.P.; Nikolova, N.K.; Hare, J.R.; Pasha, S. Machine learning techniques for the analysis of magnetic flux leakage images in pipeline inspection. IEEE Trans. Magn. 2009, 45, 3073–3084. [Google Scholar] [CrossRef]
- Piao, G.; Guo, J.; Hu, T.; Deng, Y.; Leung, H. A novel pulsed eddy current method for high-speed pipeline inline inspection. Sens. Actuators A Phys. 2019, 295, 244–258. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, J.; Huang, S.; Peng, L.; Wang, W.; Wang, S.; Zhao, W. A novel crack quantification method for ultra-high-definition magnetic flux leakage detection in pipeline inspection. IEEE Sens. J. 2022, 22, 16402–16413. [Google Scholar] [CrossRef]
- Ma, Q.; Tian, G.; Zeng, Y.; Li, R.; Song, H.; Wang, Z.; Gao, B.; Zeng, K. Pipeline in-line inspection method, instrumentation and data management. Sensors 2021, 21, 3862. [Google Scholar] [CrossRef] [PubMed]
- Fei, C.; Bai, G.; Chao, T. Extremum Response Surface Method for Casing Radial Deformation Probabilistic Analysis. J. Aerosp. Inf. Syst. 2013, 10, 1. [Google Scholar] [CrossRef]
- Cuan, Y.; Wang, S.; Han, J. Research on Deformation Detection Method of Oil and Gas Well Casing Based on Curve Fitting. J. Phys. Conf. Ser. 2019, 1325, 012218. [Google Scholar] [CrossRef]
- Cohen, A.; Migliorati, G. Optimal weighted least-squares methods. SMAI J. Comput. Math. 2017, 3, 181–203. [Google Scholar] [CrossRef]
- Hong, S.H.; Wang, L.; Truong, T.K.; Lin, T.C.; Wang, L.J. Novel approaches to the parametric cubic-spline interpolation. IEEE Trans. Image Process. 2012, 22, 1233–1241. [Google Scholar] [CrossRef]
- Maekawa, T.; Matsumoto, Y.; Namiki, K. Interpolation by geometric algorithm. Comput.-Aided Des. 2007, 39, 313–323. [Google Scholar] [CrossRef]
- Qiu, Z.; Shen, M.; Jia, C.; Chen, J.; Feng, R. Laser distance measurement technology research status and development trend. Laser J. 2023, 44, 1–8. [Google Scholar]
- Sun, Y.; Pang, Y.; Bai, Z.; Wang, Y.; Lv, Z. Application technology of laser triangulation. Laser J. 2021, 42, 1–8. [Google Scholar]
- Kienle, P.; Köhler, M.H.; Wang, K.; Jakobi, M.; Koch, A.W. Increasing the sensitivity of laser triangulation systems using structured optical surfaces. In Proceedings of the ODS 2020: Industrial Optical Devices and Systems, Online, 24 August–4 September 2020; Volume 11500, pp. 56–64. [Google Scholar]
- Suh, Y.S. Laser sensors for displacement, distance and position. Sensors 2019, 19, 1924. [Google Scholar] [CrossRef]
- Salgado, C.F.A.; Maestre, L.E.P.; Noriega, L.A.; Castro, J.R. Distance Aproximator Using IEEE 802.11 Received Signal Strength and Fuzzy Logic. In Proceedings of the 11th Mexican International Conference on Advances in Computational Intelligence—Volume Part II, San Luis Potosi, Mexico, 27 October–4 November 2012; Springer: Berlin/Heidelberg, Germany. [Google Scholar] [CrossRef]
- Reza, S.A.; Khwaja, T.S.; Mazhar, M.A.; Niazi, H.K.; Nawab, R. Improved laser-based triangulation sensor with enhanced range and resolution through adaptive optics-based active beam control. Appl. Opt. 2017, 56, 5996–6006. [Google Scholar] [CrossRef] [PubMed]
- Wallace, L. Understanding laser-based 3D triangulation methods. Vis. Syst. Des. 2015, 20, 31–35. [Google Scholar]
- Walker, C.L.; Robinson, N.E. Inline Surface Dimensional Flaw Detection and OD/Ovality Measurement Using Laser Line Triangulation on Round Product. Wire & Cable Technology International, 2 November 2022. [Google Scholar]







| Name | Length (mm) | Outer Diameter (mm) | Inner Diameter (mm) | Wall Thickness (mm) | Detection Position (mm) |
|---|---|---|---|---|---|
| casing | 700 | 127 | 114 | 13 | 550 |
| Serial Number | Measurement Value (Max) | True Value (Max) | Error Absolute Value | Serial Number | Measurement Value (min) | True Value (min) | Error Absolute Value |
|---|---|---|---|---|---|---|---|
| Lap1 | 115.6 | 115.55 | 0.05 | Lap1 | 107.0 | 106.96 | 0.04 |
| Lap2 | 115.6 | 115.55 | 0.05 | Lap2 | 107.6 | 107.55 | 0.05 |
| Lap3 | 115.6 | 115.55 | 0.05 | Lap3 | 108.5 | 108.48 | 0.02 |
| Lap4 | 115.7 | 115.68 | 0.02 | Lap4 | 108.8 | 108.71 | 0.09 |
| Lap5 | 115.5 | 115.47 | 0.03 | Lap5 | 109.7 | 109.62 | 0.08 |
| Name | Length (mm) | Outer Diameter (mm) | Inner Diameter (mm) | Wall Thickness (mm) | Detection Location (mm) |
|---|---|---|---|---|---|
| Casing | 700 | 177.8 | 157.08 | 103.6 | From the right end 200 mm |
| Serial Number | Measurement Value (Max) | True Value (Max) | Error Absolute Value | Serial Number | Measurement Value (min) | True Value (min) | Error Absolute Value |
|---|---|---|---|---|---|---|---|
| Lap1 | 159.4 | 159.37 | 0.03 | Lap1 | 154.7 | 154.68 | 0.02 |
| Lap2 | 159 | 159 | 0 | Lap2 | 155.3 | 155.31 | 0.01 |
| Lap3 | 158.8 | 158.85 | 0.05 | Lap3 | 154.4 | 154.35 | 0.05 |
| Lap4 | 158.8 | 158.9 | 0.01 | Lap4 | 154.3 | 154.23 | 0.07 |
| Lap5 | 159 | 158.97 | 0.03 | Lap5 | 154.1 | 154.14 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Mou, Y.; Cao, J.; Yan, Y. Research on Accurate Detection Algorithm for the Cross-Section of Shale Gas Casing Deformation Pipe String Based on Laser Ranging. Processes 2024, 12, 1435. https://doi.org/10.3390/pr12071435
Yang S, Mou Y, Cao J, Yan Y. Research on Accurate Detection Algorithm for the Cross-Section of Shale Gas Casing Deformation Pipe String Based on Laser Ranging. Processes. 2024; 12(7):1435. https://doi.org/10.3390/pr12071435
Chicago/Turabian StyleYang, Shangyu, Yisheng Mou, Jing Cao, and Yan Yan. 2024. "Research on Accurate Detection Algorithm for the Cross-Section of Shale Gas Casing Deformation Pipe String Based on Laser Ranging" Processes 12, no. 7: 1435. https://doi.org/10.3390/pr12071435
APA StyleYang, S., Mou, Y., Cao, J., & Yan, Y. (2024). Research on Accurate Detection Algorithm for the Cross-Section of Shale Gas Casing Deformation Pipe String Based on Laser Ranging. Processes, 12(7), 1435. https://doi.org/10.3390/pr12071435







