Abstract
In response to the trajectory tracking control problem of manipulators under measurement disturbances, a novel multi-input multi-output discrete integral terminal sliding mode control scheme is proposed. Initially, this scheme establishes a dynamic model of a two-joint manipulator based on the Lagrangian dynamics analysis method. Subsequently, a discrete integral terminal sliding mode control law based on the dynamic model of the two joints is designed, incorporating delayed estimation of unknown disturbances and discretization errors in the manipulator system. To enhance the trajectory tracking accuracy of the control scheme and suppress the impact of sliding mode chattering on the manipulator system, an adaptive switching term is introduced into the discrete integral terminal sliding mode control law. The paper derives an adaptive discrete integral terminal sliding mode control scheme and provides stability proof for the proposed approach. Simulation experiments are conducted to compare the proposed adaptive discrete integral terminal sliding mode control scheme with classical discrete sliding mode control schemes and discrete integral terminal sliding mode control schemes. The simulation results demonstrate that the designed adaptive discrete integral terminal sliding mode control scheme maintains trajectory tracking errors within 0.004 radians for each joint of the manipulator, with minimal changes in control torque for each joint. The absolute integral of the control torque variations is calculated at , which is lower than other control schemes, thereby validating the effectiveness and superiority of the proposed approach.
1. Introduction
With the rapid development of computer science and automation control technology, robotic arms have been widely utilized in high-precision industrial control applications [1]. Compared to traditional manual or semi-automatic control methods, robotic arms offer multiple advantages, such as high precision, efficiency, and versatility. However, in practical engineering applications, factors such as load conditions, external disturbances, and system friction may lead to variations in control parameters, resulting in deviations in the motion trajectory of robotic arms, especially in complex and unstructured scenarios where the precision of trajectory control may decrease, making it difficult to meet high-precision requirements [2,3,4]. Therefore, achieving adaptive high-precision trajectory control of robotic arms in complex and nonlinear environments is currently a major focus of research for the large-scale practical engineering application of robotic arms.
Currently, scholars, both domestically and internationally, have proposed numerous control strategies to address the issue of robotic arm trajectory control. For instance, in reference [5], based on the theories of RBF neural network control and iterative sliding mode control, a novel RBF neural network fractional-order iterative sliding mode control strategy is proposed. Stability analysis of the control strategy is provided. Subsequently, using a two-joint robotic arm as an example, various control strategies are simulated, compared, and analyzed. Finally, the effectiveness of the proposed strategy is verified through simulation experiments. However, neural networks are associated with drawbacks such as low computational efficiency and long training times. To address this issue, reference [6] combined extended Kalman filters with fuzzy neural networks to train fuzzy neural networks to generate feedforward torques and continuously update the output weights and center vectors of the fuzzy neural networks, thereby enhancing the computational efficiency and accuracy of the training algorithm. Additionally, in reference [7], a robust impedance controller was proposed for delayed compensation mobile robotic arms, capable of handling system non-integrity constraints, nonlinearity, system motor dynamics, and uncertainties, thus enhancing the robustness of the controller. Finally, in reference [8], a new robust finite-time tracking controller was designed for the trajectory tracking problem of manipulators with uncertainties and external disturbances, and the system uncertainties and external disturbances were estimated by the extended state observer. While these studies fully considered system nonlinearity and uncertainties, in reality, mobile robotic arms are influenced by multiple factors during operation, making it difficult to obtain accurate mathematical models. The aforementioned control algorithms are unable to meet the required control precision when the model is uncertain. Research has indicated that discrete sliding mode control (DSMC) is insensitive to changes in controlled system parameters and external disturbances, providing a simple and effective method for overcoming system disturbances [9]. The essence of DSMC is to drive the system state trajectory onto a specified sliding surface and maintain its movement along the surface. Once on the sliding surface, the controlled system exhibits robustness to certain changes in the model and external disturbances [10]. Therefore, when the model is uncertain, DSMC has significant advantages over other control methods.
For instance, reference [11] proposed an improved discrete-time fast terminal sliding surface for discrete linear single-input single-output models, designing a fast terminal sliding mode control law to achieve higher tracking accuracy. For disturbed discrete-time nonlinear systems, reference [12] introduced a model-free adaptive sliding mode control law based on an extended state observer to achieve higher precision trajectory tracking. In recent years, various discrete integral sliding mode control (ISMC) methods have been reported in the literature in different fields, as ISMC can provide smaller tracking errors compared to traditional discrete sliding mode control methods [13,14,15,16,17]. Reference [18] put forward a sliding mode control law and an approaching law for high-performance tracking of uncertain discrete-time systems, analyzing the boundary of tracking errors. In reference [19], a discrete integral terminal sliding mode control (DITSMC) approach was proposed for achieving velocity tracking control. However, the aforementioned method still suffers from the chattering phenomenon when the system encounters uncertain stochastic disturbances.
Currently, adaptive control has been successfully applied in various fields of the process industry. Adaptive control continuously extracts information about the model during system operation, gradually improving the model and correspondingly changing the controller parameters to make the system adapt over time. For example, reference [20] proposed an NTSM (Robust Adaptive Nonsingular Terminal Sliding Model) control strategy, ensuring that the position and velocity tracking errors of the system converge to zero within a finite time and eliminating the chattering caused by the terminal sliding mode controller. Addressing the lower control precision and sliding mode chattering phenomenon in robotic arm trajectory tracking, reference [21] addressed the trajectory tracking problem of a robotic arm with uncertainties and external disturbances. It proposed a novel robust finite-time tracking control scheme and designed an adaptive backstepping nonsingular fast terminal sliding mode controller to achieve finite-time convergence of tracking errors while avoiding singularity issues. Additionally, an adaptive updating law for switch gains was devised to further mitigate chattering problems. In summary, combining adaptive control with an approaching law in discrete terminal sliding mode control to eliminate sliding mode chattering is entirely feasible.
In consideration of the actual operating conditions of robotic arms, this paper proposes a new algorithm, Adaptation Discrete Integral Terminal Sliding Mode Control (ADITSMC), for the motion control of robotic arm systems under complex operating environments. The proposed scheme achieves precise motion control of robotic arm systems in complex operating environmental conditions. Simulation results demonstrate that the ADITSMC scheme outperforms DITSMC and DSMC controllers in terms of motion tracking precision.
The main contributions of this paper are as follows:
- (1)
- A novel ADITSMC algorithm is proposed, which uses a one-step delay estimation method to compensate for disturbances in the controlled object and adopts the idea of adaptive control to improve the trajectory tracking precision of robotic arm systems and suppress system chattering.
- (2)
- Compared to previous approaches utilizing robust control, neural networks, fuzzy control, etc. [5,6,7,8,9], the proposed scheme features a simpler controller design and higher tracking precision. In comparison to reference [11], the proposed scheme is applicable to multi-input and multi-output systems, thus offering higher system accuracy. In contrast to reference [12], the proposed scheme does not require a state observer, and the data-driven control algorithm is less sensitive to changes in system parameters, maintaining high tracking precision. When compared to references [18,19], the proposed scheme exhibits smaller chattering in the presence of high disturbances. In comparison to references [20,21], the proposed scheme requires fewer parameter adjustments and achieves slightly higher tracking precision.
- (3)
- The primary advantage of the proposed ADITSMC scheme is to provide an easily implemented control method for multi-input and multi-output systems, capable of handling uncertainties and disturbances.
The rest of this paper is structured as follows: Section 2 elaborates on the modeling issues of the two-degree-of-freedom robotic arm motion system. Section 3 details the design process of the DITSMC and ADITSMC schemes. Section 4 presents a series of simulation experiments. Section 5 concludes the paper.
2. Two-Joint Manipulator Model and Its Discrete State Space Expression
2.1. Two-Joint Manipulator Model
The research this paper reports focuses on the control of a two-degree-of-freedom robotic arm system as depicted in Figure 1. The lengths of the individual links, joint angular displacements, and link masses are specified in the diagram. The dynamic model of the robotic arm is established using the Lagrangian equation method, with the following dynamic equations:
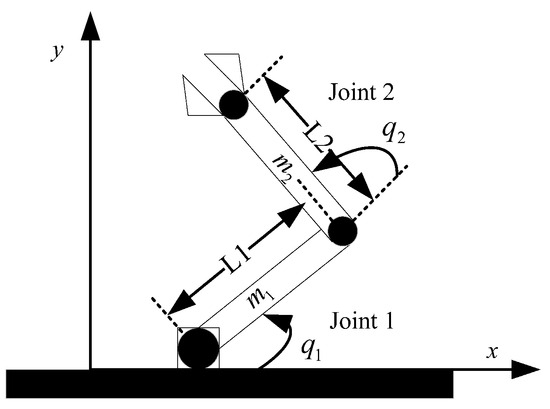
Figure 1.
Two-joint manipulator model diagram.
Here, represents the inertia mass matrix of the system; represents the Coriolis and centrifugal force matrix; represents the gravitational term matrix; stands for the control input; and denotes external unknown disturbances and model uncertainties.
; ; ; . The displacement of joint 1 and joint 2 of the manipulator are denoted as , respectively; the angular velocity of the robotic arm joints 1 and 2 are denoted as , respectively; the angular acceleration of the robotic arm joints 1 and 2 are denoted as , respectively; the driving torque of the robotic arm joints 1 and 2 are denoted as , respectively; the uncertain disturbances of the robotic arm joints 1 and 2 are denoted as , respectively.
2.2. Discrete State Space Expression of Two-Joint Manipulator
Equation (1) yields the nonlinear dynamic equation of the robotic arm. Subsequently, the state vector is defined as the joint angular displacement and angular velocity of the robotic arm, the control input variable represents the control torque of the robotic arm, and the output vector signifies the output values of the robotic arm joint angular displacement achieved through torque control. Therefore, the state–space equations of the robotic arm system are expressed as follows:
Next, the Jacobian linearization of Equation (2) is conducted. Based on the state vector defined earlier, the Jacobian sub-matrix of the derivative functions for its components is derived as follows:
After obtaining the Jacobian matrices from Equations (3) and (4), the system at the desired equilibrium point is linearized using the Jacobian linearization method.Assuming the control vector at this equilibrium point is denoted as , the state vector as , and the time derivative as , the system is linearized around the equilibrium point where the Jacobian sub-matrices in Equations (3) and (4) are linearized at .
Firstly, the linearized state vector is defined as and the control vector is defined as . Then, the system equation is
The constant term in Equation (5) can be expressed by . Then, the linearized system is as follows:
Discretizing Equation (6) using a zero-order hold with a sampling period of and incorporating an error disturbance term, the discrete-time state-space representation of the multi-input, multi-output robotic arm is as follows:
Here, the matrix parameters are as follows: , .
The factors not accounted for in the modeling and errors introduced by discretization, collectively termed disturbances , along with external interferences to the system, are represented below.
Assumption 1.
Assuming that the disturbance before sampling is smooth and bounded, the discrete uncertainty has the following properties [22]: as the sampling time is small, the variation in disturbances between adjacent sampling intervals is minimal [23,24].
3. Design of Adaptive Discrete Integral Terminal Sliding Mode Controller for Two-Joint Manipulator
3.1. Trajectory Tracking Control Structure of Two-Joint Manipulator
This section introduces the discrete integral terminal sliding mode control based on the adaptive reaching law. This control law ensures that the discrete sliding mode surface enters a quasi-sliding mode after a finite number of steps, meaning that although the state of the discrete sliding mode system cannot strictly lie on the sliding mode surface, it can move within a certain neighborhood of the sliding mode surface while maintaining a sliding motion state near the sliding mode surface. This achieves the goal of trajectory tracking control for the robotic arm. Under reasonable assumptions, the rigorous convergence proof process for this control law is provided. Figure 2 illustrates the control block diagram of the system.
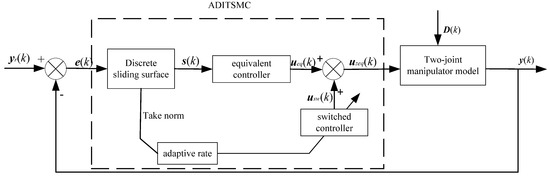
Figure 2.
ADITSMPC scheme control block diagram.
3.2. Design of Adaptive Discrete Integral Terminal Sliding Mode Control Law
Define the trajectory velocity tracking error of the manipulator:
where is the controller output trajectory and is the desired trajectory.
The design of the discrete integral terminal sliding mode surface is as follows:
The integral terminal error term in the formula is as follows:
The parameter value in the formula is . In addition, is selected as the ratio of two odd numbers [25].
The discrete integral terminal sliding mode control law of the manipulator is derived from the following conditions:
In the equation:
In the equation:
Due to the uncertainty of the disturbance in the robotic arm, a one-step ahead estimation method is employed for estimation, as shown in Equation (16).
By combining Equations (9)–(16), the discrete integral terminal sliding mode control law for the robotic arm can be derived as follows:
In order to enhance the disturbance rejection capability of the robotic arm system (7), a nonlinear switching term is introduced.
where is a parameter that can be adjusted.
The value of parameter will affect the magnitude of the sliding mode chatter in the robotic arm system (7). When parameter is small, the sliding mode chatter of the system (7) will decrease. However, if is too small, it will also affect the convergence speed of the system (7). Therefore, the value of should be variable [11]. Hence, an adaptive law is designed to allow the parameter to change with variation of the system (7). The specific adaptive law is as follows:
In the equation, is a constant; is chosen as a constant of magnitude.
In conclusion, the adaptive discrete integral terminal sliding mode control law for robotic arms is as follows:
In the equation:
3.3. Proof of Convergence for the Robotic Arm Adaptive Discrete Integral Terminal Sliding Mode Controller
Theorem 1.
For the nonlinear system of robotic arms with external disturbances (6), if the disturbance d(k) satisfies Assumption 1, the system possesses the following property.
The sliding mode state starting from any initial state can enter the region within at most k steps, where and k are defined as follows:
Proof 1.
For the convenience of calculation definition:
Moreover, for multi-input multi-output systems, matrix A can be expressed in terms of matrix and sub-elements as follows:
According to Assumption 1, it can be inferred that there exists a minimal positive number such that Equation (29) holds true, and is a constant of magnitude. Let us choose , and rewrite Equation (25) in terms of matrix sub-elements.
The reaching condition for the discrete sliding mode, as referenced in [5], is illustrated by Equation (31). When the system (7) is not on the sliding surface, Equations (32) and (33) can be derived.
Based on Equations (31)–(33), it can be concluded that the system (7) satisfies the reaching condition of discrete sliding mode.
Next, we will demonstrate that the system (7) will enter the quasi-sliding mode with a band of width centered around the sliding switching surface in a finite number of steps.
The Lyapunov function is designed as follows:
Differentiating the Lyapunov function yields:
Because is certain to be established, the signs of and are the same. Therefore, it suffices to prove proposition . We will discuss the following two cases:
When , (35) can be written as
In the equation:
Therefore, it can be deduced that
If , ,
When implies , after taking the integer steps through rounding , the system (6) enters a quasi-sliding mode centered on the sliding mode switching surface with as the bandwidth of the quasi-sliding mode.
By utilizing Equation (41), we can solve for
Let be defined as the largest integer not exceeding .
Therefore, we can conclude that when , the system (7) will enter the quasi-sliding mode with as the bandwidth of the quasi-sliding mode, centered on the sliding mode switching surface in a finite number of steps, with the step count being k.
When , the following is similarly available:
In the equation:
Therefore, it can be deduced that
Furthermore, due to the fact that
Given the similarity in expression to , it can likewise be derived that follows. That is, after integer steps of taking , the system (7) enters a quasi-sliding mode centered around the sliding mode switching surface with as the bandwidth of the quasi-sliding mode.
Similarly, we can obtain:
Let be defined as the largest integer not exceeding .
Based on Equation (50), it can be deduced that at , the system (7) will enter a quasi-sliding mode centered around the sliding mode switching surface with as the bandwidth of the quasi-sliding mode, in a finite number of steps denoted as k.
Therefore, starting from any initial state, the system (7) will reach the switching surface within a finite number of steps, and then traverse along it. However, its motion comprises three stages: an approaching mode, a quasi-sliding mode, and a steady state. Consequently, it is essential to prove that once the system (7) enters the switching surface, it will not escape from it.
To begin with, a switching band enclosing the switching surface is defined:
Subsequently, the analysis is divided into the following two cases:
- (1)
- If
- (2)
- If
Based on Equations (52)–(55), the conclusion can be drawn that once the system (7) enters region (51), it will never escape from that region. Here, represents the bandwidth of the quasi-sliding mode, with a magnitude of .
Next, we will demonstrate that the designed adaptive discrete integral terminal sliding mode control is stable and will enter the quasi-sliding mode within a finite number of steps.
Given that the system bandwidth is , is bounded. Therefore, as long as Equation (56) is satisfied, the system (7) will be stable and enter the quasi-sliding mode within a finite number of steps.
In conclusion, it can be stated that the system (7) satisfies the conditions for discrete sliding mode reaching and will enter the quasi-sliding mode with quasi-sliding mode bandwidth centered around the sliding mode switching surface within a finite number of steps, denoted as k. The proof of Theorem 1 is thus completed. □
4. Simulation Experiment and Analysis
4.1. Related Introduction of Two-Joint Manipulator
The dual-joint robotic arm is a type of mechanical arm system with two joints, commonly employed in industrial automation and robotic applications. This robotic arm can move along two axes, providing enhanced flexibility in operation and capability for executing more complex tasks. Typically composed of a series of joints, links and actuators, dual-joint robotic arms are controlled via various transmission systems. This design allows the robotic arm to perform precise positioning, handling, and assembly tasks in diverse work environments, thereby maximizing production efficiency.
4.2. Simulation Parameter Setting
In order to validate the effectiveness of the proposed adaptive discrete integral terminal sliding mode control method, this section focuses on a two-joint manipulator as the research subject and conducts simulation verification of the proposed manipulator trajectory tracking control strategy. The specific parameters are as follows:
The parameters in the equation are shown as in Equations (58)–(60).
In this study, the parameters of the manipulator model are consistent with those in reference [5], where , , , . These parameters serve as the original parameters for the model discretization. The system is discretized using the sampling time to obtain the discretized parameters of the system (7).
During simulation, the desired trajectories for the two axes are denoted as and , with initial positions set at 0 and 1, respectively. Comparative experiments are conducted using the adaptive discrete integral terminal sliding mode controller, the discrete integral terminal sliding mode controller, and the classic discrete sliding mode controller.
The classical discrete sliding mode control scheme is as follows,
In the equation:
The simulation parameters are detailed in Table 1.

Table 1.
Simulation parameters.
4.3. Simulation Results and Analysis
Under the simulation conditions outlined in Section 4.2, the following ideal simulation results were obtained, wherein Figure 3 and Figure 4 illustrate the mechanical arm trajectory tracking performance of the three control methods: ADITSMC, DITSMC, and DSMC. Figure 5, Figure 6 and Figure 7 display the tracking errors of the mechanical arm for the three control methods. In Figure 8, Figure 9 and Figure 10, the control inputs for the mechanical arm under the three control methods, ADITSMC, DITSMC, and DSMC, are presented.
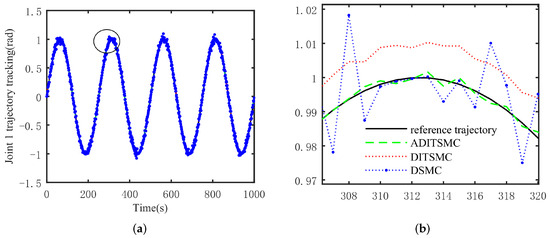
Figure 3.
Comparison of three control methods for joint 1 tracking. (a) Joint 1 tracking, (b) partial enlarged detail.
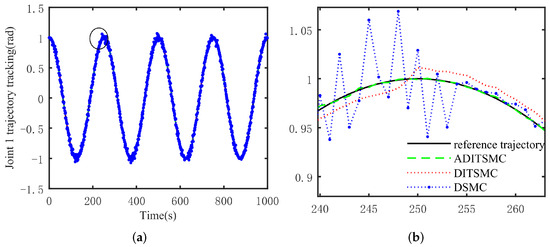
Figure 4.
Comparison of three control methods for joint 2 tracking. (a) Joint 2 tracking, (b) partial enlarged detail.
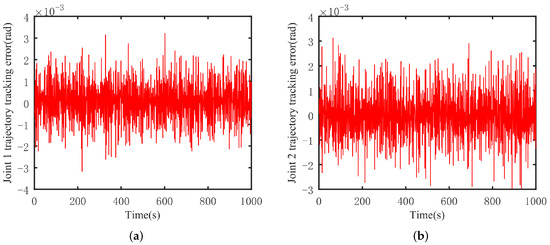
Figure 5.
ADITSMC robot arm trajectory tracking error. (a) Joint 1, (b) joint 2.
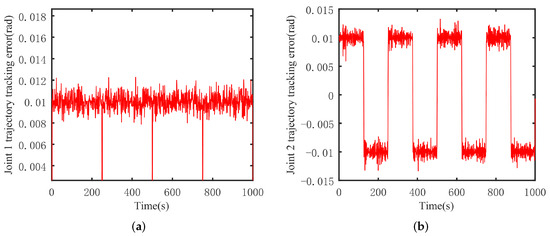
Figure 6.
DITSMC robot arm trajectory tracking error. (a) Joint 1, (b) joint 2.
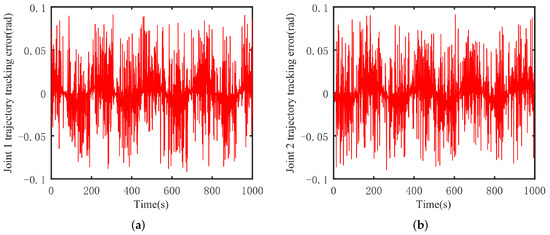
Figure 7.
DSMC robot arm trajectory tracking error. (a) Joint 1, (b) joint 2.
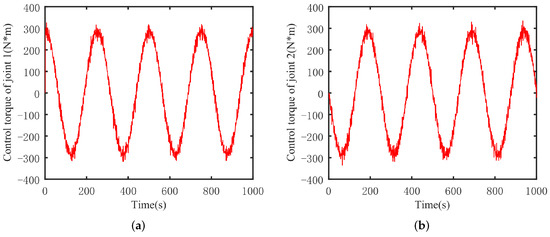
Figure 8.
ADITSMC robot arm control torque. (a) Joint 1, (b) joint 2.
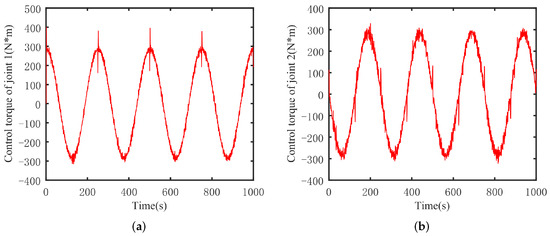
Figure 9.
DITSMC robot arm control torque. (a) Joint 1, (b) joint 2.
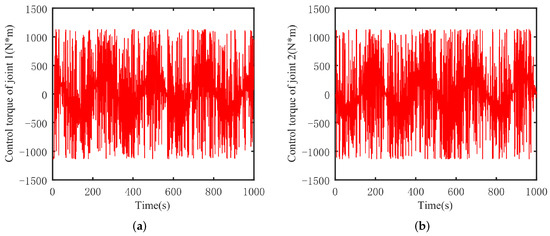
Figure 10.
DSMC robot arm control torque. (a) Joint 1, (b) joint 2.
From Figure 3, it can be observed that the control effectiveness of ADITSMC is superior to that of DITSMC, while the control effectiveness of the DSMC scheme exhibits significant oscillations. Specifically, within the time interval of [308 s, 320 s], noticeable jitter occurs in the trajectory tracking performance of DSMC. In contrast, the control effectiveness of ADITSMC closely approximates the reference trajectory compared to DITSMC. This trend is also evident from Figure 4. Concerning joint 2 of the mechanical arm, during the time span of [240 s, 260 s], ADITSMC continues to outperform DITSMC in terms of control effectiveness, whereas the DSMC control scheme shows pronounced oscillations. The graph prominently illustrates the severe oscillations in the DSMC control scheme, whereas the control effectiveness of DITSMC is relatively good but inferior to ADITSMC. Subsequent sections will present the trajectory tracking error situations for the three control schemes to validate the differences in control effectiveness as discussed earlier.
Based on Figure 5, Figure 6 and Figure 7, it can be observed that for both joint 1 and joint 2 of the mechanical arm, the control effectiveness of the ADITSMC scheme surpasses that of DITSMC, demonstrating its disturbance rejection capability. In the presence of white noise disturbances, the trajectory tracking error in the DITSMC control scheme is larger and exhibits significant oscillations compared to ADITSMC. As for the DSMC control scheme, the tracking errors are excessively large due to its pronounced oscillations, indicating significant tracking errors compared to the former two methods. Specifically, the trajectory tracking error of joint 1 in the DITSMC control scheme stabilizes only within the range of [0.005 rad, 0.015 rad], highlighting severe oscillations. This situation is more pronounced for joint 2, where the trajectory tracking error oscillates above and below zero, rendering the mechanical arm unable to function properly in practical engineering scenarios.
In contrast, the proposed ADITSMC control scheme exhibits no oscillations in control effectiveness. Even under white noise disturbances, it effectively reduces the trajectory tracking errors of joint 1 and joint 2 within the range of [−0.004 rad, 0.004 rad], showcasing faster convergence, robust disturbance rejection capabilities, and excellent control performance. These attributes make it suitable for practical engineering applications, as they ensure the mechanical arm operates smoothly without the risk of failures attributed to the control algorithm itself.
Based on Figure 8, Figure 9 and Figure 10, it is evident that the torque variation oscillation in the control scheme of DSMC is particularly severe. This is also the reason for the poor trajectory tracking performance of the DSMC scheme. Fundamentally, this issue arises from the insufficient convergence speed of the discrete sliding mode surface. On the other hand, while DITSMC enhances the convergence speed of the discrete sliding mode surface, some oscillations occur during trajectory transitions of the robotic arm, as evidenced in Figure 6. These oscillations are due to the oscillations of the sliding mode surface.
In contrast, for the ADITSMC designed in this study, whether it is joint 1 or joint 2 of the robotic arm, under white noise disturbances, the variation in its control torque is not as significant as that of DITSMC and DSMC. Furthermore, no oscillations occur during trajectory transitions. Therefore, compared to DITSMC and DSMC, ADITSMC exhibits better disturbance rejection capabilities, faster convergence speed, and effectively eliminates the influence of sliding mode oscillations.
In order to visually demonstrate the advantages of the proposed method in this paper, two metrics, namely, the mean square error (MSE) performance and the integral of the absolute force variation (IAFV), are employed to quantitatively evaluate the control methods presented in this study.
Firstly, and are expressed in matrix sub-element form as follows:
Next, the index functions of MSE and IAFV are given:
- (1)
- MSE
- (2)
- IAFV
The computation results of the two performance indices for each control method are presented in Table 2. Both performance indices of the ADITSMC control scheme outperform those of the DITSMC control scheme. This superiority is attributed to the larger tracking error and control force variation induced by the inherent chattering of DITSMC, while the classical discrete sliding mode control exhibits larger tracking errors during direction changes of the robotic arm due to its inferior convergence compared to other control schemes.

Table 2.
Performance indexes.
Finally, when the robotic arm faces more complex trajectories, the proposed control scheme’s trajectory tracking performance is verified. During simulation, the desired trajectories for the two axes are artificially set as . The remaining simulation conditions remain unchanged and the simulation results are as follows:
From Figure 11 and Figure 12, it can be observed that even when faced with more complex trajectories, ADITSMC can still track the reference trajectory with small tracking errors. Even with frequent changes in trajectory direction, the magnitude of errors does not exhibit significant abrupt changes. Therefore, it can be concluded that the proposed approach in this paper can still stably track the reference trajectory even when the system (7) is confronted with more complex trajectories.
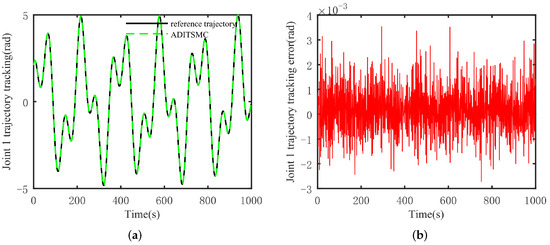
Figure 11.
Joint 1 tracking situation and error. (a) Tracking situation, (b) error.
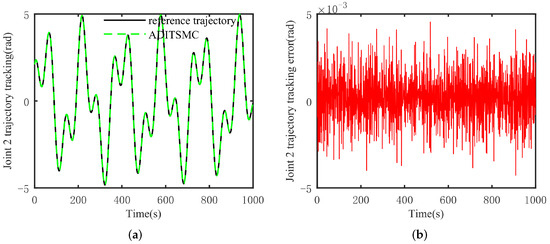
Figure 12.
Joint 2 tracking situation and error. (a) Tracking situation, (b) error.
5. Conclusions
This paper establishes a two-degree-of-freedom robotic arm model based on the characteristics of robotic arm dynamics, and proposes an adaptive discrete integral terminal sliding mode control method. In order to enhance the convergence speed of the sliding mode and reduce tracking errors, this method incorporates a sliding mode integral operator and a sliding mode terminal operator into the classical discrete sliding mode control. Given the variability of operational environments in practical robotic arm engineering, it is essential to strengthen the control algorithm’s disturbance rejection capability. Therefore, the combination of adaptive control and discrete integral terminal sliding mode control, along with the use of delay estimation to estimate system disturbances, not only improves the system’s robustness but also enhances the trajectory tracking accuracy of the robotic arm while reducing the occurrence of sliding mode chattering.
Comparative results with other control schemes demonstrate the advantages of the proposed control method as follows:
- (1)
- Achieving more precise trajectory tracking control than DITSMC and DSMC, with an error range within [−0.004 rad, 0.004 rad], ensuring the stable operation of the robotic arm in practical engineering applications.
- (2)
- After replacing the disturbances that the robotic arm may encounter in its operational environment with white noise, the control force variation becomes smaller and smoother compared to DITSMC and DSMC.
Subsequent research based on this paper will address the following:
- (1)
- Considering the multi-degree-of-freedom robotic arm model as the research object, the effectiveness of this control scheme in complex environments will be investigated.
- (2)
- Considering the incorporation of state observers for disturbance estimation, the current one-step delay estimation method in the algorithm may not fully estimate disturbances. Therefore, the use of state observers or disturbance observers for disturbance estimation will be explored to further improve the algorithm’s disturbance rejection capability.
Author Contributions
Conceptualization, J.X. and Z.S.; validation, Z.S.; formal analysis, F.X.; data curation, W.W.; writing—original draft, J.X.; writing—review and editing, Z.S.; supervision, Z.S. and W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Quzhou City Science and Technology Plan project (2023K263, 2023K265, 2023K045) and the General Research Project of the Zhejiang Provincial Department of Education (2023) (Y202353440, Y202353289).
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
Author Wenduo Wang was employed by the company China Railway Wuhan Bureau Group Co., Ltd. Wuhan EMU Depot. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Meng, G.; Han, L.L.; Zhang, C.F. Research progress and technical challenges of space robot. Acta Aeronaut. Astronaut. Sin. 2021, 42, 1–27. [Google Scholar]
- Nash, B.; Walker, A.; Chambers, T. A simulator based on virtual reality to dismantle a research reactor assembly using master-slave manipulators. Ann. Nucl. Energy 2018, 120, 1–7. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, Y.; Jiang, L.; Li, G.; Meng, J.; Huang, Y. Fault-tolerant dynamic control of a four-wheel redundantly-actuated mobile robot. IEEE Access 2019, 7, 157909–157921. [Google Scholar] [CrossRef]
- Sacchi, N.; Incremona, G.P.; Ferrara, A. Sliding mode based fault diagnosis with deep reinforcement learning add-ons for intrinsically redundant manipulators. Int. J. Robust Nonlinear Control 2023, 33, 9109–9127. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, W.; Lu, W. Fractional-order iterative sliding mode control based on the neural network for manipulator. Math. Probl. Eng. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Xia, K.; Gao, H.; Ding, L.; Liu, G.; Deng, Z.; Liu, Z.; Ma, C. Trajectory tracking control of wheeled mobile manipulator based on fuzzy neural network and extended Kalman filtering. Neural Comput. Appl. 2018, 30, 447–462. [Google Scholar] [CrossRef]
- Souzanchi-K, M.; Arab, A.; Akbarzadeh-T, M.R.; Fateh, M.M. Robust impedance control of uncertain mobile manipulators using time-delay compensation. IEEE Trans. Control Syst. Technol. 2017, 26, 1942–1953. [Google Scholar] [CrossRef]
- Reboucas Filho, P.P.; da Silva, S.P.P.; Praxedes, V.N.; Hemanth, J.; de Albuquerque, V.H.C. Control of singularity trajectory tracking for robotic manipulator by genetic algorithms. J. Comput. Sci. 2019, 30, 55–64. [Google Scholar] [CrossRef]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef]
- Hou, H.; Yu, X.; Xu, L.; Chuei, R.; Cao, Z. Discrete-time terminal sliding-mode tracking control with alleviated chattering. IEEE/ASME Trans. Mechatronics 2019, 24, 1808–1817. [Google Scholar] [CrossRef]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lü, J. Discrete-Time Fast Terminal Sliding Mode Control for Permanent Magnet Linear Motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Huang, X.; Dong, Z.; Zhang, F.; Zhang, L. Discrete-time extended state observer-based model-free adaptive sliding mode control with prescribed performance. Int. J. Robust Nonlinear Control 2022, 32, 4816–4842. [Google Scholar] [CrossRef]
- Zhai, J.; Xu, G. A novel non-singular terminal sliding mode trajectory tracking control for robotic manipulators. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 391–395. [Google Scholar] [CrossRef]
- Dachang, Z.; Baolin, D.; Puchen, Z.; Wu, W. Adaptive backstepping sliding mode control of trajectory tracking for robotic manipulators. Complexity 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- He, J.; Yang, X.; Zhang, C.; Liu, J.; Zhang, Q.; Chen, X. Tracking control via sliding mode for heavy-haul trains with input saturation. Meas. Control 2020, 53, 1720–1729. [Google Scholar] [CrossRef]
- Dong, H.; Yang, X.; Gao, H.; Yu, X. Practical terminal sliding-mode control and its applications in servo systems. IEEE Trans. Ind. Electron. 2022, 70, 752–761. [Google Scholar] [CrossRef]
- Xu, D.; Shi, Y.; Ji, Z. Model-Free Adaptive Discrete-Time Integral Sliding-Mode-Constrained-Control for Autonomous 4WMV Parking Systems. IEEE Trans. Ind. Electron. 2017, 65, 834–843. [Google Scholar] [CrossRef]
- Yuan, L.; Li, J. Consensus of discrete-time nonlinear multiagent systems using sliding mode control based on optimal control. IEEE Access 2022, 10, 47275–47283. [Google Scholar] [CrossRef]
- Kang, S.; Wu, H.; Yang, X.; Li, Y.; Yao, J.; Chen, B.; Lu, H. Discrete-time predictive sliding mode control for a constrained parallel micropositioning piezostage. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3025–3036. [Google Scholar] [CrossRef]
- Yao, X.; Park, J.H.; Dong, H.; Guo, L.; Lin, X. Robust adaptive nonsingular terminal sliding mode control for automatic train operation. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2406–2415. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, X.; Zhou, S.; Zhang, W.; Zhang, W.; Yang, S.; Liu, P.X. Extended state observer based adaptive backstepping nonsingular fast terminal sliding-mode control for robotic manipulators with uncertainties. Int. J. Control. Autom. Syst. 2022, 20, 2972–2982. [Google Scholar] [CrossRef]
- Bartoszewicz, A. Discrete-time quasi-sliding-mode control strategies. IEEE Trans. Ind. Electron. 1998, 45, 633–637. [Google Scholar] [CrossRef]
- Abidi, K.; Xu, J.X.; Xinghuo, Y. On the discrete-time integral sliding-mode control. IEEE Trans. Autom. Control 2007, 52, 709–715. [Google Scholar] [CrossRef]
- Xu, Q.S. Digital integral terminal sliding mode predictive control ofpiezoelectric-driven motion system. IEEE Trans. Ind. Electron. 2016, 63, 3976–3984. [Google Scholar] [CrossRef]
- Abidi, K.; Xu, J.X.; She, J.H. A discrete-time terminal sliding-mode control approach applied to a motion control problem. IEEE Trans. Ind. Electron. 2008, 56, 3619–3627. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).