Dynamic Reserve Calculation Method of Fractured-Vuggy Reservoir Based on Modified Comprehensive Compression Coefficient

Abstract

The low comprehensive compressibility coefficient characteristic of fracture-vuggy reservoirs often leads to imprecise dynamic reserve calculations. This study introduces a novel method for estimating dynamic reserves, which incorporates a modified comprehensive compressibility coefficient to enhance accuracy. This methodology has been applied to 23 wells in the Tahe Oilfield, resulting in error rates substantially lower than those associated with traditional techniques, thereby markedly enhancing the accuracy of dynamic reserve estimations. Specifically, for karst cave and fracture-vuggy reservoirs, the error rate in dynamic reserve calculations is reduced to under 10%, surpassing conventional methods by more than fivefold. In the case of fractured reservoirs, despite minor fluctuations in error rates due to stress sensitivity, diversion capacity, and channel variations, the proposed method still demonstrates a significant reduction in error rates compared to standard practices.

1. Introduction

Fractured and vuggy carbonate reservoirs, one of the major global sources of oil and gas production, are extremely heterogeneous, with distinct fluid distribution within the reservoir, intricate and variable fluid flow characteristics, and numerous uncertainties regarding reservoir space, fluid distribution, the oil–water interface, etc., which complicate the evaluation of the reservoir’s dynamic reserves [1,2].

The computation of dynamic reserves in fracture-cave oil reservoirs predominantly adheres to the material balance theory, initially formulated by R.J. Schilthuis in 1936 based on the law of conservation of mass and subsequently linearized by D.H. Havlena and A.S. Odeh, which has since been widely adopted for reserve estimation, analysis of driving mechanisms, and prediction of reservoir dynamics [3,4,5]. Research conducted with the Tahe Oilfield as a case study has introduced pore volume parameters specific to the heterogeneous fracture-vuggy carbonate reservoirs. Linear regression is utilized to estimate the reserves of a typical block [3,4,5]. The material balance principle is utilized to derive an equation that captures stress sensitivity, such as fracture porosity and permeability, by incorporating the elastic properties of the matrix and fractures [6,7,8,9]. The dynamic reserve calculation method is refined to align with the distribution and fluid properties of fracture-vuggy carbonate reservoirs [10,11,12]. The impact of fluid characteristics on cavity and seam elements leads to the identification of four driving types, with corresponding material balance equations for each type [13,14,15,16]. The curve’s slope, intercept, and inflection point are used to analyze reservoir size, pressure loss before water injection, wellbore conditions, and the potential for a secondary reservoir set [11,17,18,19,20,21]. The Tahe Oilfield’s water injection method for oil production is applied to establish the relationship between water injection and pressure, using the pressure change law from wellhead to bottom-hole flow pressure to formation pressure, to calculate controlled reserves for individual wells [22,23]. The fracture-vuggy carbonate reservoir is segmented into units based on the similarity principle, and dynamic reserves are calculated for each reservoir at various stages [24,25,26]. The D type water drive characteristic curve is derived from the relationship between the oil–water relative permeability ratio and water saturation, with the linear proportional coefficient inversely related to geological reserves [27,28]. The Blasingame method and the flow material balance method are used to study reservoir reserves under quasi-steady water invasion, proposing a method for dynamic reserves and water size evaluation based on the dynamic identification of water invasion [29,30,31,32,33]. A dynamic reserve calculation method for single-cavity and fracture-cavity reservoirs, considering formation water and fracture elastic energy, is established using the water injection indicator curve method and validated with production data from over 30 wells [34,35]. Based on total production reserves of well groups, cumulative oil production before gas injection, plane sweep coefficient, irregular pattern shape factor correction, and longitudinal production degree, a calculation method for gas-driven reserves of well groups and well groups under various karst backgrounds is developed [36,37]. The dynamic reserves of fracture-cavity type reservoirs in the Tahe Oilfield, under different fracture-cavity combinations and the influence of bottom water, are calculated and analyzed using production and water injection indicator curves, with the changes in reserves during multiple rounds of production and water injection demonstrated by high-pressure physical models [38,39].

Numerous techniques have been put forth by researchers to determine the dynamic reserves of fracture-vuggy carbonate reservoirs, but the value of the comprehensive compressibility coefficient has not been sufficiently investigated. In 1991, Kemeny introduced the relationship between porosity and permeability into the calculation of pore volume compressibility coefficient, deduced the pore volume compressibility coefficient, and proposed the influence of porosity and permeability on pore volume compressibility coefficient. However, due to the strong heterogeneity of fracture-cave distribution in fractured reservoirs, this method is not fully applicable to fractured reservoirs [40]. In 2009, Li proposed a new method for calculating dynamic reserves using water injection and oil replacement data for fracture-vuggy reservoirs, which requires oil wells to be drilled to the highest part of the karst cave to ensure that all reservoir crude oil is replaced, so as to determine the dynamic reserves and backcalculate the comprehensive compressibility coefficient. The limitations of this method are that there are fewer wells that can produce all the crude oil, and the production cycle is too long [41]. In 2018, Zheng established a comprehensive compressibility coefficient formula for fracture-vuggy reservoirs, but only directly added the compressibility coefficients of rock and crude oil, and did not consider the contribution ratio of rock and fluid elastic energy [42]. In 2019, Liu studied the effects of high temperature and temperature cycle changes of steam injection and production on the comprehensive compressibility coefficient of Bohai heavy oil reservoir. However, the research object was loose sandstone, and the main variable was temperature, which was not suitable for fracture-vuggy reservoirs [43]. In 2022, Wu solved the comprehensive compressibility coefficient of fracture-vuggy reservoirs through the elastic yield of water injection production to calculate the dynamic reserves. But this method did not carry out targeted research on different types of fracture-vuggy structures [44].

Therefore, the previous research on the comprehensive compressibility coefficient of fracture-vuggy reservoirs is based on the traditional reservoir engineering methods, but the fracture-cave structure and water injection development process of fracture-vuggy reservoirs are not fully considered, and the comprehensive compressibility coefficient under different fracture-vuggy structures and water–oil volume ratios should be different. In contrast to conventional methodologies, this research presents a novel strategy that uses production data to improve the comprehensive compressibility coefficient and, as a result, improves the accuracy of dynamic reserve calculations for fractured reservoirs.

2. Modification of Comprehensive Compression Coefficient

Building upon the material balance theory, predecessors have established methods for calculating the dynamic reserves of fracture-vuggy reservoirs using production and water injection indicator curves, derived from field production dynamic monitoring data. The comprehensive nature of this data has led to its widespread application.

The material balance equation represents a zero-dimensional model, which disregards flow dynamics; thus, it is unrelated to pipe flow and seepage. The oil reservoir in question is not degassed and lacks a gas cap. In scenarios where water encroachment and water injection occur concurrently, the material balance equation can be formulated as follows [3,4,5]:

$$N_{\mathrm{p}}{B}_{\mathrm{o}}+W_{\mathrm{p}}{B}_{\mathrm{w}}=N{B}_{\mathrm{oi}}{C}_{\mathrm{t}}\left(P_{\mathrm{i}}-P\right)+W_{\mathrm{e}}{B}_{\mathrm{w}}+W_{\mathrm{i}}{B}_{\mathrm{w}}$$

(1)

where N_p represents the cumulative oil production in units of 10⁴ m³; B_o denotes the volume factor of crude oil, which is dimensionless; W_p signifies the cumulative water production, also in units of 10⁴ m³; B_w is the volume factor for formation water, dimensionless; N stands for dynamic reserves, expressed in 10⁴ m³; B_oi is the initial volume factor of crude oil, dimensionless; C_t is the comprehensive reservoir compressibility coefficient, with units of 10⁻⁴ MPa⁻¹; P_i is the initial reservoir pressure in MPa; P indicates the current reservoir pressure, also in MPa; We is the volume of water intrusion, in units of 10⁴ m³; and W_i is the volume of water injected, again in units of 10⁴ m³.

The production and water injection indicator curves represent the simplified versions of the mass balance equation, with expressions described below:

$$N_{\mathrm{p}}{B}_{\mathrm{o}}+W_{\mathrm{p}}{B}_{\mathrm{w}}=N{B}_{\mathrm{oi}}{C}_{\mathrm{t}}\left(P_{\mathrm{i}}-P\right)$$

(2)

$$W_{\mathrm{i}}{B}_{\mathrm{w}}=N{B}_{\mathrm{oi}}{C}_{\mathrm{t}}\left(P-P_{\mathrm{i}}\right)$$

(3)

Production and water injection indicator curves are constructed using formulas (2) and (3), based on the available data. The slopes of these curves are determined as follows:

$$\begin{array}{l}\mathrm{Production} \mathrm{indicator} \mathrm{curve} \mathrm{slope}:K_{\mathrm{p}}=\frac{B_{\mathrm{o}}}{N{B}_{\mathrm{oi}}{C}_{\mathrm{t}}};\\ \mathrm{Water} \mathrm{injection} \mathrm{indicator} \mathrm{curve} \mathrm{slope}:K_{\mathrm{w}}=\frac{B_{\mathrm{w}}}{N{B}_{\mathrm{oi}}{C}_{\mathrm{t}}}\end{array}$$

(4)

The slope encompasses dynamic reserves N, facilitating the calculation of deployed reserves during production and swept reserves throughout the water injection process:

$$\mathrm{Productive} \mathrm{reserves}:N=\frac{B_{\mathrm{o}}}{K_{\mathrm{p}}{B}_{\mathrm{oi}}{C}_{\mathrm{t}}};\mathrm{Waterflood} \mathrm{swept} \mathrm{reserve}:N=\frac{B_{\mathrm{w}}}{K_{\mathrm{w}}{B}_{\mathrm{oi}}{C}_{\mathrm{t}}}$$

(5)

Equation (5) demonstrates that the comprehensive reservoir compressibility coefficient (C_t) is an indispensable parameter for calculating dynamic reserves, with its precision directly impacting the reliability of the outcomes. However, the application of two standard curves typically considers only the compressibility coefficient of crude oil (C_o), equating C_t with C_o. This approach overlooks that the compressibility coefficients of formation water and reservoir rock are not significantly different from that of crude oil. An underestimation of C_t can lead to an overestimation of dynamic reserves. Therefore, it is necessary to adjust the comprehensive compressibility coefficient accordingly.

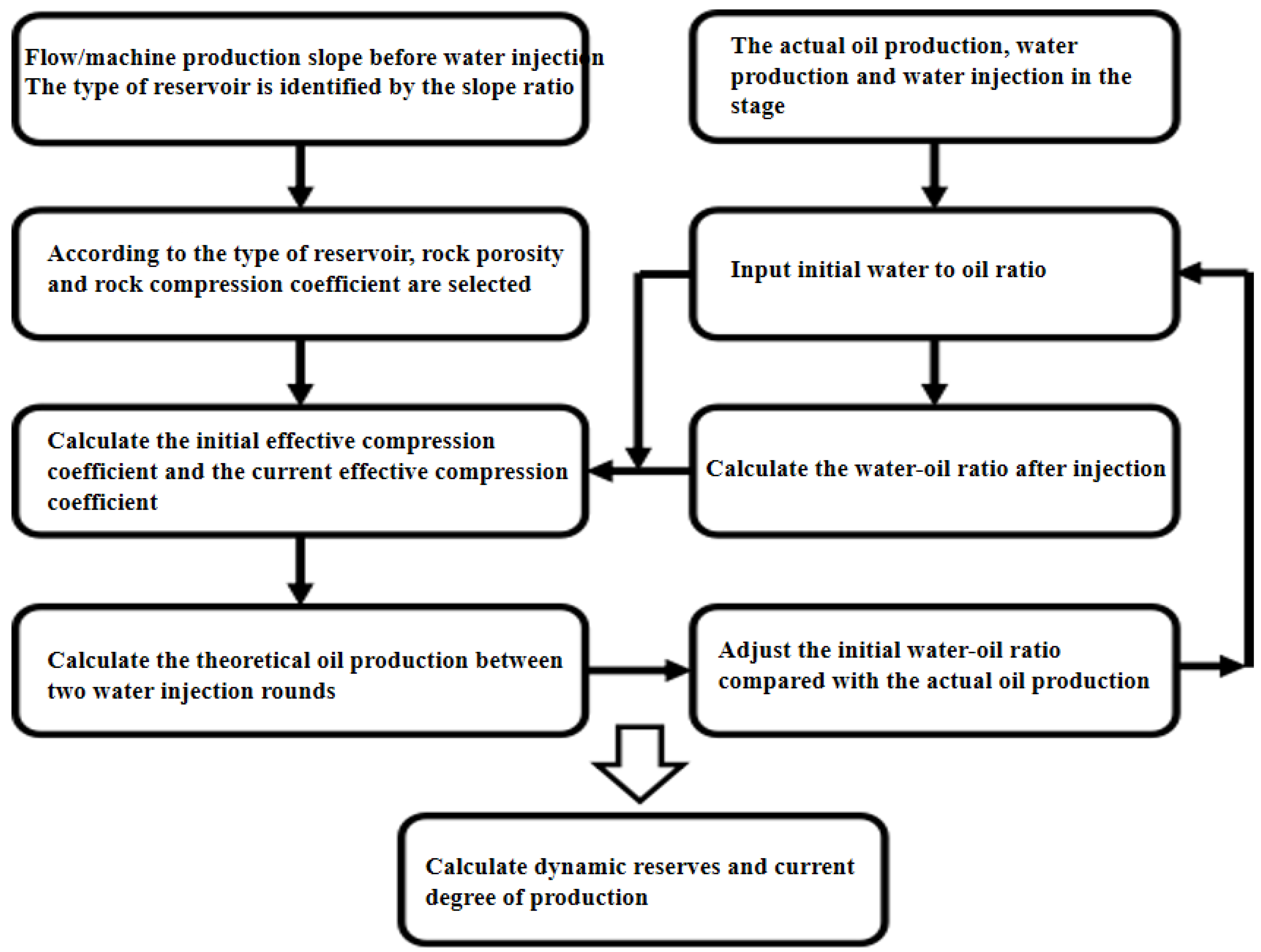
2.1. Main Research Methods

The calculation of dynamic reserves of fracture-vuggy reservoir by modifying comprehensive compressibility includes three steps:

(1)

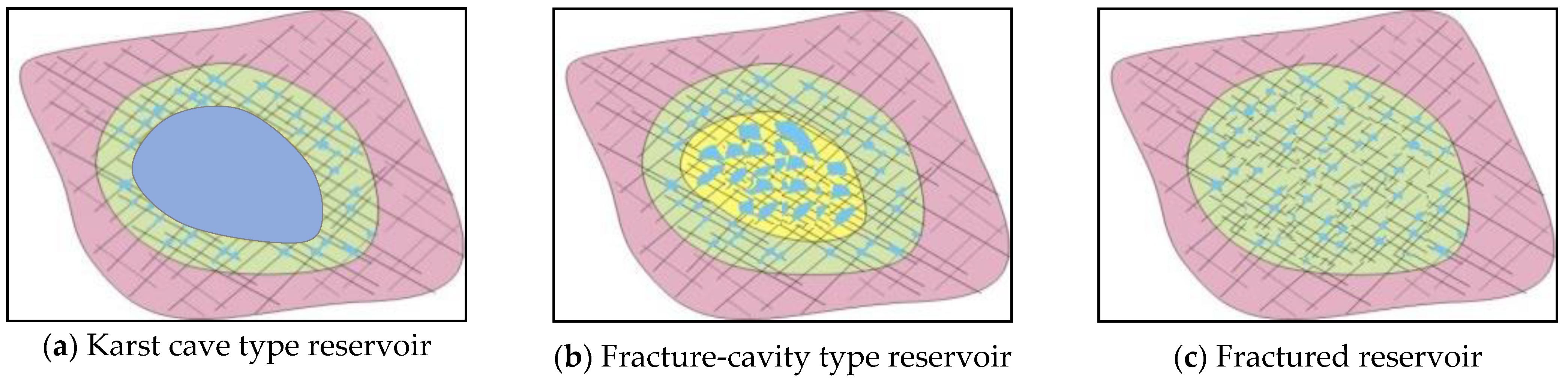
Utilizing production indicator and water injection curves, the reservoir group type is determined as follows: karst cave type exhibits minimal changes in slope across multiple water injection cycles and a stable supply radius; fracture-vuggy type shows significant slope variation and an increased supply radius with each cycle; and fractured type experiences substantial reserve loss with each additional water injection cycle, attributed to fracture closure.

(2)

The reservoir’s comprehensive compression coefficient (C_t) is meticulously determined by correlating rock porosity with the dynamic water–oil ratio, which is derived from the initial water–oil ratio data and adjusted in response to variations in oil and water production rates.

(3)

By constraining the water–oil ratio with stage oil production data and calculating the relative error rate and dynamic reserves, the current degree of extraction is analyzed, involving the input of stage oil production data, fitting theoretical stage oil production volumes for various initial water–oil ratios, and refining the initial water–oil ratio based on the relative error rate of stage oil production, followed by computing dynamic reserves under low error rate conditions.

The dynamic reserve calculation method described herein, grounded in the three aforementioned steps, is depicted in Figure 1.

2.2. Classification of Reservoir Types

Drawing from the early development experience, fracture-cavity interplay, and production dynamics of the Tahe Oilfield, the fracture-cavity carbonate reservoirs are categorized into three types: the first type, characterized by significant leakage and blowout during drilling, maintains a relatively stable volume performance during both production and water injection, with a consistent oil blowout radius between the spontaneous flow and mechanical production periods; the second type exhibits reduced leakage and blowout radius during drilling, with gradual pressure transmission and a substantially larger oil blowout radius during mechanical production; and the third type features an interwoven development and morphology that bridges the characteristics of the first two. The structures of these reservoir types are depicted in Figure 2 and Figure 3.

The analysis of production data from 23 oil wells across the 10th and 12th districts of Tahe Oilfield, based on the slope ratio of the production indicator curve between the spontaneous flow and mechanical production periods, delineates the boundary ranges for karst cave, fracture-cave, and fractured reservoirs, as depicted in

Table 1. Statistical results of oil well production data.

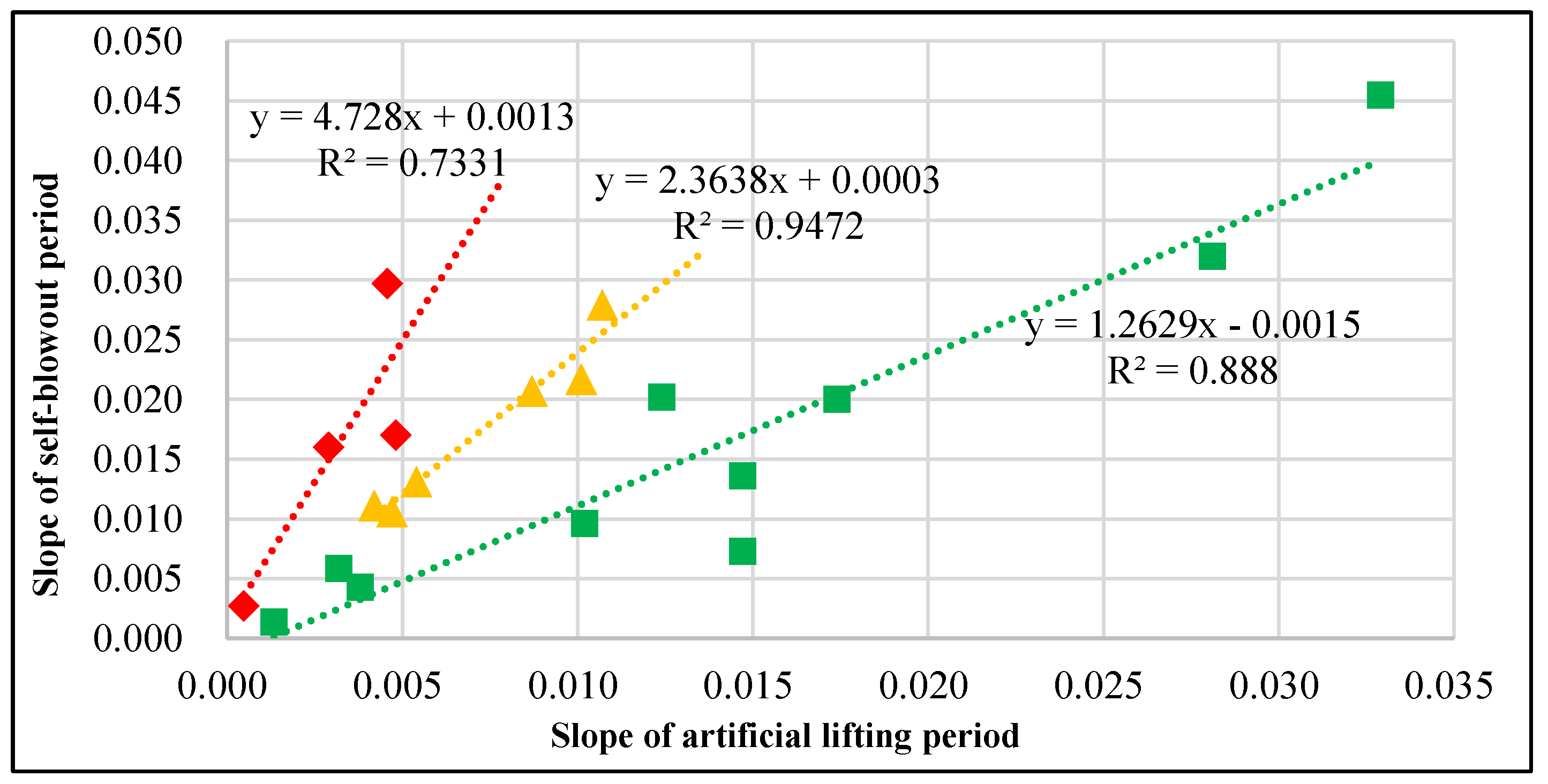
Type of Reservoir	Well Name	Self-Blowout Period Slope	Artificial Lifting Period Slope	Slope Ratio
Karst cave type reservoir	TH1	0.0136	0.0147	0.93
	TS1	0.0200	0.0174	1.15
	TH2	0.0202	0.0124	1.63
	TH3	0.0043	0.0038	1.13
	TH4	0.0059	0.0032	1.84
	TH5	0.0320	0.0281	1.14
	AD1	0.0096	0.0102	0.94
	TH6	0.0221	0.0485	0.46
	TH7	0.0073	0.0147	0.5
	TH8	0.0014	0.0013	1.02
	TH9	0.0455	0.0329	1.38
	Average			1.10
Fracture-cavity type reservoir	TH10	0.0207	0.0087	2.38
	T1	0.0622	0.0214	2.91
	TH11	0.0111	0.0042	2.64
	TH12	0.0217	0.0101	2.15
	TH13	0.0106	0.0047	2.26
	TH14	0.0279	0.0107	2.61
	TH15	0.0131	0.0054	2.43
	Average			2.48
Fractured reservoir	TH16	0.0160	0.0029	5.52
	TH17	0.0027	0.0005	5.66
	TH18	0.0170	0.0048	3.53
	TH19	0.0297	0.0046	6.5
	TH20	0.0515	0.0170	3.03
	Average			4.85

and Figure 4:

The statistical analysis of oil well production data presented in Table 1 reveals distinct patterns in the spontaneous flow slope, mechanical production slope, and their ratios for karst cave, fracture-cave, and fractured reservoirs: (1) karst cave type exhibits a slope ratio below 2, with an average of 1.10, and a relatively constant pressure relief radius; (2) fracture-cave type shows a slope ratio typically ranging from 2 to 3, averaging 2.48, with an expanded pressure relief radius during the mechanical production phase; and (3) fractured type demonstrates a slope ratio generally exceeding 3, averaging 4.85, with a continuously expanding supply radius throughout the mechanical production phase.

The distinct porosity and compressibility of the three reservoirs are discernible through the analysis of their production profiles. The classification of reservoir groups is determined by the range of the slope ratio of the production indicator curve between the mechanical extraction and spontaneous flow phases, followed by a targeted modification of the comprehensive compression coefficient.

2.3. Compression Coefficient Correction

Utilizing the empirical formula for carbonate rock compressibility and porosity under strata conditions (60 MPa), established by Zheng [45,46] based on 65 rock sample test data (as depicted in Figure 5), the porosity and rock compressibility coefficients of the three types of reservoirs were calibrated.

The rock compression coefficient is calibrated using the empirical formula shown in Figure 5: the porosity of the karst cavern reservoir is large (typically greater than 50%), and the rock compression coefficient tends to 0; the porosity of the fracture-cavity reservoir is 15–25%, and the rock compression coefficient is 3.5 × 10⁻⁴ MPa⁻¹; the rock’s compression co-efficient is 6.8 × 10⁻⁴ MPa⁻¹, and the porosity of the fractured reservoir is very low at 5%. It should be noted, nonetheless, that further core experiments are required because the calibration approach cannot accurately reflect the actual conditions of Tahe Oilfield due to the small number of experiments.

Drawing upon the calibrated rock compression coefficients, the comprehensive reservoir compression coefficient is accordingly revised.

$$C_{\mathrm{t}}=\varphi C_{\mathrm{o}}+\varphi R{C}_{\mathrm{w}}+\left(1-\varphi \right)\left(1+R\right)C_{\mathrm{p}}$$

(6)

where Φ represents porosity in percent (%); C_o is the compressibility coefficient for crude oil, which is generally 12 × 10⁻⁴ MPa⁻¹ for the heavy oil in the Tahe Oilfield; R denotes the water–oil ratio, a dimensionless quantity; C_w is the compressibility coefficient for formation water, typically around 6 × 10⁻⁴ MPa⁻¹ in the Tahe region; and C_p is the compressibility coefficient for rock, which varies with porosity as described in

Table 2. Calibration of rock compressibility in fracture-cavity reservoir.

Reservoir type	Karst Cave Reservoir	Fracture-Cavity Reservoir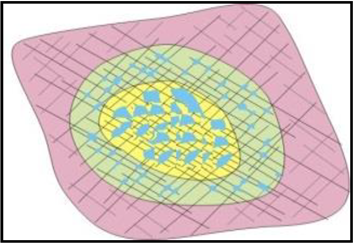	Fractured reservoir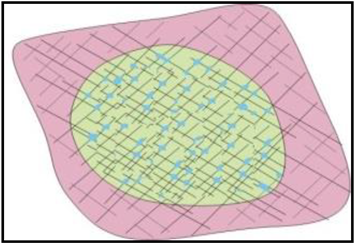
Porosity $\varphi$/%	50	20	5
Rock compressibility Cp/10−4 MPa−1	Tends to 0	3.5	6.8

, with units of 10⁻⁴ MPa⁻¹.

The comprehensive compressibility coefficient expression in Equation (6) can be refined according to the different types of reservoirs as follows:

$$C_{\mathrm{t}}=\left\{\begin{array}{c}6\times {10}^{-4}+3\times {10}^{-4}R\\ 5.2\times {10}^{-4}+4\times {10}^{-4}R\\ 7.06\times {10}^{-4}+6.76\times {10}^{-4}R\end{array}\right.\begin{array}{c}\mathrm{Cavern} \mathrm{type}\\ \mathrm{Vug} \mathrm{type}\\ \mathrm{Fracture} \mathrm{type}\end{array}$$

(7)

Equation (7) elucidates that the comprehensive compressibility coefficient correlates with the oil–water ratio within the reservoir. Fluctuations in this ratio, resulting from oil and water production alongside water injection, are observed to directly influence the coefficient’s variation, as shown in Figure 6.

2.4. Calculation of Dynamic Reserves

When employing Equation (5) to calculate the mobilized reserves during production or the extent of water injection based on production or injection data, the use of the revised comprehensive compressibility coefficient necessitates the initial determination of the reservoir’s initial oil–water ratio (R₀). Subsequently, the current oil–water ratio (R₁) is computed based on the cumulative oil production, water production, and water injection volumes:

$$R_1=\frac{\left(R_{0}N+W_{\mathrm{i}}-W_{\mathrm{p}}\right)B_{\mathrm{w}}}{N{B}_{\mathrm{oi}}-N_{\mathrm{p}}{B}_{\mathrm{o}}}$$

(8)

This research ascertains the precise oil–water ratio by initially hypothesizing a ratio, which is then used in Equation (8) to ascertain the current ratio. The initial (C_t0) and current (C_t1) comprehensive compressibility coefficients are derived from Equation (7). These coefficients are subsequently applied in Equation (5) to determine the variance between initial and current reserves (ΔN) or the change in formation water volumes pre- and post-water injection (ΔW). An error rate (ε) is established for precision control:

$$\begin{array}{l}\Delta N=\frac{B_{\mathrm{o}}}{K_{\mathrm{p}}{B}_{\mathrm{oi}}{C}_{\mathrm{t}0}}-\frac{B_{\mathrm{o}}}{K_{\mathrm{p}}{B}_{\mathrm{oi}}{C}_{\mathrm{t}1}}\\ \Delta W=\frac{R_1{B}_{\mathrm{o}}}{K_{\mathrm{p}}{B}_{\mathrm{oi}}{C}_{\mathrm{t}1}}-\frac{R_0{B}_{\mathrm{o}}}{K_{\mathrm{p}}{B}_{\mathrm{oi}}{C}_{\mathrm{t}0}}\end{array}$$

(9)

$$\epsilon =\left\{\begin{array}{c}\begin{array}{cc}\frac{\Delta N-N_{\mathrm{p}}}{N_{\mathrm{p}}}\times 100\%& \mathrm{Oil} \mathrm{production} \mathrm{error} \mathrm{rate}\end{array}\\ \begin{array}{cc}\frac{\Delta W-W_{\mathrm{i}}}{W_{\mathrm{i}}}\times 100\%& \mathrm{Error} \mathrm{rate} \mathrm{of} \mathrm{water} \mathrm{injection}\end{array}\end{array}\right.$$

(10)

In the production process, the reserve difference (ΔN) is compared against the actual stage oil production (N_p). If the discrepancy exceeds the acceptable threshold, the initial water–oil ratio (R₀) is adjusted, and iterative calculations for the current water–oil ratio (R₁) and ΔN are performed until the error meets the specified criteria. The same procedure is followed during water injection, where the water volume difference (ΔW) is compared with the actual stage water injection volume (W_i), and adjustments to R₀ are made as needed, with subsequent iterations for R₁ and ΔW until the error is within the acceptable range. This methodology ensures that the actual oil production or water injection volumes are accurately calibrated to the changes in the reservoir’s oil–water volume, yielding dynamic reserves that closely match the production data.

3. Application for Calculating Dynamic Reserves of Fracture-Vuggy Reservoir

3.1. Well Introduction

This study analyzes 23 production wells in the Tahe Oilfield, each situated within the Ordovician Yijianfang Formation and spanning depths of 6000 to 6500 m. Characterized as heavy oil wells, they exhibit crude oil viscosities ranging from 150 to 200 mPa·s under reservoir conditions. The wells are predominantly karst cave reservoirs, with karst formations accounting for more than 70% of the well structure. A strong association is observed between well types and fault lines, with karst caves primarily developing along faults, particularly at intersections. Karst cave and fracture-cave wells are often located within the same fault zones, while fractured wells are typically found at their peripheries.

3.2. Karst Cave Reservoir

Well TH7 serves as a case study, demonstrating a self-blowout/artificial lifting slope ratio of 0.5 after more than thirty water injection cycles. With an initial water–oil ratio set to zero, the error rate between the third and twentieth cycles was recorded at −3.8%. Employing the comprehensive compressibility coefficient, the dynamic reserve was calculated as 135,900 tons. To date, the well has produced 67,000 tons of oil, achieving a recovery rate of 49.3%, consistent with the expectation of higher recovery rates in karst cave storage complexes.

3.3. Fracture-Cave Reservoir

Well TH15, having undergone over 20 water injection rounds, exemplifies a self-blowout/artificial lifting slope ratio of 2.43. An initial water–oil ratio of 1.2 resulted in a 1.6% error rate across the first to fourteenth rounds, with the aggregate near-well and far-well reserves totaling 152,300 tons. To date, the well has achieved a 26.9% recovery rate, producing 40,000 tons of oil. Notably, the near-well reserves stand at 62,700 tons, with a recovery degree of 65.2% for the near-well area.

3.4. Fractured Type Reservoir

Well TH18 exemplifies a self-blowout/artificial lifting slope ratio of 3.53, with over 10 water injection rounds conducted. During the initial to ninth rounds, an initial water–oil ratio of 0.9 resulted in a 9.7% error rate, and the dynamic reserves in the well’s vicinity were estimated at 192,400 tons. To date, the well has produced 21,000 tons of oil, with a recovery rate of 11.3%, consistent with the low recovery rates expected from fractured reservoirs.

3.5. Error Analysis

The efficacy of this methodology is substantiated through a comparison with the conventional approach, which assumes a constant comprehensive compressibility coefficient. (

Table 3. Error comparison between actual oil production and theoretical oil production (unit: ten thousand tons) by different calculation methods.

Type of Reservoir	Well Name	Actual Oil Production	The Comprehensive Compression Coefficient is 0.001 MPa−1		The Comprehensive Compression Coefficient is 0.00182 MPa−1		Method of Calculation in This Paper
			The Oretical Oil Production	Error/%	The Oretical Oil Production	Error/%	The Oretical Oil Production	Error/%	Dynamc Reserves
Karst cave type	TH1	2.5	1.3	47.7	0.7	71.2	2.45	2.0	6.7
	TS1	1.16	1.7	47.8	0.9	18.7	1.13	2.2	3.8
	TH2	0.9	0.9	3.5	0.5	46.9	0.86	4.2	4.9
	TH3	4.9	10.6	100.0	5.8	19.2	5.02	2.4	12.4
	TH4	1.2	1.7	42.5	0.9	21.7	1.21	0.9	12.1
	TH5	2.5	0.5	81.9	0.2	90.0	2.53	1.4	3.4
	AD1	1.1	0.5	53.1	0.3	74.2	1.22	10.7	10.3
	TH6	1.3	0.5	60.0	0.3	78.0	1.26	3.4	4.5
	TH7	2.9	1.2	58.7	0.7	77.3	2.79	3.8	13.6
	TH8	1.7	6.3	100.0	3.5	100.0	1.72	1.1	19.8
	TH9	0.21	0.3	34.3	0.2	26.1	0.22	2.5	1.7
Fracture-cavity type	TH10	3.67	4.6	25.3	2.5	31.1	3.91	6.6	9.8
	T1	0.59	0.9	57.2	0.5	13.5	0.60	1.9	3.0
	TH11	1.32	1.1	18.7	0.6	55.3	1.33	0.8	11.2
	TH12	1.14	1.4	18.8	0.7	34.7	1.19	4.7	8.7
	TH13	1.33	1.1	19.2	0.6	55.6	1.33	0.2	26.4
	TH14	0.9	0.6	28.5	0.4	60.7	0.89	1.4	4.9
	TH15	1.4	0.3	77.7	0.2	87.7	1.54	1.6	6.3
Fractured type	TH16	2.69	2.2	17.3	1.2	54.5	2.74	10.6	42.4
	TH17	9.5	21.7	100.0	12.0	25.9	9.63	25.0	16.4
	TH18	1.6	1.7	8.9	1.0	40.1	1.61	9.7	19.2
	TH19	0.7	0.4	44.2	0.2	69.3	0.65	6.7	5.6
	TH20	0.2	0.9	100.0	3.2	100.0	0.21	4.4	1.4

).

The results indicate a substantial reduction in the error rate for dynamic reserve calculations using the modified comprehensive compressibility coefficient, particularly for karst cave and fracture-cave reservoirs where the error rate is minimal (below 10%). In contrast, fractured reservoirs exhibit greater error fluctuations due to influences of stress sensitivity, flow conductivity, and variations in near-well and far-well channeling.

4. Conclusions

(1)

This study introduces a novel method for calculating dynamic reserves in fracture-cave reservoirs, predicated on an amended comprehensive compressibility coefficient. The approach commences with the identification of reservoir types through the analysis of production data, followed by the precise calibration of rock compressibility coefficients tailored to each type. Subsequently, the method employs the relative error rate of cumulative oil production to constrain the water–oil ratio of the reservoir, which in turn refines the comprehensive compressibility coefficient for dynamic reserve computation. This methodology enhances both the accuracy and reliability of reserve estimations.

(2)

The application of this refined methodology to the dynamic reserve calculations of 23 wells in the Tahe Oilfield has yielded a notably reduced error rate compared to existing methods, thereby enhancing the accuracy of these calculations. Specifically, for karst cave and fracture-vuggy reservoirs, the error rate for dynamic reserve estimation is below 10%, surpassing the conventional method’s error rate by over fivefold. In fractured reservoirs, while the error rate experiences minor fluctuations due to stress sensitivity, diversion capacity, and channel variation, it remains significantly lower than that of traditional methods.