The DMF: Fault Diagnosis of Diaphragm Pumps Based on Deep Learning and Multi-Source Information Fusion
Abstract
1. Introduction
2. Basic Theory
2.1. Signal Demodulation Algorithm DPCA
- (a)
- Time–frequency distribution matrix
- (b)
- Covariance matrix
- (c)
- Eigenvalue decomposition
- (d)
- Principal component reconstruction
2.2. Deep Learning Models
2.2.1. Auto Encoder (AE)
2.2.2. CNN
2.2.3. SVM
2.3. Model Evaluation Indicators
2.4. DSET
- (a)
- Identification framework
- (b)
- Trust distribution
- (c)
- Synthesis rules
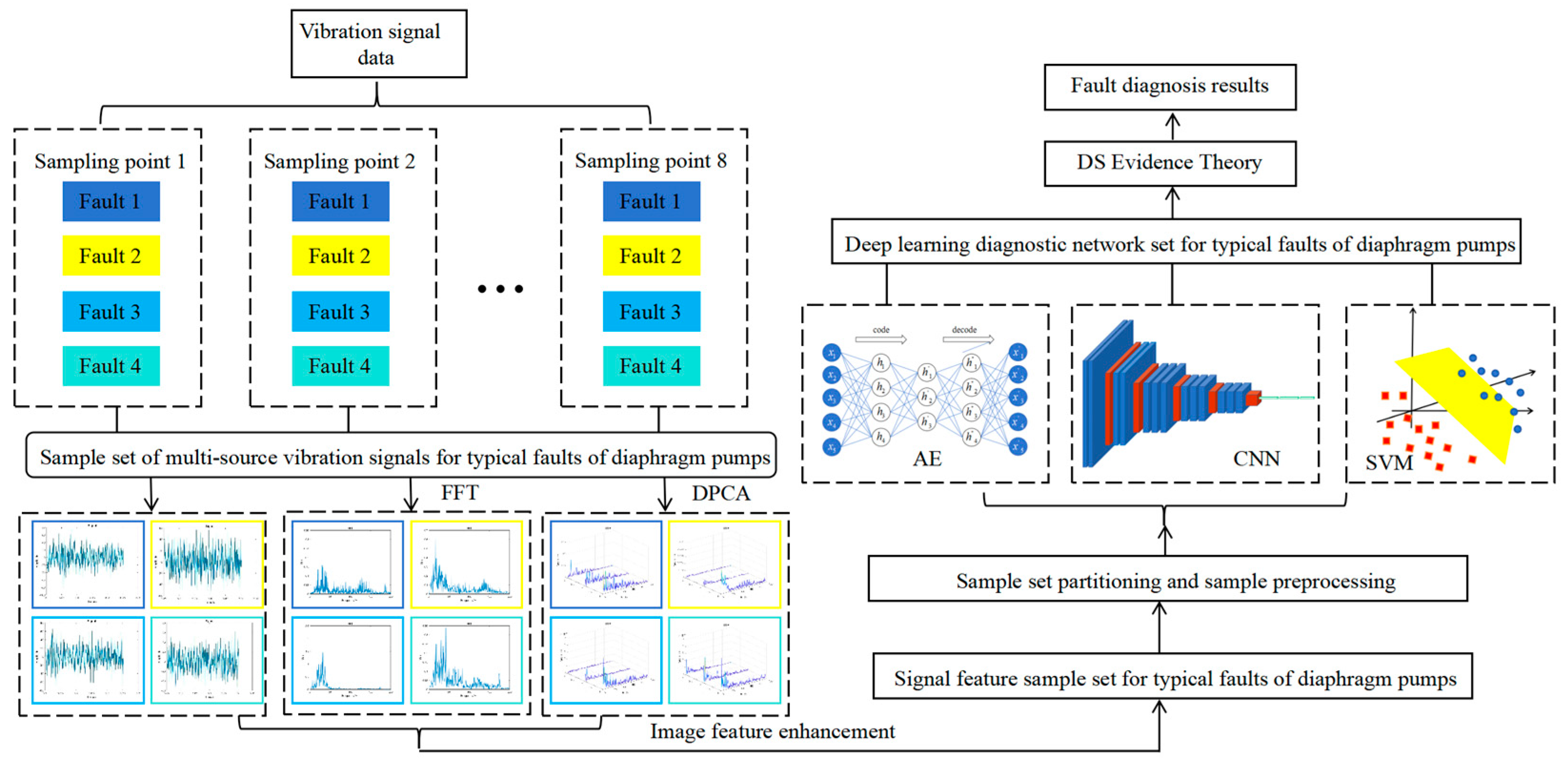
3. Experiments
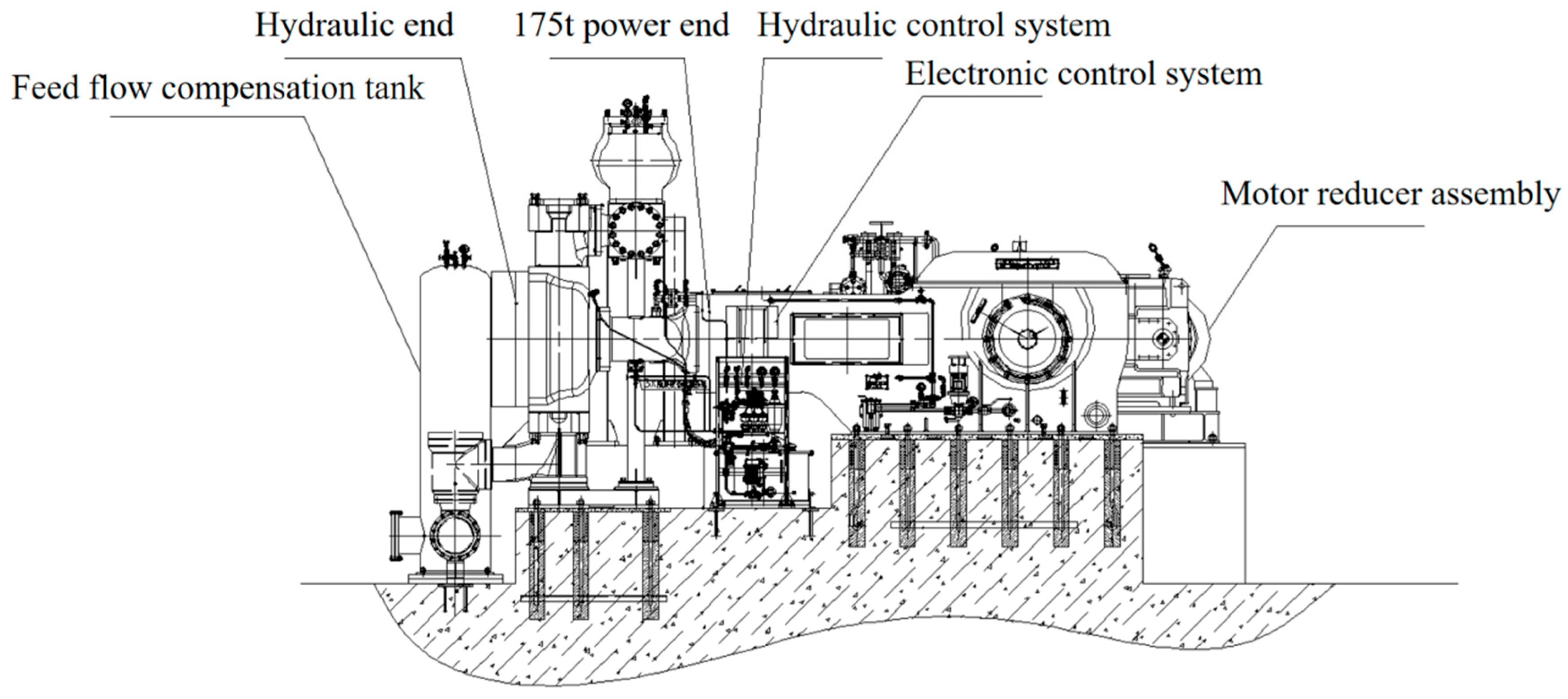
3.1. Experimental Setup
3.2. Fault Setting
- (a)
- Lubrication Pump Failure
- (b)
- Check Valve Failure
- (c)
- Diaphragm Degradation
- (d)
- Gearbox Cooling Fan Fault
3.3. Data Processing
3.4. Parameter Settings
4. Model Fusion and Discussion
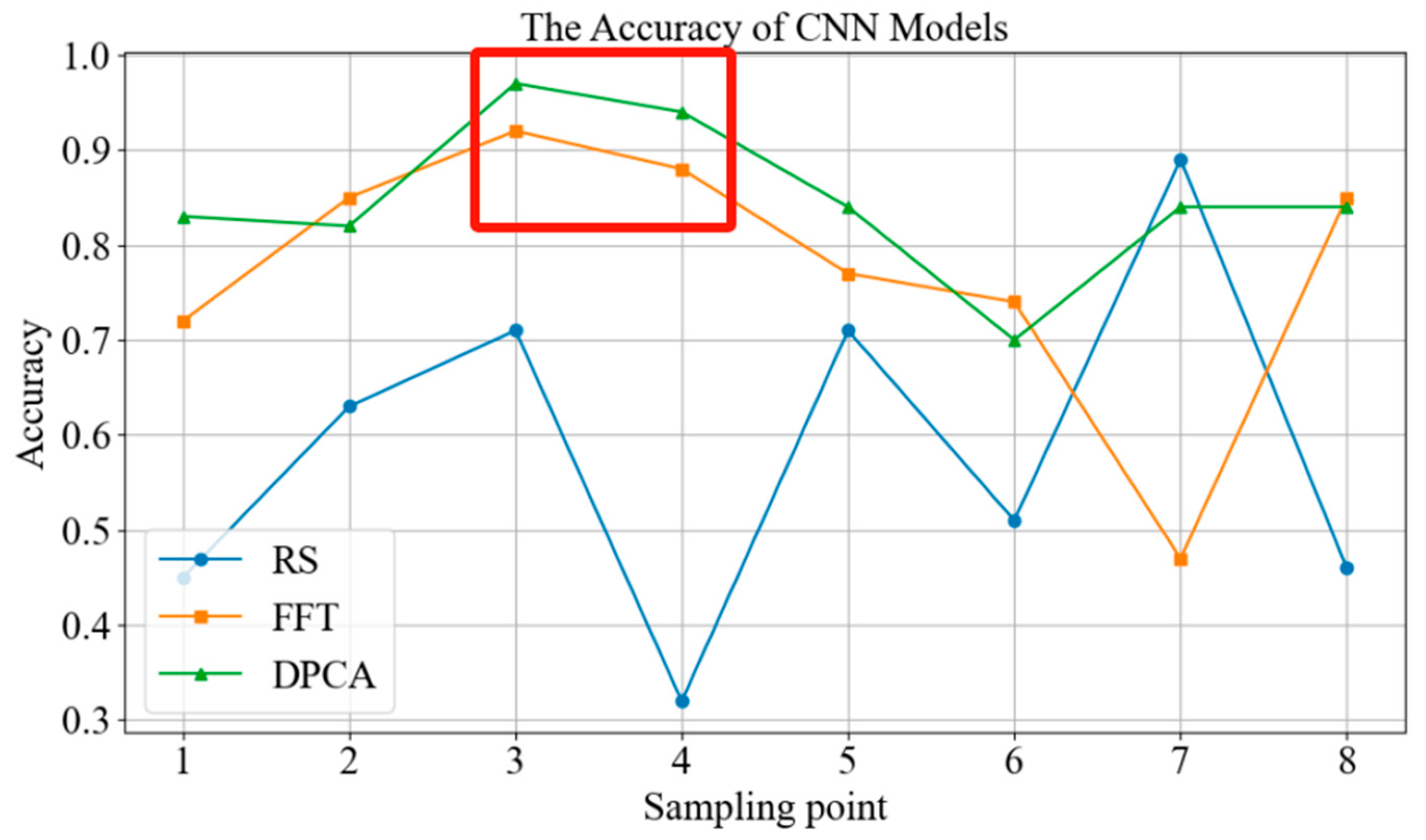
4.1. Model Selection
4.2. Decision Fusion
4.3. Model Fusion Results and Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, K.; Lou, Y.; Peng, G.; Liu, C.; Chang, H. A Review of the Development and Research Status of Symmetrical Diaphragm Pumps. Symmetry 2023, 15, 2091. [Google Scholar] [CrossRef]
- Thalhofer, T.; Keck, M.; Kibler, S.; Hayden, O. Capacitive sensor and alternating drive mixing for microfluidic applications using micro diaphragm pumps. Sensors 2022, 22, 1273. [Google Scholar] [CrossRef]
- Zhou, C.; Jia, Y.; Bai, H.; Xing, L.; Yang, Y. Sliding dispersion entropy-based fault state detection for diaphragm pump parts. Coatings 2021, 11, 1536. [Google Scholar] [CrossRef]
- Feng, Z.; Xiong, X.; Wang, X. Fault diagnosis of diaphragm pump check valve based on impulse and cyclostationary analysis. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), IEEE 2021, Kunming, China, 22–24 May 2021; pp. 2092–2097. [Google Scholar]
- Li, X.; Chen, J.; Wang, Z.; Jia, X.; Peng, X. A non-destructive fault diagnosis method for a diaphragm compressor in the hydrogen refueling station. Int. J. Hydrogen Energy 2019, 44, 24301–24311. [Google Scholar] [CrossRef]
- Xu, X.; Guo, Z.; Liang, X. Intelligent fault diagnosis system design and implementation of diaphragm pump based on artificial intelligence. J. Phys. Conf. Ser. 2022, 2181, 012046. [Google Scholar] [CrossRef]
- Jia, Y.; Qingmao, L.; Xuyi, Y. The diaphragm pump spindle fault diagnosis using HHT based on EMD. Open Autom. Control Syst. J. 2015, 7, 640–645. [Google Scholar] [CrossRef][Green Version]
- Chen, Y.; Huang, G.; Feng, Z. Early Fault Diagnosis of High Pressure Diaphragm Pump Check Valve Based on VMD-HMM. In Proceedings of the 2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), IEEE, Dali, China, 24–27 May 2019; pp. 808–813. [Google Scholar]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Ding, S.X.; Huang, B. Data-driven fault diagnosis for traction systems in high-speed trains: A survey, challenges, and perspectives. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1700–1716. [Google Scholar] [CrossRef]
- Hongm, W.; Tian-You, C.; Jan-Liang, D.; Brown, M. Data driven fault diagnosis and fault tolerant control: Some advances and possible new directions. Acta Autom. Sin. 2009, 35, 739–747. [Google Scholar]
- MacGregor, J.; Cinar, A. Monitoring, fault diagnosis, fault-tolerant control and optimization: Data driven methods. Comput. Chem. Eng. 2012, 47, 111–120. [Google Scholar] [CrossRef]
- Li, W.; Zhu, Z.; Jiang, F.; Zhou, G.; Chen, G. Fault diagnosis of rotating machinery with a novel statistical feature extraction and evaluation method. Mech. Syst. Signal Process. 2015, 50, 414–426. [Google Scholar] [CrossRef]
- Rauber, T.W.; do Nascimento, E.M.; Wandekokem, E.D.; Varejão, F.M.; Herout, A. Pattern recognition based fault diagnosis in industrial processes: Review and application. Pattern Recognit. Recent Adv. 2010, 483–508. [Google Scholar] [CrossRef]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Challenges and opportunities of deep learning models for machinery fault detection and diagnosis: A review. IEEE Access 2019, 7, 122644–122662. [Google Scholar] [CrossRef]
- Carraro, G.; Pallis, P.; Leontaritis, A.D.; Karellas, S.; Vourliotis, P.; Rech, S.; Lazzaretto, A. Experimental performance evaluation of a multi-diaphragm pump of a micro-ORC system. Energy Procedia 2017, 129, 1018–1025. [Google Scholar] [CrossRef]
- D’Amico, F.; Pallis, P.; Leontaritis, A.D.; Karellas, S.; Kakalis, N.M.; Rech, S.; Lazzaretto, A. Semi-empirical model of a multi-diaphragm pump in an Organic Rankine Cycle (ORC) experimental unit. Energy 2018, 143, 1056–1071. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Xu, W.; Jing, L.; Tan, J.; Dou, L. A multimodel decision fusion method based on DCNN-IDST for fault diagnosis of rolling bearing. Shock. Vib. 2020, 2020, 8856818. [Google Scholar] [CrossRef]
- Zeng, D.; Xu, J.; Xu, G. Data Fusion for Traffic Incident Detector Using DS Evidence Theory with Probabilistic SVMs. J. Comput. 2008, 3, 36–43. [Google Scholar] [CrossRef]
- Fu, Y.; Chen, X.; Liu, Y.; Son, C.; Yang, Y. Gearbox fault diagnosis based on multi-sensor and multi-channel decision-level fusion based on SDP. Appl. Sci. 2022, 12, 7535. [Google Scholar] [CrossRef]
- Wu, J.; Hu, K.; Cheng, Y.; Zhu, H.; Shao, X.; Wang, Y. Data-driven remaining useful life prediction via multiple sensor signals and deep long short-term memory neural network. ISA Trans. 2020, 97, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Xu, L.; Li, J.; Fang, C.; Ouyang, M. Faults diagnosis for PEM fuel cell system based on multi-sensor signals and principle component analysis method. Int. J. Hydrog. Energy 2017, 42, 18524–18531. [Google Scholar] [CrossRef]
- Song, Y.; Ma, Q.; Zhang, T.; Li, F.; Yu, Y. Research on Fault Diagnosis Strategy of Air-Conditioning Systems Based on DPCA and Machine Learning. Processes 2023, 11, 1192. [Google Scholar] [CrossRef]

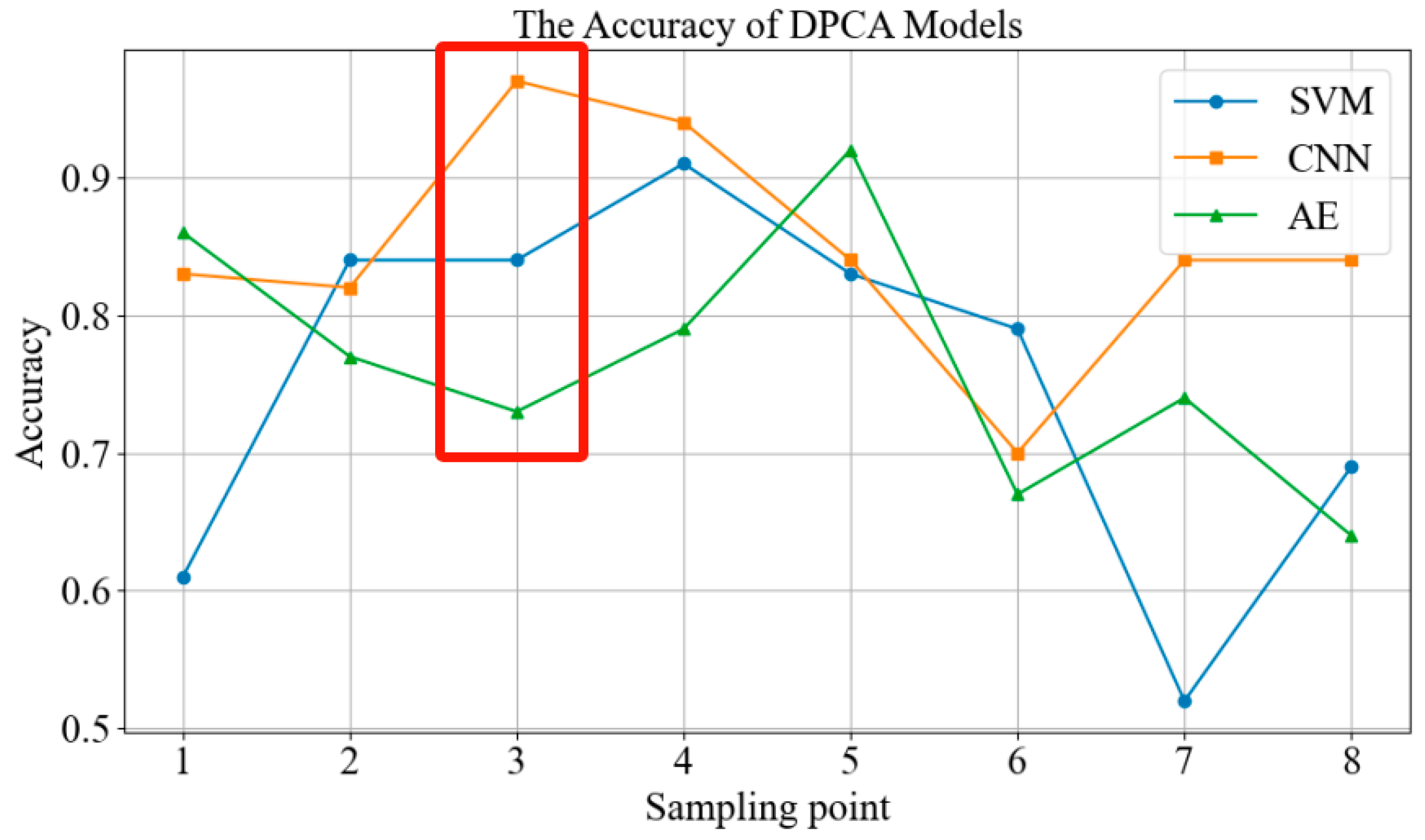
| Sampling point | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Sampling location | Pump body | Motor drive section | Reduction gearbox | |||||
| Collection direction | Level | Vertical | Level | Vertical | Vertical | Level | Level | Axial |
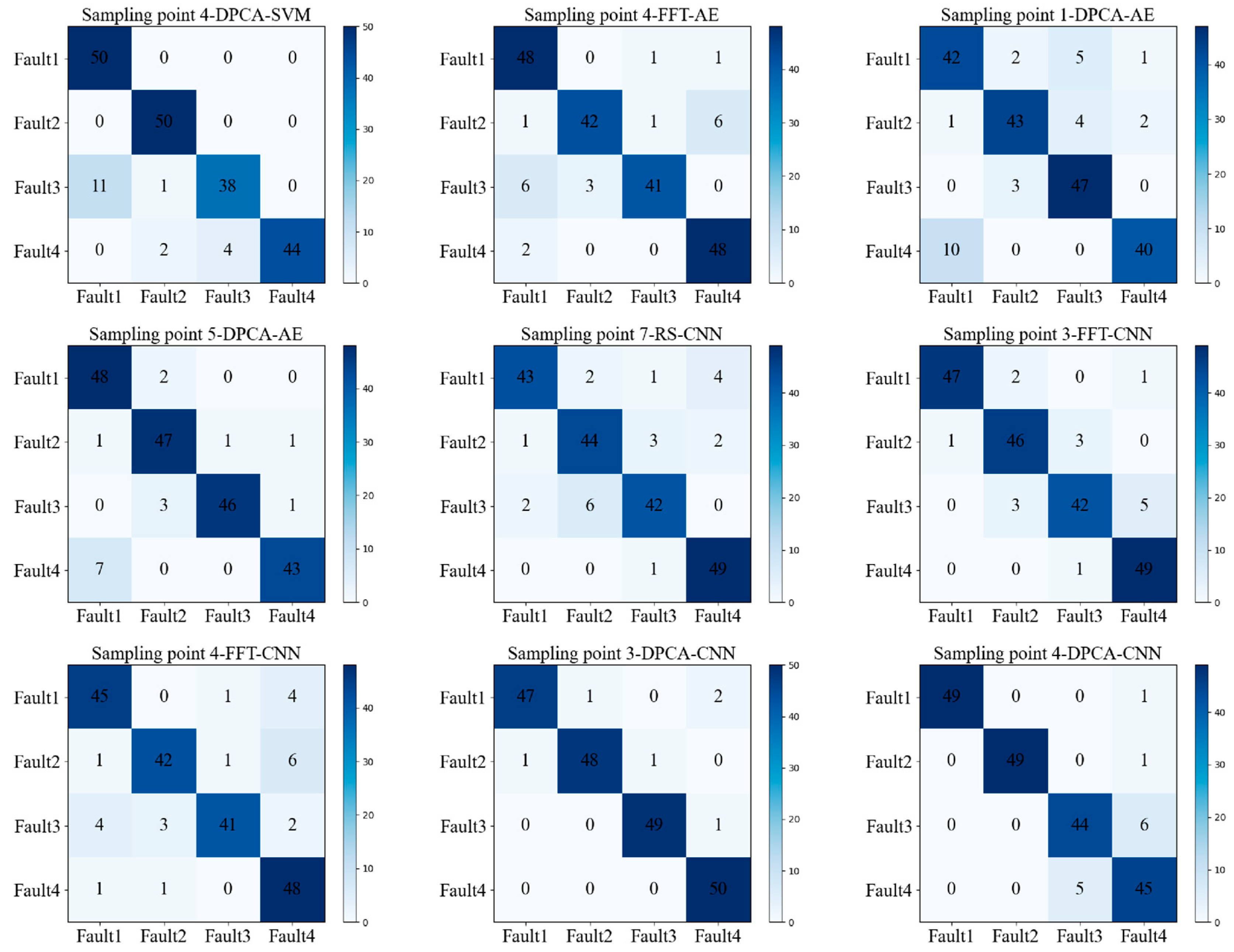
| Number | Sampling Point | Feature Extraction Methods | Deep Learning Models | Accuracy | F1 Score |
|---|---|---|---|---|---|
| 1 | 4 | DPCA | SVM | 91.00% | 0.91 |
| 2 | 4 | FFT | AE | 89.50% | 0.89 |
| 3 | 1 | DPCA | AE | 86.00% | 0.86 |
| 4 | 5 | DPCA | AE | 92.00% | 0.92 |
| 5 | 7 | RS | CNN | 89.00% | 0.89 |
| 6 | 3 | FFT | CNN | 92.00% | 0.92 |
| 7 | 4 | FFT | CNN | 88.00% | 0.88 |
| 8 | 3 | DPCA | CNN | 97.00% | 0.97 |
| 9 | 4 | DPCA | CNN | 93.50% | 0.93 |
| Model | Local Credibility | Global Credibility | |||
|---|---|---|---|---|---|
| LPF | CVF | DD | GCFF | ||
| Model 1 | 1.00 | 1.00 | 0.76 | 0.88 | 91.00% |
| Model 2 | 0.96 | 0.84 | 0.82 | 0.96 | 89.50% |
| Model 3 | 0.84 | 0.86 | 0.94 | 0.80 | 86.00% |
| Model 4 | 0.96 | 0.94 | 0.92 | 0.86 | 92.00% |
| Model 5 | 0.86 | 0.88 | 0.84 | 0.98 | 89.00% |
| Model 6 | 0.94 | 0.92 | 0.84 | 0.98 | 92.00% |
| Model 7 | 0.90 | 0.84 | 0.82 | 0.96 | 88.00% |
| Model 8 | 0.94 | 0.96 | 0.98 | 1.00 | 97.00% |
| Model 9 | 0.98 | 0.98 | 0.88 | 0.90 | 93.50% |
| Model | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | Model 7 | Model 8 | Model 9 |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.91 | 0.895 | 0.86 | 0.92 | 0.89 | 0.92 | 0.88 | 0.97 | 0.935 |
| BPA | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 | 0.12 | 0.11 |
| Fusion Method | Accuracy |
|---|---|
| RS fusion | 89.00% |
| FFT fusion | 96.74% |
| DPCA fusion | 99.53% |
| RS and FFT | 99.19% |
| RS and DPCA | 99.89% |
| FFT and DPCA | 99.90% |
| SVM fusion | 91.00% |
| CNN fusion | 99.52% |
| AE fusion | 96.45% |
| SVM and CNN | 99.90% |
| SVM and AE | 99.89% |
| CNN and AE | 99.90% |
| ALL models | 99.98% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, F.; Shi, Z.; Song, Y. The DMF: Fault Diagnosis of Diaphragm Pumps Based on Deep Learning and Multi-Source Information Fusion. Processes 2024, 12, 468. https://doi.org/10.3390/pr12030468
Meng F, Shi Z, Song Y. The DMF: Fault Diagnosis of Diaphragm Pumps Based on Deep Learning and Multi-Source Information Fusion. Processes. 2024; 12(3):468. https://doi.org/10.3390/pr12030468
Chicago/Turabian StyleMeng, Fanguang, Zhiguo Shi, and Yongxing Song. 2024. "The DMF: Fault Diagnosis of Diaphragm Pumps Based on Deep Learning and Multi-Source Information Fusion" Processes 12, no. 3: 468. https://doi.org/10.3390/pr12030468
APA StyleMeng, F., Shi, Z., & Song, Y. (2024). The DMF: Fault Diagnosis of Diaphragm Pumps Based on Deep Learning and Multi-Source Information Fusion. Processes, 12(3), 468. https://doi.org/10.3390/pr12030468







