1. Introduction
Nuclear energy is a clean energy source, which has profound significance in reducing carbon emissions and ensuring energy supplies. In the process of nuclear energy development, nuclear safety is most critical, and the emergence of dispersed particles greatly improves nuclear safety. Dispersed fuels [
1] can withstand higher temperatures under some extreme accident conditions and provide excellent intrinsic safety. It is gradually gaining attention in applications due to its excellent characteristics mentioned above. However, the addition of dispersed particles leads to the traditional single heterogeneity becoming a double heterogeneity. Due to the presence of double heterogeneity, traditional neutronics calculation programs are unable to characterize the particle-based dispersion system. To solve the problem of double heterogeneity, reactor physics researchers have proposed numerous approaches. Among many methods, the RPT (reactivity-equivalent physical transformation) method has gradually become a popular topic of research due to its simplicity and efficiency.
In 2005, the concept of the RPT [
2] method was introduced to tackle the complexity of fuels with dispersed particles. The strategy entails condensing the dispersed particles into a smaller area while preserving the system’s reactivity at the beginning of the burnup depth, followed by the application of the VWH (volume homogenization method) to the particles located in the condensed region. Thus, the double heterogeneity system is converted to a single heterogeneity system. This method involves no alterations to the existing program’s computational algorithms. Instead, it enhances the accuracy of the results by simply adjusting the geometrical configurations. Furthermore, a novel resonance approach [
3] has been introduced to tackle dual heterogeneity. It has been successfully incorporated into the ALPHA program’s resonance module, designed to address the dual heterogeneity challenges, and has shown that the results are of high accuracy. An improved reactivity-equivalent physical transformation (IRPT) method [
4] has been put forward to precisely handle FCM fuel with burnable poison particles. This IRPT method is designed to be effective for both criticality and burnup evaluations, and it remains stable regardless of changes in operational parameters. Yet, the conventional RPT approach encounters challenges when attempting to depict systems featuring two types of particles containing poisons. To achieve a uniform distribution of TRISO fuel in high-temperature reactors, the RPT method is applied. For these calculations, the WIMS [
5] and Serpent [
6] have been employed to address the calculations of the homogenized and double heterogeneous models of TRISO fuel. To manage excessive reactivity and even out the power distribution across the radius, an innovative concept has been put into practice. This involves the application of varying thicknesses of IFBA coating onto the exterior surface of the TRISO particle fuel kernel [
7]. Subsequently, neutronic assessments have been carried out, encompassing both two-dimensional full core [
8] and three-dimensional full core [
9] configurations, where the IFBA coating is uniformly dispersed. Furthermore, the ring reactivity-equivalent physical transformation method (RRPT) has been introduced [
10,
11], which more accurately simulates the stratified impact of burnable poisons compared to the traditional RPT method. In 2023, the reactive equivalent physical transformation method based on particle diameter (DRPT) [
12] was introduced. This DRPT method has demonstrated high precision in dealing with plate heterogenous systems. It is characterized by its straightforward implementation, enhanced outcomes, and broad applicability. The impact of simulating different fuel shapes for the material testing reactor (MTR) is evaluated by building two OpenMC codes [
13]. Upon examining the calculations from the two OpenMC models, it was noted that there is a minimal variation in the radial flux distribution, attributable to the similarity in fuel mass. The rapid fitting RPT methods based on the rod fuel elements [
14] and the plate fuel elements [
15] are proposed. The results show that the model with high fitting accuracy has practical engineering application value.
As the technology continues to evolve, machine learning is now expanding into the field of reactor analysis as a key tool for building alternative models for complex large-scale numerical computational programs. In 2022, Suubi Racheal [
16] proposed a novel approach to train machine learning model and use augmented datasets reflecting sensor states. This study develops, trains, and compares three machine learning models: support vector machines (SVMs), decision trees (DTs), and multilayer perceptrons (MLPs). The results show that SVM and DT models perform better than MLP models. In 2023, Zhenhai Liu [
17] carried out research on machine learning-based methods for constructing equivalent models for fuel rod temperature distribution. This study aimed to improve the computational efficiency of large-scale fuel rod performance simulation, and the construction strategy of the equivalent model for predicting the temperature distribution of fuel rods was discussed and analyzed in detail using fuel rod temperature prediction as a research example. The results show that the constructed equivalent model has a computational speedup of about 204 times compared to the COPERNIC program with high accuracy. In 2023, Guanghu [
18] elaborated five DDML algorithms such as linear regression (LR), principal component analysis (PCA), and artificial neural network (ANN), and DDML showed good applicability in the simulation of multi-scale and multi-physics fields. Artificial intelligence and machine learning (AI/ML) technologies offer unique opportunities to transform nuclear plant operations and power generation. In 2024, the barriers to AI/ML adoption within the nuclear power industry were discussed [
19], with a focus on existing commercial reactors. In 2024, HaoWu [
20] developed an automated tree-based machine learning method for the nuclear pebble bed of the high temperature gas-cooled reactor (HTGR) to explore the complex thermal radiation behavior. The findings indicate that the AutoML model operates approximately 5 to 10 times more swiftly compared to conventional techniques. Additionally, the Pareto front of the AutoML model reveals that the mean square error diminishes as the model complexity is reduced, culminating in the attainment of the optimal solution. At present, the application of machine learning and artificial intelligence in the field of nuclear engineering is in a developing state, and there is still room for improvement. For example, in calculating the
kinf of a reactor, deterministic calculations for the core under a two-step framework have a computation cost at the level of around ten minutes, which provides sufficiently accurate results. Using machine learning for prediction can be faster, but it requires a large amount of simulated data for training initially, and the trained system cannot be used for different reactor types.
Through research and analysis, it has been found that the RPT method has been widely studied due to its simple and efficient advantages. However, most of them adopt traditional methods to obtain the similarity ratio of the RPT model, which requires the calculation of a large number of Monte Carlo program results and consumes a significant amount of time. Therefore, this paper connects machine learning with the RPT model; machine learning algorithms can automatically establish the RPT model, significantly improving the efficiency of obtaining the similarity ratio of the RPT model. The obtained RPT model can be calculated by using a conventional neutronics program.
2. Materials and Methods
This section provides an introduction to RPT methods and machine learning, and the RPT method based on machine learning is proposed.
2.1. Reactivity-Equivalent Physical Transformation
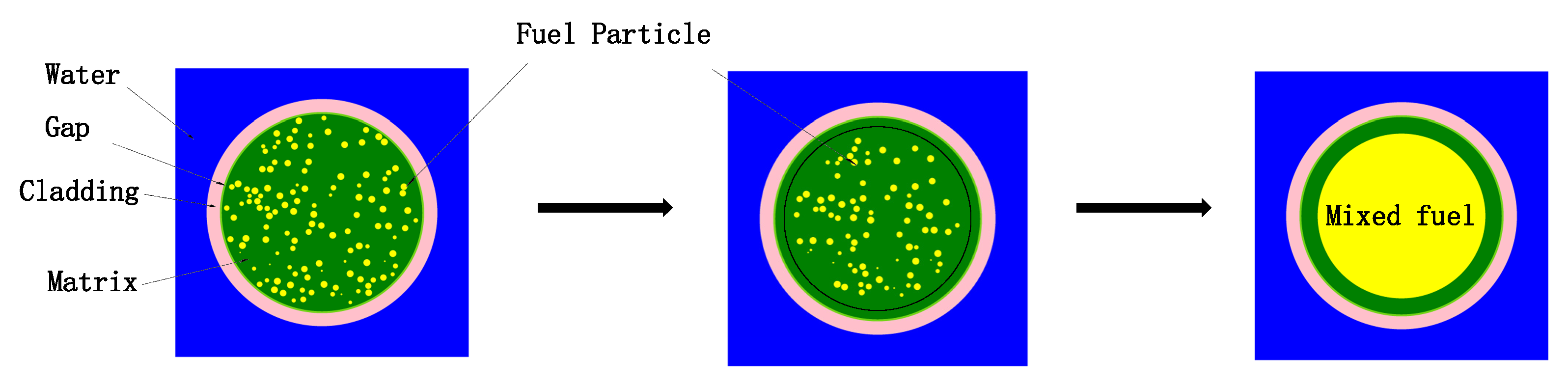
Figure 1 is a schematic diagram of the traditional RPT method. Initially, all the dispersed particles are compressed within a smaller fuel region; subsequently, for the compressed fuel region, homogenization is performed by using the volume weighting method, and the conventional pressurized water reactor physics calculation procedures are applied. In the RPT method, by ensuring that the
kinf of the system is equal to the reference solution, the radius of the compressed fuel region is determined. The reference solution is obtained through high-fidelity deterministic codes or Monte Carlo procedures.
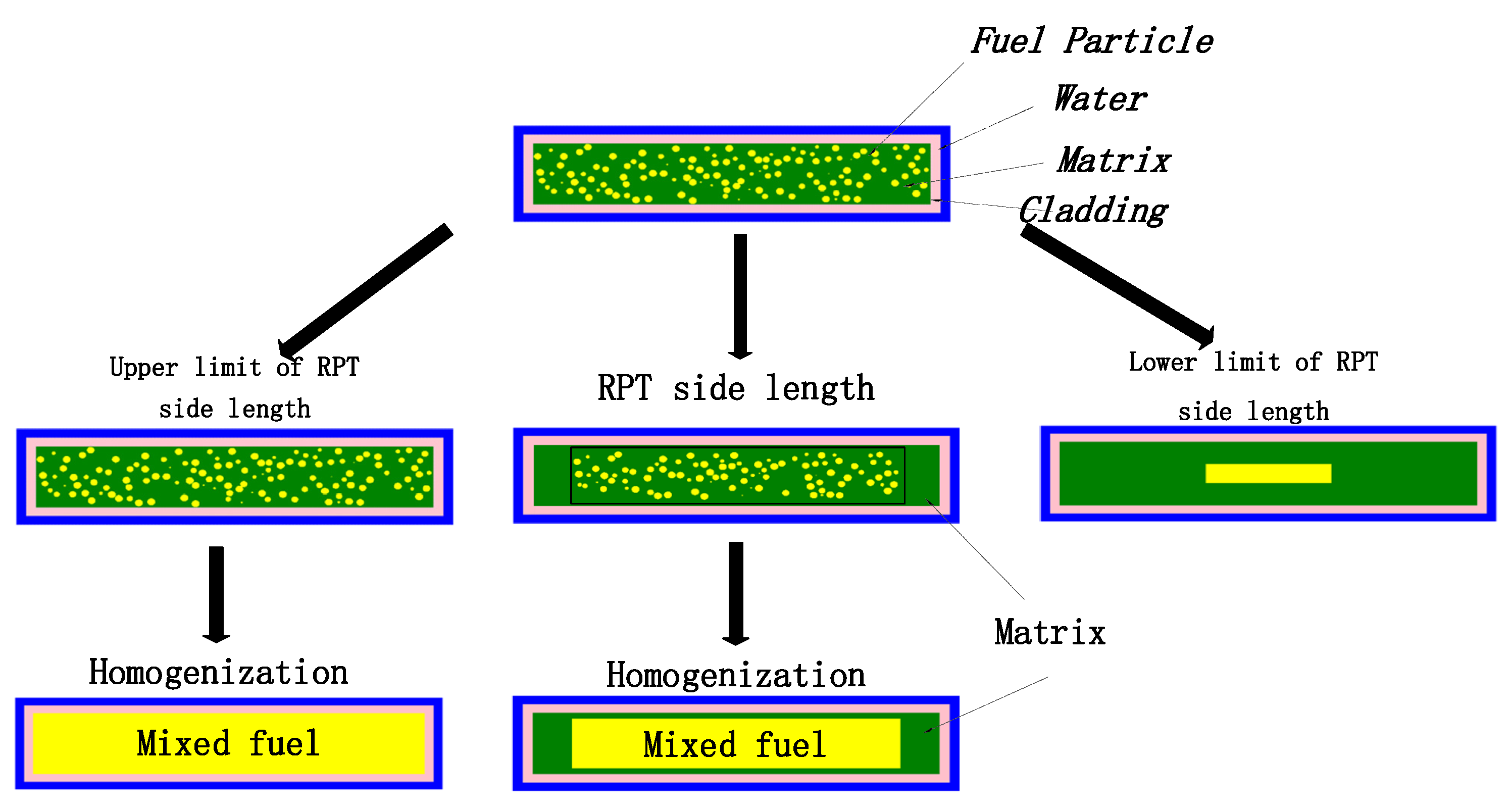
As depicted in
Figure 2, a conventional RPT method for plate-shaped structures is introduced, which is an extension of the RPT method designed for cylindrical geometries. The principle behind the plate geometry RPT closely mirrors that of the cylindrical counterpart, with the key distinction being the rectangular fuel region in the plate, influenced by both its length and width dimensions. To address this, the concept of equivalent side lengths is introduced. These lengths represent the dimensions of the fuel area after reduction, where both the length and width are scaled down uniformly. The equivalent edge lengths are also bounded by the upper and lower bounds. The upper bound should not surpass the original fuel area’s dimensions, while the lower bound corresponds to the minimal length and width when all fuel particles are compressed to the fuel zone’s center. Typically, the exact equivalent side lengths fall within these upper and lower bounds.
A straightforward computational illustration of applying the RPT method to fuel plates with dispersed particles is provided in the central part of
Figure 2. It is supposed that the fuel region of the plate element has a length of
a, a width of
b, and a height of
H, with a packing fraction
f for the dispersed particles.
1. The dispersed particles are compacted within a certain area, with both the length and width being reduced proportionally. Both a and b are scaled down by factor s, resulting in the new dimensions as and bs. The factor s is the similarity ratio (SR) of the fuel plate with its maximum value. Equation (1) is derived from the principle of maintaining the volume consistency of the dispersed particles.
2. The novel composite fuel material is synthesized via volumetric blending within the compacted fuel zone, with the matrix between the original and the newly formed fuel zones remaining unchanged. The nuclear number density is preserved across both the downsized fuel area and the initial fuel area. Consequently, the final RPT model for the fuel plate incorporating dispersed particles is formulated for this particular similarity ratio.
Range of similarity ratios: (,1).
2.2. Introduction to Machine Learning RPT Method Based on Linear Regression Model
Machine learning based on linear regression modeling is a common supervised learning method used to predict the output of a continuous value. In linear regression, a linear relationship is assumed between the dependent variable (output) and the independent variable (characteristics). The model describes the relationship between the features and outputs by fitting the best possible straight line that minimizes the error between the predicted outputs and the actual observations. The basic form of the linear regression model can be expressed as Equation (2).
where
is the predicted value,
,
,
, .....,
are the parameters (weights) of the model, and
,
, ...,
are the input features. The essence of a linear regression model is to use the explanatory variables to estimate the mean of the explanatory variables through the least squares method. Find the best-fit straight line by obtaining the sum of the squares of the residuals between the minimized observations and the model predictions. By extracting the independent variables and creating and fitting a linear regression model, the predictions are made to the model to obtain the predicted values. In order to assess the performance of a model, it can be validated by using various metrics, such as the mean square error or coefficient of determination. These metrics measure the fit of the model to the observed data and its predictive ability, and then finally, the optimal parameters are adjusted to obtain the best prediction value required. In the RPT method, the compressed fuel equivalent radius is determined by ensuring that the
kinf of the system is equal to the reference solution. The reference solution is again obtained by a high-fidelity deterministic program or a Monte Carlo program. However, all are currently obtained empirically by spending a lot of time iterating in order to obtain the corresponding
k∞. Therefore, this paper is based on the machine learning approach that can quickly derive the similarity ratios of the corresponding dispersed fuel particles. The principle of obtaining the similarity ratio is that the
kinf of the equivalent model is equal to the
kinf under the direct explicit particle modeling condition. The computational predictions are made by linear regression modeling for the parameters in the plate fuel element and rod fuel element that have a significant effect on the RPT model. The similarity ratios corresponding to them are finally obtained. The modeling process is described below: This model trains and predicts a linear regression model for a given dataset by using the Linear Regression model of the sklearn library.
First, the training data are loaded from the training set file by using the loadtxt function of the numpy library, and spaces are used as separators. We need to preprocess the data to extract features f, R, and S and target variable SR by a slicing operation.
- 2.
Linear regression model creation and training
By importing the LinearRegression class in the sklearn.linear_model module and instantiating the LinearRegression object after the data are preprocessed, a linear regression model is created. The fit method of the model pass the feature matrix x and the target variable y as parameters into the model for training in order to observe the model parameters by printing the coefficients coef_ and intercept intercept_ of the model.
- 3.
Model Prediction and Evaluation
After training the model, the model can be used to predict new data. First, load the test data in the test set file, extract the features f, R, S and the target variable SR, and then call the predicted method of the model to obtain the predicted values. In order to evaluate the performance of the model, the error calculation is also added, in addition to using the matplotlib library to plot the graphs of the true target and predicted values in order to compare the difference between them more intuitively.
- 4.
Prediction of new data
In addition to making predictions on the test data, we can also use the trained model to make predictions on unseen data. By creating a dataFrame object in pandas containing new feature values and using the model to make predictions, we can quickly apply the model to a new dataset and obtain predictions. In the next section, we will analyze the prediction of new rod and plate element parameters.
4. Conclusions
In this paper, the reactive-equivalent physical transformation method, which is based on machine learning, is used to calculate and predict the RPT parameters of plate-dispersed fuel particles and rod-dispersed fuel particles through a linear regression model, and the similarity ratio of the corresponding parameters is derived. The equivalent radius or equivalent side length of the RPT model is calculated using the similarity ratios. The burnup verification, density verification, fission rate verification, and neutron energy spectrum analysis are carried out by OpenMC programs.
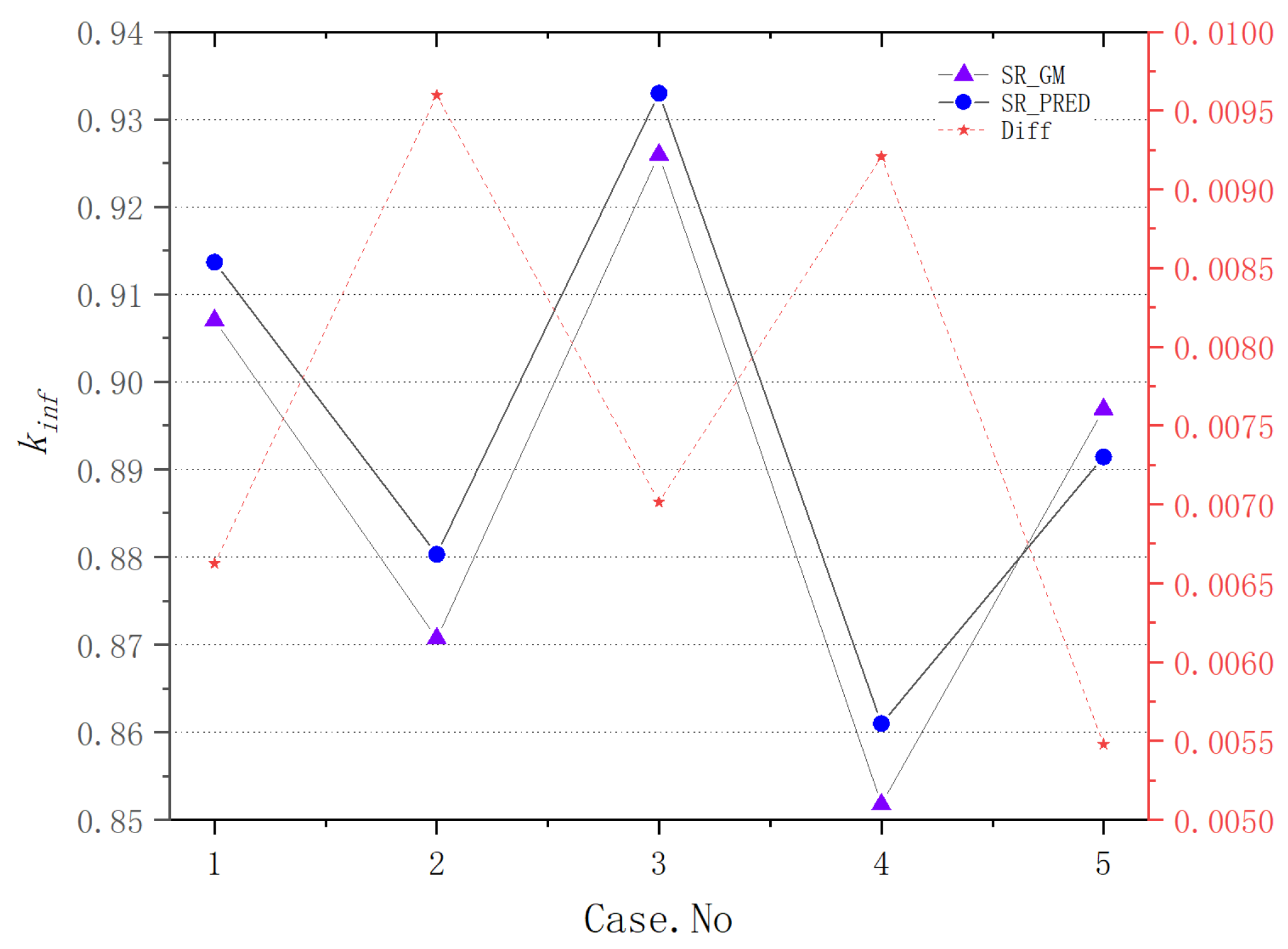
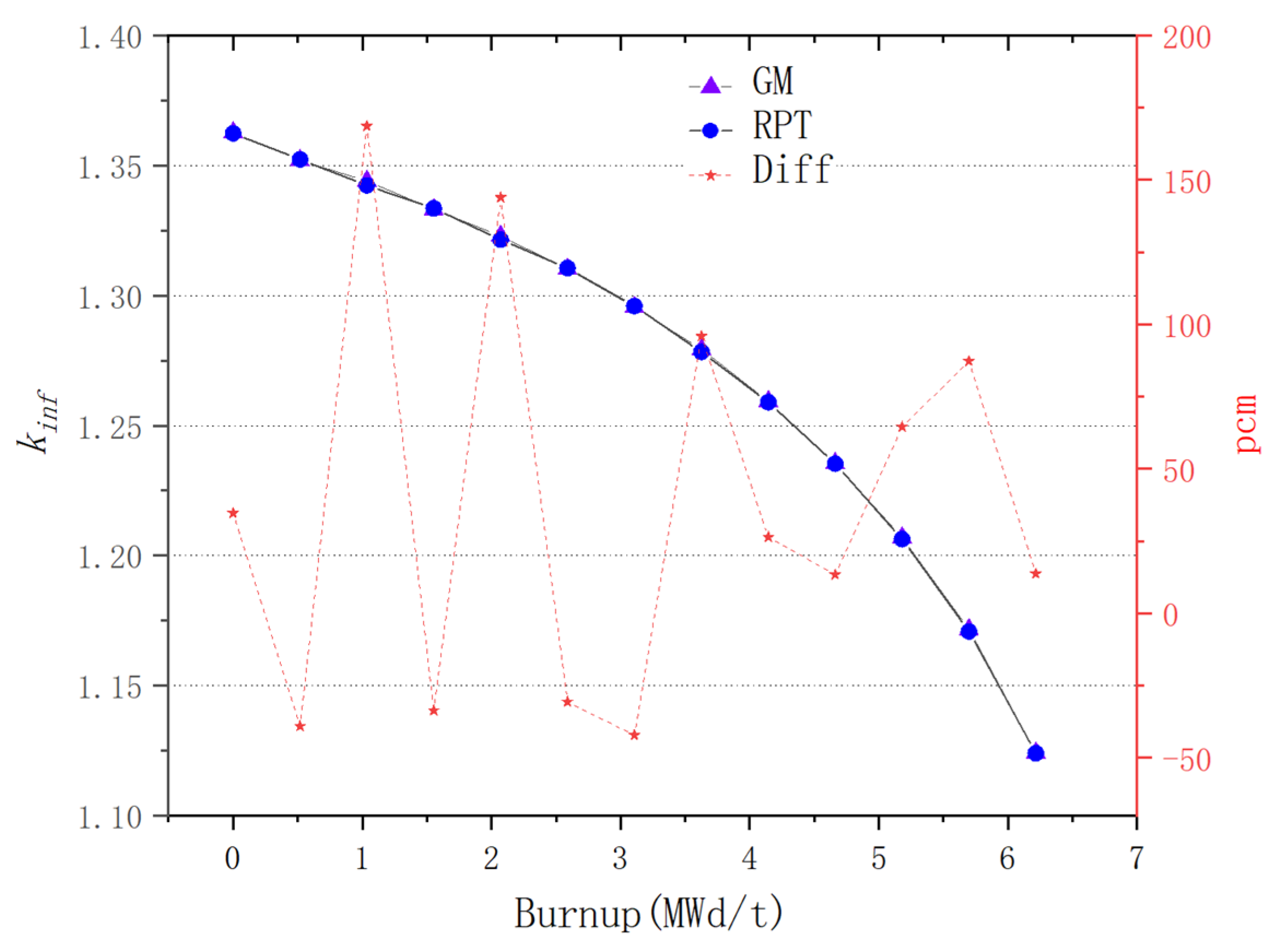
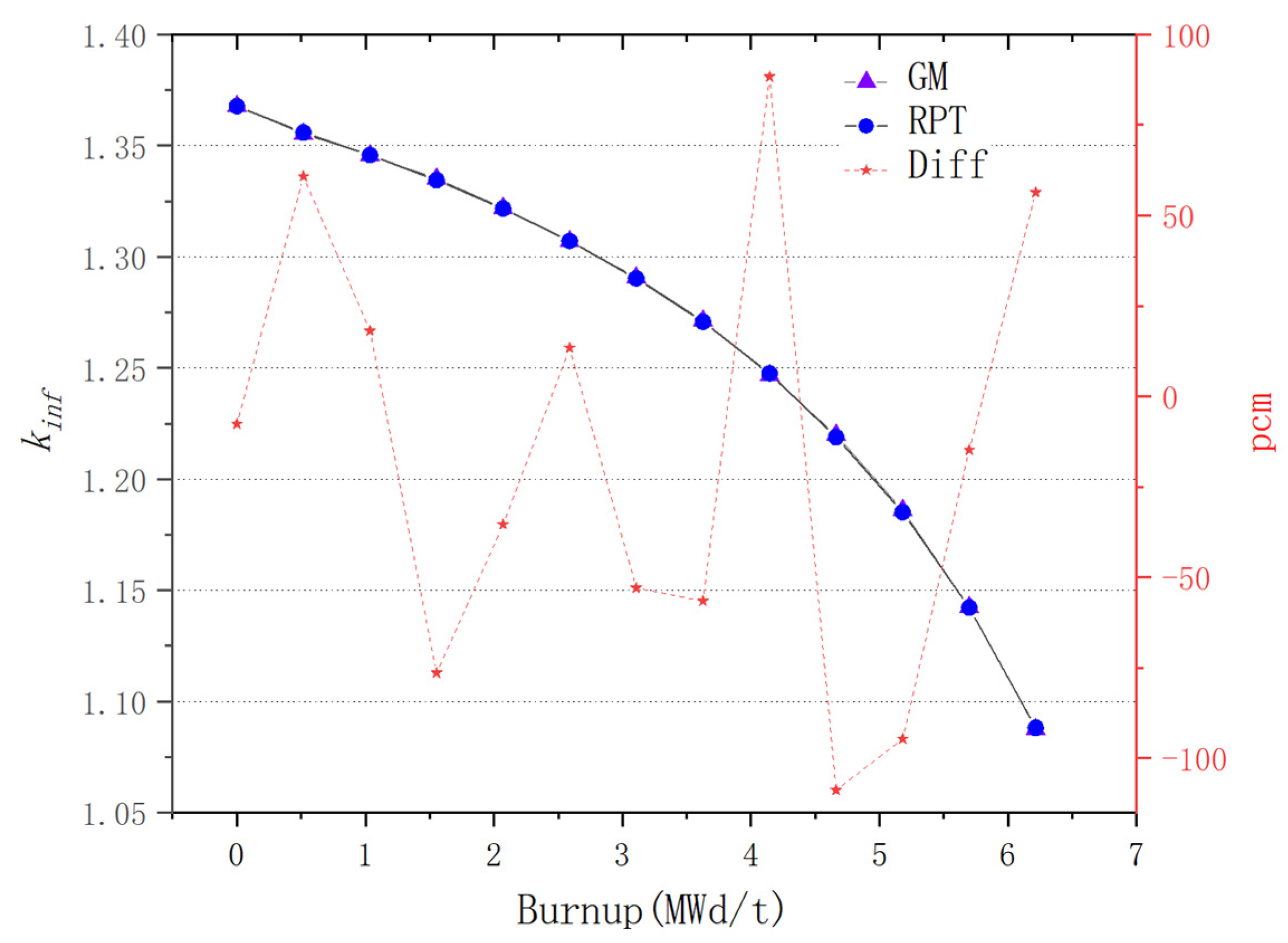
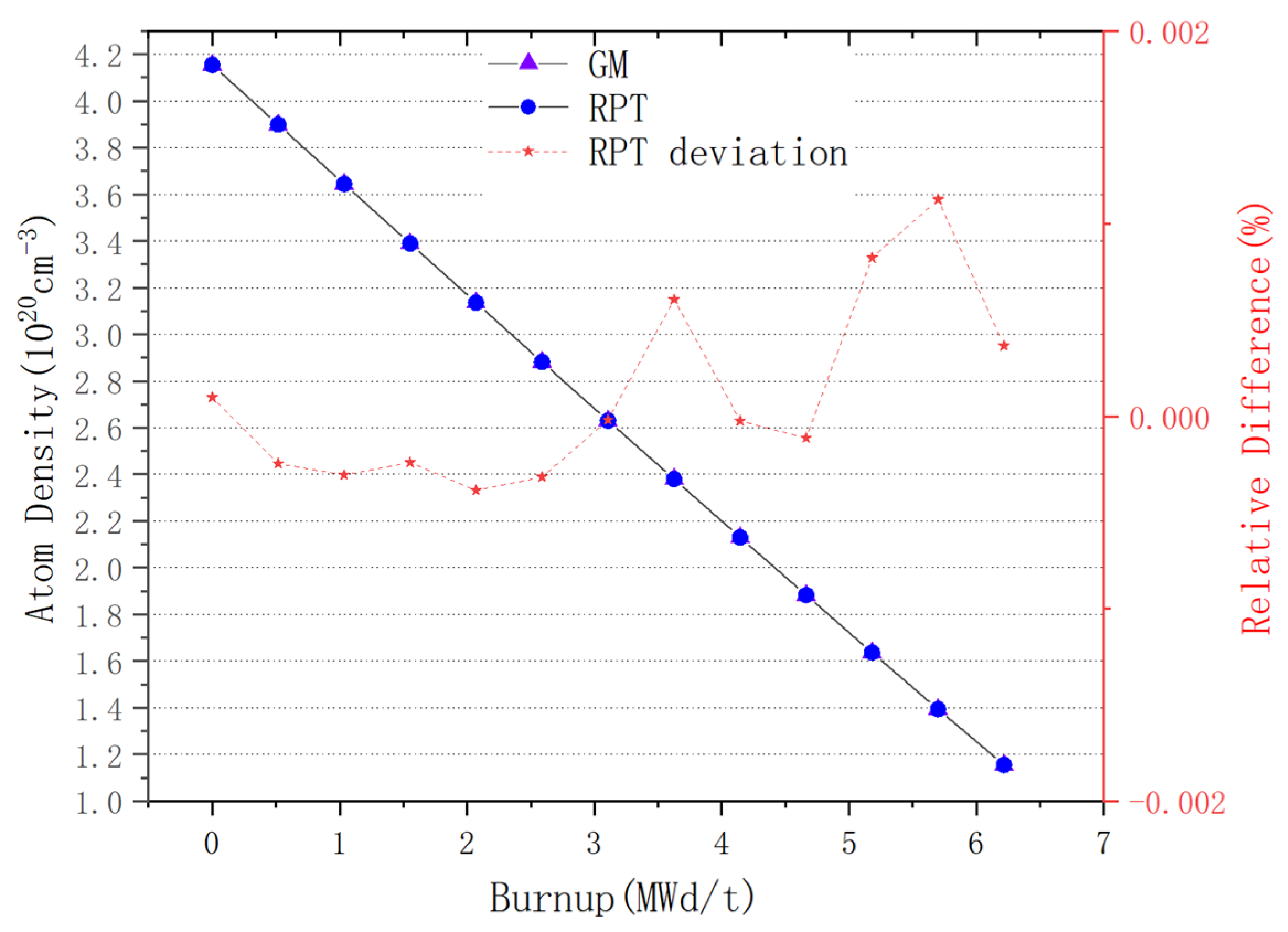
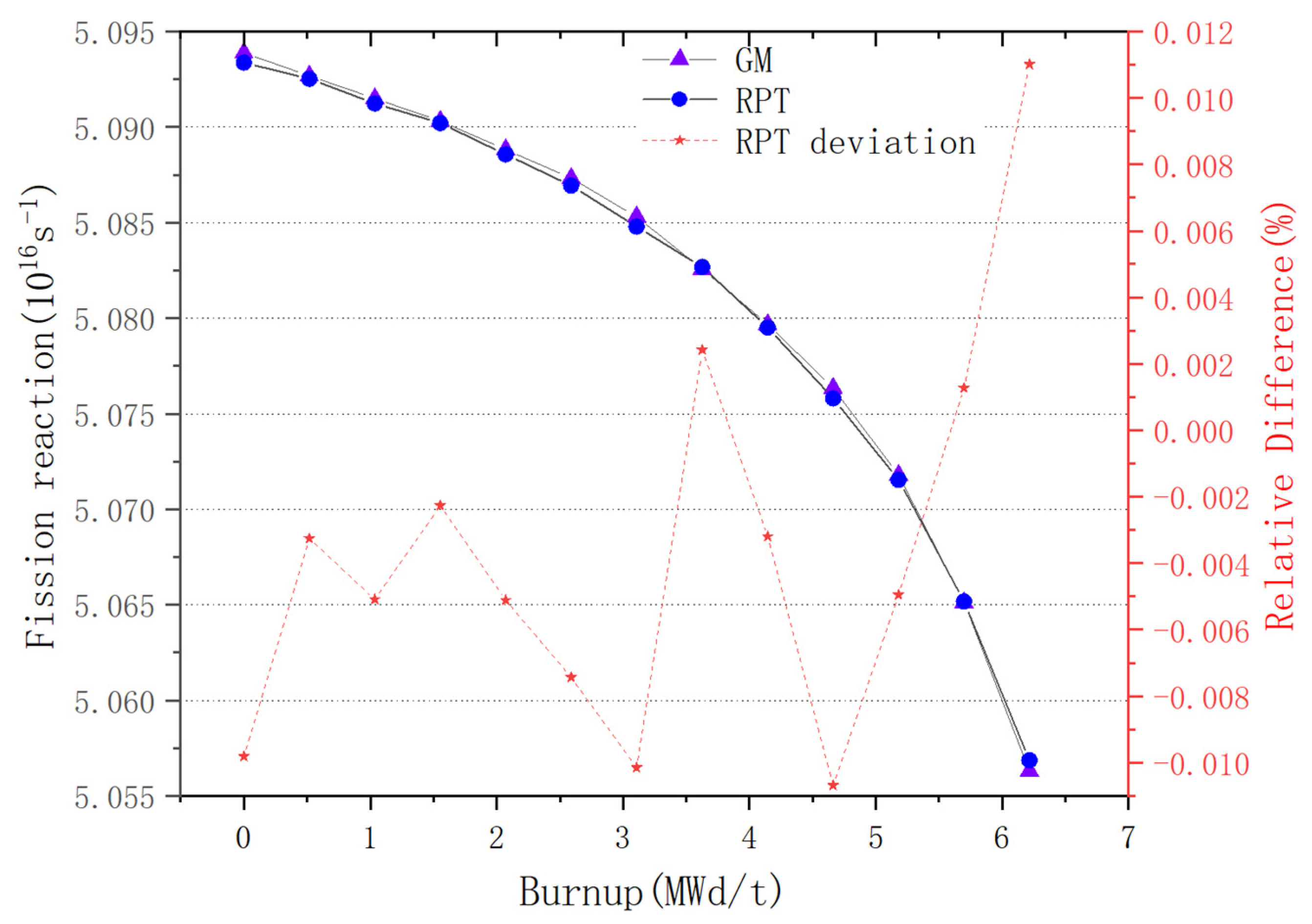
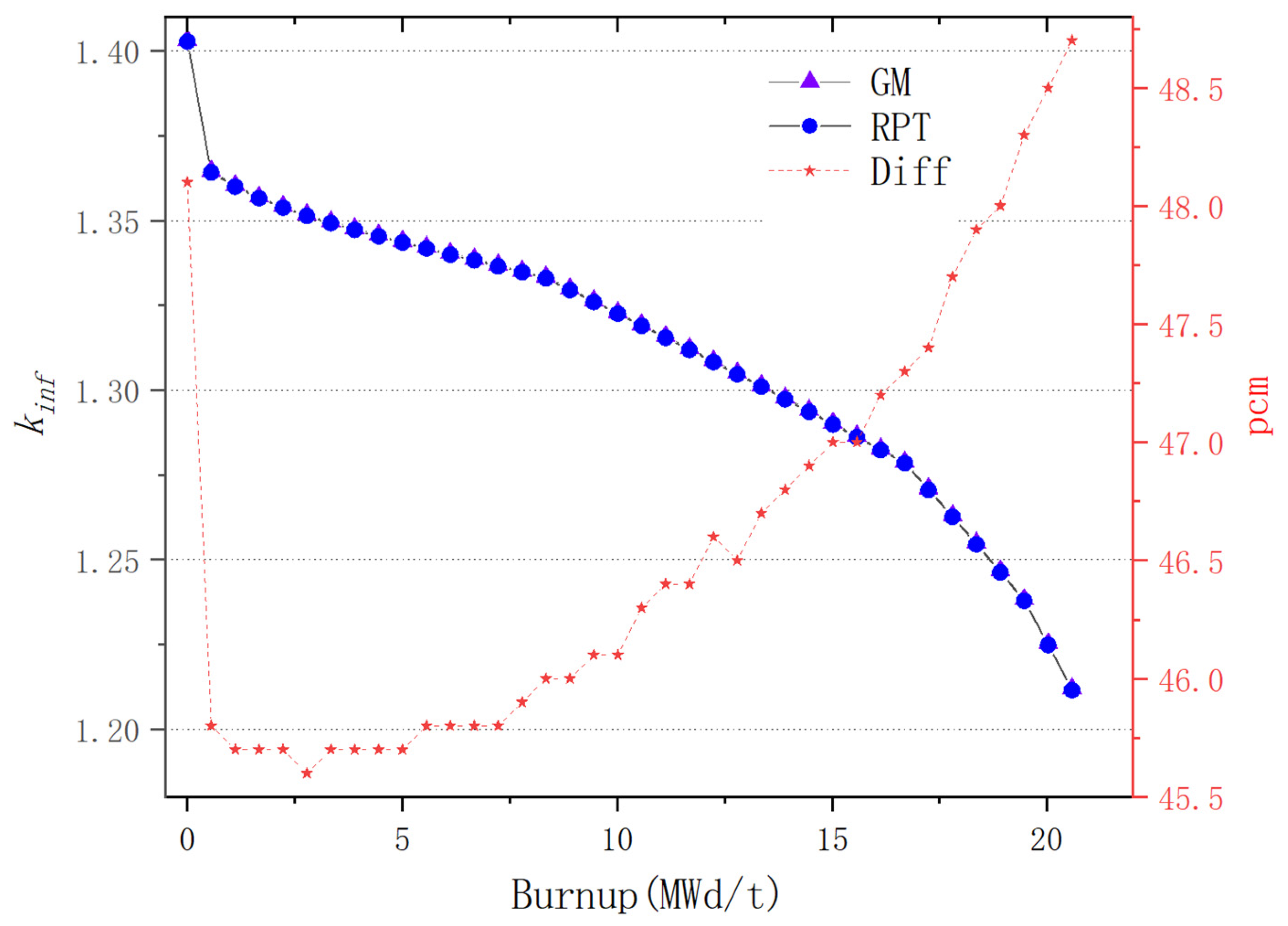
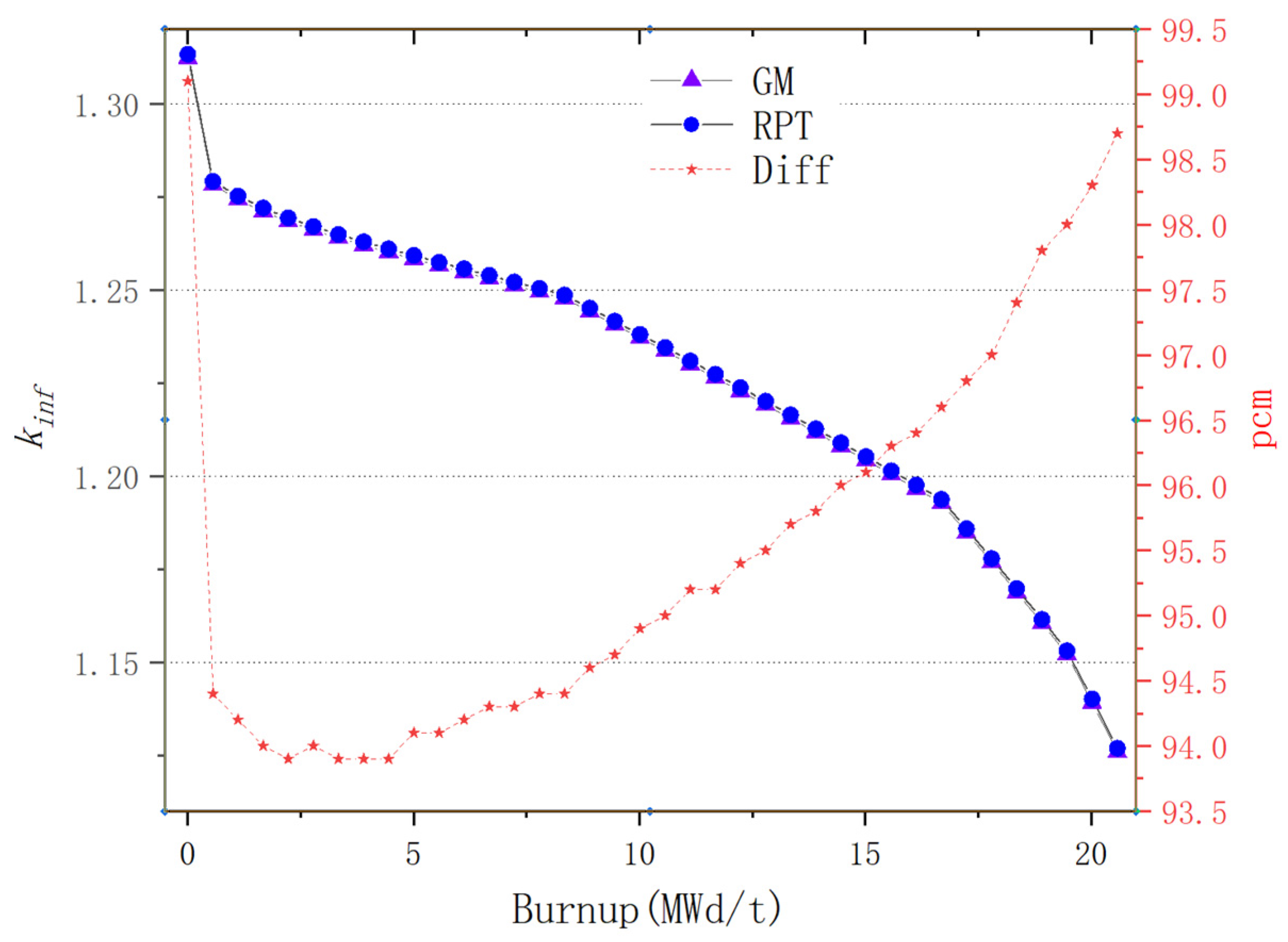
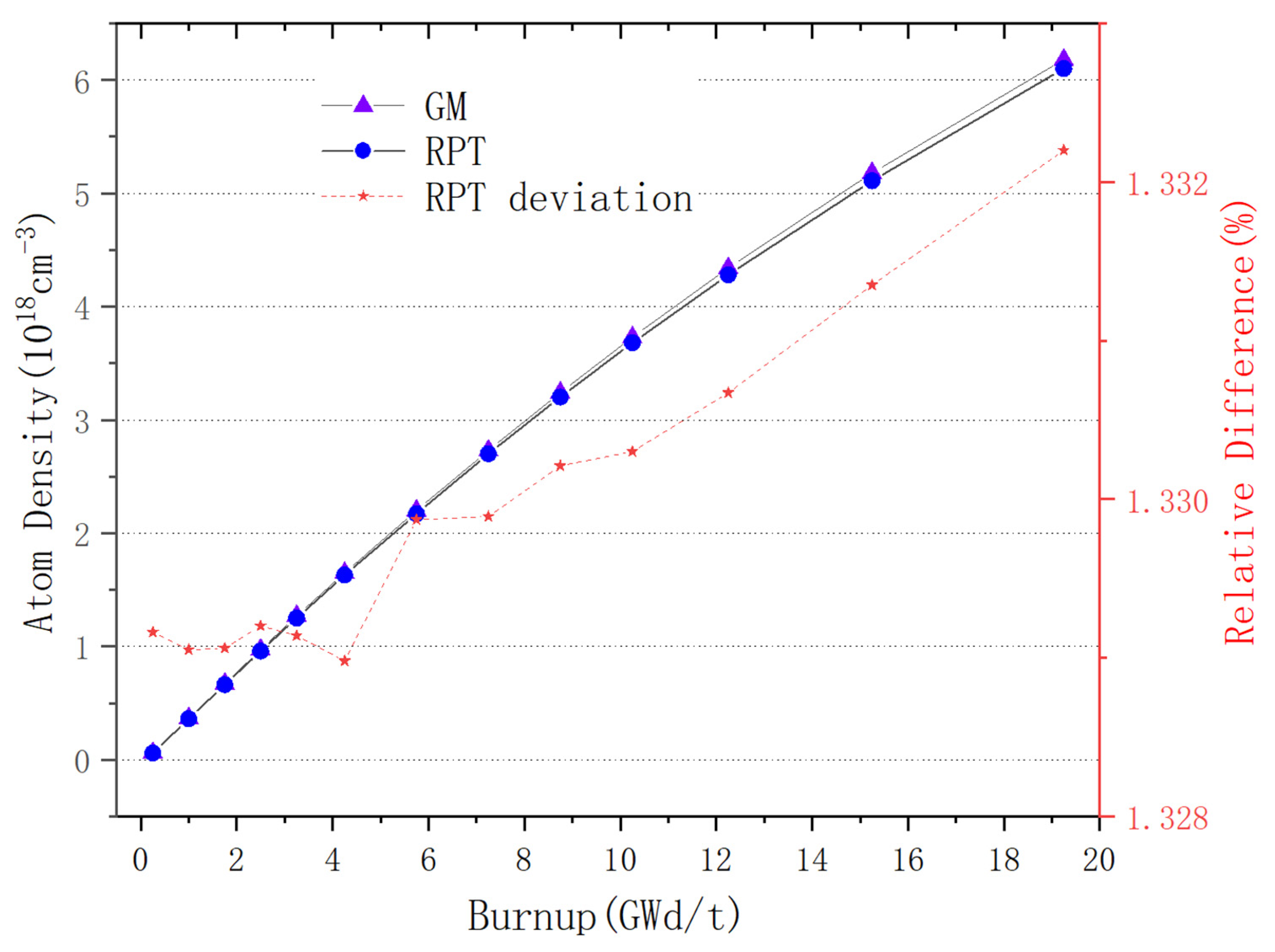
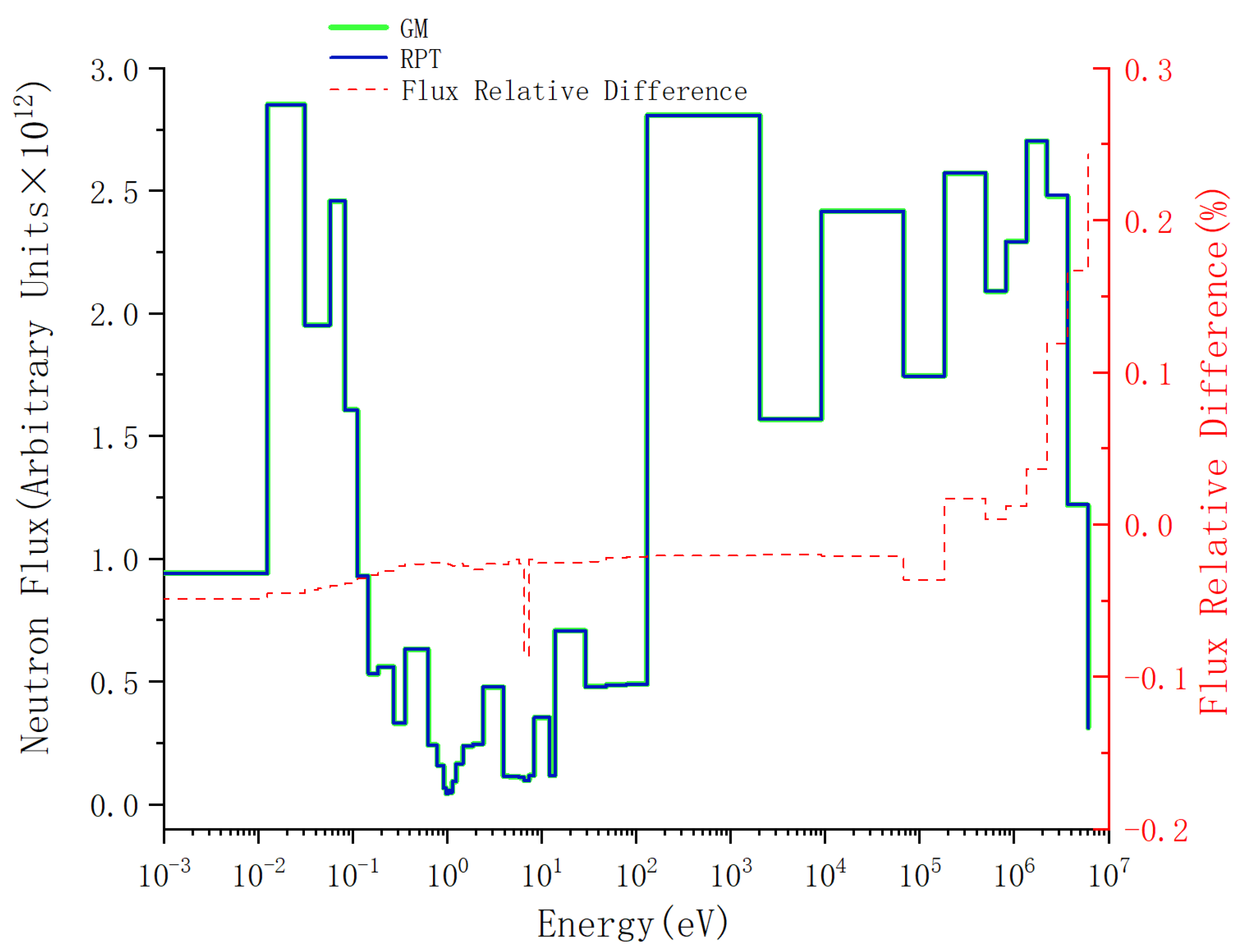
For plate-type fuel elements, among the five cases used for verification, the maximum error is 146 pcm and the minimum error is 18 pcm. These two cases with the maximum and minimum errors are selected for further verification. Both cases maintain a high level of accuracy during depletion, with the maximum errors being 168 pcm and 109 pcm, respectively. It stays within 200 pcm during depletion. Additionally, both cases maintain a high level of accuracy in the 235U density and fission rate, with errors within 0.1%. Regarding the neutron energy spectrum, the maximum errors for both cases occur in the low-energy range, at 6.55% and 5.1%, respectively. High accuracy is maintained in the medium- and high-energy ranges, with errors within 2%. For rod-type fuel elements, among the five cases used for verification, the maximum error is 99 pcm and the minimum error is 48 pcm. These two cases with the maximum and minimum errors are selected for further verification. Both cases maintain a high level of accuracy during depletion, with the maximum errors being 99 pcm and 49 pcm, respectively. It stays within 100 pcm during depletion. For the 235U and 239Pu density, the maximum error in both cases is within 1.5%. Regarding the neutron energy spectrum, unlike the plate-type fuel elements, high accuracy is maintained in the low-energy range, and while the error increases in the high-energy range, it remains within 1%. The data results show that the reactivity-equivalent physics transformation method based on the linear regression model not only has greatly improved the computational efficiency, but also ensures a very high accuracy, which meets the needs of practical usage.