Research on Reactivity-Equivalent Physical Transformation Method for Double Heterogeneity in Pressurized Water Reactors Based on Machine Learning

Abstract

Traditional computational methods for pressurized water reactors are unable to handle dispersed fuel particles as the double heterogeneity and the direct volumetric homogenization can result in significant errors. In contrast, reactivity-equivalent physical transformation techniques offer high precision for addressing the double heterogeneity introduced by dispersed fuel particles. This approach converts the double heterogeneity problem into a single heterogeneity problem, which is then subsequently investigated by using the conventional pressurized water reactor computational procedure. However, it is currently empirical and takes a lot of time to obtain the right k_∞. In this paper, we train the RPT model by using the existing dataset of plate-dispersed fuel and rod-dispersed fuel by a machine learning method based on a linear regression model, and we then use the new data to make predictions and derive the corresponding similarity ratios. The burnup verification, density verification, fission rate verification, and neutron energy spectrum analysis are calculated through the OpenMC program. For plate-type fuel elements, the method maintains an accuracy within 200 pcm during depletion, with deviations in the ²³⁵U density and ²³⁵U fission rate within 0.1% and neutron energy spectrum errors within 6%. For rod-type fuel elements, the method maintains an accuracy within 100 pcm during depletion, with deviations in ²³⁵U and ²³⁹Pu density within 1.5% and neutron energy spectrum errors within 1%. The numerical validation indicates that the reactivity-equivalent physical transformation method based on the linear regression model not only greatly improves the computational efficiency, but also ensures a very high accuracy to deal with double heterogeneity in nuclear reactors.

1. Introduction

Nuclear energy is a clean energy source, which has profound significance in reducing carbon emissions and ensuring energy supplies. In the process of nuclear energy development, nuclear safety is most critical, and the emergence of dispersed particles greatly improves nuclear safety. Dispersed fuels [1] can withstand higher temperatures under some extreme accident conditions and provide excellent intrinsic safety. It is gradually gaining attention in applications due to its excellent characteristics mentioned above. However, the addition of dispersed particles leads to the traditional single heterogeneity becoming a double heterogeneity. Due to the presence of double heterogeneity, traditional neutronics calculation programs are unable to characterize the particle-based dispersion system. To solve the problem of double heterogeneity, reactor physics researchers have proposed numerous approaches. Among many methods, the RPT (reactivity-equivalent physical transformation) method has gradually become a popular topic of research due to its simplicity and efficiency.

In 2005, the concept of the RPT [2] method was introduced to tackle the complexity of fuels with dispersed particles. The strategy entails condensing the dispersed particles into a smaller area while preserving the system’s reactivity at the beginning of the burnup depth, followed by the application of the VWH (volume homogenization method) to the particles located in the condensed region. Thus, the double heterogeneity system is converted to a single heterogeneity system. This method involves no alterations to the existing program’s computational algorithms. Instead, it enhances the accuracy of the results by simply adjusting the geometrical configurations. Furthermore, a novel resonance approach [3] has been introduced to tackle dual heterogeneity. It has been successfully incorporated into the ALPHA program’s resonance module, designed to address the dual heterogeneity challenges, and has shown that the results are of high accuracy. An improved reactivity-equivalent physical transformation (IRPT) method [4] has been put forward to precisely handle FCM fuel with burnable poison particles. This IRPT method is designed to be effective for both criticality and burnup evaluations, and it remains stable regardless of changes in operational parameters. Yet, the conventional RPT approach encounters challenges when attempting to depict systems featuring two types of particles containing poisons. To achieve a uniform distribution of TRISO fuel in high-temperature reactors, the RPT method is applied. For these calculations, the WIMS [5] and Serpent [6] have been employed to address the calculations of the homogenized and double heterogeneous models of TRISO fuel. To manage excessive reactivity and even out the power distribution across the radius, an innovative concept has been put into practice. This involves the application of varying thicknesses of IFBA coating onto the exterior surface of the TRISO particle fuel kernel [7]. Subsequently, neutronic assessments have been carried out, encompassing both two-dimensional full core [8] and three-dimensional full core [9] configurations, where the IFBA coating is uniformly dispersed. Furthermore, the ring reactivity-equivalent physical transformation method (RRPT) has been introduced [10,11], which more accurately simulates the stratified impact of burnable poisons compared to the traditional RPT method. In 2023, the reactive equivalent physical transformation method based on particle diameter (DRPT) [12] was introduced. This DRPT method has demonstrated high precision in dealing with plate heterogenous systems. It is characterized by its straightforward implementation, enhanced outcomes, and broad applicability. The impact of simulating different fuel shapes for the material testing reactor (MTR) is evaluated by building two OpenMC codes [13]. Upon examining the calculations from the two OpenMC models, it was noted that there is a minimal variation in the radial flux distribution, attributable to the similarity in fuel mass. The rapid fitting RPT methods based on the rod fuel elements [14] and the plate fuel elements [15] are proposed. The results show that the model with high fitting accuracy has practical engineering application value.

As the technology continues to evolve, machine learning is now expanding into the field of reactor analysis as a key tool for building alternative models for complex large-scale numerical computational programs. In 2022, Suubi Racheal [16] proposed a novel approach to train machine learning model and use augmented datasets reflecting sensor states. This study develops, trains, and compares three machine learning models: support vector machines (SVMs), decision trees (DTs), and multilayer perceptrons (MLPs). The results show that SVM and DT models perform better than MLP models. In 2023, Zhenhai Liu [17] carried out research on machine learning-based methods for constructing equivalent models for fuel rod temperature distribution. This study aimed to improve the computational efficiency of large-scale fuel rod performance simulation, and the construction strategy of the equivalent model for predicting the temperature distribution of fuel rods was discussed and analyzed in detail using fuel rod temperature prediction as a research example. The results show that the constructed equivalent model has a computational speedup of about 204 times compared to the COPERNIC program with high accuracy. In 2023, Guanghu [18] elaborated five DDML algorithms such as linear regression (LR), principal component analysis (PCA), and artificial neural network (ANN), and DDML showed good applicability in the simulation of multi-scale and multi-physics fields. Artificial intelligence and machine learning (AI/ML) technologies offer unique opportunities to transform nuclear plant operations and power generation. In 2024, the barriers to AI/ML adoption within the nuclear power industry were discussed [19], with a focus on existing commercial reactors. In 2024, HaoWu [20] developed an automated tree-based machine learning method for the nuclear pebble bed of the high temperature gas-cooled reactor (HTGR) to explore the complex thermal radiation behavior. The findings indicate that the AutoML model operates approximately 5 to 10 times more swiftly compared to conventional techniques. Additionally, the Pareto front of the AutoML model reveals that the mean square error diminishes as the model complexity is reduced, culminating in the attainment of the optimal solution. At present, the application of machine learning and artificial intelligence in the field of nuclear engineering is in a developing state, and there is still room for improvement. For example, in calculating the k_inf of a reactor, deterministic calculations for the core under a two-step framework have a computation cost at the level of around ten minutes, which provides sufficiently accurate results. Using machine learning for prediction can be faster, but it requires a large amount of simulated data for training initially, and the trained system cannot be used for different reactor types.

Through research and analysis, it has been found that the RPT method has been widely studied due to its simple and efficient advantages. However, most of them adopt traditional methods to obtain the similarity ratio of the RPT model, which requires the calculation of a large number of Monte Carlo program results and consumes a significant amount of time. Therefore, this paper connects machine learning with the RPT model; machine learning algorithms can automatically establish the RPT model, significantly improving the efficiency of obtaining the similarity ratio of the RPT model. The obtained RPT model can be calculated by using a conventional neutronics program.

2. Materials and Methods

This section provides an introduction to RPT methods and machine learning, and the RPT method based on machine learning is proposed.

2.1. Reactivity-Equivalent Physical Transformation

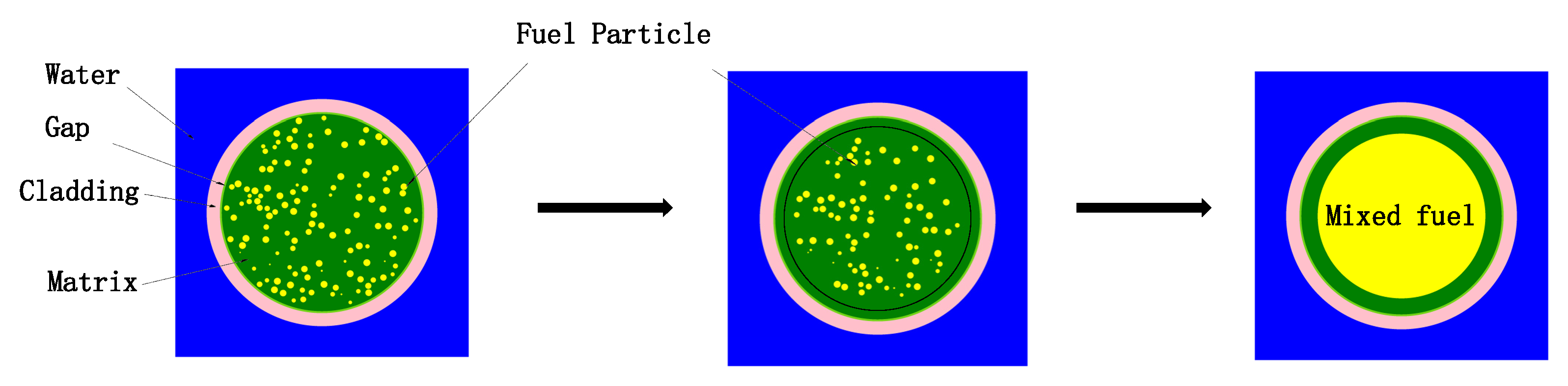
Figure 1 is a schematic diagram of the traditional RPT method. Initially, all the dispersed particles are compressed within a smaller fuel region; subsequently, for the compressed fuel region, homogenization is performed by using the volume weighting method, and the conventional pressurized water reactor physics calculation procedures are applied. In the RPT method, by ensuring that the k_inf of the system is equal to the reference solution, the radius of the compressed fuel region is determined. The reference solution is obtained through high-fidelity deterministic codes or Monte Carlo procedures.

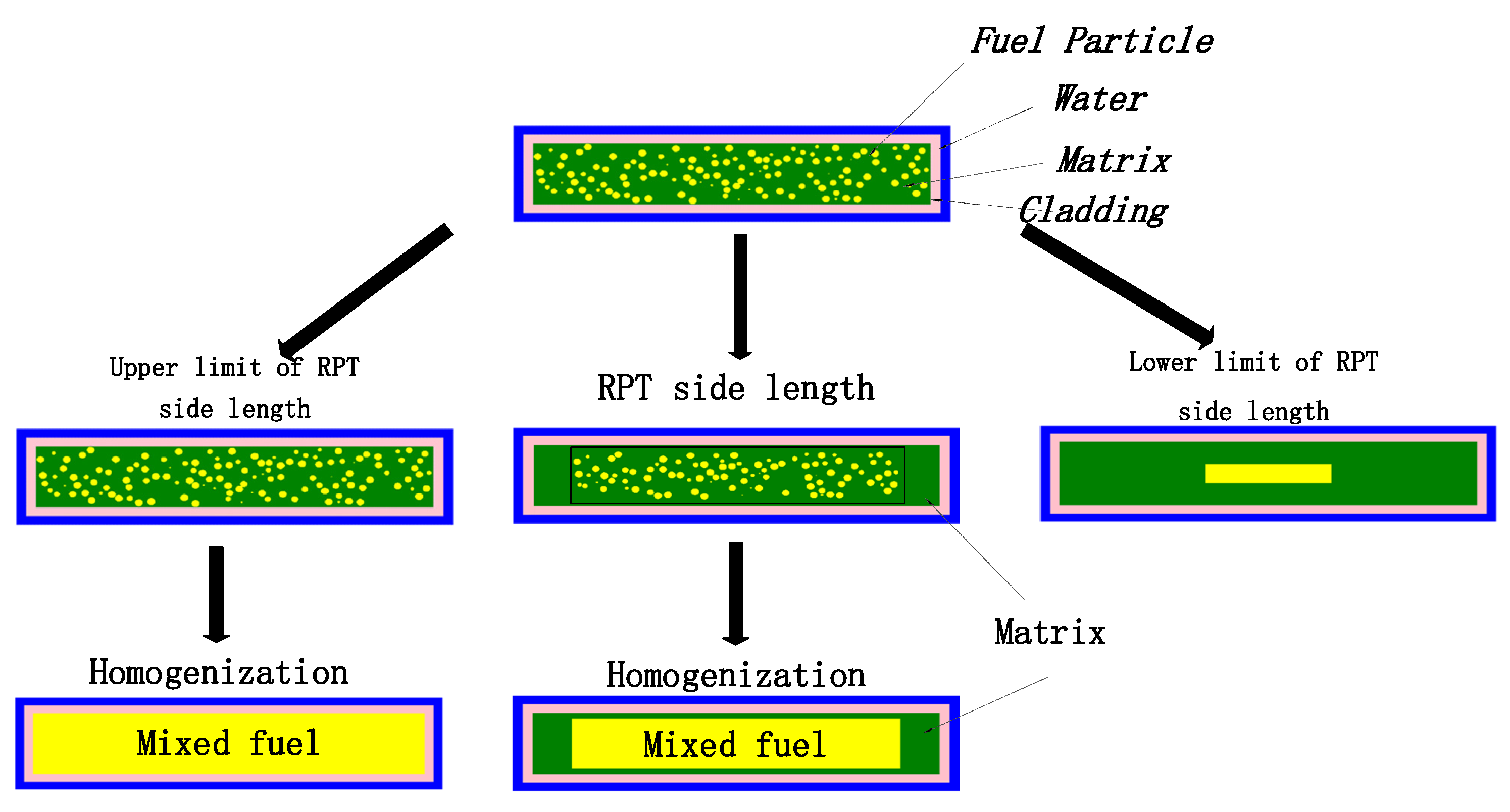
As depicted in Figure 2, a conventional RPT method for plate-shaped structures is introduced, which is an extension of the RPT method designed for cylindrical geometries. The principle behind the plate geometry RPT closely mirrors that of the cylindrical counterpart, with the key distinction being the rectangular fuel region in the plate, influenced by both its length and width dimensions. To address this, the concept of equivalent side lengths is introduced. These lengths represent the dimensions of the fuel area after reduction, where both the length and width are scaled down uniformly. The equivalent edge lengths are also bounded by the upper and lower bounds. The upper bound should not surpass the original fuel area’s dimensions, while the lower bound corresponds to the minimal length and width when all fuel particles are compressed to the fuel zone’s center. Typically, the exact equivalent side lengths fall within these upper and lower bounds.

A straightforward computational illustration of applying the RPT method to fuel plates with dispersed particles is provided in the central part of Figure 2. It is supposed that the fuel region of the plate element has a length of a, a width of b, and a height of H, with a packing fraction f for the dispersed particles.

1. The dispersed particles are compacted within a certain area, with both the length and width being reduced proportionally. Both a and b are scaled down by factor s, resulting in the new dimensions as and bs. The factor s is the similarity ratio (SR) of the fuel plate with its maximum value. Equation (1) is derived from the principle of maintaining the volume consistency of the dispersed particles.

2. The novel composite fuel material is synthesized via volumetric blending within the compacted fuel zone, with the matrix between the original and the newly formed fuel zones remaining unchanged. The nuclear number density is preserved across both the downsized fuel area and the initial fuel area. Consequently, the final RPT model for the fuel plate incorporating dispersed particles is formulated for this particular similarity ratio.

$$f\times a\times b\times H=a\times b\times H\times s^2$$

(1)

$$s=\sqrt{f}$$

Range of similarity ratios: ($\sqrt{f}$,1).

2.2. Introduction to Machine Learning RPT Method Based on Linear Regression Model

Machine learning based on linear regression modeling is a common supervised learning method used to predict the output of a continuous value. In linear regression, a linear relationship is assumed between the dependent variable (output) and the independent variable (characteristics). The model describes the relationship between the features and outputs by fitting the best possible straight line that minimizes the error between the predicted outputs and the actual observations. The basic form of the linear regression model can be expressed as Equation (2).

$$y={\omega }_0+{\omega }_1{x}_1+{\omega }_2{x}_2+\dots \dots +{\omega }_n{x}_n$$

(2)

where $y$ is the predicted value, ${\omega }_0$, ${\omega }_1$, ${\omega }_2$, ....., ${\omega }_n$ are the parameters (weights) of the model, and $x_1$, $x_2$, ..., $x_n$ are the input features. The essence of a linear regression model is to use the explanatory variables to estimate the mean of the explanatory variables through the least squares method. Find the best-fit straight line by obtaining the sum of the squares of the residuals between the minimized observations and the model predictions. By extracting the independent variables and creating and fitting a linear regression model, the predictions are made to the model to obtain the predicted values. In order to assess the performance of a model, it can be validated by using various metrics, such as the mean square error or coefficient of determination. These metrics measure the fit of the model to the observed data and its predictive ability, and then finally, the optimal parameters are adjusted to obtain the best prediction value required. In the RPT method, the compressed fuel equivalent radius is determined by ensuring that the k_inf of the system is equal to the reference solution. The reference solution is again obtained by a high-fidelity deterministic program or a Monte Carlo program. However, all are currently obtained empirically by spending a lot of time iterating in order to obtain the corresponding k∞. Therefore, this paper is based on the machine learning approach that can quickly derive the similarity ratios of the corresponding dispersed fuel particles. The principle of obtaining the similarity ratio is that the k_inf of the equivalent model is equal to the k_inf under the direct explicit particle modeling condition. The computational predictions are made by linear regression modeling for the parameters in the plate fuel element and rod fuel element that have a significant effect on the RPT model. The similarity ratios corresponding to them are finally obtained. The modeling process is described below: This model trains and predicts a linear regression model for a given dataset by using the Linear Regression model of the sklearn library.

• Data loading and preprocessing

First, the training data are loaded from the training set file by using the loadtxt function of the numpy library, and spaces are used as separators. We need to preprocess the data to extract features f, R, and S and target variable SR by a slicing operation.

2.

Linear regression model creation and training

By importing the LinearRegression class in the sklearn.linear_model module and instantiating the LinearRegression object after the data are preprocessed, a linear regression model is created. The fit method of the model pass the feature matrix x and the target variable y as parameters into the model for training in order to observe the model parameters by printing the coefficients coef_ and intercept intercept_ of the model.

3.

Model Prediction and Evaluation

After training the model, the model can be used to predict new data. First, load the test data in the test set file, extract the features f, R, S and the target variable SR, and then call the predicted method of the model to obtain the predicted values. In order to evaluate the performance of the model, the error calculation is also added, in addition to using the matplotlib library to plot the graphs of the true target and predicted values in order to compare the difference between them more intuitively.

4.

Prediction of new data

In addition to making predictions on the test data, we can also use the trained model to make predictions on unseen data. By creating a dataFrame object in pandas containing new feature values and using the model to make predictions, we can quickly apply the model to a new dataset and obtain predictions. In the next section, we will analyze the prediction of new rod and plate element parameters.

3. Results

In this section, the RPT method is investigated based on machine learning for both rod fuel elements and plate fuel elements. For the plate fuel element, three of the RPT parameters will be analyzed and calculated, which are shown in

Table 1. Plate-type element parameters.

No	Parameters	Comment
1	R	Outer radius of the fuel kernel
2	f	Packing fraction
3	S	Fuel area size

. For the rod fuel element, six of the RPT parameters will be analyzed and calculated, which are shown in

Table 2. Rod-type element parameters.

No	Parameters	Comment
1	Rpf	Outer radius of the fuel kernel
2	Rpar	Outer radius of the particle
3	Rcf	Outer radius of the cell fuel zone
4	L	Length of the cell
5	ρmod	Density of moderator
6	f	Packing fraction

. The results are validated and analyzed with conventional Monte Carlo calculations.

3.1. Plate-Type Component RPT Calculation Based on Linear Regression Model

Among the three parameters of the selected plate element, the value range of R is 0.015–0.04, the value range of S is 0.72–0.72 × 1.52, and the value range of f is 0.1–0.3. The SR is the actual similarity ratio calculated from these three parameters. The three parameters R, S, and f and the corresponding similarity ratio SR are selected from the existing data, and a total of 19 groups are shown in

Table 3. Plate element RPT training parameters.

Case	f	R (cm)	S (cm2)	SR
1	0.15	0.02	0.8712	0.896
2	0.25	0.03	1.0368	0.925
3	0.3	0.035	1.62	0.943
4	0.2	0.04	0.72	0.845
5	0.25	0.02	1.2168	0.952
6	0.15	0.025	1.62	0.89
7	0.2	0.03	1.4112	0.915
8	0.1	0.015	1.0368	0.89
9	0.15	0.03	1.4112	0.87
10	0.2	0.035	1.0368	0.875
11	0.25	0.035	1.2168	0.91
12	0.15	0.025	0.8712	0.868
13	0.25	0.02	0.8712	0.953
14	0.1	0.015	1.62	0.905
15	0.25	0.04	1.0368	0.895
16	0.25	0.025	1.0368	0.94
17	0.2	0.02	1.62	0.952
18	0.3	0.035	1.0368	0.92
19	0.15	0.025	1.2168	0.89

, which are used for training the model. The prediction results are shown in Figure 3 and

Table 4. Plate element RPT training parameters.

Case	SR	SR_PRED	Absolute Error
1	0.907027	0.91365155	0.00662455
2	0.870681	0.88027745	0.00959645
3	0.92595	0.93297148	0.00701248
4	0.85175	0.86095752	0.00920752
5	0.896875	0.89139689	0.00547811

.

A quantitative and qualitative analysis of the machine learning model’s process will be provided here. Table 3 and

Table 5. Rod element RPT parameters (training).

Case	Rpf	Rpar	Rcf	f	L	ρmod	SR
1	0.032	0.053	0.6	0.36	1.597	0.53	0.791587
2	0.038	0.052	0.59	0.41	1.689	0.85	0.88578
3	0.029	0.055	0.6	0.39	1.602	0.94	0.771288
4	0.034	0.05	0.6	0.47	1.683	0.67	0.879322
5	0.029	0.056	0.56	0.38	1.669	0.9	0.758034
6	0.036	0.053	0.61	0.51	1.661	0.96	0.872503
7	0.03	0.049	0.59	0.43	1.72	0.6	0.867403
8	0.03	0.055	0.55	0.34	1.68	0.61	0.750047
9	0.027	0.049	0.56	0.47	1.758	0.98	0.871202
10	0.038	0.051	0.59	0.52	1.605	0.61	0.886234
11	0.036	0.049	0.56	0.41	1.728	0.78	0.922807
12	0.029	0.053	0.58	0.5	1.745	0.64	0.841566
13	0.032	0.052	0.61	0.51	1.753	0.91	0.882943
14	0.034	0.049	0.6	0.37	1.72	0.67	0.887217
15	0.032	0.049	0.58	0.53	1.623	0.52	0.870648
16	0.03	0.055	0.57	0.43	1.622	0.98	0.777879
17	0.037	0.05	0.56	0.42	1.617	0.7	0.886357
18	0.034	0.049	0.56	0.46	1.713	0.7	0.908090
19	0.028	0.05	0.56	0.39	1.608	0.53	0.794398
20	0.032	0.05	0.55	0.36	1.634	0.74	0.828195
21	0.032	0.049	0.55	0.34	1.762	0.52	0.866093

represent the data used for model prediction for rod-type and plate-type fuel elements, respectively. For plate-type elements, the f, R, and S are the independent variables while SR is the dependent variable. For rod-type elements, R_pf, R_par, R_cf, ρ_mod, f, and L are the independent variables, while SR is the dependent variable. After the data are preprocessed, a LinearRegression object is instantiated by using the LinearRegression class in the sklearn.linear_model module. With this, a linear model is trained. Table 4 and

Table 6. Rod element RPT training parameters.

Case	SR_GM	SR_PRED	Absolute Error
1	0.763909	0.76932157	0.00541257
2	0.836235	0.83230878	0.00392622
3	0.849329	0.85283524	0.00350624
4	0.878268	0.88498019	0.00671219
5	0.899911	0.90717844	0.00726744

display the similarity ratios and absolute deviations between the two, thereby analyzing the relevant physical properties through the similarity ratios. This is a flowchart to facilitate the understanding of the paper’s structure which is shown in Figure 4.

Through Figure 3, it can be seen that the linear regression model has a better training effect, and the predicted data curves are basically close to overlap. It shows that the method of machine learning to deal with the plate element RPT is more accurate and can meet the practical needs.

3.2. Calculation of RPT for Rod Elements Based on Linear Regression Modeling

The six parameters and the corresponding similarity ratio SR are selected from the existing data, and a total of 21 groups are shown in Table 5, which are used for training the model. The trained model is used to predict five new datasets in Table 6.

In comparison of the final obtained results, the absolute errors are kept in the thousandths of a percentile, and the relative errors are kept within 1%. It can be seen through Figure 5 that the linear regression model is trained better and that the predicted data curves basically overlap. This indicates that the machine learning approach handles the rod element with high accuracy and meets the practical requirements.

3.3. Numerical Validation and Analysis

3.3.1. Plate Fuel Element Validation Analysis

In this section, the OpenMC [21] program is used to validate the similarity ratios of the predicted RPT parameters of the plate elements above. It includes the $k_{\inf ,GM}$ calculated by the actual similarity ratio and the $k_{\inf ,RPT}$ calculated by the predicted similarity ratio. SR_PRED is the predicted similarity ratio. The results of the k_inf -deviation are shown in

Table 7. Deviation in verification of plate fuel elements.

Case	${\mathit{k}}_{\mathbf{i}\mathbf{n}\mathbf{f},\mathit{G}\mathit{M}}$	${\mathit{k}}_{\mathbf{i}\mathbf{n}\mathbf{f},\mathit{R}\mathit{P}\mathit{T}}$	SR_PRED	kinf-Deviation (pcm)
1	1.33493	1.33516	0.913652	23
2	1.39146	1.39263	0.880277	117
3	1.36264	1.36282	0.932971	18
4	1.36938	1.37048	0.860958	110
5	1.36639	1.36751	0.891397	146

, and the k_inf -deviation is shown in Equation (3).

$$k-deviation=(k_{{\inf }_{RPT}}-k_{{\inf }_{GM}})\times {10}^5$$

(3)

From Table 7, it can be concluded that both k_inf deviations are small and that the deviations are kept within 200 pcm, which meets the actual accuracy requirements. Among them, Case5 has the largest deviation of 146 pcm and Case3 has the smallest deviation of 18 pcm.

Burnup Verification

In Section 3.3.1, Case3 and Case5 are selected to validate the GM model and RPT model for burnup, and Figure 6 and Figure 7 demonstrate the variation of k_inf during the burnup process.

The overall trend in both remains consistent: the k_inf decreases with increasing burnup depth. In Case3, the RPT model curves basically overlap with the GM model curves, the maximum deviation is less than 200 pcm, and they overall were maintained within 100 pcm. The maximum error is 168.62 pcm at a burnup depth of 1.037 MWd/t, and the minimum deviation is 13.384 pcm at a burnup depth of 4.666 MWd/t. In Case5, the RPT model curves basically coincide with the GM model curves and the maximum deviation is 108.85 pcm at a burnup depth of 4.66575 MWd/t. The minimum deviation is 13.357 pcm at a burnup depth of 2.592 MWd/t. This indicates that the RPT model maintains a high accuracy over the full lifetime of the burnup.

²³⁵U Density Verification

Case3 with the smallest k_inf deviation and Case5 with the largest k_inf deviation in Table 7 are selected to validate the ²³⁵U density against the GM model and the RPT model, and Figure 8 and Figure 9 demonstrate the variation of ²³⁵U density with burnup.

The general trend remains consistent for both, with the ²³⁵U density decreasing as the depth of burnup increases. It is obvious in both figures that the GM model curves overlap completely with the RPT model curves, and the relative errors show an increasing trend but are of a small order of magnitude. At a burnup depth of 5.869 MWd/t, the maximum error is 0.00284% which is negligible. This indicates that the ²³⁵U density of the RPT model is basically unaffected by the fit over the full lifetime of the burnup and meets the practical accuracy requirements.

²³⁵U Fission Rate Validation

Case3 with the smallest k_inf deviation and Case5 with the largest k_inf deviation in Table 7 are selected to validate the ²³⁵U fission rate for the GM model and RPT model, and Figure 10 and Figure 11 demonstrate the variation of the ²³⁵U fission rate with burnup.

In the case with the smallest k_inf deviation, the maximum error is 0.021% at a burnup depth of 2.592 MWd/t. In the case with the largest k_inf deviation, the maximum error is 0.011% when the burnup depth reaches 6.221 MWd/t. This indicates that the ²³⁵U fission rate of the RPT model is basically unaffected by the fit over the full life of the burnup and meets the practical accuracy requirements.

Neutron Energy Spectrum Analysis

The neutron energy spectrum delineates the spread of neutrons within the reactor based on their energy levels. Case3 with the smallest k_inf deviation and Case5 with the largest k_inf deviation in Table 7 are selected to analyze the neutron energy spectrum of the GM model and the RPT model. Figure 12 and Figure 13 demonstrate the variation in neutron fluxes with neutron energies and the relative errors.

In the low-energy region, the relative errors of the GM model and the RPT model are large. For Case3, the relative error is 6.55% at an energy of 1.23 × 10⁻³ eV. For Case5, the relative error is 5.10% at an energy of 1.23 × 10⁻³ eV. The trends of the energy spectra of the GM and RPT models are basically the same in the middle- and high-energy regions. The deviation of the RPT model in the resonance region fluctuates significantly in both cases due to the partial loss of the self-shielding effect, but the deviation is within 2%.

3.3.2. Rod Fuel Element Validation Analysis

In this section, the OpenMC program will be used to validate the similarity ratios of the five sets of data for the rod element, and the results of its k_inf deviation are shown in

Table 8. Actual and predicted k_inf and deviation of k_inf for rod fuel.

Case	${\mathit{k}}_{\mathbf{i}\mathbf{n}\mathbf{f},\mathit{G}\mathit{M}}$	${\mathit{k}}_{\mathbf{i}\mathbf{n}\mathbf{f},\mathit{R}\mathit{P}\mathit{T}}$	SR_PRED	kinf-Deviation (pcm)
1	1.312222	1.313213	0.76932157	99.1
2	1.360558	1.359970	0.83230878	58.8
3	1.402700	1.403181	0.85283524	48.1
4	1.452812	1.453629	0.88498019	81.7
5	1.470916	1.471734	0.90717844	81.8

.

From Table 8, it can be concluded that the deviation between $k_{\inf ,RPT}$ calculated by the model and the actual value of rod fuel $k_{\inf ,GM}$ is small, being kept within 100 pcm. It indicates that the linear regression model fits well and meets the requirement of practical accuracy.

Burnup Verification

Case3 with the smallest k_inf deviation and Case1 with the largest k_inf deviation in Table 8 are selected to validate the GM model and RPT model with burnup, and Figure 14 and Figure 15 show the variation of $k_{\inf ,GM}$ and $k_{\inf ,RPT}$ with burnup.

For Case3 and Case1, the general trends remain consistent, both decreasing with an increasing burnup depth. In Case3, the RPT model curve basically coincides with the GM model curve, and the pcm shows a monotonically increasing trend. The maximum deviation is less than 50 pcm. The maximum error is 48.7 pcm at a burnup depth of 19.25 MWd/t, and the minimum error is 45.7 pcm at a burnup depth of 1.75 MWd/t. In Case1, the RPT model curve is basically coincident with the GM model curve, and the pcm shows a monotonically increasing trend, with the maximum deviation not exceeding 100 pcm. The maximum error is 98.7 pcm at a burnup depth of 19.25 MWd/t, and the minimum error is 93.6 pcm at a burnup depth of 1 MWd/t. This indicates that the fitting effect of the RPT model is very stable and can maintain a high accuracy during the burnup lifetime.

²³⁵U, ²³⁹Pu Density Verification

Case3 with the smallest k_inf deviation and Case5 with the largest k_inf deviation in Table 8 are selected to validate the ²³⁵U and ²³⁹Pu densities of the GM model and the RPT model, Figure 16 and Figure 17 illustrate the variation in the ²³⁵U density with burnup, and Figure 18 and Figure 19 illustrate the variation in the ²³⁹Pu density with burnup.

As can be seen from the figure, the general trend remains the same for both, with the ²³⁵U density decreasing during the burnup. In Case3, the maximum error is 0.1965% when the burnup depth reaches 0.25 MWd/t; in Case5, the maximum error is negligible at 0.2216% when the burnup depth is at the initial value.

As can be seen from the figure, the general trend remains the same for both, with the ²³⁹Pu density decreasing during the burnup. In Case3, the maximum error is 0.643% when the burnup depth reaches 19.25 MWd/t; in Case5, the maximum error is 0.823% when the burnup depth reaches 19.25 MWd/t, which is negligible. This indicates that the ²³⁵U density and ²³⁹Pu density of the RPT model are basically unaffected by the fitting during the burnup lifetime and meet the practical accuracy requirements.

Neutron Energy Spectrum Analysis

The distribution of neutrons within a reactor based on their energy is represented by the neutron energy spectrum. Case3 with the smallest k_inf deviation and Case1 with the largest k_inf deviation in Table 8 are selected to analyze the neutron energy spectrum of the GM model and the RPT model, and the variation in neutron fluxes with neutron energies and the flux relative errors are demonstrated in Figure 20 and Figure 21.

The relative errors between the GM model and the RPT model are smaller in the low-energy and medium-energy regions. The fluctuations in the resonance region of the high-energy region are obvious, but the relative errors are all within 0.445%, which is negligible and meets the actual accuracy requirements.

4. Conclusions

In this paper, the reactive-equivalent physical transformation method, which is based on machine learning, is used to calculate and predict the RPT parameters of plate-dispersed fuel particles and rod-dispersed fuel particles through a linear regression model, and the similarity ratio of the corresponding parameters is derived. The equivalent radius or equivalent side length of the RPT model is calculated using the similarity ratios. The burnup verification, density verification, fission rate verification, and neutron energy spectrum analysis are carried out by OpenMC programs.

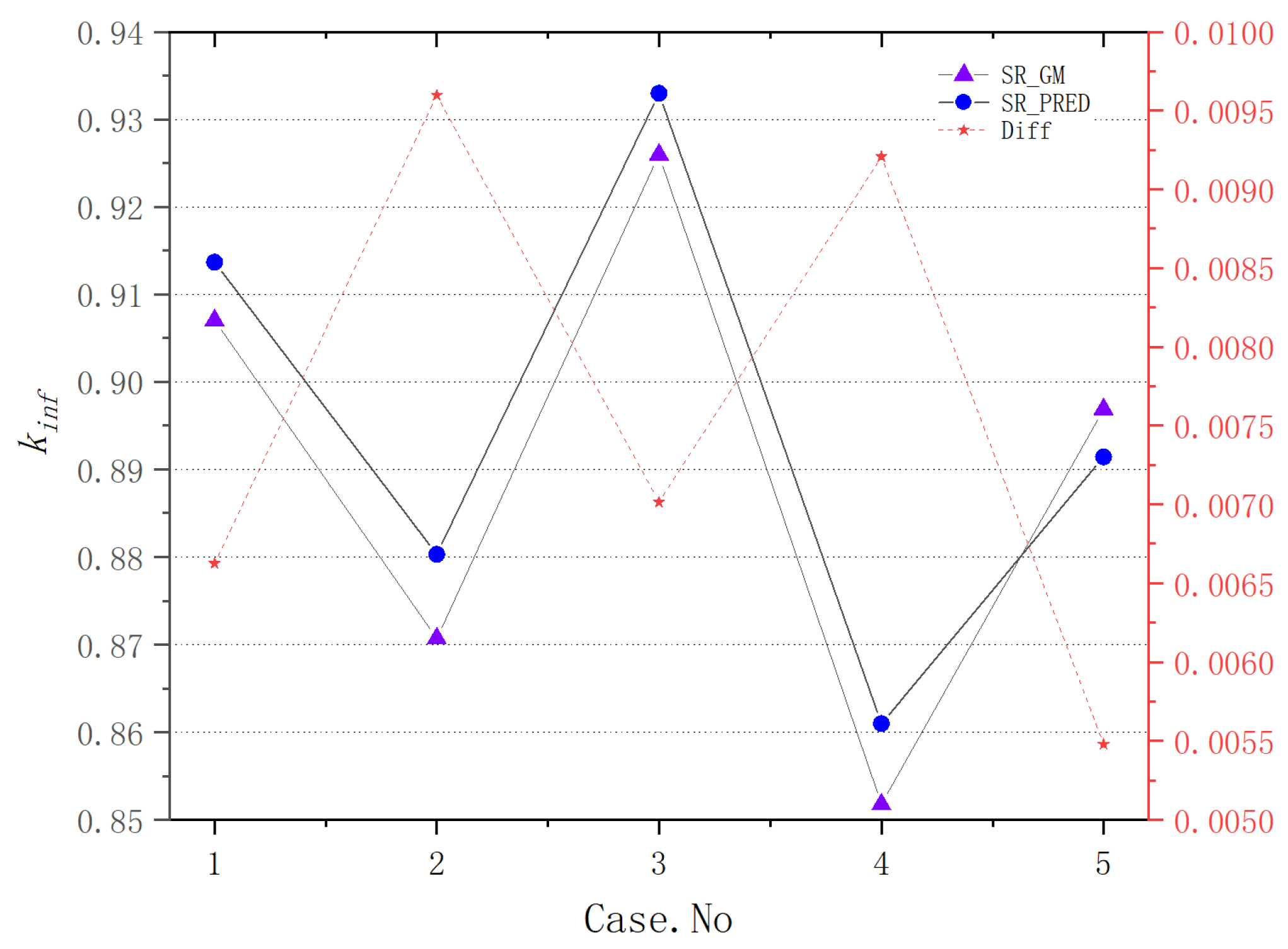
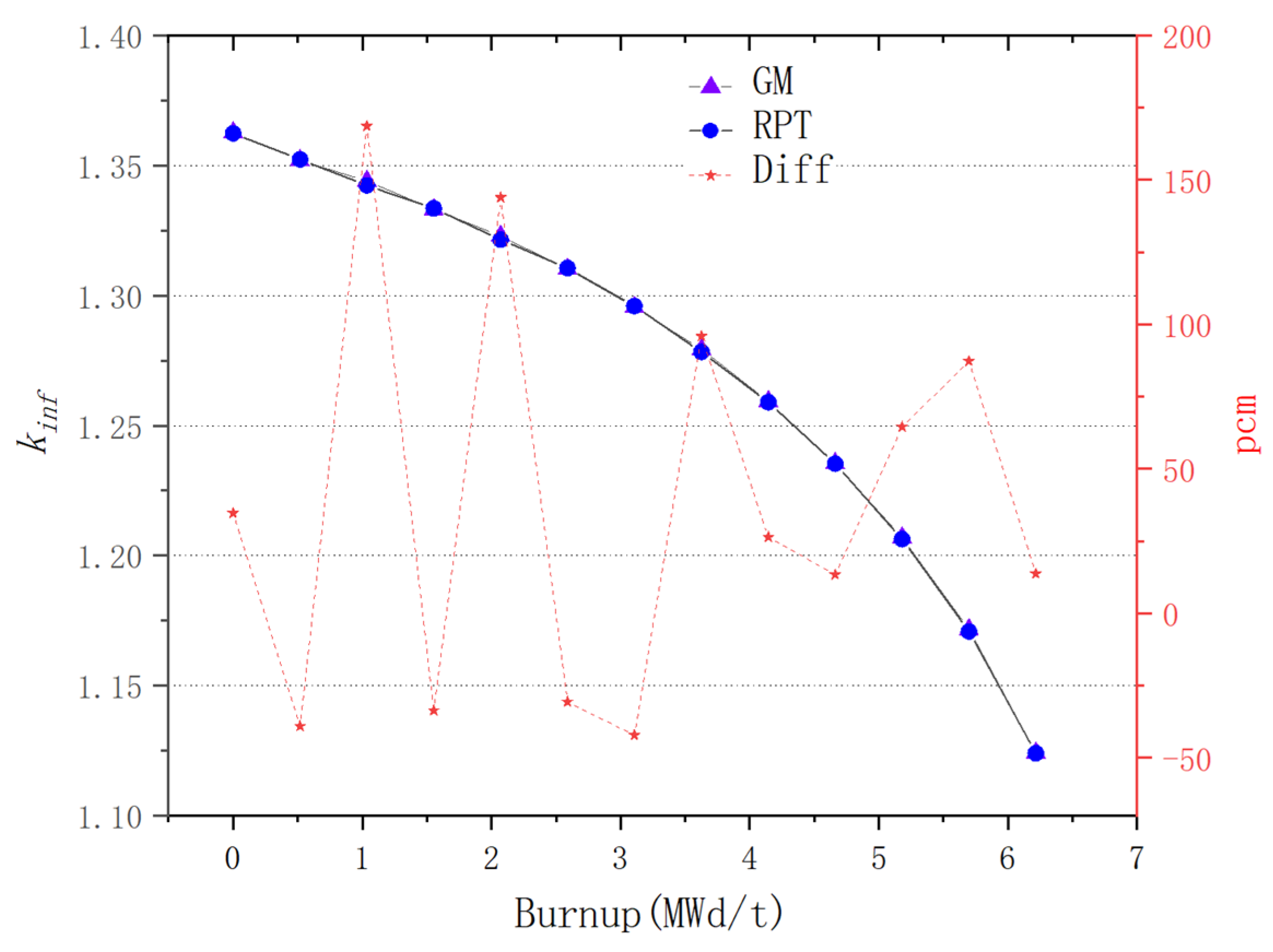
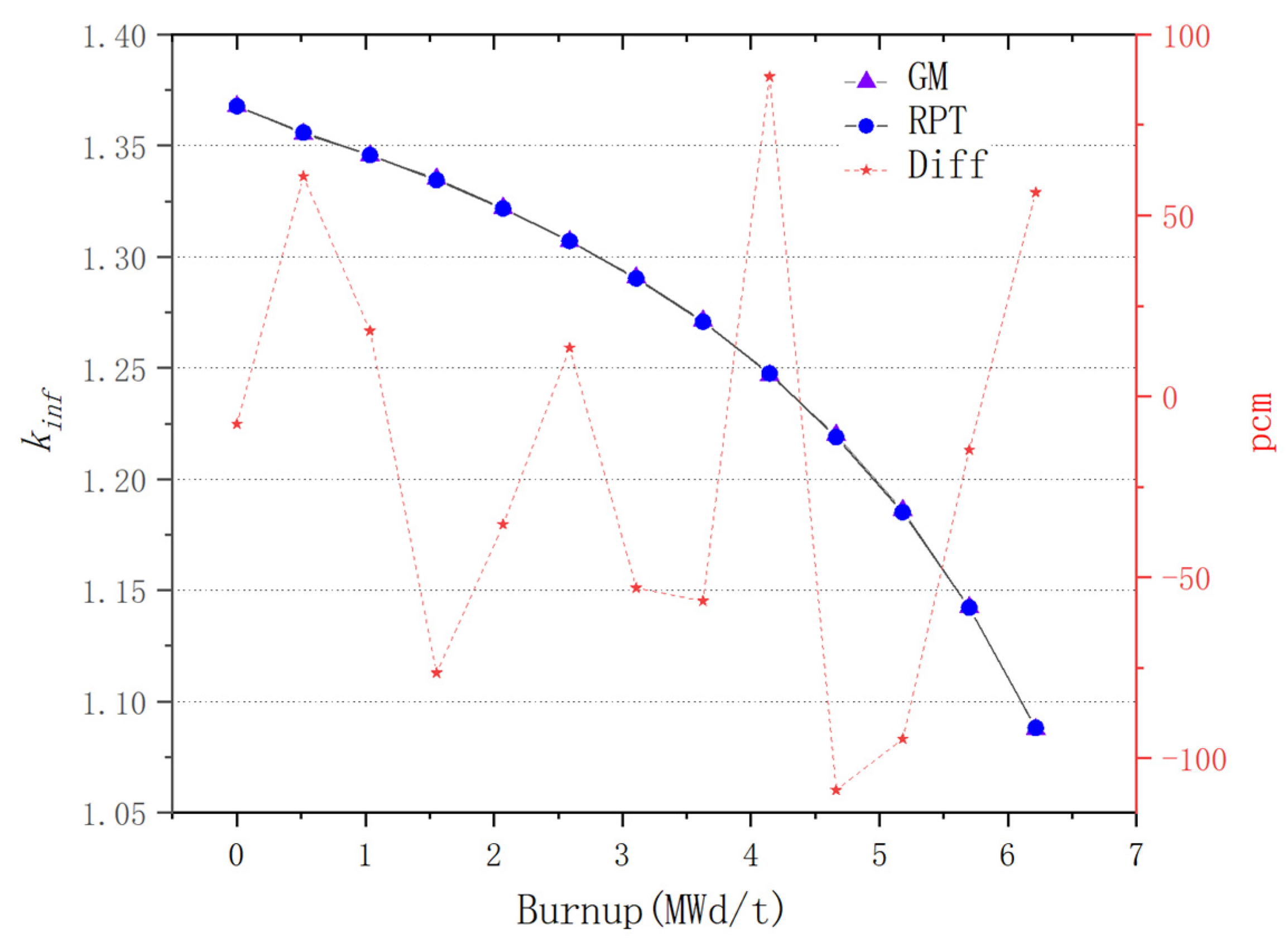
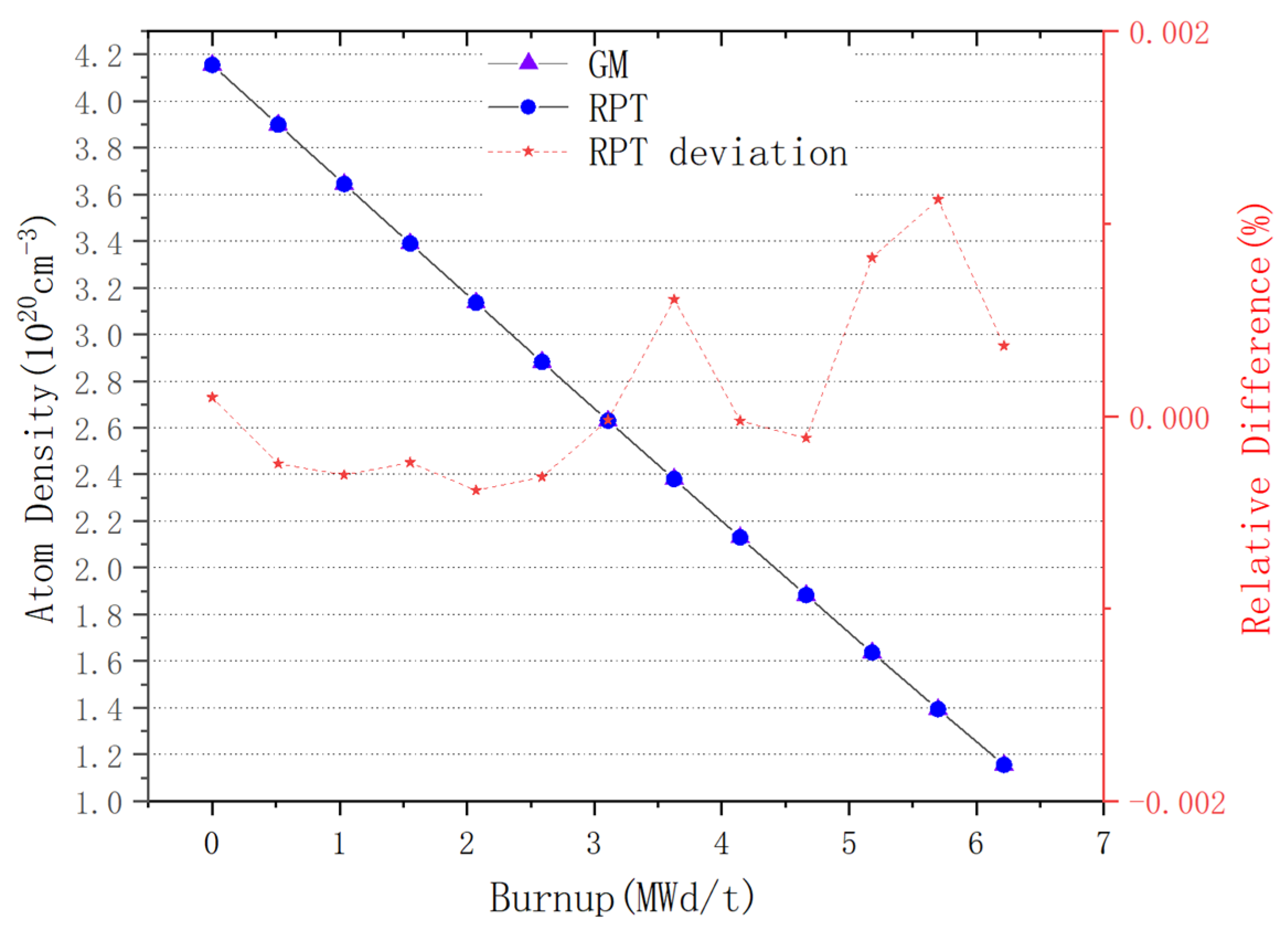
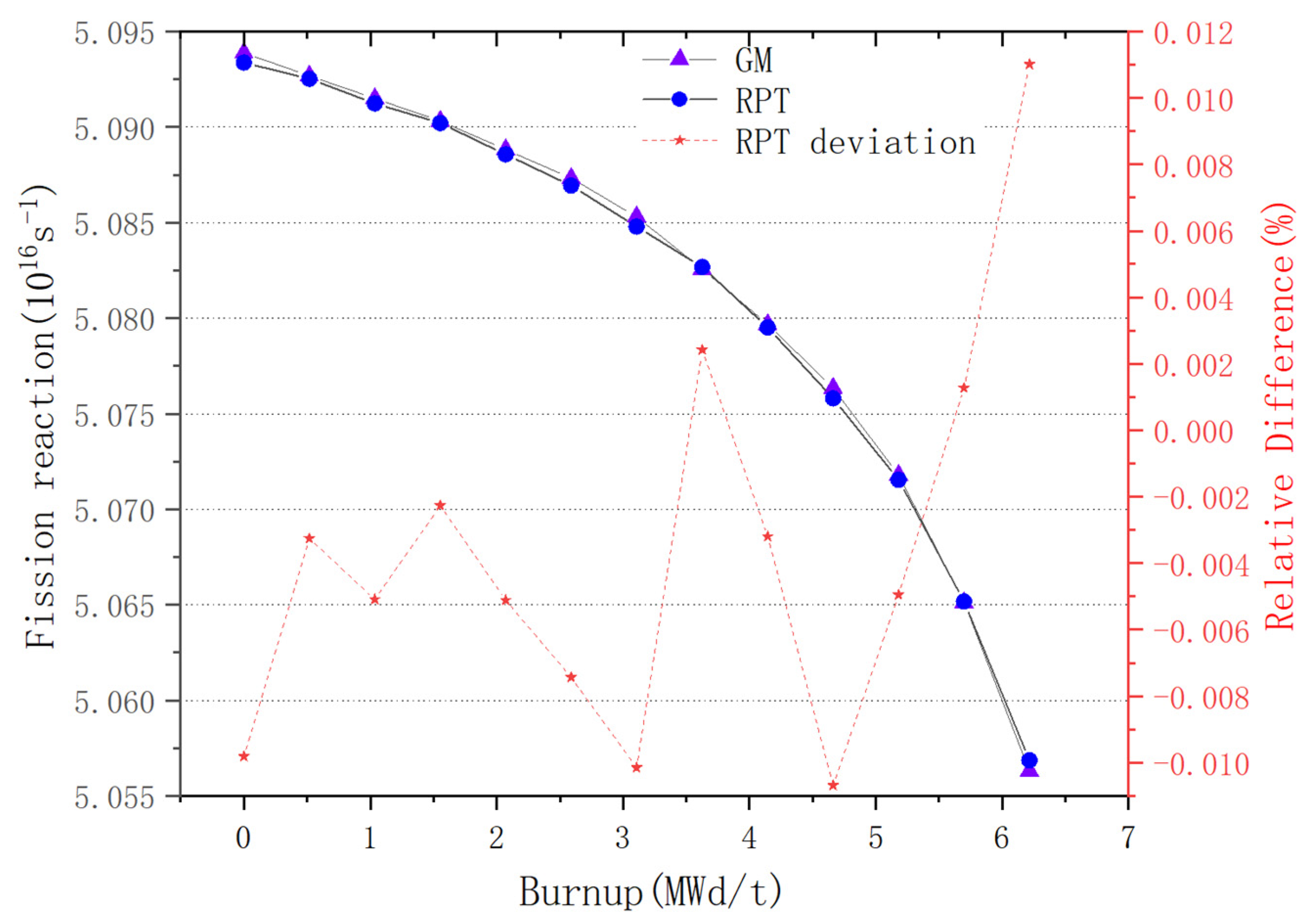
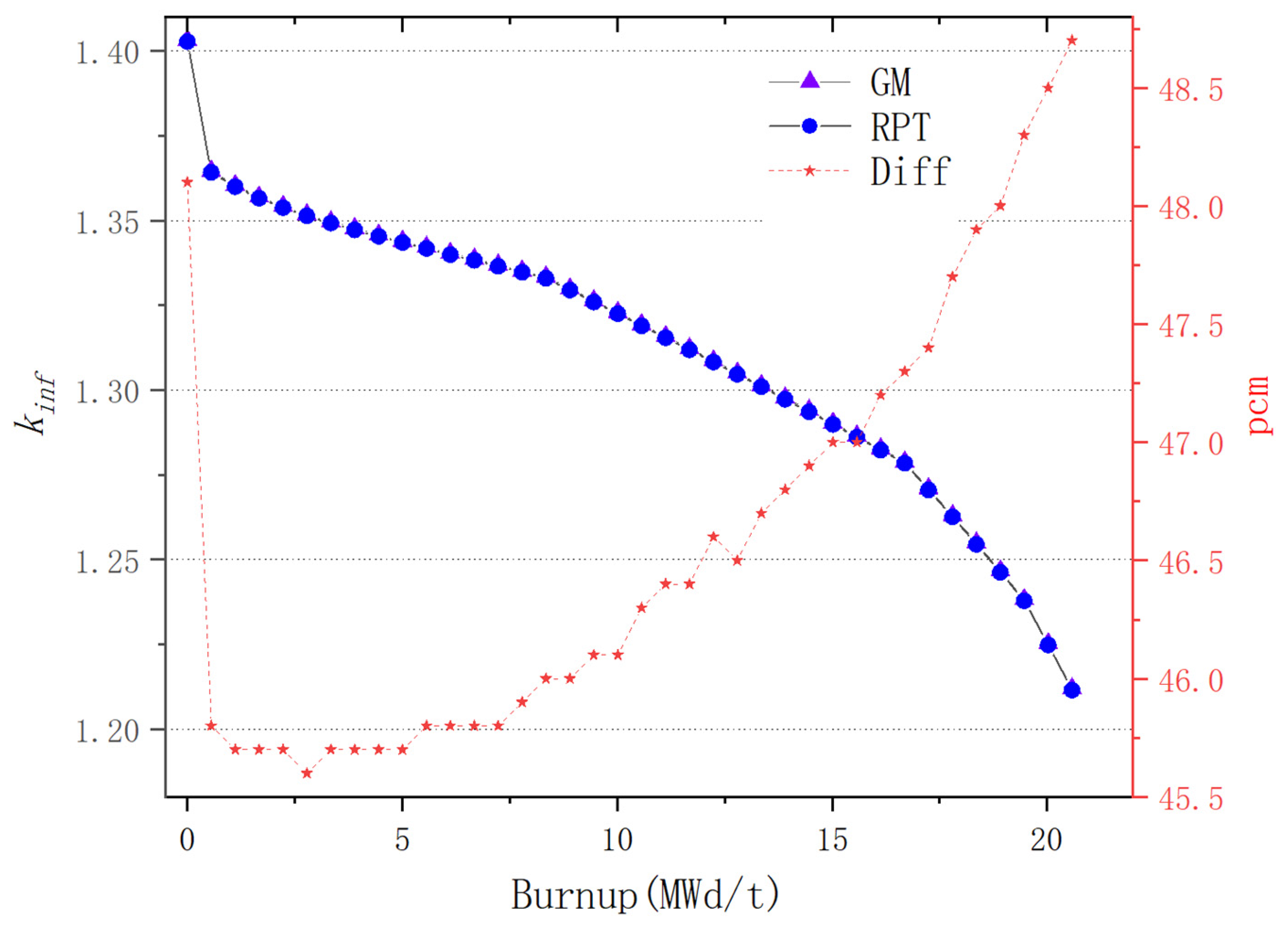
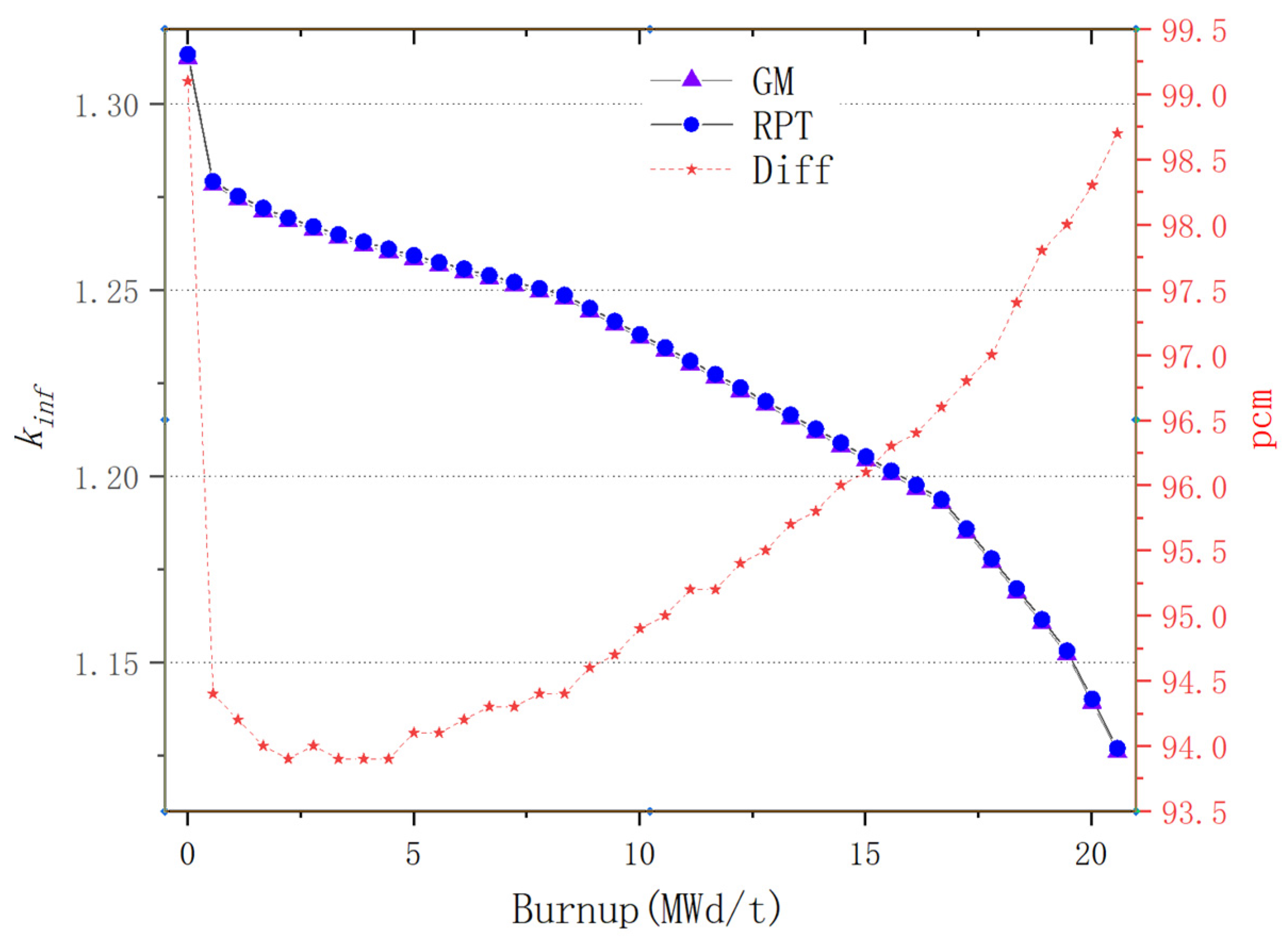
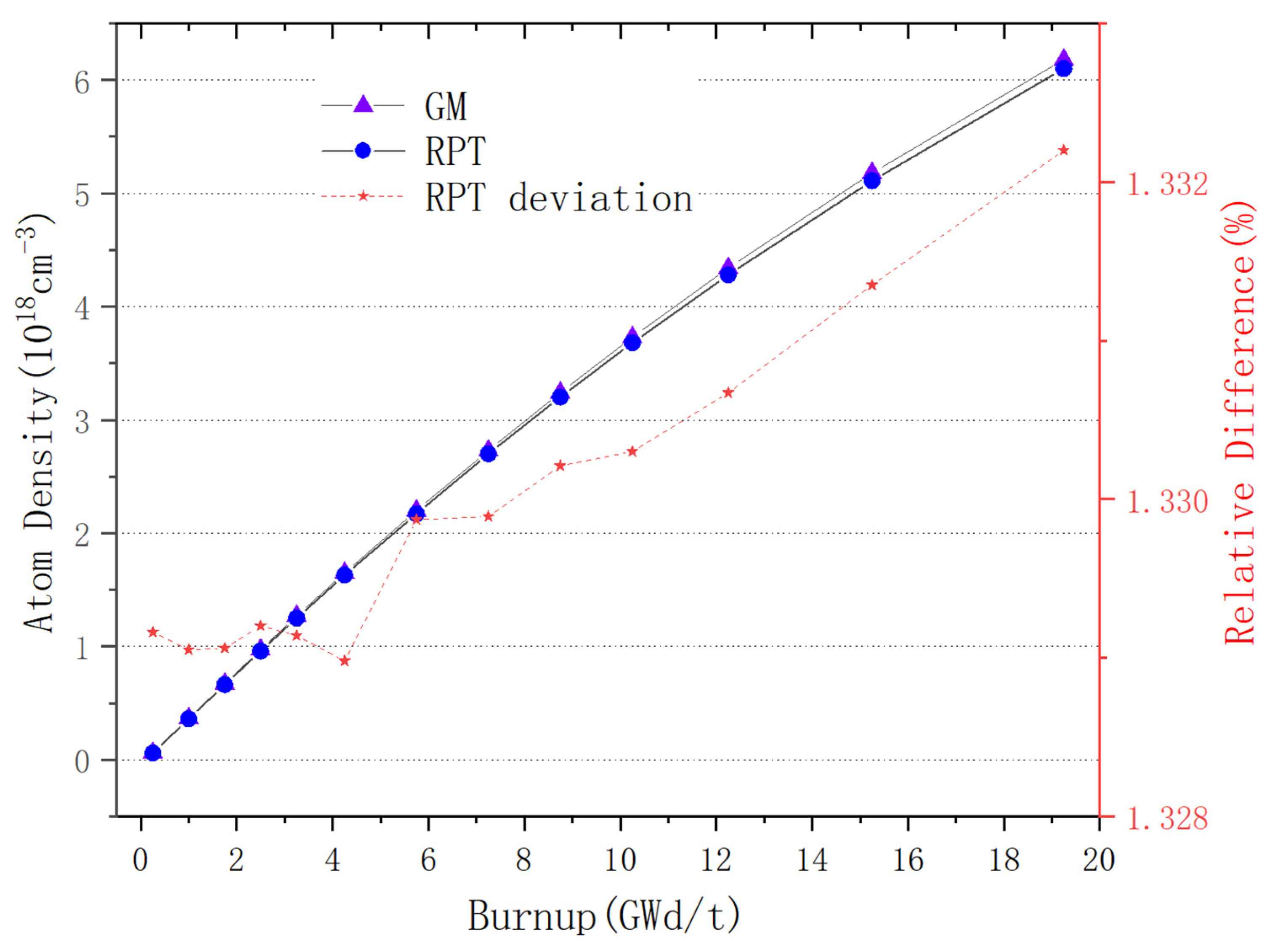
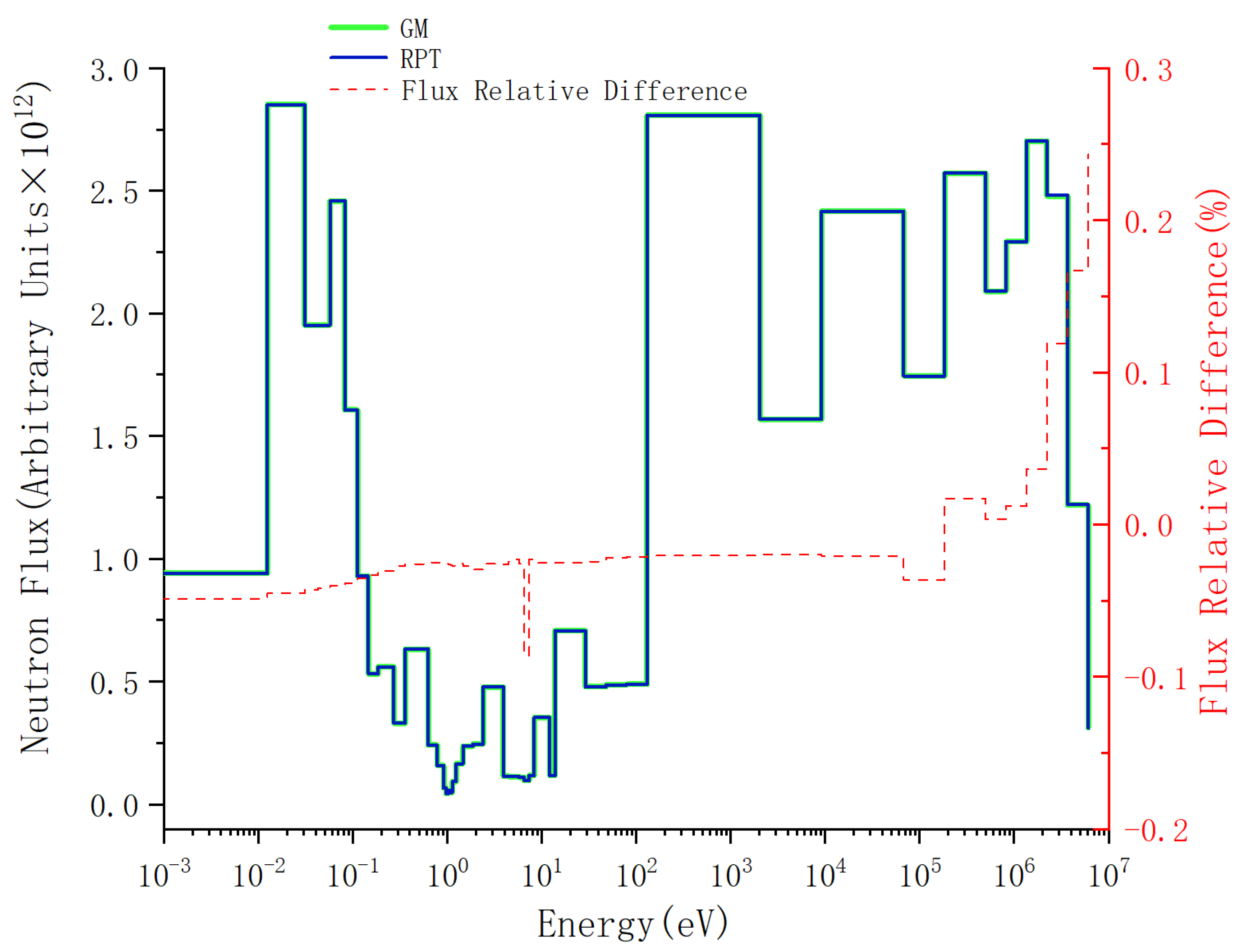
For plate-type fuel elements, among the five cases used for verification, the maximum error is 146 pcm and the minimum error is 18 pcm. These two cases with the maximum and minimum errors are selected for further verification. Both cases maintain a high level of accuracy during depletion, with the maximum errors being 168 pcm and 109 pcm, respectively. It stays within 200 pcm during depletion. Additionally, both cases maintain a high level of accuracy in the ²³⁵U density and fission rate, with errors within 0.1%. Regarding the neutron energy spectrum, the maximum errors for both cases occur in the low-energy range, at 6.55% and 5.1%, respectively. High accuracy is maintained in the medium- and high-energy ranges, with errors within 2%. For rod-type fuel elements, among the five cases used for verification, the maximum error is 99 pcm and the minimum error is 48 pcm. These two cases with the maximum and minimum errors are selected for further verification. Both cases maintain a high level of accuracy during depletion, with the maximum errors being 99 pcm and 49 pcm, respectively. It stays within 100 pcm during depletion. For the ²³⁵U and ²³⁹Pu density, the maximum error in both cases is within 1.5%. Regarding the neutron energy spectrum, unlike the plate-type fuel elements, high accuracy is maintained in the low-energy range, and while the error increases in the high-energy range, it remains within 1%. The data results show that the reactivity-equivalent physics transformation method based on the linear regression model not only has greatly improved the computational efficiency, but also ensures a very high accuracy, which meets the needs of practical usage.