Artificial Intelligence for Hybrid Modeling in Fluid Catalytic Cracking (FCC)
Abstract
:1. Introduction
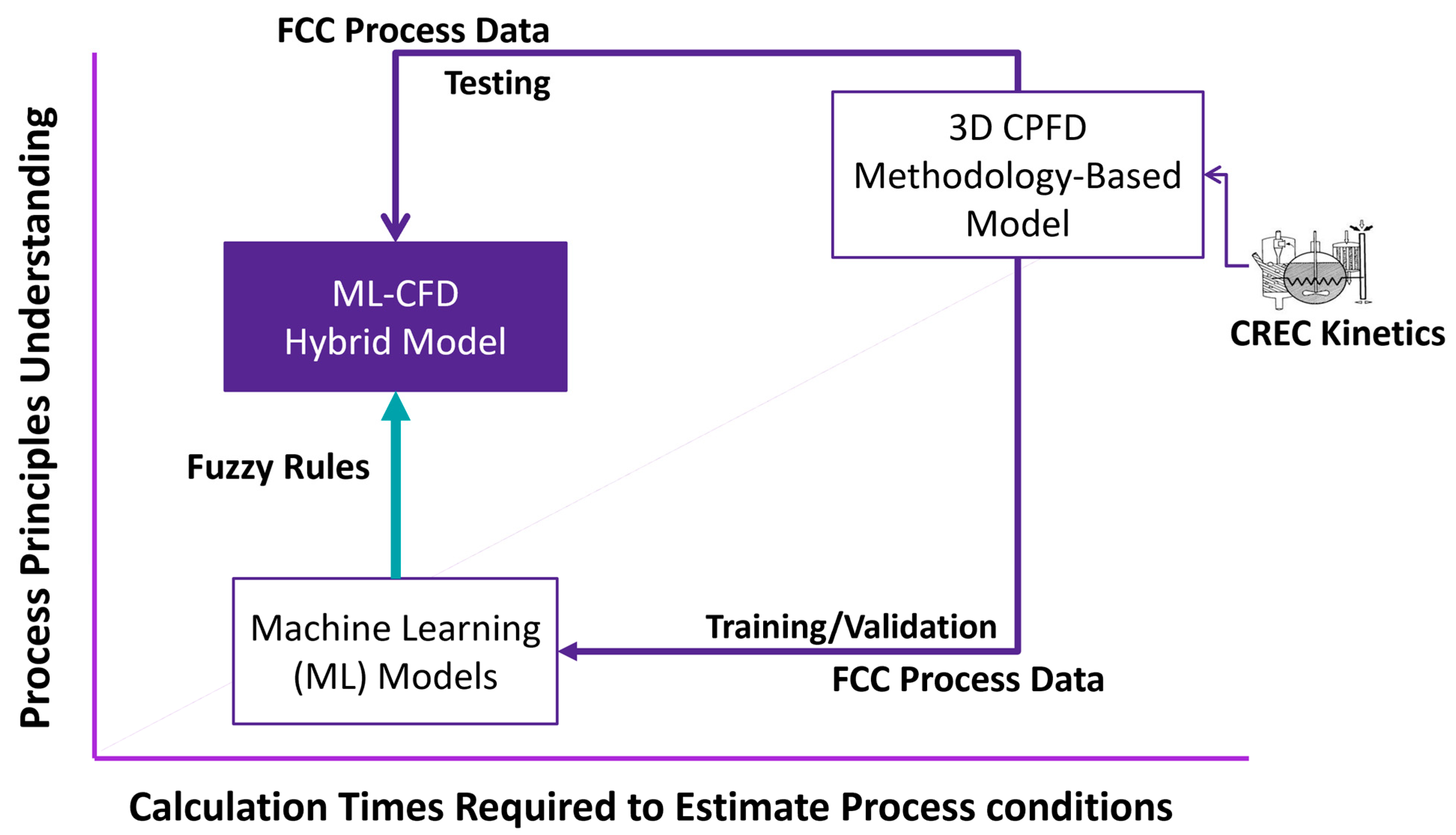
- The development and implementation of a reliable CPFD model to simulate an industrial-scale FCC riser reactor unit, including trustable kinetics determined in a CREC riser simulator.
- The establishment of AI-based models for the prediction of FCC riser reactor unit performance under a wide range of typical FCC riser operating conditions.
- It is our understanding that there is no study in the open literature addressing such a significant topic.
2. Methodology
2.1. Computational Particle-Fluid Dynamics (CPFD)
- Fluid and catalyst particle properties,
- Fluid momentum balances using averaged Navier–Stokes equations coupled with the particle phase,
- Particle-fluid interactions using an energy minimization multiscale (EMMS) drag model,
- Particle interactions via a particle stress function ,
- Enthalpy balances, including gas and particles contributions,
- FCC catalyst particle size distribution,
- Suitable FCC VGO cracking reaction kinetics.
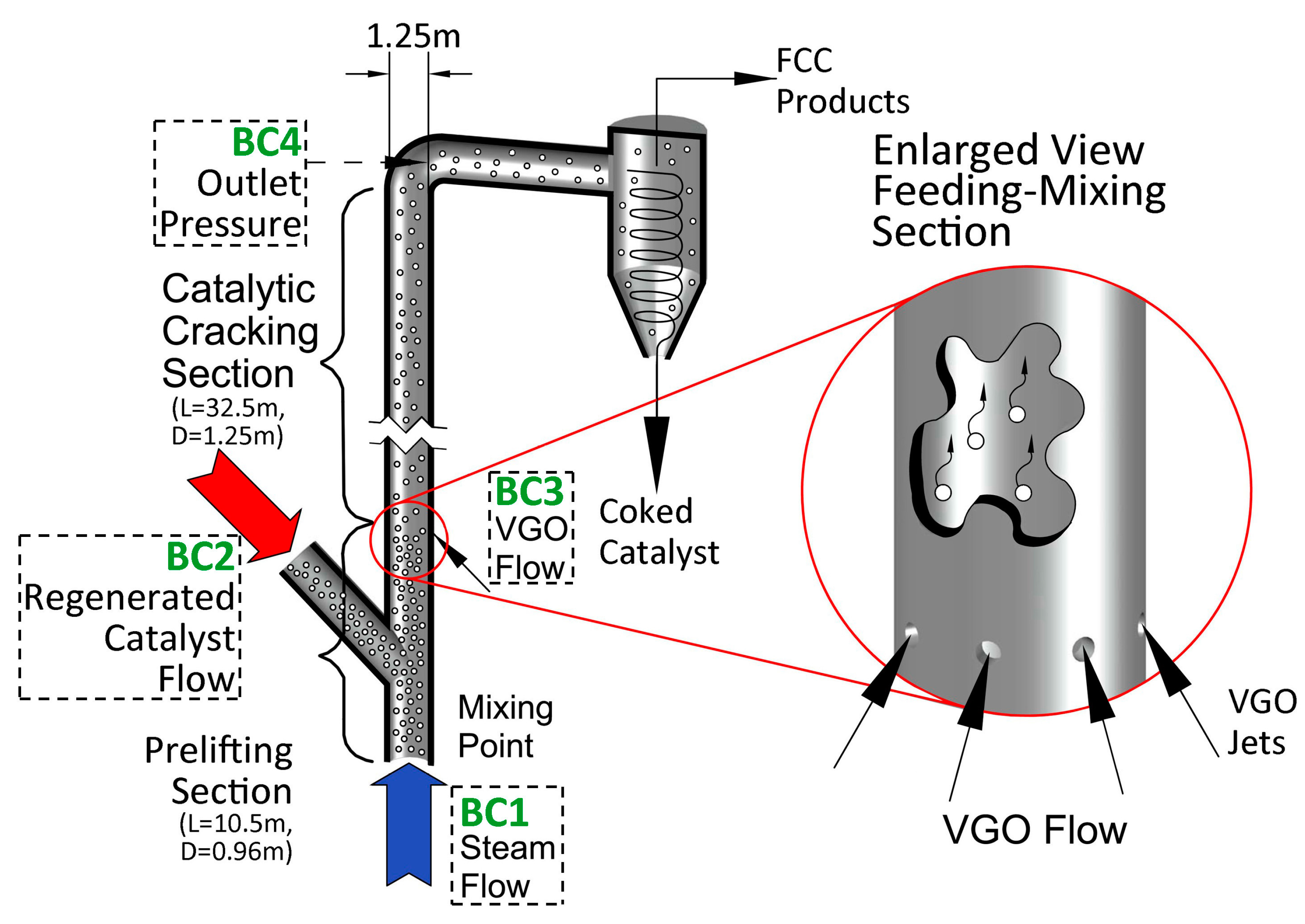
2.1.1. FCC Riser Unit
2.1.2. Operating Conditions
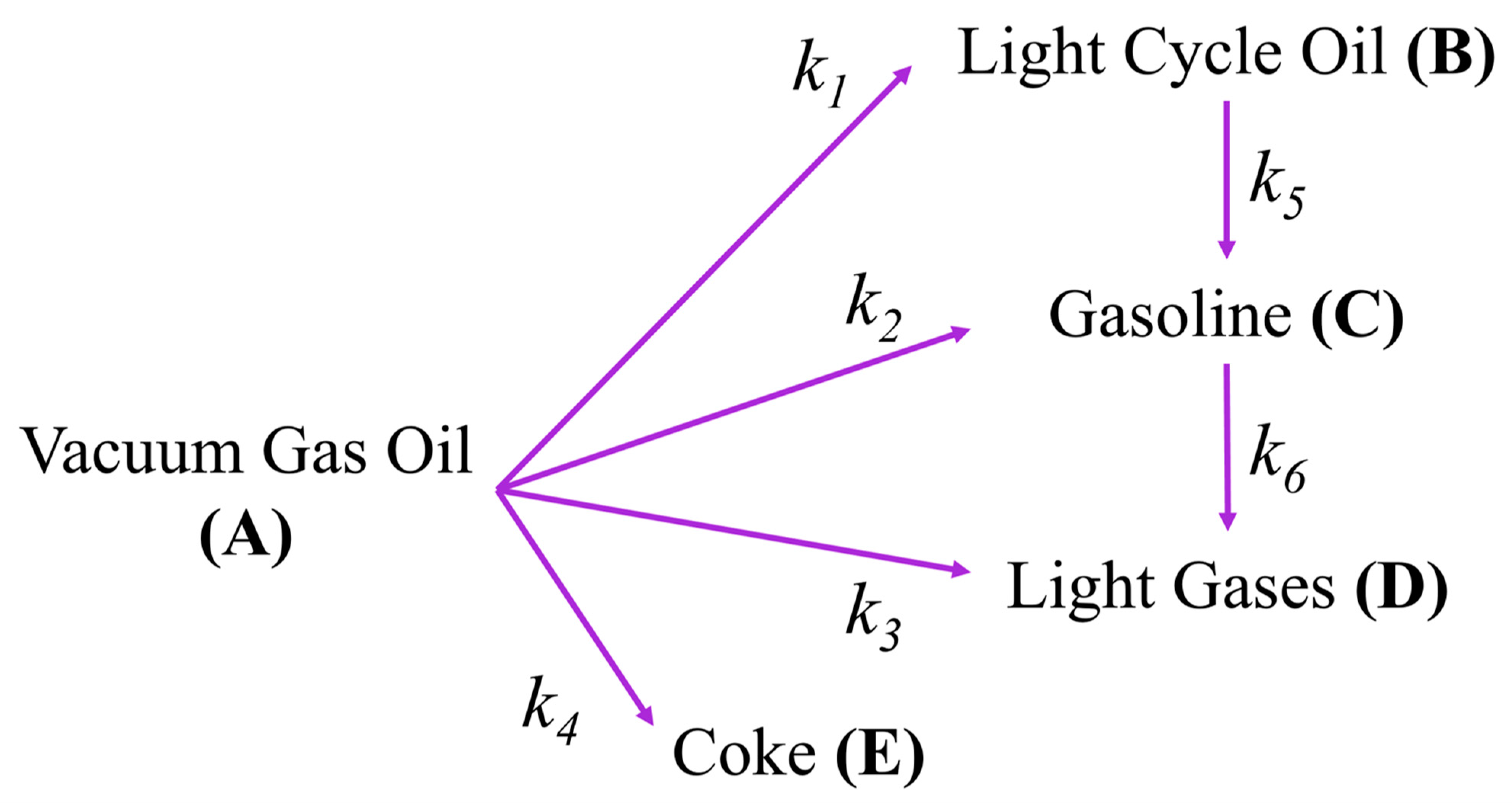
2.1.3. Catalytic Cracking Kinetics
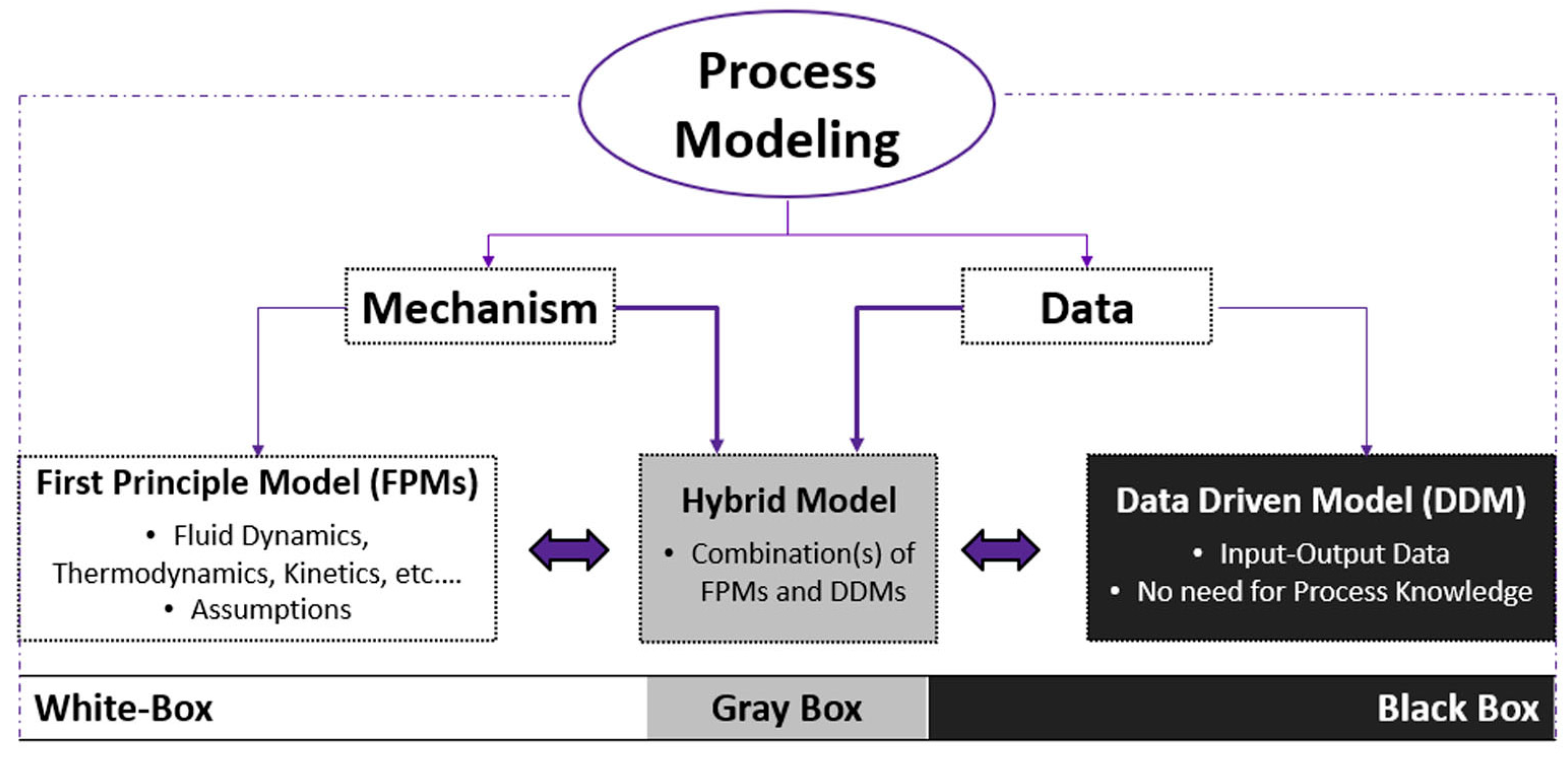
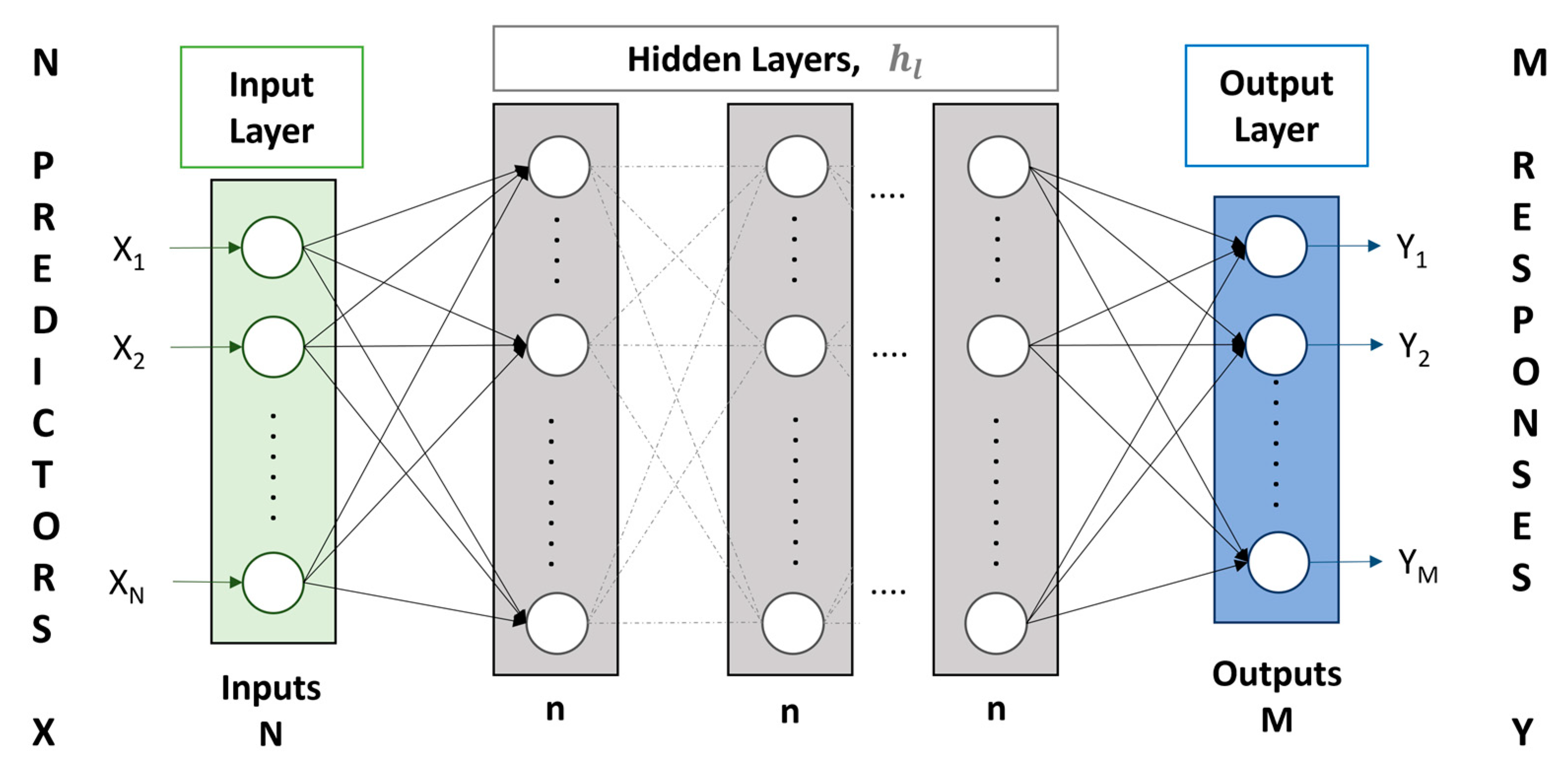
2.2. AI-Based Model
- First, the sets of operating conditions leading to temperatures at the mixing bottom section higher than 570 °C or lower than 510 °C are discarded from the original dataset. This was performed by considering the limits of the temperature range used for the VGO cracking kinetics as reported by [27].
- Then, a “hold-out” method considered 90% of all the data randomly selected for AI training. The remaining 10% of data is kept aside to be used for the final testing of the AI model.
- In addition, the entire training data is split into 10 different subsets, or folds. This is performed for the K-fold cross-validation implementation and based on the reduced number of data points available, as recommended by [37]. Regarding the selected 10-folds, 90% of the data are considered for AI training and 10% for validation.
- Following this, the AI model is developed and validated for each one of the selected K-folds.
- Once this step is completed, the various AI model parameters established for each one of the K-folds are averaged with the selection of the best fitting parameters, providing a designated “ensemble” model with the corresponding statistical indicators.
- Finally, the developed “ensemble” model was evaluated by comparing it with 10% of the original data randomly chosen, as described in step 2.
2.2.1. Artificial Neural Network (ANN)
2.2.2. Fuzzy Rules
| Temperature: | Low Temperature Regime (LTR) | |
| Medium Temperature Regime (MTR) | ||
| High Temperature Regime (HTR) | ||
| C/O Ratio: | Low CO Ratio | |
| Medium CO Ratio | ||
| High CO Ratio |
3. Results and Discussion
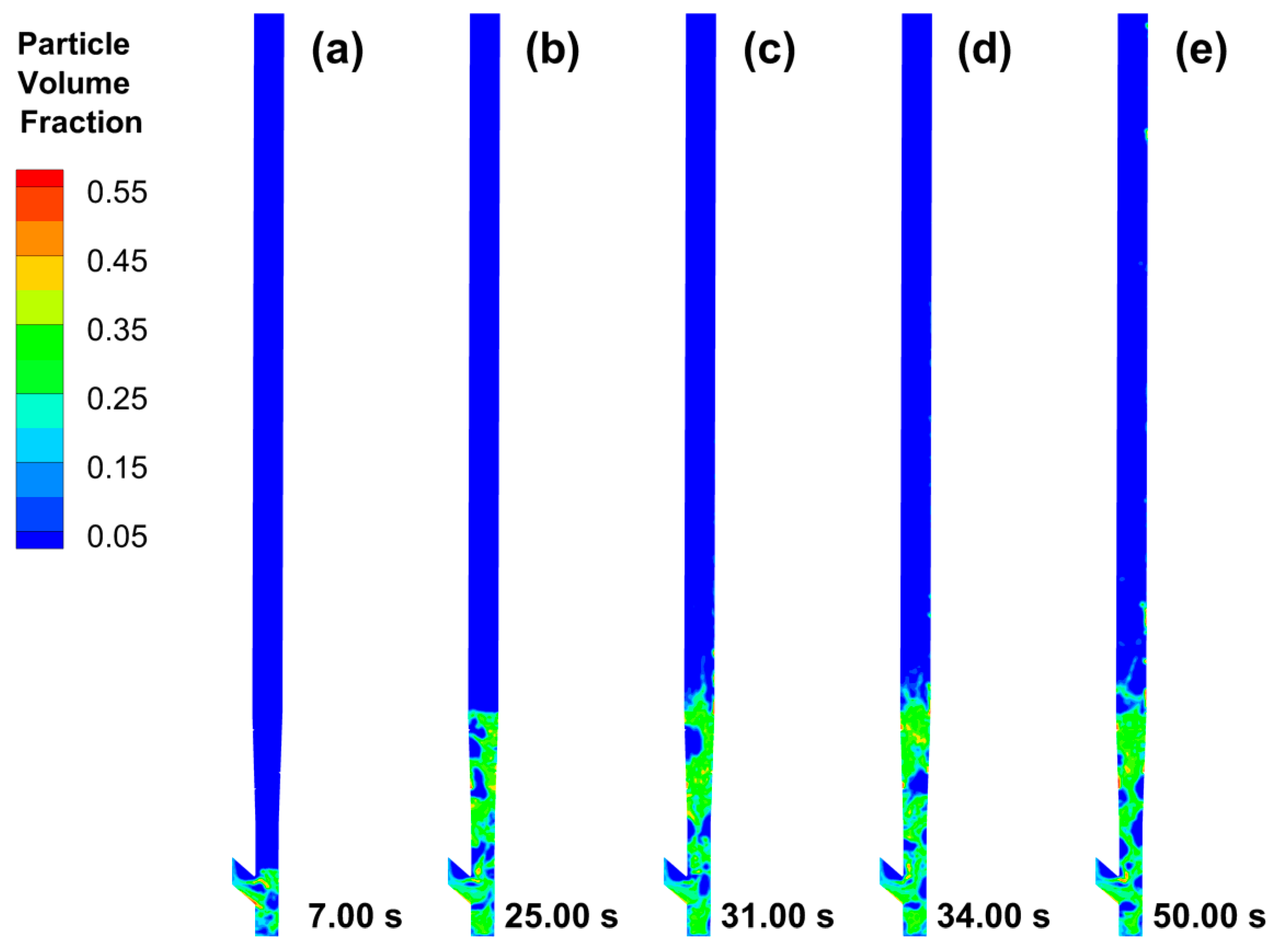
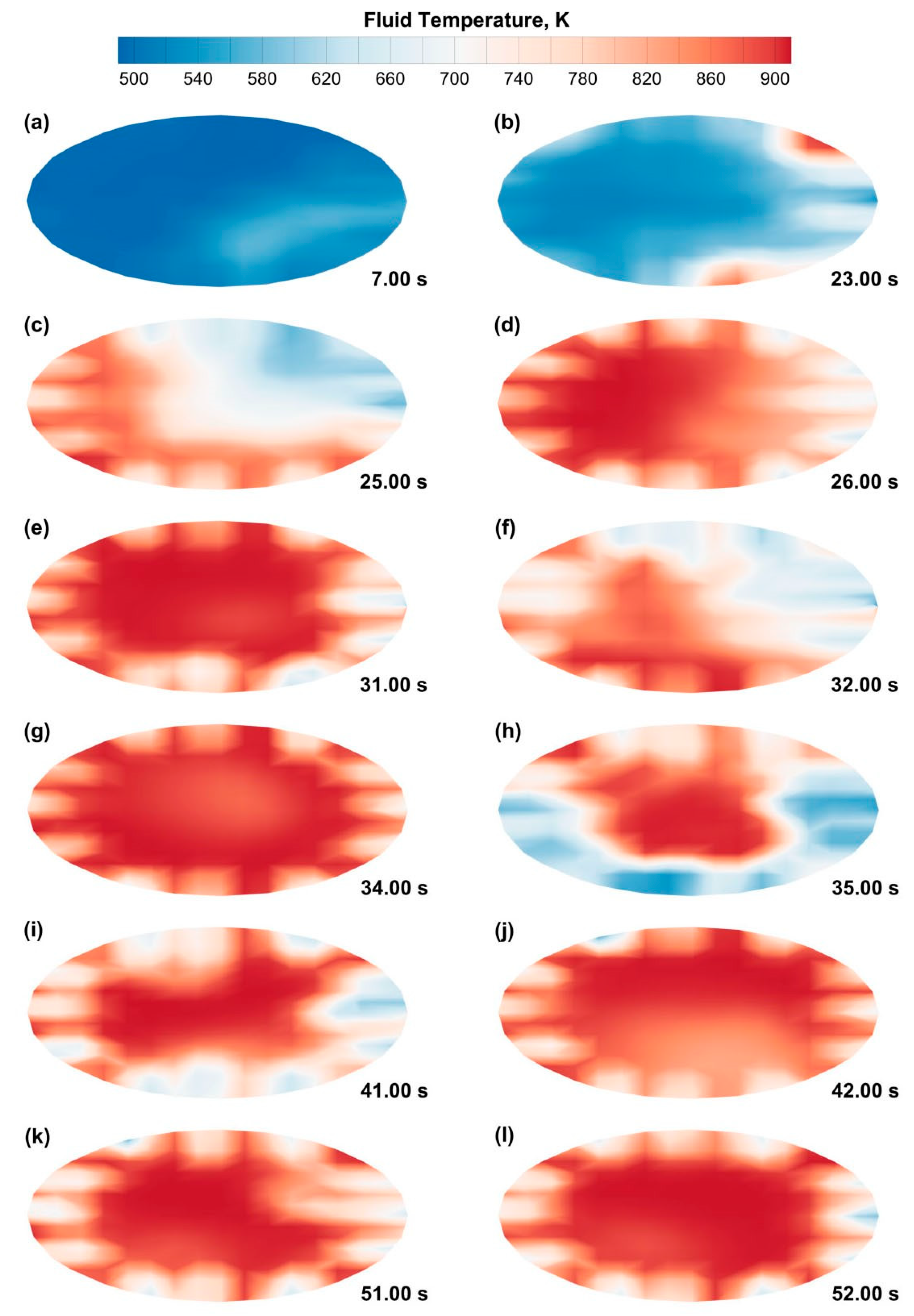
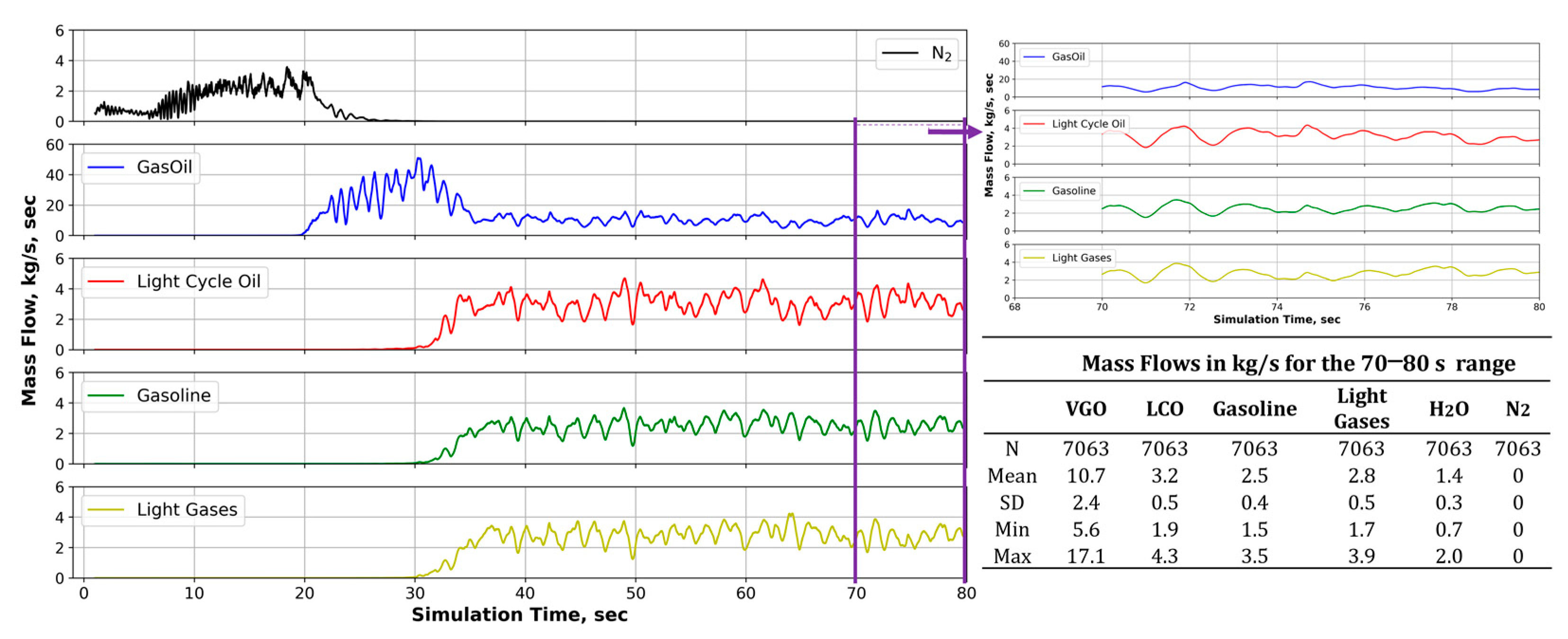
3.1. CPFD Simulation Results
Data Quality Evaluation
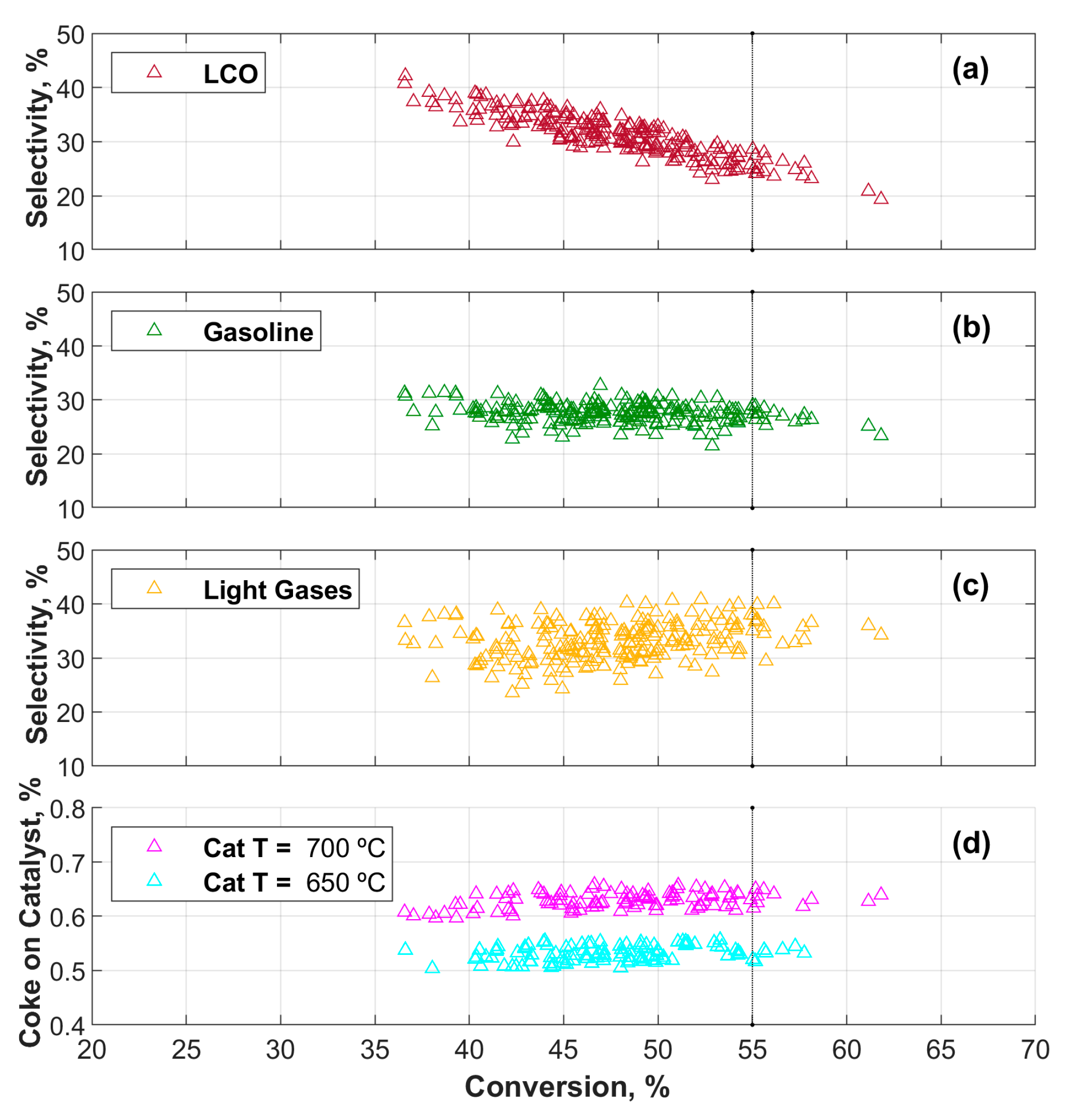
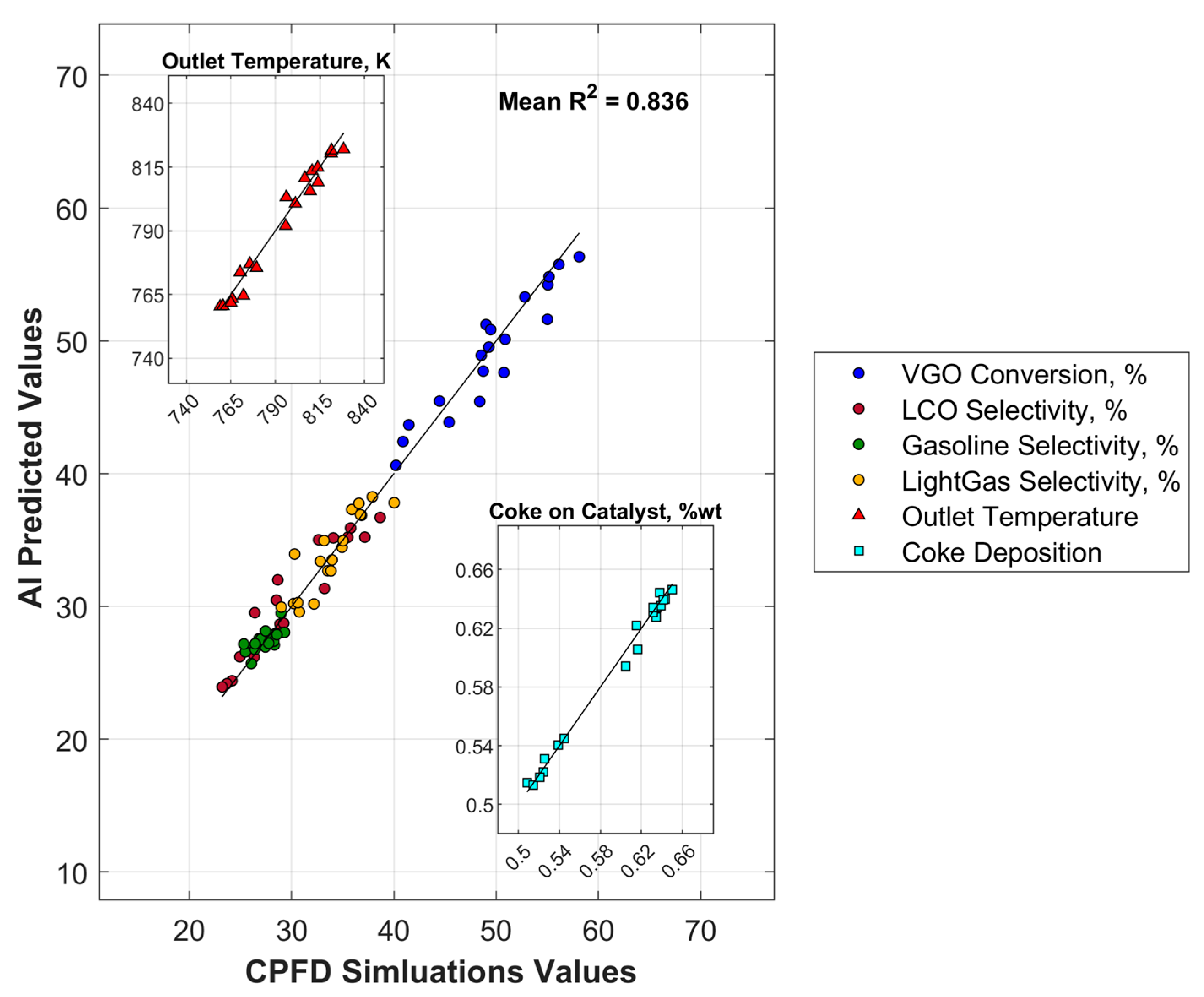
3.2. Machine Learning (ML) Results
Fuzzy Rules Results
4. Conclusions
- CPFD simulations are valuable to assess the performance of industrial-scale FCC riser reactors under a spectrum of possible operation conditions.
- CPFD simulations, including CREC-UWO kinetics obtained in a minifluidized CREC riser simulator, can contribute to significant advances in AI development. This approach provides valuable datasets for AI model development and AI model validation.
- Fuzzy logic constraints in AI can add additional confidence to the postulated AI hybrid models for FCC.
- FNNs for FCC units need to be considered with a limited number of hidden layers to involve a tractable number of AI model parameters.
- Optimized FNN hybrids for FCC units can deliver excellent performance estimations and lump species predictions with high coefficients of determination ().
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Variables | |
| Particle external surface area, m2 | |
| Specific heat capacity of particle, J/(kg·K) | |
| Mass diffusivity | |
| Drag function | |
| Activation energy, J/mol | |
| Particle distribution function | |
| Interphase momentum exchange rate per volume, N | |
| Coke mass flow, kg/s | |
| VGO mass flow, kg/s | |
| Mass flow for species , kg/s | |
| VGO mass flow, kg/s | |
| Mass flows of solids, kg/s | |
| Acceleration due to gravity, m/s2 | |
| Fluid enthalpy, J/mol | |
| Solid enthalpy, J/mol | |
| Pre-exponential factor | |
| Mass of a particle cloud, kg | |
| Chemical source term for species i | |
| Reaction order | |
| Nusselt number for heat transfer from the fluid to the solid | |
| Fluid pressure, Pa | |
| Solids pressure term (Equation (11)), Pa | |
| Fluid heat flux, J/m2 | |
| Enthalpy diffusion term | |
| Energy source per volume, J/m3 | |
| Particle radius, m | |
| Apparent rate for reaction path th | |
| Universal gas constant, J/(mol·K) | |
| Coefficient of determination | |
| Conservative energy exchange from particle phase to fluid phase, J/m3 | |
| Selectivity for species, | |
| Time, s | |
| Mean temperature of the fluid and solid phases, K | |
| Fluid temperature, K | |
| Particle temperature, K | |
| Fluid velocity, m/s | |
| Particle velocity, m/s | |
| Local mass-averaged particle velocity, m/s | |
| Particle acceleration, m/s2 | |
| Particle position, m | |
| VGO conversion | |
| Output variable value from the CPFD data | |
| Average of | |
| Predicted output variable value | |
| Mass fraction of species i | |
| Greek Symbols | |
| Solids stress function term (Equation (11)) | |
| Solids stress function term (Equation (11)) | |
| Stoichiometric coefficient for species | |
| Fluid volume fraction | |
| Particle volume fraction | |
| Solid-phase volume fraction at close packing | |
| Fluid thermal conductivity, J/(m⋅s⋅K) | |
| Fluid density, kg/m3 | |
| Particle density, kg/m3 | |
| Fluid stress tensor, Pa | |
| Particle normal stress, Pa | |
| Particle collision damping time, s | |
| Viscous dissipation | |
| Catalyst deactivation factor | |
| Acronyms | |
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| BC | Boundary condition |
| CFD | Computational fluid dynamics |
| CPFD | Computational particle-fluid dynamics |
| C/O | Catalyst to oil ratio |
| DDM | Data driven model |
| EMMS | Energy minimization multiscale |
| FCC | Fluid catalytic cracking |
| FNN | Feedforward neural network |
| FPM | First principle model |
| HM | Hybrid model |
| HTR | High temperature regime |
| LCO | Light cycle oil |
| LTR | Low temperature regime |
| ML | Machine learning |
| MP-PIC | Multiphase particle-in-cell |
| MTR | Medium temperature regime |
| ORMSE | Overall root mean square error |
| R&D | Research and Development |
| RMSE | Root mean square error |
| VGO | Vacuum gas oil |
Appendix A
| Lump | Range of Hydrocarbons | Boiling Point Range (°C) at 1 atm | Molecular Weight (g/mol) |
|---|---|---|---|
| Gas Oil | >C20 | >342.7 | 397 |
| Light cycle Oil | C12–C20 | 216.3–342.7 | 226 |
| Gasoline | C5–C12 | 36.1–216.3 | 114 |
| Light gases | C1–C4 | <36.1 | 46 |
| Coke | 800 |
| Value | 95% CFL | Units | |
|---|---|---|---|
| k1 | 1.16 × 10−2 | ±2.1% | m6/(kgCrystallite molGasOil s) |
| E1 | 97.01 | ±11.9% | kJ/molGasOil |
| k2 | 5.04 × 10−3 | ±2.4% | m6/(kgCrystallite molGasOil s) |
| E2 | 120.61 | ±4.1% | kJ/molGasOil |
| k3 | 4.06 × 10−3 | ±3.1% | m6/(kgCrystallite molGasOil s) |
| E3 | 136.17 | ±4.8% | kJ/molGasOil |
| k4 | 1.49 × 10−3 | ±4.0% | m6/(kgCrystallite molGasOil s) |
| E4 | 139.65 | ±5.1% | kJ/molGasOil |
| k5 | 7.60 × 10−2 | ±6.4% | m3/(kgCrystallite s) |
| E5 | 90.43 | ±15.4% | kJ/molLCO |
| k5 | 4.70 × 10−2 | ±8.3% | m3/(kgCrystallite s) |
| E6 | 82.86 | ±21.6% | kJ/molGasoline |
| 26.1 | ±4.5% | - |
| Name | State | Molecular Weight (g/mol) | Heat of Formation (J/kg) | Density (kg/m3) | Heat Capacity (J/kg K) |
|---|---|---|---|---|---|
| VGO | Gas | 400 | −820,000 | - | 3430 |
| Light Cycle Oil | Gas | 200 | −600,000 | - | |
| Gasoline | Gas | 100 | −550,000 | - | |
| Light Gases | Gas | 50 | −75,000 | - | |
| Coke | Solid | 800 | 0 | 1200 | 850 |
| FCC Catalyst Base | Solid | ~102 | 0 | 1722 | 1046 |
References
- Pinheiro, C.I.C.; Fernandes, J.L.; Domingues, L.; Chambel, A.J.S.; Graça, I.; Oliveira, N.M.C.; Cerqueira, H.S.; Ribeiro, F.R. Fluid Catalytic Cracking (FCC) Process Modeling, Simulation, and Control. Ind. Eng. Chem. Res. 2012, 51, 1–29. [Google Scholar] [CrossRef]
- Sadeghbeigi, R. Fluid catalytic cracking process description—Converter section. In Fluid Catalytic Cracking Handbook; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–22. [Google Scholar] [CrossRef]
- Guan, H.; Ye, L.; Shen, F.; Song, Z. Economic operation of a fluid catalytic cracking process using self-optimizing control and reconfiguration. J. Taiwan Inst. Chem. Eng. 2019, 96, 104–113. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, Y.; Li, S. Enhancing incremental deep learning for FCCU end-point quality prediction. Inf. Sci. 2020, 530, 95–107. [Google Scholar] [CrossRef]
- Khaldi, M.K.; Al-Dhaifallah, M.; Taha, O. Artificial intelligence perspectives: A systematic literature review on modeling, control, and optimization of fluid catalytic cracking. Alex. Eng. J. 2023, 80, 294–314. [Google Scholar] [CrossRef]
- Han, I.-S.; Chung, C.-B. Dynamic modeling and simulation of a fluidized catalytic cracking process. Part I: Process modeling. Chem. Eng. Sci. 2001, 56, 1951–1971. [Google Scholar] [CrossRef]
- Liu, A.Y.; Chang, A.-F.; Kiran, P. Predictive Modeling of the Fluid Catalytic Cracking (FCC) Process. In Petroleum Refinery Process Modeling—Integrated Optimization Tools and Applications; Wiley: Hoboken, NJ, USA, 2018; ISBN 9783527344239. [Google Scholar]
- Olafadehan, O.A.; Sunmola, O.P.; Jaiyeola, A.; Efeovbokhan, V.; Abatan, O.G. Modelling and simulation of an industrial RFCCU-riser reactor for catalytic cracking of vacuum residue. Appl. Petrochem. Res. 2018, 8, 219–237. [Google Scholar] [CrossRef]
- Ali, H.; Rohani, S.; Corriou, J. Modelling and Control of a Riser Type Fluid Catalytic Cracking (FCC) Unit. Chem. Eng. Res. Des. 1997, 75, 401–412. [Google Scholar] [CrossRef]
- Kim, S.; Urm, J.; Kim, D.S.; Lee, K.; Lee, J.M. Modeling, simulation and structural analysis of a fluid catalytic cracking (FCC) process. Korean J. Chem. Eng. 2018, 35, 2327–2335. [Google Scholar] [CrossRef]
- Khandalekar, P.; Riggs, J. Nonlinear process model based control and optimization of a model IV FCC unit. Comput. Chem. Eng. 1995, 19, 1153–1168. [Google Scholar] [CrossRef]
- Arbel, A.; Huang, Z.; Rinard, I.H.; Shinnar, R.; Sapre, A.V. Dynamic and Control of Fluidized Catalytic Crackers. 1. Modeling of the Current Generation of FCC’s. Ind. Eng. Chem. Res. 1995, 34, 1228–1243. [Google Scholar] [CrossRef]
- Araujo-Monroy, C.; López-Isunza, F. Modeling and Simulation of an Industrial Fluid Catalytic Cracking Riser Reactor Using a Lump-Kinetic Model for a Distinct Feedstock. Ind. Eng. Chem. Res. 2006, 45, 120–128. [Google Scholar] [CrossRef]
- Bollas, G.; Papadokonstadakis, S.; Michalopoulos, J.; Arampatzis, G.; Lappas, A.; Vasalos, I.; Lygeros, A. Using hybrid neural networks in scaling up an FCC model from a pilot plant to an industrial unit. Chem. Eng. Process.-Process Intensif. 2003, 42, 697–713. [Google Scholar] [CrossRef]
- Alaradi, A.; Rohani, S. Identification and control of a riser-type FCC unit using neural networks. Comput. Chem. Eng. 2002, 26, 401–421. [Google Scholar] [CrossRef]
- Wang, X.; Chen, B.; Yang, S.; McGreavy, C. Neural nets, fuzzy sets and digraphs in safety and operability studies of refinery reaction processes. Chem. Eng. Sci. 1996, 51, 2169–2178. [Google Scholar] [CrossRef]
- Yang, S.; Chen, B.; Wang, X. Neural network based fault diagnosis using unmeasurable inputs. Eng. Appl. Artif. Intell. 2000, 13, 345–356. [Google Scholar] [CrossRef]
- Michalopoulos, J.; Papadokonstadakis, S.; Arampatzis, G.; Lygeros, A. Modelling of an Industrial Fluid Catalytic Cracking Unit Using Neural Networks. Chem. Eng. Res. Des. 2001, 79, 137–142. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Rezaei, N.; Lohi, A. Applications of hybrid models in chemical, petroleum, and energy systems: A systematic review. Appl. Energy 2018, 228, 2539–2566. [Google Scholar] [CrossRef]
- Ali, J.M.; Hussain, M.; Tade, M.O.; Zhang, J. Artificial Intelligence techniques applied as estimator in chemical process systems—A literature survey. Expert Syst. Appl. 2015, 42, 5915–5931. [Google Scholar] [CrossRef]
- Abdollahi, S.A.; Ranjbar, S.F.; Jahromi, D.R. Applying feature selection and machine learning techniques to estimate the biomass higher heating value. Sci. Rep. 2023, 13, 16093. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, Z.; Zhao, Y.; Lv, M.; Lan, X.; Shi, X.; Gao, J.; Li, C.; Yuan, Z.; Lin, Y. A hybrid safety monitoring framework for industrial FCC disengager coking rate based on FPM, CFD, and ML. Process Saf. Environ. Prot. 2023, 175, 17–33. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, Y.; Lu, C. CPFD simulation on wear mechanisms in disk–donut FCC strippers. Powder Technol. 2015, 279, 269–281. [Google Scholar] [CrossRef]
- McIntyre, C.; Hughes, R.; Macchi, A.; Mehrani, P. Computational modeling of high pressure bubbling fluidized bed hydrodynamics using ilmenite particles. Powder Technol. 2022, 402, 117332. [Google Scholar] [CrossRef]
- Snider, D. An Incompressible Three-Dimensional Multiphase Particle-in-Cell Model for Dense Particle Flows. J. Comput. Phys. 2001, 170, 523–549. [Google Scholar] [CrossRef]
- Medina-Pedraza, C.; de Lasa, H. Hybrid Particle Cluster CPFD Simulation in the Acceleration and Stabilized Sections of a Downflow Circulating Fluidized Bed. Ind. Eng. Chem. Res. 2020, 59, 20325–20336. [Google Scholar] [CrossRef]
- Al-Sabawi, M.; Atias, J.A.; de Lasa, H. Kinetic Modeling of Catalytic Cracking of Gas Oil Feedstocks: Reaction and Diffusion Phenomena. Ind. Eng. Chem. Res. 2006, 45, 1583–1593. [Google Scholar] [CrossRef]
- Snider, D.M.; Clark, S.M.; O’Rourke, P.J. Eulerian–Lagrangian method for three-dimensional thermal reacting flow with application to coal gasifiers. Chem. Eng. Sci. 2011, 66, 1285–1295. [Google Scholar] [CrossRef]
- Oloruntoba, A.; Zhang, Y.; Xiao, H. Study on effect of gas distributor in fluidized bed reactors by hydrodynamics-reaction-coupled simulations. Chem. Eng. Res. Des. 2022, 177, 431–447. [Google Scholar] [CrossRef]
- Di Nardo, A.; Savuto, E.; Calchetti, G.; Stendardo, S. Computational particle fluid dynamics 3D simulation of the sorption-enhanced steam methane reforming process in a dual fluidized bed of bifunctional sorbent-catalyst particles. Powder Technol. 2023, 424, 118568. [Google Scholar] [CrossRef]
- Chang, S.-L.; Zhou, C.Q. Simulation of FCC riser flow with multiphase heat transfer and cracking reactions. Comput. Mech. 2003, 31, 519–532. [Google Scholar] [CrossRef]
- Arandes, J.M.; Azkoiti, M.J.; Bilbao, J.; de Lasa, H.I. Modelling FCC units under steady and unsteady state conditions. Can. J. Chem. Eng. 2000, 78, 111–123. [Google Scholar] [CrossRef]
- Behjat, Y.; Shahhosseini, S.; Marvast, M.A. CFD analysis of hydrodynamic, heat transfer and reaction of three phase riser reactor. Chem. Eng. Res. Des. 2011, 89, 978–989. [Google Scholar] [CrossRef]
- Du, Y.; Chen, X.; Li, S.; Berrouk, A.S.; Ren, W.; Yang, C. Revisiting a large-scale FCC riser reactor with a particle-scale model. Chem. Eng. Sci. 2022, 249, 117300. [Google Scholar] [CrossRef]
- Hajjar, Z.; Tayyebi, S.; Ahmadi, M.H.E. Application of AI in Chemical Engineering. In Artificial Intelligence—Emerging Trends and Applications; IntechOpen Ltd.: London, UK, 2018. [Google Scholar] [CrossRef]
- Venkatasubramanian, V. The promise of artificial intelligence in chemical engineering: Is it here, finally? AIChE J. 2019, 65, 466–478. [Google Scholar] [CrossRef]
- García, J.A.; Gómez, J.F.; Castellanos, N.T. Properties prediction of environmentally friendly ultra-high-performance concrete using artificial neural networks. Eur. J. Environ. Civ. Eng. 2022, 26, 2319–2343. [Google Scholar] [CrossRef]
- Du, C.; Han, C.; Yang, Z.; Wu, H.; Luo, H.; Niedzwiecki, L.; Lu, B.; Wang, W. Multiscale CFD Simulation of an Industrial Diameter-Transformed Fluidized Bed Reactor with Artificial Neural Network Analysis of EMMS Drag Markers. Ind. Eng. Chem. Res. 2022, 61, 8566–8580. [Google Scholar] [CrossRef]
- Lopez-Ramirez, E.; Lopez-Zamora, S.; Escobedo, S.; de Lasa, H. Artificial Neural Networks (ANNs) for Vapour-Liquid-Liquid Equilibrium (VLLE) Predictions in N-Octane/Water Blends. Processes 2023, 11, 2026. [Google Scholar] [CrossRef]
- Schubert, J.; Simutis, R.; Dors, M.; Havlik, I.; Lübbert, A. Bioprocess optimization and control: Application of hybrid modelling. J. Biotechnol. 1994, 35, 51–68. [Google Scholar] [CrossRef]
- Souza, P.V.d.C.; Lughofer, E.; Guimaraes, A.J. An interpretable evolving fuzzy neural network based on self-organized direction-aware data partitioning and fuzzy logic neurons. Appl. Soft Comput. 2021, 112, 107829. [Google Scholar] [CrossRef]


| Fluid-Phase Equations | ||
| Continuity equation of fluid phase: | ||
| (1) | ||
| Momentum equation of fluid phase: | ||
| (2) | ||
| Enthalpy: | ||
| (3) | ||
| Species transport: | ||
| (4) | ||
| Solid-Phase Equations | ||
| Liouville equation for finding the particle distribution function , at each time: | ||
| (5) | ||
| Particle acceleration: | ||
| (6) | ||
| Particle mass: | ||
| (7) | ||
| Particle volume fraction: | ||
| (8) | ||
| Particle energy: | ||
| (9) | ||
| Fluid-Solid Interphase Equations | ||
| Momentum transfer between phases: | ||
| (10) | ||
| Particle-Particle Interaction Equation | ||
| Particle collision normal stress model: | ||
| (11) | ||
| No. | Variables | Unit | Condition | ||
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| 1 | Catalyst Mass Flow | kg/s | 133.80 | 147.20 | 160.60 |
| 2 | Catalyst Temperature | °C | - | 650 | 700 |
| 3 | VGO Mass Flow | kg/s | 19.50 | 21.45 | 23.50 |
| 4 | VGO Temperature | °C | 210 | 230 | 250 |
| 5 | Bottom Steam Mass Flow | kg/s | - | 0.120 | 0.132 |
| 6 | Bottom Steam Temperature | °C | - | 250 | 300 |
| No. | Condition | Units | Type |
|---|---|---|---|
| 1 | Catalyst Mass Flow | kg/s | Independent |
| 2 | Catalyst Temperature | K | |
| 3 | VGO Mass Flow | kg/s | |
| 4 | VGO Temperature | K | |
| 5 | Bottom Steam Mass Flow | kg/s | |
| 6 | Bottom Steam Temperature | K | |
| 7 | C/O Ratio | kg Catalyst/kg VGO | Dependent |
| 8 | Mixing Point Temperature | K |
| Type | Hyperparameter | Value | Description |
|---|---|---|---|
| Performance | performFcn | RMSE | This provides the root mean square error (RMSE) as performance function. |
| performParam.regularization | 0.15 | This considers a performance ratio for regularization. | |
| performParam.normalization | ‘standard’ | This provides a standard normalization of the target variables values. | |
| Training | trainParam.goal | 0.01 | This considers a RMSE desired value as the goal for the training. |
| trainFcn | traingdx | This provides training by using gradient descent with momentum and adaptive learning rate backpropagation | |
| trainParam.lr | 0.01 | This considers an initial learning rate for the training. | |
| trainParam.lr_inc | 1.005 | This enhances training by employing an increase ratio in the learning rate. | |
| trainParam.lr_dec | 0.05 | This enhances training by employing a decrease ratio in the learning rate. | |
| trainParam.mc | 0.75 | This incorporates a momentum value for updating weights during training. | |
| divideFcn | ‘dividerand’ | This involves training with a data division function for training and validation. | |
| divideParam.trainRatio | 0.9 | This considers a data split ratio for training. | |
| divideParam.valRatio | 0.1 | This considers a data split ratio for validation. | |
| trainParam.max_fail | 20 | This considers a maximum validation cap for failures. | |
| Architecture | transferFcn | ‘tansig’ | This involves a hyperbolic tangent sigmoid activation function for nodes connections. |
| Hidden Layers | 1, 2, 3 | Up to a maximum of three hidden layers are considered. | |
| Hidden Layers Nodes | 1–12 | Up to a maximum of 12 nodes for each hidden layer are considered. | |
| Parameters | <200 | Up to a maximum of 200 parameters are selected to prevent overparameterization. |
| Condition | Value | Units |
|---|---|---|
| Catalyst mass flow | 133.80 | kg/s |
| Catalyst temperature | 923 | K |
| VGO mass flow | 19.50 | kg/s |
| VGO temperature | 483 | K |
| Bottom steam mass flow | 0.120 | kg/s |
| Bottom steam temperature | 523 | K |
| Variable of Interest | Value | Units |
|---|---|---|
| VGO conversion | 45.19 | % |
| LCO selectivity | 36.34 | % |
| Gasoline selectivity | 28.87 | % |
| Light gases selectivity | 31.60 | % |
| Mixing temperature | 785 | K |
| Outlet temperature | 757 | K |
| Variable of Interest | Raw Data from CPFD | Units | |||
|---|---|---|---|---|---|
| Max | Min | Mean | SD | ||
| VGO conversion | 61.82 | 36.57 | 47.84 | 4.86 | % |
| LCO selectivity | 42.17 | 19.36 | 31.15 | 4.01 | % |
| Gasoline selectivity | 32.69 | 21.50 | 27.54 | 1.80 | % |
| Light gases selectivity | 40.81 | 23.57 | 33.15 | 3.48 | % |
| Mixing temperature | 869 | 754 | 814 | 24 | K |
| Outlet temperature | 831 | 742 | 785 | 20 | K |
| Coke on catalyst | 0.66 | 0.5 | 0.58 | 0.05 | % |
| FNN1 | FNN2 | FNN3 | FNN4 | FNN5 | ||
|---|---|---|---|---|---|---|
| Architecture | Hidden Layers | 1 | 2 | 2 | 3 | 3 |
| Nodes | [10] | [6, 9] | [10, 5] | [3, 10, 7] | [6, 10, 4] | |
| Parameters | 156 | 177 | 181 | 192 | 198 | |
| 2.38 | 2.00 | 1.98 | 2.37 | 2.24 | ||
| VGO Conversion | 0.86 | 0.86 | 0.85 | 0.80 | 0.85 | |
| LCO selectivity | 0.80 | 0.85 | 0.84 | 0.81 | 0.86 | |
| Gasoline selectivity | 0.09 | 0.15 | 0.17 | 0.23 | 0.29 | |
| Light Gases selectivity | 0.65 | 0.69 | 0.66 | 0.68 | 0.68 | |
| Outlet Temperature | 0.96 | 0.97 | 0.98 | 0.96 | 0.96 | |
| Coke on Catalyst | 0.96 | 0.99 | 0.99 | 0.99 | 0.99 | |
| Average | 0.721 | 0.752 | 0.749 | 0.745 | 0.772 | |
| FNN1 | FNN2 | FNN3 | FNN4 | ||
|---|---|---|---|---|---|
| Architecture | Hidden Layers | 1 | 2 | 2 | 2 |
| Nodes | [10] | [5, 5] | [5, 8] | [8, 5] | |
| Parameters | 196 | 131 | 167 | 185 | |
| 1.78 | 1.93 | 2.02 | 1.93 | ||
| VGO Conversion | 0.84 | 0.85 | 0.85 | 0.89 | |
| LCO selectivity | 0.79 | 0.84 | 0.88 | 0.89 | |
| Gasoline selectivity | 0.37 | 0.14 | 0.68 | 0.49 | |
| Light Gases selectivity | 0.80 | 0.69 | 0.78 | 0.79 | |
| Outlet Temperature | 0.99 | 0.98 | 0.96 | 0.97 | |
| Coke on Catalyst | 0.99 | 0.99 | 0.99 | 0.99 | |
| Average | 0.796 | 0.749 | 0.859 | 0.836 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acosta-López, J.G.; de Lasa, H. Artificial Intelligence for Hybrid Modeling in Fluid Catalytic Cracking (FCC). Processes 2024, 12, 61. https://doi.org/10.3390/pr12010061
Acosta-López JG, de Lasa H. Artificial Intelligence for Hybrid Modeling in Fluid Catalytic Cracking (FCC). Processes. 2024; 12(1):61. https://doi.org/10.3390/pr12010061
Chicago/Turabian StyleAcosta-López, Jansen Gabriel, and Hugo de Lasa. 2024. "Artificial Intelligence for Hybrid Modeling in Fluid Catalytic Cracking (FCC)" Processes 12, no. 1: 61. https://doi.org/10.3390/pr12010061
APA StyleAcosta-López, J. G., & de Lasa, H. (2024). Artificial Intelligence for Hybrid Modeling in Fluid Catalytic Cracking (FCC). Processes, 12(1), 61. https://doi.org/10.3390/pr12010061








