A Novel Thermal Lattice Boltzmann Method for Numerical Simulation of Natural Convection of Non-Newtonian Fluids

Abstract

A modified thermal Bhatnagar–Gross–Krook Lattice Boltzmann (BGK-LB) model was developed to study the convection phenomenon of non-Newtonian fluids (NNFs). This model integrates the local shear rate into the equilibrium distribution function (EDF) of the flow field and keeps the relaxation time from varying with fluid viscosity by introducing an additional parameter. In addition, a modified temperature EDF was constructed for the evolution equation of the temperature field to ensure the precise recovery of the convection–diffusion equation. To validate the accuracy and effectiveness of the proposed model, numerical simulations of benchmark problems were performed. Subsequently, we investigated the natural convection of power–law (PL) fluids and examined the impact of the PL index (n = 0.7–1.3) and Rayleigh number (Ra = 10³–5 × 10⁵) on the flow and temperature fields while holding the Prandtl number (Pr = 7) constant. The obtained results indicate that, for a given value of n, the convective intensity exhibits a positive correlation with Ra, which is illustrated by the rising trend in the average Nusselt number ($\overline{Nu}$) with increasing Ra. Additionally, shear-thinning fluid (n < 1) exhibited increased $\overline{Nu}$ values compared to the Newtonian case, indicating an enhanced convection effect. Conversely, shear-thickening fluid (n > 1) exhibits reduced $\overline{Nu}$ values, indicating weakened convective behavior.

1. Introduction

Natural convection (NC) is a crucial mechanism for cooling electronic devices, facilitating thermal management in solar collectors and building insulation, as well as promoting efficient food processing applications, among others. Consequently, NC has received significant attention in recent decades [1,2]. However, many practical fluids in nature and engineering applications exhibit non-Newtonian behavior. Compared to extensive research on Newtonian fluids (NFs), research on the NC phenomena of non-Newtonian fluids (NNFs) has been relatively limited [3].

There have been some efforts to study the NC of NNFs using traditional computational fluid dynamic (CFD) methods despite the difficulties in simulating NNFs. Ozoe et al. [4] were pioneers in investigating heat transfer (HT) involving NNFs. They conducted a study specifically targeting the HT behavior of PL and Ellis fluids within a rectangular enclosure with a heated bottom wall and concluded that there was a positive correlation between the critical Ra value and the PL index. In a related study, Ohta et al. [5] explored the NC of pseudoplastic fluid in a square enclosure and observed that the convective flow of NNFs was more complex compared to that of NFs. Building on this work, Kim et al. [6] investigated the NC of PL fluids in a square cavity and discovered distinct variations in the HT rate and convective intensity between NNFs and NFs at a given Ra number. Extending this line of research, Lamsaadi et al. [7] conducted numerical simulations of NC for PL fluids in a shallow cavity. These findings demonstrate that the HT rate is enhanced for a pseudo-plastic fluid and weakened for a dilatant fluid compared to the Newtonian case. Furthermore, Turan et al. [8] investigated the NC in square and rectangular cavities filled with PL fluids. Their findings revealed a positive correlation between Nu and Ra, indicating that Nu increased as Ra increased. Conversely, they observed a negative correlation between the Nu and the PL index, as a rise in the PL index corresponded to a decline in the Nu value. Khezzar et al. [9] conducted numerical investigations on NC in tilted rectangular cavities filled with NFs and NNFs. Their findings showed that decreasing the PL index resulted in a significant increase in the HT rate while increasing the PL index caused a notable decrease in the HT rate. In separate research conducted by Matin et al. [10], they investigated the NC phenomenon of NNFs between two horizontally placed eccentric square ducts. The results showed that as the Ra number increased, the cooling effect of shear-thinning fluids became more pronounced, while the insulating effect of shear-thickening fluids became more prominent. According to their research, NNFs have more complicated flow and HT properties than NFs because their dynamic viscosity varies with the shear stress [11,12].

The lattice Boltzmann method (LBM) has potential beyond traditional methods for modeling complicated flows and associated phenomena as a numerical technique. Distinct from the traditional macroscopic approaches that treat fluid as a continuous medium, LBM is a mesoscale numerical technique that uses the probability of finding molecules in a lattice-discrete domain to provide a statistical description of molecular dynamics [13]. This unique kinetic framework gives the LBM numerous advantages, including its straightforward implementation, capability for parallelization, easy handling of complex boundary conditions, and exceptional computational efficiency [14]. As a result, the LBM has made major advances in the simulation of complex hydrodynamic phenomena when coupled with thermodynamics [15,16]. For instance, Kefayati et al. [17] utilized the LBM to examine the behavior of NFs within a rectangular cavity. The authors observed an increase in the HT rate as the Ra number increased. Dash et al. [18] employed a combination of LBM and the immersed boundary method to investigate NC within an eccentric annulus formed between heated square inner cylinders. Sheikholeslami et al. [19] employed the LBM to investigate the HT of Newtonian copper oxide nanofluids under NC conditions. They focused on a specific cavity that was subject to constant and angular magnetic flux, studying the impact of various parameters on the velocity and temperature distributions. The findings demonstrated that increasing the Ra number resulted in an augmentation in the HT rate while increasing the Hartmann number resulted in a decrease in the HT rate.

Inspired by the achievements of LBM in simulating flows of NFs, endeavors have been undertaken to expand its capabilities to simulate flows of NNFs as well. NNFs, in contrast to NFs, possess a variable viscosity that is contingent upon derivatives of the velocity field. Numerical accuracy diminishes, and instability may arise in the solution process due to the differentiation of the velocity field. The LBM offers notable advantages for NNFs. Specifically, the LBM allows the shear rate to be determined directly from the distribution function, eliminating the need for derivation from the velocity field [20].

It can be noted that the majority of existing LB models used to simulate thermal flow and non-Newtonian flow employs the BGK collision operator due to its efficiency and simplicity [21]. However, it is necessary to recognize that the tradeoff for such efficiency and simplicity is the compromise in numerical stability. To overcome the deficiencies of the BGK-LB model, alternative approaches such as the MRT-LBM (Multiple-Relaxation-Time LBM) or hybrid approaches combining traditional numerical methods with LBM should be employed. Kefayati et al. [22] utilized a finite-difference LBM (FD-LBM) to investigate the convection flow properties of non-Newtonian molten polymers characterized by PL fluids. Zhang et al. [23] used the same approach to investigate the influence of a magnetic field on the NC and the entropy formation of non-Newtonian PL fluids within an L-shaped chamber. Their approach used a conventional numerical scheme to derive the shear stress equation. However, this needed to solve the Poisson equation, which made the solution procedure more complicated. Boutra et al. [24] used a combination of MRT-LBM and FDM to analyze the fluid flow of Bingham plastic fluids inside a side-heated cube. To solve the equations for dynamics and energy, they adopted the MRT-LBM and the FDM, respectively. Jahanbakhshi et al. [25] investigated the magneto-hydrodynamic convective flow inside an L-shaped chamber containing NNFs by adopting the finite volume method and LBM. Their approach deviated from the traditional kinetic-based LBM and spoiled computational efficiency. Rahman et al. [26] analyzed the impact of a magnetic field on non-Newtonian flow within a side-heated rectangular enclosure using the MRT-LBM. Despite its improved stability, the MRT-LBM requires more computational resources than the BGK-LB model, especially for NNFs [20].

In summary, despite its simplicity and efficiency making it the most popular model, the BGK-LB model has not gained substantial popularity in the field of the thermal flow of NNFs due to its numerical instability under low viscosity conditions. Therefore, it is imperative to develop a numerically stable BGK-LB model to study the thermal flow characteristics of NNFs. This paper aims to address this need by developing a non-Newtonian thermal BGK-LB model and utilizing it to investigate the NC of PL fluids, demonstrating its ability to simulate the thermal flow of NNFs. In Section 2, we present an improved BGK-LB model for the thermal flow of NNFs. This method incorporates the shear rate into the EDF of the velocity field and allows the relaxation time to be invariant to the fluid viscosity by introducing an additional parameter. Section 3 describes the physical model of natural convection and the setting of the boundary conditions. In Section 4, we conduct a grid independence analysis and validate the proposed method. We then systematically analyzed the impacts of the Ra and PL index on the NC of PL fluids in a square cavity.

2. Numerical Method

2.1. BGK-LB Equations for the Flow Field

The LBM is a flexible numerical technique that can be utilized to address a wide range of challenges in relation to fluid dynamics, convective heat transfer, and mass diffusion. Within the framework of LBM, the fluid domain was discretized and represented as a collection of virtual particles that underwent discrete velocity-based movements in predefined directions influenced by the lattice structure. Furthermore, these particles collide with each other at lattice nodes. The LB equation for the velocity field is expressed as:

$$f_i\left(\mathit{x}+{\mathit{e}}_i{\delta }_t,t+{\delta }_t\right)-f_i\left(\mathit{x},t\right)=-\frac{1}{{\tau }_f}\left[f_i\left(\mathit{x},t\right)-f_i^{eq}\left(\mathit{x},t\right)\right]+{\delta }_t{F}_i\left(\mathit{x},t\right)$$

(1)

in which $f_i$ is the particle distribution function (DF) that describes the probability of finding fluid molecules at time t and at point x with the discrete velocity ${\mathit{e}}_i$ while ${\tau }_f$ denotes the dimensionless relaxation time, $F_i$ denotes the external force term.

The equilibrium distribution function (EDF) $f_i^{eq}$ has the following form:

$$f_i^{eq}\left(\mathit{x},t\right)=f_i^{e\left(0\right)}\left(\mathit{u}\right)+s_i\left(\mathit{u}\right)$$

(2)

where

$$f_i^{e\left(0\right)}\left(\mathit{u}\right)={\omega }_i\rho \left[1+\frac{{\mathit{e}}_i\cdot \mathit{u}}{c_s^2}+\frac{\mathit{u}\mathit{u}:\left({\mathit{e}}_i{\mathit{e}}_i-c_s^2\mathit{I}\right)}{2c_s^4}\right], s_i\left(\mathit{u}\right)={\omega }_i\rho {\delta }_t\frac{A\mathit{S}:\left({\mathit{e}}_i{\mathit{e}}_i-c_s^2\mathit{I}\right)}{2c_s^2}$$

(3)

in which S represents the shear rate, I represents the unit tensor, and A is an adjustable additional parameter. It is evident that the present model is based on the standard LBM with the addition of the term s_i.

$F_i$ takes the following form to obtain the fluid dynamics equations:

$$F_i\left(\mathit{x},t\right)={\omega }_i\rho \left(1-\frac{1}{2{\tau }_f}\right)\left[\frac{{\mathit{e}}_i\cdot \mathit{u}}{c_s^2}+\frac{\left(\mathit{u}\mathit{a}+\mathit{a}\mathit{u}\right):({\mathit{e}}_i{\mathit{e}}_i-c_s^2\mathit{I})}{2c_s^4}\right]$$

(4)

where a stands for the acceleration resulting from the external force, which is determined by Equation (9).

The fluid density $\rho$ and velocity u are obtained through:

$$\rho ={\displaystyle \sum _i{f}_i}, \mathit{u}=\frac{1}{\rho }{\displaystyle \sum _i{f}_i{\mathit{e}}_i}+\frac{1}{2}{\delta }_t\mathit{a}$$

(5)

In this paper, the D2Q9 model (as shown in Figure 1) [27] is adopted, and the corresponding ${\mathit{e}}_i$ is defined as:

$${\mathit{e}}_i=c\left[\begin{array}{ccccccccc}0& 1& 0& -1& 0& 1& -1& -1& 1\\ 0& 0& 1& 0& -1& 1& 1& -1& 1\end{array}\right]$$

(6)

with $c={\delta }_x/{\delta }_t$, where ${\delta }_x$ and ${\delta }_t$ denote the step sizes for the spatial and temporal, respectively, both of which are set to 1. The weight factors are given by ${\omega }_0=4/9$, ${\omega }_{1\text{–}4}=1/9$, ${\omega }_{5\text{–}8}=1/36$ and $c_s=c/\sqrt{3}$.

By applying the Chapman–Enskog expansion, the macroscopic equations for the flow field could be derived from the LB Equation (1) (the details are presented in Appendix A):

$$\frac{\mathit{\partial }\rho }{\mathit{\partial }t}+\nabla \cdot \left(\rho \mathit{u}\right)=0$$

(7)

$$\frac{\mathit{\partial }\left(\rho \mathit{u}\right)}{\mathit{\partial }t}+\nabla \cdot \left(\rho \mathit{u}\mathit{u}\right)=-\nabla P+\nabla \cdot \mathit{\tau }+\mathit{F}$$

(8)

where $\mathit{\tau }=\rho \nu \mathit{S}$ is shear stress. The shear rate $\mathit{S}=2\mathit{\epsilon }=\nabla \mathit{u}+{\left(\nabla \mathit{u}\right)}^T$, $\mathit{\epsilon }$ refers to the strain rate tensor, and F is the external force.

The Boussinesq approximation is employed for NC. Correspondingly, the forcing term in Equation (8) takes the form:

$$\mathit{F}=\rho \mathit{a}=-\rho g\beta \left(T-T_0\right)\mathit{j}$$

(9)

where g denotes the gravitational acceleration, $\beta$ represents the thermal expansion coefficient, j denotes a unit vector pointing in the gravitational direction, and T₀ denotes a reference temperature.

The kinematic viscosity $\nu$ is determined by:

$$\nu =c_s^2\left({\tau }_f-A-0.5\right){\delta }_t$$

(10)

In the conventional BGK-LB model, the viscosity of the fluid can be determined solely by the relaxation time (A = 0). In order to simulate the behavior of NNFs accurately, it was necessary to dynamically adjust the relaxation time in the BGK collision term to reflect real-time variations in viscosity. Nevertheless, it should be emphasized that numerical instability phenomena arise when the relaxation time approaches 1/2 [28]. This restriction limits the applications of the BGK-LB model in non-Newtonian simulations. Equation (10) shows that the fluid viscosity in the improved BGK-LB model was not only determined by the relaxation time. This characteristic provided the model with superior numerical stability compared to the traditional BGK-LB model. To describe the behavior of NNFs in this study, we employed the PL model, where the apparent viscosity is given by:

$$\mu =K{\left|\mathit{S}\right|}^{n-1}$$

(11)

where $\mu =\rho \nu$. The consistency index K and PL index n are measures of consistency and the non-Newtonian characteristics of a fluid, respectively. For n values less than 1, the fluid’s apparent viscosity decreased with the increasing strain rate, which characterized it as shear-thinning or pseudo-plastic. Conversely, when n values exceeded 1, the apparent viscosity increased with higher strain rates, categorizing them as shear-thickening or dilatant. When n equals 1, the PL fluid exhibits Newtonian behavior. $\left|\mathit{S}\right|$ is given as

$$\left|\mathit{S}\right|=\sqrt{2\left(\mathit{\epsilon }:\mathit{\epsilon }\right)}=\sqrt{\left(\mathit{S}:\mathit{S}\right)/2}$$

(12)

The localization of DF’s evolutionary process in this model was ensured by calculating the shear rate S using the following formula (as presented in Appendix A):

$$\mathit{S}=\frac{{\displaystyle {\sum }_i{\mathit{e}}_i{\mathit{e}}_i\left[f_i-f_i^{e\left(0\right)}\right]+\frac{{\delta }_t}{2}}\rho \left(\mathit{u}\mathit{a}+\mathit{a}\mathit{u}\right)}{c_s^2\rho \left(A-{\tau }_f\right){\delta }_t}$$

(13)

According to Equation (13), the calculation of the strain rate tensor is not dependent on velocity gradients. This advantageous property simplifies the calculation process and reduces the required computational resources compared to traditional CFD methods.

2.2. BGK-LB Equations for the Temperature Field

The transport of energy due to diffusion processes was modeled using the convection-diffusion equation (CDE), which takes the following form:

$$\frac{\mathit{\partial }T}{\mathit{\partial }t}+\nabla \cdot \left(\mathit{u}T\right)=\nabla \cdot \left(\alpha \nabla T\right)$$

(14)

where $\alpha$ denotes the thermal diffusivity. For most existing LB models used to solve CDE, some assumptions were required to eliminate the deviation terms in order to recover Equation (14). However, for most practical cases that do not satisfy the assumptions, the deviation term may still exist. To remove this drawback, a modified EDF was constructed, and the temperature evolution equations were adjusted by incorporating a source term inspired by Chai’s proposal [29]. The LB equation for the temperature field is given by:

$$g_i\left(\mathit{x}+{\mathit{e}}_i{\delta }_t,t+{\delta }_t\right)-g_i\left(\mathit{x},t\right)=-\frac{1}{{\tau }_g}\left[g_i\left(\mathit{x},t\right)-g_i^{eq}\left(\mathit{x},t\right)\right]+{\delta }_t{R}_i\left(\mathit{x},t\right)$$

(15)

The temperature DF is referred to as $g_i\left(\mathit{x},t\right)$, and ${\tau }_g$ denotes the dimensionless relaxation time. $g_i^{eq}$ is expressed as:

$$g_i^{eq}={\omega }_{i}T\left(1+\frac{{\mathit{e}}_i\cdot \mathit{u}}{c_s^2}+\frac{{\left({\mathit{e}}_i\cdot \mathit{u}\right)}^2}{2c_s^4}-\frac{\mathit{u}\cdot \mathit{u}}{2c_s^2}\right)+{\lambda }_{i}T$$

(16)

where ${\lambda }_{1\text{–}8}={\omega }_{1\text{–}8}$, ${\lambda }_0=-{\displaystyle \sum _{i=1}^8{\lambda }_i}$.

The source term $R_i$ is defined as:

$$R_i={\omega }_i\left(1-\frac{1}{2{\tau }_g}\right)\left[\frac{{\mathit{e}}_i\cdot \left(T\mathit{F}+P\nabla T\right)}{c_s^2\rho }\right]$$

(17)

The temperature can be obtained by the temperature DF:

$$T\left(x,t\right)={\displaystyle \sum _i{g}_i}$$

(18)

By applying the Chapman–Enskog technique to Equation (15), the CDE could be precisely deduced. The thermal diffusion coefficient D is related to ${\tau }_g$ through:

$$\alpha =c_s^2\left({\tau }_g-0.5\right){\delta }_t$$

(19)

To ensure the localization of the evolutionary process of the present model, the gradient term in $R_i$ can be computed through:

$$\nabla T=-\frac{2{\displaystyle {\sum }_i{\mathit{e}}_i\left[g_i-g_i^{eq}\right]+{\delta }_t\mathit{a}T}}{c_s^2\left(1+2{\tau }_g\right){\delta }_t}$$

(20)

3. Physical Problem

In Figure 2, the physical model of NC within a square cavity is presented. The cavity, with a side length of L, contained a non-Newtonian PL fluid. The left boundary of the cavity was subjected to a prescribed temperature of $T_h$, while the right boundary was maintained at a temperature of $T_c$ ($T_h>T_c$). Both temperatures remained constant throughout the analysis. The top and bottom boundaries of the square cavity were considered adiabatic. Initially, the fluid within the cavity was stationary, with a uniform temperature denoted as $T_0=\left(T_h+T_c\right)/2$. Additionally, the solid boundaries of the cavity adhered to the no-slip condition, ensuring zero velocity at these interfaces.

It is worth mentioning that the current work involves two essential parameters, the Rayleigh number and the Prandtl number, which have the following definitions [30]:

$$Ra=\frac{g\beta \left(T_h-T_c\right)L^{2n+1}}{{\alpha }^n\left(K/\rho \right)}, Pr=\left(\frac{K}{\rho }\right){\alpha }^{n-2}{L}^{2-2n}$$

(21)

The Ra number is a measure of the relative magnitudes of thermal transport induced by the buoyancy force and thermal diffusion. It characterizes the relative influence of these two mechanisms on HT. The Pr number serves as a measure of the relative importance of momentum diffusivity and thermal diffusivity in a fluid.

When the system reaches stability, the HT rate is quantified using the $\overline{Nu}$ number, which represents the ratio of the convection-induced HT rate to the conduction-induced HT rate. It is defined as [31]:

$$\overline{Nu}=1+〈u_{x}T〉\frac{L}{\alpha \left(T_h-T_c\right)}$$

(22)

where 〈 ▪ 〉 denotes the average over the whole flow domain.

4. Results and Discussion

4.1. Research on Independence from the Grid

In our study, the basic length unit is the lattice unit (lu), and the time unit is the time step (ts). Unless otherwise stated, ${\tau }_f$ and ${\tau }_g$ are set to one. We conducted a grid independence analysis in order to find an optimal grid that could ensure acceptable computational accuracy while minimizing computational costs.

Table 1. Grid dependence research for n = 0.7, 1.0, 1.3, Ra = 10⁵ and Pr = 7.

Nx × Ny (lu)	$\overline{\mathit{N}\mathit{u}}$
	$\mathit{n}=0.7$	$\mathit{n}=1.0$	$\mathit{n}=1.3$
64 × 64	9.4011	4.8734	3.6996
96 × 96	9.3896	4.7816	3.6619
128 × 128	9.3812	4.7309	3.6324
160 × 160	9.3768	4.6867	3.5982
192 × 192	9.3745	4.6702	3.5803
224 × 224	9.3725	4.6582	3.5624
256 × 256	9.3719	4.6578	3.5620

displays the $\overline{Nu}$ number for Pr = 7, n = 0.7, 1.0, 1.3, Ra = 10⁵, and the different grid sizes. The results indicate that a grid size of Nx × Ny = 256 × 256 (lu) is good enough for numerical calculations. Similar analyses for Ra = 10³, 10⁴, and 5 × 10⁵ determined their computational grids to be 128 × 128 (lu), 192 × 192 (lu), and 256 × 256 (lu).

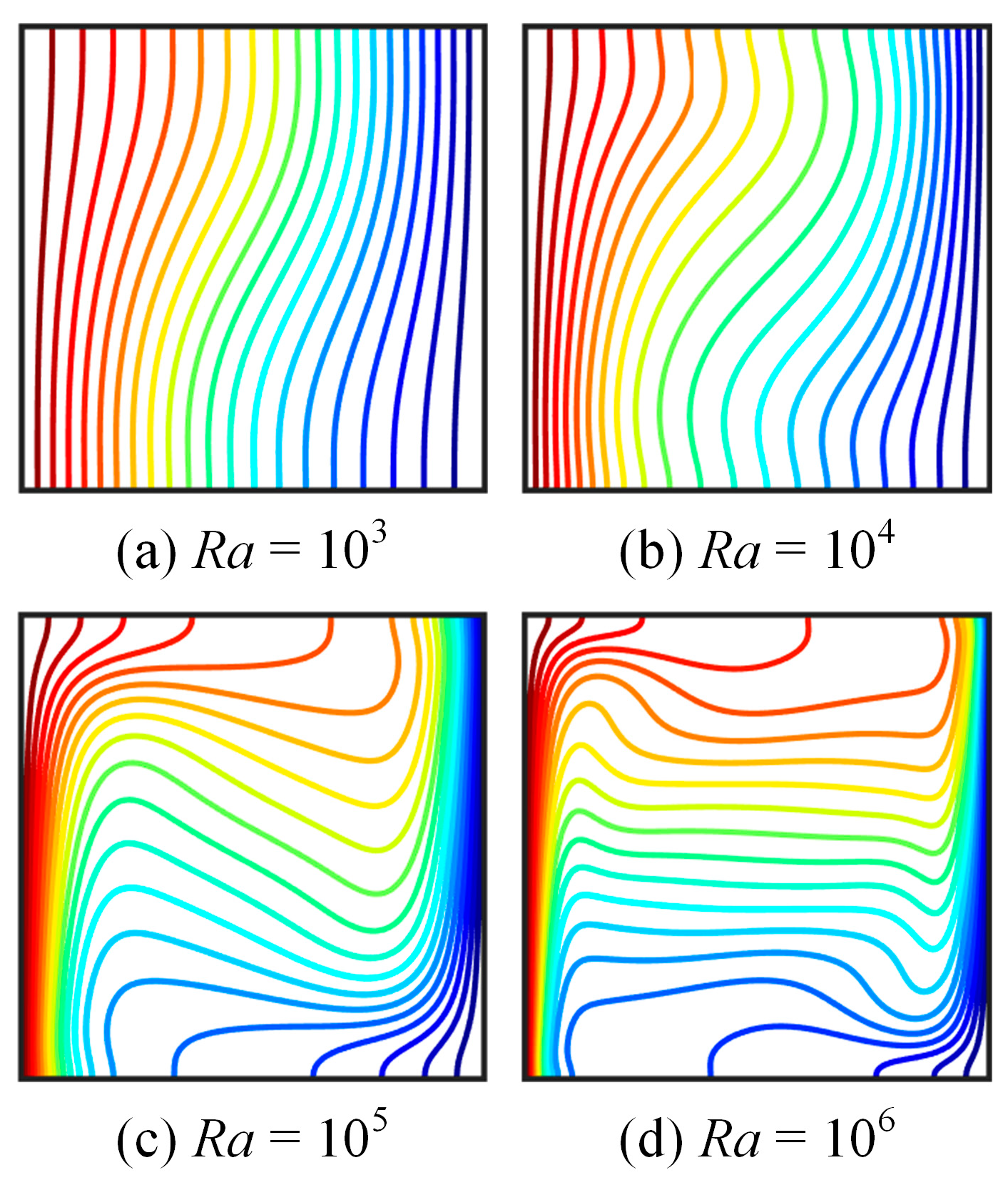
4.2. Numerical Validation

To verify the correctness of the model, simulations of NC were conducted for Pr = 0.71 and n = 1. $T_h=1$ and $T_c=0$ were maintained for the vertical boundaries while the horizontal boundaries remained adiabatic. Figure 3 and Figure 4 depict the streamlines and isotherms, revealing several important features of the flow behavior at different Ra values. At low Ra values, the heated fluid ascended along the left boundary, encountering the adiabatic top boundary, moving toward the cold boundary, and then descending, forming a steady clockwise rotational flow and a central single vortex. This vortex formation corresponds to the characteristic NC flow pattern. As Ra increases, the single vortex becomes elliptical, and at Ra = 10⁵, it splits into two smaller vortices. Further increasing Ra to 10⁶ leads to the movement of these two vortices toward the walls, which is accompanied by the appearance of a third vortex at the cavity center. The isotherms at low Ra values indicate that HT occurs predominantly through conduction between the vertical boundaries, leading to nearly vertical isotherm lines. However, with increasing the Ra, convection becomes the dominant HT mechanism. This transition causes the isotherms to assume a horizontal orientation in the central region of the cavity while remaining vertical only within the thin boundary layers adjacent to the hot and cold boundaries. Overall, the findings depicted in the figures align well with previous works [32,33,34], validating the presented model.

Detailed comparisons for $\overline{Nu}$ along the heated sidewall were performed to quantify the results, as shown in

Table 2. Comparisons of $\overline{Nu}$ obtained from the present method with previous works for n = 1 and Pr = 0.71.

Ra	$\overline{\mathit{N}\mathit{u}}$
	Present Study	Turan et al. [32]	Guo et al. [33]	de Vahl Davis, G [34]
103	1.1182	1.118	1.1195	1.118
104	2.2453	2.245	2.2545	2.243
105	4.5239	4.520	4.5278	4.519
106	8.8342	8.823	8.7746	8.800

. The $\overline{Nu}$ values obtained in our work are consistent with the results from earlier studies, providing further confirmation of the accuracy and reliability of the current scheme.

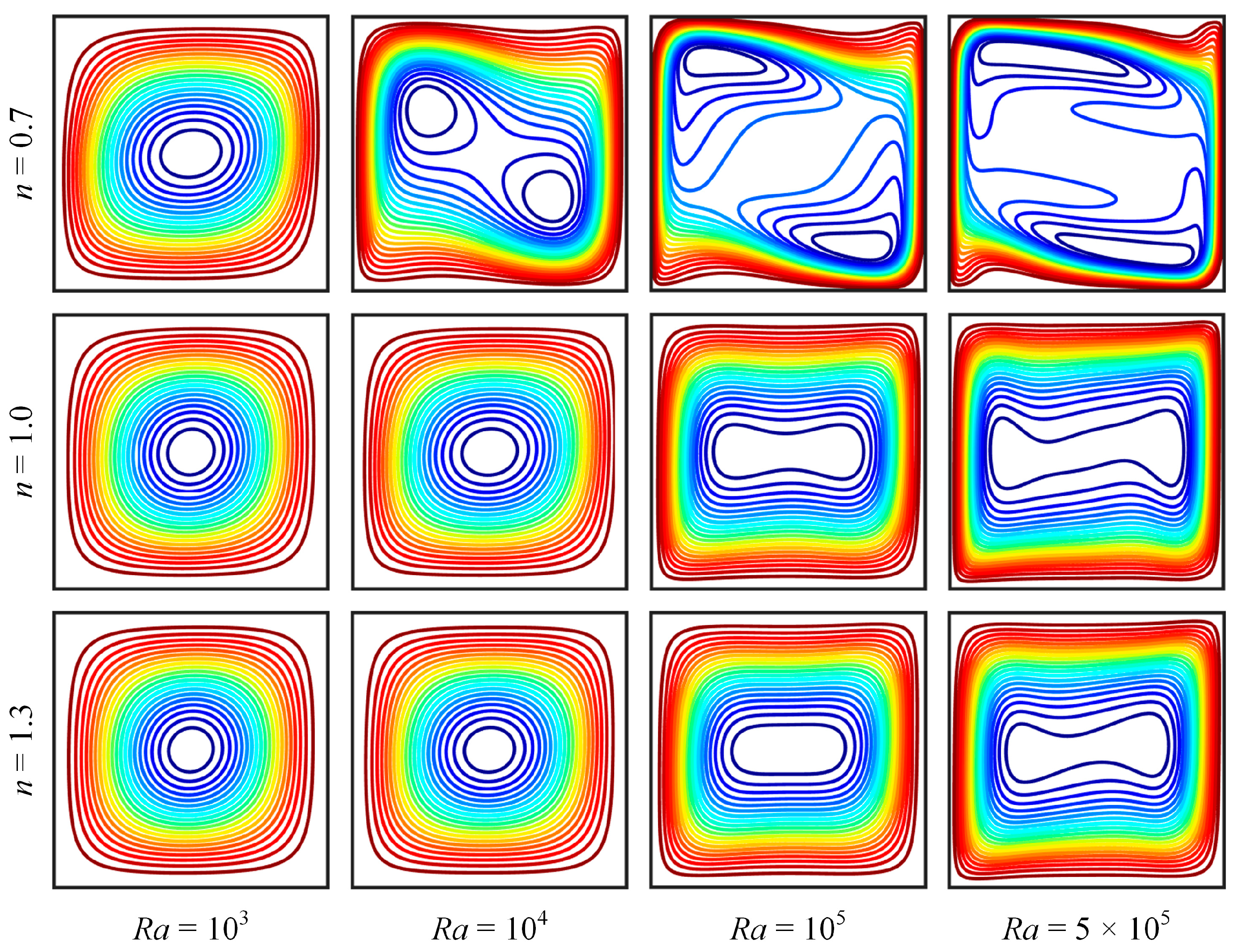
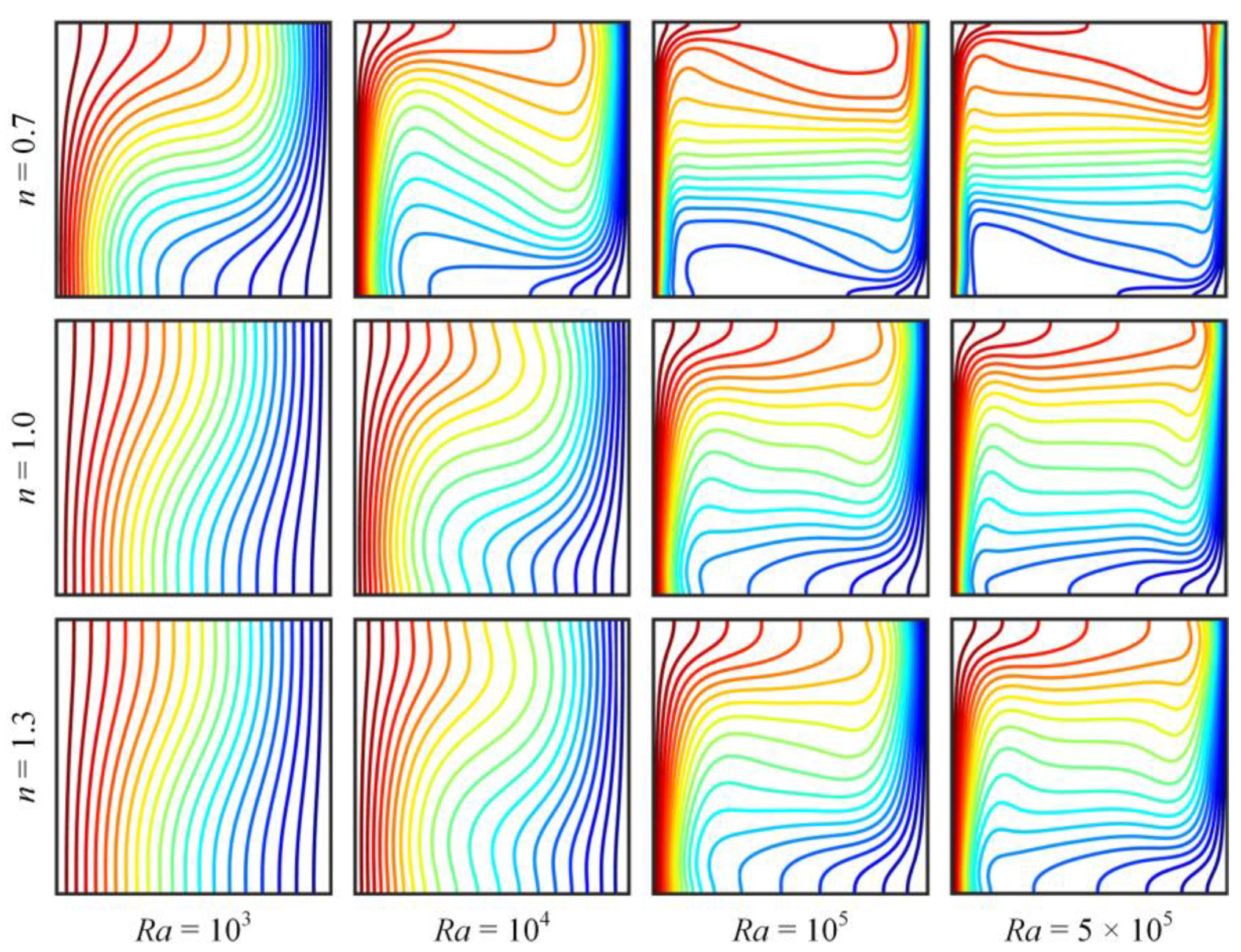
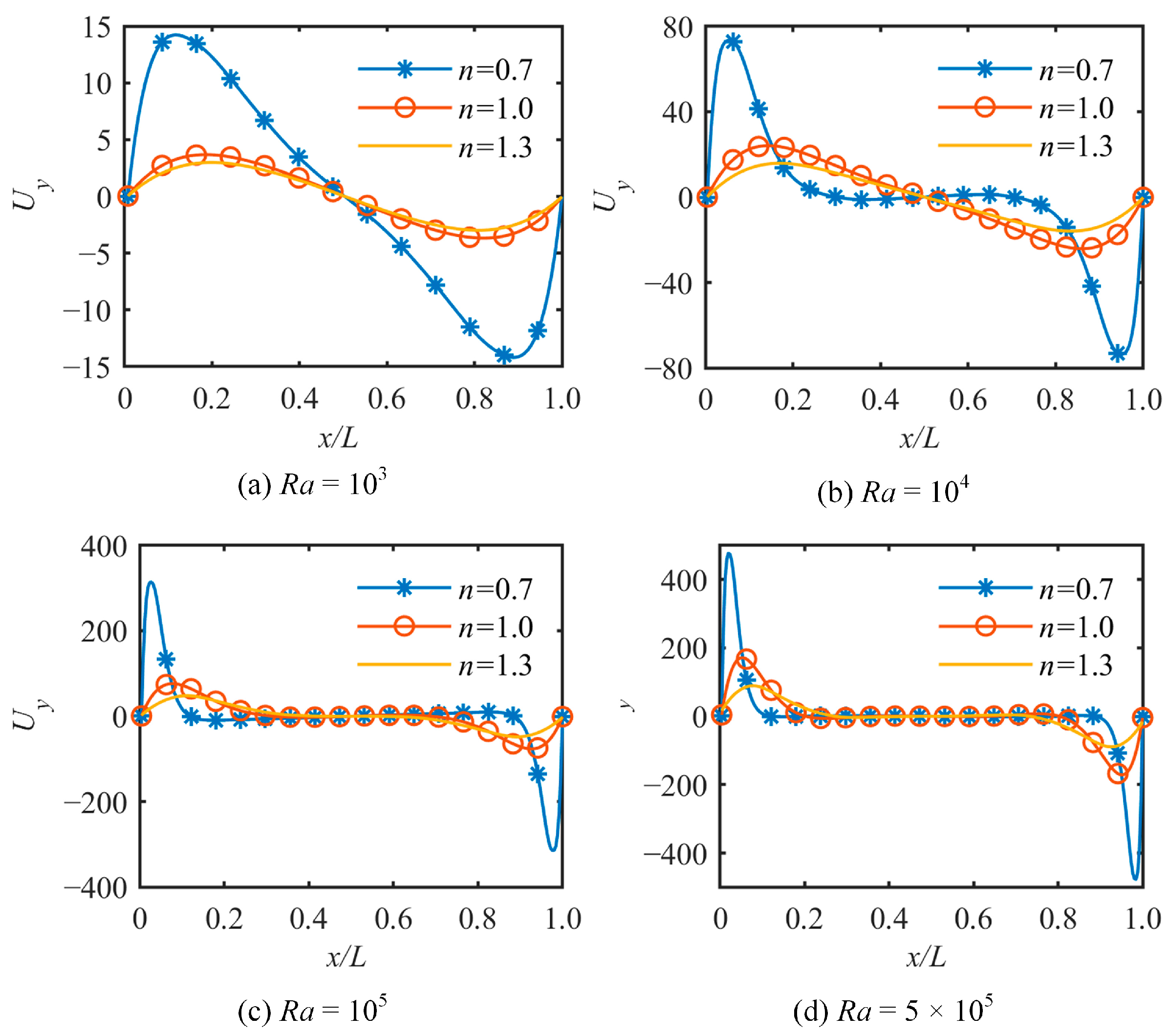
4.3. NC of Power-Law Fluids

The streamline and isotherm distributions obtained from NNFs (n ≠ 1) were compared to those obtained from NFs (n = 1) to explore the influence of non-Newtonian behavior on the flow and HT within the cavity, as shown in Figure 5 and Figure 6.

Figure 5 illustrates the flow field for Ra = 10³, 10⁴, 10⁵, 5 × 10⁵, n = 0.7, 1.0, 1.3, and Pr = 7. According to Figure 5, for a given value of n, both the streamline density along the walls and the convective intensity increased as Ra rose. Furthermore, for a given Ra number, an increase in n led to a rise in the apparent viscosity and a decrease in convection intensity. Note that for Ra = 10³, due to the poor convection within the cavity, the increase in n had no obvious influence on the velocity field. However, for large Ra values, the convective intensity was strong, and increasing n resulted in a considerable drop in velocity.

Figure 6 shows the temperature field for Ra = 10³, 10⁴, 10⁵, 5 × 10⁵, n = 0.7, 1.0, 1.3, and Pr = 7. At low Ra numbers, heat conduction dominated HT, leading to only slightly distorted isotherms. However, as Ra rose, convection took over as the primary mode of heat transmission, causing the isotherms to deform more drastically. When Ra increased to 10⁵, the isotherms within the main cavity region became almost horizontal, while only in the thin border layers were they parallel to the vertical walls. When Ra reached 5 × 10⁵, thermal stratification occurred. In addition, for any given Ra number, an increase in n led to the dominance of shear-thickening behavior, which, in turn, weakened the convection effect and resulted in a decrease in the flow velocity.

Figure 7 depicts the non-dimensional temperature ($\theta =\left(T-T_c\right)/\left(T_h-T_c\right)$) in the vertical direction at the mid-section (y = L/2). As seen in Figure 7, for a given Ra number, the temperature distribution became increasingly linear as n increased. In contrast, for a given value of n, the degree of nonlinearity for the temperature distribution increased as Ra increased. The linear temperature profile suggests that HT was primarily dominated by conduction, while the increase in its nonlinearity indicated an enhancement in the convection intensity at the cavity.

Figure 8 illustrates the changes in non-dimensional vertical velocity ($U_y=u_{y}L/\alpha$) at the cavity’s mid-section (y = L/2) for various Ra and n values. The changes in the shape of these curves reflect variations in the flow patterns. From the figure, it can be observed that as the n value increased for fixed Ra, there was a noticeable decrease in the strength of the rotating cells, which could be attributed to the increased viscosity of the fluid. Therefore, the amplitude of the vertical velocity decreased. In addition, for a given n value, the highest and lowest values of the velocity component increased with Ra. This trend indicated that the intensity of the convection increased with Ra.

Figure 9 depicts how the $\overline{Nu}$ number was influenced by Ra and n. As previously stated, at low Ra numbers, conduction was the primary mechanism for heat transmission, resulting in a small $\overline{Nu}$ number. As Ra increased, however, convection became more dominant, leading to a higher HT rate and an increased $\overline{Nu}$ number. Figure 9 also shows that as the n value increased, the convective effect weakened, resulting in a decrease in the HT rate and a subsequent decline in the $\overline{Nu}$ number.

5. Conclusions

This paper introduces a novel thermal BGK-LB model for NNFs. The proposed model incorporated the local shear rate into the EDF of the flow field. Additionally, the introduction of an adjustable parameter allowed for the determination of fluid viscosity based on the relaxation time in conjunction with the adjustable parameter. This enabled better numerical stability under conditions of low viscosity.

The present model was verified by simulating the NC of Newtonian fluids and comparing the results with those of previous works. Subsequently, the model was employed to examine thermal convection in PL fluids, with a systematic examination of the impacts of Ra and n on both the velocity and temperature fields. The outcomes of the analysis showed that:

(1)

Increasing the Ra number could improve the convective strength and HT rate of both NFs and NNFs.

(2)

A decrease in the n value (0 < n < 1) improved the convective strength and HT rate compared to Newtonian fluids (n = 1), whereas an increase in the n value (n > 1) had the opposite effect.

(3)

The current study presents a more efficient and simplified non-Newtonian thermal BGK-LB model, which proved valuable for studying the mass or heat transfer in NNFs. The model’s ability to accurately capture convective heat transfer phenomena and its computational efficiency contributed to its practical applications in optimizing the design and performance of heat transfer systems using NNFs. Furthermore, this model can serve as a framework for future research addressing more complex non-Newtonian fluid behaviors and extending its application to different flow scenarios.