1. Introduction
A plant factory is one of the most advanced development technologies of modern agriculture; it is characterized by higher unit output, a higher degree of production automation, a higher resource utilization rate, and green health [
1,
2,
3]. A nutrient solution is an indispensable source of nutrients for crop growth in plant factories that is designed to provide suitable ionic elements for crop growth. Hydroponics is a system in which the nutrient solution supplies water, nutrients, and oxygen to crops instead of natural soil so that crops can grow healthily during the life cycle [
4,
5]. The advantage of hydroponic systems is that they can avoid continuous cropping obstacles and diseases that often occur in soil cultivation [
6,
7]. The four essential indicators of nutrient solutions for plant factories are pH, EC, temperature, and oxygen. Significantly, the pH value of the nutrient solution is crucial for determining the health and productivity of crops. The pH value is a measure of the acidity or alkalinity of a solution, representing the concentration of hydrogen ions (H
+) in the solution. Different crops in plant factories have specific pH requirements for optimal nutrient absorption. Moreover, maintaining the appropriate pH level in nutrient solutions ensures that crops can readily absorb essential nutrients [
8,
9]. However, it is a challenging task for the pH control problem due to the strong nonlinearity, parameters uncertainty, and multi-disturbances for the nutrient solution process.
Many forms of pH modeling for nutrient solutions have been proposed, which can be represented by the continuous stirred tank reactor (CSTR) model [
10]. The typical pH general model has been developed from the perspective of these mechanisms [
11]. The abovementioned mathematical model can be described by the dynamic model and static nonlinear model. The dynamic model describes the dynamic change of the concentration of each chemical component in CSTR. The nonlinear model reflects the balance of chemical components in a system at equilibrium. A bilinear model of a pH model was approached [
12]. A pH model was presented by solving a non-linear algebraic equations system based on chemical equilibrium equations, mass balances, and the electroneutrality principle [
13]. To accurately predict the behavior of pH processes in tubular mixers and in-line systems, a distributed parameter model has been proposed in [
14]. It should be noted that an accurate mathematical model was difficult to obtain owing to a mismatch in model parameters. In addition, there are also limitations when applying pH modeling in plant factories. These include the significant upfront investment required for system installation and the continuous requirement for monitoring system operations, particularly in terms of electricity supply.
Over the past few years, many academics have put forward control strategies, such as robust control [
15,
16], feedforward control [
17], adaptive control [
18,
19,
20], fuzzy control [
21,
22,
23], optimal control [
24,
25], and so on. However, the control strategy proposed in aforementioned papers can only deal with systems whose dynamics are linearly characteristic. Therefore, the classical linear control strategy can only achieve a good control effect within a small range of working points for weak nonlinear systems. The controller design for the pH value of nutrient solutions encounters a significant challenge due to its inherent complexity. There are three main reasons, as follows:
(1) The nutrient solution process can be described as a dynamic system with strong nonlinearity characterized by significant gain fluctuation at different working points. In particular, the sensitivity of pH changes is very large when the pH reaches the neutral point. A small input change may cause a great output change [
26].
(2) Furthermore, the pH of nutrient solutions is severely influenced by multi-disturbances and parameters uncertainty, such as fluctuations of fertilizer flow and irrigation water flow, instable factors including acid concentration, and the alkali concentration of the feed solution [
27].
(3) The pH value of a nutrient solution is highly dynamic and primarily influenced by the absorption of ions by crops roots, the hydrolysis of carbon dioxide (CO2), and the loss of H+ ions, resulting in elevated cation levels. As a result, the pH variation in the nutrient solution becomes intricate and challenging to control.
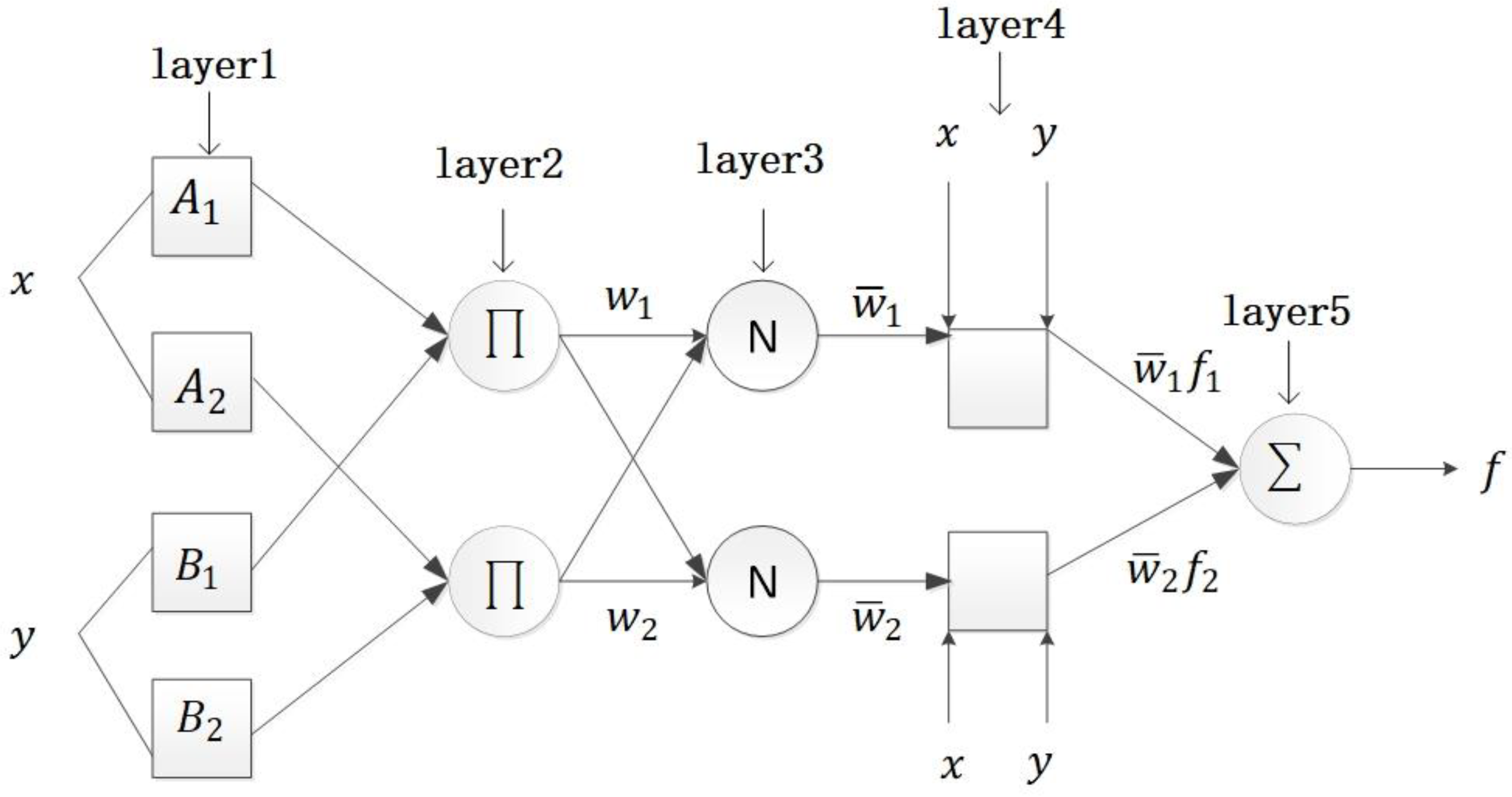
Artificial intelligence theories, such as neural networks, are utilized as a promising approach for control problems. Because neural networks can approximate any continuous functions between finite-dimensional spaces and arbitrary accuracy, many scholars have tried to apply neural networks to nonlinear control. To stabilize certain types of nonlinear strict-feedback systems with uncertain dynamics while considering full-state constraints, an adaptive neural network control method was investigated [
28]. A nonlinear multi-agent adaptive neural network controller with constraints was presented [
29]. Aiming at a specific class of nonlinear systems that feature multiple-input and multiple-output (MIMO) variables, an adaptive output feedback fault-tolerant controller based on a neural network was proposed [
30]. A control strategy based on neural networks was proposed for adaptive decoupling of nonlinear systems to enhance evaporation efficiency [
31]. A feedback-based adaptive controller based on a neural network was presented for improved control performance [
32].
By building upon the control strategy presented in references [
33,
34,
35,
36], a nonlinear adaptive control scheme utilizing ANFIS is proposed to address the control problem related to regulating the pH value of nutrient solutions. This article makes several contributions to the field, including:
(1) To achieve precise control of pH value and ensure that the pH value of the nutrient solution is suitable for crop growth, a dynamic model for nutrient solution pH is established based on the actual conditions of the factory.
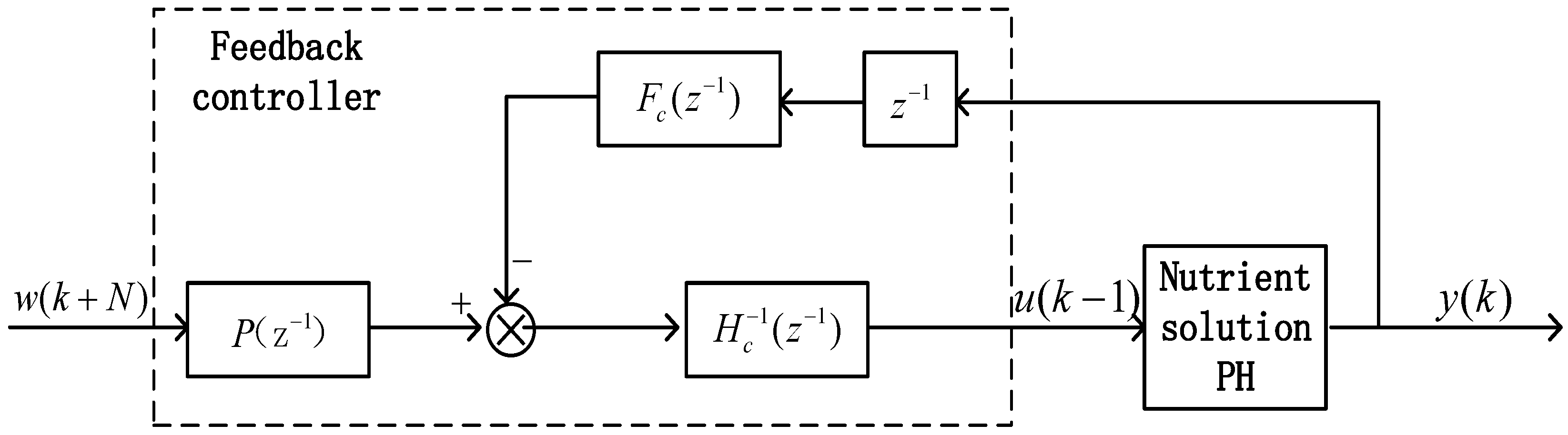
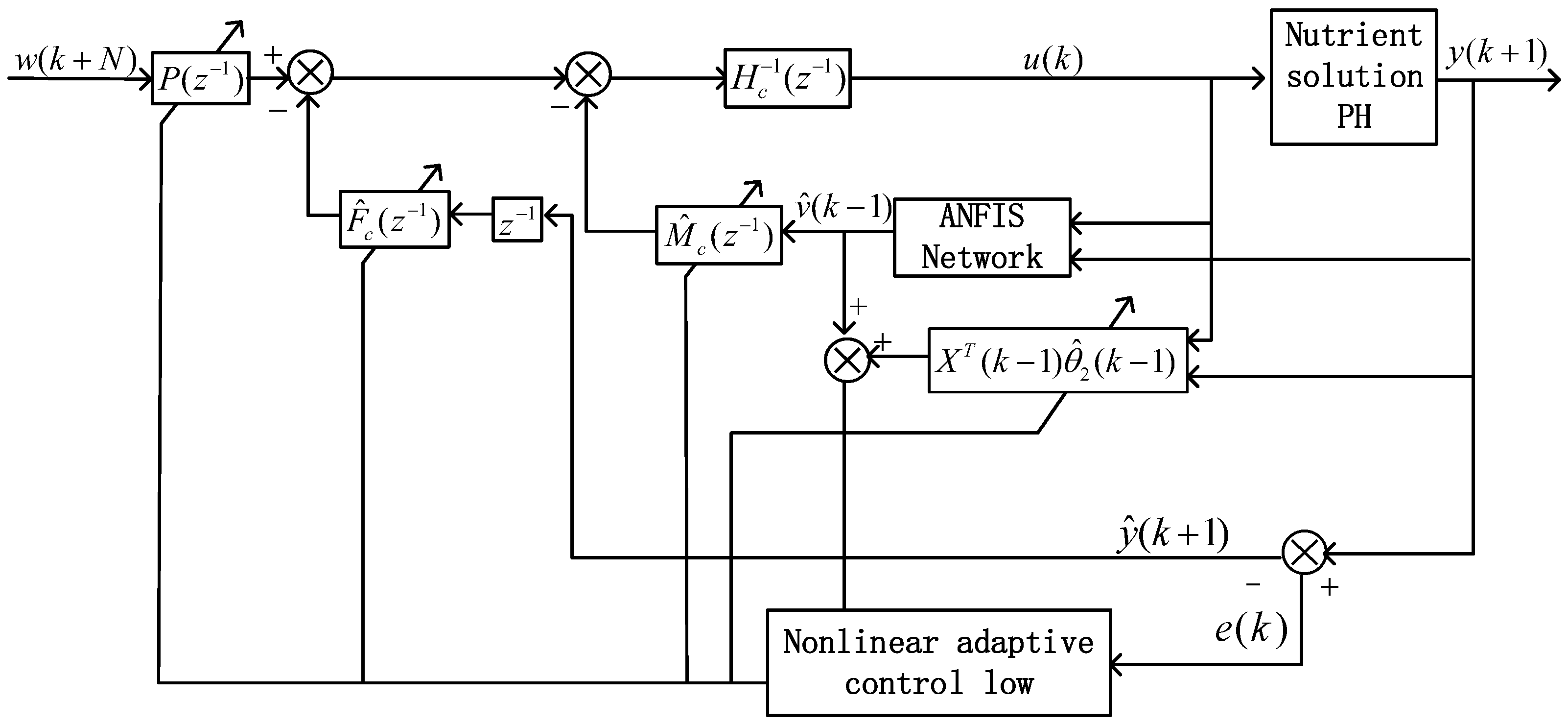
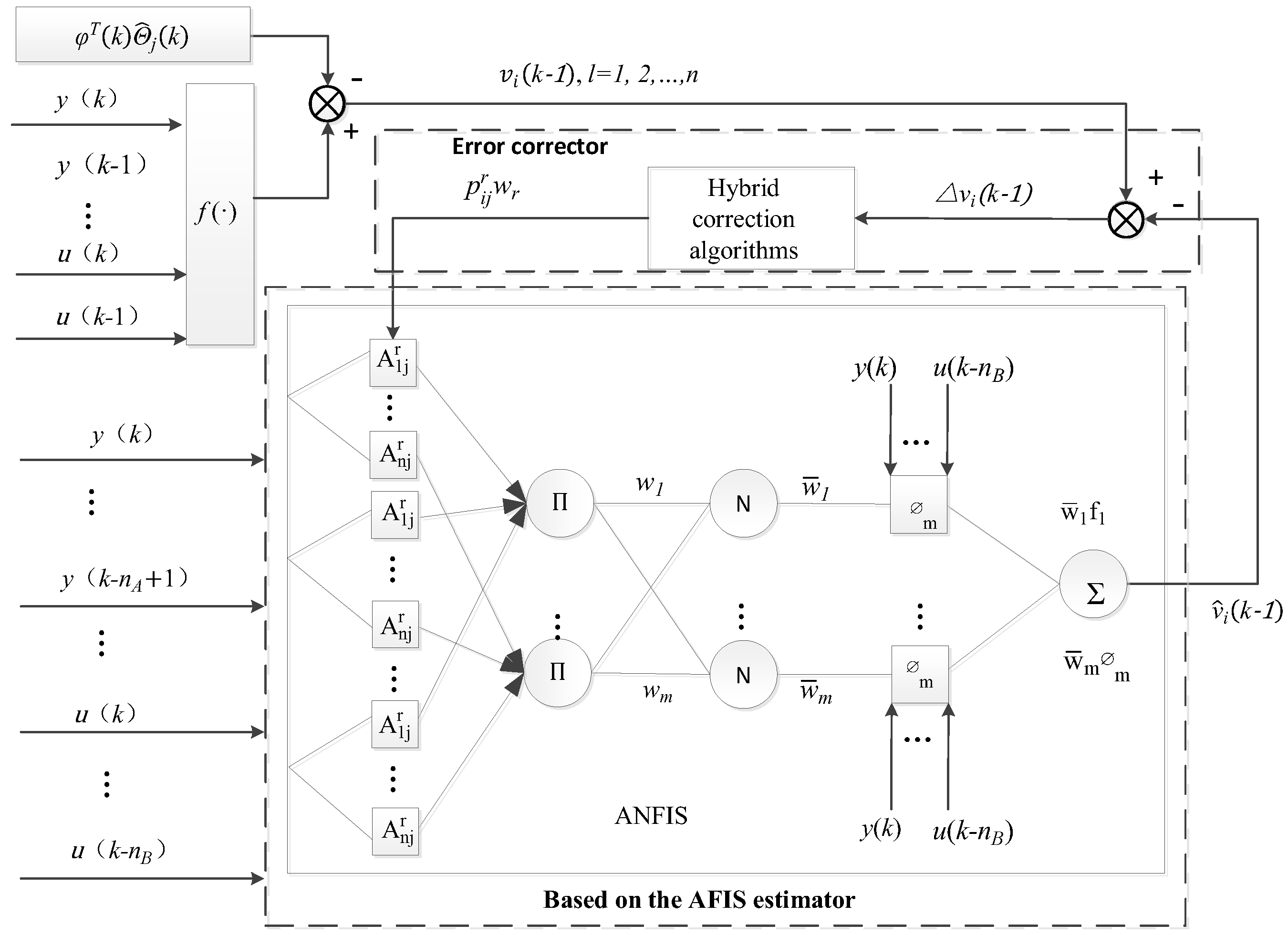
(2) To the best of our knowledge, there is a significant lack of research exploring the potential application of the nonlinear generalized prediction adaptive control method on the basis of ANFIS in pH control of nutrient solutions. The control method comprises a linear adaptive generalized predictive controller, a nonlinear adaptive generalized predictive controller, and a switching mechanism. The parameters of the controller are adjusted by GPC laws. In this approach, ANFIS is used to estimate the unmodeled dynamics to depress the influence of nonlinearity on the system.
2. Process Description of the Nutrient Solution
The model and control of the research are experimented on in the plant factory (
Figure 1a) located at Haicheng Sanxing Ecological Agriculture Co., Ltd. in Liaoning Province. The size of the plant factory is 16 m in length, 6 m in width, and 3 m in height. The interior of the plant factory (
Figure 1b) has three cultivation racks, which are 14 m long, 0.3 m wide, and 0.5 m high. The nutrient solution process system in the plant factory is shown in
Figure 1c. From left to right, the four tanks contain fertilizer, acid, alkali, and a mixed nutrient solution, and the volumes of the four tanks are 300 L, 300 L, 300 L, and 500 L, respectively. The initially composition of the fertilizer includes Ca(NO
3)
2 4H
2O—315 mg/L; KNO
3—712 mg/L; MgSO
4 7H
2O—542 mg/L; and (NH
4)
2HPO
4—301 mg/L. For pH control, the acid solution uses HCL—0.36 mol/L, while the alkaline solution uses NaOH—0.1 mol/L. The transmission pipe (
Figure 1d) of the nutrient solution system is made of polyvinyl chloride (PVC), with a diameter of 8 cm.
A construction diagram of the nutrient solution system is displayed, as shown in
Figure 2. The system takes place at the reaction center and has four inputs and one output. The inputs are acid solution, alkali solution, fertilizer solution, and irrigation water. The output is mixed nutrient solution, which is sent to the cultivation rack under pressure by the fertilization pump. The symbols in
Figure 2 are explained as follows: GL—filter; JL—metering pump; PH—sensor;
,
,
,
—electromagnetism valve.
In the actual configuration process of the nutrient solution, the controller regulates the input flow rate of acid liquid (), alkali liquid (), fertilizer liquid (), and irrigation water () by the metering pumps (JL). In order to be well mixed for the nutrient solution, the stirring device is activated when the liquid flows into the mixing tank (). The pH value is detected by the sensor. After comparing the measurement value of pH with the setpoint value, the controller adjusts each input flow and configures the qualified nutrient solution. Finally, the qualified nutrient solution is extracted through the fertilization pump supplied to the crops of the plant factory through the electromagnetism valve.
4. Dynamic Characteristics
The dynamic model of the pH of the nutrient solution is denoted in Equations (3)–(5).
Table 1 contains the parameters utilized in the simulations of the model. To design a control strategy of the system, the dynamic characteristics, parameters uncertainty, and nonlinearity are discussed in this section.
4.1. Parameters Uncertainty
It is significant to notice that the model parameters are constant for many ideal assumptions in establishing the pH model of the nutrient solution. Although it is possible to avoid significant fluctuations by controlling the quantity of nutritional elements through the monitoring system, there are many uncertainties for some parameters in the actual system of the nutrient solution as time goes on. For example, ,, and vary with time in Equation (3). Subsequently, parameters uncertainty experiments are discussed below.
The initial value of the system is
= 3.6 L/min;
y = 7 and the input and output of the system are not changed in the experimental process. The parameter
is adjusted from the initial value of 0.36 mol/L to 0.32 mol/L, 0.34 mol/L, 0.38 mol/L, and 0.40 mol/L for investigating the output response of the system. The results of the experiment are depicted in
Figure 4.
The results show that the pH value has fluctuated dramatically with the change of the model parameter
. As shown in
Figure 4, the pH value changed from 7 to 11.5 at
= 0.32 mol/L and varied from 7 to 11 at
= 0.34 mol/L. The pH value of the nutrient solution changed from 7 to 3 at
= 0.38 mol/L and varied from 7 to 2.3 at
= 0.4 mol/L.
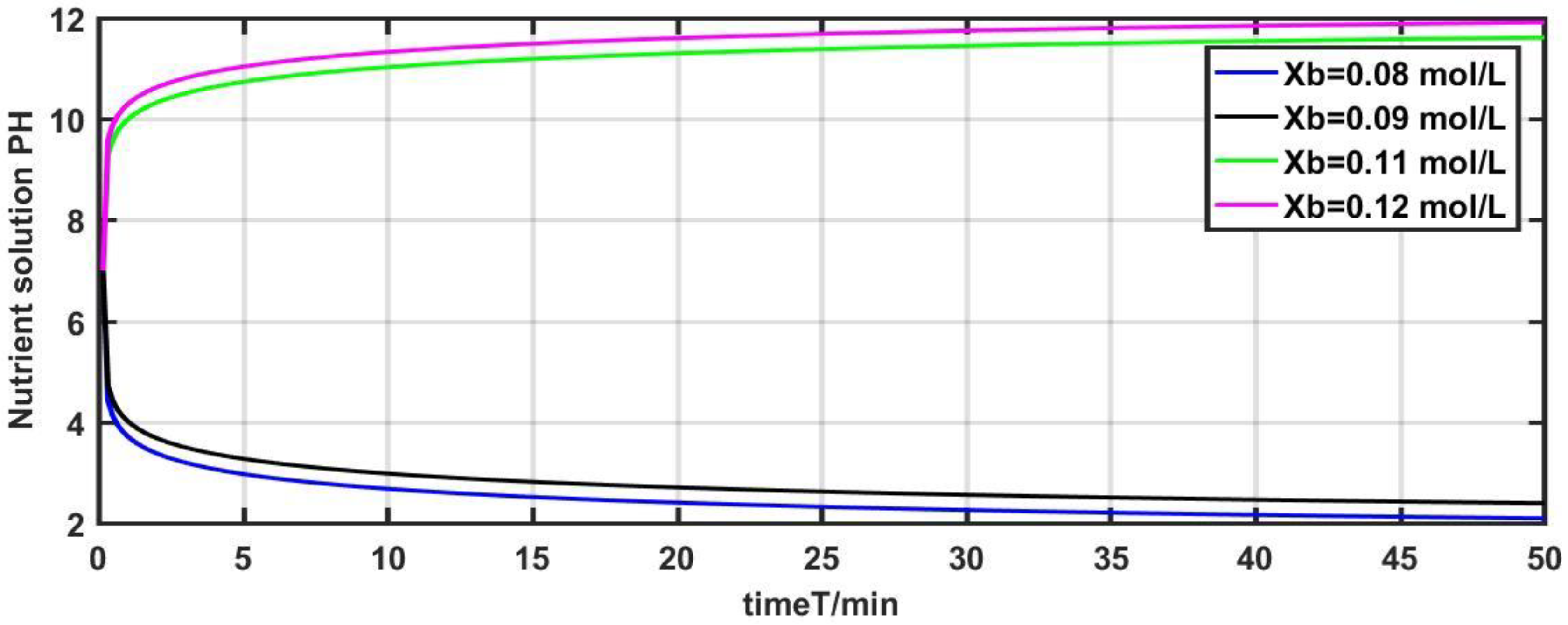
The model parameter
is adjusted from the initial value of 0.1 mol/L to 0.08 mol/L, 0.09 mol/L, 0.11 mol/L, and 0.12 mol/L for investigating the output response of the system. The results of the experiment are depicted in
Figure 5.
The results show that the pH value has changed significantly with the modification of the model parameter
simultaneously. As shown in
Figure 5, the pH value changed from 7 to 2 at
= 0.08 mol/L and varied from 7 to 2.5 at
= 0.09 mol/L. The pH value of the nutrient solution changed from 7 to 11.5 at
= 0.11 mol/L and varied from 7 to 12 at
0.12 mol/L.
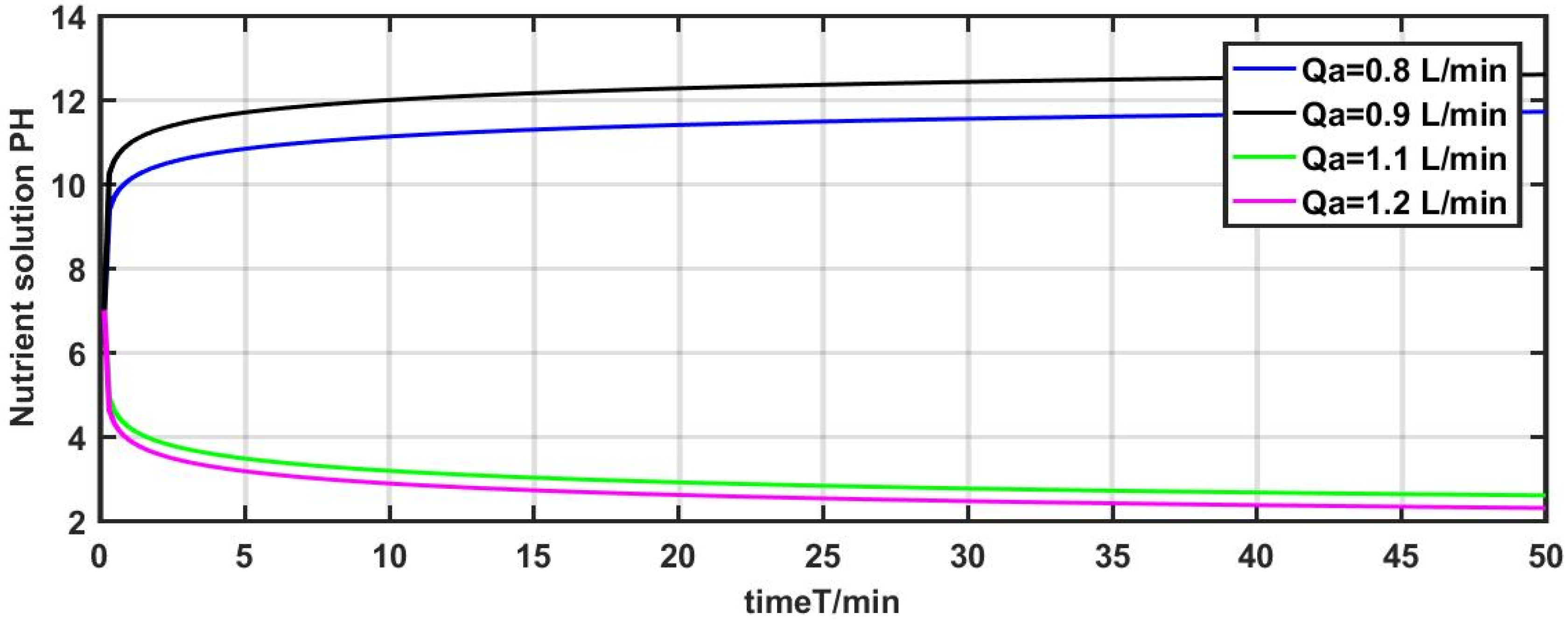
The model parameter
is adjusted from the initial value of 1 L/min to 0.8 L/min, 0.9 L/min, 1.1 L/min, and 0.13 L/min for investigating the output response of the system. The results of the experiment are depicted in
Figure 6.
The results show that the pH value has a similar response with the change of the model parameter
. As shown in
Figure 6, the pH value of the nutrient solution changed from 7 to 12 at
= 0.8 L/min and varied from 7 to 11 at
= 0.9 L/min. The pH value of the nutrient solution changed from 7 to 3 at
= 1.1 L/min and varied from 7 to 2.3 at
= 1.2 L/min.
It is evident from the aforementioned three experiments that the pH value of the system has changed remarkably with the slight modification of the model parameters , , and . Furthermore, fluctuations of fertilizer flow and irrigation water flow also affect the dynamic characteristics of the pH of the nutrient solution. Therefore, it is necessary to depress the influence of multi-disturbances and parameters uncertainty on the system.
4.2. Nonlinearity of the System
Figure 7 shows the titration curve for the pH value, which describes the static input–output relationship of the system [
37]. It is seen clearly that the pH of the solution has a small change where the reaction process is far away from the neutral point (pH = 7), even if a large amount of alkali liquid is added. However, the sensitivity of the pH becomes very large when the reaction process is around the neutral point. Adding a small amount of alkali liquid can cause a large change in the pH value. As shown in
Figure 7, the pH of the solution system exhibits strong output multiplicity. The static curve increases from nearly 0 degrees to nearly 90 degrees and then reduces from almost 90 degrees to almost 0 degrees. Based on the concept in [
38], the pH of the nutrient solution system has strong static nonlinearity.
In order to further illustrate the nonlinear characteristic of the nutrient solution system, this paper uses the gap metric method to measure the nonlinear strength of the pH of the nutrient solution [
39]. The working space of the nutrient solution system
can be meshed with
working points in the working space. The linearization model at the
point and the
point of the system is
,
in the working area. Select the largest gap
as the nonlinearity measure of the system in its working area. The degree of nonlinearity can be expressed using the following formula:
By following the steps for calculating the gap metric, one can obtain a measure of nonlinearity:
(1) By leveraging existing knowledge about the system, distribute working points in the whole working space.
(2) Linearize the nonlinear systems and obtain linearized models corresponding to all working points.
(3) Calculate the gap metric values between the linearized models, and the gap-matrix is computed.
(4) Compare the matrix components one by one and use the largest element to represent the nonlinearity measure of the system in the working space.
The pH of the nutrient solution system is divided within the range of pH
[
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
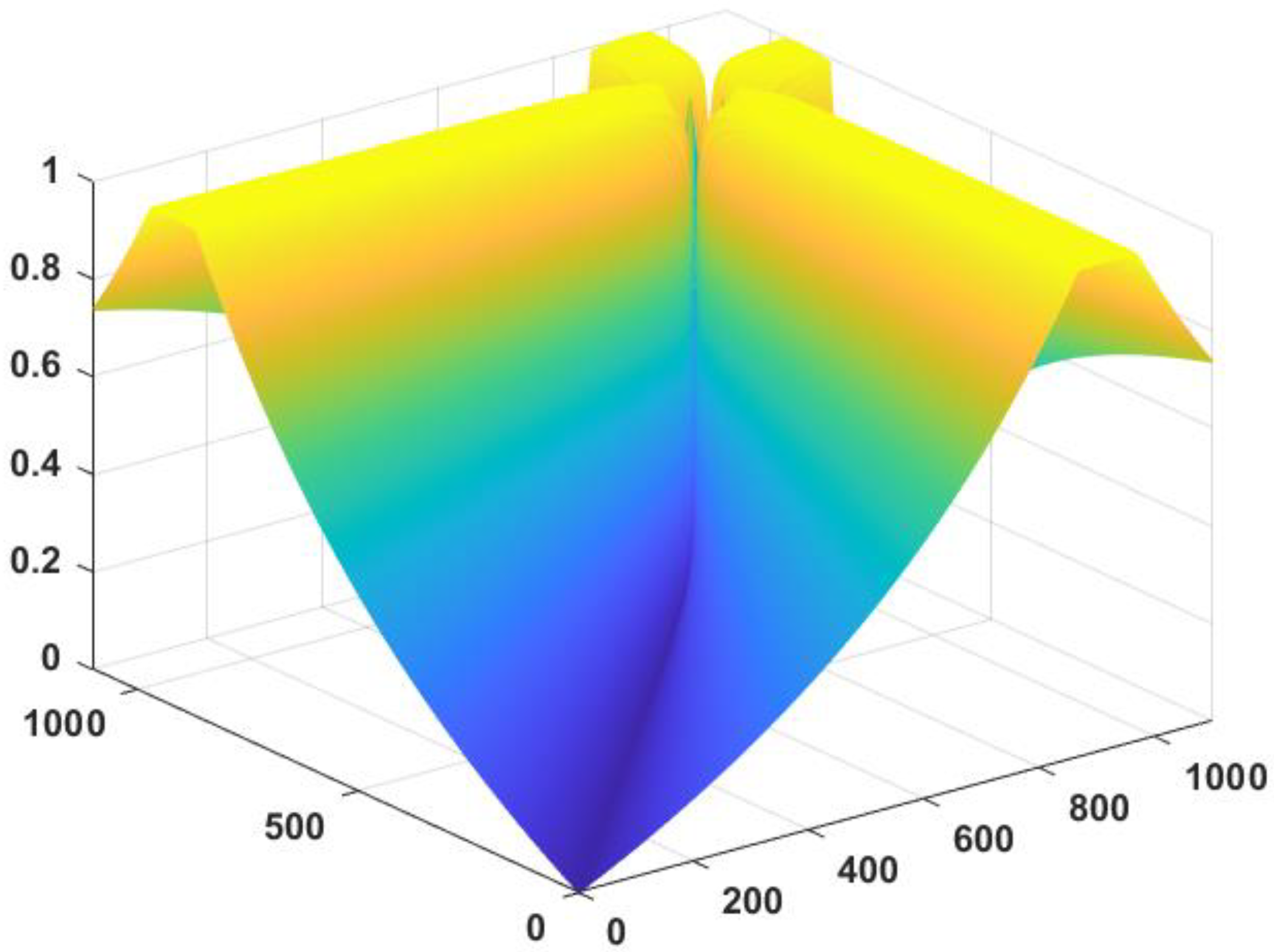
12]. The number of working points is
= 1100, where 1100 linear models can be obtained by linearizing the dynamics of the nonlinear system near these points. Gap metric values are calculated for 1100 different linear systems, and the maximum gap among the
gaps is selected as the nonlinearity degree. The gaps are displayed in
Figure 8.
The results show that the nonlinearity measure = 1. Furthermore, there are great differences in characteristics of the nutrient solution system at different working points in the given working space. Thus, as the system exhibits significant nonlinearity in its working range, a nonlinear control approach is required.
6. Simulation Results
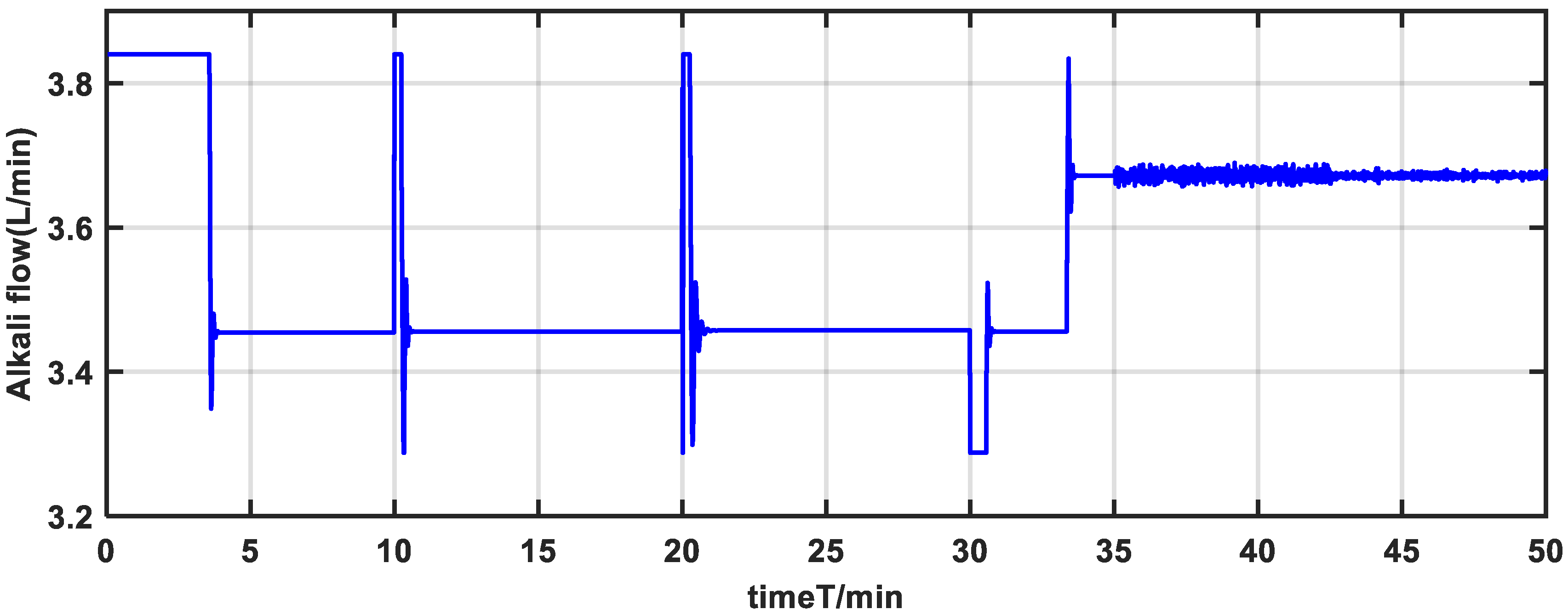
To validate the effectiveness of the present method, the nonlinear adaptive control strategy was applied to the nutrient solution pH value system. In this paper, two kinds of experiments were carried out in the simulation research: (1) A setpoint tracking experiment was devised to examine the tracking effect of the present method. (2) A parameter uncertainty experiment was devised to investigate the control performance under the condition of time-varying parameters. (3) A noise and unmeasurable disturbances experiment was devised to validate the feasibility of the nonlinear adaptive strategy.
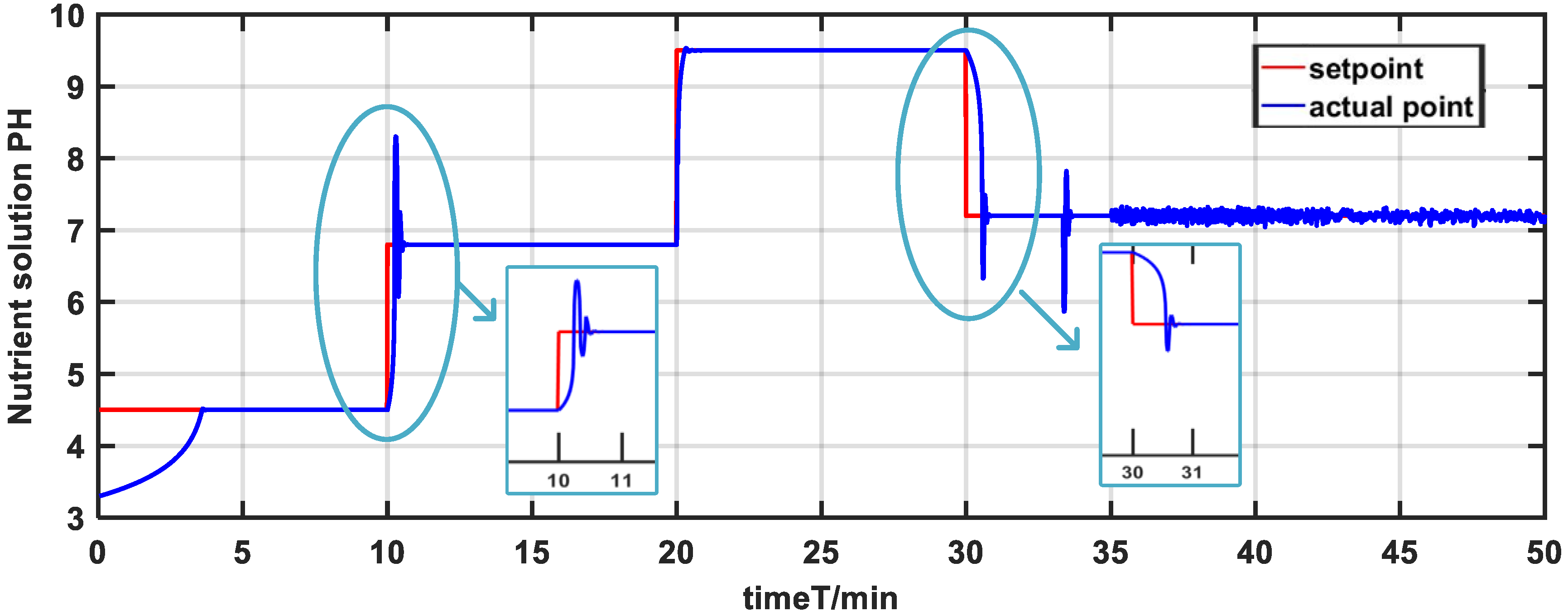
(1) Setpoint tracking experiment. To further illustrate the availability and feasibility of the method put forward in this paper, the pH scale was designed to be adjusted from 3 to 10. The experimental design is outlined as follows. The pH setpoint of the nutrient solution was changed every 10 min during a 50 min experimental process. The set value of the pH is changed from 3.3 to 4.5 at t = 0–10 min and then was designed from 4.5 to 6.8 at 10–20 min. Subsequently, the setpoint of pH was changed from 6.8 to 9.5 at t = 20–30 min. In the end, the set value of pH was changed from 9.5 to 7.2 at t = 30–50 min.
The initial parameters of the model are given as follows: = 0.36 mol/L, = 0.1 mol/L, = 1.0 L/min, = 500 L, = 0.5 L/min, = 0.1 mol/L, = 1.5 L/min, and = 0.1 mol/L. The initial working point is as follows: = 3.42 L/min and = 3.3; the open-loop step experiment was carried out at this working point to obtain the experimental data, and the system order is expressed as = 2, = 1. The model of the system is obtained around the working point through system identification: , . The parameters of the nonlinear adaptive controller are designed as follows: = 0.1, the parameters of switching criterion . The membership function of ANFIS is arranged as the Gaussian function which the training time is set to 40. The input of ANFIS is divided into three fuzzy intervals.
In comparison, the gain-scheduling PID control method was adopted in this process. The experiments were devised as follows. The pH setpoint of the nutrient solution was changed every 50 min due to the long adjustment time for the PID control method. The set value of the pH was changed from 3.1 to 4.5 at t = 0–50 min and then was designed from 4.5 to 6.8 at 50–100 min. Subsequently, the setpoint of the pH was changed from 6.8 to 9.5 at t = 100–150 min. In the end, the set value of the pH was changed from 9.5 to 7.2 at t = 150–250 min. In this paper, the classic incremental PID structure is applied to the nutrient solution and the PID controller as follows:
where
, and
denote the proportional gain, integral gain, and derivative gain, respectively.
To mitigate the impact of nonlinearity and varying dynamics on the system, the gain-scheduling PID strategy was applied to the process by modifying the proportional, integral, and derivative gains in specific operating conditions. The parameters of the PID controller are provided in
Table 2 at different operating points.
(2) Parameters uncertainty experiment. In fact, the parameters, such as acid flow rate, are very difficult to be obtained precisely in advance and may vary with different operation conditions on the basis of actual production for the nutrient solution. To prove the effectiveness of the present method, the abovementioned parameters were changed during the experiment when the system was in steady-stage. The experimental design is outlined as follows. Acid flow was changed from 1.0 to 1.1 L at t = 33 min. The gain-scheduling PID control method was also adopted here for comparison. The changes in the parameter amplitude were similar to the above experiment and were designed as follows. The acid flow was changed from 1.0 to 1.1 L at t = 158 min.
(3) Noise and unmeasurable disturbances experiment. As a matter of fact, the actual process has noise and additional unmeasurable interferences in the plant factory. The acidity and alkalinity concentrations are difficult to detect in real-time in practical systems. The above factors belong to unmeasurable disturbances. Moreover, to further prove the feasibility of the present method, the noise was also added for testing purposes during the experiment when the system was in steady-stage. The experimental design is outlined as follows. The acidity and alkalinity concentrations were added random disturbances with amplitudes ranging from [−0.05 +0.05] around their operating point at t = 35 min. The noise was added to the pH measurement with amplitudes ranging from [−0.1 +0.1] at t = 42.5 min. The gain-scheduling PID control method is also adopted here for comparison. The acidity and alkalinity concentrations were added random disturbances with amplitudes ranging from [−0.05 +0.05] around their operating point at t = 170 min. The noise was added to the pH measurement with amplitudes ranging from [−0.1 +0.1] at t = 210 min.
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19 and
Figure 20 display the simulation results.
Figure 15,
Figure 16,
Figure 17 and
Figure 18 show the control effect using a gain-scheduling PID control strategy, and
Figure 18,
Figure 19 and
Figure 20 show the control effect by nonlinear adaptive control strategy. The gain-scheduling PID control strategy does not produce a desirable control effect, as can be observed. Due to the uncertainties and strong nonlinearity in the nutrient solution system, the pH value has a long adjustment time and reaches the steady state very slowly, especially at the setpoint of 4.5 and 9.5. However, the adjustment time of the nonlinear adaptive control strategy is short and reaches the steady state within 5 min. In additional, the pH has small overshoot, which greatly enhances the control effect of the system.
Regarding the situation of parameter uncertainties, the pH value features large fluctuations based on the gain-scheduling PID control strategy from
Figure 15. However, as depicted in
Figure 18, the pH value undergoes less fluctuations and rapidly adjusts towards the setpoint during parameter variations. Therefore, the pH is capable of fast setpoint tracking and mitigating the effects of uncertainties on the system.
Concerning the situation of noise and unmeasurable disturbances, the proposed method has good robustness similar to the gain-scheduling PID controller, as depicted in
Figure 18. Therefore, the nonlinear adaptive controller is not sensitive to interference and noise. The precise control of pH for the nutrient solution can adjust the acidity or alkalinity of the nutrient solution to regulate the solubility and stability of the nutrients, thereby promoting nutrient absorption and utilization, maintaining healthy root development, and, ultimately, enhancing crops yield.
To further substantiate the control performance of the nonlinear adaptive control strategy, the average error and standard error are selected to measure the control effect. The formula for calculating the average error and standard error is as follows and the results of two methods are show in
Table 3.
The above table shows the average error and standard error of the gain-scheduling PID control strategy and the nonlinear adaptive control strategy, respectively. The average error and standard error of the gain-scheduling PID control strategy are 0.1338 and 0.4784, respectively. The average error and standard error of the nonlinear adaptive control strategy are 0.1046 and 0.3009, respectively.
By comparing with two control strategies, it can be deduced that the nonlinear adaptive control strategy has a good control effect on the actual nutrient solution pH in many aspects. For one thing, the nonlinear adaptive controller enhances the setpoint tracking performance that shortens the adjustment time and decreases overshoot; for another, it has a better adaptability of parameter uncertainties. Therefore, the proposed method can improve the dynamic performance and has good robustness in the face of strong nonlinearity and parameters uncertainty.
The setpoint tracking experiment, the parameters uncertainty experiment, and the noise and unmeasurable disturbances experiments are conducted to validate the effectiveness and feasibility of the proposed control method for the plant factory. Precisely regulating the pH value under various complex situations promotes nutrient transformation and metabolism, improving crops’ nutrient utilization efficiency while creating a suitable environment for plant growth. Furthermore, it can reduce nutrient waste and loss, increasing crops yield and thereby enhancing the economic efficiency of plant factories.