Nonlinear Adaptive Back-Stepping Optimization Control of the Hydraulic Active Suspension Actuator
Abstract
1. Introduction
2. Nonlinear Modeling of Hydraulic Active Suspension Actuator
3. Nonlinear ABC Controller Design and Stability Testing for Hydraulic Active Suspension Actuator
3.1. Design of Nonlinear ABC Controller
3.2. Stability Analysis
- (1)
- , positive definite.
- (2)
- Let , just .
- (3)
- is semi-negative definite and bounded.
- (4)
- The derivative of yields the following: , and satisfies the uniformly continuous as .
4. PSO Improvement and Controller Parameters Optimization
4.1. PSO Basic Principles
- (1)
- Assume the population size is , the particle diameter is , the position of each particle is , and the velocity is to begin the particle swarm;
- (2)
- Determine each particle’s fitness value ;
- (3)
- Compare each particle’s fitness value to its unique extreme value , and , replace with ;
- (4)
- Compare each particle’s fitness value to the global extreme value . , replace with ;
- (5)
- Iteratively update particle position and velocity, using formulae (33) and (34):
- (6)
- Determine whether the algorithm satisfies the termination criteria. If this is the case, terminate the process and report the optimization results; otherwise, proceed to step 2.
4.2. Improvement of PSO Algorithm
4.3. Designing Performance Index Functions for Controller Parameter Optimization
4.4. PSO+CP+TVAC Optimization ABC Parameters , and Processes
5. Simulation Test Verification
5.1. Parameter Setting
5.2. Simulation Results Analysis
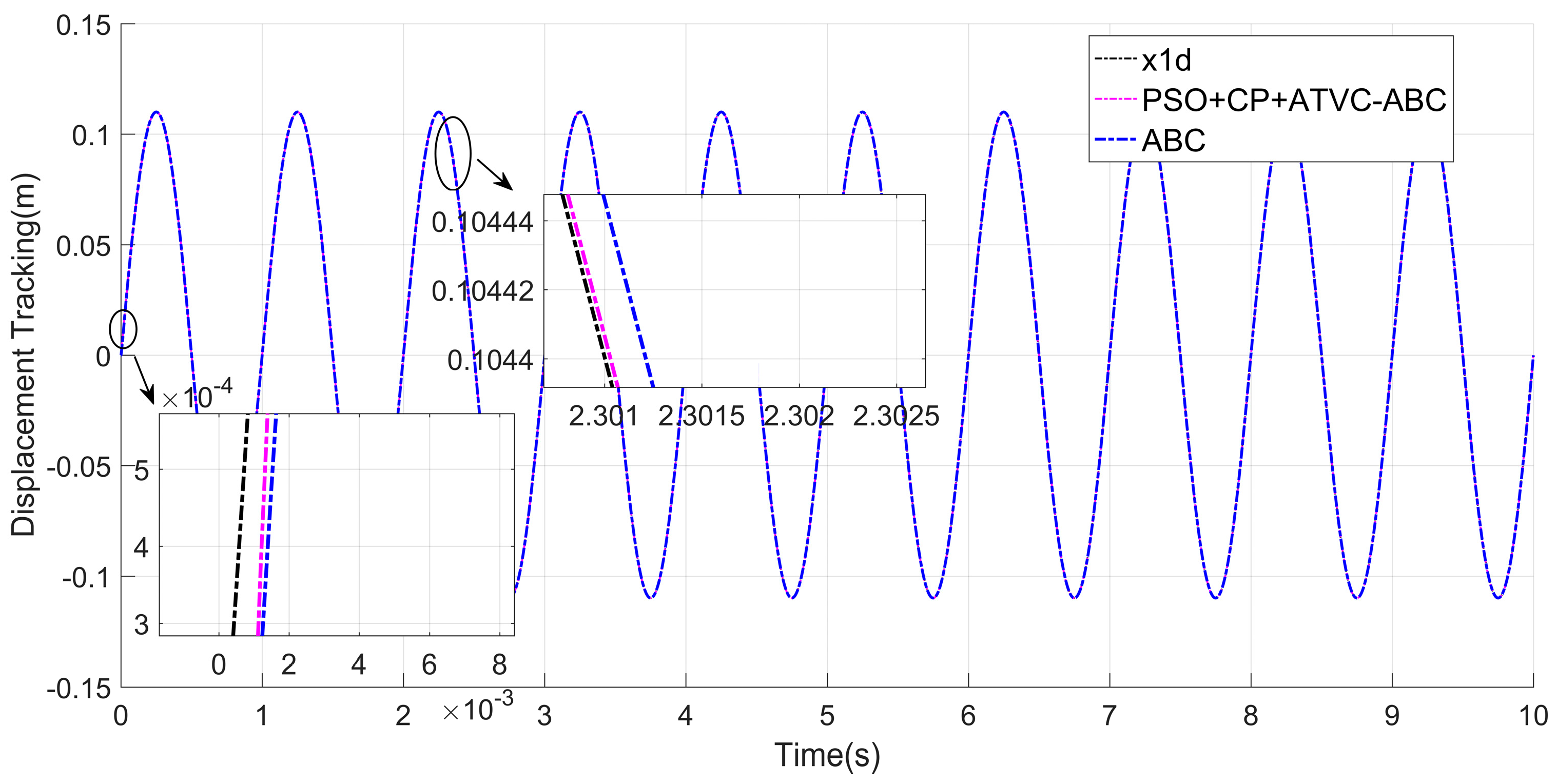
5.3. Displacement Tracking Performance Comparison
- (1)
- The maximum tracking error is defined as
- (2)
- The average value of the displacement tracking error is defined as
- (3)
- The standard deviation of the displacement tracking error is defined as
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hrovat, D. Survey of advanced suspension developments and related optimal control applications. Automatica 1997, 33, 1781–1817. [Google Scholar] [CrossRef]
- Balamurugan, L.; Jancirani, J. An Investigation on semi-active suspension damper and control strategies for vehicle ride comfort and road holding. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2012, 226, 1119–1129. [Google Scholar] [CrossRef]
- Huang, Y.B.; Hou, H.D.; Na, J.; He, H.R.; Zhao, J.; Shi, Z.H. Output Feedback Control of Hydraulic Active Suspensions with Experimental Validation. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 631–635. [Google Scholar] [CrossRef]
- Na, J.; Huang, Y.B.; Wu, X.; Liu, Y.J.; Li, Y.P.; Li, G. Active Suspension Control of Quarter-Car System with Experimental Validation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4714–4726. [Google Scholar] [CrossRef]
- Yan, S.; Sun, W.C.; Yu, X.H.; Gao, H.J. Adaptive Sensor Fault Accommodation for Vehicle Active Suspensions via Partial Measurement Information. IEEE Trans. Cybern. 2022, 52, 12290–12301. [Google Scholar] [CrossRef]
- Mahyar, D.; Fateh, M.M.; Ghalehonie, M. A Fuzzy-Supervised Impedance Control for an Active Suspension System. J. Vib. Eng. Technol. 2022, 1–10. [Google Scholar] [CrossRef]
- Shaer, B.; Kenné, J.P.; Kaddissi, C.; Fallaha, C. A chattering-free fuzzy hybrid sliding mode control of an electro hydraulic active suspension. Trans. Inst. Meas. Control 2018, 40, 222–238. [Google Scholar] [CrossRef]
- Shaer, B.; Kenné, J.P.; Kaddissi, C.; Mintsa, H.A. Real-time hybrid control of electrohydraulic active suspension. Int. J. Robust Nonlinear Control 2017, 27, 4968–4991. [Google Scholar] [CrossRef]
- Zhao, D.X.; Liu, S.; Gong, M.D.; Sun, Z.G.; Zhang, Z.X.; Ni, T.; Yang, B.; Guo, Q.H.; Yang, M.K. Vehicle-Mounted Motion Simulation Platform Based on Active Suspension, and Control Method Therefor. U.S. Patent 11,280,703, 22 March 2022. [Google Scholar]
- Patil, K.S.; Gambhire, V.R. Design and development of double wishbone electro-hydraulic active suspension system. Int. J. Sci. Eng. Technol. 2014, 3, 760–764. [Google Scholar]
- Cytrynski, S.; Neerpasch, U.; Bellmann, R.; Danner, B. The active suspension of the new mercedes-benz GLE. ATZ Worldw. 2018, 120, 42–45. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.Y. Adaptive Backstepping Control of Uncertain Systems; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Wei, Y.H.; Sheng, D.; Chen, Y.Q.; Wang, Y. Fractional order chattering-free robust adaptive backstepping control technique. Nonlinear Dyn. 2019, 95, 2383–2394. [Google Scholar] [CrossRef]
- Wei, Y.H.; Tse, P.W.; Yao, Z.; Wang, Y. Adaptive backstepping output feedback control for a class of nonlinear fractional order systems. Nonlinear Dyn. 2016, 86, 1047–1056. [Google Scholar] [CrossRef]
- Yu, X.W.; Lin, Y. Adaptive backstepping quantized control for a class of nonlinear systems. IEEE Trans. Autom. Control 2017, 62, 981–985. [Google Scholar] [CrossRef]
- Shi, X.Y.; Cheng, Y.H.; Yin, C.; Huang, X.G.; Zhong, S.M. Design of adaptive backstepping dynamic surface control method with RBF neural network for uncertain nonlinear system. Neurocomputing 2018, 330, 490–503. [Google Scholar] [CrossRef]
- Yue, F.F.; Li, X.F. Robust adaptive integral backstepping control for opto-electronic tracking system based on modified LuGre friction model. ISA Trans. 2018, 80, 312–321. [Google Scholar] [CrossRef]
- Ma’arif, A.; Márquez-Vera, M.A.; Mahmoud, M.S.; Ladaci, S.; Çakan, A.; Nino-Parada, J. Backstepping sliding mode control for inverted pendulum system with disturbance and parameter uncertainty. J. Robot. Control 2022, 3, 86–92. [Google Scholar] [CrossRef]
- Xu, W.; Ismail, M.M.; Liu, Y.; Islam, M.R. Parameter optimization of adaptive flux-weakening strategy for permanent-magnet synchronous motor drives based on particle swarm algorithm. IEEE Trans. Power Electron. 2019, 34, 12128–12140. [Google Scholar] [CrossRef]
- Ghogare, M.G.; Patil, S.L.; Patil, C.Y. Experimental validation of optimized fast terminal sliding mode control for level system. ISA Trans. 2022, 126, 486–497. [Google Scholar] [CrossRef]
- Jin, Z.J.; Sun, X.D.; Lei, G.; Guo, Y.G.; Zhu, J.G. Sliding mode direct torque control of SPMSMs based on a hybrid wolf optimization algorithm. IEEE Trans. Ind. Electron. 2021, 69, 4534–4544. [Google Scholar] [CrossRef]
- Mohanty, B.; Panda, S.; Hota, P.K. Controller parameters tuning of differential evolution algorithm and its application to load frequency control of multi-source power system. Int. J. Electr. Power Energy Syst. 2014, 54, 77–85. [Google Scholar] [CrossRef]
- Song, J.; Zheng, W.X.; Niu, Y.G. Self-triggered sliding mode control for networked PMSM speed regulation system: A PSO-Optimized super-twisting algorithm. IEEE Trans. Ind. Electron. 2022, 69, 763–773. [Google Scholar] [CrossRef]
- Yin, Z.G.; Gong, L.; Du, C.; Liu, J.; Zhong, Y.R. Integrated position and speed loops under sliding mode control optimized by differential evolution algorithm for PMSM drives. IEEE Trans. Power Electron. 2019, 34, 8994–9005. [Google Scholar] [CrossRef]
- Yao, B.; Bu, F.P.; Reedy, J.; Chiu, G.T.-C. Adaptive robust motion control of single rod hydraulic actuators: Theory and experiments. IEEE/ASME Trans. Mechatron. 2000, 5, 79–91. [Google Scholar]
- Slotine, J.J.E.; Li, W.P. Applied Nonlinear Control; China Machine Press: Beijing, China, 1991. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Shi, Y.H.; Eberhart, R.C. Empirical Study of Particle Swarm Optimization. In Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Victoire, T.A.A.; Jeyakumar, A.E. Reserve constrained dynamic dispatch of units with valve-point effects. IEEE Trans. Power Syst. 2005, 20, 1273–1282. [Google Scholar] [CrossRef]
- Chaturvedi, K.T.; Pandit, M.; Srivastava, L. Particle swarm optimization with crazy particles for nonconvex economic dispatch. Appl. Soft Comput. J. 2009, 9, 962–969. [Google Scholar] [CrossRef]
- Shukla, A.; Singh, S.N. Advanced three-stage pseudo-inspired weight-improved crazy particle swarm optimization for unit commitment problem. Energy 2016, 96, 23–36. [Google Scholar] [CrossRef]
- Suganthan, P.N. Particle Swarm Optimiser with Neighbourhood Operator. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No.99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1958–1962. [Google Scholar]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Liu, J.K. Advanced PID Control MATLAB Simulation, 4th ed.; Electronic Industry Press: Beijing, China, 2016. [Google Scholar]
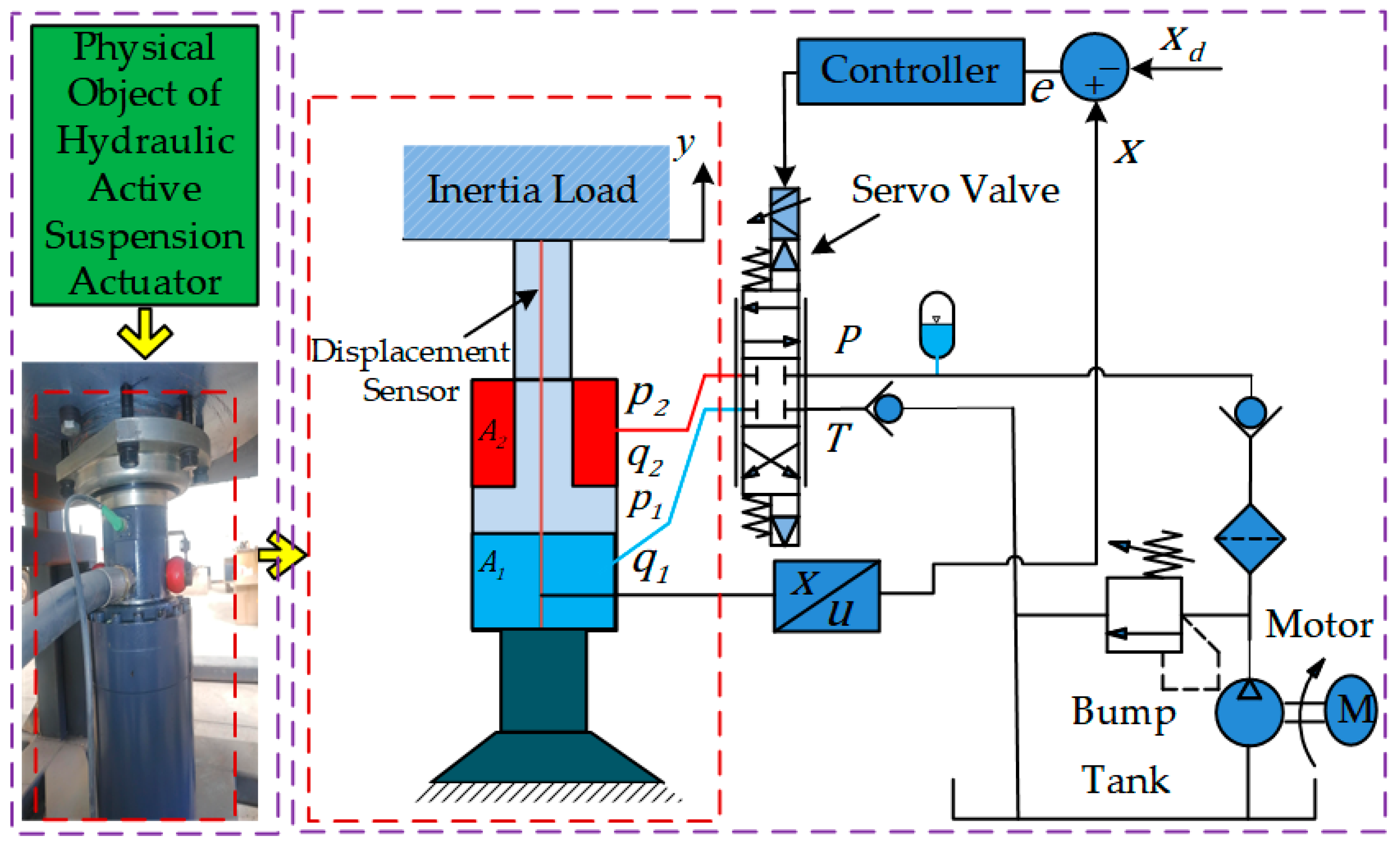
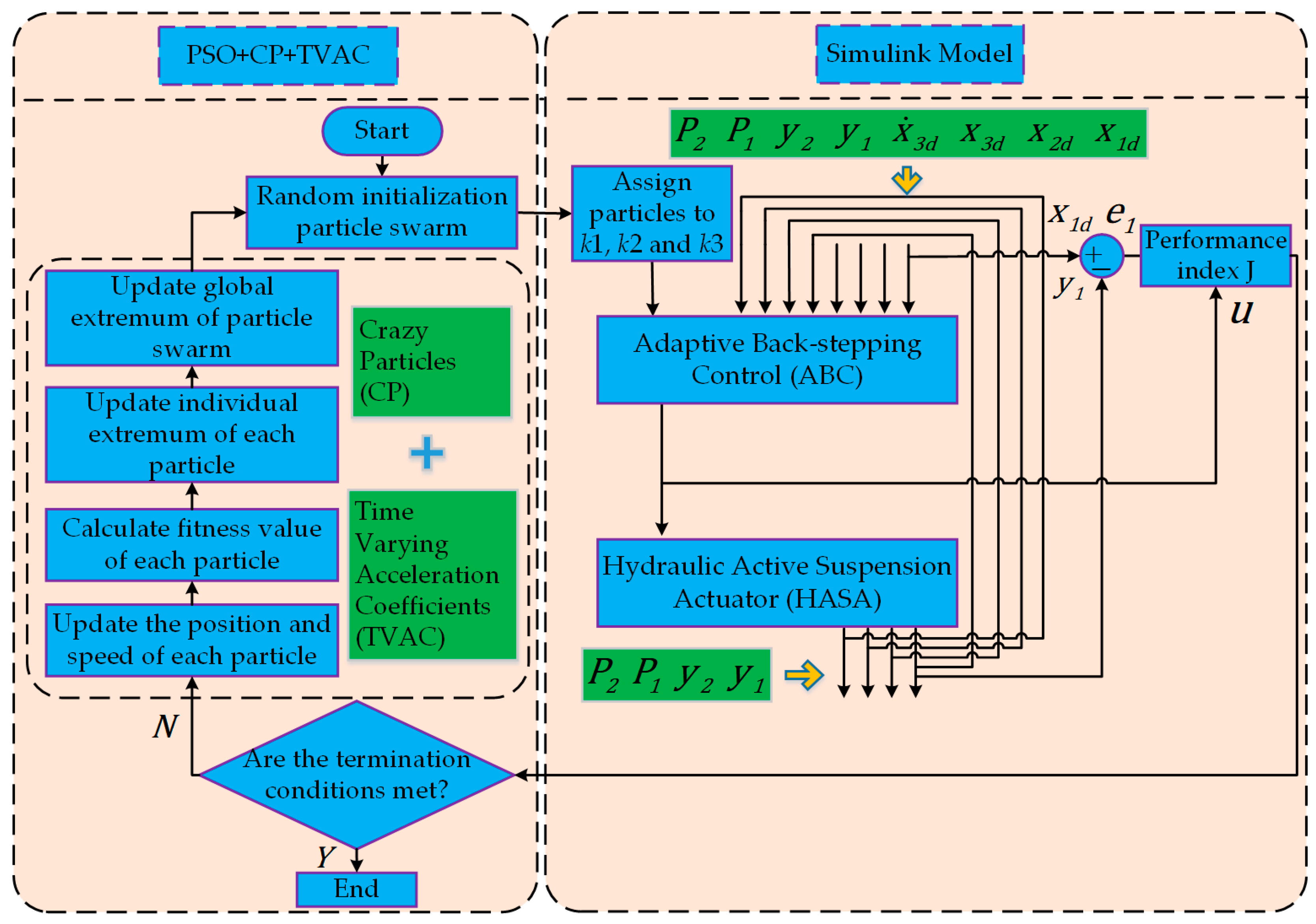


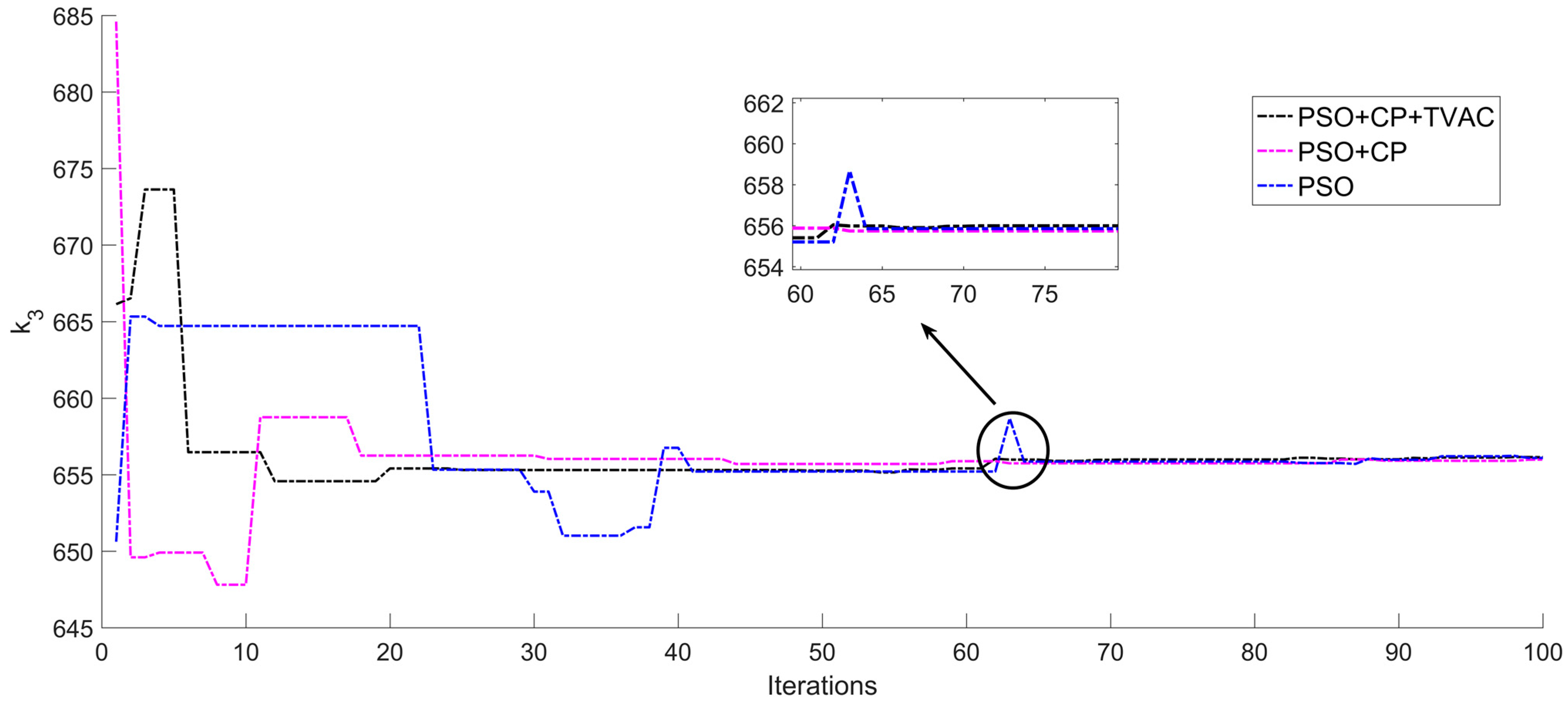
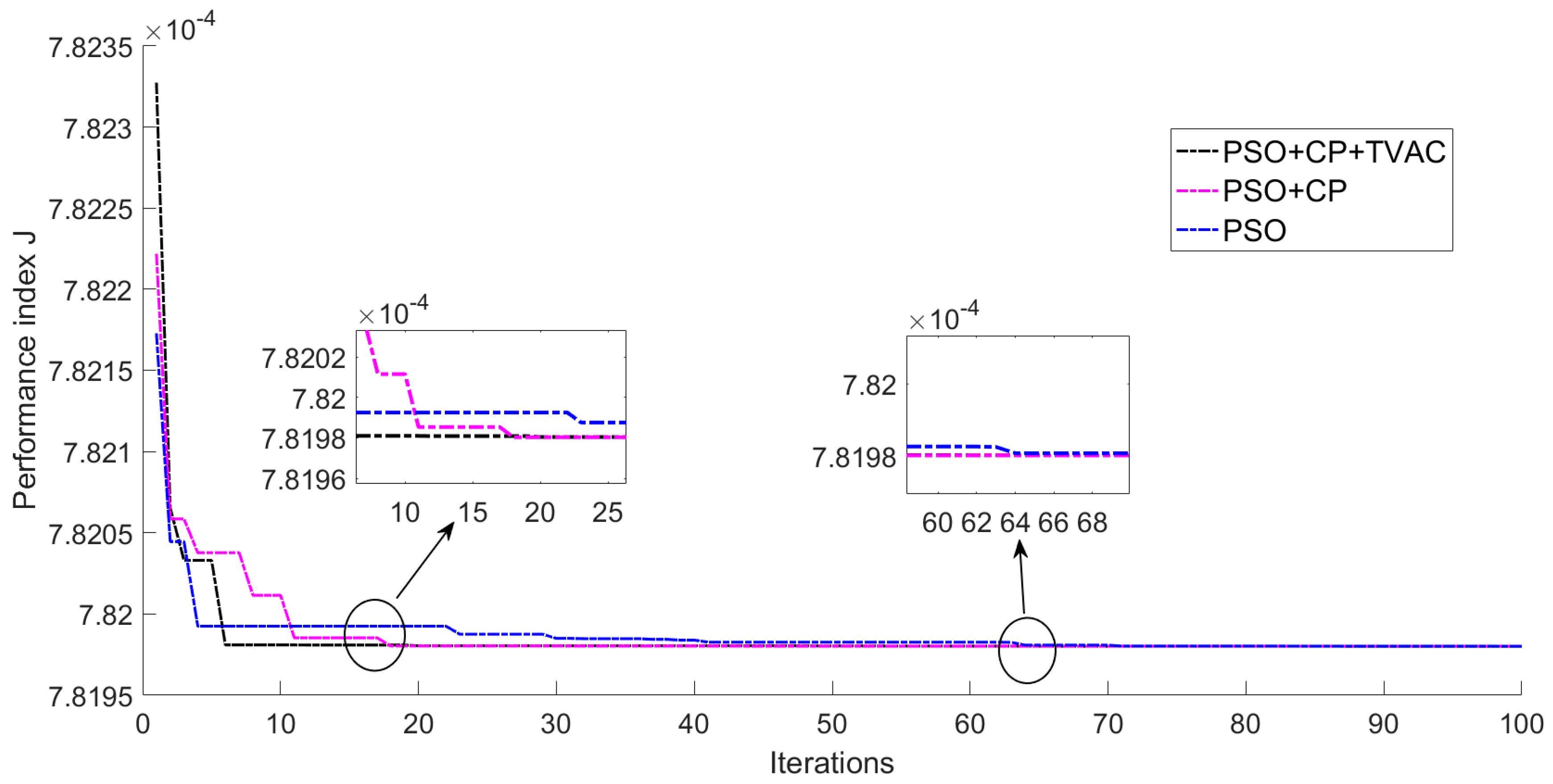

| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Parameters | PSO | PSO+CP | PSO+CP+ATVC |
|---|---|---|---|
| Controller | |||
|---|---|---|---|
| PSO+CP+ATVC-ABC | |||
| ABC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zhao, D.; Zhao, X.; Qin, Y. Nonlinear Adaptive Back-Stepping Optimization Control of the Hydraulic Active Suspension Actuator. Processes 2023, 11, 2020. https://doi.org/10.3390/pr11072020
Wu L, Zhao D, Zhao X, Qin Y. Nonlinear Adaptive Back-Stepping Optimization Control of the Hydraulic Active Suspension Actuator. Processes. 2023; 11(7):2020. https://doi.org/10.3390/pr11072020
Chicago/Turabian StyleWu, Lizhe, Dingxuan Zhao, Xiaolong Zhao, and Yalu Qin. 2023. "Nonlinear Adaptive Back-Stepping Optimization Control of the Hydraulic Active Suspension Actuator" Processes 11, no. 7: 2020. https://doi.org/10.3390/pr11072020
APA StyleWu, L., Zhao, D., Zhao, X., & Qin, Y. (2023). Nonlinear Adaptive Back-Stepping Optimization Control of the Hydraulic Active Suspension Actuator. Processes, 11(7), 2020. https://doi.org/10.3390/pr11072020







