Abstract
The simulated moving bed (SMB) is a well-established, fully continuous process for chromatographic separation of difficult tasks with overlapping peaks, but it is relatively complex. The 1-SMB, which uses only one column but includes residence time zones to preserve concentration profiles, is a simpler semi-continuous alternative. This work examines the possible design of these residence time zones. Simulation studies were conducted to investigate the dependence of process metrics, such as purity, yield, productivity, and eluent consumption, on fluid dynamics. No deterioration in purity was observed, and the other variables remained constant over a wide range of axial dispersion before decreasing sharply. Pilot-scale experiments were conducted with various devices, including coiled flow inverters, eluate recycling devices, packed columns, and tank arrangements, to validate possible apparatus implementations with fluid dynamic measurements. It was demonstrated that the 1-SMB offers similar performance to the 4-SMB, albeit with reduced yield and lower apparatus complexity.
1. Introduction
Simulated moving bed chromatography (SMB) is an established continuous separation process. Explaining its basic principles would go beyond the scope of this article, and it can be read about in detail elsewhere [1,2,3,4].
Nevertheless, the basic principle will be briefly outlined. A binary separation and isocratic operation are assumed.
In general, classical column chromatography is a batch process. A single chromatography column cannot be continuously loaded. This would result in the mixing of the faster-moving components of the second injection with the slower-moving components of the first injection and, thus, no separation would occur. The simulated moving bed process overcomes this problem by using a periodic counter-current flow. For this purpose, usually, four or more columns are operated, as shown in Figure 1A. The columns are “moved” in a counter-current manner to the liquid phase. This is performed by switching the inlet and outlet ports with a relatively large number of valves. Usually, at least six valves are needed per column as well as a minimum of four to five pumps, depending on the specific design. This relatively complex setup is rewarded with high purity and yield as well as productivity, even for mixtures where no baseline separation could be accomplished in batch chromatography. In addition, the process is fully continuous in terms of feed loading and product elution. This is hardly achieved by any other chromatography process.
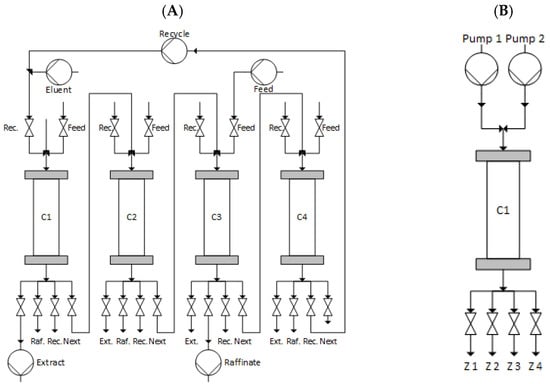
Figure 1.
(A) Simplified process flow diagram of a 4-SMB with 5 pumps. (B) Simplified process flow diagram of a 1-SMB with 2 pumps.
The single-column or one-column SMB (1-SMB) represents a less complex equipment variant (Figure 1B) but can only be operated in a semi-continuous mode [5,6,7].
Figure 2 shows schematically the sequence of a 1-SMB cycle. The column undergoes the same steps as any column in the classical SMB process. However, unlike the classical SMB process, the column is not connected to other columns. The exchange of concentration profiles from column to column is achieved through vessels, which can be retention time devices of any sort. These are investigated in this paper. The column does not take the mixture from the previous column but rather its own eluate from the previous cycle. The zones are run through in the order Zone III, Zone II, Zone I, and Zone IV [7].
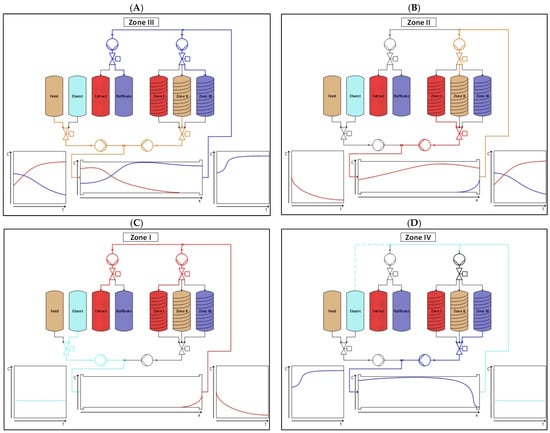
Figure 2.
Process flow charts of one cycle of a 1-SMB. Depicted is the end of the cycle just before switching to the next zone.
Figure 2A Zone III: The column is loaded with the feed out of the feed tank and the eluate from Zone II. This was stored in the Zone II retention time device. It originates from the previous cycle. Pure raffinate leaves the column. This product stream is split. One part is stored in the residence time vessel for Zone III to be used in the next cycle, while the other part is gathered as the product.
Figure 2B Zone II: The column is loaded from the Zone I tank. Again, the contents of this tank come from the previous cycle. The incompletely separated mixture is eluted and stored in the Zone II tank.
Figure 2C Zone I: The column is regenerated with fresh eluent. The pure extract is washed from the column and also split into a product and a storage stream.
Figure 2D Zone IV: The empty column is pre-loaded with raffinate from the Zone III tank. This corresponds to the closed-loop concept. Pre-loading the column also improves the separation in many cases due to displacement effects [8]. Although it is only implied with dashed lines in Figure 1, it would be possible to recycle the eluent. Whether recycling is advisable depends on the specific application.
The configuration shown in Figure 2 is one of many possibilities. In fact, using four pumps would result in the system being hydrodynamically overdetermined. As shown in Figure 1 and Figure 2 accordingly, two pumps are needed to load and elute the column. Pump 1 would switch through the residence time zones, while pump 2 would pump feed or fresh eluant in Zone III or Zone I, respectively. The split of the outlet streams in Zones III and I could be achieved with throttle valves. One can argue that this would be true for the 4-SMB as well. Nevertheless, in the case of the 4-SMB, there are at least three columns located downstream in the flow direction after Zone I, and there is one column located downstream after Zone III after the outlet ports of the product streams (extract and raffinate). As a result, the circulation path exhibits a significantly higher resistance or pressure drop. This makes precise splitting using valves challenging. In the case of the one-column SMB, both paths are relatively pressure-free. This is advantageous overall since it reduces the system pressure as well as the pressure exerted by Pump 1 or the circulation pump. Additionally, in the 1-SMB configuration, the column can be operated at relatively constant pressures, whereas in the 4-SMB configuration, the pressure decreases continuously from Zone I to Zone IV.
The basic principle has already been developed by research groups led by Wankat and Mota [5,6,9,10,11].
The implementation and performance of the 1-SMB idea obviously strongly depend on the conservation of the concentration profile in the residence time sections. Chibèrio et al. solved this with a column-like device called an eluate recycling device (ERD) [12,13]. The results were promising as long as attention was paid to good liquid distributors.
This work will investigate residence time sections for 1-SMB on a more general basis. Basically, one might think of three types of devices: pipes, columns, and tanks. All of these should have as little backmixing as possible. Thus, the pipes should be long and thin, the columns need some sort of bed, and the stirred tanks should be arranged in a cascade or sequentially.
The feasibility will be tested through chromatography modelling on a well-known SMB test separation of cyclopentanone and cycloheptanone on normal phase columns [14]. The process design is performed based on triangle theory [15,16,17,18,19,20,21].
2. Materials and Methods
2.1. Chromatography Columns, Buffers and Feed
Normal phase chromatography was performed with LiChroprep® SI 60 material (15–25 µm, Merck KGaA, Darmstadt, Germany) using Superformance® 600-16 columns (Götec-Labortechnik GmbH, Bickenbach, Germany) with a 12.5 cm bed length. All the chromatography runs were isocratic, with 85% (v/v) hexane (LiChrosolv®, Merck KGaA) and 15% (v/v) ethyl acetate (LiChrosolv®, Merck KGaA). A mixture of cyclopentanone (purity 99%) and cycloheptanone (purity 98%) from Alfa Aesar (Haverhill, MA, USA) was used as a test substance. For the overloaded conditions, a selectivity α of 1.29 and a resolution Rs of 0.46 were found, which were calculated with Equations (1) and (2):
2.2. Chromatography Modeling
The general rate model was utilized for the purpose of chromatography modeling. Orthogonal collocation on finite elements and the GEAR algorithm were used to solve the differential equations. The model comprises two target components. Since the SMB is typically operated with isocratic elution, there is no need to consider modifiers.
2.2.1. General Rate Model
The chromatography model used in this study, along with the overall modeling methodology, parameter determination, and model validation are comprehensively explained in Zobel-Roos et al. [22]. The general rate model can be broken down into three components: the mass balance equation for the mobile phase, the mass balance equation for the stationary phase, and the equilibrium description. For information regarding the derivation process, assumptions, and additional details, please refer to [1,2,4,23,24,25].
2.2.2. Mass Balance of Mobile Phase
The mass balance equation for the mobile phase comprises four terms that are arranged from left to right as follows: storage, convective flow, axial dispersion, and mass transport [2]:
with as the interstitial velocity, as the axial dispersion coefficient, as the voidage, as the particle diameter, and as the film mass transport coefficient. In order to account for pore diffusion in the mass balance equation of the stationary phase, the use of a film mass transport coefficient is required. However, film mass transport and pore diffusion can be integrated by utilizing the lumped pore diffusion model [25]. This approach involves replacing the film mass transport coefficient, , with an effective mass transport coefficient, , thereby simplifying the model. Although this simplification is commonly used during the early stages of process development to reduce the effort required to determine the model parameters, it often results in a tradeoff between model accuracy and process understanding. An even greater simplification can be achieved using the lumped kinetic model, which completely neglects intraparticle pores [25].
2.2.3. Mass Balance of Stationary Phase
The mass balance of the stationary phase is mostly dominated by pore diffusion, Dp,I, and surface diffusion, DS,i [23,26]:
with as the concentration of component i within the pores, and as the surface loading of component i. In the case of larger molecules, surface diffusion is often disregarded and instead combined with pore diffusion to yield a single effective diffusion coefficient, Deff [26,27]:
Combining Equations (4) and (5) results in:
For the lumped pore diffusion model, the mass balance for the stationary phase reads [25]:
2.2.4. Adsorption Equilibrium
There are numerous approaches available for describing adsorption equilibrium, which largely depend on the mechanism of adsorption and the mode of operation [28,29,30,31,32,33,34,35,36,37,38,39,40]. For this simulation study, competitive Langmuir isotherms were used [27,41]:
Here, represents the Langmuir coefficient, while denotes the maximum loading capacity of component i. It is worth noting that different notations are utilized in the literature, e.g., with the use of the Henry coefficient, Hi. However, it is possible to convert between these different notations using the following equation:
2.3. Model Parameter Determination
A detailed description of the model parameter determination can be found here for reference: [4,22,42,43].
2.3.1. Fluid Dynamics
The fluid dynamic parameters and are obtained via tracer experiments using toluene as the tracer substance. In order to determine the axial dispersion coefficients, the peak is evaluated using the following equations [44]:
where denotes the mean residence time, is the variance, v is the velocity, and l is the column length. It is worth noting that both equations tend to yield similar results. While Equation (10) is applicable to closed vessel boundary conditions, Equation (11) is valid for open vessel boundary conditions. In most cases, the assumption of a closed vessel boundary condition is reasonable, particularly for small chromatography columns. Porosities can be determined using the following Equation (12):
2.3.2. Adsorption Equilibrium
Frontal analysis and perturbation experiments [2,28] were carried out on LiChroprep® SI 60 material to determine the isotherms of the cyclopentanone/cycloheptanone mixture. A mixture of 85 vol.-% hexane and 15 vol.-% ethyl acetate was used as the eluent at a flow rate of 12.5 mL/min. The adsorbent was packed in Götec glass columns with an inner diameter of 1.6 cm and a length of 10 cm.
The columns were first equilibrated with the pure eluent, followed by a stepwise change to a mixture of eluent and the target components. For this purpose, individual concentrations of 0.5 g/L, 1 g/L, 2 g/L, 4 g/L, 7.8 g/L, 31.3 g/L, 62.5 g/L, and 125 g/L were used in multiple series of measurements. Cyclopentanone and cycloheptanone were present in equal mass fractions at the respective concentrations. The breakthrough curve resulting from the concentration jump was recorded using a diode array detector (DAD) and fractionated in six-second intervals. These fractions were analyzed offline and evaluated as frontal analysis. At the end of the breakthrough curve, a new equilibrium state was established. Once this was achieved, the perturbation experiments were initiated. For this purpose, 100 μL of pure eluent and 50 μL of pure cyclopentanone or cycloheptanone were injected in sequence, and the resulting peaks were recorded with the DAD detector. This was performed twice per component.
2.3.3. Mass Transport
Given that all the other parameters were known following the previous measurements, the mass transfer coefficient, , was determined by fitting simulations to experimental batch runs with varying velocities.
2.3.4. Model Validation
Again, the model validation for this test mixture and this separation was performed in previous work [22]. In short, a large set of simulations was compared to a set of experiments. The input parameters of the simulations varied with the error of the experimental parameter determination, while the variation in the experiments lies in the nature of the experiment itself. Both the simulations and experiments need to be and were in good agreement.
2.4. Triangle Theory
In addition to the usual process parameters known for chromatography, such as column dimensions, buffer composition, or fraction cut points, the SMB process has five parameters that need to be optimized with respect to each other. These are the volumetric flow in Zones I-IV and the switching time, . This can be achieved with the help of the triangle theory [15,16,17,18,19,20,21]. A good summary is provided by Mazzotti [15].
In general, to obtain high purity and yield, a few constraints need to be fulfilled: considering more than one column per zone before reaching the switching time, the extract must be completely displaced from the first column of Zone I, and the raffinate must be completely displaced from the first column of Zone II. The adsorption front of the extract in the last column of Zone III, as well as the adsorption front of the raffinate in the last column of Zone IV, must be retained in this column.
It is known from the equilibrium theory of Rhee et al. [45] that there is a relation between the residence time of component I, , and its Henry coefficient, , as given in Equations (13) and (14) [2]:
If Formula (13) is inserted into Formula (14) and solved for , Formula (15) is obtained as follows:
Extended with the column volume, one obtains:
Considering the formula for the zone-specific mass flow ratios, i.e., the ratio of the mass/volume flow of the mobile phase to the pseudo mass/volume flow of the stationary phase from Formula (17),
The relationship between the Henry coefficients and the mass flow ratios becomes visible. This gives a set of inequalities for the separation of two components 1 and 2, under which the conditions for achieving high purities mentioned above are fulfilled [46]:
The index, i, of the components is assigned in ascending order according to the retention time. Component 1 is the weak binding component, and component 2 is the strong binding component. These inequalities can also be represented in a triangle diagram (see Figure 3) [47]. For this purpose, the mass flow ratios m2 and m3 are plotted on the x- and y-axes, respectively.
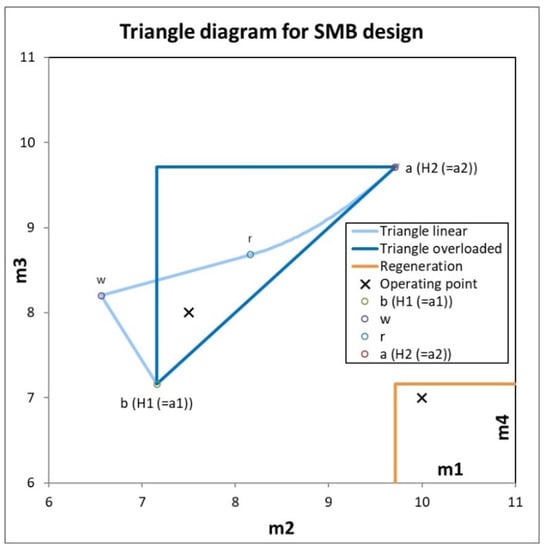
Figure 3.
Triangle diagram for cyclopentanone/cycloheptanone. The dark blue triangle is valid for low concentrations representing the linear region of the Langmuir isotherm. For higher concentrations, the triangle shifts to the right, as depicted with the light blue lines. The orange triangle represents the working condition for Zones I and IV.
All of the conditions and restrictions mentioned above apply to linear isotherms. In this case, a right-angled triangle (dark blue) is obtained in the operating diagram, with the Henry coefficients of each component, , as vertices. These vertices are labeled a and b in Figure 3. If the parameters m2 and m3 are chosen in such a way that the operating point lies within the triangle, both the extract and the raffinate can be obtained with 100% purity and yield [1,3,15,18]. This triangle corresponds to the inequalities (19) and (20). Outside the triangle, but above the bisector, either only pure raffinate, only pure extract, or no pure phase can be obtained. A working point for m2/m3 below the bisector is not possible. This would require the feed stream to be negative.
Figure 3 also shows the region where conditions (18) and (21) are fulfilled for m1/m4. This orange triangle indicates the regeneration region [48,49,50].
For non-linear isotherms, the shape of the triangle changes depending on the feed concentration, . The type of isotherm determines the location of points w and r. The derivations for this can be found in Storti et al. [20,21,47] and Mazzotti et al. [16,17,18,19], and they were summarized by the latter [15].
In this work, only Langmuir isotherms are considered. The equations for these are taken from Mazzotti et al. [15] and summarized in Table 1.

Table 1.
Equations for the characteristic points in the triangle diagram under Langmuir conditions.
The triangle theory is a shortcut method that neglects mass transport phenomena and fluid dynamic effects. As a result, it only provides a basic foundation and serves as a starting point for a detailed process design. Additionally, it provides a good visualization of the working points. Both effects are covered in the process model, which is, therefore, used for detailed process design.
2.5. Axial Dispersion Coefficient for Residence Time Sections
The axial dispersion coefficients were measured with tracer experiments. Water was used as the liquid phase, and acetone was used as the tracer. The injection was performed with an L-2200 Autosampler (VWR International, Radnor, PA, USA) and the detection was performed with two diode array detectors, Smartline DAD 2600 (Knauer Wissenschaftliche Geräte GmbH, Berlin, Germany). The axial dispersion coefficient was calculated with Equations (10) and (11) and fitted with the pipe flow model.
3. Results and Discussion
3.1. Simulated Moving Bed Design
The design of the simulated moving bed was performed according to the triangle theory. The corresponding working diagram can be found in Figure 4. The feed concentration of the test mixture was set to 5 g/l. This is in the overloaded region of the Langmuir isotherm. Thus, the triangle warps to the left side. The column dimensions can be chosen freely. In order to reflect at least the pilot scale, ID16 columns were used. The length is theoretically freely selectable, although a packing under 10 cm seems to make little sense. Each zone could be equipped with more than one column. However, in this case, only one column per zone was planned. Thus, four columns with dimensions of 100 × 16 were used.
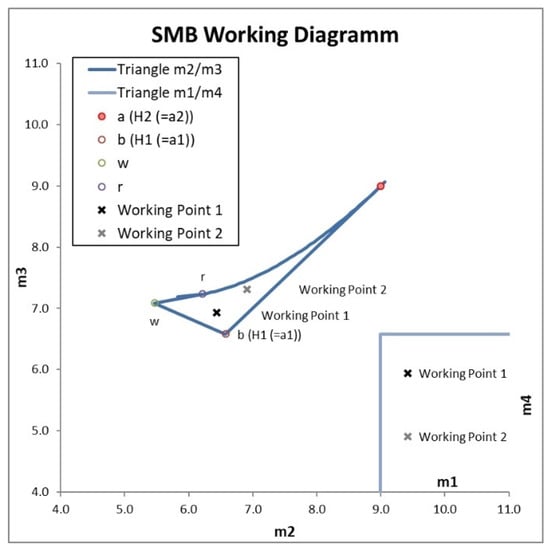
Figure 4.
Working diagram for the test mixture cyclopentanone/cycloheptanone with 5 g/L feed concentration.
The feed flow was chosen to be 1 mL/min. This leads to linear velocities short below 1000 cm/h in the most strongly flown through Zone I.
Two different operation points (see Figure 4) were chosen to reflect both operating ranges of the SMB. Working point 1 is in favor of the raffinate, working point 2 is focused on the extract. Both are on the safe side of the operation with a safety margin to the boundaries of the triangle. Detailed simulation studies showed the purity and yield to be 100% (see Tables in Section 3.2). The mass flow ratios for both points are given in Table 2.

Table 2.
Mass flow ratios for each zone for working points 1 and 2.
3.2. Simulation Studies
As previously stated, the 1-SMB has been demonstrated to function. The remaining question is: How simple or complex must the retention sections be to maintain separation efficiency? For this purpose, simulation studies were conducted. Ultimately, all the concepts for retention sections can be traced back to tanks or pipes with varying axial backmixing. Therefore, simulation studies were initially performed with these parameters.
The chromatography column was modeled as described above. Additionally, a retention section was implemented for each zone. These sections were designed as either continuous stirred-tank reactors or plug flow tubes. The latter was modeled according to Equation (3) but without the mass transport term. Simulation studies were conducted with different axial dispersion values ranging from 10−4 cm2/s to 100 cm2/s.
The resulting chromatograms for working point 1 are provided in Figure 5. It can be seen that just concerning the SMB profile, the 1-SMB will work fine with a variety of pipes. The deviation between 1-SMB and 4-SMB is low for the axial dispersion coefficients between 10−4 cm2/s and 1 cm2/s. Higher axial dispersion coefficients result in a significant mass loss in the retention sections because the concentration profiles spread too much. The front of the profiles does not remain in the retention section but is pushed beyond it into the waste. This mass loss results in lower concentrations and, therefore, accounts for the differences in the concentration profiles, as can be seen in Figure 5A. This mass loss also takes place for the lower dispersion coefficients, hence the deviation in the concentrations there but to a much smaller extent.
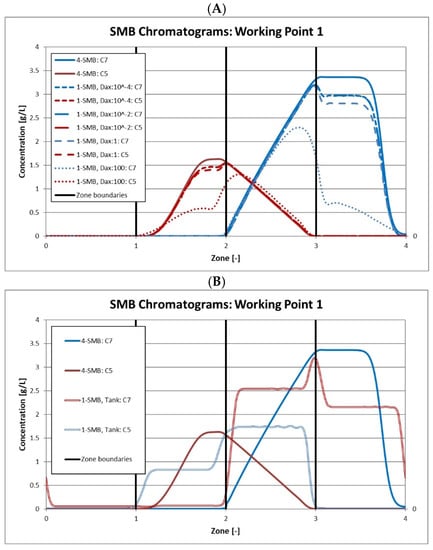
Figure 5.
SMB chromatograms for working point 1. The signal is measured at the column outlet. The red lines indicate the extract, the blue lines indicate raffinate. (A): 1-SMB with plug flow with varying axial dispersion. The solid lines represent the classical 4-column SMB, the dashed lines represent 1-SMB with pipes. (B) 1-SMB with tanks (double lines).
All the process metrics are provided in Table 3 and visualized in Figure 6. The product purity for the raffinate (C7) is 100%, and the column yield is 100% for Dax values < 1 and then decreases gradually to 99.7. The column yield is calculated as the amount of product leaving the column divided by the amount of product entering the column.

Table 3.
Process metrics for working point 1.
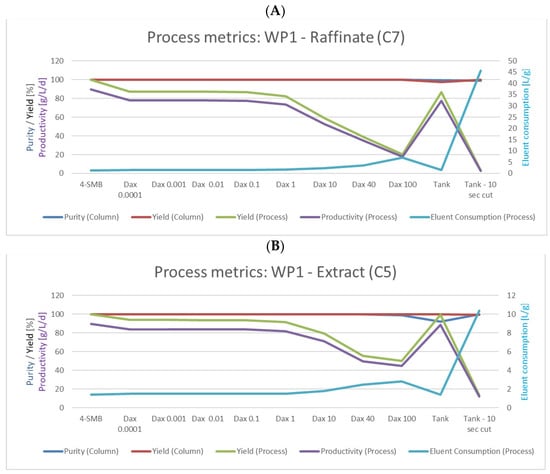
Figure 6.
Process metrics for working point 1. (A) for raffinate/cycloheptanone (C7) and (B) for extract/cyclopentanone (C5). On the primary axis: purity (%, blue), yield (%, red for column yield, green for process yield) and productivity (g/L/d, purple). On the secondary axis: eluent consumption (L/g, turquoise).
The overall process yield, however, is only between 87% for Dax = 10−4 cm2/s and decreases to 20% for the highest axial dispersion, compared to 100% for the 4-SMB. The overall yield is calculated as the amount of product gained entirely divided by the amount of product entering the whole setup.
Figure 5B shows the chromatograms for the 1-SMB with stirred tanks compared to the 4-SMB. Due to the complete equalization of the concentration profile in the stirred tanks, the chromatograms look quite different. This especially affects the product purity due to the breakthrough of the concentration fronts. This problem can be addressed by discarding the product stream a few seconds after switching. The yield and process yield, however, are good since the effect described for the pipes is limited.
Similar results were achieved for working point 2. The chromatograms are shown in Figure 7. Here, the deviation between 1-SMB and 4-SMB is more pronounced. There is significantly more mass loss for the extract. This is due to the fact that the concentration front of the extract in Zone III is steeper. Hence, the amount of product lost in the residence time devices is higher.
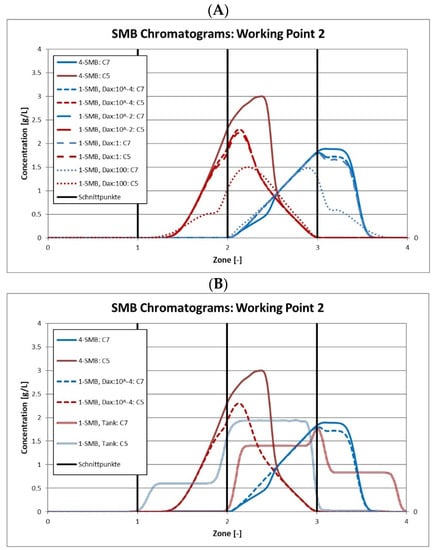
Figure 7.
SMB Chromatograms for working point 2. The signal is measured at the column outlet. The red lines indicate the extract, the blue lines indicate raffinate. (A) 1-SMB with plug flow with varying axial dispersion. The solid lines represent the classical 4-column SMB, the dashed lines represent 1-SMB with pipes. (B) 1-SMB with tanks (double lines).
The process metrics for working point 2 are provided in Table 4 and Figure 8. Again, it can be noted that both the purity and the column yield do not deviate from that of the 4-SMB up to a Dax of 1 m2/s. The process yield, however, is roughly 10% less and decreases with increasing axial dispersion.

Table 4.
Process metrics for working point 2.
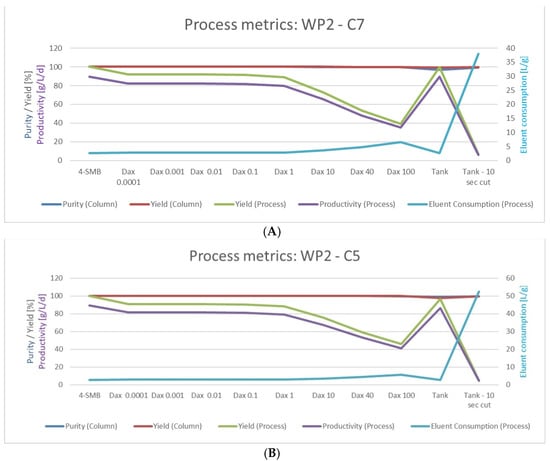
Figure 8.
Process metrics for working point 2. (A) for raffinate/cycloheptanone (C7) and (B) for extract/cyclopentanone (C5). On the primary axis: purity (%, blue), yield (%, red for column yield, green for process yield) and productivity (g/L/d, purple). On the secondary axis: eluent consumption (L/g, turquoise).
Nevertheless, the productivity of the 1-SMB is comparable in both processes, and the eluent consumption also does not deviate much.
Interim conclusion: It is possible to create a 1-SMB process comparable to the 4-SMB with no deviations in the product purity and only minor deviations in the overall yield, productivity, and eluent consumption as long as the axial dispersion is lower than 1 cm2/s. Thus, a brief evaluation of different residence time devices is needed.
3.3. Retention Time Device Concepts
In this study, several storage zone concepts were tested, all of which operate according to the first in, first out (FIFO) principle. This means that the volume elements that enter a storage zone first will also be the first to leave. FIFO is intended to ensure the best possible preservation of the concentration profile. The following are the different types of storage zones, all designed for a storage volume of approximately 40 mL.
3.3.1. Coiled Flow Inverter (CFI)
Besides the tank, the pipe as a storage zone represents the simplest concept investigated in this study. The implementation is achieved through flexible silicone hoses rather than rigid piping, providing advantages in terms of ease of availability and deformability. Due to the small diameter, the volume of the storage zones results in relatively long pipes. Any arbitrary arrangement is not recommended since it leads to different flow velocities across the cross-sectional area in curved channels. To counteract these effects, the arrangement is selected as coiled flow inverters (CFI). The principle is based on flow reversal by changing the direction of the centrifugal force in spirally wound tubes. The main mechanism involves the generation of a spatially chaotic path by changing the flow direction through a 90° bend in helical turns [51,52].
For a CFI with ID 0.2 cm, thus 1275 cm pipe length l, the measured axial dispersion coefficient was 48 cm2/s, and the simulation-based estimation provided 42 cm2/s. Saxena and Nigam found a correlation in 1984 [51]:
With
where n is the number of bends. This correlation yields .
3.3.2. Packed Bed Columns
The axial dispersion of chromatography columns is known to be low. The columns in this study had around Dax = 10−4 cm2/s. Additionally, columns packed with 0.5 mm glass beads were tested. These had a measured Dax of 0.016 cm2/s. The model estimate was 0.022 cm2/s and a correlation of Chung and Wen ([53], Equation (24)) would yield 0.077 cm2/s.
3.3.3. Tank Cascades or Sequential Setups
As shown above, a single tank does not retain the concentration profile. This could be achieved with a cascade of tanks, continuously flown through, with one loading into the next, or a sequential setup. Here, the elution profile is loaded to the first tank until this is full, and then it is switched to the next tank until the whole profile is captured. Both setups are relatively complex. The advantage of complexity reduction from 4-SMB to 1-SMB is thereby countered. We tested setups with 1, 3, 6, and 9 tanks without success. The axial dispersion values for the sequential setup exceeded 100 cm2/s.
3.3.4. Eluate Recycling Device
This device, introduced by Chibério et al. [12,13], is cleverly designed and can be built relatively easily on a small scale out of glass columns. Nevertheless, we ran into the same problems as the original inventors. Without proper fluid distribution, a lot of channeling is observed.
4. Conclusions
It can be concluded that the 1-SMB provides similar performance compared to the 4-SMB. As long as the concentration profiles are approximately retained in the storage zones, the separation performance of the column itself is identical to that of the 4-SMB. However, losses occur within the storage zones or at their ends, increasing with increasing axial dispersion coefficient due to increased peak broadening. This problem could be addressed with simple process analytical technologies to reduce yield losses. For classical design and operation, the axial dispersion coefficient should be less than 1 cm2/s. No changes in performance data were observed between Dax = 10−4 cm2/s and 10−1. At a Dax of 1 cm2/s, the yield and productivity decrease slightly. With a further increase, the trend intensifies significantly.
However, compared to the 4-SMB, a 10–20% lower yield can still be expected with the 1-SMB. This is countered by a significant reduction in equipment complexity. Classical SMBs are typically operated with at least four, usually five, pumps and at least six valves per column, depending on the interconnection. Since at least 4 columns are required, at least 24 valves are installed. The 1-SMB is ready for use with two pumps and a total of six valves. The periphery with the pumps and valves for the feed, eluent, and product tanks is not included in this consideration. However, these are the same for both processes.
It should be noted that the 1-SMB is not continuously loaded with feed, but only in one of the four steps of a cycle. Therefore, the diameter of one column should be double that of the columns of the 4-SMB, resulting in four times the surface area/volume to process the same amount of product. Column-wise, the difference between the 1-SMB and 4-SMB is, therefore, one column with double the diameter versus four columns, which must be packed as precisely as possible, as changes in the fluid dynamics between the columns have a drastic effect on the performance.
The study of possible residence time devices identified packed columns as a good solution. Glass beads are sufficient as packing material. The quality of the packing is less critical than for separation columns.
In conclusion, the 1-SMB is a less complex alternative to the conventional SMB. The low complexity, especially the use of only one column, makes it easier to transition from batch processes. The separation efficiency remains identical. Even strongly overlapping peaks can be separated with 100% purity.
Author Contributions
Conceptualization, S.Z.-R. and J.S.; methodology, S.Z.-R. and F.V.; experiments: S.Z.-R. and F.V.; validation, S.Z.-R. and F.V.; writing—original draft preparation, S.Z.-R.; writing—review and editing, J.S.; supervision, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this article.
Acknowledgments
The authors gratefully acknowledge the support of S. Mallon during his master’s thesis and thank the workshop, F. Steinhäuser, V. Strohmeyer, N. Hoffmann, and T. Knebel for building the prototypes.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| α | Selectivity | |
| (g/L) | Concentration of component i | |
| (g/L) | Concentration of component i inside the pores | |
| (cm2/s) | Axial dispersion coefficient | |
| Deff | (cm2/s) | Effective diffusion coefficient |
| (cm) | Particle diameter | |
| Dp,i | (cm2/s) | Pore diffusion coefficient |
| DS,i | (cm2/s) | Surface diffusion coefficient |
| (-) | Porosity | |
| (-) | Voidage | |
| (-) | Total porosity | |
| Hi | (-) | Henry coefficient of component i |
| Ki | (L/g) | Langmuir coefficient of component i |
| (cm/s) | Effective mass transport coefficient | |
| kf | (cm/s) | Mass transport coefficient |
| l | (cm) | Length |
| mj | Mass flow ratio of zone j | |
| n | Number of bends | |
| PAT | Process analytical technology | |
| qi | (g/L) | Loading of component i |
| qmax,i | (g/L) | Maximum loading capacity of component i |
| r | (cm) | Radius |
| Re | (-) | Reynolds number |
| (cm) | Particle radius | |
| Rs | Resolution | |
| t | (s); (min) | Time |
| t0 | (s); (min) | Dead time |
| tR1 | (s); (min) | Retention time peak 1 |
| tR2 | (s); (min) | Retention time peak 2 |
| (s); (min) | Mean residence time | |
| (cm/s) | Interstitial velocity | |
| v | (cm/s) | Velocity |
| (mL/min) | Volumetric flow | |
| (mL) | Volume of column | |
| (mg/cm*s) | Dynamic viscosity | |
| (g/L) | Density | |
| (s2) | Variance | |
| Mass fraction of component i | ||
| wb1 | (s); (min) | Peak width peak 1 |
| wb2 | (s); (min) | Peak width peak 1 |
References
- Strube, J. Technische Chromatographie: Auslegung, Optimierung, Betrieb und Wirtschaftlichkeit; Shaker: Aachen, Germany, 2000; ISBN 3826568974. [Google Scholar]
- Guiochon, G.; Felinger, A.; Shirazi, D.G.; Katti, A.M. Fundamentals of Preparative and Nonlinear Chromatography, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Rodrigues, A. Simulated Moving Bed Technology: Principles, Design and Process Applications; Elsevier Science: Burlington, NJ, USA, 2015; ISBN 9780128020241. [Google Scholar]
- Zobel-Roos, S. Entwicklung, Modellierung und Validierung von Integrierten Kontinuierlichen Gegenstrom-Chromatographie-Prozessen, 1. Auflage; Shaker: Herzogenrath, Germany, 2018; ISBN 3844061878. [Google Scholar]
- Abunasser, N.; Wankat, P.C.; Kim, Y.-S.; Koo, Y.M. One-Column Chromatograph with Recycle Analogous to a Four-Zone Simulated Moving Bed. Ind. Eng. Chem. Res. 2003, 42, 5268–5279. [Google Scholar] [CrossRef]
- Mota, J.P.B.; Araújo, J.M.M. Single-column simulated-moving-bed process with recycle lag. AIChE J. 2005, 51, 1641–1653. [Google Scholar] [CrossRef]
- Zobel, S.; Helling, C.; Ditz, R.; Strube, J. Design and Operation of Continuous Countercurrent Chromatography in Biotechnological Production. Ind. Eng. Chem. Res. 2014, 53, 9169–9185. [Google Scholar] [CrossRef]
- Seidel-Morgenstern, A. Mathematische Modellierung der Präparativen Flüssigchromatographie; Deutscher Universitäts-Verlag: Wiesbaden, Germany, 1995; ISBN 3824420643. [Google Scholar]
- Abunasser, N.; Wankat, P. Ternary Separations with One-Column Analogs to SMB. Sep. Sci. Technol. 2005, 40, 3239–3259. [Google Scholar] [CrossRef]
- Abunasser, N.; Wankat, P.C. Improving the performance of one column analogs to SMBs. AIChE J. 2006, 52, 2461–2472. [Google Scholar] [CrossRef]
- de Araújo, J.M.; Rodrigues, R.C.; Silva, R.; Mota, J. Single-Column Simulated Moving-Bed Process with Recycle Lag: Analysis and Applications. Adsorpt. Sci. Technol. 2007, 25, 647–659. [Google Scholar] [CrossRef]
- Chibério, A.S.; Policarpo, G.F.; Antunes, J.C.; Santos, T.P.; Ribeiro, R.P.; Mota, J.P. Batch chromatography with recycle lag. II—Physical realization and experimental validation. J. Chromatogr. A 2020, 1623, 461211. [Google Scholar] [CrossRef]
- Chibério, A.S.; Santos, T.P.; Ribeiro, R.P.; Mota, J.P. Batch chromatography with recycle lag. I—Concept and design. J. Chromatogr. A 2020, 1623, 461199. [Google Scholar] [CrossRef]
- Juza, M. Development of a high-performance liquid chromatographic simulated moving bed separation from an industrial perspective. J. Chromatogr. A 1999, 865, 35–49. [Google Scholar] [CrossRef]
- Mazzotti, M. Equilibrium theory based design of simulated moving bed processes for a generalized Langmuir isotherm. J. Chromatogr. A 2006, 1126, 311–322. [Google Scholar] [CrossRef]
- Mazzotti, M.; Storti, G.; Morbidelli, M. Robust design of countercurrent adsorption separation processes: 2. Multicomponent systems. AIChE J. 1994, 40, 1825–1842. [Google Scholar] [CrossRef]
- Mazzotti, M.; Storti, G.; Morbidelli, M. Robust design of countercurrent adsorption separation: 3. Nonstoichiometric systems. AIChE J. 1996, 42, 2784–2796. [Google Scholar] [CrossRef]
- Mazzotti, M.; Storti, G.; Morbidelli, M. Optimal operation of simulated moving bed units for nonlinear chromatographic separations. J. Chromatogr. A 1997, 769, 3–24. [Google Scholar] [CrossRef]
- Mazzotti, M.; Storti, G.; Morbidelli, M. Robust design of countercurrent adsorption separation processes: 4. Desorbent in the feed. AIChE J. 1997, 43, 64–72. [Google Scholar] [CrossRef]
- Storti, G.; Baciocchi, R.; Mazzotti, M.; Morbidelli, M. Design of Optimal Operating Conditions of Simulated Moving Bed Adsorptive Separation Units. Ind. Eng. Chem. Res. 1995, 34, 288–301. [Google Scholar] [CrossRef]
- Storti, G.; Mazzotti, M.; Morbidelli, M.; Carrà, S. Robust design of binary countercurrent adsorption separation processes. AIChE J. 1993, 39, 471–492. [Google Scholar] [CrossRef]
- Zobel-Roos, S.; Mouellef, M.; Ditz, R.; Strube, J. Distinct and Quantitative Validation Method for Predictive Process Modelling in Preparative Chromatography of Synthetic and Bio-Based Feed Mixtures following a Quality-by-Design (QbD) Approach. Processes 2019, 7, 580. [Google Scholar] [CrossRef]
- Kaczmarski, K.; Cavazzini, A.; Szabelski, P.; Zhou, D.; Liu, X.; Guiochon, G. Application of the general rate model and the generalized Maxwell–Stefan equation to the study of the mass transfer kinetics of a pair of enantiomers. J. Chromatogr. A 2002, 962, 57–67. [Google Scholar] [CrossRef]
- Kaczmarski, K.; Gubernak, M.; Zhou, D.; Guiochon, G. Application of the general rate model with the Maxwell–Stefan equations for the prediction of the band profiles of the 1-indanol enantiomers. Chem. Eng. Sci. 2003, 58, 2325–2338. [Google Scholar] [CrossRef]
- Felinger, A.; Guiochon, G. Comparison of the Kinetic Models of Linear Chromatography. Chromatographia 2004, 60, S175–S180. [Google Scholar] [CrossRef]
- Piątkowski, W.; Antos, D.; Kaczmarski, K. Modeling of preparative chromatography processes with slow intraparticle mass transport kinetics. J. Chromatogr. A 2003, 988, 219–231. [Google Scholar] [CrossRef]
- Carta, G.; Jungbauer, A. Protein Chromatography: Process Development and Scale-Up; WILEY-VCH: Weinheim, Germany, 2010; ISBN 978-3-527-31819-3. [Google Scholar]
- Seidel-Morgenstern, A. Experimental determination of single solute and competitive adsorption isotherms. J. Chromatogr. A 2004, 1037, 255–272. [Google Scholar] [CrossRef]
- Asnin, L. Adsorption models in chiral chromatography. J. Chromatogr. A 2012, 1269, 3–25. [Google Scholar] [CrossRef] [PubMed]
- Blümel, C.; Kniep, H.; Seidel-Morgenstern, A. Measuring adsorption isotherms using a closed-loop perturbation method to minimize sample consumption. In 6th International Conference of Fundamentals of Adsorption—FOA 6; Elsevier: Amsterdam, The Netherlands, 1998; pp. 449–454. [Google Scholar]
- Cavazzini, A.; Felinger, A.; Guiochon, G. Comparison between adsorption isotherm determination techniques and overloaded band profiles on four batches of monolithic columns. J. Chromatogr. A 2003, 1012, 139–149. [Google Scholar] [CrossRef] [PubMed]
- Ching, C.B.; Chu, K.H.; Ruthven, D.M. A study of multicomponent adsorption equilibria by liquid chromatography. AIChE J. 1990, 36, 275–281. [Google Scholar] [CrossRef]
- Gamba, G.; Rota, R.; Storti, G.; Carra, S.; Morbidelli, M. Absorbed solution theory models for multicomponent adsorption equilibria. AIChE J. 1989, 35, 959–966. [Google Scholar] [CrossRef]
- Hu, X.; Do, D.D. Comparing various multicomponent adsorption equilibrium models. AIChE J. 1995, 41, 1585–1592. [Google Scholar] [CrossRef]
- Heinonen, J.; Landa, H.O.R.; Sainio, T.; Seidel-Morgenstern, A. Use of Adsorbed Solution theory to model competitive and co-operative sorption on elastic ion exchange resins. Sep. Purif. Technol. 2012, 95, 235–247. [Google Scholar] [CrossRef]
- Emerton, D.A. Profitability in the Biosimilars Market: Can You Translate Scientific Excellence into a Healthy Commercial Return? BioProcess Int. 2013, 11, 6–23. [Google Scholar]
- Erto, A.; Lancia, A.; Musmarra, D. A modelling analysis of PCE/TCE mixture adsorption based on Ideal Adsorbed Solution Theory. Sep. Purif. Technol. 2011, 80, 140–147. [Google Scholar] [CrossRef]
- Myers, A.L.; Prausnitz, J.M. Thermodynamics of mixed-gas adsorption. AIChE J. 1965, 11, 121–127. [Google Scholar] [CrossRef]
- Costa, E.; Calleja, G.; Marron, C.; Jimenez, A.; Pau, J. Equilibrium adsorption of methane, ethane, ethylene, and propylene and their mixtures on activated carbon. J. Chem. Eng. Data 1989, 34, 156–160. [Google Scholar] [CrossRef]
- Brooks, C.A.; Cramer, S.M. Steric mass-action ion exchange: Displacement profiles and induced salt gradients. AIChE J. 1992, 38, 1969–1978. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Zobel-Roos, S.; Schmidt, A.; Mestmäcker, F.; Mouellef, M.; Huter, M.; Uhlenbrock, L.; Kornecki, M.; Lohmann, L.; Ditz, R.; Strube, J. Accelerating Biologics Manufacturing by Modeling or: Is Approval under the QbD and PAT Approaches Demanded by Authorities Acceptable without a Digital-Twin? Processes 2019, 7, 94. [Google Scholar] [CrossRef]
- Zobel-Roos, S.; Schmidt, A.; Uhlenbrock, L.; Ditz, R.; Köster, D.; Strube, J. Digital Twins in Biomanufacturing. In Digital Twins: Tools and Concepts for Smart Biomanufacturing; Herwig, C., Pörtner, R., Möller, J., Eds.; Springer: Cham, Switzerland, 2021; pp. 181–262. ISBN 978-3-030-71660-8. [Google Scholar]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1998; ISBN 978-0471254249. [Google Scholar]
- Rhee, H.-K.; Aris, R.; Amundson, N.R. Multicomponent adsorption in continuous countercurrent exchangers. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1971, 269, 187–215. [Google Scholar] [CrossRef]
- Fanali, S. Editorial on “Simulated moving bed chromatography for the separation of enantiomers” by A. Rajendran, G. Paredes and M. Mazzotti. J. Chromatogr. A 2009, 1216, 708. [Google Scholar] [CrossRef] [PubMed]
- Storti, G.; Masi, M.; Carrà, S.; Morbidelli, M. Optimal design of multicomponent countercurrent adsorption separation processes involving nonlinear equilibria. Chem. Eng. Sci. 1989, 44, 1329–1345. [Google Scholar] [CrossRef]
- Kaspereit, M.; Seidel-Morgenstern, A. Auslegung der Regenerationszonen des SMB-Verfahrens. Chem. Ing. Tech. 2002, 74, 591–592. [Google Scholar] [CrossRef]
- Kaspereit, M.; Neupert, B. Vereinfachte Auslegung der simulierten Gegenstromchromatographie mittels des Hodographenraums. Chem. Ing. Tech. 2016, 88, 1628–1642. [Google Scholar] [CrossRef]
- Kaspereit, M.; Jandera, P.; Škavrada, M.; Seidel-Morgenstern, A. Impact of adsorption isotherm parameters on the performance of enantioseparation using simulated moving bed chromatography. J. Chromatogr. A 2001, 944, 249–262. [Google Scholar] [CrossRef] [PubMed]
- Saxena, A.K.; Nigam, K.D.P. Coiled configuration for flow inversion and its effect on residence time distribution. AIChE J. 1984, 30, 363–368. [Google Scholar] [CrossRef]
- Kumar, V.; Nigam, K. Numerical simulation of steady flow fields in coiled flow inverter. Int. J. Heat Mass Transf. 2005, 48, 4811–4828. [Google Scholar] [CrossRef]
- Chung, S.F.; Wen, C.Y. Longitudinal dispersion of liquid flowing through fixed and fluidized beds. AIChE J. 1968, 14, 857–866. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).