Accelerated Arithmetic Optimization Algorithm by Cuckoo Search for Solving Engineering Design Problems

Abstract

Several metaheuristic algorithms have been implemented to solve global optimization issues. Nevertheless, these approaches require more enhancement to strike a suitable harmony between exploration and exploitation. Consequently, this paper proposes improving the arithmetic optimization algorithm (AOA) to solve engineering optimization issues based on the cuckoo search algorithm called AOACS. The developed approach uses cuckoo search algorithm operators to improve the ability of the exploitation operations of AOA. AOACS enhances the convergence ratio of the presented technique to find the optimum solution. The performance of the AOACS is examined using 23 benchmark functions and CEC-2019 functions to show the ability of the proposed work to solve different numerical optimization problems. The proposed AOACS is evaluated using four engineering design problems: the welded beam, the three-bar truss, the stepped cantilever beam, and the speed reducer design. Finally, the results of the proposed approach are compared with state-of-the-art approaches to prove the performance of the proposed AOACS approach. The results illustrated an outperformance of AOACS compared to other methods of performance measurement.

1. Introduction

Increasingly complicated optimization issues have arisen due to the rapid expansion of numerous application domains. Traditional optimization techniques take too much time and money to solve these new optimization challenges. It is common knowledge that exact and rigorous answers are not required in most situations [1]. That is, due to the significantly reduced time and costs, estimated ideal solutions can be acceptable in practice. In order to address these non-convex, non-linear limitations and difficult optimization problems, numerous optimization algorithms have been introduced in recent years. These algorithms have proven to be quite successful in solving these real-world problems.

The use of optimization techniques to address issues in the actual world is common. These challenging, nonlinear, and multimodal real-world issues often need the use of metaheuristic algorithms, which have proven to be reliable optimization techniques in such circumstances. Metaheuristic algorithms are popular because of their simplicity in design and implementation, gradient-freeness, and ability to work around obstacles.

Metaheuristic algorithms efficiently solve a wide range of real-world problems; this comes from the nature of these algorithms and adopts a gradient-free method. Various metaheuristic techniques have been released recently based on natural procedures, collaborative behavior, or scientific laws.

Four general categories can be used to categorize metaheuristic algorithms, as shown in Figure 1:

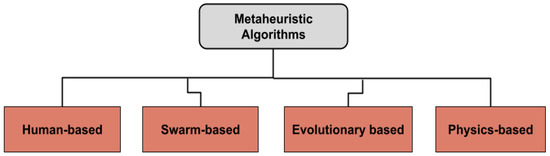
Figure 1. Metaheuristic algorithms.

Human-based algorithms: Fireworks Algorithm (FW) [2], Child Drawing Development Optimization Algorithm (CDD) [3], Teaching-based learning algorithm (TBLA) [4], Socio Evolution & Learning Optimizer (SELO) [5], Genetic algorithm (GA) [6], and Harmony Search (HS) [7]. Swarm-based algorithms: Particle Swarm Optimization (PSO) [8], Prairie Dog Optimization Algorithm (PDOA) [9], Grasshopper Optimization Algorithm (GOA) [10], Moth Flame Optimization (MFO) [11], Firefly Algorithm (FA) [12], Aquila Optimizer (AO) [13], and Ant lion optimizer [14]. Evolutionary algorithms (EA): Backtracking Search Optimization Algorithm (BTSO) [15], Evolutionary Strategies algorithm (ES) [15], Differential evolution (DE) [16], Genetic Algorithm (GA) [6], and Tree Growth Algorithm (TGA) [17]. Physics-based algorithms: Multi-verse Optimizer (MVO) [18], Black Hole Algorithm (BHA) [19], Space Gravitational Algorithm (SGA) [20], The arithmetic optimization algorithm (AOA) [21], and Henry Gas Solubility Optimization (HGSO) [22]. An overview of the given method is presented in Table 1.

Table 1. An overview of the presented methods.

Ref.	Method Name	Abbreviation	Idea	Year
[1]	Fireworks Algorithm	FW	There are two different sorts of explosion (search) procedures used and there are well-designed devices for containing a variety of sparks.	2010
[2]	Child Drawing Development Optimization Algorithm	CDD	By applying the golden ratio to enhance the beauty of their work, the learning behavior and cognitive development of the child are optimized.	2022
[3]	Teaching-based learning algorithm	TBLA	The suggested approach is based on how a teacher’s influence affects students’ performance in a class.	2012
[4]	Socio Evolution & Learning Optimizer	SELO	This approach draws its inspiration from how people develop social skills when they are arranged into families in a societal setting.	2018
[8]	Prairie Dog Optimization Algorithm	PDOA	This approach using prairie dogs behaves as they would in their native environment.	2022
[9]	Aquila optimizer	AO	This technique draws inspiration from the way aquilas grab their prey in the wild.	2021
[19]	The arithmetic optimization algorithm	AOA	This technique makes use of the distributional properties of the primary mathematical arithmetic operators.	2021

Still, not all of the issues can be resolved by these techniques [23,24]. Heuristic algorithms are currently used to address optimization problems in many different disciplines, including optimal power flow problems and parameter optimization of photovoltaic models [25,26]. Therefore, in the face of complex difficulties, we must provide algorithms with more efficiency [27].

A population-based metaheuristic method called the arithmetic optimization algorithm (AOA) was just recently proposed. The approach is based on how the addition, subtraction, multiplication, and division arithmetic operators behave with respect to distributivity [21].

The AOA algorithm proves its stable and robust performance in different fields, such as data clustering, power systems, power controllers, feature selection, and image processing. In this paper [28], the authors propose an improved AOA algorithm based on flow direction for data clustering. The proposed algorithm is validated on different data clustering problems and outperforms compared to other algorithms. Elkasem, Ahmed HA, et al. present an approach to using fuzzy logic and AOA algorithms to enhance the performance of power controllers, such as the proportional-integral-derivative (PID); the conducted results show the superiority of the PID based on fuzzy logic and AOA [29]. A binary version of AOA extracts and selects features from images to detect osteosarcoma. AOA with different algorithms accurately classifies the images [30]. Ewees, Ahmed A., et al. accelerated the AOA algorithm with hybridization of AOA and genetic algorithms to enhance the algorithm search method. The proposed algorithm is implemented on the Cox proportional hazards method [31].

The AOA algorithm is widely used for solving several optimization problems because of the simplicity, robustness, and effectiveness of the results in terms of solving optimization problems [32]. However, AOA would also easily fall in the local optima for optimizing some complex issues, and the exploration and exploitation capabilities are less significant [33].

The primary function in avoiding local optima and balancing exploitation and exploration in the fundamental AOA algorithm is played by the control parameter and the position vectors C_Iter. In order to integrate the advantages of AOA and CS, we present a hybrid approach in this study. To improve AOA’s search procedure and find solutions that are close to optimal, the AOACS is created. Specifically, a new formulation of the C_ Iter uses the CS algorithm.

This paper proposes a novel optimization algorithm based on the cuckoo search algorithm for solving engineering design problems. The algorithm is specifically designed to optimize arithmetic expressions that arise in engineering design problems, such as mathematical models for physical systems, circuits, or mechanical systems. The cuckoo search algorithm is a nature-inspired optimization algorithm that is based on the behavior of cuckoo birds. The algorithm is known for its ability to efficiently search large solution spaces and find optimal or near-optimal solutions. The proposed algorithm in this work enhances the cuckoo search algorithm by introducing an accelerated arithmetic optimization technique that exploits the mathematical structure of the optimization problem. The main objective of the proposed algorithm is to minimize the objective function, which represents the cost or performance of the system being optimized. The algorithm iteratively searches the solution space using a set of cuckoo nests, each of which contains a potential solution. The nests are updated using a set of optimization operators, such as mutation and crossover, which are used to generate new potential solutions. The performance of the proposed algorithm is evaluated using several benchmark functions and compared with other state-of-the-art optimization algorithms. The results show that the proposed algorithm outperforms other algorithms in terms of solution quality and convergence speed. The proposed algorithm has potential applications in various fields, such as aerospace engineering, mechanical engineering, and electrical engineering, where optimization of complex mathematical models is necessary.

The following is a summary of this paper’s significant contributions:

• We suggest a brand-new hybrid algorithm called AOACS based on the arithmetic optimization algorithm (AOA) and cuckoo search (CS) approach inspired by the AOA and CS algorithm design.
• CS aids the suggested algorithm in increasing the diversity of the original population and its capacity to depart from the local optimum.
• Enhanced AOA exploration and exploitation to increase convergence accuracy.
• Twenty-three benchmark functions and CEC-2019 functions are implemented to increase the ability of AOACS to solve several numerical optimization problems.
• The performance of AOACS is validated using three engineering optimization issues: the welded beam, the three-bar truss, the stepped cantilever beam, and the speed reducer design.
• The results indicate the out-performance of AOACS over the basic AOA, CS, and other metaheuristic approaches.

The following is the order of the paper: The AOA algorithm is presented in Section 2. The search algorithm for cuckoo is introduced in Section 3. Section 4 description of the proposed AOACS algorithm. Section 5 discusses the outcomes of applying the AOACS to engineering challenges. This article is concluded in Section 6.

2. Arithmetic Optimization Algorithm (AOA)

Using several equations and mathematical operators, Abualigah presented this approach in 2020 [21]. AOA mimics four basic arithmetic operators (i.e., Subtraction (S), Addition (A), Multiplication (M), Division (D)) and is used to update the positions and search for the optimal global solutions. For the exploration search, the Multiplication and Division operators are employed; on the other hand, the Addition and Subtraction operators are used to execute the exploitation search. Figure 2 shows the AOA optimization technique.

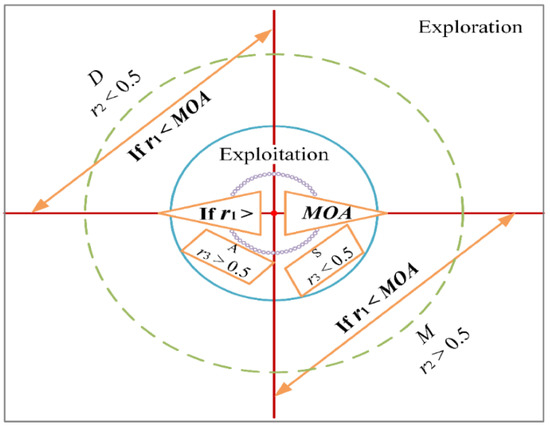
Figure 2. The AOA optimization technique.

The AOA method begins with a population of unanticipated solutions, just like other metaheuristics. The objective value of each solution is computed after each iteration. Before changing the position of keys, two regulating parameters named MOA and MOP in this method should be modified as follows:

$$\mathrm{MOA}\left(t\right)=\mathrm{Min}+t\times \left(\frac{\mathrm{Max}-\mathrm{Min}}{T}\right)$$

(1)

where MOA(t) denotes the result of the ith iteration of the function, the maximum number of repetitions is T, and the current number of repetitions is represented by t. Min and Max are accelerated processes of the minimum and maximum values.

$$MOP\left(t\right)=1-{\left(\frac{t}{T}\right)}^{\frac{1}{\alpha }}$$

(2)

where math optimizer probability (MOP) is a coefficient, MOP(t) is the procedure’s weight at the tth repetition, T is the highest repetitions number, t is the current repetition, and α illustrates a controlling value. Here, r1 is an integer that is created at random and MOP is a scaling parameter that encourages further exploration.

A random number named r1 is created to switch between exploitation and exploration after following MOA and MOP. The following formula is employed for exploration:

$$x_{i,J}\left(t+1\right)=\{\begin{array}{c}\frac{best\left(x_j\right)}{MOP+ϵ}÷\left(U{B}_j-L{B}_J\right)\times \mu +L{B}_j if r2<0.5\\ best\left(x_j\right)\times MOP\times \left(U{B}_j-L{B}_j\right)\times \mu +L{B}_{j }if r2 \ge 0.5\end{array}$$

(3)

The current repetition is presented as t, µ is used as controlling element, ϵ is a small numeral to evade division by 0, and r3 is an arbitrary value in the range [0, 1]. The following formula is used for the exploitation.

$$x_{i,J}\left(t+1\right)=\{\begin{array}{c}best\left(x_j\right)-MOP\times \left(U{B}_j-L{B}_j\right)\times \mu +L{B}_j if r3<0.5\\ best\left(x_j\right)+MOP\times \left(U{B}_j-L{B}_j\right)\times \mu +L{B}_j if r3\ge 0.5\end{array}$$

(4)

where x_i,j(t) demonstrates the jth placements of the ith answer at the recent repetition. The optimal (x_j) is the jth placement in the optimal solution. Here, x_i (t + 1) denotes the ith answer in the following repetition. Respectively, $U{B}_j$ and $L{B}_j$ define the $j^{th}$ placements upper and lower bound values. Algorithm 1 shows the pseudocode for the AOA algorithm.

Algorithm 1 Pseudo-code of AOA algorithm.
Initialize the population size N and the maximum iteration T
Initialize the population size of each search agent Xi (I = 1,2, …, N)
While  t$\le$T
	Check if the position goes beyond the search space boundary and the adjust it.
	Evaluate the fitness values of all search agents
	Set Xbest as the position of current best solution
	Calculate the MOA value using Equation (1)
	Calculate the MOP value using Equation (2)
	For i = 1 to N
		If r1 $>$ MOA then
		Update the search agent’s position using Equation (3)
		Else
		Update the search agent’s position using Equation (4)
		End If
	End For
	t = t + 1
End While
Return  Xbest

3. Cuckoo Search Algorithm

We initially idealize the main elements of the cuckoo-host strategy as a population of n cuckoos with n nests to discuss the cuckoo search algorithm as simply as possible. In true cuckoo-host systems, host bird nests usually contain three to four eggs or more, and by laying its eggs in such nests, a cuckoo can attack many nests. Because each cuckoo may only affect one host nest at a time while also applying one egg, the number of eggs, nests, and cuckoos is similar. Thus, an optimization problem’s solution vector, x, can be thought of as the location of an egg. As a result, there is no longer a need to distinguish between eggs, cuckoos, and nests. We essentially have the equivalence “egg = cuckoo = nest” as a result [34]. Algorithm 2 shows the pseudocode for AOA algorithm.

The initial population of the CS algorithm is generated by the Lévy flight algorithm. In the 1930s, the French mathematician Paul Pierre proposed the Lévy flight, a random walk mechanism whose walk steps fit the stable heavy-tail distribution that can make big jumps at nearby sites with a high probability. Sharp peaks, asymmetry, and lagging were features of the possibility density allocation of the Lévy flight. It moved in a rhythm that rotated between periodic short-distance jumps and sporadic long-distance hops, which can widen the search region for the population and jump out of the local optimal. In nature, numerous insects and animals, including flies and reindeer, fly in a manner resembling Lévy flying.

Algorithm 2 Pseudo-code of Cuckoo search algorithm.
Objective function f$\left(\overrightarrow{x}\right), \overrightarrow{x}={\left(x_1,x_2, \mathrm{\dots }, x_d\right)}^T$
Generation t = 1
Initial a population of n host nests $x_i \left( i=1,2,\mathrm{\dots },n\right)$
While (t $<$ Stop criterion)
	Get a cuckoo (i) randomly by Lévy flight
	Evaluate the fitness values of all search agents F
	Choose a nest among n (such as c) randomly
	If $(F_i>F_c$)
		Replace c by the new solution
	End If
	Abandon a faction ($P_a$) of the worst nests and build new ones
	Keep the optimal solutions.
	Rank the solutions an find the current best.
	Update the generation number t = t + 1
End While

4. Hybridization of AOA with CS Algorithm

The elements in AOA swarms would hunt more randomly than CS swarms. However, elements in the AOA would execute poorer performance than those in the CS swarms during the exploitation operation. The exploitation ability of elements in AOA swarms would not be sufficient, and elements in CS swarms would be less qualified than those in AOA swarms despite the fact that both of these algorithms show a significant performance in optimization several problems. Therefore, it could be preferable if the exploitation process of people in CS swarms and the exploration process of elements in AOA swarms are coupled. Figure 3 illustrates the proposed AOACS algorithm.

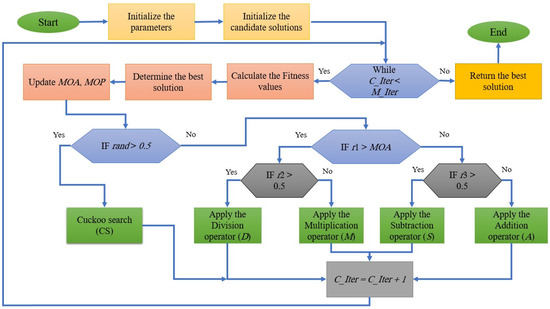
Figure 3. The proposed AOACS algorithm.

5. Results and Discussion

5.1. Benchmark Functions Description

Table 2 lists the 23 mathematical functions used, their categories, and their mathematical formulation. The unimodal benchmark functions in Table 2 are used because they only have one optimal solution, making them a good choice for testing the effectiveness of the proposed optimizer. Table 2 illustrates several mathematical functions. Multimodal functions contain some peaks, a few local optimums, and only one global optimum, which makes these benchmark functions the best option when assessing the exploration of the optimization process. Further, balancing the exploration and exploitation of any algorithm is a challenging assignment; thus, the fixed dimension numerical multimodal is used to prove the outperformance of the proposed algorithm. The minimum value for each function (f_min), the defined search space limitations, and the considered dimensions are demonstrated in Table 2.

Table 2. Benchmark functions.

Fun.	Fun. Description	Dim.	Range	fmin
Unimodal Benchmark Functions
F1	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}{x}_i^2$	10,100	[−100, 100]	0
F2	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=0}^n}\left|x_i\right|+{\displaystyle {\displaystyle \prod }_{i=0}^n}\left|x_i\right|$	10,100	[−10, 10]	0
F3	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^d}{\left({\displaystyle {\displaystyle \sum }_{j=1}^i}{x}_j\right)}^2$	10,100	[−100, 100]	0
F4	$f\left(x\right)=ma{x}_i\left\{\left|x_i\right|,1\le i\le n\right\}$	10,100	[−100, 100]	0
F5	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^{n-1}}\left[100{\left(x_i^2-x_{i+1}\right)}^2+{\left(1-x_i\right)}^2\right]$	10,100	[−30, 30]	0
F6	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}{\left(\left[x_i+0.5\right]\right)}^2$	10,100	[−100, 100]	0
F7	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=0}^n}{\mathit{ix}}_i^4+\mathrm{random}\left[0,1\right)$
Multimodal Benchmark Functions
F8	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left(-x_i\sin \left(\sqrt{\left|x_i\right|}\right)\right)$	10,100	[−500, 500]	−418.9829
F9	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}\left[x_i^2-10\cos \left(2{\mathsf{\pi }x}_i\right)+10\right]$	10,100	[−5.12, 5.12]	0
F10	$f\left(x\right)=-20\exp \left(-0.2\sqrt{\frac{1}{n}{\displaystyle {\displaystyle \sum }_{i=1}^n}{x}_i^2}\right)-\exp \left(\frac{1}{n}{\displaystyle {\displaystyle \sum }_{i=1}^n}\cos \left(2{\mathsf{\pi }x}_i\right)\right)+20+\mathrm{e}$	10,100	[−32, 32]	0
F11	$f\left(x\right)=1+\frac{1}{4000}{\displaystyle {\displaystyle \sum }_{i=1}^n}{x}_i^2-{\displaystyle {\displaystyle \prod }_{i=1}^n}\cos \left(\frac{x_i}{\sqrt{i}}\right)$	10,100	[−600, 600]	0
F12	$f\left(x\right)=\frac{\mathsf{\pi }}{n}10\sin \left({\mathsf{\pi }y}_1\right)+{\displaystyle {\displaystyle \sum }_{i=1}^{n-1}}{\left(y_i-1\right)}^2\left[1+10{\sin }^2\left({\mathsf{\pi }y}_{i+1}\right)+{\displaystyle {\displaystyle \sum }_{i=1}^n}u\left(x_i,10,100,4\right)\right]$ $y_i=1+\frac{x_i+1}{4},u\left(x_i,a,k,m\right)\{\begin{array}{cc}K{\left(x_i-a\right)}^m& \mathrm{if} x_i>a\\ 0& -a\le x_i\ge a\\ K{\left(-x_i-a\right)}^m& -a\le x_i\end{array}$	10,100	[−50, 50]	0
F13	$\begin{array}{c}f\left(x\right)=0.1({\sin }^2\left(3{\mathsf{\pi }x}_1\right)+{{\displaystyle \sum }}_{i=1}^n{\left(x_i-1\right)}^2\left[1+{\sin }^2\left(3{\mathsf{\pi }x}_i+1\right)\right]+\\ {\left(x_n-1\right)}^{2}1+{\sin }^2\left(2{\mathsf{\pi }x}_n\right))+{{\displaystyle \sum }}_{i=1}^{n}u\left(x_i,5,100,4\right)\end{array}$	10,100	[−50, 50]	0
Fixed-Dimension Multimodal Benchmark Functions
F14	$f\left(x\right)={\left(\frac{1}{500}+{\displaystyle {\displaystyle \sum }_{\mathrm{j}=1}^{25}}\frac{1}{\mathrm{j}+{{\displaystyle \sum }}_{i=1}^2}\left(x_i-{\mathrm{a}}_{\mathrm{ij}}\right)\right)}^{-1}$	2	[−65, 65]	1
F15	$f\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^{11}}{\left[{\mathrm{a}}_{\mathrm{i}}-\frac{x_1\left({\mathrm{b}}_{\mathrm{i}}^2+{\mathrm{b}}_{\mathrm{i}}{x}_2\right)}{{\mathrm{b}}_{\mathrm{i}}^2+{\mathrm{b}}_{\mathrm{i}}{x}_3+x_4}\right]}^2$	4	[−5, 5]	0.398
F16	$f\left(x\right)=4x_1^2-2.1x_1^4+\frac{1}{3}{x}_1^6+x_1{x}_2-4x_2^2+4x_2^{}$	2	[−5, 5]	−1.0316
F17	$f\left(x\right)={\left(x_2-\frac{5.1}{4{\pi }^2}{x}_1^2+\frac{5}{\pi }{x}_1-6\right)}^2+10\left(1-\frac{1}{8\pi }\right)cos{x}_1+10$	2	[−5, 5]	0.398
F18	$\begin{array}{c}f\left(x\right)=\left[1+{\left(x_1+x_2+1\right)}^2\left(19-14x_1+3x_1^2-14x_2+6x_1{x}_2+3x_2^2\right)\right]\\ \times \left[30+{\left(2x_1-3x_2\right)}^2\times \left(18-32x_i+12x_1^2+48x_2-36x_1{x}_2+27x_2^2\right)\right]\end{array}$	2	[−2, 2]	3
F19	$f\left(x\right)=-{\displaystyle {\displaystyle \sum }_{i=1}^4}{\mathrm{c}}_{\mathrm{i}}\exp \left(-{\displaystyle {\displaystyle \sum }_{i=1}^3}{\mathrm{a}}_{\mathrm{ij}}{\left({\mathrm{x}}_{\mathrm{j}}-{\mathrm{p}}_{\mathrm{ij}}\right)}^2\right)$	3	[−1, 2]	−3.86
F20	$f\left(x\right)=-{\displaystyle {\displaystyle \sum }_{i=1}^4}{\mathrm{c}}_{\mathrm{i}}\exp \left(-{\displaystyle {\displaystyle \sum }_{i=1}^6}{\mathrm{a}}_{\mathrm{ij}}{\left({\mathrm{x}}_{\mathrm{j}}-{\mathrm{p}}_{\mathrm{ij}}\right)}^2\right)$	6	[0, 1]	−0.32
F21	$f\left(x\right)=-{\displaystyle {\displaystyle \sum }_{i=1}^5}{\left[\left(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}\right){\left(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}\right)}^{\mathrm{T}}+{\mathrm{c}}_{\mathrm{i}}\right]}^{-1}$	4	[0, 1]	−10.1532
F22	$f\left(x\right)=-{\displaystyle {\displaystyle \sum }_{i=1}^7}{\left[\left(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}\right){\left(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}\right)}^{\mathrm{T}}+{\mathrm{c}}_{\mathrm{i}}\right]}^{-1}$	4	[0, 1]	−10.4028
F23	$f\left(x\right)=-{\displaystyle {\displaystyle \sum }_{i=1}^{10}}{\left[\left(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}\right){\left(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}\right)}^{\mathrm{T}}+{\mathrm{c}}_{\mathrm{i}}\right]}^{-1}$	4	[0, 1]	−10.5363

The proposed AOACS algorithm’s performance in this part is assessed in two steps; the first involves processing a complex set of mathematical benchmark functions. Second, two real word problems are solved using the proposed method to show the performance of the proposed work. The results are compared with different well-known algorithms, such as the original AOA, Whale optimization algorithm (WOA), Harris hawks optimization (HHO), Salp swarm algorithm (SSA), particle swarm optimization (PSO), and Slime mould algorithm (SMA). The selected methods are the most related and new in this domain. The worst, best, average, and standard deviation of the finesse values are the four metrics employed in the comparisons. Furthermore, the Wilcoxon summation rank is utilized to show the statistical distinctions between AOACS and the rest of the algorithms. Table 3 provides the values for the essential parameters for the used algorithms.

Table 3. Parameter values of the proposed AOACS algorithm and other algorithms.

Algorithm	Parameters
AOACS	μ = 0.5;
	α = 5;
PSO	wMax  =  0.9;
	wMin  =  0.2;
	c1  =  2;
	c2  =  2
WOA	a1 ∈ [2, 0];
	a2 ∈ [−1, −2];
	b = 1
SSA	Random values c2 and c3 [1, 0]
SMA	z = 0.01
HHO	α = 1.5
AOA	μ = 0.5; α = 5;

5.2. The Global Optimization Results

The suggested AOACS has been evaluated utilizing 23 more widely used mathematical functions in this area. With the help of several statistical analyses, the proposed AOACS’s results have been compared with many contemporary state-of-the-art methods to evaluate and show how well it handles problems involving global optimization. The original AOA [21], Whale optimization algorithm (WOA) [35], Harris hawks optimization (HHO) [36], Salp swarm algorithm (SSA) [37,38], particle swarm optimization (PSO), and Slime mould algorithm (SMA) [39] are among the algorithms that were taken into consideration.

The algorithms were applied with the same settings to ensure the fairness of the experimental results: population size was set to 30, and the maximum number of iterations was 500 for 30 separate instances. The study and simulations were conducted using Windows 10 and an Intel Core i7 processor running at 2.3 GHz with 16 GB of RAM. For a fair comparison, all competitors were run on the MATLAB 2018 platform.

5.2.1. Achieved Qualitative Results

The AOACS behaviors regarding the trajectories and convergence are illustrated in Figure 4 to confirm the effectiveness of the proposed algorithm. The figure shows several results: functions plotted in 2D fashion appear in the first column. The second column represents the trajectory of the solution, followed by two columns, the fitness significance, and convergence, respectively.

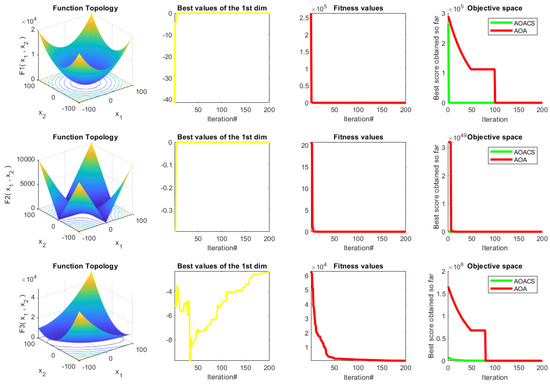
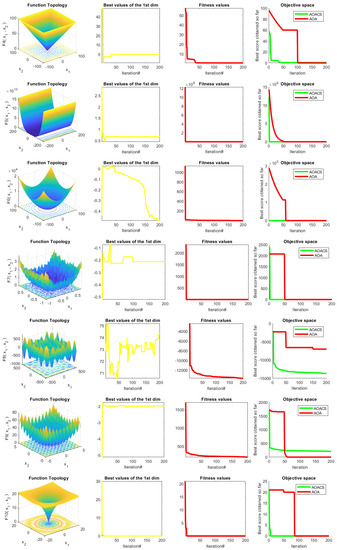
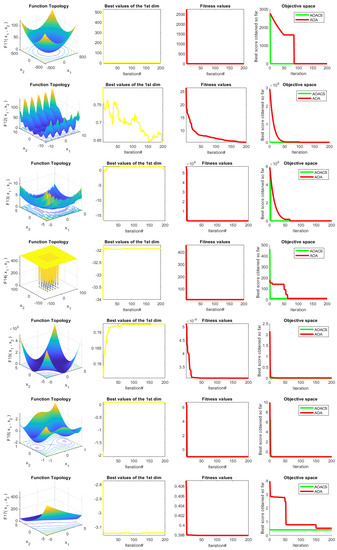
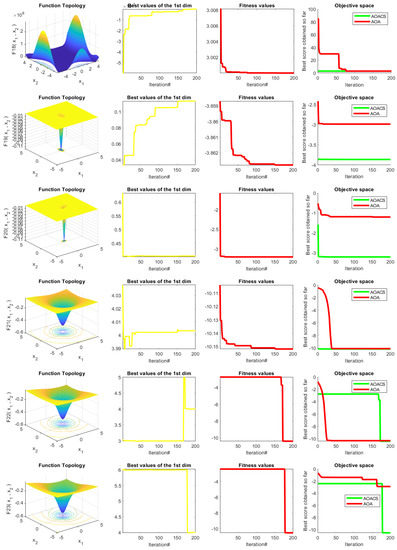
Figure 4. The achieved results of the tested qualitative analysis for 23 benchmark functions.

The solution’s magnitude and frequency in the initial iterations may be seen from the second column (trajectory behavior). They have almost completely disappeared in recent versions. This shows how AOACS had strong exploration capabilities in the early versions and strong exploitation capabilities in the later iterations. This tendency suggests that AOACS can find the ideal answer well. The ability of the AOACS to converge to highly qualified explanations in fewer repetitions is demonstrated by the average fitness value across all solutions among the number of repetitions shown in the third column of Figure 4. The average fitness value for the AOACS starts high in the early generations.

5.2.2. Results of Simulation of 23 Benchmark Functions and Discussions

Figure 5 compares the convergence curves of the proposed AOACS with those of the basic AOA and cutting-edge methods to evaluate the effectiveness of the AOACS for the main balance target exploitation and exploration. In contrast to the SMA, PSO, SSA, WOA, and HHO, which experienced severe dormancy at the optimal local explanations, the results demonstrate the smooth convergence of the AOACS by reaching superior quality solutions.

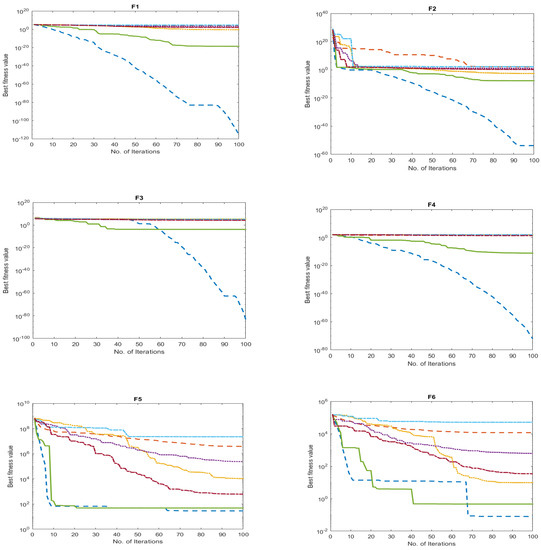
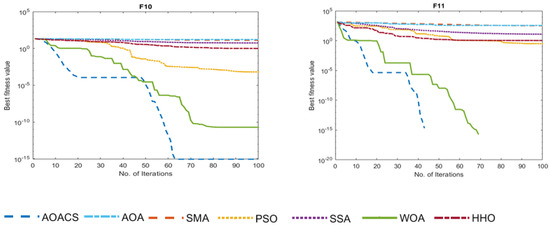
Figure 5. The comparison approaches behaved in terms of convergence for the test functions (F1–F6, F10, and F11), where the dimension was 10.

Table 4 statistics compare the performance of the AOACS to that of the standard AOA, PSO, WOA, SSA, SMA, HHO, and AOACS. It displayed the lowest values of the computed metrics in the functions of the worst, best, average, and standard deviation (STD) values by AOACS, demonstrating that it can outperform all other algorithms in around 50% of all the benchmarks that were taken into consideration (F: 2, 3, 5, 8, 9, 11, 12, 14, 19, 22). Furthermore, it performs similarly well in the other 50% of the relevant functions. The P-values acquired utilizing Wilcoxon summation rank with a significant value of 0.05, which is less than 0.05, demonstrate that the AOACS is superior to the SSA in 18 approaches. The null hypothesis test is therefore not accepted (h = 1 indicates a significant difference between the examined optimizers, AOACS and SSA). The P-values for PSO, SMA, HHO, WOA, SSA, and basic AOA demonstrate that the AOACS outperforms other algorithms in handling about 13 of the 23 functions; as a result, the null assumption examination is rejected (h = 1). Additionally, the proposed AOACS is compared to its equivalents while processing the 23 functions using the Friedman ranking test to determine where it ranks among them for further investigation. Table 5 lists the classes that were gained.

Table 4. Results from methods of comparison on 23 benchmark functions (F1–F23), where the dimension is 10.

Function	Measure	Algorithm
		PSO	WOA	SSA	SMA	HHO	AOA	AOACS
F1	Best	6.12 × 103	3.64 × 102	6.51 × 103	2.76 × 101	1.15 × 102	3.66 × 10−9	3.64 × 10−68
	Average	3.00 × 103	1.60 × 102	1.49 × 103	1.11 × 101	5.95 × 101	7.88 × 10−10	7.28 × 10−69
	Worst	1.43 × 103	1.81 × 101	3.92 × 101	5.57 × 10−1	2.70 × 101	6.73 × 10−17	1.06 × 10−76
	STD	2.07 × 103	1.28 × 102	2.81 × 103	1.25 × 101	3.69 × 101	1.61 × 10−9	1.63 × 10−68
	p-value	1.19 × 10−2	2.36 × 10−2	2.69 × 10−1	8.04 × 10−2	6.89 × 10−3	1	3.05 × 10−1
	h	1	1	0	0	1	0	0
F2	Best	3.76 × 101	1.14 × 101	0.452 × 101	0.238 × 101	0.494 × 101	9.87 × 10−5	3.77 × 10−27
	Average	1.98 × 101	0.450 × 101	0.226 × 101	5.38 × 10−1	0.260 × 101	2.06 × 10−5	7.54 × 10−28
	Worst	0.907 × 10−1	0.203 × 101	5.15 × 10−1	2.38 × 10−2	0.103 × 101	2.19 × 10−10	9.73 × 10−39
	STD	1.34 × 101	0.394 × 101	0.160 × 101	0.103 × 101	0.162 × 101	4.37 × 10−5	1.68 × 10−27
	p-valu×10	1.07 × 10−2	3.39 × 10−2	1.34 × 10−2	2.76 × 10−1	7.03 × 10−3	1	3.23 × 10−1
	h	1	1	1	0	1	0	0
F3	B×10 st	1.74 × 104	7.62 × 103	5.40 × 103	3.15 × 104	2.01 × 103	9.11 × 10−2	8.27 × 10−55
	Average	7.44 × 103	3.19 × 103	3.94 × 103	1.75 × 104	7.80 × 102	1.82 × 10−2	1.69 × 10−55
	Worst	4.24 × 103	1.19 × 103	1.26 × 103	6.84 × 103	8.88 × 101	5.68 × 10−14	1.54 × 10−63
	STD	5.60 × 103	2.60 × 103	1.80 × 103	9.39 × 103	8.89 × 102	4.08 × 10−2	3.68 × 10−55
	p-value	1.79 × 10−2	2.54 × 10−2	1.19 × 10−3	3.17 × 10−3	8.56 × 10−2	1	3.46 × 10−1
	h	1	1	1	1	0	0	0
F4	Best	6.21 × 101	1.94 × 101	6.43 × 101	7.67 × 101	9.86 × 100	6.42 × 10−5	4.95 × 10−33
	Average	3.67 × 101	1.58 × 101	3.64 × 101	5.19 × 101	0.697 × 101	1.93 × 10−5	2.13 × 10−33
	Worst	2.10 × 101	1.34 × 101	1.61 × 101	2.52 × 101	0.400 × 101	4.89 × 10−7	7.72 × 10−38
	STD	1.65 × 101	0.263 × 101	2.12 × 101	1.98 × 101	0.275 × 101	2.64 × 10−5	2.45 × 10−33
	p-value	1.09 × 10−3	9.00 × 10−7	4.89 × 10−3	3.78 × 10−4	4.74 × 10−4	1	1.40 × 10−1
	h	1	1	1	1	1	0	0
F5	Best	1.08 × 107	7.00 × 103	4.19 × 105	3.79 × 104	3.63 × 103	0.894 × 101	8.99 × 100
	Average	2.98 × 106	2.02 × 103	2.42 × 105	1.94 × 104	2.71 × 103	0.734 × 101	8.94 × 100
	Worst	5.59 × 104	3.23 × 102	8.08 × 104	6.84 × 102	5.27 × 102	0.107 × 101	8.79 × 100
	STD	4.51 × 106	2.86 × 103	1.34 × 105	1.74 × 104	1.30 × 103	0.351 × 101	8.25 × 10−2
	p-value	1.77 × 10−1	1.55 × 10−1	3.72 × 10−3	3.68 × 10−2	1.65 × 10−3	1	3.39 × 10−1
	h	0	0	1	1	1	0	0
F6	Best	1.12 × 104	2.32 × 103	1.87 × 103	6.20 × 101	7.76 × 101	4.03 × 10−1	1.54 × 100
	Average	4.23 × 103	9.19 × 102	6.91 × 102	2.29 × 101	4.00 × 101	1.22 × 10−1	1.24 × 100
	Worst	1.11 × 103	7.32 × 101	1.27 × 101	0.149 × 101	1.30 × 101	1.90 × 10−5	9.72 × 10−1
	STD	4.19 × 103	8.99 × 102	7.22 × 102	2.55 × 101	2.80 × 101	1.76 × 10−1	2.16 × 10−1
	p-value	5.39 × 10−2	5.16 × 10−2	6.49 × 10−2	8.03 × 10−2	1.29 × 10−2	1	1.90 × 10−5
	h	0	0	0	0	1	0	1
F7	Best	5.41 × 10−1	2.84 × 100	5.88 × 10−1	9.58 × 10−1	1.99 × 10−1	8.87 × 10−3	1.61 × 10−2
	Average	2.93 × 10−1	9.32 × 10−1	3.12 × 10−1	3.23 × 10−1	1.01 × 10−1	6.33 × 10−3	6.06 × 10−3
	Worst	1.89 × 10−1	3.70 × 10−1	5.34 × 10−2	5.25 × 10−3	6.27 × 10−2	3.89 × 10−3	4.13 × 10−4
	STD	1.53 × 10−1	0.107 × 101	2.04 × 10−1	3.80 × 10−1	5.78 × 10−2	1.83 × 10−3	6.38 × 10−3
	p-value	3.03 × 10−3	8.90 × 10−2	1.00 × 10−2	9.95 × 10−2	6.26 × 10−3	1	9.31 × 10−1
	h	1	0	1	0	1	0	0
F8	Best	−1.46 × 103	−1.17 × 103	−1.38 × 103	−1.65 × 103	−1.72 × 103	−1.73 × 103	−1.93 × 103
	Average	−1.78 × 103	−1.40 × 103	−1.59 × 103	−2.10 × 103	−1.93 × 103	−3.17 × 103	−3.64 × 103
	Worst	−2.17 × 103	−2.01 × 103	−1.91 × 103	−2.95 × 103	−2.15 × 103	−4.19 × 103	−4.17 × 103
	STD	3.15 × 102	3.47 × 102	2.02 × 102	5.25 × 102	2.00 × 102	1.04 × 103	9.60 × 102
	p-value	2.10 × 10−2	6.86 × 10−3	1.04 × 10−2	7.48 × 10−2	3.04 × 10−2	1	4.82 × 10−1
	h	1	1	1	0	1	0	0
F9	Best	9.21 × 101	7.14 × 101	8.80 × 101	9.44 × 101	6.90 × 101	4.21 × 10−8	0
	Average	6.63 × 101	5.48 × 101	6.21 × 101	6.80 × 101	3.92 × 101	1.03 × 10−8	0
	Worst	3.98 × 101	4.02 × 101	2.28 × 101	0.292 × 101	1.09 × 101	0	0
	STD	1.94 × 101	1.15 × 101	2.62 × 101	3.78 × 101	2.76 × 101	1.80 × 10−8	0
	p-value	6.08 × 10−5	5.32 × 10−6	7.28 × 10−4	3.80 × 10−3	1.30 × 10−2	1	2.35 × 10−1
	H	1	1	1	1	1	0	0
F10	Best	9.21 × 101	7.14 × 101	8.80 × 101	9.44 × 101	6.90 × 101	4.21 × 10−8	0
	Average	6.63 × 101	5.48 × 101	6.21 × 101	6.80 × 101	3.92 × 101	1.03 × 10−8	0
	Worst	3.98 × 101	4.02 × 101	2.28 × 101	0.292 × 101	1.09 × 101	0	0
	STD	1.94 × 101	1.15 × 101	2.62 × 101	3.78 × 101	2.76 × 101	1.80 × 10−8	0
	p-value	6.08 × 10−5	5.32 × 10−6	7.28 × 10−4	3.80 × 10−3	1.30 × 10−2	1	2.35 × 10−1
	h	1	1	1	1	1	0	0
F11	Best	6.43 × 101	1.63 × 102	2.53 × 101	1.19 × 100	0.316 × 101	2.76 × 10−4	0
	Average	2.38 × 101	1.01 × 102	1.09 × 101	8.03 × 10−1	0.204 × 101	8.53 × 10−5	0
	Worst	0.933 × 101	6.30 × 101	0.211 × 101	3.49 × 10−1	0.144 × 101	5.20 × 10−12	0
	STD	2.29 × 101	3.76 × 101	0.997 × 101	3.38 × 10−1	6.59 × 10−1	1.25 × 10−4	0
	p-value	4.90 × 10−2	3.31 × 10−4	4.00 × 10−2	7.18 × 10−4	1.23 × 10−4	1	1.65 × 10−1
	h	1	1	1	1	1	0	0
F12	Best	6.31 × 106	0.832 × 101	2.61 × 107	1.34 × 104	1.57 × 101	2.78 × 10−1	0.151 × 101
	Average	1.36 × 106	0.337 × 101	5.81 × 106	2.70 × 103	0.712 × 101	6.93 × 10−2	4.46 × 10−1
	Worst	3.92 × 101	1.51 × 10−1	5.10 × 104	2.50 × 10−1	9.75 × 10−1	3.31 × 10−4	4.55 × 10−2
	STD	2.78 × 106	0.369 × 101	1.14 × 107	5.98 × 103	0.542 × 101	1.19 × 10−1	6.00 × 10−1
	p-value	3.07 × 10−1	8.08 × 10−2	2.85 × 10−1	3.42 × 10−1	1.97 × 10−2	1	2.05 × 10−1
	h	0	0	0	0	1	0	0
F13	Best	1.95 × 107	2.03 × 102	4.85 × 106	4.44 × 106	1.42 × 101	2.35 × 10−1	9.56 × 10−1
	Average	5.77 × 106	5.72 × 101	1.58 × 106	1.30 × 106	0.648 × 101	8.06 × 10−2	8.84 × 10−1
	Worst	7.02 × 105	4.66 × 10−1	1.36 × 103	6.52 × 101	0.179 × 101	9.17 × 10−5	8.04 × 10−1
	STD	7.97 × 106	8.72 × 101	1.97 × 106	1.89 × 106	0.469 × 101	9.47 × 10−2	6.08 × 10−2
	p-value	1.44 × 10−1	1.81 × 10−1	1.11 × 10−1	1.65 × 10−1	1.57 × 10−2	1	2.39 × 10−7
	h	0	0	0	0	1	0	1
F14	Worst	2.20 × 101	1.27 × 101	1.27 × 101	1.56 × 101	1.65 × 101	1.17 × 101	1.64 × 101
	Average	1.72 × 101	0.471 × 101	0.646 × 101	0.993 × 101	1.15 × 101	0.848 × 101	0.957 × 101
	Best	1.46 × 101	9.98 × 10−1	0.199 × 101	0.595 × 101	0.397 × 101	0.320 × 101	0.298 × 101
	STD	0.311 × 101	0.535 × 101	0.568 × 101	0.424 × 101	0.515 × 101	0.352 × 101	0.524 × 101
	p-value	2.00 × 10−3	1	6.29 × 10−1	1.26 × 10−1	7.54 × 10−2	2.25 × 10−1	1.85 × 10−1
	H	1	0	0	0	0	0	0
F15	Worst	6.17 × 10−2	5.59 × 10−3	7.91 × 10−3	2.64 × 10−2	3.60 × 10−2	3.62 × 10−3	1.64 × 10−2
	Average	2.54 × 10−2	2.81 × 10−3	4.61 × 10−3	1.42 × 10−2	1.11 × 10−2	1.43 × 10−3	6.05 × 10−3
	Best	5.03 × 10−3	7.93 × 10−4	1.52 × 10−3	5.74 × 10−4	1.78 × 10−3	6.44 × 10−4	1.90 × 10−3
	STD	2.35 × 10−2	1.95 × 10−3	2.63 × 10−3	1.04 × 10−2	1.43 × 10−2	1.24 × 10−3	5.93 × 10−3
	p-value	6.49 × 10−2	1	2.54 × 10−1	4.28 × 10−2	2.36 × 10−1	2.20 × 10−1	2.79 × 10−1
	H	0	0	0	1	0	0	0
F16	Worst	−0.103 × 101	−0.102 × 101	−0.100 × 101	−0.101 × 101	−9.49 × 10−1	−0.103 × 101	−0.103 × 101
	Average	−0.103 × 101	−0.103 × 101	−0.102 × 101	−0.102 × 101	−9.99 × 10−1	−0.103 × 101	−0.103 × 101
	Best	−0.103 × 101	−0.103 × 101	−0.103 × 101	−0.103 × 101	−0.103 × 101	−0.103 × 101	−0.103 × 101
	STD	7.72 × 10−5	3.88 × 10−3	1.63 × 10−2	1.03 × 10−2	3.42 × 10−2	4.18 × 10−5	4.17 × 10−4
	p-value	1.07 × 10−1	1	2.25 × 10−1	2.58 × 10−1	9.53 × 10−2	1.07 × 10−1	1.35 × 10−1
	h	0	0	0	0	0	0	0
F17	Worst	3.98 × 10−1	4.09 × 10−1	5.19 × 10−1	0.277 × 10−1	0.150 × 10−1	0.411 × 10−1	3.98 × 10−1
	Average	3.98 × 10−1	4.03 × 10−1	4.23 × 10−1	0.104 × 10−1	8.57 × 10−1	0.114 × 10−1	3.98 × 10−1
	Best	3.98 × 10−1	3.98 × 10−1	3.98 × 10−1	4.08 × 10−1	4.00 × 10−1	3.98 × 10−1	3.98 × 10−1
	STD	1.18 × 10−4	4.52 × 10−3	5.39 × 10−2	9.82 × 10−1	4.61 × 10−1	0.166 × 10−1	7.87 × 10−6
	p-value	3.59 × 10−2	1	4.45 × 10−1	1.87 × 10−1	5.89 × 10−2	3.46 × 10−1	3.34 × 10−2
	h	1	0	0	0	0	0	1
F18	Worst	9.18 × 101	0.453 × 10−1	3.00 × 101	2.51 × 101	1.79 × 101	9.37 × 101	0.323 × 10−1
	Average	3.77 × 101	0.331 × 10−1	1.53 × 101	1.03 × 101	0.629 × 10−1	2.13 × 101	0.305 × 10−1
	Best	0.30 × 10−1	0.30 × 10−1	0.30 × 10−1	0.30 × 10−1	0.30 × 10−1	0.304 × 10−1	0.300 × 10−1
	STD	4.75 × 101	6.78 × 10−1	1.38 × 101	1.03 × 101	0.649 × 10−1	4.05 × 101	1.03 × 10−1
	p-value	1.44 × 10−1	1	8.72 × 10−2	1.68 × 10−1	0.338 × 10−1	3.49 × 10−1	4.09 × 10−1
	H	0	0	0	0	0	0	0
F19	Worst	−0.270 × 10−1	−0.329 × 10−1	−0.385 × 10−1	−0.297 × 10−1	−0.261 × 10−1	−0.377 × 10−1	−0.386 × 10−1
	Average	−0.330 × 10−1	−0.368 × 10−1	−0.386 × 10−1	−0.348 × 10−1	−0.346 × 10−1	−0.382 × 10−1	−0.386 × 10−1
	Best	−0.386 × 10−1	−0.385 × 10−1	−0.386 × 10−1	−0.378 × 10−1	−0.384 × 10−1	−0.386 × 10−1	−0.386 × 10−1
	STD	4.92 × 10−1	2.26 × 10−1	4.27 × 10−3	3.26 × 10−1	4.96 × 10−1	4.24 × 10−2	1.01 × 10−3
	p-value	1.49 × 10−1	1.00 × 100	1.24 × 10−1	2.83 × 10−1	3.83 × 10−1	2.12 × 10−1	1.15 × 10−1
	h	0	0	0	0	0	0	0
F20	Worst	−0.114 × 10−1	−0.151 × 10−1	−0.259 × 10−1	−0.213 × 10−1	−0.171 × 10−1	−0.311 × 10−1	−0.313 × 10−1
	Average	−0.197 × 10−1	−0.211 × 10−1	−0.287 × 10−1	−0.260 × 10−1	−0.217 × 10−1	−0.319 × 10−1	−0.322 × 10−1
	Best	−0.303 × 10−1	−0.262 × 10−1	−0.327 × 10−1	−0.314 × 10−1	−0.255 × 10−1	−0.331 × 10−1	−0.331 × 10−1
	STD	9.04 × 10−1	4.55 × 10−1	2.90 × 10−1	4.25 × 10−1	3.07 × 10−1	8.36 × 10−2	7.78 × 10−2
	p-value	7.56 × 10−1	1	1.36 × 10−2	1.19 × 10−1	8.27 × 10−1	8.12 × 10−4	6.63 × 10−4
	h	0	0	1	0	0	1	1
F21	Worst	−0.267 × 10−1	−0.221 × 10−1	−0.489 × 10−1	−3.51 × 10−1	−4.84 × 10−1	−0.256 × 10−1	−0.253 × 10−1
	Average	−0.612 × 10−1	−0.348 × 10−1	−0.698 × 10−1	−9.24 × 10−1	−0.201 × 10−1	−0.580 × 10−1	−0.497 × 10−1
	Best	−0.986 × 10−1	−0.467 × 10−1	−1.01 × 101	−0.293 × 10−1	−0.382 × 10−1	−1.01 × 101	−1.01 × 101
	STD	0.339 × 10−1	0.115 × 10−1	0.274 × 10−1	0.112 × 10−1	0.142 × 10−1	0.348 × 10−1	0.343 × 10−1
	p-value	1.37 × 10−1	1	3.02 × 10−2	7.44 × 10−3	1.10 × 10−1	1.94 × 10−1	3.83 × 10−1
	h	0	0	1	1	0	0	0
F22	Worst	−0.150 × 10−1	−0.303 × 10−1	−0.271 × 10−1	−5.20 × 10−1	−3.75 × 10−1	−0.364 × 10−1	−0.274 × 10−1
	Average	−0.209 × 10−1	−0.368 × 10−1	−0.666 × 10−1	−0.122 × 10−1	−9.71 × 10−1	−0.702 × 10−1	−0.494 × 10−1
	Best	−0.275 × 10−1	−0.442 × 10−1	−1.03 × 101	−0.207 × 10−1	−0.181 × 10−1	−0.980 × 10−1	−0.989 × 10−1
	STD	5.19 × 10−1	5.86 × 10−1	0.340 × 10−1	5.91 × 10−1	5.21 × 10−1	0.268 × 10−1	0.288 × 10−1
	p-value	1.89 × 10−3	1	8.86 × 10−2	1.72 × 10−4	5.68 × 10−5	2.60 × 10−2	3.63 × 10−1
	h	1	0	0	1	1	1	0
F23	Worst	−0.144 × 10−1	−0.329 × 10−1	−0.514 × 10−1	−4.06 × 10−1	−0.107 × 10−1	−0.222 × 10−1	−0.241 × 10−1
	Average	−0.377 × 10−1	−0.398 × 10−1	−0.932 × 10−1	−0.152 × 10−1	−0.262 × 10−1	−0.409 × 10−1	−0.287 × 10−1
	Best	−0.509 × 10−1	−0.470 × 10−1	−1.05 × 101	−0.453 × 10−1	−0.454 × 10−1	−0.973 × 10−1	−0.381 × 10−1
	STD	0.163 × 10−1	5.79 × 10−1	0.235 × 10−1	0.170 × 10−1	0.162 × 10−1	0.322 × 10−1	5.69 × 10−1
	p-value	7.90 × 10−1	1	1.13 × 10−3	1.56 × 10−2	1.16 × 10−1	9.45 × 10−1	1.54 × 10−2
	h	0	0	1	1	0	0	1

Table 5. Twenty-three benchmark functions are used for the Friedman ranking test for comparative approaches, with a dimension of 10.

Fun.	Algorithm
	PSO	WOA	SSA	SMA	HHO	AOA	AOACS
F1	7	5	6	3	4	2	1
F2	7	6	4	3	5	2	1
F3	6	4	5	7	3	2	1
F4	6	4	5	7	3	2	1
F5	7	3	6	5	4	1	2
F6	7	6	5	3	4	1	2
F7	4	7	5	6	3	2	1
F8	5	7	6	3	4	2	1
F9	6	4	5	7	3	2	1
F10	7	4	6	3	5	2	1
F11	6	7	5	3	4	2	1
F12	6	3	7	5	4	1	2
F13	7	4	6	5	3	1	2
F14	7	1	2	5	6	3	4
F15	7	2	3	6	5	1	4
F16	2	4	6	5	7	1	3
F17	2	3	4	6	5	7	1
F18	7	2	5	4	3	6	1
F19	7	4	2	5	6	3	1
F20	7	6	3	4	5	2	1
F21	2	5	1	7	6	3	4
F22	5	4	2	6	7	1	3
F23	4	3	1	7	6	2	5
Sum	131	98	100	115	105	51	44
Mean	5.70	4.26	4.35	5.00	4.57	2.22	1.91
Rank	6	2	3	5	4	2	1

5.2.3. Scalability Study

In this section, the effectiveness of AOACS is assessed using 13 functions from Table 1 and the 10 CEC2019 benchmark functions.

1.

Experiments on 13 benchmark functions:

The performance of AOACS is evaluated using 13 functions from Table 1 with a heightened size of 100 to determine the optimizer’s resilience as the size of the optimization issues it handles grows.

Table 6 presents the effects of the offered variant and the other techniques (PSO, WOA, SSA, SMA, HHO, and AOA) for the worst, best, average, and STD values. Additionally, Table 6 provides the P-value and null hypothesis test result for AOACS compared to the other methods using the Wilcoxon rank summation examination with a substantial difference of 0.05.

Table 6. Results from methods of comparison on 23 benchmark functions (F1–F13), where the dimension is 50.

Function	Measure	Algorithm
		PSO	WOA	SSA	SMA	HHO	AOA	AOACS
F1	Worst	3.10 × 105	1.15 × 105	3.94 × 105	3.44 × 103	1.56 × 105	4.33 × 10−6	2.33 × 10−41
	Average	2.27 × 105	1.05 × 105	2.63 × 105	1.28 × 103	1.27 × 105	1.32 × 10−6	4.66 × 10−42
	Best	1.91 × 105	9.80 × 104	1.69 × 105	1.36 × 102	9.96 × 104	7.18 × 10−17	5.83 × 10−65
	STD	4.92 × 104	6.61 × 103	9.40 × 104	1.29 × 103	2.13 × 104	1.94 × 10−6	1.04 × 10−41
	p-value	6.61 × 10−6	4.20 × 10−10	2.42 × 10−4	5.69 × 10−2	9.44 × 10−7	1	1.69 × 10−1
	h	1	1	1	0	1	0	0
F2	Worst	6.06 × 102	4.47 × 1053	1.40 × 102	0.563 × 10−1	1.50 × 103	4.07 × 10−4	1.40 × 10−16
	Average	5.30 × 102	8.94 × 1052	1.03 × 102	0.308 × 10−1	6.19 × 102	1.29 × 10−4	2.80 × 10−17
	Best	3.82 × 102	8.35 × 1043	5.81 × 101	3.37 × 10−1	3.89 × 102	5.89 × 10−7	3.36 × 10−35
	STD	9.34 × 101	2.00 × 1053	3.12 × 101	0.214 × 10−1	4.93 × 102	1.73 × 10−4	6.27 × 10−17
	p-value	1.39 × 10−6	3.47 × 10−1	8.03 × 10−5	1.24 × 10−2	2.28 × 10−2	1	0
	h	1	0	1	1	1	0	0
F3	Worst	6.01 × 106	2.75 × 106	5.01 × 106	1.75 × 107	1.47 × 106	2.40 × 106	6.37 × 10−17
	Average	4.15 × 106	1.14 × 106	3.67 × 106	1.03 × 107	1.00 × 106	1.36 × 106	1.27 × 10−17
	Best	2.22 × 106	6.02 × 105	3.00 × 106	3.78 × 106	7.71 × 105	8.11 × 101	8.96 × 10−57
	STD	1.39 × 106	9.05 × 105	8.07 × 105	5.07 × 106	3.02 × 105	9.86 × 105	2.85 × 10−17
	p-value	6.45 × 10−3	7.20 × 10−1	3.70 × 10−3	4.86 × 10−3	4.61 × 10−1	1	1.49 × 10−2
	h	1	0	1	1	0	0	1
F4	Worst	9.93 × 101	6.16 × 101	9.94 × 101	9.09 × 101	9.28 × 101	2.59 × 10−4	1.05 × 10−18
	Average	9.30 × 101	5.82 × 101	9.91 × 101	7.76 × 101	8.26 × 101	5.26 × 10−5	2.10 × 10−19
	Best	8.07 × 101	5.59 × 101	9.87 × 101	3.37 × 101	7.34 × 101	5.34 × 10−9	1.77 × 10−33
	STD	0.841 × 10−1	0.225 × 10−1	3.13 × 10−1	2.47 × 101	0.832 × 10−1	1.15 × 10−4	4.71 × 10−19
	p-value	7.67 × 10−9	8.67 × 10−12	1.80 × 10−20	1.12 × 10−4	1.80 × 10−8	1	3.38 × 10−1
	h	1	1	1	1	1	0	0
F5	Worst	1.16 × 109	2.75 × 108	2.59 × 109	2.88 × 105	3.91 × 108	1.98 × 102	1.99 × 102
	Average	5.56 × 108	1.93 × 108	2.39 × 109	1.57 × 105	1.77 × 108	1.58 × 102	1.99 × 102
	Best	2.38 × 108	1.17 × 108	2.05 × 109	7.67 × 102	6.54 × 107	0.105 × 10−1	1.99 × 102
	STD	3.67 × 108	5.86 × 107	2.05 × 108	1.30 × 105	1.32 × 108	8.78 × 101	1.40 × 10−2
	p-value	9.59 × 10−3	7.77 × 10−5	5.04 × 10−9	2.67 × 10−2	1.71 × 10−2	1	3.27 × 10−1
	h	1	1	1	1	1	0	0
F6	Worst	2.72 × 105	1.15 × 105	3.76 × 105	1.79 × 103	1.72 × 105	1.51 × 101	4.94 × 101
	Average	2.26 × 105	1.02 × 105	2.66 × 105	7.60 × 102	1.20 × 105	3.53 × 100	4.81 × 101
	Best	1.80 × 105	9.46 × 104	1.12 × 105	1.05 × 102	8.26 × 104	6.33 × 10−2	4.73 × 101
	STD	3.98 × 104	7.80 × 103	1.15 × 105	7.07 × 102	3.39 × 104	0.652 × 10−1	9.28 × 10−1
	p-value	1.38 × 10−6	1.97 × 10−9	8.65 × 10−4	4.38 × 10−2	4.80 × 10−5	1	3.57 × 10−7
	h	1	1	1	1	1	0	1
F7	Worst	4.08 × 103	1.00 × 104	1.01 × 104	1.41 × 102	1.12 × 103	5.47 × 10−2	2.21 × 10−2
	Average	1.94 × 103	9.34 × 103	6.56 × 103	3.46 × 101	9.18 × 102	1.48 × 10−2	1.24 × 10−2
	Best	4.29 × 102	8.65 × 103	4.09 × 103	2.19 × 100	6.34 × 102	5.30 × 10−4	2.16 × 10−3
	STD	1.46 × 103	6.00 × 102	2.43 × 103	5.96 × 101	2.02 × 102	2.27 × 10−2	8.80 × 10−3
	p-value	1.77 × 10−2	5.07 × 10−10	3.15 × 10−4	2.31 × 10−1	7.61 × 10−6	1.00 × 100	8.30 × 10−1
	h	1	1	1	0	1	0	0
F8	Worst	−7.26 × 103	−3.51 × 103	−6.05 × 103	−4.99 × 104	−6.34 × 103	−2.84 × 104	−2.42 × 104
	Average	−9.61 × 103	−5.16 × 103	−6.77 × 103	−5.51 × 104	−9.25 × 103	−4.74 × 104	−5.90 × 104
	Best	−1.32 × 104	−8.14 × 103	−7.99 × 103	−5.98 × 104	−1.12 × 104	−7.61 × 104	−8.33 × 104
	STD	2.26 × 103	1.89 × 103	7.39 × 102	3.61 × 103	2.57 × 103	2.00 × 104	2.44 × 104
	p-value	3.00 × 10−3	1.54 × 10−3	1.90 × 10−3	4.20 × 10−1	2.88 × 10−3	1	4.34 × 10−1
	h	1	1	1	0	1	0	0
F9	Worst	2.42 × 103	3.24 × 103	2.57 × 103	1.98 × 103	2.20 × 103	3.14 × 10−6	0
	Average	2.26 × 103	3.17 × 103	1.05 × 103	6.35 × 102	2.06 × 103	7.15 × 10−7	0
	Best	2.19 × 103	3.09 × 103	3.84 × 102	1.50 × 10−1	1.90 × 103	0	0
	STD	9.29 × 101	6.11 × 101	8.69 × 102	8.10 × 102	1.40 × 102	1.37 × 10−6	0
	p-value	1.44 × 10−11	3.38 × 10−14	2.69 × 10−2	1.18 × 10−1	8.01 × 10−10	1	2.76 × 10−1
	h	1	1	1	0	1	0	0
F10	Worst	2.00 × 101	1.86 × 101	2.09 × 101	0.472 × 10−1	1.83 × 101	1.18 × 10−4	8.88 × 10−16
	Average	1.89 × 101	1.80 × 101	1.87 × 101	0.234 × 10−1	1.77 × 101	4.16 × 10−5	8.88 × 10−16
	Best	1.83 × 101	1.75 × 101	1.35 × 101	1.90 × 10−2	1.69 × 101	3.37 × 10−7	8.88 × 10−16
	STD	7.16 × 10−1	4.39 × 10−1	0.306 × 10−1	0.222 × 10−1	6.69 × 10−1	5.44 × 10−5	0.00 × 100
	p-value	7.67 × 10−12	2.27 × 10−13	7.94 × 10−7	4.59 × 10−2	7.59 × 10−12	1	1.26 × 10−1
	h	1	1	1	1	1	0	0
F11	Worst	2.11 × 103	2.46 × 103	3.12 × 103	1.82 × 102	1.27 × 103	5.67 × 10−6	0
	Average	1.61 × 103	2.29 × 103	2.22 × 103	4.26 × 101	1.15 × 103	1.14 × 10−6	0
	Best	6.87 × 102	2.17 × 103	7.28 × 102	0.125 × 10−1	1.06 × 103	6.66 × 10−16	0
	STD	5.94 × 102	1.28 × 102	9.58 × 102	7.82 × 101	8.29 × 101	2.53 × 10−6	0
	p-value	3.06 × 10−4	1.65 × 10−10	8.50 × 10−4	2.58 × 10−1	1.30 × 10−9	1	3.46 × 10−1
	h	1	1	1	0	1	0	0
F12	Worst	9.71 × 108	8.83 × 107	6.94 × 109	3.29 × 107	5.27 × 108	2.75 × 10−2	0.347 × 10−1
	Average	5.21 × 108	6.96 × 107	5.60 × 109	6.90 × 106	2.57 × 108	9.13 × 10−3	0.144 × 10−1
	Best	2.13 × 108	4.81 × 107	4.79 × 109	4.74 × 10−1	1.16 × 108	1.33 × 10−3	8.87 × 10−2
	STD	3.17 × 108	1.71 × 107	8.83 × 108	1.46 × 107	1.62 × 108	1.07 × 10−2	0.124 × 10−1
	p-value	6.24 × 10−3	1.71 × 10−5	5.97 × 10−7	3.20 × 10−1	7.54 × 10−3	1	3.26 × 10−2
	h	1	1	1	0	1	0	1
F13	Worst	1.62 × 109	5.92 × 108	1.29 × 1010	1.50 × 108	1.14 × 109	0.367 × 10−1	2.00 × 101
	Average	1.19 × 109	3.66 × 108	1.04 × 1010	3.70 × 107	6.67 × 108	0.103 × 10−1	1.73 × 101
	Best	1.72 × 108	1.97 × 108	8.31 × 109	6.51 × 102	1.08 × 108	1.77 × 10−2	0.660 × 10−1
	STD	6.06 × 108	1.64 × 108	1.70 × 109	6.36 × 107	3.92 × 108	0.151 × 10−1	0.598 × 10−1
	p-value	2.27 × 10−3	1.07 × 10−3	8.07 × 10−7	2.29 × 10−1	5.23 × 10−3	1	3.63 × 10−4
	h	1	1	1	0	1	0	1

The statistics from Table 6 show how stable and effective the suggested AOACS is because it offers the best answers for all six functions (F1, F2, F3, F4, F9, and F11). In addition, compared to the other algorithms, it produces the most comparable outcomes for the best solutions of the other methods (F5, F6, F7, F8, F10). For 85% of the examined functions, the stated P-values are smaller than 0.05. AOACS is highly stable and superior for handling situations with high dimensions.

Table 7 computes the Friedman ranking test to highlight the noteworthiness of the suggested AOACS. The AOACS has the top rankings in nine of the thirteen benchmark functions that were analyzed as problems; as a result, it finally occupies the top spot in the queue of other high-dimensional problem-solving strategies. With an average rank almost as high as AOACS’s, unmodified AOA holds down the second spot. As a result, AOA offers higher-quality solutions for high-dimensional issues than modern state-of-the-art approaches.

Table 7. Thirteen benchmark functions are used for the Friedman ranking test for comparative approaches, with a dimension of 50.

Fun.	Algorithm
	PSO	WOA	SSA	SMA	HHO	AOA	AOACS
F1	6	4	7	3	5	2	1
F2	5	7	4	3	6	2	1
F3	6	3	5	7	2	4	1
F4	6	3	7	4	5	2	1
F5	6	5	7	3	4	1	2
F6	6	4	7	3	5	1	2
F7	5	7	6	3	4	2	1
F8	4	7	6	2	5	3	1
F9	6	7	4	3	5	2	1
F10	7	5	6	3	4	2	1
F11	5	7	6	3	4	2	1
F12	6	4	7	3	5	1	2
F13	6	4	7	3	5	1	2
Sum	74	67	79	43	59	25	17
Mean	5.69	5.15	6.08	3.31	4.54	1.92	1.31
Rank	6	5	7	3	4	2	1

Figure 6 compares the proposed AOACS’s convergence curves to the original AOA and cutting-edge methods to evaluate the effectiveness of the AOACS’s exploration and exploitation. In contrast to the WOA, PSO, SSA, SMA, and HHO, which experienced severe recession at the local optimal solutions, the curves demonstrate the soft convergence of the AOACS by reaching superior quality solutions.

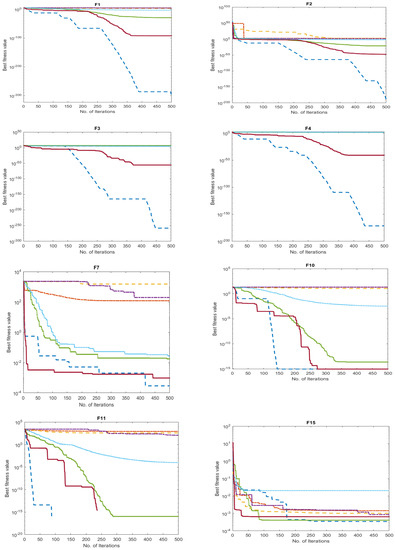
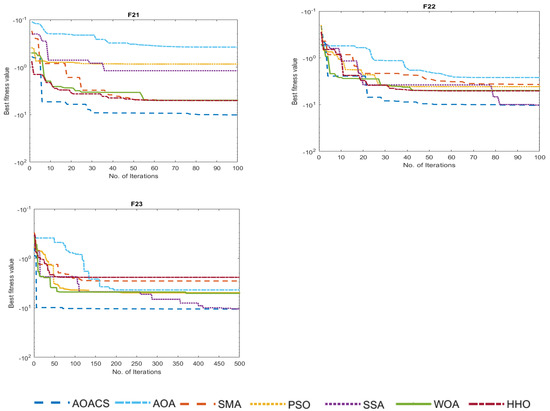
Figure 6. Comparison of methods’ behavior regarding convergence on the test functions (F1–F4, F7, F10, F11, F15, F21–F23), where dimension 10 is present.

2.

Experiments on 10 CEC2019 benchmark functions.

The translation trajectory function, the translation trajectory Schwefel function, the translation trajectory Lunacek double grating function, and the comprehensive Rosenbrock plus Griewangk function are the CEC1 through CEC4 test functions for CEC2020. These functions are divided into mixed functions (CEC5–CEC7) and compound functions (CEC8–CEC10). The best value, average value, and standard deviation for each algorithm were determined after 30 independent runs.

The output of each algorithm for each test function in the CEC2019 is shown in Table 8. The table shows that, regardless of the ideal or average value, the AOACS algorithm produced the best results in 10 benchmark functions and seven of the best outcomes. This demonstrates the AOACS algorithm’s powerful optimization impact. The AOACS algorithm was less stable than most other algorithms for CEC3, CEC8, and CEC9, but it was still better for STD in terms of numerical value.

Table 8. Results from methods of comparison on 2019 benchmark functions (F1–F10).

Function	Measure	Algorithm
		PSO	WOA	SSA	SMA	HHO	AOA	AOACS
CEC−1	Best	1.81 × 1012	6.00 × 1013	3.11 × 1012	4.03 × 108	1.78 × 1012	2.15 × 1011	1.61 × 106
	Average	7.75 × 1011	2.19 × 1013	9.46 × 1011	8.10 × 107	7.64 × 1011	7.88 × 1010	6.70 × 105
	Worst	1.88 × 1011	2.95 × 1012	1.23 × 1011	7.83 × 104	6.40 × 1010	1.94 × 1010	1.36 × 105
	STD	6.72 × 1011	2.22 × 1013	1.23 × 1012	1.80 × 108	7.85 × 1011	8.00 × 1010	5.89 × 105
	p-value	3.27 × 10−2	5.87 × 10−2	1.24 × 10−1	1.00 × 100	6.13 × 10−2	5.91 × 10−2	3.48 × 10−1
	h	1	0	0	0	0	0	0
CEC−2	Best	1.54 × 103	3.00 × 104	1.43 × 102	1.82 × 101	8.88 × 103	1.96 × 102	1.93 × 101
	Average	4.41 × 102	2.38 × 104	6.98 × 101	1.77 × 101	4.51 × 103	8.25 × 101	1.82 × 101
	Worst	3.97 × 101	1.56 × 104	1.97 × 101	1.74 × 101	6.72 × 102	3.02 × 101	1.75 × 101
	STD	6.27 × 102	7.27 × 103	5.72 × 101	3.29 × 10−1	3.31 × 103	6.79 × 101	7.53 × 10−1
	p-value	1.69 × 10−1	8.22 × 10−5	7.56 × 10−2	1	1.62 × 10−2	6.55 × 10−2	1.79 × 10−1
	h	0	1	0	0	1	0	0
CEC−3	Best	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101
	Average	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101
	Worst	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101	1.27 × 101
	STD	1.33 × 10−3	5.29 × 10−4	9.19 × 10−4	3.52 × 10−4	2.78 × 10−3	1.74 × 10−3	1.12 × 10−3
	p-value	7.92 × 10−3	4.87 × 10−1	7.25 × 10−3	1.00 × 100	2.25 × 10−1	1.82 × 10−1	1.97 × 10−1
	h	1	0	1	0	0	0	0
CEC−4	Best	1.14 × 104	1.53 × 104	1.48 × 104	3.00 × 104	1.70 × 104	5.07 × 103	5.16 × 103
	Average	8.61 × 103	1.10 × 104	9.93 × 103	1.73 × 104	1.24 × 104	4.18 × 103	3.84 × 103
	Worst	3.42 × 103	7.25 × 103	3.68 × 103	6.73 × 103	4.36 × 103	3.54 × 103	2.32 × 103
	STD	3.29 × 103	3.24 × 103	4.79 × 103	9.86 × 103	4.74 × 103	6.80 × 102	1.04 × 103
	p-value	9.96 × 10−2	2.15 × 10−1	1.73 × 10−1	1	3.46 × 10−1	1.81 × 10−2	1.64 × 10−2
	h	0	0	0	0	0	1	1
CEC−5	Best	0.521 × 10−1	0.466 × 10−1	0.787 × 10−1	0.666 × 10−1	0.973 × 10−1	0.324 × 10−1	0.359 × 10−1
	Average	0.454 × 10−1	0.367 × 10−1	0.528 × 10−1	0.594 × 10−1	0.539 × 10−1	0.260 × 10−1	0.318 × 10−1
	Worst	0.400 × 10−1	0.265 × 10−1	0.336 × 10−1	0.528 × 10−1	0.336 × 10−1	0.200 × 10−1	0.200 × 10−1
	STD	4.89 × 10−1	8.49 × 10−1	0.189 × 10−1	5.94 × 10−1	0.262 × 10−1	5.09 × 10−1	6.68 × 10−1
	p-value	3.59 × 10−3	1.20 × 10−3	4.81 × 10−1	1	6.62 × 10−1	1.20 × 10−5	1.27 × 10−4
	h	1	1	0	0	0	1	1
CEC−6	Best	1.53 × 101	1.43 × 101	1.34 × 101	1.52 × 101	1.38 × 101	1.56 × 101	1.49 × 101
	Average	1.42 × 101	1.31 × 101	1.23 × 101	1.33 × 101	1.21 × 101	1.38 × 101	1.27 × 101
	Worst	1.37 × 101	1.19 × 101	1.07 × 101	1.10 × 101	1.02 × 101	1.29 × 101	1.06 × 101
	STD	6.34 × 10−1	8.80 × 10−1	0.138 × 10−1	0.172 × 10−1	0.144 × 10−1	0.110 × 10−1	0.168 × 10−1
	p-value	3.24 × 10−1	7.87 × 10−1	3.38 × 10−1	1	2.52 × 10−1	6.52 × 10−1	5.91 × 10−1
	h	0	0	0	0	0	0	0
CEC−7	Best	1.65 × 103	1.12 × 103	1.87 × 103	1.87 × 103	1.96 × 103	1.97 × 103	9.70 × 102
	Average	1.53 × 103	8.71 × 102	1.56 × 103	1.33 × 103	1.47 × 103	1.37 × 103	6.03 × 102
	Worst	1.38 × 103	6.45 × 102	1.25 × 103	6.71 × 102	1.07 × 103	6.12 × 102	1.84 × 102
	STD	1.07 × 102	2.14 × 102	2.62 × 102	4.47 × 102	3.33 × 102	5.81 × 102	3.46 × 102
	p-value	3.72 × 10−1	7.04 × 10−2	3.58 × 10−1	1	6.04 × 10−1	9.18 × 10−1	2.03 × 10−2
	h	0	0	0	0	0	0	1
CEC−8	Best	0.816 × 10−1	0.757 × 10−1	0.840 × 10−1	0.764 × 10−1	0.769 × 10−1	0.795 × 10−1	0.781 × 10−1
	Average	0.763 × 10−1	0.710 × 10−1	0.761 × 10−1	0.709 × 10−1	0.689 × 10−1	0.723 × 10−1	0.684 × 10−1
	Worst	0.703 × 10−1	0.622 × 10−1	0.658 × 10−1	0.581 × 10−1	0.614 × 10−1	0.676 × 10−1	0.615 × 10−1
	STD	4.54 × 10−1	5.13 × 10−1	7.60 × 10−1	7.38 × 10−1	5.77 × 10−1	4.67 × 10−1	6.32 × 10−1
	p-value	2.02 × 10−1	9.76 × 10−1	3.03 × 10−1	1	6.59 × 10−1	7.20 × 10−1	5.93 × 10−1
	h	0	0	0	0	0	0	0
CEC−9	Best	2.05 × 103	2.19 × 103	3.55 × 103	3.92 × 103	3.73 × 103	3.15 × 103	7.79 × 102
	Average	1.29 × 103	1.03 × 103	2.86 × 103	3.24 × 103	2.20 × 103	1.08 × 103	3.50 × 102
	Worst	4.92 × 102	2.60 × 102	2.35 × 103	1.55 × 103	4.66 × 102	5.46 × 101	6.60 × 101
	STD	5.84 × 102	7.93 × 102	5.24 × 102	9.72 × 102	1.19 × 103	1.26 × 103	3.01 × 102
	p-value	4.93 × 10−3	4.39 × 10−3	4.73 × 10−1	1	1.70 × 10−1	1.66 × 10−2	2.23 × 10−4
	h	1	1	0	0	0	1	1
CEC−10	Best	2.11 × 101	2.10 × 101	2.08 × 101	2.09 × 101	2.10 × 101	2.10 × 101	2.09 × 101
	Average	2.08 × 101	2.08 × 101	2.07 × 101	2.07 × 101	2.07 × 101	2.09 × 101	2.06 × 101
	Worst	2.07 × 101	2.06 × 101	2.04 × 101	2.05 × 101	2.04 × 101	2.06 × 101	2.04 × 101
	STD	1.83 × 10−1	1.65 × 10−1	2.00 × 10−1	1.34 × 10−1	2.19 × 10−1	1.55 × 10−1	1.75 × 10−1
	p-value	2.45 × 10−1	2.53 × 10−1	6.77 × 10−1	1.00 × 100	7.75 × 10−1	1.37 × 10−1	3.06 × 10−1
	h	0	0	0	0	0	0	0

The Friedman ranking test is computed in Table 9 to show how noteworthy the suggested AOACS are. The AOACS finally holds the top position in the queue of other high-dimensional problem-solving strategies since it has the highest rankings in six of the ten benchmark functions that were analyzed for problems. Unmodified AOA takes the runner-up position with an average rank nearly as high as AOACS’s.

Table 9. Ten benchmark functions are used for the Friedman ranking test for comparative approaches.

Function	Algorithm
	PSO	WOA	SSA	SMA	HHO	AOA	AOACS
cec01	6	4	5	2	7	3	1
cec02	3	6	5	1	7	4	2
cec03	5	6	7	1	2	4	3
cec04	4	6	3	7	5	2	1
cec05	5	6	4	7	3	1	2
cec06	2	1	7	5	4	6	3
cec07	7	5	6	3	2	4	1
cec08	6	2	7	3	4	5	1
cec09	6	5	4	7	2	3	1
cec10	2	3	6	4	5	7	1
Sum	46	44	54	40	41	39	16
Mean	4.6	4.4	5.4	4.0	4.1	3.9	1.6
Rank	6	5	7	3	4	2	1

6. AOACS for Solving Real Word Engineering Optimization Problems

This section uses the suggested algorithm to resolve four engineering design issues: the welded beam, the three-bar truss, the stepped cantilever beam, and the speed reducer design. A set of 30 solutions and 500 iterations are employed in each run to solve these issues.

The acquired results are contrasted with some related methods described in the literature. The results of the presented AOACS are contrasted with those of the most recent techniques in the subsections that follow. In order to assess the effectiveness of the suggested AOACS, bound-constrained and generally constrained optimization problems are used in this study. Each pattern variable is frequently required to give a boundary restriction for the bound-constrained optimization problems:

$$l{b}_j \le x_{ij} \le u{b}_j, j=1,2,3,\dots ,n$$

(5)

where $n$ is the total number of places given, and $l{b}_j$ and $u{b}_j$ stand for the position’s lower and upper bounds, respectively. Additionally, a general constrained problem is typically formulated as:

$$\begin{gathered} \mathit{m}\mathit{i}\mathit{n} \mathit{f}\left(\mathit{x}\right) \\ X=\left\{x_{11},x_{1j},x_{1j},\dots ,x_{1n}\right\} \\ subject to \\ {g}_i\left(x\right)\le 0, j=1,2,3,\dots ,k \\ {s}_t\left(X\right)=0,t=1,2,\dots ,p \end{gathered}$$

(6)

where there are p equilibrium constraints, and k different types of constraints. All of the constrained optimization issues in Equation (6) are mapped into the bound-constrained design in the performance evaluation of the proposed AOA by using the static cost function. A cost function will be incorporated into the underlying objective function for any infeasible solution. The static cost function is streamlined for ease of employment, and it is appropriate for all kinds of issues and calls for an auxiliary cost function. The aforementioned constrained optimization problem can be expressed as follows:

$$f\left(X\right)=f\left(x\right){\displaystyle \sum }_{j=1}^m\mu e_{p}max\left\{g_i\left(X\right),0\right\}+{\displaystyle \sum }_{t=1}^n\mu e_t\left\{\left|S_t\left(X\right)-\delta \right|,0\right\}$$

(7)

where $\mu e_p$ and $\mu e_t$ are typically charged a high amount; $\delta$ is the inaccuracy of equilibrium constraints and in this paper, we set it to ${10}^{-6}$. In optimization problems, constraints are used to restrict the values that the variables can take on. By properly handling constraints, we can find the optimal values of the variables that satisfy the constraints and obtain meaningful solutions to real-world problems [40].

Real word engineering design issues comprise nonlinear optimization problems attended by numerous complicated constraints and geometry. The proposed AOACS method is implemented in four issues (the welded beam design problem, the three-bar truss design problem, the stepped cantilever beam design, and the speed reducer design) to demonstrate how well it performs in optimization situations related to engineering problems. The proposed AOACS simulation is set as follows: the maximum iterations number is 200, the population size is set to 30, and the simulation runs 20 times. These details are well known to solve this kind of problem.

6.1. Welded Beam

One of the considerably well-known problem studies to assess algorithms’ effectiveness is the welded beam design problem. It was first put forth in [41] and sought to decrease the overall fabricating value of a welded beam by using four decision variables, as shown in Figure 7. These variables are the weld thickness (h), the joint beam’s length (l), its height (t), and its thickness (b).

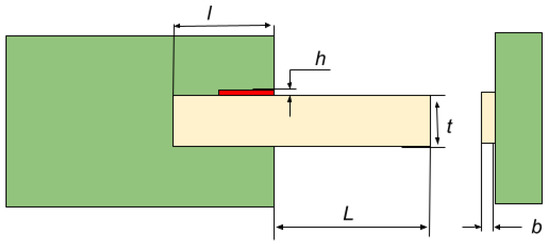
Figure 7. Welded beam.

The problem’s mathematical formulation and constraint functions are as follows:

Consider

$$\overrightarrow{\mathsf{\lambda }}=\left[{\mathsf{\lambda }}_1,{\mathsf{\lambda }}_2,{\mathsf{\lambda }}_3,{\mathsf{\lambda }}_4\right]=\left[h,l,t,b\right]$$

Minimize

$$f\left(\overrightarrow{\mathsf{\lambda }}\right)=1.10471{\mathsf{\lambda }}_1^2{\mathsf{\lambda }}_2+0.04811{\mathsf{\lambda }}_3{\mathsf{\lambda }}_4\left(14.0+{\mathsf{\lambda }}_2\right)$$

Subject to

$$g1\left(\overrightarrow{\mathsf{\lambda }}\right)=\mathsf{\tau }\left(\mathsf{\lambda }\right)-{\mathsf{\tau }}_{max}\le 0$$

$$g2\left(\overrightarrow{\mathsf{\lambda }}\right)=\mathsf{\sigma }-{\mathsf{\sigma }}_{max}\le 0$$

$$g3\left(\overrightarrow{\mathsf{\lambda }}\right)=\mathsf{\delta }-{\mathsf{\delta }}_{max}\le 0$$

$$g4\left(\overrightarrow{\mathsf{\lambda }}\right)={\mathsf{\lambda }}_1-{\mathsf{\lambda }}_4\le 0\le 0$$

$$g5\left(\overrightarrow{\mathsf{\lambda }}\right)=P-P_C\left(\overrightarrow{\mathsf{\lambda }}\right)\le 0$$

$$g6\left(\overrightarrow{\mathsf{\lambda }}\right)=0.125-{\mathsf{\lambda }}_1\le 0$$

$$g7\left(\overrightarrow{\mathsf{\lambda }}\right)=1.10471{\mathsf{\lambda }}_1^2+0.04811{\mathsf{\lambda }}_3{\mathsf{\lambda }}_4\left(14+{\mathsf{\lambda }}_2\right)-5\le 0$$

Variable range

$$0.1\le {\mathsf{\lambda }}_1,{\mathsf{\lambda }}_2\le 2,0.1\le {\mathsf{\lambda }}_2,{\mathsf{\lambda }}_3\le 10$$

where

$$\mathsf{\tau }\left(\overrightarrow{\mathsf{\lambda }}\right)=\sqrt{{\left( {\mathsf{\tau }}^{\prime }\right)}^2+2 {\mathsf{\tau }}^{\prime } {\mathsf{\tau }}^{″}\frac{{\mathsf{\lambda }}_2}{2R}+{\left( {\mathsf{\tau }}^{″}\right)}^2}, {\mathsf{\tau }}^{\prime }=\frac{P}{\sqrt{2}{\mathsf{\lambda }}_1{\mathsf{\lambda }}_2}, {\mathsf{\tau }}^{\prime }=\frac{MR}{J},M=P\left(L+\frac{{\mathsf{\lambda }}_2}{2}\right)$$

$$R=\sqrt{\frac{{\mathsf{\lambda }}_1^2}{4}+{\left(\frac{{\mathsf{\lambda }}_1+{\mathsf{\lambda }}_3}{2}\right)}^2},J=2\left\{\sqrt{2}{\mathsf{\lambda }}_1{\mathsf{\lambda }}_2\left[\frac{{\mathsf{\lambda }}_2^2}{4}+{\left(\frac{{\mathsf{\lambda }}_1+{\mathsf{\lambda }}_3}{2}\right)}^2\right]\right\},$$

$$\mathsf{\sigma }\left(\overrightarrow{\mathsf{\lambda }}\right)=\frac{6PL}{E{\mathsf{\lambda }}_3^2{\mathsf{\lambda }}_4}, \mathsf{\delta }\left(\overrightarrow{\mathsf{\lambda }}\right)=\frac{6{\mathrm{PL}}^3}{{\mathrm{E}\mathsf{\lambda }}_3^2{\mathsf{\lambda }}_4},$$

$$P_C\left(\overrightarrow{\mathsf{\lambda }}\right)=\frac{4.013E\sqrt{\frac{{\mathsf{\lambda }}_3^2{\mathsf{\lambda }}_4^6}{36}}}{L^2}\left(1-\frac{z_3}{2L}\sqrt{\frac{E}{4G}}\right)$$

$${\mathsf{\sigma }}_{max}=3000psi,{ \mathsf{\delta }}_{max}=0.25in,{ \mathsf{\tau }}_{max}=30,000psi.$$

$$E=30\times {10}^{6}psi, G=12\times {10}^{6}psi$$

$$L=14in, P=6000lb,$$

The proposed AOACS is implemented on the welded beam problem, and the result is compared with other metaheuristic approaches such as AOA, HHO, SSA, WOA, PSO, and SMA. Table 10 shows the achieved results; the variables h, l, t, and b are set as 1.96 × 10⁻¹, 0.335 × 10⁻¹, 0.904 × 10⁻¹, and 2.06 × 10⁻¹, respectively, and the optimal manufacturing cost of AOACS is 1.96 × 10⁻¹. In this comparison, it is clear that AOACS produces better outcomes than all the other techniques. This demonstrates that AOACS is competitive in solving the welded beam design challenge.

Table 10. Comparison of the achieved outcomes of different algorithms when solving the welded beam problem.

Algorithm	Optimal Estimated Values				Optimal Cost
	$\mathbf{h} \left({\mathit{\lambda }}_1\right)$	$\mathbf{l} ({\mathit{\lambda }}_2)$	$\mathbf{t} ({\mathit{\lambda }}_3)$	$\mathbf{b} ({\mathit{\lambda }}_4)$
HHO	2.05 × 10−1	0.348 × 10−1	0.904 × 10−1	2.06 × 10−1	1.730
AOA	1.94 × 10−1	0.257 × 10−1	0.100 × 10−1	2.02 × 10−1	1.720
WOA	2.05 × 10−1	0.347 × 10−1	0.904 × 10−1	2.06 × 10−1	1.730
SSA	2.06 × 10−1	0.348 × 10−1	0.904 × 10−1	2.06 × 10−1	1.730
PSO	2.00 × 10−1	0.337 × 10−1	0.901 × 10−1	2.07 × 10−1	1.710
SMA	2.08 × 10−1	0.323 × 10−1	0.899 × 10−1	2.08 × 10−1	1.700
AOACS	1.96 × 10−1	0.335 × 10−1	0.904 × 10−1	2.06 × 10−1	1.690

6.2. Three-Bar Truss

The three-bar truss design’s optimization goal is to reduce overall weight. Figure 8 depicts the three-bar truss construction together with its primary parameters, element 1’s cross-sectional site (X1) and element 2’s cross-sectional site (X2). Buckling, deflection, and stress are further limits on the issue.

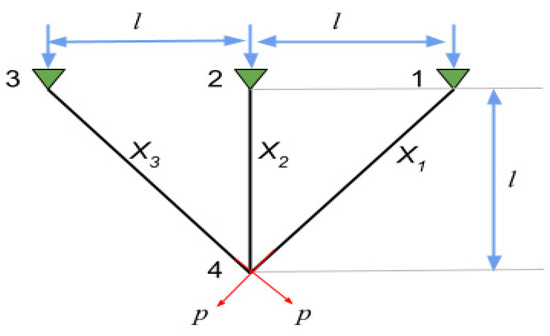
Figure 8. Three-Bar Truss Design.

The mathematical formulation is expressed as follows:

Consider

$$\overrightarrow{\mathsf{\lambda }}=\left[{\mathsf{\lambda }}_1,{\mathsf{\lambda }}_2\right]=\left[X_1,X_2\right]$$

Minimize

$$f\left(\overrightarrow{\mathsf{\lambda }}\right)=\left(2\sqrt{2}{\mathsf{\lambda }}_1+{\mathsf{\lambda }}_2\right)\times l$$

Subject to

$$g1\left(\overrightarrow{\mathsf{\lambda }}\right)=\frac{\sqrt{2}{\mathsf{\lambda }}_1+{\mathsf{\lambda }}_2}{\sqrt{2}{\mathsf{\lambda }}_1^2+2{\mathsf{\lambda }}_1{\mathsf{\lambda }}_2}P-\mathsf{\sigma }\le 0$$

$$g2\left(\overrightarrow{\mathsf{\lambda }}\right)=\frac{{\mathsf{\lambda }}_2}{\sqrt{2}{\mathsf{\lambda }}_1^2+2{\mathsf{\lambda }}_1{\mathsf{\lambda }}_2}P-\mathsf{\sigma }\le 0$$

$$g3\left(\overrightarrow{\mathsf{\lambda }}\right)=\frac{1}{\sqrt{2}{\mathsf{\lambda }}_2+{\mathsf{\lambda }}_1}P-\mathsf{\sigma }\le 0$$

Variable range

$$0\le {\mathsf{\lambda }}_1,{\mathsf{\lambda }}_2\le 1$$

where

$$\sigma =2 \mathrm{KN}/{\mathrm{cm}}^2, l=100 \mathrm{cm}, P=2 \mathrm{KN}/{\mathrm{cm}}^2$$

Table 11 shows the performance of several algorithms, such as HHO, AOA, WOA, SSA, PSO, SMA, and the proposed AOACS algorithm for solving the problem of the three-bar truss design problem. The results demonstrate that the AOACS algorithm indicates an outperformance compared to other algorithms. The minimum weight is 2.6387 × 10², and the optimal values for X1(${\lambda }_1$) and X2(${\lambda }_2$) are 7.8859 × 10⁻¹ and 4.0825 × 10⁻¹, respectively. Thus, the AOACS has the promising prospect of solving such an issue with a minimal search area.

Table 11. The achieved outcomes of several algorithms when solving the three-bar truss optimization issue.

Algorithm	Optimal Estimated Values		Lowest Weight
	$\mathbf{X}1 \left({\mathit{\lambda }}_1\right)$	$\mathbf{X}2 \left({\mathit{\lambda }}_2\right)$
HHO	7.8867 × 10−1	4.0828 × 10−1	2.6390 × 102
AOA	7.9369 × 10−1	3.9426 × 10−1	2.6392 × 102
WOA	7.8866 × 10−1	4.0828 × 10−1	2.6390 × 102
SSA	7.8860 × 10−1	4.0845 × 10−1	2.6390 × 102
PSO	7.8867 × 10−1	4.0826 × 10−1	2.6390 × 102
SMA	7.8890 × 10−1	4.0762 × 10−1	2.6390 × 102
AOACS	7.8859 × 10−1	4.0825 × 10−1	2.6387 × 102

6.3. Stepped Cantilever Beam Design

As depicted in Figure 9, a stepped cantilever beam is kept at one end and loaded at the other. At a predetermined distance from the support, the beam must be capable of supporting the specified load. Each section’s width ($\lambda$) can be altered by the beam’s designers. We assume that the length of each part of the cantilever is the same. The cantilever’s weight must be kept to a minimum in order to solve the cantilever beam design problem.

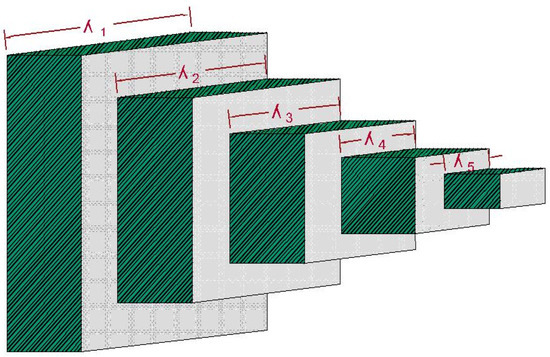
Figure 9. Stepped Cantilever Beam Design.

The problem’s mathematical formulation and constraint functions are as follows:

Consider:

$$\lambda =\left[{\lambda }_1{\lambda }_2{\lambda }_3{\lambda }_4{\lambda }_5\right]$$

Minimize:

$$f\left(x\right)=0.0624\left({\lambda }_1+{\lambda }_2+{\lambda }_3+{\lambda }_4+{\lambda }_5\right)$$

Subject to:

$$g\left(x\right)=\frac{61}{{\lambda }_1^3}+\frac{37}{{\lambda }_2^3}+\frac{19}{{\lambda }_3^3}+\frac{7}{{\lambda }_4^3}+\frac{1}{{\lambda }_5^3}-1\le 0$$

Variable range:

$$0.01\le {\lambda }_i\le 100\left(i=1,2,\dots 5\right)$$

Table 12 displays the test findings for the cantilever beam design issue. The table shows that the weight acquired by the AOACS algorithm was the best weight (0.134 × 10⁻¹) when compared to the HHO, WOA, SSA, PSO, and SMA algorithms, demonstrating the AOACS algorithm’s viability and efficiency in addressing the cantilever beam design problem.

Table 12. The achieved outcomes of several algorithms when solving the stepped cantilever beam design issue.

Algorithm	Optimal Estimated Values					Lowest Weight
	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$	${\mathit{\lambda }}_4$	${\mathit{\lambda }}_5$
HHO	0.513 × 10−1	0.562 × 10−1	0.510 × 10−1	0.393 × 10−1	0.232 × 10−1	0.138 × 10−1
AOA	0.621 × 10−1	0.621 × 10−1	0.621 × 10−1	0.621 × 10−1	0.621 × 10−1	0.194 × 10−1
WOA	0.600 × 10−1	0.530 × 10−1	0.449 × 10−1	0.351 × 10−1	0.217 × 10−1	0.134 × 10−1
SSA	0.561 × 10−1	0.496 × 10−1	0.566 × 10−1	0.320 × 10−1	0.320 × 10−1	0.141 × 10−1
PSO	0.605 × 10−1	0.526 × 10−1	0.451 × 10−1	0.346 × 10−1	0.219 × 10−1	0.134 × 10−1
SMA	0.511 × 10−1	0.599 × 10−1	0.502 × 10−1	0.371 × 10−1	0.327 × 10−1	0.144 × 10−1
AOACS	0.601 × 10−1	0.531 × 10−1	0.449 × 10−1	0.350 × 10−1	0.215 × 10−1	0.134 × 10−1

6.4. Speed Reducer Design

The tooth surface width ${\lambda }_1$, gear module ${\lambda }_2$, the number of teeth on the pinion ${\lambda }_3$, the length of the first shaft between bearings ${\lambda }_4$, the length of the second shaft between bearings ${\lambda }_5$, the diameter of the first shaft ${\lambda }_6$, and the diameter of the second shaft ${\lambda }_7$ are the seven variables in the reducer design problem. In Figure 10, the variable diagram is displayed. The reducer design problem aims to determine the reducer’s smallest weight while adhering to four design restrictions. The four design limitations are stress in the shaft, lateral shaft deflection, stress on the shaft, and bending stress on the gear teeth.

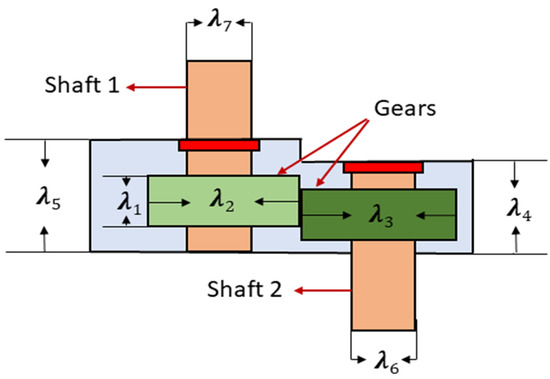
Figure 10. Speed Reducer Design.

The problem’s mathematical formulation and constraint functions are as follows:

Consider:

$$\lambda =\left[{\lambda }_1{\lambda }_2{\lambda }_3{\lambda }_4{\lambda }_5{\lambda }_6{\lambda }_7\right]$$

Minimize:

$$\begin{gathered} f\left(\overrightarrow{\lambda }\right)=07854\times {\lambda }_1\times {\lambda }_2^2\times \left(3.3333\times {\lambda }_3^2+14.9334\times {\lambda }_3-43.0934\right)-1.508\times {\lambda }_1\times \left({\lambda }_6^2+{\lambda }_7^2\right)+ \\ 7.4777\times {\lambda }_6^3+{\lambda }_7^3+0.7854\times {\lambda }_4\times {\lambda }_6^2+{\lambda }_5\times {\lambda }_7^2 \end{gathered}$$

Subject to:

$$g_1\left(\overrightarrow{\lambda }\right)=\frac{27}{{\lambda }_1\times {\lambda }_2^2\times {\lambda }_3}-1\le 0$$

$$g_2\left(\overrightarrow{\lambda }\right)=\frac{397.5}{{\lambda }_1\times {\lambda }_2^2\times {\lambda }_3^2}-1\le 0$$

$$g_3\left(\overrightarrow{\lambda }\right)=\frac{1.93\times {\lambda }_4^3}{{\lambda }_2\times {\lambda }_3\times {\lambda }_6^4}-1\le 0$$

$$g_4\left(\overrightarrow{\lambda }\right)=\frac{1.93\times {\lambda }_5^3}{{\lambda }_2\times {\lambda }_3\times {\lambda }_7^4}-1\le 0$$

$$g_5\left(\overrightarrow{\lambda }\right)=\frac{1}{110\times {\lambda }_6^3}\sqrt{{\left(\frac{745\times {\lambda }_4}{{\lambda }_2\times {\lambda }_3}\right)}^2+16.9\times {10}^6}-1\le 0$$

$$g_6\left(\overrightarrow{\lambda }\right)=\frac{1}{85\times {\lambda }_7^3}\sqrt{{\left(\frac{745\times {\lambda }_5}{{\lambda }_2\times {\lambda }_3}\right)}^2+16.9\times {10}^6}-1\le 0$$

$$g_7\left(\overrightarrow{\lambda }\right)=\frac{{\lambda }_2\times {\lambda }_3}{40}-1\le 0$$

$$g_8\left(\overrightarrow{\lambda }\right)=\frac{5\times {\lambda }_2}{{\lambda }_1}-1\le 0$$

$$g_9\left(\overrightarrow{\lambda }\right)=\frac{{\lambda }_1}{12\times {\lambda }_2}-1\le 0$$

$$g_{10}\left(\overrightarrow{\lambda }\right)=\frac{1.5\times {\lambda }_6+1.9}{{\lambda }_4}-1\le 0$$

$$g_{11}\left(\overrightarrow{\lambda }\right)=\frac{1.1\times {\lambda }_7+1.9}{{\lambda }_5}-1\le 0$$

Variable range:

$$\begin{gathered} 2.6\le {\lambda }_1\le 3.6,0.7\le {\lambda }_2\le 0.8,17\le {\lambda }_3\le 28,7.3\le {\lambda }_4\le 8.3,7.3\le {\lambda }_5\le \\ 8.3,2.9\le {\lambda }_6\le 3.9,5{\lambda }_7\le 5.5 \end{gathered}$$

The results of the AOACS and the compared methods are listed in Table 13. From this table, the AOACS is ranked first and outperformed all methods in solving this problem, whereas the SMA is ranked second, followed by PSO, AOA, and HHO, respectively.

Table 13. The achieved outcomes of several algorithms when solving the speed reducer issue.

Algorithm	Optimal Estimated Values							Lowest Weight
	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$	${\mathit{\lambda }}_4$	${\mathit{\lambda }}_5$	${\mathit{\lambda }}_6$	${\mathsf{\lambda }}_7$
HHO	3.606129	0.7	17	7.2	7.98141	3.462569	5.296749	3028.873076
AOA	3.5	0.7	17	7.2	7.680396	3.552421	5.255814	3020.583365
WOA	3.518765	0.7	17	7.2	7.9	3.45102	5.299213	3031.563
SSA	3.530134	0.7	17	8.36	7.9	3.37697	5.298719	3030.002
PSO	3.537485	0.7002	17	7.729684	8.090954	3.361512	5.297051	3011.137492
SMA	3.526152	0.700005	17	7.559136	7.95833	3.375576	5.299773	3009.08
AOACS	3.5032	0.7	17	7.2198	7.7375	3.3741	5.2994	3007.7328

This work presents an innovative optimization algorithm for solving engineering design problems. The performance of the proposed algorithm is evaluated using several benchmark functions and compared with other state-of-the-art optimization algorithms. Here is a brief discussion of the results obtained in the study. The results demonstrate that the proposed algorithm outperforms other optimization algorithms in terms of solution quality and convergence speed. The proposed algorithm is more efficient in finding the global optimum and has a faster convergence rate compared to the other algorithms. The study also presents a comparison between the standard cuckoo search algorithm and the proposed algorithm, which shows that the proposed algorithm performs better than the standard cuckoo search algorithm in terms of solution quality and convergence speed. The proposed algorithm achieves a better balance between exploration and exploitation of the solution space, leading to improved optimization performance. Moreover, the study shows that the proposed algorithm is robust and effective in solving different types of engineering design problems. The algorithm successfully optimizes various engineering design problems, including mathematical models for physical systems, circuits, and mechanical systems.

In summary, the results of the study demonstrate that the proposed algorithm is a powerful optimization tool that can efficiently solve complex engineering design problems. The algorithm offers superior performance in terms of solution quality and convergence speed compared to other state-of-the-art optimization algorithms. Therefore, the proposed algorithm has the potential to be widely applied in different fields, such as aerospace engineering, mechanical engineering, and electrical engineering, where optimization of complex mathematical models is necessary.

7. Conclusions

In this work, we propose an accelerated AOA algorithm approach called AOACS, which hybridizes the AOA with the cuckoo search algorithm. The CS is used to enhance the performance of AOA by balancing the exploitation and exploration to acquire more reasonable convergence accuracy. The proposed algorithm provides significant results in solving numerical optimization problems compared to other algorithms. The performance of the AOACS is examined using 23 benchmark functions to show the ability of the proposed work to solve different numerical optimization problems. Further, to verify the outperformance of the AOACS algorithm, AOACS is implemented to solve two examples of engineering optimization design problems, welded beam and three-bar truss design. AOACS is compared with the essential AOA and well-known algorithms such as HHO, SSA, WOA, PSO, and SMA and demonstrates superior performance in terms of minimum manufacturing cost for the welded beam and minimum weight for the three-bar truss design.

This work proposes a novel optimization algorithm that shows promising results in solving complex engineering design problems. Here are some future research directions that could build upon this work:

• Hybridization with other optimization algorithms: The proposed algorithm could be combined with other optimization algorithms, such as the Genetic Algorithm (GA) or Particle Swarm Optimization (PSO), to create hybrid algorithms that leverage the strengths of both approaches. Hybrid algorithms may lead to even better optimization performance for certain types of engineering design problems.
• Parameter tuning: The performance of the proposed algorithm is highly dependent on the values of its parameters, such as the population size and the number of iterations. Future work could focus on finding optimal parameter settings that can improve the performance of the algorithm.
• Application to real-world engineering problems: The proposed algorithm has the potential to be applied to real-world engineering design problems, such as designing efficient aircraft or optimizing the performance of renewable energy systems. Future research could focus on applying the proposed algorithm to such problems and evaluating its performance in comparison to other optimization algorithms.
• Further theoretical analysis: Theoretical analysis of the proposed algorithm, such as convergence analysis or complexity analysis, could provide deeper insights into its behavior and limitations. Such analysis could also guide the development of more efficient optimization algorithms in the future.
• Extension to multi-objective optimization: The proposed algorithm is currently designed to optimize single-objective problems. Future research could focus on extending the algorithm to solve multi-objective optimization problems, where multiple conflicting objectives need to be optimized simultaneously.

In conclusion, this work presents a promising optimization algorithm that can be further developed and applied to real-world engineering problems. Future research can build upon this work to improve the algorithm’s performance and expand its application domain.