A Peptide Potential Based on a Bond Dipole Representation of Electrostatics
Abstract
1. Introduction
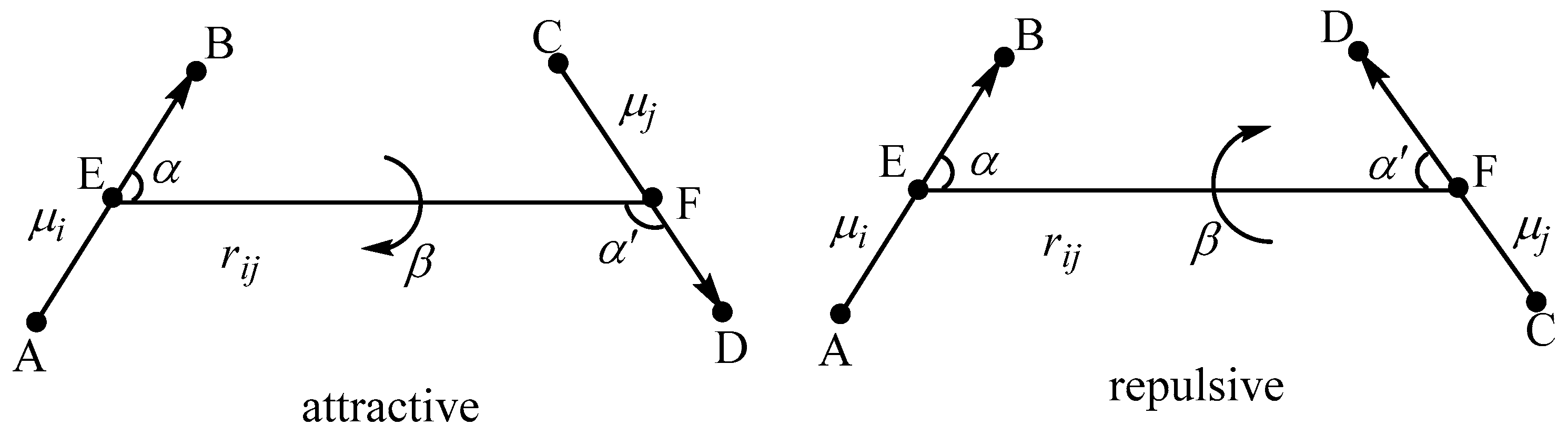
2. Theoretical Model
3. Parameterization
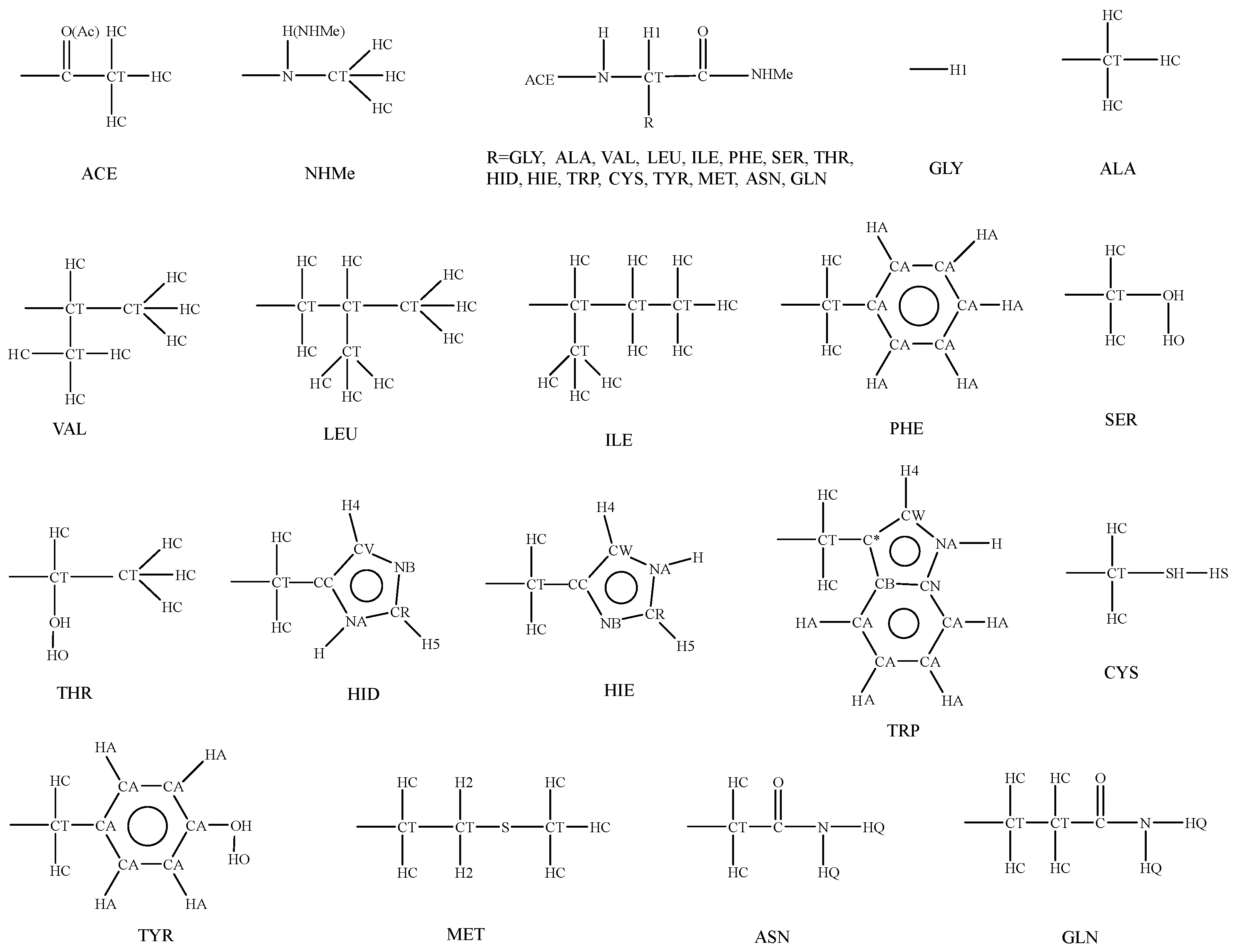
3.1. Parameters for Electrostatics
3.2. Parameters for Van Der Waals
3.3. Parameters for Bonded Terms
3.4. Scale Factors for Intramolecular Dipole–Dipole Interactions
4. Applications
4.1. Conformational Energy
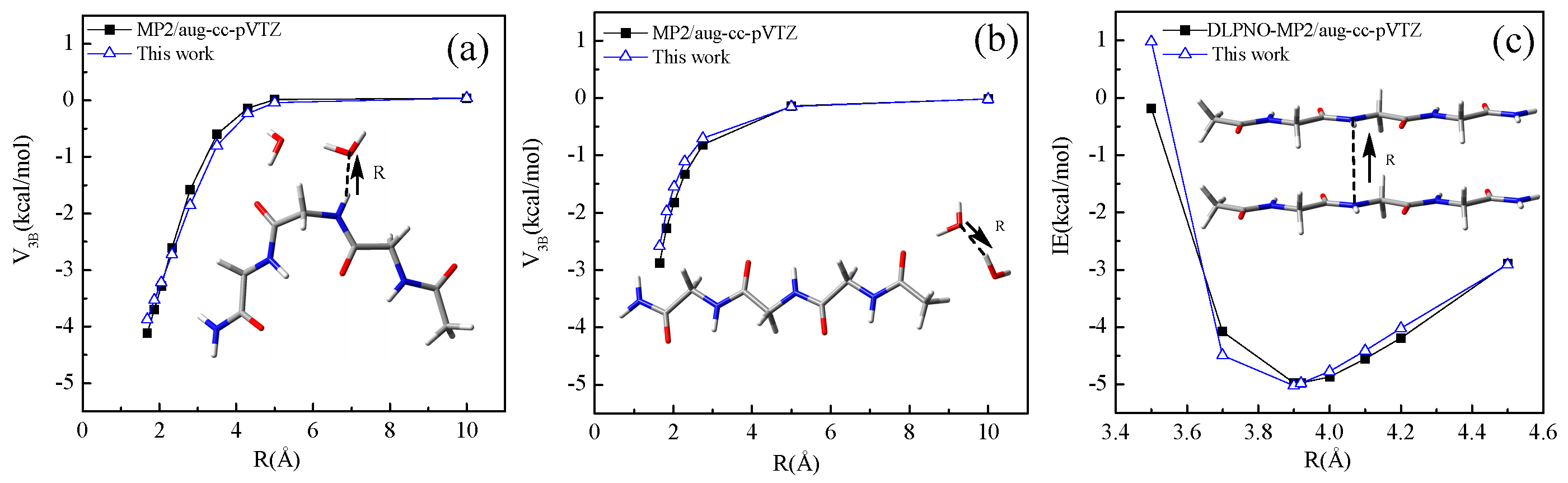
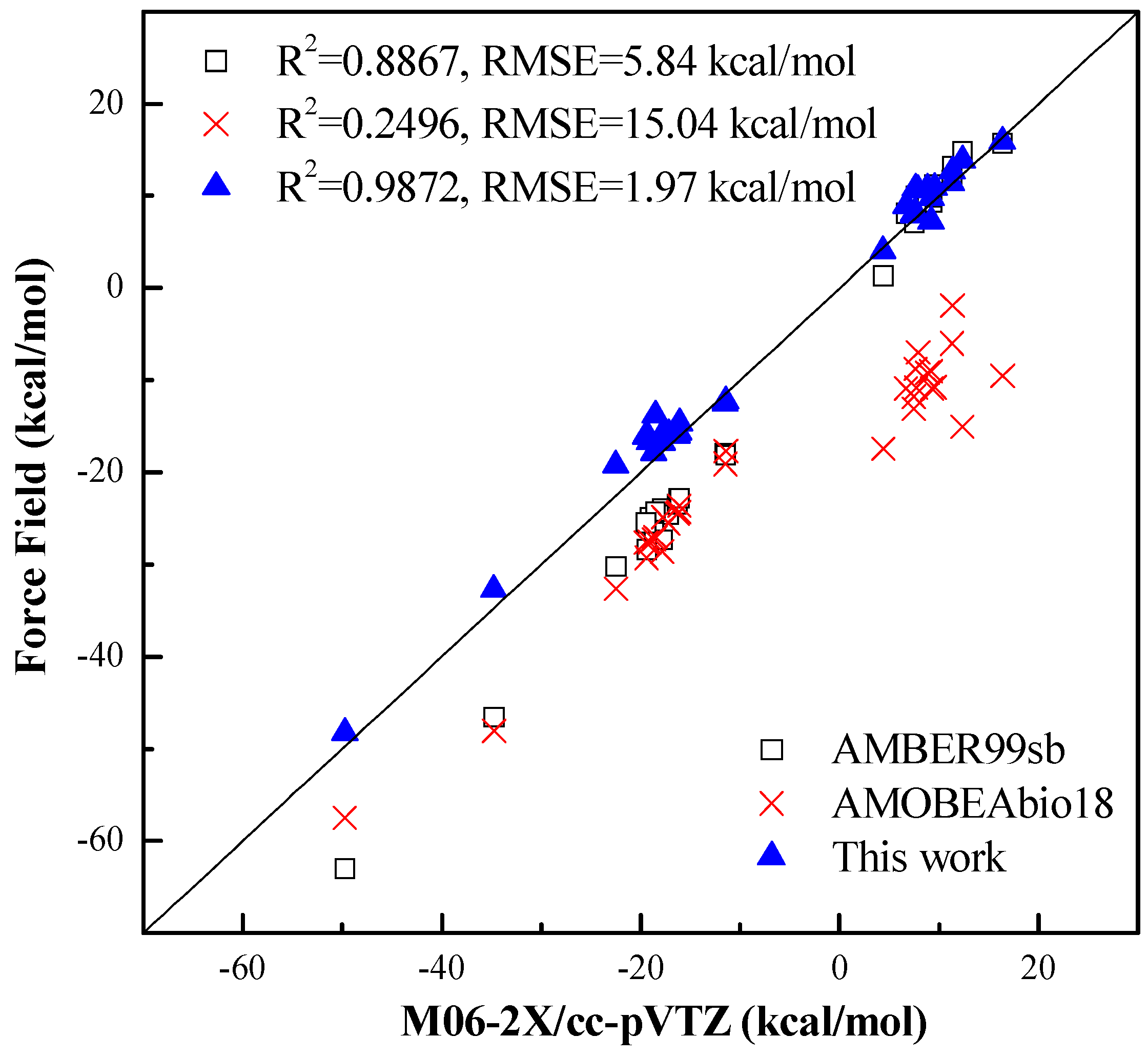
4.2. Intermolecular Interaction Energy
4.3. Structures
4.4. Efficiency
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- MacKerell, A.D.; Wiórkiewicz-Kuczera, J.; Karplus, M. An All-Atom Empirical Energy Function for the Simulation of Nucleic Acids. J. Am. Chem. Soc. 1995, 117, 11946–11975. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grübmuller, H.; MacKerell, A.D., Jr. CHARMM36M: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; van Gunsteren, W.F. A Biomolecular Force Field Based on the Free Enthalpy of Hydration and Solvation: The GROMOS Force-Field Parameter Sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; van Gunsteren, W.F. Definition and Testing of the GROMOS Force-Field Versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843–856. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef]
- Shi, Y.; Xia, Z.; Zhang, J.; Best, R.; Wu, C.; Ponder, J.W.; Ren, P. Polarizable Atomic Multipole-Based AMOEBA Force Field for Proteins. J. Chem. Theory Comput. 2013, 9, 4046–4063. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, C.; Jing, Z.; Wu, C.; Piquemal, J.P.; Ponder, J.W.; Ren, P. AMOEBA Polarizable Atomic Multipole Force Field for Nucleic Acids. J. Chem. Theory Comput. 2018, 14, 2084–2108. [Google Scholar] [CrossRef]
- Lopes, P.E.M.; Huang, J.; Shim, J.; Luo, Y.; Li, H.; Roux, B.; MacKerell, A.D. Polarizable Force Field for Peptides and Proteins Based on the Classical Drude Oscillator. J. Chem. Theory Comput. 2013, 9, 5430–5449. [Google Scholar] [CrossRef]
- Kognole, A.A.; Aytenfisu, A.H.; MacKerell, A.D. Extension of the CHARMM Classical Drude Polarizable Force Field to N- and O-Linked Glycopeptides and Glycoproteins. J. Phys. Chem. B 2022, 126, 6642–6653. [Google Scholar] [CrossRef]
- Lemkul, J.A.; Huang, J.; Roux, B.; MacKerell, A.D., Jr. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev. 2016, 116, 4983–5013. [Google Scholar] [CrossRef]
- Marshall, G.R. Limiting Assumptions in Molecular Modeling: Electrostatics. J. Comput. Aided Mol. Des. 2013, 27, 107–114. [Google Scholar] [CrossRef]
- Cisneros, G.A.; Karttunen, M.; Ren, P.; Sagui, C. Classical Electrostatics for Biomolecular Simulations. Chem. Rev. 2014, 114, 779–814. [Google Scholar] [CrossRef]
- Barker, J.A. Statistical Mechanics of Interacting Dipoles. Proc. R. Soc. A 1953, 219, 367–372. [Google Scholar]
- Buckingham, A.D.; Pople, J.A. The Statistical Mechanics of Imperfect Polar Gases. Part 1.—Second Virial Coefficients. Trans. Faraday Soc. 1955, 51, 1173–1179. [Google Scholar] [CrossRef]
- Ren, P.; Ponder, J.W. Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J. Phys. Chem. B 2003, 107, 5933–5947. [Google Scholar] [CrossRef]
- Lamoureux, G.; MacKerell, A.D.; Roux, B.T. A Simple Polarizable Model of Water Based on Classical Drude Oscillators. J. Chem. Phys. 2003, 119, 5185–5197. [Google Scholar] [CrossRef]
- Liu, C.; Piquemal, J.P.; Ren, P. AMOEBA+ Classical Potential for Modeling Molecular Interactions. J. Chem. Theory Comput. 2019, 15, 4122–4139. [Google Scholar] [CrossRef]
- Liu, C.; Piquemal, J.P.; Ren, P. Implementation of Geometry-Dependent Charge Flux into the Polarizable AMOEBA+ Potential. J. Phys. Chem. Lett. 2020, 11, 419–426. [Google Scholar] [CrossRef] [PubMed]
- Medders, G.R.; Babin, V.; Paesani, F. A Critical Assessment of Two-Body and Three-Body Interactions in Water. J. Chem. Theory Comput. 2013, 9, 1103–1114. [Google Scholar] [CrossRef] [PubMed]
- Bull-Vulpe, E.F.; Riera, M.; Götz, A.W.; Paesani, F. MB-Fit: Software Infrastructure for Data-Driven Many-Body Potential Energy Functions. J. Chem. Phys. 2021, 155, 124801–124817. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.-L.; Jiang, X.-N.; Wang, C.-S. An Analytic Potential Energy Function for the Amide-Amide and Amide-Water Intermolecular Hydrogen Bonds in Peptides. J. Comput. Chem. 2009, 30, 2567–2575. [Google Scholar] [CrossRef]
- Jiang, X.-N.; Sun, C.-L.; Wang, C.-S. A Scheme for Rapid Prediction of Cooperativity in Hydrogen Bond Chains of Formamides, Acetamides, and N-Methylformamides. J. Comput. Chem. 2010, 31, 1410–1420. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, X.-N.; Wang, C.-S. Rapid Evaluation of the Binding Energies in Hydrogen-Bonded Amide-Thymine and Amide-Uracil Dimers in Gas Phase. J. Comput. Chem. 2011, 32, 953–966. [Google Scholar] [CrossRef]
- Li, S.-S.; Huang, C.-Y.; Hao, J.-J.; Wang, C.-S. A Polarizable Dipole-Dipole Interaction Model for Evaluation of the Interaction Energies for N-H···O=C and C-H···O=C Hydrogen-Bonded Complexes. J. Comput. Chem. 2014, 35, 415–426. [Google Scholar] [CrossRef]
- Gao, X.-C.; Hao, Q.; Wang, C.-S. Improved Polarizable Dipole-Dipole Interaction Model for Hydrogen Bonding, Stacking, T-Shaped, and X-H···π Interactions. J. Chem. Theory Comput. 2017, 13, 2730–2741. [Google Scholar] [CrossRef]
- Huang, C.; Hao, Q.; Wang, C. Rapid Prediction of Interaction Energies for Nucleoside-Containing Hydrogen-Bonded Complexes: Lone-Pair Dipole Moment Treatment for Adenine, Cytosine and Guanine. Chem. Res. Chin. Univ. 2017, 33, 94–99. [Google Scholar] [CrossRef]
- Li, X.-L.; Li, C.-M.; Zhu, J.-Y.; Zhou, Z.; Hao, Q.; Wang, C.-S. A Scheme for Rapid Evaluation of the Intermolecular Three-body Polarization Effect in Water Clusters. J. Comput. Chem. 2023, 44, 677–686. [Google Scholar] [CrossRef]
- Li, X.-L.; Sun, Y.-J.; Ying, T.; Wang, C.-S. Rapid and Accurate Calculation of the Three⁃body Interaction Strength in the Hydrogen-bonded Complexes of Alcohols or Deoxyribose with Water. Chem. J. Chin. Univ. 2021, 42, 3664–3671. [Google Scholar]
- Buckingham, A.D. Molecular Quadrupole Moments. Q. Rev. Chem. Soc. 1959, 13, 183–214. [Google Scholar] [CrossRef]
- Speight, J.G. Lange’s Handbook of Chemistry, 16th ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins Struct. Funct. Bioinf. 2006, 65, 712–725. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Neese, F. Software Update: The ORCA Program System—Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Ponder, J.W. TINKER Molecular Modeling Package, V8.10.1; Washington University Medical School: St. Louis, MO, USA, 2021. [Google Scholar]
- PBFF Is an In-House Developed Fortran Code Which Is Publicly. Available online: http://cswang.home.lnnu.edu.cn (accessed on 20 October 2022).
- Wu, Y.-D.; Zhao, Y.-L. A Theoretical Study on the Origin of Cooperativity in the Formation of 310- and α-helices. J. Am. Chem. Soc. 2001, 123, 5313–5319. [Google Scholar] [CrossRef]
- Dill, K.A.; MacCallum, J.L. The Protein-Folding Problem, 50 Years On. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef]
- Gromiha, M.M.; Siebers, J.G.; Selvaraj, S.; Kono, H.; Sarai, A. Role of Inter and Intramolecular Interactions in Protein-DNA Recognition. Gene 2005, 364, 108–113. [Google Scholar] [CrossRef]

| Parameters for Electrostatics | μ0 (Debye) | c | q0 |
|---|---|---|---|
| C=O | 2.65 | 1.80 | −0.3800 |
| C=O(Ac) | 2.65 | 1.80 | −0.3720 |
| N-H | 1.51 | 1.00 | 0.2690 |
| N-H(NHMe), NA-H | 1.51 | 1.00 | 0.2360 |
| N-HQ | 1.31 | 1.80 | 0.2373 |
| CT-H1 | 0.70 | 1.00 | 0.1150 |
| CT-OH | 0.70 | 0.00 | -- |
| CA-OH | 0.70 | 0.00 | -- |
| OW-HW | 1.51 | 1.86 | 0.1942 |
| OH-HO | 1.51 | 1.00 | 0.2164 |
| CT-SH | 0.90 | 0.00 | -- |
| CT-S | 0.90 | 0.00 | -- |
| SH-HS | 0.65 | 1.00 | 0.0304 |
| Scale factors for intramolecular dipole-dipole interactions | |||
| two dipoles separated by 3 bonds | 0.75 | ||
| two dipoles separated by 4 bonds | 0.90 | ||
| Parameters for van der Waals | R*(Å) | ε (kcal/mol) | |
| C, CA, CB, CC, C*, CN, CW, CV, CR | 1.9080 | 0.0860 | |
| CT | 1.9080 | 0.1094 | |
| N, NA, NB | 1.6240 | 0.1700 | |
| O, O(Ac) | 1.6612 | 0.2100 | |
| OH | 1.7210 | 0.2104 | |
| S, SH | 2.0000 | 0.6500 | |
| H, HQ, H(NHMe) | 0.8000 | 0.0157 | |
| H1, H2, HC | 1.3000 | 0.0157 | |
| HA | 1.4590 | 0.0150 | |
| HO | 0.0000 | 0.0000 | |
| H4 | 1.4090 | 0.0150 | |
| H5 | 1.3590 | 0.0150 | |
| HS | 0.6000 | 0.0157 | |
| X | Conformer | M06-2X/cc-pVTZ | AMBER99sb | Δ | AMOEBAbio18 | Δ | This Work | Δ |
|---|---|---|---|---|---|---|---|---|
| Val | helix | −17.76 | −23.91 | −6.15 | −24.84 | −7.08 | −15.77 | 1.98 |
| C5 | 7.87 | 9.39 | 1.51 | −6.96 | −14.83 | 10.68 | 2.81 | |
| Ile | helix | −19.07 | −24.82 | −5.75 | −27.55 | −8.48 | −16.62 | 2.46 |
| C5 | 6.71 | 8.18 | 1.47 | −10.84 | −17.55 | 9.03 | 2.32 | |
| Leu | helix | −17.20 | −24.53 | −7.33 | −25.51 | −8.31 | −15.84 | 1.36 |
| C5 | 9.28 | 9.32 | 0.04 | −10.88 | −20.16 | 9.80 | 0.52 | |
| Phe | helix | −16.32 | −23.40 | −7.08 | −24.46 | −8.14 | −15.94 | 0.38 |
| C5 | 7.48 | 8.34 | 0.86 | −11.79 | −19.27 | 8.01 | 0.53 | |
| Asn | helix | −18.65 | −26.42 | −7.77 | −27.27 | −8.62 | −17.84 | 0.81 |
| C5 | 9.19 | 9.91 | 0.72 | −8.97 | −18.16 | 7.25 | −1.95 | |
| Gln | helix | −22.50 | −30.17 | −7.67 | −32.62 | −10.12 | −19.23 | 3.27 |
| C5 | 9.56 | 11.27 | 1.71 | −10.74 | −20.30 | 10.93 | 1.37 | |
| Ser | helix | −11.48 | −17.86 | −6.38 | −19.04 | −7.56 | −12.52 | −1.04 |
| C5 | 11.29 | 11.75 | 0.46 | −6.02 | −17.31 | 11.42 | 0.13 | |
| Thr | helix | −11.46 | −18.09 | −6.63 | −17.64 | −6.18 | −12.25 | −0.79 |
| C5 | 11.34 | 13.27 | 1.93 | −1.85 | −13.19 | 12.75 | 1.41 | |
| Tyr | helix | −16.14 | −22.80 | −6.66 | −24.26 | −8.12 | −15.59 | 0.55 |
| C5 | 7.62 | 10.10 | 2.48 | −8.79 | −16.41 | 10.83 | 3.21 | |
| Cys | helix | −16.11 | −22.79 | −6.68 | −23.57 | −7.46 | −14.67 | 1.44 |
| C5 | 8.85 | 10.35 | 1.50 | −9.16 | −18.01 | 10.88 | 2.03 | |
| Hid | helix | −17.85 | −27.27 | −9.42 | −28.55 | −10.70 | −16.53 | 1.32 |
| C5 | -- | -- | -- | -- | -- | -- | -- | |
| Hie | helix | −18.51 | −24.19 | −5.68 | −26.98 | −8.47 | −13.80 | 4.71 |
| C5 | 7.70 | 8.06 | 0.36 | −10.78 | −18.48 | 8.21 | 0.51 | |
| Met | helix | −19.47 | −25.47 | −6.00 | −27.61 | −8.14 | −16.10 | 3.37 |
| C5 | 7.46 | 7.16 | −0.30 | −13.08 | −20.54 | 8.18 | 0.72 | |
| Trp | helix | −19.38 | −28.34 | −8.97 | −29.24 | −9.87 | −15.87 | 3.51 |
| C5 | 4.37 | 1.36 | −3.01 | −17.42 | −21.79 | 4.06 | −0.32 | |
| Max Absolute Error | 9.42 | 21.79 | 4.71 | |||||
| RMSE | 5.22 | 14.08 | 2.04 | |||||
| Conformer | QM | AMBER99sb | Δ | AMOEBAbio18 | Δ | This Work | Δ | |
|---|---|---|---|---|---|---|---|---|
| AcAla13NH2 | helix | −34.73 | −46.57 | −11.84 | −48.05 | −13.32 | −32.73 | 2.00 |
| C5 | 12.33 | 14.91 | 2.58 | −15.06 | −27.39 | 13.86 | 1.53 | |
| Ac(Ala2GlnAla2)3NH2 | helix | −49.72 | −62.99 | −13.27 | −57.51 | −7.79 | −48.25 | 1.47 |
| C5 | 16.38 | 15.75 | −0.63 | −9.51 | −25.89 | 15.96 | −0.42 |
| Hydrogen-Bonded Dimer | QM a | AMBER99sb | Δ | AMOEBAbio18 | Δ | This Work | Δ |
|---|---|---|---|---|---|---|---|
| antiparallel glycine tripeptide | −21.65 | −21.77 (84.4%) | −0.12 | −21.54 (106.0%) | 0.11 | −22.62 (83.4%) | −0.97 |
| parallel glycine tripeptide | −16.80 | −15.31 (96.5%) | 1.49 | −15.61 (98.2%) | 1.19 | −17.25(88.7%) | −0.45 |
| antiparallel glycine pentapeptide | −33.69 | −36.08 (81.8%) | −2.39 | −36.10 (104.3%) | −2.41 | −36.26 (81.0%) | −2.57 |
| parallel glycine pentapeptide | −27.18 | −25.34 (93.6%) | 1.84 | −26.42 (95.8%) | 0.76 | −27.30 (87.3%) | −0.12 |
| antiparallel alanine tripeptide | −25.22 | −23.34 (85.4%) | 1.88 | −23.10 (113.9%) | 2.12 | −24.61 (86.2%) | 0.61 |
| parallel alanine tripeptide | −24.54 | −22.92 (85.0%) | 1.62 | −21.17 (112.4%) | 3.37 | −24.88 (85.5%) | −0.34 |
| antiparallel alanine tetrapeptide | −30.07 | −29.12 (81.0%) | 0.95 | −29.60 (109.5%) | 0.47 | −30.12 (81.9%) | −0.05 |
| parallel alanine tetrapeptide | −32.38 | −30.20 (85.4%) | 2.18 | −28.47 (111.9%) | 3.91 | −32.46 (85.0%) | −0.08 |
| RMSE | 1.70 | 2.21 | 1.02 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-M.; Zheng, X.-H.; Li, C.-M.; Liu, Q.; Wang, L.; Hao, Q.; Wang, C.-S. A Peptide Potential Based on a Bond Dipole Representation of Electrostatics. Processes 2023, 11, 1291. https://doi.org/10.3390/pr11041291
Li Y-M, Zheng X-H, Li C-M, Liu Q, Wang L, Hao Q, Wang C-S. A Peptide Potential Based on a Bond Dipole Representation of Electrostatics. Processes. 2023; 11(4):1291. https://doi.org/10.3390/pr11041291
Chicago/Turabian StyleLi, Yan-Min, Xiao-Han Zheng, Chao-Ming Li, Qi Liu, Lei Wang, Qiang Hao, and Chang-Sheng Wang. 2023. "A Peptide Potential Based on a Bond Dipole Representation of Electrostatics" Processes 11, no. 4: 1291. https://doi.org/10.3390/pr11041291
APA StyleLi, Y.-M., Zheng, X.-H., Li, C.-M., Liu, Q., Wang, L., Hao, Q., & Wang, C.-S. (2023). A Peptide Potential Based on a Bond Dipole Representation of Electrostatics. Processes, 11(4), 1291. https://doi.org/10.3390/pr11041291





