Abstract
The inventory level has a significant influence on the cost of process scheduling. The stochastic cutting stock problem (SCSP) is a complicated inventory-level scheduling problem due to the existence of random variables. In this study, we applied a model-free on-policy reinforcement learning (RL) approach based on a well-known RL method, called the Advantage Actor-Critic, to solve a SCSP example. To achieve the two goals of our RL model, namely, avoiding violating the constraints and minimizing cost, we proposed a two-stage discount factor algorithm to balance these goals during different training stages and adopted the game concept of an episode ending when an action violates any constraint. Experimental results demonstrate that our proposed method obtains solutions with low costs and is good at continuously generating actions that satisfy the constraints. Additionally, the two-stage discount factor algorithm trained the model faster while maintaining a good balance between the two aforementioned goals.
1. Introduction
The cutting stock problem (CSP) is the common problem of minimizing trim loss when cutting stock materials into pieces of required sizes to meet customer demand. It has been considered in a wide range of industrial applications, including paper, metal, and glass manufacturing. The CSP is an integer linear programming problem that can be formulated as follows:
The i-th item has a demand di (i {1, 2, …, m}) given by the customer. Items are produced to meet demand by cutting stock materials in predefined cutting patterns. The j-th cutting pattern is defined by the vector aj = [a1j, a2j,…, aij] (j {1, 2, …, n}), where aij indicates the number of i-th items produced when a stock material is cut by the j-th pattern; gj is the trim loss of the j-th pattern. The objective of the problem is to determine the number of stock materials to be cut by the j-th pattern, which is denoted as xj, to meet the demand while minimizing total trim loss [1,2,3].
In production scheduling for chemical industries, the inventory level directly affects production costs. For the stochastic CSP (SCSP), the demand is a random variable that is unknown prior to production [4,5]. Due to the presence of random event factors, the SCSP can be considered as a complex inventory-level scheduling problem. A performant algorithm for solving such a problem may minimize costs such as waste, inventory, and back-order costs, which are critical for companies. However, in traditional deterministic mathematical methods such as integer programming, calculation time increases rapidly as the amount of data increases, and random variables make such problems difficult to solve [6]. Reinforcement learning (RL) is a novel method for rapidly providing an optimal scheduling solution when handling non-deterministic problems. However, RL is doubtful when dealing with constrained problems.
Only one previous study applied RL methods to solve the CSP. Pitombeira-Neto and Murta [7] presented a model-free off-policy approximate policy iteration algorithm for solving the SCSP example. Their algorithm approximated the action-value function using two basis functions, namely, the polynomial and Fourier basis function. Their results showed the scheduling performance of RL and ensured that actions did not violate the constraints. However, for each of the two basis functions, a set of parameter matrices of unknown sizes must be tuned prior to training. Excessive mathematizations, exhaustive random iterations, and requirements for prior knowledge led to both huge training and calculation times, making this model impractical for industrial application. Some studies have solved the knapsack problem, which is a common optimization problem similar to the CSP, using RL approaches. Gu et al. proposed a RL algorithm with a pointer network to solve the single-knapsack problem [8]. Sur et al. solved the multiple-knapsack problem using a RL agent trained by the A3C algorithm [9].
The goal of this study was to adopt Advantage Actor-Critic (A2C) for continuous action space to solve the SCSP example considered in [7] for easier and more reproducible implementation in industries. In this example, seven items are produced by cutting raw materials with fixed amounts and sizes according to 15 cutting patterns. The goal is to determine the number of times to apply each pattern to satisfy the constraints and simultaneously minimize the sum of the trim loss, back-order cost, and inventory cost. There is a hyperparameter called the discount factor (γ) that significantly affects the training of a RL agent, which has a value between zero and one. The discount factor determines the extent to which future rewards should be considered. The closer it is to zero, the fewer time steps of future rewards are considered. Therefore, to achieve an effective balance between the two goals of avoiding violating the constraints and minimizing cost, we proposed a two-stage discount factor algorithm for training a RL model. Experimental results demonstrate that our proposed two-stage discount factor algorithm can accelerate model training significantly. Our model learns the SCSP and constraints accurately to provide actions continuously that satisfy the constraints and minimize cost.
2. Materials and Methods
2.1. Problem Statement
We considered the SCSP example presented in [7]. In this problem, there are 30 pieces of 1500 cm long raw material and 15 cutting patterns that may be used to cut the raw material into seven different items with random demand. The goal of the problem is to determine the number of times to apply each pattern to minimize the sum of the trim loss, back-order cost, and inventory cost. The lengths of the items are listed in Table 1. The compositions and trim losses of patterns are listed in Table 2. The total demand for all items is defined as dtotal, which follows a discrete uniform probability distribution between dmin and dmax. The demand for individual items is defined by a vector d = [d1, d2,…, di] (i {1, 2, …, m}), which follows a multinomial distribution based on the total demand and probability distribution vector p. The values of dmin, dmax, and p are listed in Table 3. The demand vector d can be formulated as follows:

Table 1.
Lengths of seven items.

Table 2.
Compositions and trim losses of 15 patterns.

Table 3.
Probability distribution of the demand for seven items.
2.2. Reinforcement Learning
RL is a decision-making method that solves problems described as Markov decision processes. A RL system involves an agent interacting with an environment. In each step, the agent observes the state of the environment and then determines the action to be taken. The environment then returns the next state and a reward (Figure 1). The sets of states, actions, rewards, and next states at time step t are presented in the following form: (st, at, rt, st+1). The (st, at, rt, st+1) sequence of an episode with several time steps is called a trajectory. The goal of the agent is to maximize the reward. Therefore, RL attempts to develop a policy for choosing an optimal action based on states [10,11,12].
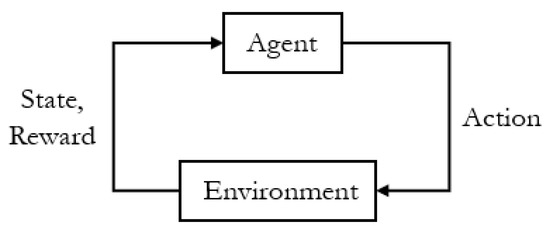
Figure 1.
Diagram of a reinforcement leaning system.
The methods of RL can be divided into value-based and policy-based. The main difference is whether an explicit policy is trained. In value-based learning, there is no explicit policy to be trained, and actions are selected based on a value function instead. In policy-based learning, an explicit policy is built to determine actions directly. RL can also be divided into on-policy and off-policy learning. The main difference is whether the policy that is improved, which is called the target policy, is the same as the policy that is used to select actions, which is called the behavior policy. In on-policy learning, the target policy and behavior policy are the same, meaning only current data can be used for training. In off-policy learning, the target policy and behavior policy may be different; hence, historical data can also be used for training [13,14].
2.3. Advantage Actor-Critic
2.3.1. Discrete Action Space
A2C is an on-policy method for RL that combines value-based and policy-based learning and is composed of two neural networks called the actor and critic. The actor represents the policy that determines actions and is trained by minimizing the actor loss, which increases the probability of taking actions with large advantage values [15,16]. This process is formulated as:
where B is the batch size; is the advantage value of taking action at state , which can be estimated using Equation (6); is the Q value representing the expected future rewards of taking action at state , which can be calculated based on the reward , discount factor , and the next state value, as shown in Equation (7); is the state value of state ; and γ is the discount factor, which is between zero and one. The closer the discount factor is to one, the more time steps of future rewards that are considered. It should be noted that the advantage value can be calculated using the state value, reward, and discount factor, indicating that only one network must be trained to estimate the state value, which is called the critic network. represents the probability of taking action at state outputted by the actor. Therefore, the actor loss can be expressed as:
The critic is updated based on the temporal difference (TD). Therefore, the critic loss is formulated as:
Additionally, entropy loss can be used during the training of actors and critics. Entropy loss allows an actor to maintain the ability to explore at the beginning of training, thereby avoiding falling into local optima. The entropy loss is formulated as follows:
where is the entropy beta, which modulates the effect of entropy loss on training.
2.3.2. Continuous Action Space
For a discrete action space, the actor network in A2C traditionally outputs the probabilities of actions. A2C is also a promising method for handling a continuous action space. Instead of outputting the probabilities of actions, the actor network outputs two scalars, each of which has the same size as the number of actions. One scalar represents the mean value µ of the Gaussian distribution, and the other represents the variance 𝜎2. When addressing a continuous action space, the critic loss is the same as that in the discrete A2C (see Equation (9)). The actor and entropy losses must be slightly different from those in the discrete A2C and are formulated as:
2.4. Environment
Our environment system for RL contains states, actions, rewards, constraints, and a variable which is called “done” and is used to solve the SCSP.
- The state , represents the inventory of item i (i {1, 2, …, 7}). The initial state (i.e., the initial inventory) follows a discrete uniform probability distribution between 0 and 35, which can be formulated as:
The state transition function is given by Equation (14). The next state is determined by the current state, action, and random demand, which is only known after executing an action.
- An action denoted as represents the number of times to apply pattern j.
- To estimate the reward, the cost is first calculated using Equation (15), where is the trim loss of pattern j, the value of which is provided in Table 2, and [x]+ = max(0,x). The values and definitions of and are provided in Table 4. The cost consists of the trim loss, inventory cost, and back-order cost. The reward is a function of the cost and is calculated by dividing the cost by 500, as shown in Equation (16). This reward function indicates that when the cost is greater than 500, a reward of less than one is returned, and when the cost is equal to 500, a reward with a value of one is returned. The reward function was designed in this manner for the following reasons:
 Table 4. Parameters of the environment system.
Table 4. Parameters of the environment system.- Based on the results presented in [7], a cost of approximately 500 is sufficiently low for this SCSP example.
- The training of the critic and actor networks may be unstable if the variance of the loss is large. Therefore, the reward should be approximately equal to one.
- There are two constraints on actions in the target environment system, as described below. First, the inventory of any item at any time cannot exceed the maximum inventory. Second, the total number of patterns to be used must be less than the number of available stock materials.
- The value of the variable depends on whether action violates the constraints (Equation (18)). The takes on a value of one if the current episode ends or a value of zero if the episode continues, and then the state is updated by the state transition function (Equation (13)). We adopted the game concept of an episode ending when an action violates any constraint and continuing when all constraints are satisfied to improve the ability of the model to deal with the constraints. For a discount factor close to one, the greater the number of future steps, the higher the accumulated reward, resulting in a training target that continuously provides actions that meet constraints.
2.5. Proposed Method
2.5.1. Two-Stage Discount Factor
When calculating the critic loss, which is based on the TD, the discount factor is critical for determining the extent to which future rewards should be considered. The closer the discount factor is to zero, the fewer time steps of future rewards are considered. With a value of zero, the actor can only consider the current step.
There are two goals for our agent to achieve:
- Avoiding violating the constraints;
- Minimizing cost.
According to these different goals, we define an adaptive discount factor in two stages, as shown in Equation (19). First, we set a high discount factor, meaning many future steps are considered. When the constraints are satisfied for multiple time steps, accumulated rewards increase. Therefore, the model is trained to satisfy the constraints continuously in this stage. When the average number of steps of continuous actions that satisfy the constraints is greater than 200, the discount factor is adjusted to 0.1. At this stage, the goal of the agent is to take an action that minimizes the cost.
2.5.2. Proposed Process
The structures of the critic and actor neural networks are presented in Figure 2. The state is not directly inputted into the actor and critic. Instead, we use a base fully connected network for feature extraction. The critic network is composed of two fully connected layers with a rectified linear unit (ReLU) activation function and a fully connected layer with no activation function. The critic output is the estimated state value corresponding to the input state and has dimensions of B × 1, where B represents the batch size. The actor is divided into two networks, where one outputs the mean value µ of the number of each pattern to use, which follows a Gaussian distribution, and the other outputs the variance 𝜎2. Both outputs have dimensions of B × 15. Both actor networks are composed of two fully connected layers with a ReLU activation function and one fully connected layer with a Softmax activation function
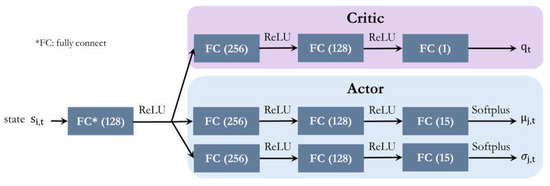
Figure 2.
Structures of the actor and critic neural networks.
The proposed process diagram is presented in Figure 3 and Algorithm 1 summarizes the steps of the proposed method. The proposed framework is composed of two parallel processes.
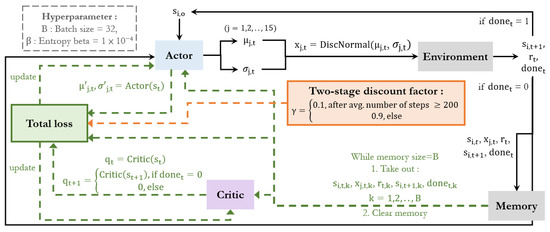
Figure 3.
Proposed process diagram.
- Interaction for data collection (solid line in Figure 3): At the beginning of an episode, the initial state is sampled and observed by the actor, and the actor then outputs the mean value and variance for sampling an action from a Gaussian distribution. After executing a sampled action, the environment returns the next state, reward, and whether the episode is finished. If the episode is finished, indicating that the constraints are violated, then the next episode starts, and an initial state is sampled. Otherwise, the next state is observed by the actor to take the next action.
- Training of the critic and actor (green dashed line in Figure 3): After each of the 32 steps of interaction between the actor and environment, the total loss, which is composed of critic, policy, and entropy losses (Equation (20)), is calculated and used to update both the actor and critic networks. It should be noted that if the episode ends at time step t, the state value of time step t + 1 must be zero. Otherwise, training will not converge. Furthermore, we propose a two-stage discount factor algorithm, as shown in the orange box in Figure 3. Once the average number of steps over the previous hundred training episodes is greater than 200, the discount factor is adjusted to 0.1. Before this point, the discount factor is 0.9.
| Algorithm 1. Proposed A2C Model for a Continuous Action Space with a Two-stage Discount Factor |
| Initialize actor network πθ and critic network Qθ with random parameters θ Input = 1 × 10−4, B = 32 Initialize discount factor γ = 0.9 Initialize memory M Initialize total game steps , total rewards , total cost = 0 for each episode: Initialize the initial state s0 While: Get 𝜇t, 𝜎2t = πθ(st) Take an action at = int(sample from a Gaussian distribution with mean 𝜇t and variance 𝜎2t) Execute action at and observe reward rt, next state st+1, and donet Store (st, at, rt, st+1, donet) in M += 1 += += /500 Update state st ← st+1 if donet: Calculate the average number of steps and mean cost over the last 100 episodes if 200: γ = 0.1 if the number of data in M = B: Calculate the total loss by Equation (20). Update critic and actor by minimizing the total loss end for |
PyTorch was used to implement the proposed algorithm. In addition to our proposed model, we trained a model with a discount factor of 0.9 and another model with a discount factor equal to 0.1 for comparison. The discount factor of 0.9 indicates that many steps of future rewards are considered, and a discount factor of 0.1 indicates that few steps of future rewards are considered. The models were trained with a fixed total number of training steps (1,500,000 steps) instead of a fixed total number of training episodes. The number of steps in each episode may vary according to the ability of the model to handle the constraints. Therefore, the total number of training episodes for each model may vary. Every model was executed on a PC with an i7-9700 3.00 GHz CPU and 32 GB of RAM.
3. Results and Discussion
3.1. Training
The results of training are discussed in terms of the average number of steps (Figure 4 and Figure 5) and mean cost (Figure 6 and Figure 7). Each point in Figure 4, Figure 5, Figure 6 and Figure 7 represents the result of averaging over the previous 100 episodes. The training of the model with a discount factor of 0.1 is slower than that of the other two models obviously, resulting in much larger training episodes, making it difficult to present those results together with others. Therefore, the results of the model with a discount factor of 0.1 are presented separately from the other two models in Figure 5 and Figure 7.
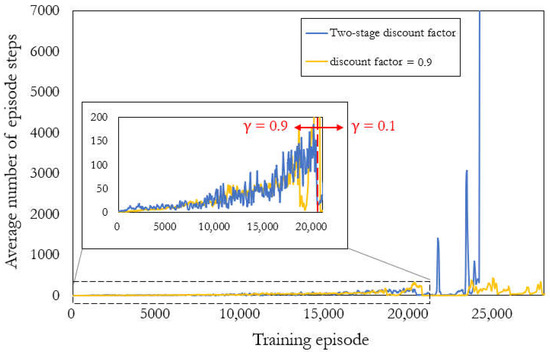
Figure 4.
Average number of steps for the last 100 training episodes with the two-stage discount factor (blue) and discount factor = 0.9 (yellow), where γ is the discount factor.
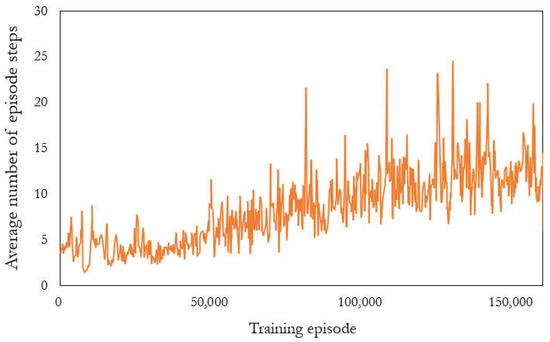
Figure 5.
Average number of steps for last 100 training episodes for discount factor = 0.1.
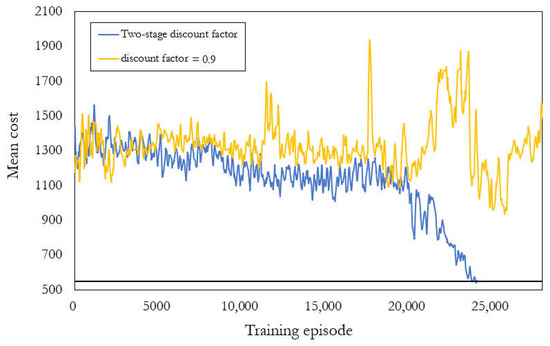
Figure 6.
Mean costs for the last 100 training episodes for the two-stage discount factor (blue) and discount factor = 0.9 (yellow).
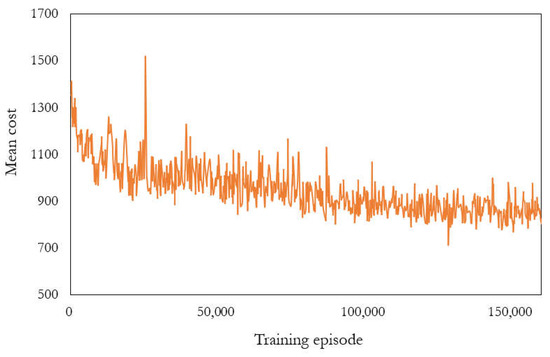
Figure 7.
Mean of cost for the last 100 training episodes for discount factor = 0.1.
3.1.1. Average Number of Steps
The higher the average number of steps, the better the ability of the agent to provide actions that satisfy the constraints continuously. Figure 4 and Figure 5 reveal a gradual increase in the average number of steps, indicating that the agent learns to take actions satisfying the constraints. The two-stage discount factor model (blue line in Figure 4) was trained the fastest with an average number of steps greater than 7000 after training. The model with a discount factor of 0.9 (yellow line in Figure 4) was trained slightly slower with an average number of steps of approximately 200 after training. The model with a discount factor of 0.1 (Figure 5) was trained the slowest with an average number of steps of approximately 15 after training. When the training episode is around 25,000, the average steps of the two-stage discount factor had significant improvement, which is better than the single discount factor. Furthermore, the partially enlarged view in Figure 4 shows the results before the 21,000th episode with an average number of steps between 0 and 200. The average number of steps reached 200 at approximately the 20,000th episode, where the discount factor was adjusted from 0.9 to 0.1 for training the two-stage discount factor model. A higher discount factor considers more future rewards, indicating that the higher the average number of steps, the higher the accumulated reward—the target for RL training. Thus, the model with a discount factor of 0.9 demonstrated a greater ability to provide actions that continuously satisfy constraints than the model with a discount factor of 0.1. Our two-stage discount factor model was trained to prioritize constraint satisfaction in the first stage, enabling it to learn more efficiently to minimize costs in the second stage. This approach allowed us to overcome the bottleneck of the average number of steps and achieve excellent results.
3.1.2. Mean Cost
The results presented in Figure 6 (blue line) demonstrate the excellent performance of our proposed method that the two-stage discount factor model reaches a sufficiently low mean cost of approximately 550 with a high average number of steps. For the model with a discount factor of 0.9, Figure 4 reveals that the agent learned to take actions satisfying the constraints. However, Figure 6 (yellow line) reveals that the mean cost does not decrease with training, indicating that this model cannot achieve a low cost while satisfying the constraints. For the model with a discount factor of 0.1, Figure 7 reveals a gradual decrease in the mean cost, indicating that this model leaks when dealing with the constraints but has the potential to reduce costs.
Overall, these results demonstrate that adjusting the value of the discount factor according to the training goals in different training stages can increase the speed of training and achieve both the goals of continuously providing actions that satisfy the constraints and minimizing cost. The model with a discount factor equal to 0.9 considers more steps of future rewards. Therefore, the results indicate that this model satisfies the constraints, but with a high cost, which proves that this model is dedicated to taking actions that satisfy the constraints continuously. With a discount factor of 0.1, the model considers fewer steps of future rewards; hence, the results indicate that this model provides actions with low costs but struggles to satisfy constraints, demonstrating that this model is devoted to adopting actions that minimize costs.
3.2. Testing
By testing the three models for 100 episodes, we obtained the results listed in Table 5, which reveal that our proposed model achieves the highest average number of steps and lowest cost. Surprisingly, our model continuously provides actions that satisfy constraints for over 10,000 interactions with a mean cost of 462.75, indicating that the proposed method is promising for balancing the tradeoff between different goals. The discount factor with a value of 0.1 yields the smallest average number of steps, indicating that it struggles to satisfy constraints. The discount factor with a value of 0.9 yields the largest mean cost, indicating that it only provides suboptimal feasible solutions.

Table 5.
Test results for the average number of steps and mean cost for the two-stage discount factor, discount factor = 0.9, and discount factor = 0.1.
Second, we tested the two-stage discount factor model over 10 simulations with 1000 steps per episode and averaged the results over previous steps. Because the other two models were unable to provide actions for 1000 steps continuously, this test was only applicable to the two-stage discount factor model. The results were compared to the results of two RL models, namely, the polynomial and Fourier models, which were proposed in [7], as well as a myopic policy, which is a reasonable heuristic for the SCSP in practice. We obtained the results presented in Figure 8 (blue line), where the final average cost of our proposed model is 456.3. The myopic policy (yellow line) has a final average cost of 2186.5, whereas the polynomial (orange line) and Fourier (green line) models have final average costs of 441.3 and 363.4, respectively. These results demonstrate that the proposed method significantly outperforms the myopic policy and is similar to the polynomial. Although our model has an average cost that is slightly higher than the Fourier, our model has several additional advantages.
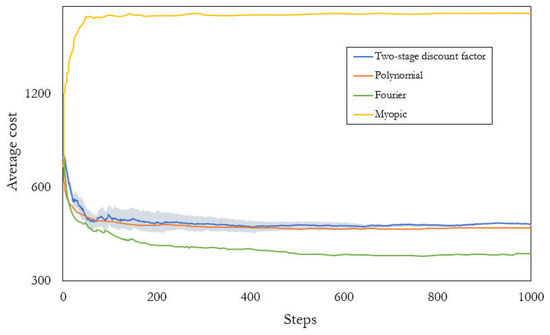
Figure 8.
Average cost over 10 simulations for 1000 steps (log scale) for our proposed model (blue line), the polynomial (orange line), Fourier (green line), and myopic policy (yellow line) models [7]. Bands represent 95% bootstrap confidence intervals for 10 simulations.
- Ability to satisfy the constraints: The results for the average number of steps demonstrate the excellent ability of our proposed model to satisfy the constraints without excessive random iterations used in the literature to ensure that the actions satisfy the constraints.
- Repeatability, practicality, and short training time: Our method has a small number of hyperparameters to be tuned, which makes it repeatable, practical, and easy to train. Furthermore, the proposed two-stage discount factor algorithm can reduce training time.
- Intelligibility: We proposed a two-stage discount factor algorithm to adjust the hyperparameter of the A2C model dynamically, so our proposed model is based on a common RL method, making it simple to understand and implement.
4. Conclusions
In this study, we proposed an A2C model, which is a RL method, for a continuous action space with a two-stage discount factor algorithm to solve a SCSP example. Our proposed method successfully solved the SCSP and obtained low-cost solutions. Our model has several advantages, including the ability to satisfy the constraints, repeatability, practicality, short training time, and intelligibility.
The two-stage discount factor algorithm trains the A2C model rapidly and achieves a suitable balance between the two goals of avoiding violating the constraints and minimizing cost. These promising results demonstrate the potential of the proposed method for application to other stochastic constrained optimization problems found in a variety of industries. Furthermore, based on the outstanding performance of the Fourier model proposed by [7], it is expected that adding the Fourier approach to the actor network might improve the results of our model, which would be implemented in the future.
Author Contributions
Conceptualization, J.-Y.S. and J.-L.K.; methodology, J.-Y.S. and J.-L.K.; software, J.-Y.S. and J.-L.K.; validation, J.-Y.S., J.-L.K. and S.-S.J.; formal analysis, J.-Y.S. and J.-L.K.; investigation, J.-Y.S.; resources, S.-S.J.; data curation, J.-Y.S.; writing—original draft preparation, J.-Y.S.; writing—review and editing, J.-L.K. and S.-S.J.; visualization, J.-Y.S.; supervision, S.-S.J.; project administration, J.-L.K. and S.-S.J.; funding acquisition, S.-S.J. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by Grant NSTC 111-2221-E-007-002 from the National Science and Technology Council of the Republic of China.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gilmore, P.C.; Gomory, R.E. A linear programming approach to the cutting-stock problem. Oper. Res. 1961, 9, 849–859. [Google Scholar] [CrossRef]
- Israni, S.; Sanders, J. Two-dimensional cutting stock problem research: A review and a new rectangular layout algorithm. J. Manuf. Syst. 1982, 1, 169–182. [Google Scholar] [CrossRef]
- Cheng, C.H.; Feiring, B.R.; Cheng, T.C.E. The cutting stock problem—A survey. Int. J. Prod. Econ. 1994, 36, 291–305. [Google Scholar] [CrossRef]
- Krichagina, E.V.; Rubio, R.; Taksar, M.I.; Wein, L.M. A dynamic stochastic stock-cutting problem. Oper. Res. 1998, 46, 690–701. [Google Scholar] [CrossRef]
- Alem, D.J.; Munari, P.A.; Arenales, M.N.; Ferreira, P.A.V. On the cutting stock problem under stochastic demand. Ann. Oper. Res. 2010, 179, 169–186. [Google Scholar] [CrossRef]
- Ikonen, T.J.; Heljanko, K.; Harjunkoski, I. Reinforcement learning of adaptive online rescheduling timing and computing time allocation. Comput. Chem. Eng. 2020, 141, 106994. [Google Scholar] [CrossRef]
- Pitombeira-Neto, A.R.; Murta, A.H. A reinforcement learning approach to the stochastic cutting stock problem. EURO J. Comput. Optim. 2022, 10, 100027. [Google Scholar] [CrossRef]
- Gu, S.; Hao, T.; Yao, H. A pointer network based deep learning algorithm for unconstrained binary quadratic programming problem. Neurocomputing 2020, 390, 1–11. [Google Scholar] [CrossRef]
- Sur, G.; Ryu, S.Y.; Kim, J.; Lim, H. A Deep Reinforcement Learning-Based Scheme for Solving Multiple Knapsack Problems. Appl. Sci. 2022, 12, 3068. [Google Scholar] [CrossRef]
- Hubbs, C.D.; Li, C.; Sahinidis, N.V.; Grossmann, I.E.; Wassick, J.M. A deep reinforcement learning approach for chemical production scheduling. Comput. Chem. Eng. 2020, 141, 106982. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Zhu, L.; Cui, Y.; Takami, G.; Kanokogi, H.; Matsubara, T. Scalable reinforcement learning for plant-wide control of vinyl acetate monomer process. Control Eng. Pract. 2020, 97, 104331. [Google Scholar] [CrossRef]
- Shao, Z.; Si, F.; Kudenko, D.; Wang, P.; Tong, X. Predictive scheduling of wet flue gas desulfurization system based on reinforcement learning. Comput. Chem. Eng. 2020, 141, 107000. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Peng, B.; Li, X.; Gao, J.; Liu, J.; Chen, Y.N.; Wong, K.F. Adversarial advantage actor-critic model for task-completion dialogue policy learning. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 6149–6153. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1928–1937. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).