Experimental Investigation and Thermodynamic Assessment of the Ternary Al–Ni–Er System
Abstract
1. Introduction
2. Literature Review
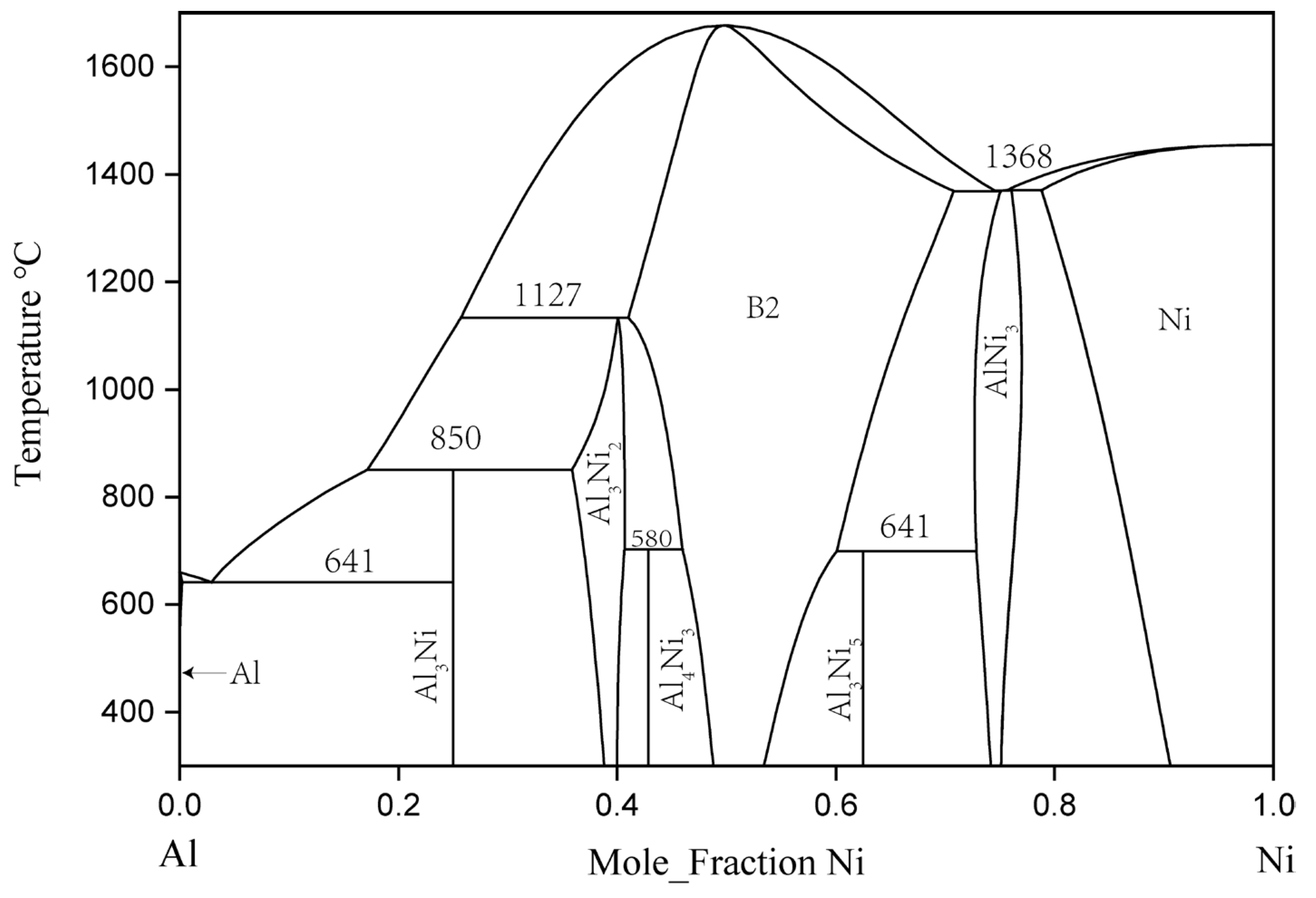
2.1. Binary Al–Ni System
2.2. Binary Er–Ni System
2.3. Binary Al–Er System
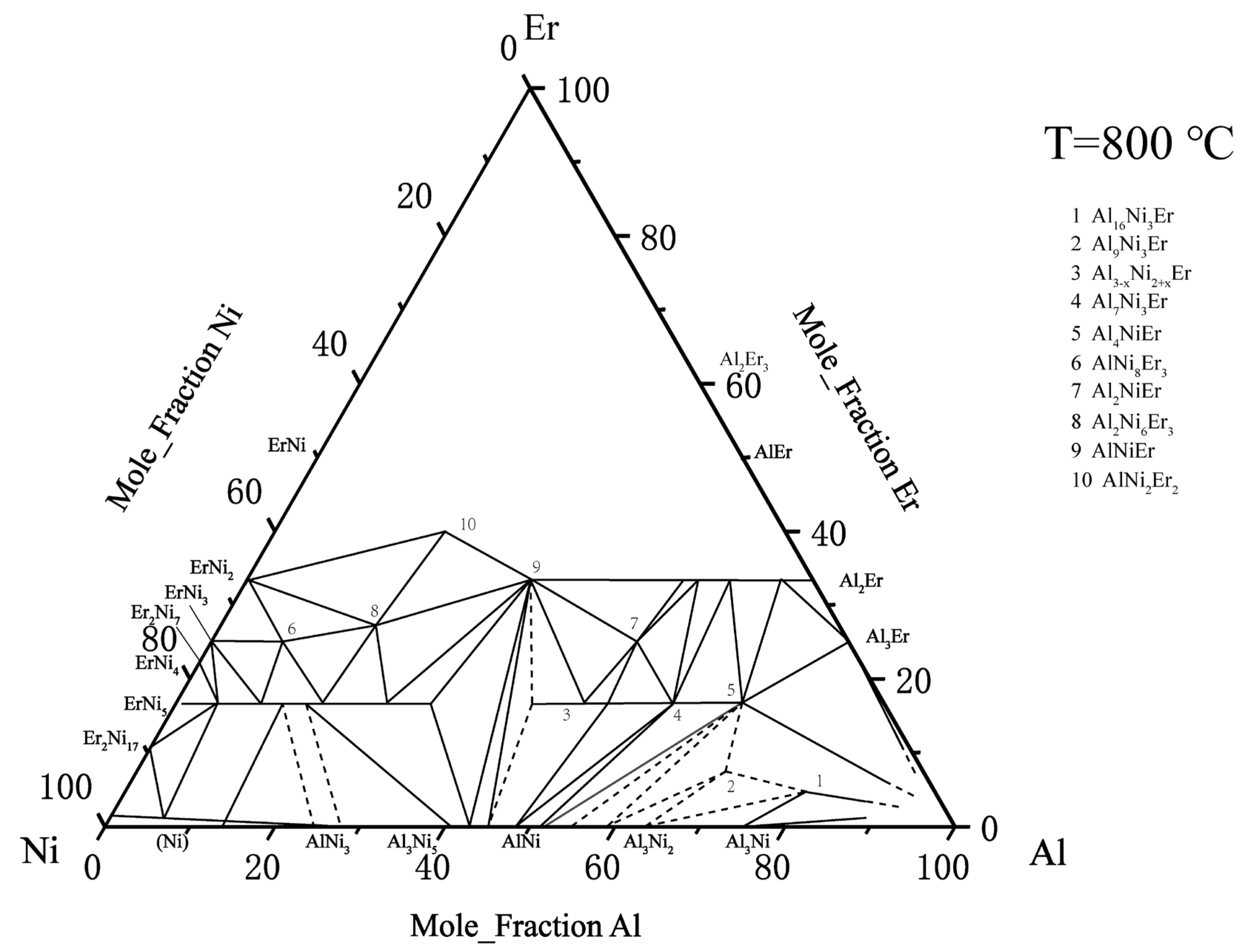
2.4. Ternary Al–Ni–Er System
3. Experimental Details
4. Calculation Methods
4.1. Thermodynamic Modeling
4.1.1. Unary Phases
4.1.2. Solution Phases
4.1.3. Binary Compounds
4.1.4. Ternary Compounds
4.2. First-Principles Calculation
5. Results and Discussion
5.1. Experimental Investigations
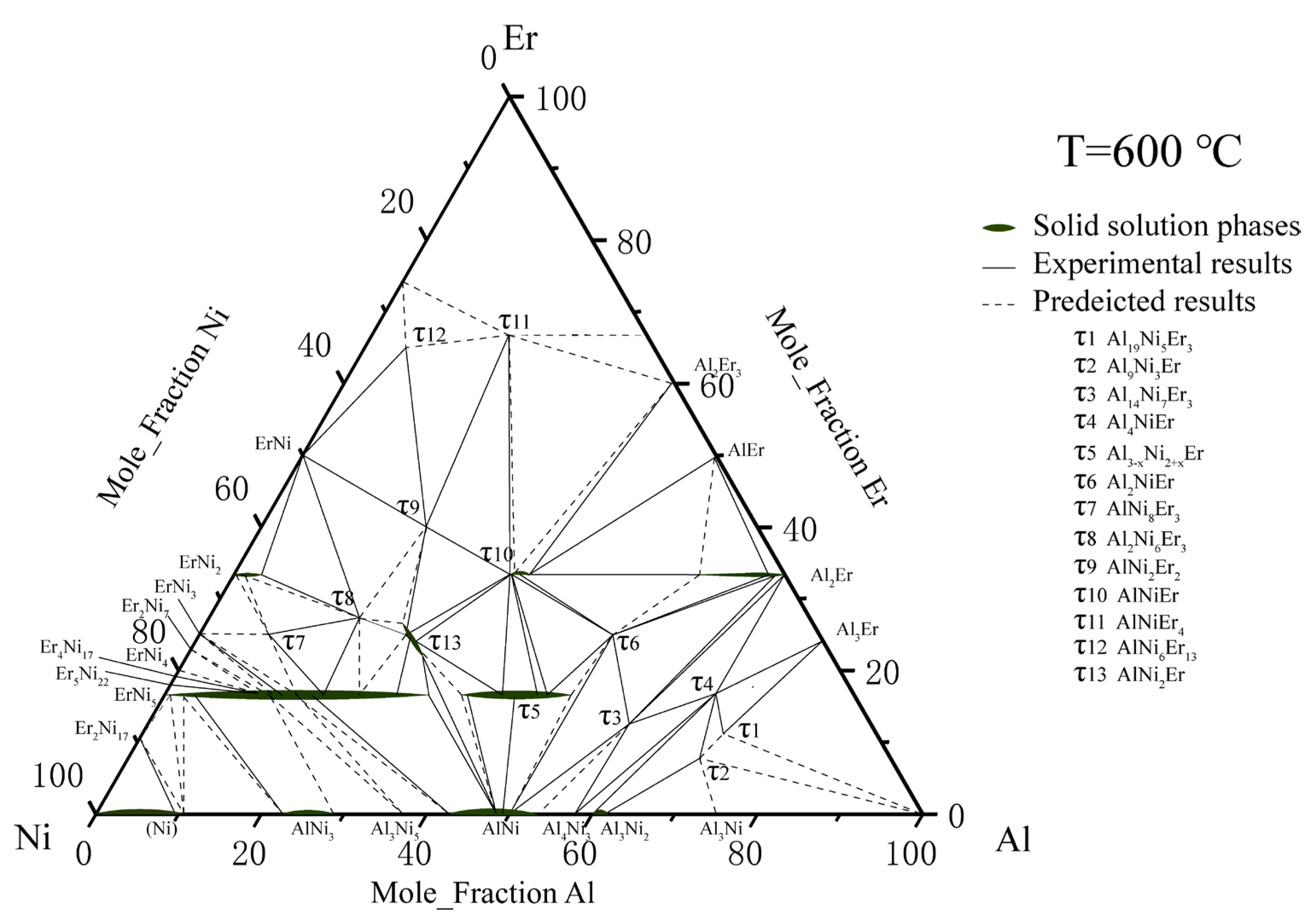
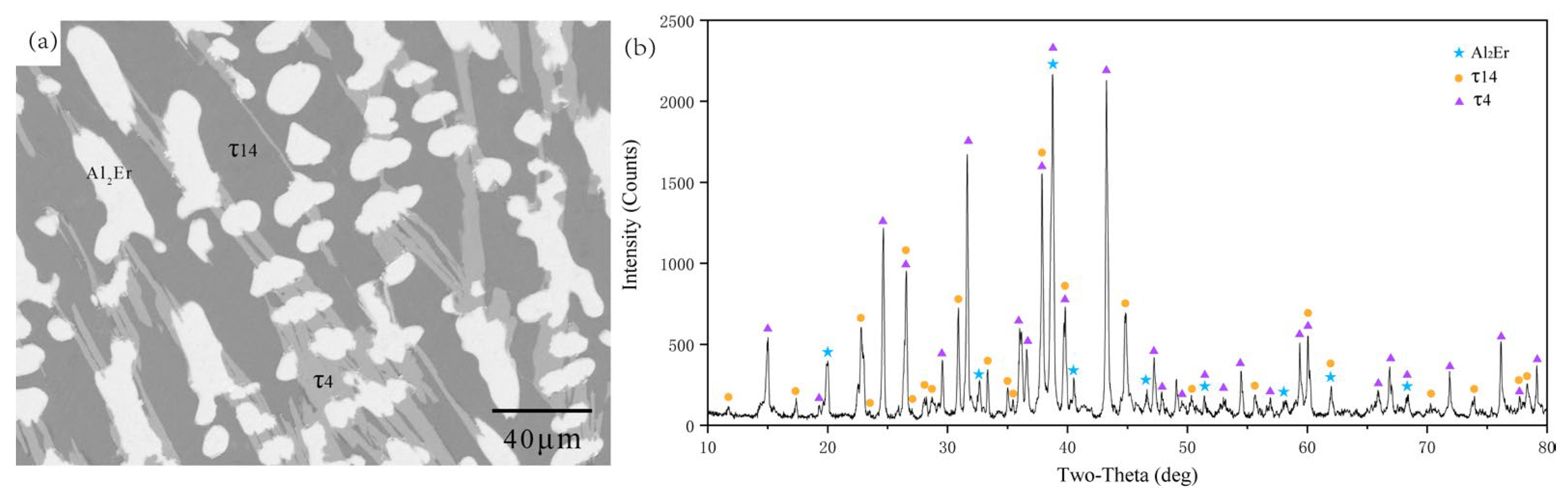
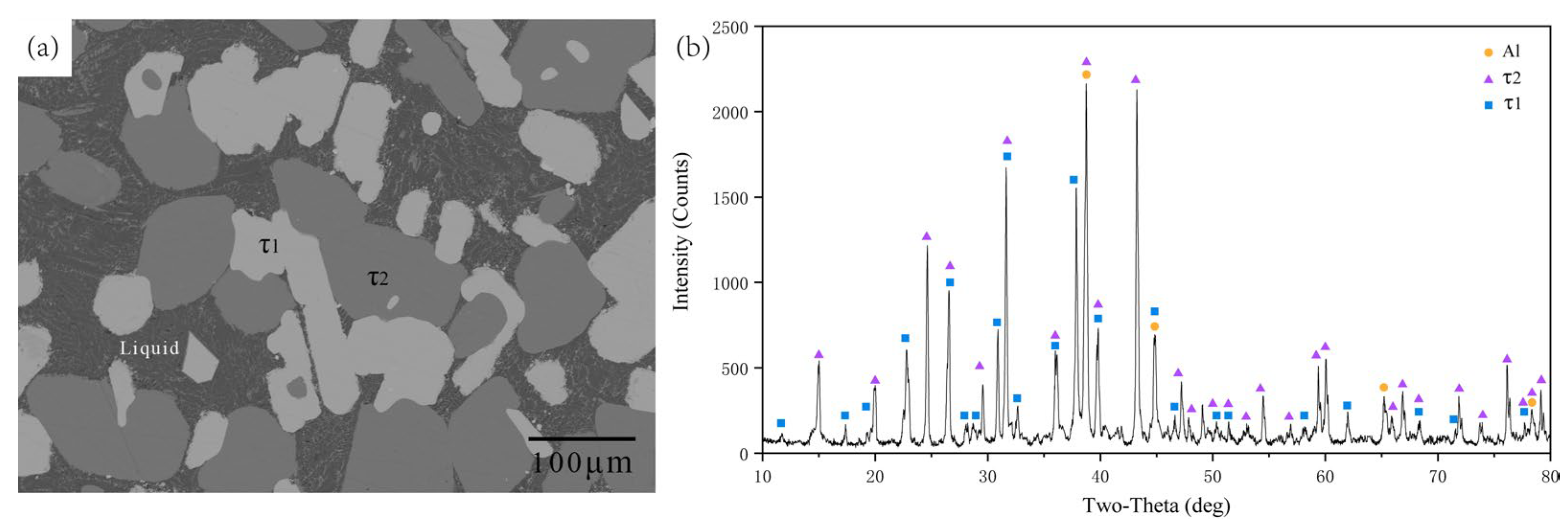
5.1.1. Isothermal Section of the Al-Rich Corner at 600 °C
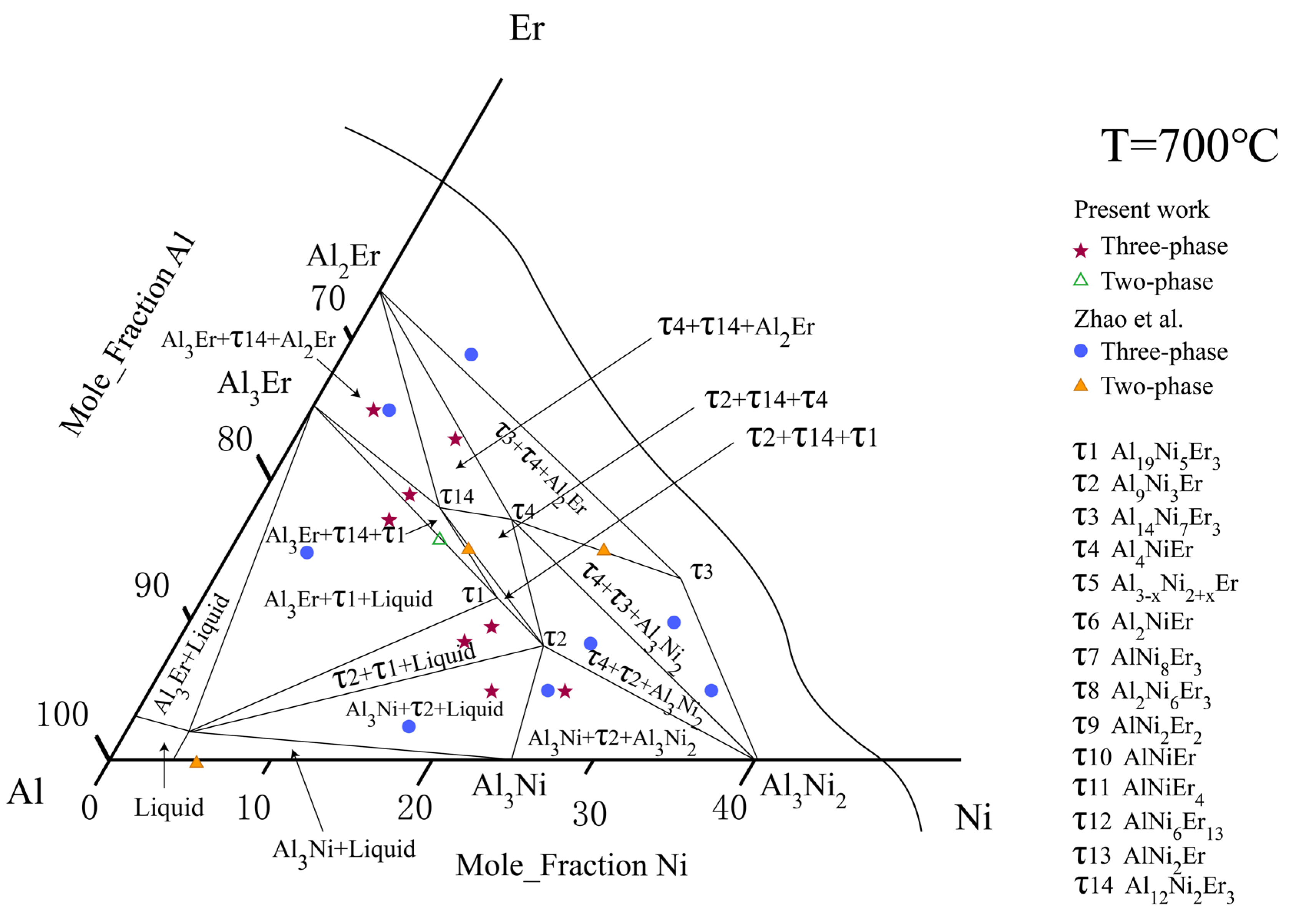
5.1.2. Isothermal Section at 700 °C
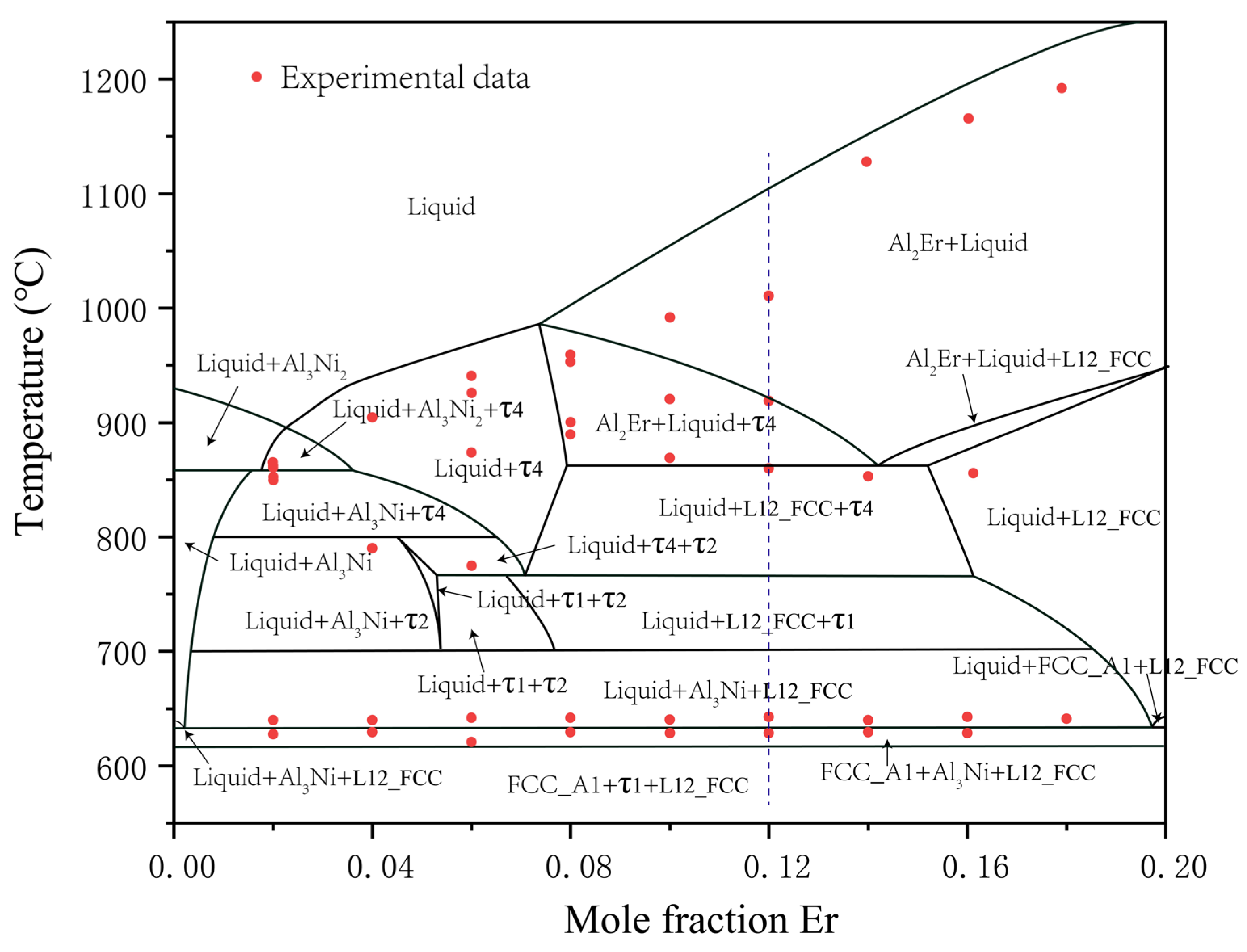
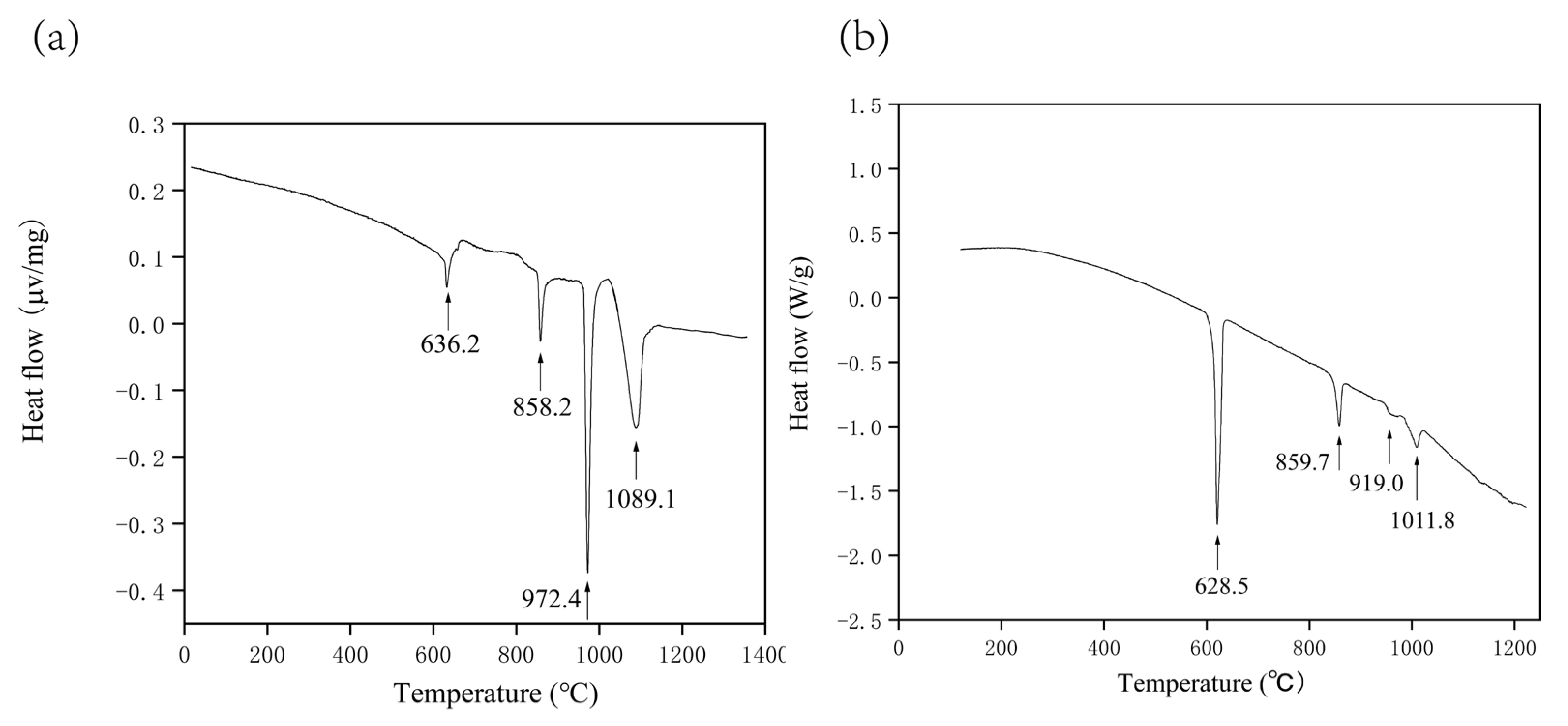
5.1.3. Study of the Vertical Section Phase Diagram
5.2. Thermodynamic Modeling
6. Conclusions
- The isothermal sections at 600 and 700 °C were measured, and a new ternary compound, τ14 (Al12Ni2Er3), was found.
- The vertical sections of the Al–Ni–Er phase diagram with 70 and 80 at. % aluminum content were detected with DSC.
- The thermodynamic database of the Al–Ni–Er system was established. The calculations reproduced the phase equilibria, isothermal sections, and vertical sections.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Deng, Y.; Zhang, Y. Development of high strength aluminum alloys and processing techniques for the materials. Acta Metall. Sin. 2015, 51, 257–271. [Google Scholar] [CrossRef]
- Kong, Y.; Jia, Z.; Liu, Z.; Liu, M.; Roven, H.J.; Liu, Q. Effect of Zr and Er on the microstructure, mechanical and electrical properties of Al-0.4Fe alloy. J. Alloys Compd. 2020, 857, 157611. [Google Scholar] [CrossRef]
- Barkov, R.Y.; Mikhaylovskaya, A.; Yakovtseva, O.; Loginova, I.; Prosviryakov, A.; Pozdniakov, A. Effects of thermomechanical treatment on the microstructure, precipitation strengthening, internal friction, and thermal stability of Al–Er-Yb-Sc alloys with good electrical conductivity. J. Alloys Compd. 2020, 855, 157367. [Google Scholar] [CrossRef]
- Shang, Q.X.; Liu, Y.R.; Su, K.P.; Hu, S.L.; Wang, H.O.; Huang, S.; Yang, D.X.; Huo, D.X.; Liu, J. The Isothermal Section of the Al–Mn–In Ternary System at 773K and Hard Magnetic Properties of MnAlIn Alloys. J. Phase Equilibria Diffus. 2021, 42, 888–897. [Google Scholar] [CrossRef]
- Shen, Y.; Perepezko, J. Al-based amorphous alloys: Glass-forming ability, crystallization behavior and effects of minor alloying additions. J. Alloys Compd. 2017, 707, 3–11. [Google Scholar] [CrossRef]
- Yang, H.; Wang, J.; Li, Y. Influence of TM and RE elements on glass formation of the ternary Al–TM–RE systems. J. Non-Cryst. Solids 2008, 354, 3473–3479. [Google Scholar] [CrossRef]
- Abrosimova, G.; Aronin, A.; Budchenko, A. Amorphous phase decomposition in Al–Ni–RE system alloys. Mater. Lett. 2015, 139, 194–196. [Google Scholar] [CrossRef]
- Chang, Y.; Chen, S.; Zhang, F.; Yan, X.; Xie, F.; Schmid-Fetzer, R.; Oates, W. Phase diagram calculation: Past, present and future. Prog. Mater. Sci. 2004, 49, 313–345. [Google Scholar] [CrossRef]
- Deffrennes, G.; Joubert, J.-M.; Oudot, B. On models to describe the volume in the context of establishing high-pressure Gibbs energy databases. Calphad 2022, 78, 102435. [Google Scholar] [CrossRef]
- Pelton, A.D. Thermodynamics and phase diagrams of materials. In Phase Transformations in Materials; Wiley Online Library: New York, NY, USA, 2001; pp. 1–80. [Google Scholar]
- Li, C.; Song, Q.; Yang, X.; Wei, Y.; Hu, Q.; Liu, L.; Zhang, L. Experimental Investigation of the Phase Relations in the Fe-Zr-Y Ternary System. Materials 2022, 15, 593. [Google Scholar] [CrossRef]
- Okamoto, H. Al-Ni (aluminum-nickel). J. Phase Equilibria Diffus. 2004, 25, 394. [Google Scholar] [CrossRef]
- Lee, K.J.; Nash, P. The Al-Ni-Ti system (Aluminum-Nickel-Titanium). J. Phase Equilibria Diffus. 1991, 12, 551–562. [Google Scholar] [CrossRef]
- Wang, Y.; Cacciamani, G. Thermodynamic modeling of the Al-Cr-Ni system over the entire composition and temperature range. J. Alloys Compd. 2016, 688, 422–435. [Google Scholar] [CrossRef]
- Gwyer, A.G.C. über die Legierungen des Aluminiums mit Kupfer, Eisen, Nickel, Kobalt, Blei und Cadmium. Z. Anorg. Chem. 1908, 57, 113–153. [Google Scholar] [CrossRef]
- Ansara, I.; Dupin, N.; Lukas, H.L.; Sundman, B. Thermodynamic assessment of the Al-Ni system. J. Alloys Compd. 1997, 247, 20–30. [Google Scholar] [CrossRef]
- Du, Y.; Clavaguera, N. Thermodynamic assessment of the AlNi system. J. Alloys Compd. 1996, 237, 20–32. [Google Scholar] [CrossRef]
- Huang, W.; Chang, Y. A thermodynamic analysis of the Ni-Al system. Intermetallics 1998, 6, 487–498. [Google Scholar] [CrossRef]
- Dupin, N.; Ansara, I.; Sundman, B. Thermodynamic re-assessment of the ternary system Al-Cr-Ni. Calphad 2001, 25, 279–298. [Google Scholar] [CrossRef]
- Lu, X.-G.; Sundman, B.; Ågren, J. Thermodynamic assessments of the Ni–Pt and Al–Ni–Pt systems. Calphad 2009, 33, 450–456. [Google Scholar] [CrossRef]
- Chen, H.-L.; Doernberg, E.; Svoboda, P.; Schmid-Fetzer, R. Thermodynamics of the Al3Ni phase and revision of the Al–Ni system. Thermochim. Acta 2011, 512, 189–195. [Google Scholar] [CrossRef]
- Ellner, M.; Kek, S.; Predel, B. ChemInform Abstract: Ni3Al4-A Phase with Ordered Vacancies Isotypic to Ni3Ga4. Less-Common Met. 1989, 154, 207–215. [Google Scholar] [CrossRef]
- Buschow, K. Crystal structures, magnetic properties and phase relations of erbium-nickel intermetallic compounds. J. Less Common Met. 1968, 16, 45–53. [Google Scholar] [CrossRef]
- Moreau, J.M.; Paccard, D.; Gignoux, D. The crystal structure of Er3Ni2. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1974, 257, 195–209. [Google Scholar] [CrossRef]
- Du, Z.; Wang, D.; Zhang, W. Thermodynamic assessment of the Co–Pr, Er–Ni and Ni–Pr systems. J. Alloys Compd. 1999, 284, 206–212. [Google Scholar] [CrossRef]
- Buschow, K.H.J.; van Vucht, J.H.N. Das System Erbium-Aluminium und ein Vergleich mit dem System Yttrıum-Aluminium. Int. J. Mater. Res. 1965, 56, 9–13. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Calderwood, F.W. The Al−Er (Aluminum-Erbium) system. Bull. Alloy Phase Diagr. 1988, 9, 676–678. [Google Scholar] [CrossRef]
- Cacciamani, G.; Saccone, A.; De Negri, S.; Ferro, R. The Al-Er-Mg ternary system Part II: Thermodynamic modeling. J. Phase Equilibria 2002, 23, 38. [Google Scholar] [CrossRef]
- Xu, L.; Shi, X.; Xia, D.; Huang, D.; Tang, H. Experimental investigation and thermodynamic assessment of the Al–Er system. Calphad 2022, 79, 102482. [Google Scholar] [CrossRef]
- Zarechnyuk, O.; Rykhal, R.; Romaka, V.; Kovalska, O.; Shazabura, G. Isothermal sections of the Holmium, erbium-nickel-aluminium ternary systems at 800 °C in the 0 to 0.333 atomic fraction range of the rare-earth metal. Dop. Akad. Nauk Ukr. RSR Ser. A Fiz. Mat. Tekh. Nauki 1982, 14, 78–80. [Google Scholar]
- Gladyshevskii, R.; Cenzual, K.; Parthé, E. The crystal structure of orthorhombic Gd3Ni5Al19, a new representative of the structure series R2+mT4+mAl15+4m. J. Solid State Chem. 1992, 100, 9–15. [Google Scholar] [CrossRef]
- Šorgić, B.; Drašner, A.; Blaẑina, Ẑ. The effect of aluminium on the structural and hydrogen sorption properties of ErNi5. J. Alloys Compd. 1996, 232, 79–83. [Google Scholar] [CrossRef]
- Riccardo, F.; Gilda, Z.; Rinaldo, M. Al-Er-Ni (aluminium–erbium–nickel). Landolt-Börnstein-Group IV Phys. Chem. 2005, 11A2, 249–256. [Google Scholar]
- Zhao, F.; Zhang, L.; Wang, H.; Liu, L. Phase equilibria investigation of the Al–Ni–Er ternary system at 600 °C and 700 °C. Calphad 2021, 75, 102353. [Google Scholar] [CrossRef]
- Massalski, T.B.; Okamoto, H.; Subramanian, P.R. Binary Alloy Phase Diagrams, 2nd ed.; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- Viklund, P.; Haussermann, U.; Lidin, S. NiAl3: A structure type of its own? In Acta Crystallographica A-Foundation and Advances; Int Union Crystallography: Chester, UK, 1996; Volume 52, p. C321. [Google Scholar]
- Bouche, K.; Barbier, F.; Coulet, A. Phase formation during dissolution of nickel in liquid aluminium. Zeitschrift Fuer Met. 1997, 88, 446–451. [Google Scholar] [CrossRef]
- Dwight, A.; Mueller, M.; Conner, R.; Downey, J.; Knott, H. Ternary compounds with the Fe2P-type structure. Trans. Am. Inst. Min. Metall. Pet. Eng. 1968, 242, 2075–2080. [Google Scholar]
- Hilpert, K.; Kobertz, D.; Venugopal, V.; Miller, M.; Gerads, H.; Bremer, F.J.; Nickel, H. Phase Diagram Studies on the Al-Ni System. Ztschrift Für Nat. A 1987, 42, 1327–1332. [Google Scholar] [CrossRef]
- Delsante, S.; Richter, K.W.; Ipser, H.; Borzone, G. Synthesis and structural characterization of ternary compounds belonging to the series RE2+mNi4+mAl15+4m (RE = rare earth metal). Z. Für Anorg. Und Allg. Chem. 2009, 635, 365–368. [Google Scholar] [CrossRef]
- Buschow, K.; Van Der Goot, A. The crystal structure of rare-earth nickel compounds of the type R2Ni7. J. Less Common Met. 1970, 22, 419–428. [Google Scholar] [CrossRef]
- Dwight, A.E. The unit-cell constants of some PuNi3-type compounds. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 2010, 24, 1395–1396. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Long, Y.; Ye, R.; Chang, Y.; Wan, F. Hydrogen induced structural and magnetic transformations in magnetic regenerator materials ErNin (n = 1, 2) and HoCu2. J. Magn. Magn. Mater. 2007, 311, 697–701. [Google Scholar] [CrossRef]
- Okamoto, H.; Massalski, T.B. guidelines for binary phase diagram assessment. J. Phase Equilibria Diffus. 1993, 14, 316–335. [Google Scholar] [CrossRef]
- Garde, C.S.; Ray, J. Magnetic and superconducting behaviour of the (R = La, Pr, Gd, Tb, Ho and Er) systems. J. Phys. Condens. Matter 1997, 9, 7419–7434. [Google Scholar] [CrossRef]
- Dinsdale, A. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A.T. Algebraic Representation of Thermodynamic Properties and the Classification of Solutions. Ind. Eng. Chem. 1948, 40, 345–348. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Liao, J.; Liao, Y.; Wang, H.; Zhang, L.; Ma, Y. Thermodynamic optimization of the Ni–Al–Nd ternary system. Calphad 2019, 64, 16–22. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, Q.; Tian, Y.; Xue, R.; Zhang, L.; Liu, L. Experimental investigation and thermodynamic assessment of the Al–Ag–Sc system. J. Alloys Compd. 2023, 934, 167980. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Tang, F.; Hallstedt, B. Using the PARROT module of Thermo-Calc with the Cr–Ni system as example. Calphad 2016, 55, 260–269. [Google Scholar] [CrossRef]
- Cao, W.; Chen, S.-L.; Zhang, F.; Wu, K.; Yang, Y.; Chang, Y.; Schmid-Fetzer, R.; Oates, W. PANDAT software with PanEngine, PanOptimizer and PanPrecipitation for multi-component phase diagram calculation and materials property simulation. Calphad 2009, 33, 328–342. [Google Scholar] [CrossRef]
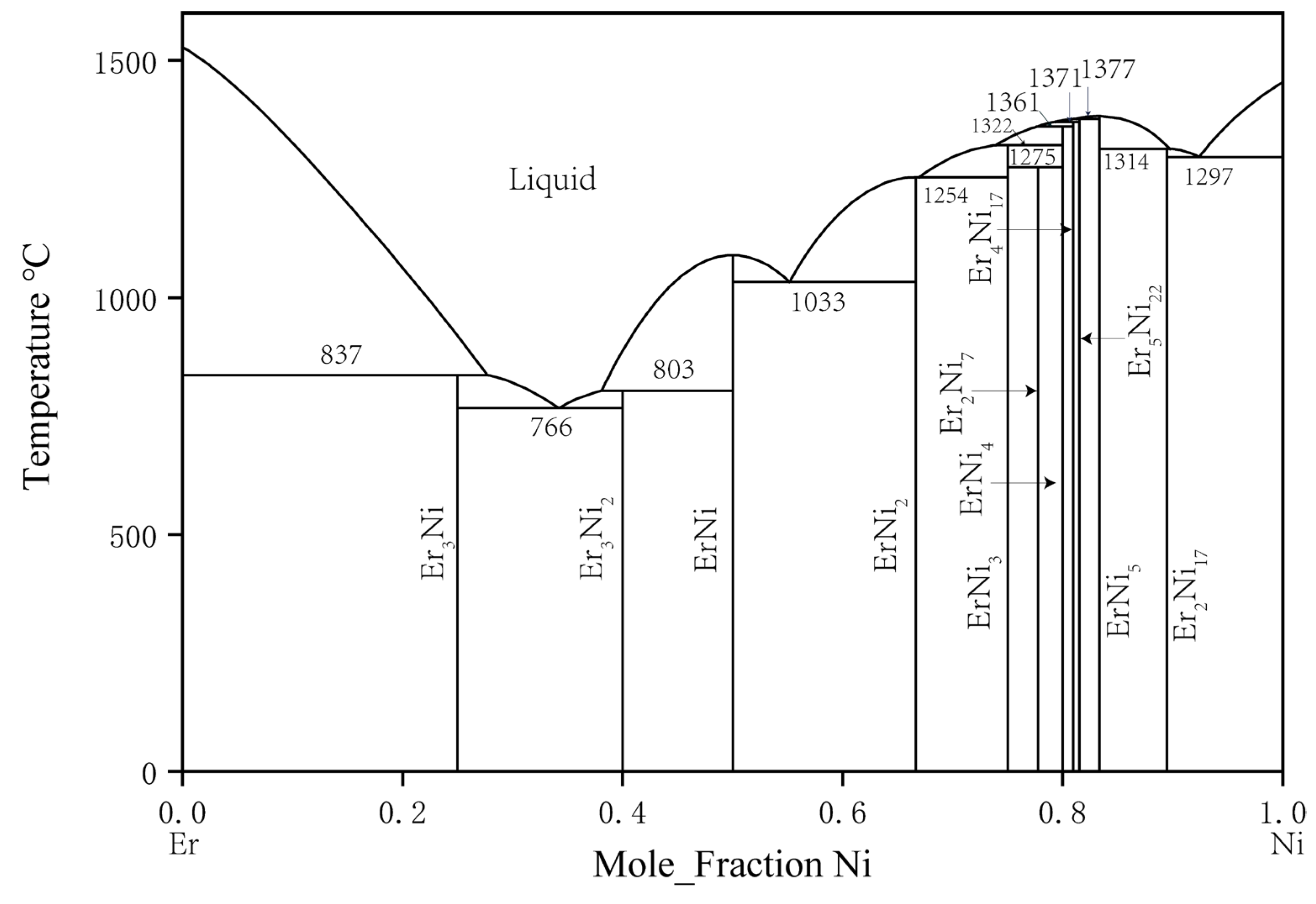
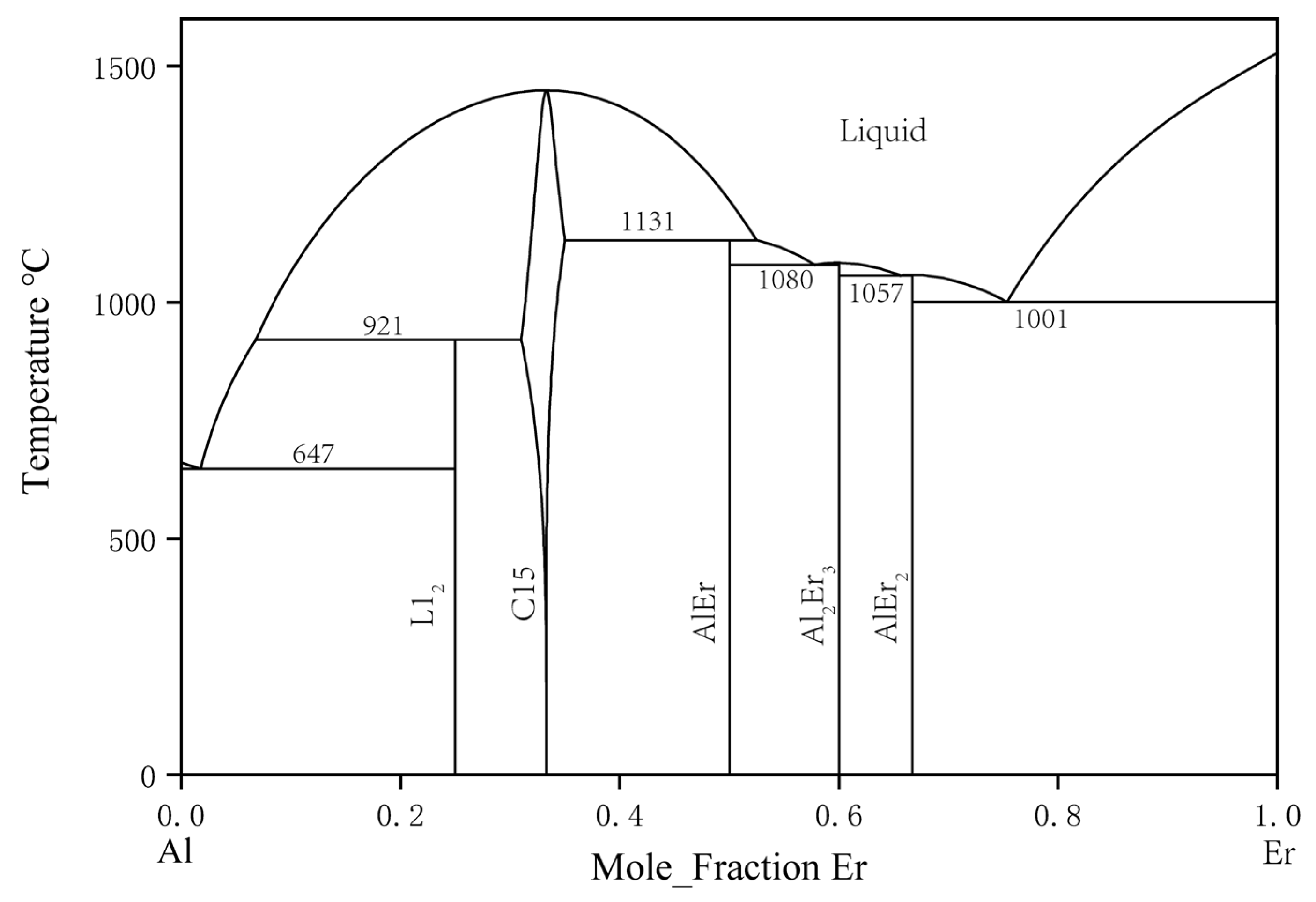




| System | Phase | Prototype | Pearson Symbol | Lattice Parameters (nm) | Refs. | ||
|---|---|---|---|---|---|---|---|
| a | b | c | |||||
| Al | Fcc_A1, (Al) | Cu | cF4 | 0.40496 | [35] | ||
| Ni | Fcc_A1, (Ni) | Cu | cF4 | 0.3524 | [35] | ||
| Er | Hcp_A3, (Er) | Mg | hP2 | 0.359 | 0.555 | [35] | |
| Al–Ni | Al3Ni | Al3Ni | oP16 | 0.6613 | 0.7367 | 0.4811 | [36] |
| Al3Ni2 | Al3Ni2 | hP5 | 0.4028 | 0.4811 | [37] | ||
| AlNi | CsCl | cP2 | 0.28872 | [35] | |||
| Al3Ni5 | Pt5Ga3 | oC16 | 0.753 | 0.661 | 0.376 | [35] | |
| AlNi3 | Cu3Au | cP4 | 0.35792 | [35] | |||
| Al4Ni3 | Ga4Ni3 | cI112 | 1.144 | [22] | |||
| Ni–Er | Er2Ni17 | Th2Ni17 | hP38 | 0.8287 | 0.8017 | [22] | |
| Er5Ni22 | hP108 | 0.4862 | 7.177 | [22] | |||
| Er4Ni17 | hP126 | 0.4869 | 8.407 | [22] | |||
| ErNi4 | PuNi4 | mS30 | 0.4855 | 0.8444 | 1.0231 | [22] | |
| Er2Ni7 | Gd2Co7 | hR54 | 0.4909 | 3.6067 | [38] | ||
| ErNi3 | PuNi3 | hR36 | 0.4941 | 2.4252 | [30] | ||
| ErNi2 | MgCu2 | cF24 | 0.71175 | [31] | |||
| Er3Ni2 | Er3Ni2 | hR45 | 0.8472 | 1.5680 | [39] | ||
| ErNi | FeB | oP8 | 0.6977 | 0.4110 | 0.5443 | [39] | |
| Er3Ni | Fe3C | oP16 | 0.6804 | 0.9432 | 0.6245 | [40] | |
| Al–Er | Al3Er | AuCu3 | cP4 | 0.4235 | [26] | ||
| Al2Er3 | Al2Zr3 | tP20 | 0.81323 | 0.75039 | [41] | ||
| AlEr2 | Co2Si | oP12 | 0.6516 | 0.5015 | 0.9279 | [42] | |
| AlEr | AlDy | oP16 | 0.55791 | 1.1277 | 0.5574 | [43] | |
| Al–Ni–Er | |||||||
| τ1 | Al19Ni5Er3 | Al119Ni5Gd3 | oS108 | 4.0565 | 15.8906 | 26.9752 | [24] |
| τ2 | Al9Ni3Er | Al9Ni3Er | hR78 | 7.2716 | 27.346 | [44] | |
| τ3 | Al14Ni7Er3 | Al14Ni7Gd3 | hP72 | 17.8776 | 4.03212 | [25] | |
| τ4 | Al4NiEr | YNiAl4 | oS24 | 4.044 | 15.08 | 6.631 | [22] |
| τ5 | Al3–xNi2+xEr | Al3Ni2Y | hP18 | 9.01 | 4.049 | [22] | |
| τ6 | Al2NiEr | MgCuAl2 | oS16 | 4.064 | 10.06 | 6.898 | [22] |
| τ7 | AlNi8Er3 | Ce3Co8Si | hP24 | 5.002 | 15.99 | [22] | |
| τ8 | Al2Ni6Er3 | Ce3Ni6Si2 | cI44 | 8.88 | [22] | ||
| τ9 | AlNi2Er2 | W2CoB2 | oI10 | 5.347 | 8.374 | 4.157 | [37] |
| τ10 | AlNiEr | AlNiZr | hP9 | 6.970 | 3.8003 | [45] | |
| τ11 | AlNiEr4 | [34] | |||||
| τ12 | AlNi6Er13 | [34] | |||||
| τ13 | AlNi2Er | [34] | |||||
| τ14 | Al12Ni2Er3 | This work | |||||
| Alloy (No.) | Nominal Composition (at. %) | Chemical Composition of the Experimentally Identified Phases (at. %) | Phase Determination | ||||
|---|---|---|---|---|---|---|---|
| Al | Ni | Er | Al | Ni | Er | ||
| A1 | 80 | 2 | 18 | 99.42 | 0.36 | 0.22 | Al |
| 72.23 | 17.21 | 10.57 | τ1 | ||||
| 76.43 | 0.15 | 23.41 | Al3Er | ||||
| A2 | 80 | 15 | 5 | 96.46 | 3.49 | 0.04 | Al |
| 70.20 | 22.52 | 7.28 | τ2 | ||||
| 75.35 | 24.64 | 0.01 | Al3Ni | ||||
| A3 | 70 | 20 | 10 | 71.32 | 17.94 | 10.74 | τ1 |
| 70.12 | 22.37 | 7.52 | τ2 | ||||
| A4 | 70 | 25 | 5 | 61.20 | 38.76 | 0.04 | Al3Ni2 |
| 74.98 | 24.96 | 0.05 | Al3Ni | ||||
| 69.71 | 23.05 | 7.24 | τ2 | ||||
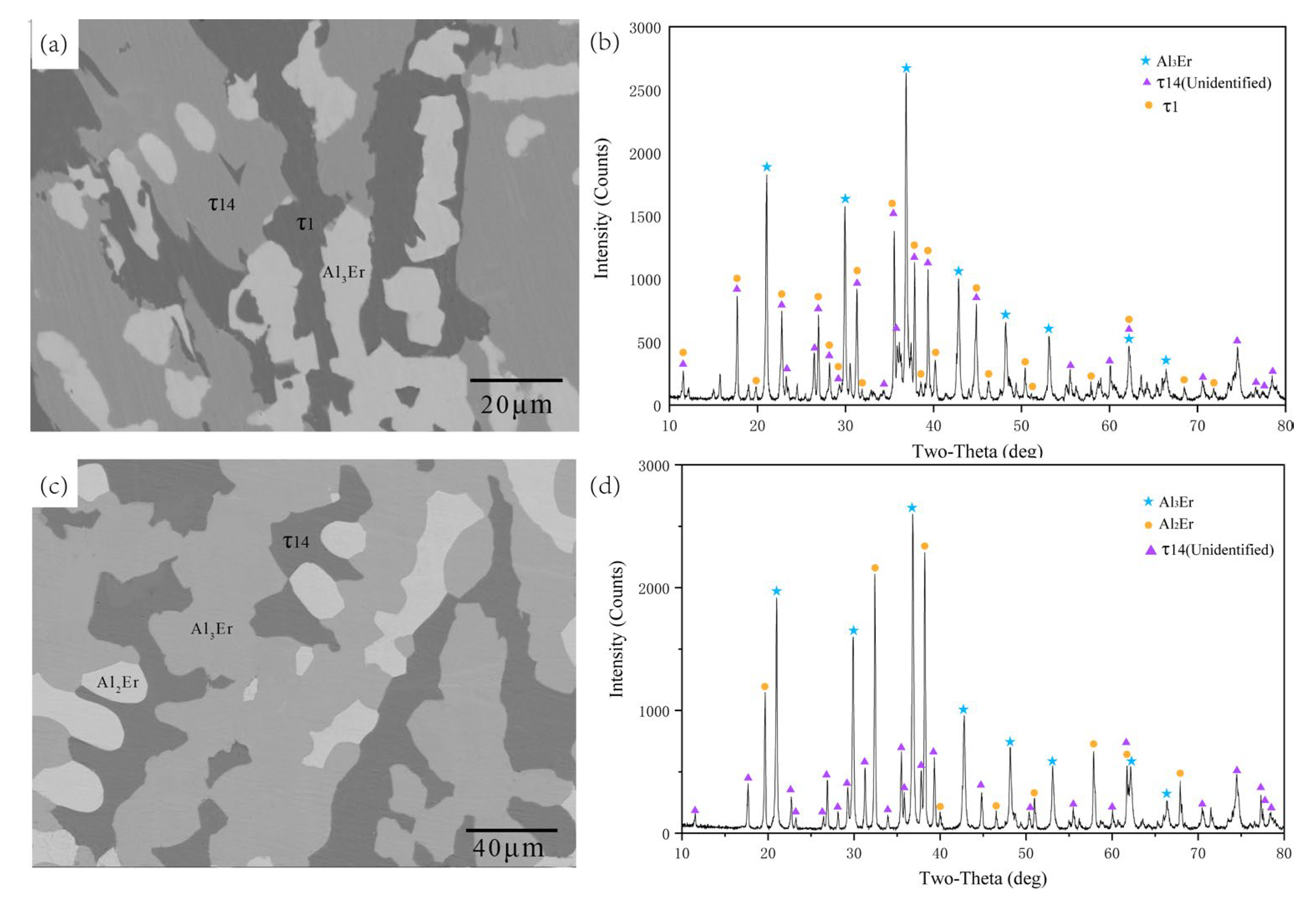
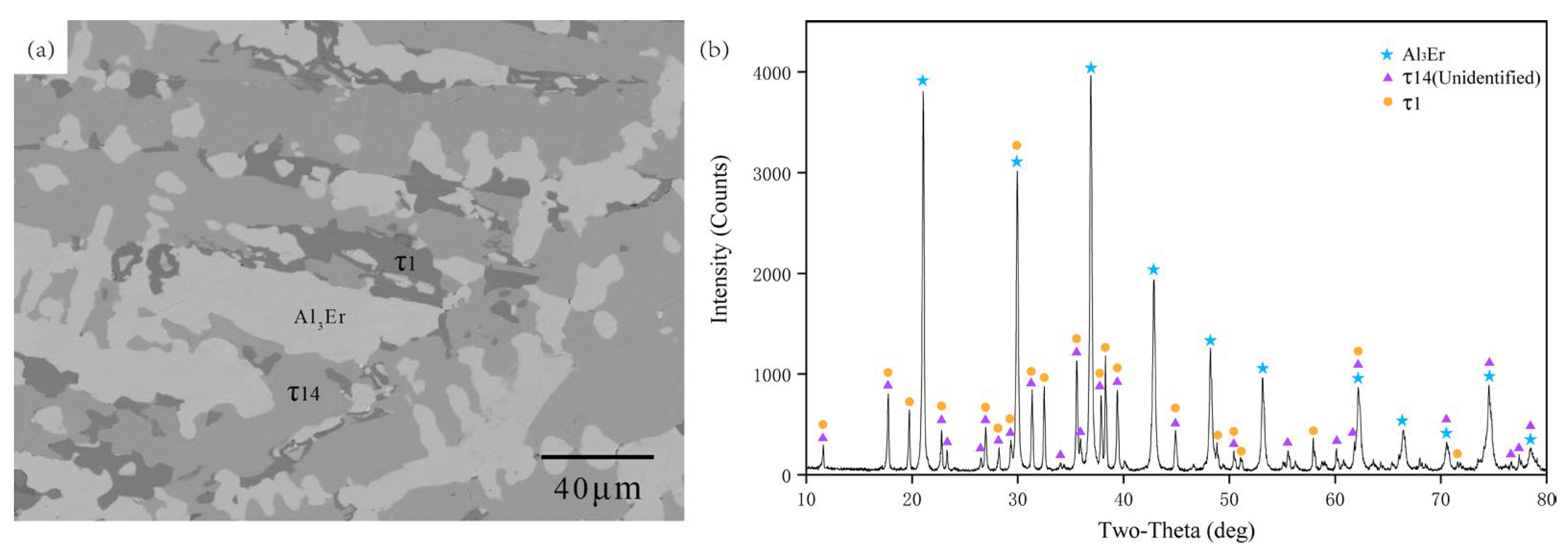
| A5 | 71 | 17 | 12 | 75.44 | 1.43 | 23.13 | Al3Er |
| 70.89 | 17.45 | 11.66 | τ1 | ||||
| A6 | 70 | 22 | 8 | 96.37 | 3.10 | 0.54 | Al |
| 70.61 | 17.76 | 11.64 | τ1 | ||||
| 69.84 | 22.51 | 7.65 | τ2 | ||||
| A7 | 71 | 12 | 17 | 75.03 | 0.00 | 24.97 | Al3Er |
| 72.40 | 14.90 | 12.69 | τ1 | ||||
| 70.02 | 12.33 | 17.65 | τ14 | ||||
| A8 | 70 | 6 | 24 | 75.57 | 0.00 | 24.43 | Al3Er |
| 70.48 | 12.04 | 17.48 | τ14 | ||||
| 66.75 | 0.00 | 33.25 | Al2Er | ||||
| Alloy (No.) | Nominal Composition (at. %) | Chemical Composition of the Experimentally Identified Phases (at. %) | Phase Determination | ||||
|---|---|---|---|---|---|---|---|
| Al | Ni | Er | Al | Ni | Er | ||
| B1 | 71.91 | 24.54 | 3.55 | 74.14 | 25.84 | 0.02 | Al3Ni |
| 70.43 | 21.55 | 8.02 | τ2 | ||||
| 60.25 | 39.75 | 0.00 | Al3Ni2 | ||||
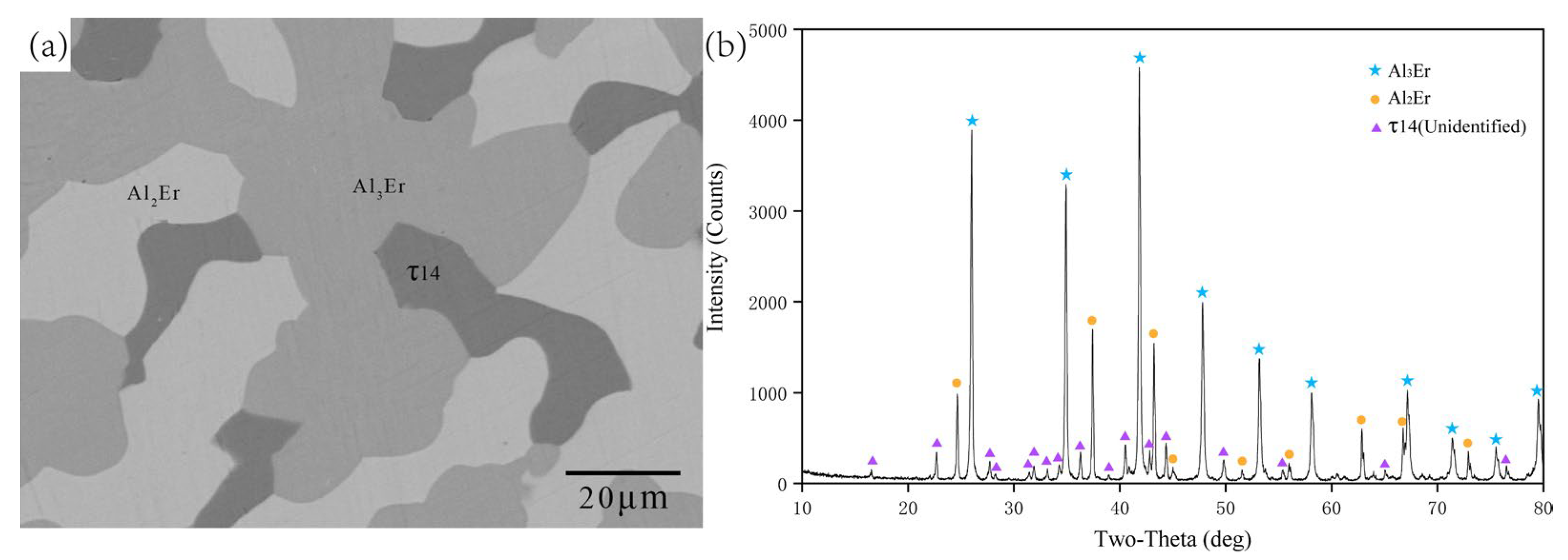
| B2 | 70.87 | 4.20 | 24.93 | 75.37 | 0.00 | 24.63 | Al3Er |
| 66.45 | 0.00 | 33.55 | Al2Er | ||||
| 70.25 | 12.39 | 17.35 | τ14 | ||||
| B3 | 72.44 | 9.21 | 18.36 | 75.03 | 0.00 | 24.97 | Al3Er |
| 70.45 | 12.17 | 17.38 | τ14 | ||||
| 72.65 | 14.78 | 12.57 | τ1 | ||||
| B4 | 74.89 | 17.56 | 7.55 | 72.88 | 15.72 | 11.40 | τ1 |
| 70.44 | 21.45 | 8.11 | τ2 | ||||
| - | - | - | Liquid | ||||
| B5 | 75.50 | 6.47 | 18.03 | 75.56 | 0.00 | 24.44 | Al3Er |
| 73.68 | 14.87 | 11.45 | τ1 | ||||
| 95.10 | 2.74 | 2.16 | Al | ||||
| B6 | 72.35 | 22.35 | 5.30 | 70.96 | 21.45 | 7.59 | τ2 |
| 74.73 | 25.20 | 0.08 | Al3Ni | ||||
| 98.91 | 0.97 | 0.12 | Al | ||||
| B7 | 74.44 | 17.83 | 7.73 | 73.03 | 15.70 | 11.27 | τ1 |
| 71.06 | 20.99 | 7.95 | τ2 | ||||
| - | - | - | Liquid | ||||
| B8 | 68.72 | 11.54 | 19.75 | 66.05 | 0.00 | 33.95 | Al2Er |
| 63.00 | 15.35 | 21.65 | τ4 | ||||
| 69.88 | 12.59 | 17.53 | τ14 | ||||
| B9 | 70.19 | 12.04 | 17.76 | 75.20 | 0.00 | 24.80 | Al3Er |
| 69.96 | 12.26 | 17.79 | τ14 | ||||
| 72.72 | 14.66 | 12.62 | τ1 | ||||
| Alloy | Nominal Composition (at. %) | DSC Peak Corresponding Temperature (°C) | ||||||
|---|---|---|---|---|---|---|---|---|
| (No.) | Al | Ni | Er | 1 | 2 | 3 | 4 | 5 |
| 1 | 70 | 4 | 26 | 915.3 | 1065.0 | 1108.2 | 1281.2 | 1395.8 |
| 2 | 70 | 5 | 25 | 511.8 | 1057.3 | |||
| 3 | 70 | 6 | 24 | 1064.8 | 1120.0 | 1265.5 | 1373.2 | |
| 4 | 72 | 8 | 20 | 911.8 | 1067.8 | 1116.9 | 1279.2 | 1313.0 |
| 5 | 70 | 10 | 20 | 906.50 | 1066.2 | 1142.6 | 1238.7 | |
| 6 | 70 | 12 | 18 | 919.0 | 1117.6 | 1133.6 | 1147.1 | |
| 7 | 70 | 15 | 15 | 636.8 | 910.5 | 1125.7 | 1152.3 | |
| 8 | 70 | 17 | 13 | 633.9 | 914.8 | 994.9 | 1127.9 | |
| 9 | 73.14 | 18.36 | 8.5 | 644.9 | 966.3 | 994.1 | 1070.9 | |
| 10 | 70 | 18.5 | 11.5 | 635.8 | 959.9 | 990.4 | 1123.5 | |
| 11 | 70 | 20 | 10 | 639.0 | 855.8 | 960.2 | 989.6 | 1096.6 |
| 12 | 70 | 23 | 7 | 636.2 | 858.2 | 972.4 | 1089.1 | |
| 13 | 70 | 25 | 5 | 861.7 | 974.9 | 1062.0 | 1111.3 | |
| 14 | 70.2 | 25.8 | 4 | 958.6 | 1091.4 | 1109.4 | ||
| 15 | 70 | 28 | 2 | 635.5 | 861.7 | 968.7 | 1128.3 | |
| 16 | 80 | 2 | 18 | 641.2 | 1204.2 | |||
| 17 | 80 | 4 | 16 | 628.2 | 641.0 | 850.5 | 1143.4 | |
| 18 | 80 | 6 | 14 | 631.1 | 853.0 | 1128.1 | ||
| 19 | 80 | 8 | 12 | 628.5 | 642.8 | 859.7 | 919.0 | 990.3 |
| 20 | 80 | 10 | 10 | 629.8 | 640.2 | 868.8 | 920.6 | 1011.8 |
| 21 | 80 | 12 | 8 | 630.0 | 641.8 | 889.5 | 899.5 | 958.1 |
| 22 | 80 | 14 | 6 | 620.8 | 642.0 | 774.2 | 873.5 | 926.0 |
| 23 | 80 | 16 | 4 | 629.3 | 639.9 | 790.0 | 904.6 | |
| 24 | 80 | 18 | 2 | 627.5 | 640.1 | 852.4 | 862.3 | |
| Phase | Model | Formula | First Principles (0K) |
|---|---|---|---|
| ErNi2 | (Er)1(Ni, Al)2 | ErNi2 | −49.9053 |
| ErNi5 | (Er)1(Ni, Al)5 | ErNi5 | −15.7665 |
| Al2Er | (Al, Ni, Er)2(Al, Ni, Al)1 | AlNi2 | −30.5421 |
| ErNi2 | 112.6254 | ||
| τ1 | (A1)19(Ni)5(Er)3 | Er3Ni5Al19 | −50.5094 |
| τ2 | (A1)9(Ni)3(Er)1 | ErAl9Ni3 | −53.6710 |
| τ3 | (A1)14(Ni)7(Er)3 | Er3Ni7Al14 | −62.7523 |
| τ4 | (A1)4(Ni)1(Er)1 | ErAl4Ni | −55.0009 |
| τ6 | (A1)2(Ni)1(Er)1 | ErAl2Ni | −65.7477 |
| τ7 | (A1)1(Ni)8(Er)3 | Er3AlNi8 | −50.858 |
| τ8 | (A1)2(Ni)6(Er)3 | Er3Al2Ni6 | −61.6016 |
| τ9 | (A1)1(Ni)2(Er)2 | Er2AlNi2 | −59.857 |
| τ10 | (A1)1(Ni)1(Er)1 | ErAlNi | −64.2862 |
| Phase | Thermodynamic Parameters | Reference |
|---|---|---|
| Liquid | model (Al, Ni, Er)1 | |
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| [25] | ||
| [25] | ||
| BCC_B2 | model (Al, Ni, VA)1 (Al, Ni, VA)1 | |
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| BCC_A2 | Model (Al, Ni, Er)1 (VA)3 | |
| [17] | ||
| FCC_A1 | Model (Al, Ni, Er)1 (VA)1 | |
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [25] | ||
| L12_FCC | Model (Al, Ni, Er)0.75 (Al, Ni, Er)0.25(VA)1 | |
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| HCP | Model (Al, Ni, Er)1 (VA)1 | |
| [25] | ||
| Al3Ni | Model (Al)0.75 (Ni)0.25 | |
| [17] | ||
| Al3Ni2 | Model (Al)3 (Al, Ni)2(Ni, VA)1 | |
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| [17] | ||
| Al3Ni5 | Model (Al)0.375 (Ni)0.625 | |
| [17] | ||
| Al4Ni3 | Model (Al)4 (Ni)3 | |
| [17] | ||
| Er3Ni | Model (Er)3 (Ni)1 | |
| [25] | ||
| Er3Ni2 | Model (Er)3 (Ni)2 | |
| [25] | ||
| ErNi | Model (Er)1 (Ni)1 | |
| [25] | ||
| ErNi3 | Model (Er)1 (Ni)3 | |
| [25] | ||
| Er2Ni7 | Model (Er)2 (Ni)7 | |
| [25] | ||
| ErNi4 | Model (Er)1 (Ni)4 | |
| [25] | ||
| Er4Ni17 | Model (Er)4 (Ni)17 | |
| [25] | ||
| Er5Ni22 | Model (Er)5 (Ni)22 | |
| [25] | ||
| Er2Ni17 | Model (Er)2 (Ni)17 | |
| [25] | ||
| AlEr | Model (Al)0.5 (Er)0.5 | |
| [52] | ||
| Al2Er3 | Model (Al)0.4 (Er)0.6 | |
| [52] | ||
| AlEr2 | Model (Al)0.33 (Er)0.667 | |
| [52] | ||
| ErNi2 | model (Er)1 (Al, Ni)2 | |
| [25] | ||
| This work | ||
| This work | ||
| This work | ||
| ErNi5 | Model (Er)1 (Ni, Al)5 | |
| [25] | ||
| This work | ||
| This work | ||
| Al2Er | Model (Al, Ni, Er)2 (Al, Ni, Er)1 | |
| [52] | ||
| [52] | ||
| [52] | ||
| [52] | ||
| This work | ||
| This work | ||
| This work | ||
| This work | ||
| This work | ||
| A119Ni5Er3 | Model (Al)19 (Ni)5 (Er)3 | |
| This work | ||
| A19Ni3Er | Model (Al)9 (Ni)3 (Er)1 | |
| This work | ||
| Al14Ni7Er3 | Model (Al)14 (Ni)7 (Er)3 | |
| This work | ||
| Al4NiEr | Model (Al)4 (Ni) (Er)1 | |
| This work | ||
| Al2NiEr | Model (Al)2 (Ni) (Er)1 | |
| This work | ||
| AlNi8Er3 | Model (Al)1 (Ni)8 (Er)3 | |
| This work | ||
| Al2Ni6Er3 | Model (Al)2 (Ni)6 (Er)3 | |
| This work | ||
| AlNi2Er2 | Model (Al)1 (Ni)2 (Er)2 | |
| This work | ||
| AlNiEr | Model (Al)1 (Ni)1 (Er)1 | |
| This work | ||
| AlNiEr4 | Model (Al)1 (Ni)1 (Er)4 | |
| This work | ||
| AlNi6Er13 | Model (Al)1 (Ni)6 (Er)13 | |
| This work | ||
| AlNi2Er | Model (Al)1 (Ni)2 (Er)1 | |
| This work | ||
| T5 | Model (Al, Ni)3 (Al, Ni)2 (Er)1 | |
| This work | ||
| This work | ||
| This work | ||
| This work | ||
| This work | ||
| This work | ||
| This work | ||
| This work | ||
| Al12Ni2Er3 | Model (Al)12 (Ni)2 (Er)3 | |
| This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q.; Li, C.; Deng, Z.; Zhang, L.; Liu, L. Experimental Investigation and Thermodynamic Assessment of the Ternary Al–Ni–Er System. Processes 2023, 11, 1061. https://doi.org/10.3390/pr11041061
Song Q, Li C, Deng Z, Zhang L, Liu L. Experimental Investigation and Thermodynamic Assessment of the Ternary Al–Ni–Er System. Processes. 2023; 11(4):1061. https://doi.org/10.3390/pr11041061
Chicago/Turabian StyleSong, Qian, Chenbo Li, Zixuan Deng, Ligang Zhang, and Libin Liu. 2023. "Experimental Investigation and Thermodynamic Assessment of the Ternary Al–Ni–Er System" Processes 11, no. 4: 1061. https://doi.org/10.3390/pr11041061
APA StyleSong, Q., Li, C., Deng, Z., Zhang, L., & Liu, L. (2023). Experimental Investigation and Thermodynamic Assessment of the Ternary Al–Ni–Er System. Processes, 11(4), 1061. https://doi.org/10.3390/pr11041061