Abstract
In this paper, taking Block G in Canada as an example, combined with the data of the working area, the Pearson–MIC comprehensive evaluation method was adopted to optimize the key parameters of productivity. Based on the analytic hierarchy process, the weight of each parameter was calculated, the grade of evaluation index of the “sweet spot” was divided, the standard of the sweet spot was established, and the distribution of the superimposed sweet spot was finally depicted. The results show that lateral length, number of stages, volume of fluid, and amount of proppant are the key engineering parameters of horizontal well, and lateral length is an independent key engineering parameter. The cumulative gas production in the first two years was normalized on the lateral length to eliminate the engineering influence, and the total organic carbon (TOC) was finally determined as the key geological parameter, whereas porosity and water saturation were the secondary key parameters. The area of Type I sweet spots accounts for 24.2% in the Series Upper and 23.1% in the Series Lower. This study proposed a new sweet spot prediction idea based on the influence of geological factors on productivity, and its results also laid a foundation for the subsequent placement of horizontal wells in Block G.
1. Introduction
The term “sweet spot” refers to an oil and gas enrichment area that can be preferentially explored and developed under existing economic and technical conditions [1,2,3]. There are three prediction methods: (1) identification of favorable reservoirs through seismic inversion technology; (2) comprehensive analysis and prediction of a sweet spot based on geological research of reservoir formation, diagenesis, sedimentation, and sequence; and (3) prediction of a sweet spot with mathematical analysis methods by analyzing the influence of reservoir physical property, reserve abundance, reservoir thickness, and other formation parameters on productivity based on existing data. With the gradual accumulation of production materials and the deepening of reservoir understanding, the “static–dynamic method” is widely adopted, which use dynamic data to screen the main control parameters and combining geological models to predict the sweet spot.
Sweet spots are divided into geological sweet spots and engineering sweet spots. The geological sweet spot manifests higher yield under the same fracturing technology, and its main parameters include porosity, permeability, gas saturation, reservoir thickness, total organic carbon, vitrinite reflectance, etc. The engineering sweet spot refers to the area conducive to fracturing construction, and its main parameters include brittle mineral content, brittleness index, fracture pressure, pore pressure, crustal stress, etc. [4,5,6,7,8]. Scholars have done a lot of research on the evaluation and prediction of the sweet spot. Pan et al. (2016) elaborated on the geological conditions of the sweet spot of shale gas reservoirs based on a large amount of data [9]. Chen et al. (2018) proposed a set of multivariate statistical methods to identify potential sweet spots based on the relationship between the production of tight oil production wells and geological factors [10]. Wei et al. (2021) quantitatively evaluated the comprehensive sweet spot of shale oil by establishing the evaluation function of sweet spot characterization parameters and calculating the comprehensive weight factor based on the BP neural network, Eaton method, and other methods [11]. Chen et al. (2016) raised the concept of shale oil and gas vertical sweet spots by comprehensively considering various factors [12]. Zhou et al. (2020) analyzed the key geological parameters of tight sandstone reservoir, and proposed the sweet spot model for qualitative identification of factor analysis and quantitative evaluation criteria [13]. Li et al. (2020) established the horizontal well section optimization model by using the combination weight method in the form of normalized index value and weight product [14]. Han et al. (2019) used RGB color fusion method to get the prediction result of sweet spot for five key attributes [15]. Liao et al. (2019) qualitatively analyzed the influence of geological and engineering sweet spot parameters on gas production, and quantitatively characterized the sweet spot coefficient by using the radar area model and weight model [16,17]. Montgomery et al. (2005) uses seven parameters for evaluation: total organic carbon, original oil and gas potential, vitrinite reflectance, content and composition of natural gas, formation temperature, and hydrocarbon conversion ratio [18]. Chalmers and Bustin (2007) used total organic carbon, organic matter type, vitrinite reflectance, mineral composition, water saturation, pore diameter, gas adsorption capacity, porosity, and permeability when evaluating the Cretaceous shale of British Columbia in the Western Canada Basin [19]. Curtis (2002) selects reservoir thickness, mineral, total organic carbon, organic matter type, vitrinite reflectance, permeability, pressure, brittle mineral content, and other parameters to optimize favorable areas in Antrim, Ohio, New Albany, Barnett, and Lewis and other blocks [20]. Pejman et al. (2017) analyzed log data through two methods of data mining and machine learning technology to identify areas containing high total organic carbon (TOC) and brittle rocks that are prone to fracture [21]. Heege et al. (2015) evaluated the underexplored shale and mapped out sweet spots across shale basins based on the properties of North American shale (Marcellus, Bakken, Haynesville, and Barnett), i.e., vitrinite reflectance, porosity, depth, thickness, absorbed gas content, and brittleness index [22]. Munther et al. (2019) simplified the complexity of unconventional resource evaluation and evaluated the oil and gas resource prospects of Goldwyer by considering the parameters of total organic carbon, total porosity, water saturation and brittleness index, and depicting the average map of different attributes in a weighted way [23]. Sahoo et al. (2020) integrated data analytics and fluid geochemical data (mainly Ph/nC18 and Pr/nC17) to map the sweet spots within a producing shale play of North America under the limited conditions of core data, logging data, and seismic data [24]. Tang et al. (2020) illustrated a new tool that uses gradient-boosting decision trees (GBDTs) and ensemble models to classify reservoir quality and identify logging curves more effectively, which further helps search and identify sweet spots automatically [25]. Yuan et al. (2022) applied advanced well logging and slim-compact microimager (SCMI) technologies to conduct high-resolution quantitative analysis of the Goldwyer Formation in the Canning Basin, Western Australia, from in situ macroscopic scale to laboratory microscale, and believed that the most favorable lithofacies in the sweet spot develop numerous organic matter/mineral nanopores for hydrocarbon storage from a microscopic view [26]. Nelson et al. (2022) proposed a workflow to quantify completion quality (CQ) and reservoir quality (RQ), and offered a method by which to compare the predicted sweet spots against available production data via their correlation coefficient, and finally resulted reasonable formation property maps, and the successful identification of sweet spots [27]. At present, the prediction of sweet spot is generally based on simple geological research without considering the factors of productivity. This paper takes the Upper Montney Formation of Block G in Canada as an example to analyze the impact of various geological parameters on the productivity of horizontal wells through Pearson correlation coefficient and maximal information coefficient (MIC) method, optimizes the key parameters, and finally determines the weight of each parameter and predicts the sweet spot by using the analytic hierarchy process. This study can not only provide technical support for efficient development of Block G in Canada, but also provide reference for similar gas fields.
2. Geology
Block G in Canada is located in the western edge of the Western Canada Basin. Three sets of strata were adopted from bottom to top, namely the Triassic, Jurassic, and Cretaceous, in which the oil-bearing strata mainly include the Triassic Montney Formation, Doig Phosphate Formation, and Cretaceous Cadomin Formation. The Triassic Montney Formation is divided into Upper Montney and Lower Montney, wherein the Upper Montney Formation is the target layer of this study and belongs to the “marine” dense siltstone deposits on the passive continental margin. The sedimentation center of sandstone migrates from northeast to southwest, and the sandstone is stacked forward on the plane, belonging to thick massive tight sandstone. Its thickness is about 150~200 m, and the altitude is −1950 m~−2880 m. The stratum shows the characteristics of multicycle sandstone progradation filling mode, which is subdivided into seven layers, AA and A~F, from bottom to top [28]. At present, two sets of development layer series are adopted: Series Upper includes three layers (F, E, D), and Series Lower includes four layers (C, B, A and AA) (Figure 1).
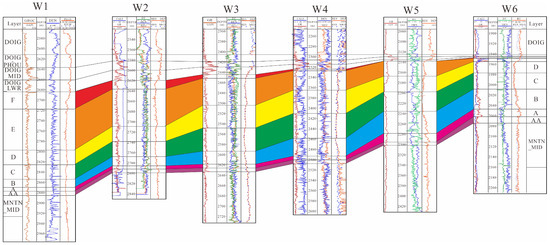
Figure 1.
Cross section of Upper Montney Formation in the Western Canada Basin.
The content of brittle minerals such as quartz and calcite in the Upper Montney Formation is relatively high, accounting for approximately 40% of the total mineral components. The pores of rock particles are small and the degree of diagenesis is high. The mudstone particles are silt with 20~50 μm particles relatively concentrated according to Udden–Wentworth classification (Table 1) [29], and the pore types are mainly intergranular pore and intercrystalline pore. The extremely fine sandstone has relatively high content of argillaceous and organic matter between grains. The gamma ray (GR) curve shows a certain sawtooth shape, indicating that it has obvious characteristics of “self-source and self-reservoir”, strong hydrocarbon generation capacity, and adsorbed gas, similar to shale [30]. The hydrogen index (HI) sample value of the reservoir ranges from 25 to 50, and the type of organic matter belongs to type II with high organic matter abundance. The TOC is generally between 2% and 4%.

Table 1.
Udden–Wentworth Scale.
3. Methodology
3.1. Pearson–MIC Comprehensive Evaluation Method
Pearson correlation coefficient is used to measure the degree of correlation between two variables. Its value is between −1 and 1, reflecting the linear relationship between variables and the direction of correlation. The greater the absolute value of correlation coefficient, the stronger the correlation. Positive values represent positive correlation and negative values represent negative correlation. It is generally believed that the relationship between the absolute value of the obtained correlation coefficient and the correlation strength is as follows: [0.0, 0.2), uncorrelated or very weak correlation; [0.2, 0.4), weak correlation; [0.4, 0.6), medium intensity correlation; [0.6, 0.8), strong correlation; and [0.8, 1.0], extremely strong correlation.
When two groups of variables with linear relationships are continuous and have normal distribution or unimodal symmetric distribution close to normal distribution, the correlation between these two groups of variables can be expressed by product difference correlation coefficient. The formula is
In the formula, is the Pearson correlation coefficient, is a parameter value of group variable and its average value, and is a parameter value of group variable and its average value.
The maximal information coefficient (MIC), is used to measure the linear or nonlinear correlation between two variables X and Y. The basic mathematical principle is: for any two variables X and Y in the sample data set D, the sample size in the sample data set is N, and the two variables have i and j possible values respectively, so that the correlation map of the two variables can be divided into i × j, and then calculate the maximum information coefficient MIC by the following formula:
In the formula, is the MIC of , in the grid, and is the number of samples.
The Fisher-z transformation is a method used in statistics to test hypotheses of correlation coefficient, and its formula is
After getting z, calculate the standard deviation of z (SDz) and select the significance threshold α, and check the standard deviation of the corresponding mean value. This article takes α as 0.95, and the corresponding inspection value is 1.95. From this, the upper limit Max and lower limit Min are calculated. If the upper and lower limits are on the same side of zero, the sample is statistically significant. We have
3.2. Analytic Hierarchy Process
The analytic hierarchy process (AHP) refers to a systematic method that takes a complex multiobjective decision-making problem as a system, decomposes the objective into multiple objectives or criteria, and then into several levels of multiple indicators, and calculates the hierarchical single ranking and total ranking through the qualitative index fuzzy quantitative method to serve as the objective and multiple scheme optimization decision-making [31]. The specific steps include establishing the hierarchical structure model, constructing the pairwise matrix, hierarchical single ranking and its consistency check, hierarchical total ranking and its consistency check.
According to the elements included in the analysis system and the relationship between the elements, a hierarchical structure model is established, which is generally divided into target layer, scheme layer and criterion layer. Then a pairwise matrix is constructed: suppose there are n factors in a layer, compare their influence on a criterion in the previous layer, and determine the proportion of the layer to a criterion. The above comparison is between two factors, i.e., aij = bi/bj. We have
Hierarchical single ranking is the process of determining the influence degree of each factor in the next layer on a factor in the previous layer, that is, the process of solving the pairwise matrix constructed above, generally including iterative method, sum product method, and square root method. The square root method is introduced here.
- (1)
- Multiply the elements of A by rows: .
- (2)
- Take the n root of the resulting product: .
- (3)
- Normalize the root vector to obtain the eigenvector W: .
- (4)
- Calculate the maximum eigenroot of the pairwise matrix:
In practice, the pairwise matrix is required to meet the general consistency, and a consistency check is required. Only through inspection can it be explained that the pairwise matrix is logically reasonable, and the analysis of the results can continue. The steps of consistency inspection are as follows.
- (1)
- Calculate consistency index CI: .
- (2)
- Look up the table to determine the corresponding average random consistency index RI (RI is the average of the maximum eigenvalue of a certain number of n-order random matrices and its value is only related to the order (n) of the matrix).
- (3)
- Calculate the consistency ratio CR and make judgment: .
When CR < 0.1, it is considered that the consistency of the pairwise matrix is acceptable. When CR > 0.1, it is considered that the pairwise matrix does not meet the consistency requirements, and the pairwise matrix needs to be revised.
4. Analysis on Key Parameters of Horizontal Well Productivity in Tight Gas Reservoir
4.1. Interfering Factor of Horizontal Well Productivity in Tight Gas Reservoir
There are many factors affecting the productivity of horizontal wells in tight gas reservoirs, and these are mainly divided into geological factors and engineering factors. Geological factors include permeability, reservoir thickness, porosity, water saturation, total organic carbon (TOC), brittle mineral content, crustal stress, etc. Engineering factors include lateral length, fracturing technology, number of stages, volume of fracturing fluid, amount of proppant, etc.
Unconventional reservoir development requires large-scale hydraulic fracturing, and the role of permeability is limited, and the data scattering about it and the cumulative production of horizontal wells in the first two years is disordered, without an obvious linear relationship, which has no obvious correlation with the productivity of horizontal wells. Reservoir thickness is an important condition for sandstone to have sufficient reservoir space, but the data scattering about it and horizontal well productivity is triangular, indicating that there is no correlation between them. Porosity is the key index to determine the abundance, and the overall scattering about it and production in the first two years is positively correlated, which has a certain impact on the productivity of horizontal wells. Water saturation is negatively correlated with horizontal well productivity. Total organic carbon (TOC) refers to the carbon content in the residual organic matter after oil and gas spill in the source rock, which is the material basis for generation of oil and gas, and the data scattering between it and production in the first two years is positively correlated, indicating that it has a certain correlation with the productivity of horizontal wells (Figure 2).
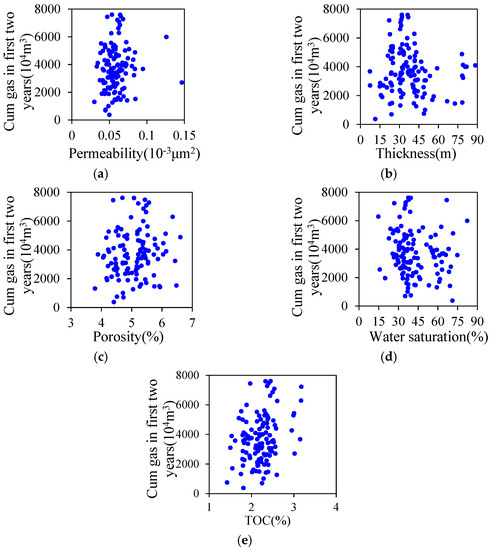
Figure 2.
Relationship between cumulative gas production of horizontal well in the first two years and geological parameters. (a) Permeability; (b) thickness; (c) porosity; (d) water saturation; (e) total organic carbon (TOC).
Under the same conditions, the longer the lateral length of a horizontal well is, the more well controlled reserves are, and the higher the production is. The data scattering of lateral length of horizontal wells and cumulative production in the first two years shows a good positive linear correlation. Similarly, the greater the number of stages, the number of clusters, volume of fracturing fluid and amount of proppant, the larger the reconstruction volume formed by fracturing, the stronger the conductivity of artificial fractures, and the higher the production of wells. These parameters have obvious positive correlation with cumulative production in the first two years. The relationship between flowback rate and productivity is complex. In matrix, flowback rate and productivity are negatively correlated. In fractures, they are positively correlated. In addition, slippage effect, stress sensitivity, production system, etc. will also affect their correlation. The data scattering of flowback rate and productivity is disorder, indicating that there is no single correlation between them (Figure 3).
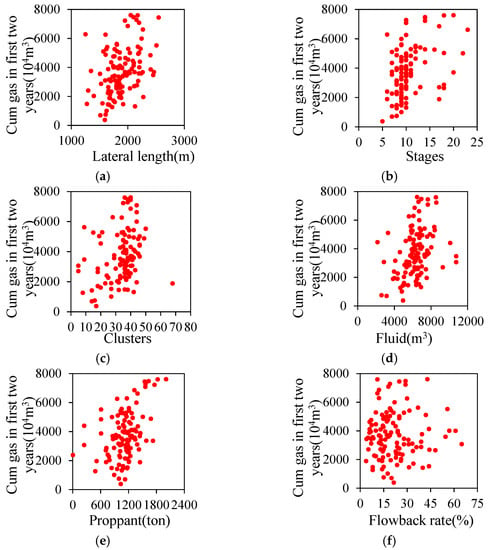
Figure 3.
Relationship between cumulative gas production of horizontal well in the first two years and engineering parameters. (a) Lateral length; (b) number of stages; (c) number of clusters; (d) volume of fracturing fluid; (e) amount of proppant; (f): flowback rate.
4.2. Analysis on Engineering Parameters of Horizontal Wells in Tight Gas Reservoirs
The physical property distribution of the same layer in Block G is relatively stable. In order to reduce the influence of geological factors, the correlation between the cumulative gas production in the first two years of horizontal wells and various engineering parameters is calculated by layers (the purpose of calculation for each layer is only to eliminate the influence of geological factors on engineering factors, and then analyze the influence of engineering parameters on horizontal well productivity. The results of each layer are consistent in theory.). In order to eliminate the impact caused by the difference of fracturing technology, horizontal wells with similar fracturing technology are selected that were put into production from 2010 to 2013. Fisher’s z-transform shows that there are few wells in Layer AA, A, B, C, D, and F, and the samples do not obey the normal distribution and have no statistical significance, so they are not considered. There are most wells in Layer E, which is statistically significant. Moreover, the impact of absolute engineering factors on productivity is not affected by geological factors, so take Layer E as an example to analyze the impact of engineering parameters on productivity (Table 2).

Table 2.
Correlation between cumulative gas production in the first two years of horizontal wells in Layer E and engineering parameters.
These engineering parameters are selected as the key engineering parameters whose Pearson correlation coefficient and MIC are greater than 0.5 with the cumulative gas production in the first two years of the horizontal wells. Finally, the optimized key engineering parameters are lateral length, number of stages, volume of fracturing fluid, and amount of proppant.
4.3. Analysis on Geological Parameters of Horizontal Wells in Tight Gas Reservoirs
In order to analyze the impact of geological parameters on the productivity of horizontal wells, it is necessary to eliminate the impact of engineering factors on the productivity of horizontal wells. Therefore, the cumulative gas production in the first two years of horizontal wells is normalized to the optimized engineering parameters.
The engineering parameters are mutually independent and mutual influence. For example, the longer the lateral length of horizontal well is, the more the number of stages may be. The greater the volume of fracturing fluid is, the greater the amount of proppant may be. Through cluster analysis, it is found that the correlation coefficient between the lateral length and the number of stages, volume of fracturing fluid, and amount of proppant is greater than 0.5, so the lateral length is determined as an independent key engineering parameter (Table 3).

Table 3.
Correlation between each key engineering parameter.
The cumulative gas production in the first two years of the horizontal well is normalized on the lateral length, and the Pearson correlation coefficient and MIC between normalized production and various geological parameters are calculated. It is found that the correlation between the normalized cumulative gas production in the first two years and various geological parameters is weak (Table 4). Therefore, the requirements for correlation are reduced. The key geological parameter is the parameter whose Pearson correlation coefficient and MIC are greater than 0.3, and the secondary key parameter is the parameter whose Pearson correlation coefficient or MIC is greater than 0.3. Finally, TOC is determined as the key geological parameter, and porosity and water saturation are the secondary key parameters.

Table 4.
Correlation between geological parameters and normalized cumulative gas production in the first two years.
5. Prediction of Longitudinal Superimposed Sweet Spot of Tight Gas Reservoir
The steps to predict the longitudinal superimposed sweet spot based on the analytic hierarchy process include: establishing hierarchical structure model, constructing a pairwise matrix, hierarchical ranking and consistency check, grading of evaluation indicators, and comprehensive evaluation and index division of longitudinal superimposed sweet spot.
- (1)
- Establishing hierarchical structure model: Block G has been effectively developed with clear geological understanding. This prediction of sweet spot further determines the favorable development area in the determined geological area. The target layer is the sweet spot. The criterion layer is the TOC, porosity, water saturation. The scheme layer is as follows: Type I sweet spot, Type II sweet spot, Type III sweet spot and nonsweet spot.
- (2)
- Constructing pairwise matrix: According to the results of Pearson-MIC comprehensive evaluation, the scale of TOC is set as 1, and the scale of porosity and water saturation is set as 2, so as to construct a pairwise matrix (Table 4).
- (3)
- Hierarchical ranking and consistency check: Calculate the weight of each evaluation parameter according to the principle of analytic hierarchy process. The calculation meets the consistency check and is consistent with the actual production (Table 5).
 Table 5. Pairwise matrix and weight of Block G.
Table 5. Pairwise matrix and weight of Block G. - (4)
- Grading of evaluation indicators: This paper involves the evaluation of three parameters, and the value range of each parameter is quite different. For the convenience of comparison, the evaluation index of the sweet spot is divided into three grades: excellent, medium, and poor (Table 6). Each cell in the Petrel work area of Block G corresponds to the index parameter value. Judge the range of evaluation indicator parameter values of each cell, divide the grade of evaluation indicators, and assign values.
 Table 6. Pairwise matrix and weight of Block G.
Table 6. Pairwise matrix and weight of Block G. - (5)
- Comprehensive evaluation and index division of longitudinal superimposed sweet spot: The comprehensive score M of each cell in the Petrel work area of Block G is calculated by summing up the weights of each parameter. Based on the weighted average of the thickness of each layer in corresponding series, the plane distribution of the cell comprehensive score S of the Series Upper and the Series Lower is depicted. On this basis, referring to the existing sweet spot standard, the comprehensive score is divided into four grades to determine the longitudinal superimposed sweet spot standard of Block G (Table 7). According to the standards in Table 6, the longitudinal superimposed sweet spot of Series E and Series Lower in Block G is depicted (Figure 4). We have
 Table 7. Comprehensive evaluation grade table of sweet spot in Block G.
Table 7. Comprehensive evaluation grade table of sweet spot in Block G.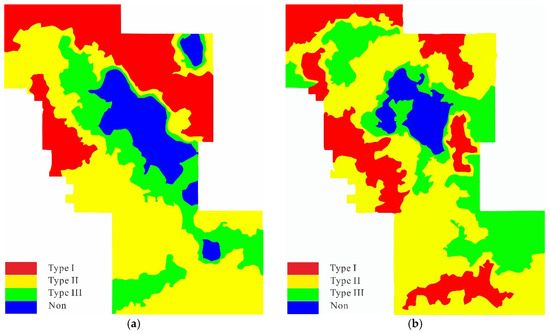 Figure 4. Plane distribution maps of longitudinal superimposed sweet spot in Block G. (a) Series Upper. (b) Series Lower.
Figure 4. Plane distribution maps of longitudinal superimposed sweet spot in Block G. (a) Series Upper. (b) Series Lower.
In the formula, is the comprehensive score of each cell, is the weight of evaluation index, is the score of evaluation index, is the comprehensive score of each cell in the series, and is the thickness weight of each layer in the series.
In the Series Upper, Layer E has the best physical properties and the largest thickness, making the most outstanding contribution to the sweet spot. The Type I sweet spot accounts for 24.2% in the Series Upper, which is mainly distributed in the north and northeast of the reservoir with good physical properties. The Type II sweet spot accounts for 42.4%, mainly distributed in the south where the physical property is slightly inferior but the reservoir thickness is relatively thick. The Type III sweet spot accounts for 22.8%, and the non-sweet spot accounts for 10.6%. These two areas are mainly concentrated in the middle of the reservoir with ordinary physical properties and thin thickness.
In the Series Lower, Type I sweet spot accounts for 23.1%, which is relatively scattered, and the southern part is greatly affected by thin Layer AA and Layer A with good reservoir physical properties. The Type II sweet spot accounts for 48.0%, and its distribution is relatively scattered. The Type III sweet spot accounts for 21.7%, mainly distributed in the southeast and northwest. The non-sweet spot accounts for 7.2%, concentrated in the middle.
6. Conclusions
- (1)
- The influence of engineering parameters on productivity is more significant. According to Pearson–MIC comprehensive evaluation method, the lateral length of horizontal well, number of stages, volume of fracturing fluid, and amount of proppant are determined as the key engineering parameters.
- (2)
- Through cluster analysis, the lateral length is selected as an independent key engineering parameter, and the cumulative gas production in the first two years is normalized on the lateral length to eliminate the impact of the engineering. After calculating the correlation between the normalized cumulative gas production in the first two years and geological parameters, the TOC is determined as the key geological parameter, and porosity and water saturation are the secondary key parameters.
- (3)
- The sweet spot standard of Block G is formulated based on the weight of each parameter obtained by AHP and the sweet spot evaluation index grade. The distribution of longitudinal superimposed sweet spot in Block G of Series Upper and Series Lower is obtained by thickness weighted average, laying a foundation for the subsequent placement of new wells.
Author Contributions
Writing—review and editing, Y.J.; supervision, W.H.; methodology, P.S.; project administration, P.W.; data curation, X.K. and L.L.; visualization, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Major National Science and Technology Projects (No. 2016ZX05029-005), Major Science and Technology Projects of CNPC (No. 2019D-4412), and Special Science and Technology Project of CNPC (No. 2021DJ3303).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Our data presented is original and not inappropriately selected, manipulated, enhanced, or fabricated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, S.; Zhang, J.; Huang, W.; Zhang, Y.; Tang, X. “Sweet spot” types of reservoirs and genesis of tight sandstone gas in Kekeya area, Turpan-Hami Basin. Acta Pet. Sin. 2013, 34, 272–282. [Google Scholar] [CrossRef]
- Ma, Y.; Cai, X.; Zhao, P. China’s shale gas exploration and development: Understanding and practice. Pet. Explor. Dev. 2018, 45, 561–574. [Google Scholar] [CrossRef]
- Kumar, A.; Seth, P.; Shrivastava, K.; Manchanda, R.; Sharma, M.M. Integrated Analysis of Tracer and Pressure-Interference Tests to Identify Well Interference. SPE J. 2020, 25, 1623–1635. [Google Scholar] [CrossRef]
- Zhao, Z.; Du, J. Tight Oil and Gas; Petroleum Industry Press: Beijing, China, 2012; pp. 100–128. [Google Scholar]
- Zou, C.; Tao, S.; Hou, L. Unconventional Oil and Gas Geology; Geological Publishing House: Beijing, China, 2014. [Google Scholar]
- Sun, L.; Zou, C.; Jia, A.; Wei, Y.; Zhu, R.; Wu, S.; Guo, Z. Development characteristics and orientation of tight oil and gas in China. Pet. Explor. Dev. 2019, 46, 1015–1026. [Google Scholar] [CrossRef]
- Xu, M. Research on the Geological and Engineering Sweet Spot Index of Shale Gas; China University of Petroleum: Beijing, China, 2016. [Google Scholar]
- Zhao, W.; Jia, C.; Jiang, L.; Zhang, T.; He, M.; Zhang, F.; Jiang, Z.; Li, X.; Wu, K. Fluid charging and hydrocarbon accumulation in the sweet spot, Ordos Basin, China. J. Pet. Sci. Eng. 2021, 200, 108391. [Google Scholar] [CrossRef]
- Pan, R.; Gong, Q.; Yan, J.; Jin, J. Elements and gas enrichment laws of sweet spots in shale gas reservoir: A case study of the Longmaxi Fm in Changning block, Sichuan Basin. Nat. Gas Ind. 2016, 36, 7–13. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, C.; Jiang, C.; Dan, K.; Kezhen, H.; Liu, X.; Melinda, Y. Production characteristics and sweet-spots mapping of the Upper Devonian Lower Mississippian Bakken Formation tight oil in southeastern Saskatchewan, Canada. Pet. Explor. Dev. 2018, 45, 626–635. [Google Scholar] [CrossRef]
- Wei, Y.; Li, J.; Lu, S.; Song, Z.; Zhao, R.; Zhang, Y.; Wang, J.; Liu, X. Comprehensive evaluation method of sweet spot zone in Lacustrine shale oil reservoir and its application: A case study of shale oil in lower 1st member of the Shahejie formation in the Raoyang sag. J. China Univ. Min. Technol. 2021, 1–12. [Google Scholar] [CrossRef]
- Chen, G.; Bai, Y.; Chen, X.; Xu, B.; Zhu, Y.; Feng, R.; Chen, L. A new identification method for the longitudinal integrated shale oil/gas sweet spot and its quantitative evaluation. Acta Pet. Sin. 2016, 37, 1337–1342+1360. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, H.; Zhou, K.; Hao, J.; Wang, X. “Sweet spot” identification and evaluation of tight sandstone reservoir. Bull. Geol. Sci. Technol. 2020, 39, 165–173. [Google Scholar] [CrossRef]
- Li, M.; Sun, J.; Hu, J.; Liu, D.; Yuan, B. Sweet spot selection model for horizontal shale gas well section. Sci. Technol. Eng. 2020, 20, 9844–9850. [Google Scholar]
- Han, F.; Song, G.; Wu, Z.; Shen, X.; Han, F. Multi-attribute Fusion Prediction Technique for Tight Oil “Sweets”. Spec. Oil Gas Reserv. 2019, 26, 94–99. [Google Scholar] [CrossRef]
- Liao, D.; Lu, B. An evaluation method of engineering sweet spots of shale gas reservoir development: A case study from the Jiaoshiba Gas Field, Sichuan Basin. Nat. Gas Ind. 2018, 38, 43–50. [Google Scholar] [CrossRef]
- Liao, D.; Lu, B.; Chen, Y. An evaluation method of geological sweet spots of shale gas reservoir development: A case study from the Jiaoshiba Gas Field, Sichuan Basin. Acta Pet. Sin. 2019, 40, 144–151. [Google Scholar] [CrossRef]
- Montgomery, S.L.; Jarvie, D.M.; Bowker, K.A.; Pollastro, R.M. Mississippian Barnett Shale, Fort Worth basin, north-central Texas: Gas-shale play with multi-trillion cubic foot potential. Am. Assoc. Pet. Geol. 2005, 89, 155–175. [Google Scholar] [CrossRef]
- Chalmers, G.R.L.; Bustin, R.M. The organic matter distribution and methane capacity of the Lower Cretaceous strata of northeastern British Columbia, Canada. Int. J. Coal Geol. 2007, 70, 223–239. [Google Scholar] [CrossRef]
- Curtis, J.B. Fractured shale gas systems. AAPG 2002, 86, 1921–1938. [Google Scholar] [CrossRef]
- Pejman, T.; Farzam, J.; Muhammad, S. Data Mining and Machine Learning for Identifying Sweet Spots in Shale Reservoirs. Expert Syst. Appl. 2017, 88, 435–477. [Google Scholar] [CrossRef]
- Heege, J.T.; Zijp, M.; Nelskamp, S.; Douma, L.; Verreussel, R.; Veen, J.T.; Bruin, G.; Peters, R. Sweet spot identification in underexplored shales using multidisciplinary reservoir characterization and key performance indicators: Example of the Posidonia Shale Formation in the Netherlands. J. Nat. Gas Sci. Eng. 2015, 27, 558–577. [Google Scholar] [CrossRef]
- Munther, A.; Reza, R. Sweet-spot mapping through formation evaluation and property modelling using data from the Goldwyer Formation of the Barbwire Terrace, Canning Basin. Petroleum 2019, 5, 13–29. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Basu, S.; Vishal, V.; Srivastava, M. Hierarchical clustering of Pristane and Phytane data to identify the sweet spots in the shale reservoirs. Energy Clim. Chang. 2020, 1, 100011. [Google Scholar] [CrossRef]
- Tang, J.; Fan, B.; Xiao, L.; Weitz, D. A New Ensemble Machine-Learning Framework for Searching Sweet Spots in Shale Reservoirs. SPE J. 2020, 26, 482–497. [Google Scholar] [CrossRef]
- Yuan, Y.; Rezaee, R.; Gu, J.; Wu, S.; Al-Khdheeawi,, E.A.; Wang, J.; Pan, B. High-resolution coupling of stratigraphic sweet spot lithofacies and petrophysical properties: A multiscale study of Ordovician Goldwyer Formation, Western Australia. Pet. Sci. 2022, 11, 011. [Google Scholar] [CrossRef]
- Tatsipie, N.R.K.; Sheng, J.J. Statistical distribution of geomechanical properties and ‘Sweet Spots’ identification in part of the upper Bakken. Pet. Res. 2022, 10, 005. [Google Scholar] [CrossRef]
- Mu, L.; Zhang, M.; Xia, Z.; Qu, L.; Jiang, P. Quantitative characterization technique for tight gas reservoir in Groundbirch, Canada. Acta Pet. Sin. 2017, 38, 363–374. [Google Scholar] [CrossRef]
- Haldar, S.K. Introduction to Mineralogy and Petrology; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Jiang, P.; Mu, L.; Zhang, M.; Zhao, W. Difference of reservoir characteristics between domestic and oversea tight gas of CNPC and its developing trends. Nat. Gas Geosci. 2015, 26, 1095–1105. [Google Scholar] [CrossRef]
- Xu, S. Practical Decision-Making Method: The Principle of Analytic Hierarchy Process; Tianjin University Press: Tianjin, China, 1989. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).