Large-Eddy Simulation of Flow Separation Control in Low-Speed Diffuser Cascade with Splitter Blades
Abstract
:1. Introduction
2. Geometric Model and Splitter Blades
2.1. Low-Speed Diffuser Cascade
2.2. Splitter Blade Designs
3. Computational Methods and Validations
3.1. Numerical Models and Boundary Conditions
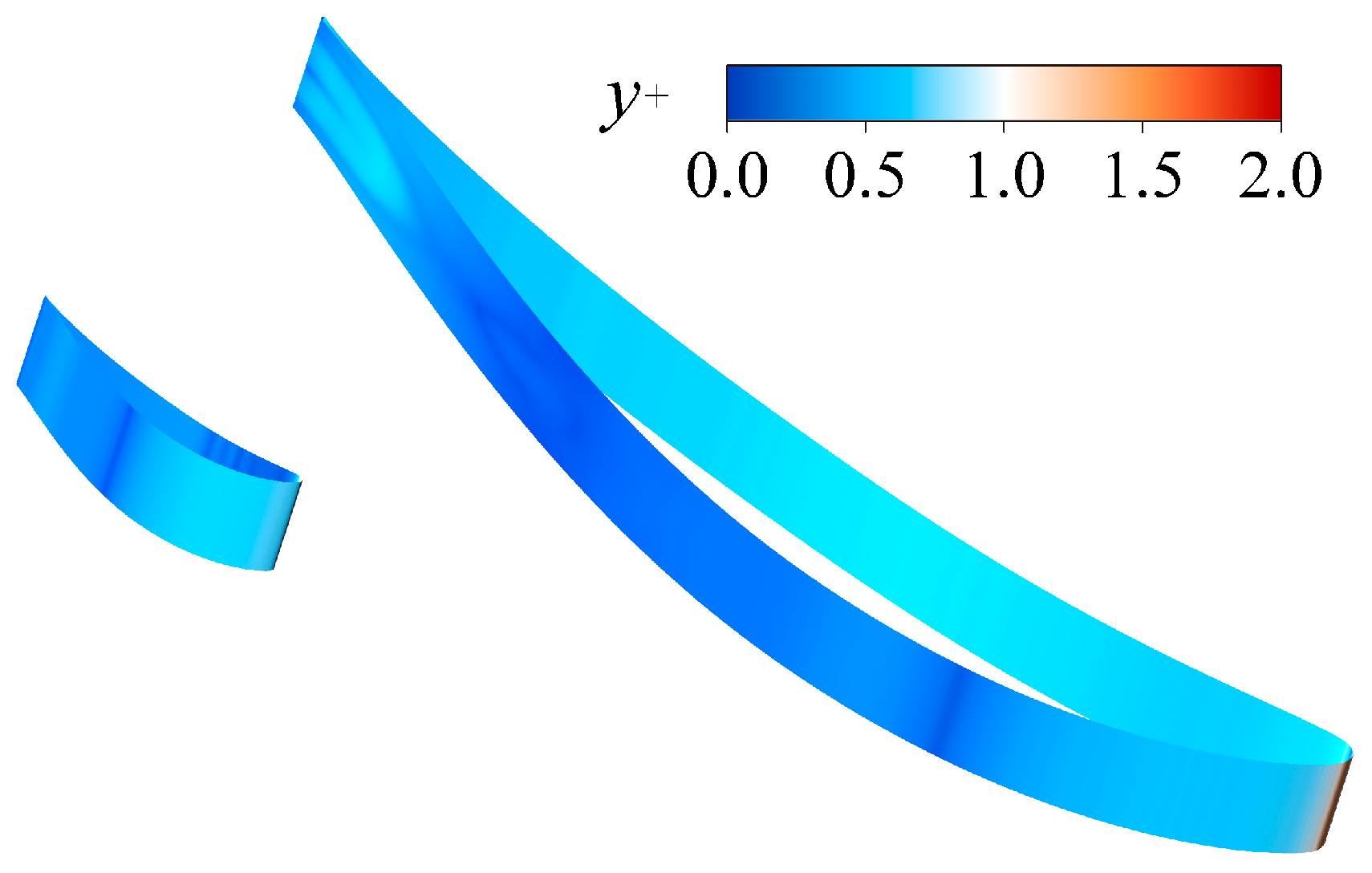
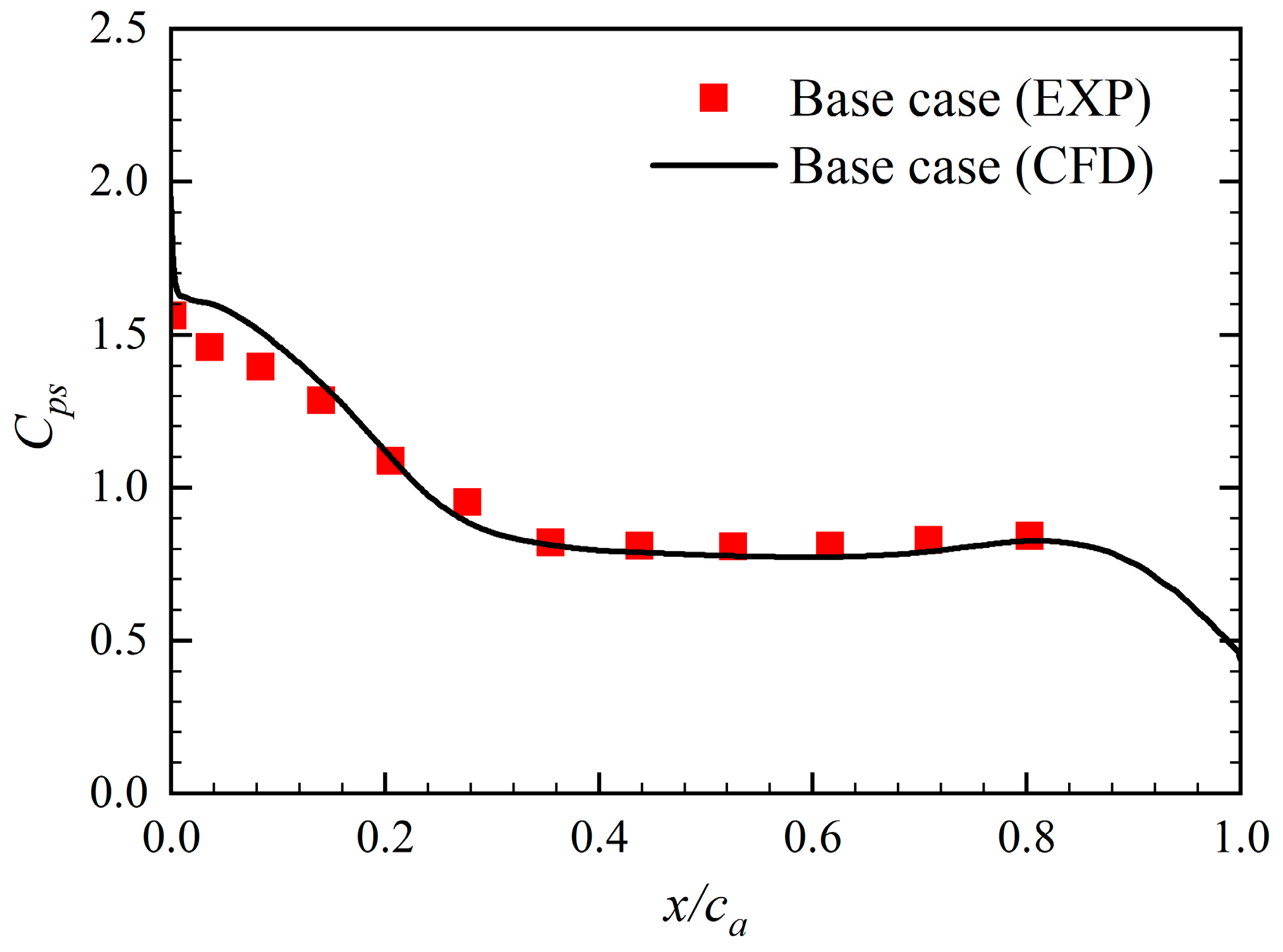
3.2. Grid Sensitivity Study and Validations
4. Results and Discussions
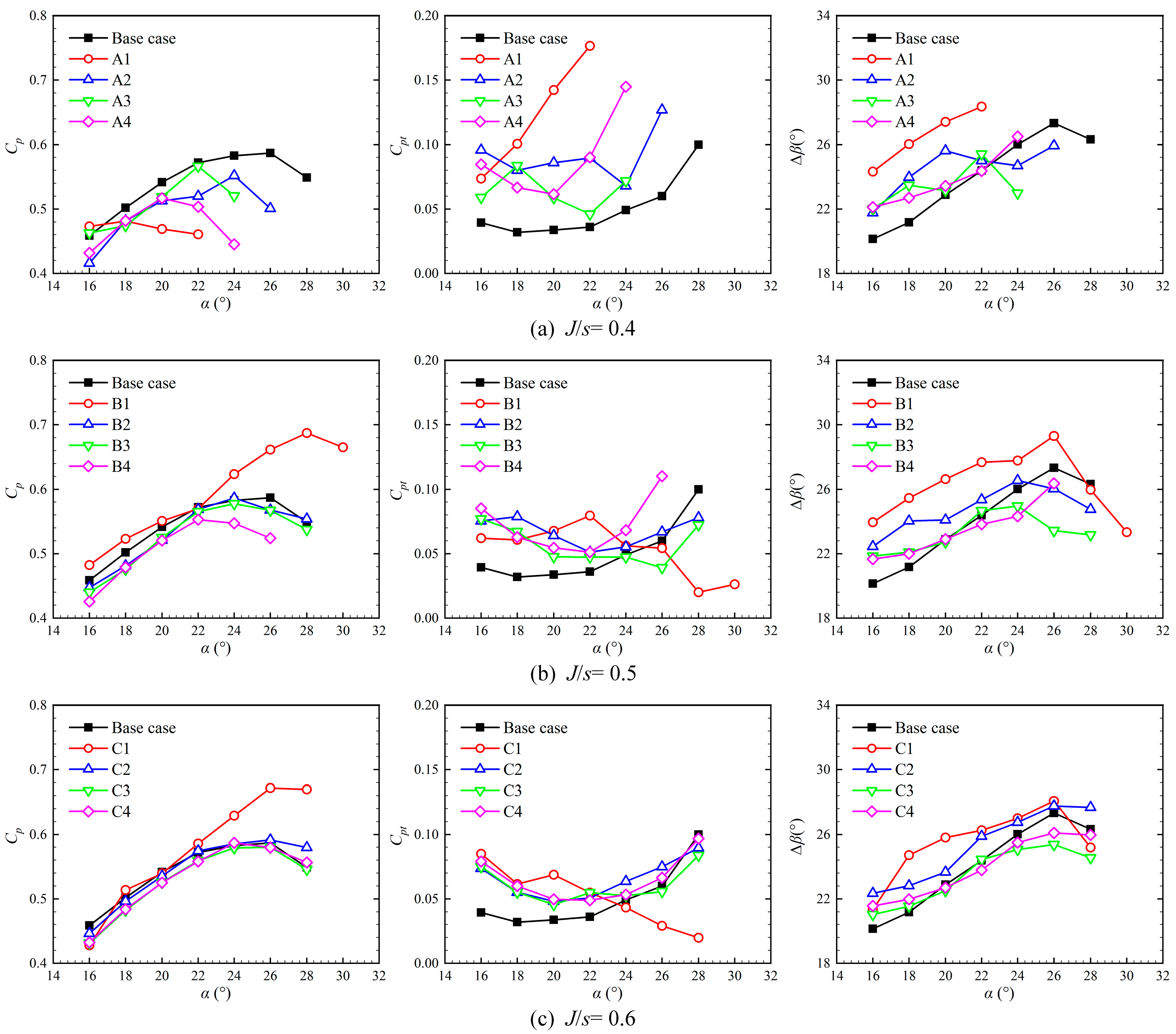
4.1. Effect of Splitter Blade Arrangement
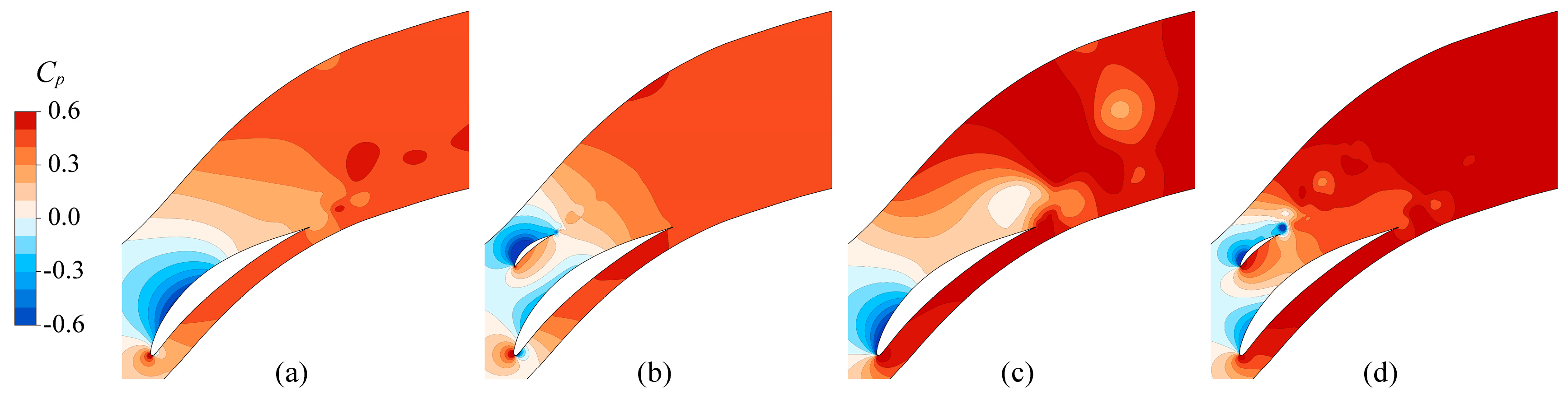
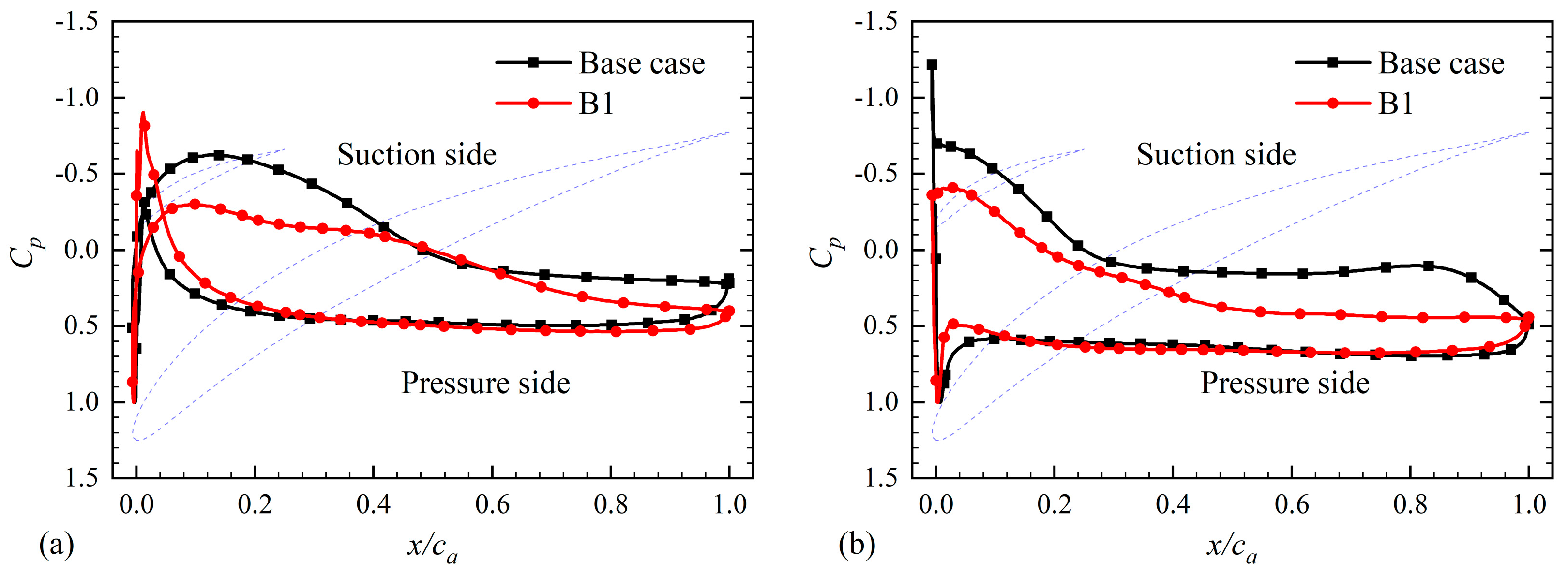
4.2. Effect of Splitter Blades on the Flow Field
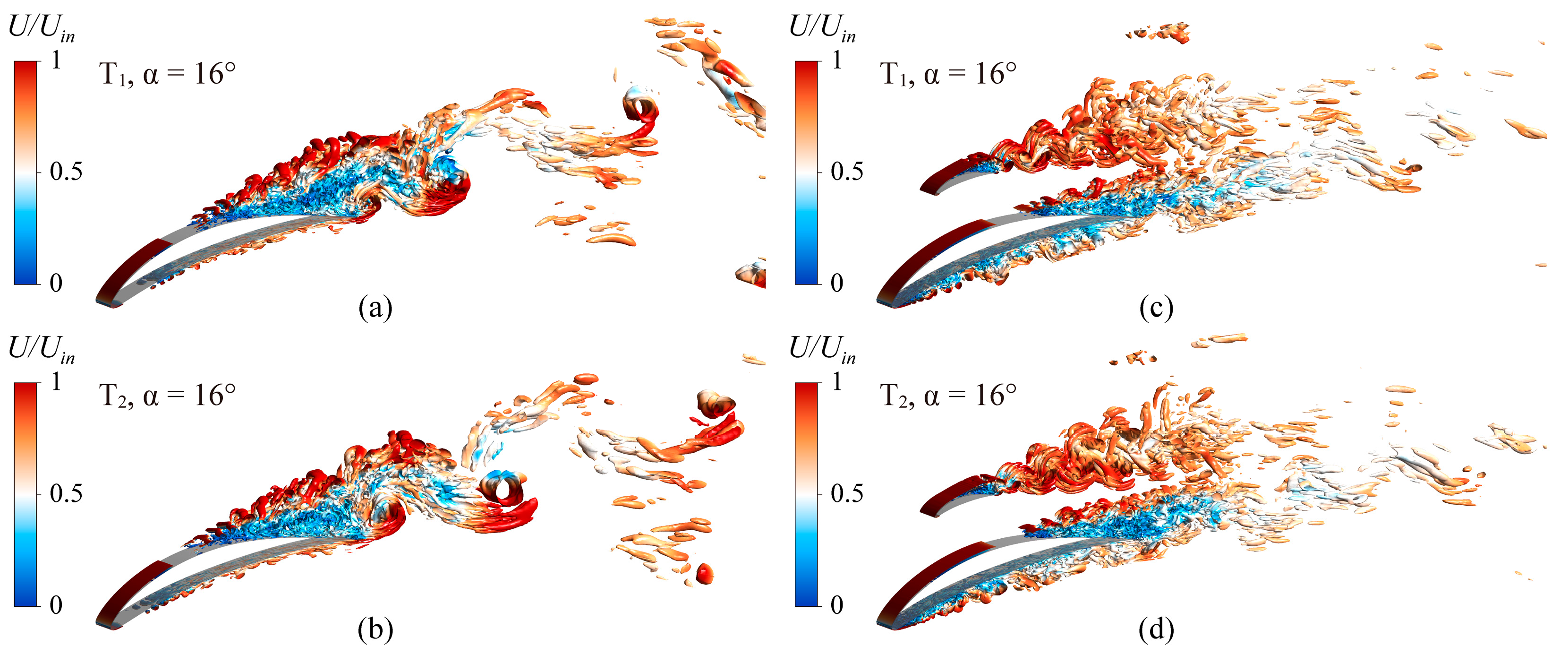
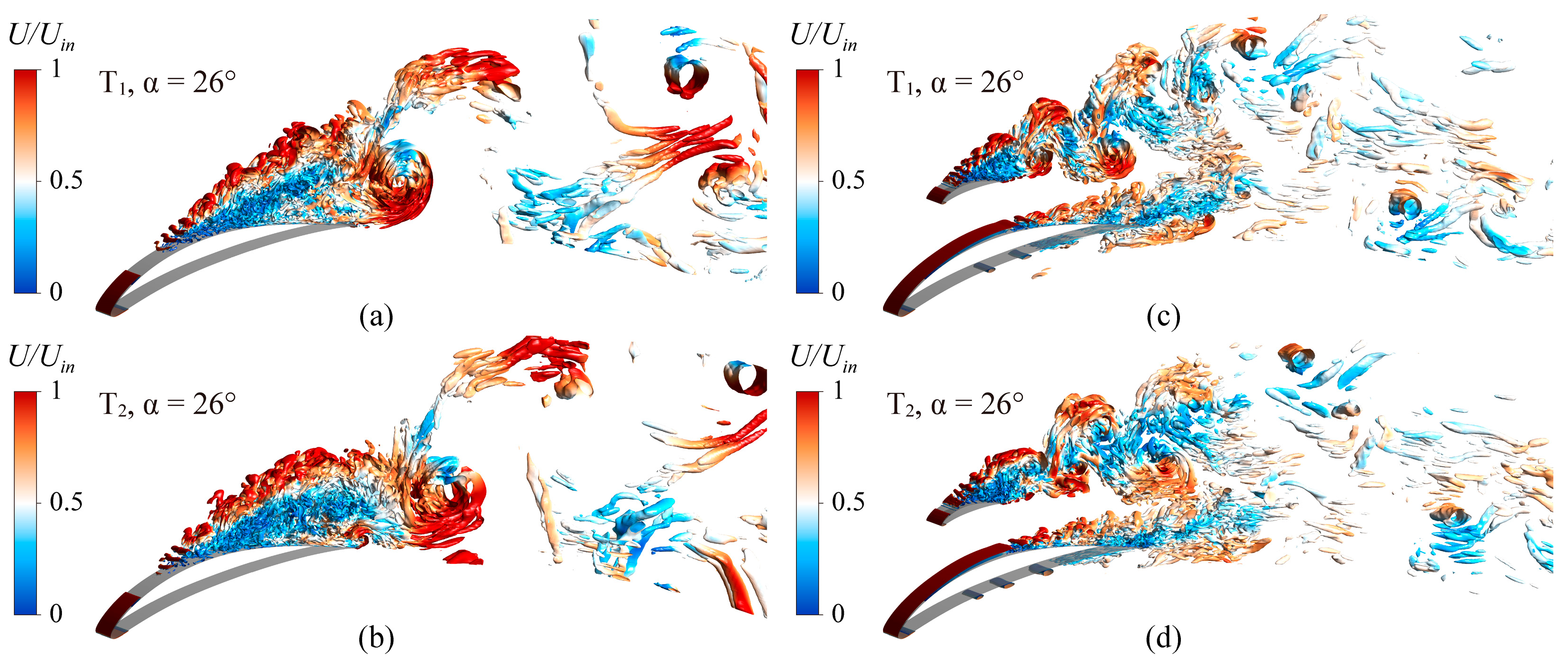
4.3. Effect of Splitter Blades on the Instantaneous Flow Structures
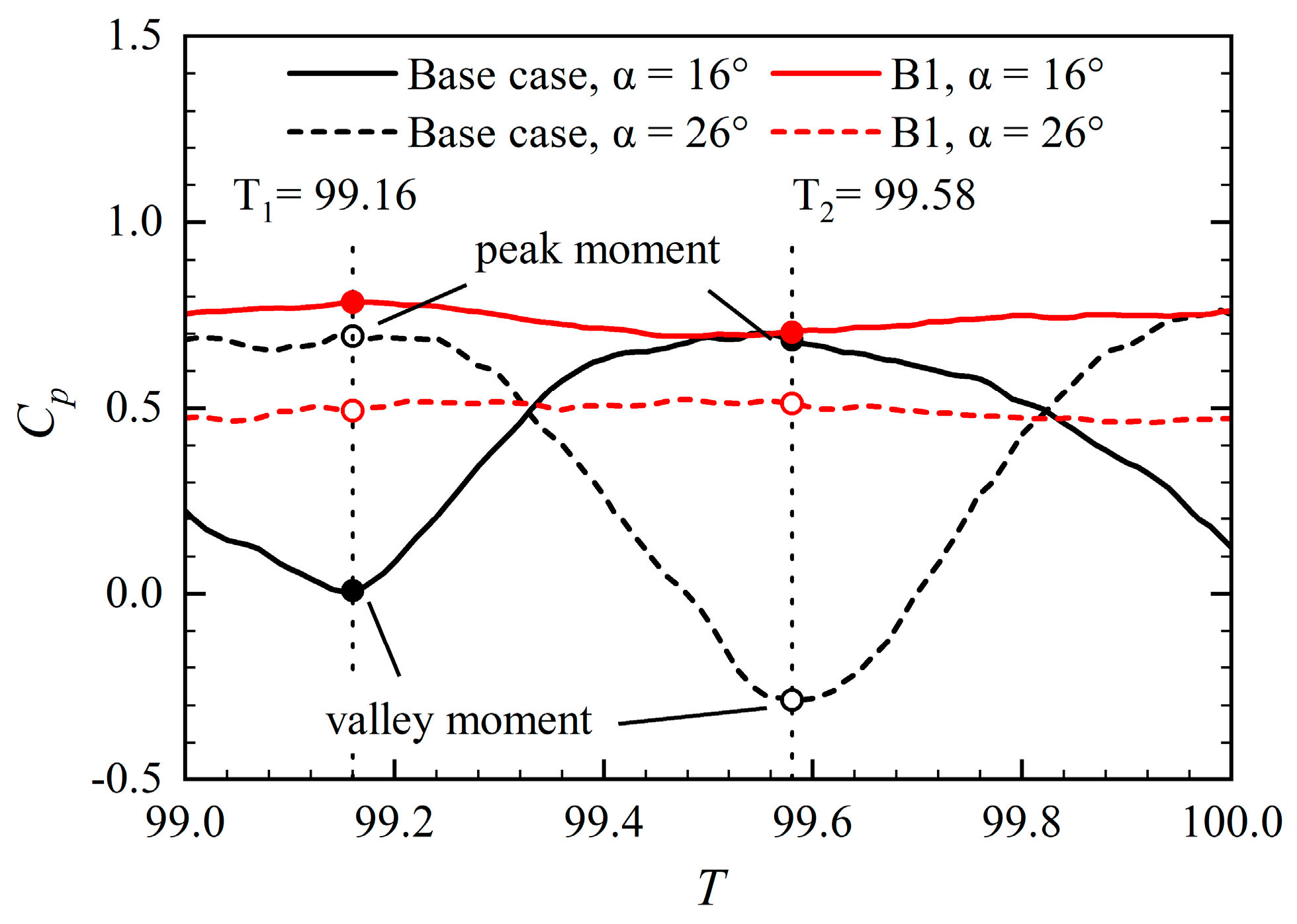
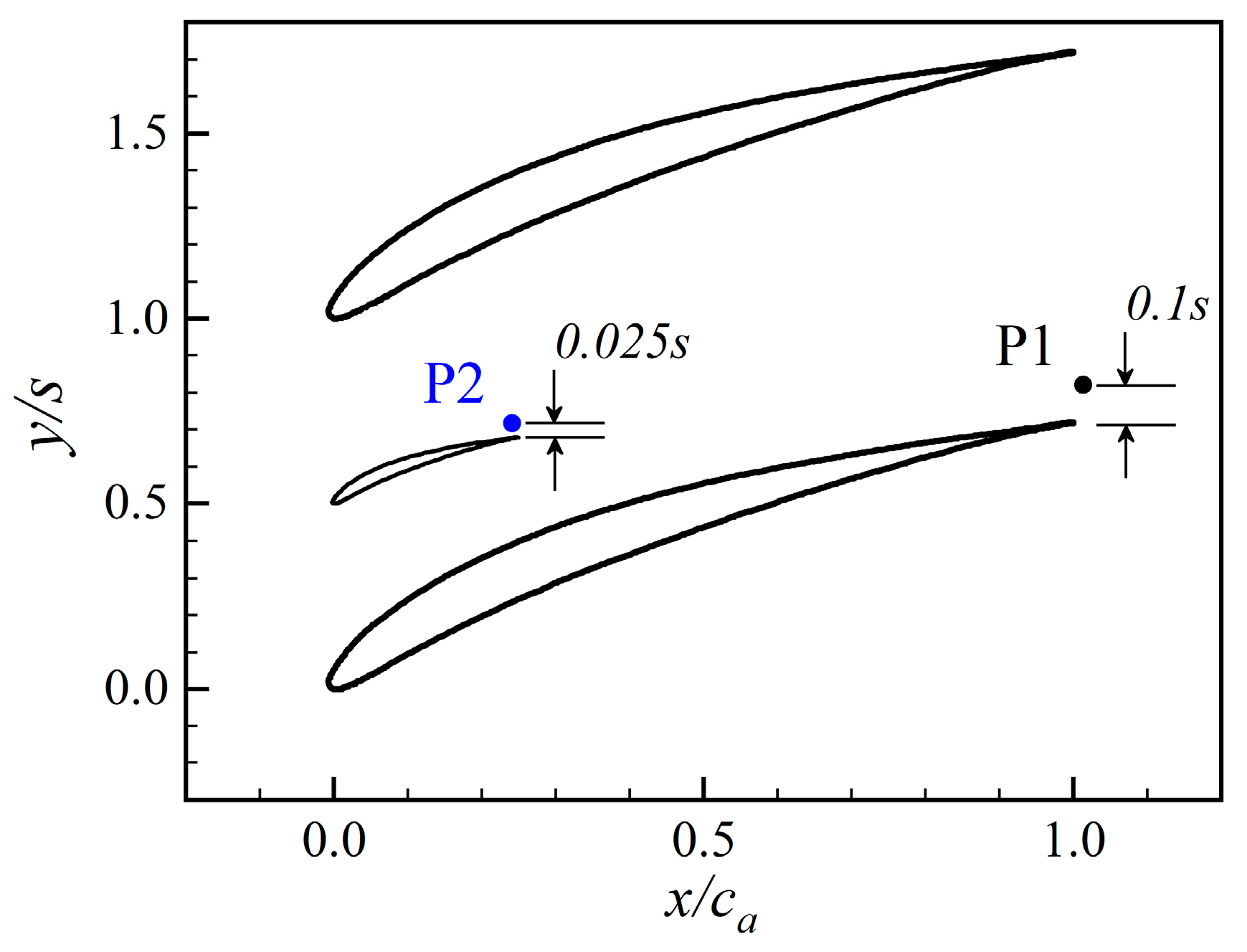
4.4. Effect of Splitter Blades on the Pressure Fluctuation
5. Conclusions
- The aerodynamic performance of the low-speed diffuser cascade was susceptible to the position of the splitter blades. The optimal position of the splitter blade was located in the middle of the main blades near the leading edge (B1, I/c = 0, J/s = 0.5). The aerodynamic performance of the cascade system was effectively improved.
- The arrangement of the splitter blades changed the pressure distribution on the main blades. Decreasing the reverse pressure gradient on the main blade suction surface weakened the separation flow. The main separation flow occurred on the splitter blade suction surface. All the separation points of B1 were about 0.2 axial chord length behind the base case.
- The LES results show that the splitter blades improved the stability of the cascade system, especially at the stall angle of attack. With the arrangement of splitter blades, the scale and intensity of the separation vortices generated on the suction surface of the main blade decreased. In addition, the separation vortices of the main blade and the splitter blade interacted and rapidly decomposed into small-scale vortices downstream of the cascade, reducing the flow loss.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cp | Static pressure coefficient, Cp = (Ps,out − Ps,in)/(Pt,in − Ps,in) |
| Cps | Blade surface pressure coefficient, Cps = (Pt,in − Ps)/(Pt,in − Ps,in) |
| Cpt | Total pressure loss coefficient, Cpt = (Pt,in − Pt,out)/(Pt,in − Ps,in) |
| ε(Cp) | Static pressure coefficient variable rate, ε(Cp) = (Cp,i − Cp,i−1)/(Cp,i−1) × 100% |
| ∆β | Flow turning angle, ° |
| Uin | Flow velocity at the cascade inlet, m/s |
| Ps | Static pressure, Pa |
| Pt | Total pressure, Pa |
| c | Blade chord length, mm |
| ca | Blade axial chord length, mm |
| s | Pitch spacing, mm |
| φ | Camber angle, ° |
| γ | Stagger angle, ° |
| h | Blade span, mm |
| i | Incidence angle, ° |
| α | Attack angle, ° |
| β1 | Design inflow angle, ° |
| β2 | Design outflow angle, ° |
| T | The dimensionless time |
| ∆t | Physical time step, s |
| T1 | Valley moment, s |
| T2 | Peak moment, s |
| P1 | Main blade monitor |
| P2 | Splitter blade monitor |
| DAA | Design attack angle |
| SAA | Stall attack angle |
| RANS | Reynolds averaged Navier-Stokes |
| LES | Large-eddy simulation |
| FFT | Fast Fourier transform |
References
- Zhou, B. Investigation on the Instability and the Mechanism of Its Induced Noise in an Axial-Flow Fan. Ph.D. Thesis, Jiangsu University, Zhenjiang, China, 2017. [Google Scholar]
- Luo, D. Passive flow control of a stalled airfoil using a microcylinder. J. Wind Eng. Ind. Aerodyn. 2017, 170, 256–273. [Google Scholar] [CrossRef]
- Emmons, H.W.; Pearson, C.E.; Grant, H.P. Compressor Surge and Stall Propagation. Trans. Am. Soc. Mech. Eng. 2022, 77, 455–467. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, L.; Zhou, L.; Sun, S. Effect of blended blade tip and winglet on aerodynamic and aeroacoustic performances of a diagonal fan. Aerosp. Sci. Technol. 2020, 98, 105688. [Google Scholar] [CrossRef]
- Gad-el-Hak, M. Modern developments in flow control. Appl. Mech. Rev. 1996, 49, 365–379. [Google Scholar] [CrossRef]
- Joshi, S.N.; Gujarathi, Y.S. A Review on Active and Passive Flow Control Techniques. Int. J. Recent Technol. Mech. Electr. Eng. 2016, 4, 1–6. [Google Scholar]
- Ortiz-Tarin, J.L.; Nidhan, S.; Sarkar, S. High-Reynolds-number wake of a slender body. J. Fluid Mech. 2021, 918, A30. [Google Scholar] [CrossRef]
- Ortiz-Tarin, J.L.; Nidhan, S.; Sarkar, S. The high-Reynolds-number stratified wake of a slender body and its comparison with a bluff-body wake. J. Fluid Mech. 2023, 957, A7. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Z. Analytical study on the synthetic jet control of asymmetric flow field of flying wing unmanned aerial vehicle. Aerosp. Sci. Technol. 2016, 56, 90–99. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Z. Study on longitudinal stability improvement of flying wing aircraft based on synthetic jet flow control. Aerosp. Sci. Technol. 2015, 46, 287–298. [Google Scholar] [CrossRef]
- Zhu, H.; Hao, W.; Li, C.; Ding, Q.; Wu, B. Application of flow control strategy of blowing, synthetic and plasma jet actuators in vertical axis wind turbines. Aerosp. Sci. Technol. 2019, 88, 468–480. [Google Scholar] [CrossRef]
- Kamari, D.; Tadjfar, M.; Madadi, A. Optimization of SD7003 airfoil performance using TBL and CBL at low Reynolds numbers. Aerosp. Sci. Technol. 2018, 79, 199–211. [Google Scholar] [CrossRef]
- Brüderlin, M.; Zimmer, M.; Hosters, N.; Behr, M. Numerical simulation of vortex generators on a winglet control surface. Aerosp. Sci. Technol. 2017, 71, 651–660. [Google Scholar] [CrossRef]
- Yang, X.; Wang, J.; Jiang, B.; Li, Z.A.; Xiao, Q. Numerical Study of Effect of Sawtooth Riblets on Low-Reynolds-Number Airfoil Flow Characteristic and Aerodynamic Performance. Processes 2021, 9, 2102. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, X.; Chao, Y.; Li, Q.; Li, M.; Zheng, W.; Chen, T. Effects of leading edge slat on flow separation and aerodynamic performance of wind turbine. Energy 2019, 182, 988–998. [Google Scholar] [CrossRef]
- Chen, T.; Jiang, X.; Wang, H.; Li, Q.; Li, M.; Wu, Z. Investigation of leading-edge slat on aerodynamic performance of wind turbine blade. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1329–1343. [Google Scholar] [CrossRef]
- Mostafa, W.; Abdelsamie, A.; Sedrak, M.; Thévenin, D.; Mohamed, M.H. Quantitative impact of a micro-cylinder as a passive flow control on a horizontal axis wind turbine performance. Energy 2022, 244, 122654. [Google Scholar] [CrossRef]
- Malik, A.; Zheng, Q. Effect of double splitter blades position in a centrifugal compressor impeller. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 689–701. [Google Scholar] [CrossRef]
- Malik, A.; Qun, Z.; Zaidi, A.A.; Fawzy, H. Performance Enhancement of Centrifugal Compressor with Addition of Splitter Blade Close to Pressure Surface. J. Appl. Fluid Mech. 2018, 11, 919–928. [Google Scholar] [CrossRef]
- Zhang, J.; Li, G.; Mao, J.; Yuan, S.; Qu, Y.; Jia, J. Numerical investigation of the effects of splitter blade deflection on the pressure pulsation in a low specific speed centrifugal pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 420–432. [Google Scholar] [CrossRef]
- Jia, Y.; Wei, X.; Wang, Q.; Cui, J.; Li, F. Experimental Study of the Effect of Splitter Blades on the Performance Characteristics of Francis Turbines. Energies 2019, 12, 1676. [Google Scholar] [CrossRef]
- Wennerstrom, A.J.; Frost, G.R. Design of a Rotor Incorporating Splitter Vanes for a High Pressure Ratio Supersonic Axial Compressor Stage; Aerospace Research Laboratories, Air Force Systems Command, United States Air Force: Washington, DC, USA, 1974. [Google Scholar]
- Tzuoo, K.L.; Hingorani, S.S.; Sehra, A.K. Design Methodology for Splittered Axial Compressor Rotors. In Proceedings of the ASME 1990 International Gas Turbine and Aeroengine Congress and Exposition, Brussels, Belgium, 11–14 June 1990. [Google Scholar]
- Li, H.; Zou, Z.; Liu, H. Flow Analysis on a Single-Stage Axial Compressor with a Splitter Rotor. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; pp. 365–373. [Google Scholar]
- Clark, C.J.; Pullan, G.; Curtis, E.; Goenaga, F. Secondary Flow Control in Low Aspect Ratio Vanes Using Splitters. J. Turbomach. 2017, 139, 091003. [Google Scholar] [CrossRef]
- Liu, B.; Fu, D.; Yu, X. Development of a Preliminary Design Method for Subsonic Splittered Blades in Highly Loaded Axial-Flow Compressors. Appl. Sci. 2017, 7, 283. [Google Scholar] [CrossRef]
- Pham, K.Q.; Le, X.T.; Dinh, C.T. Effects of stator splitter blades on aerodynamic performance of a single-stage transonic axial compressor. J. Mech. Eng. Sci. 2020, 14, 7369–7378. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, J.; Wang, W.; Jiang, B.; Ding, Y.; Qin, W. Numerical and Experimental Investigations of Axial Flow Fan with Bionic Forked Trailing Edge. Machines 2023, 11, 155. [Google Scholar] [CrossRef]
- Qingyi, S.A.I.; Yuanjia, Z.H.U.; Ailing, Y.; Ren, D.A.I. Experimental Study on Aerodynamic Performance and Flow Structure of a Diffuser Cascade with Splitter Blades. J. Chin. Soc. Power Eng. 2013, 33, 847–852. [Google Scholar]
- Kumar, P.; Mahesh, K. Large-eddy simulation of flow over an axisymmetric body of revolution. J. Fluid Mech. 2018, 853, 537–563. [Google Scholar] [CrossRef]
- Plasseraud, M.; Kumar, P.; Mahesh, K. Large-eddy simulation of tripping effects on the flow over a 6:1 prolate spheroid at angle of attack. J. Fluid Mech. 2023, 960, A3. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, B.; Wang, J.; Huang, Y.; Yang, W.; Yuan, K.; Shi, X. Multi-objective optimization of dual-arc blades in a squirrel-cage fan using modified non-dominated sorting genetic algorithm. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 1053–1068. [Google Scholar] [CrossRef]
- Foo, K.; Liang, Y.Y.; Tan, C.K.; Fimbres Weihs, G.A. Coupled effects of circular and elliptical feed spacers under forced-slip on viscous dissipation and mass transfer enhancement based on CFD. J. Membr. Sci. 2021, 637, 119599. [Google Scholar] [CrossRef]
- Rostamzadeh-Renani, M.; Rostamzadeh-Renani, R.; Baghoolizadeh, M.; Khabazian Azarkhavarani, N. The effect of vortex generators on the hydrodynamic performance of a submarine at a high angle of attack using a multi-objective optimization and computational fluid dynamics. Ocean Eng. 2023, 282, 114932. [Google Scholar] [CrossRef]
- Haller, G. An objective definition of a vortex. J. Fluid Mech. 2005, 525, 1–26. [Google Scholar] [CrossRef]
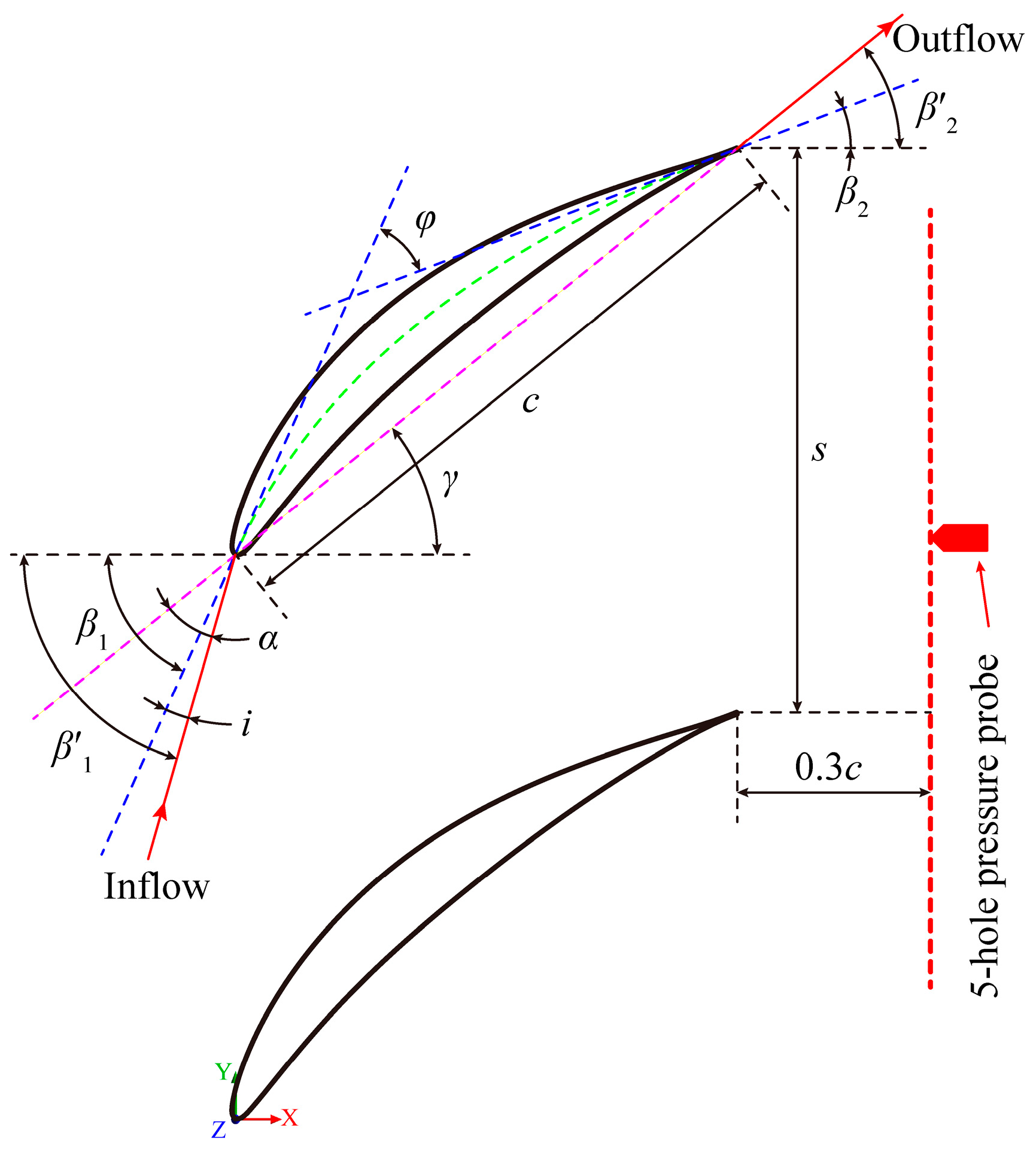
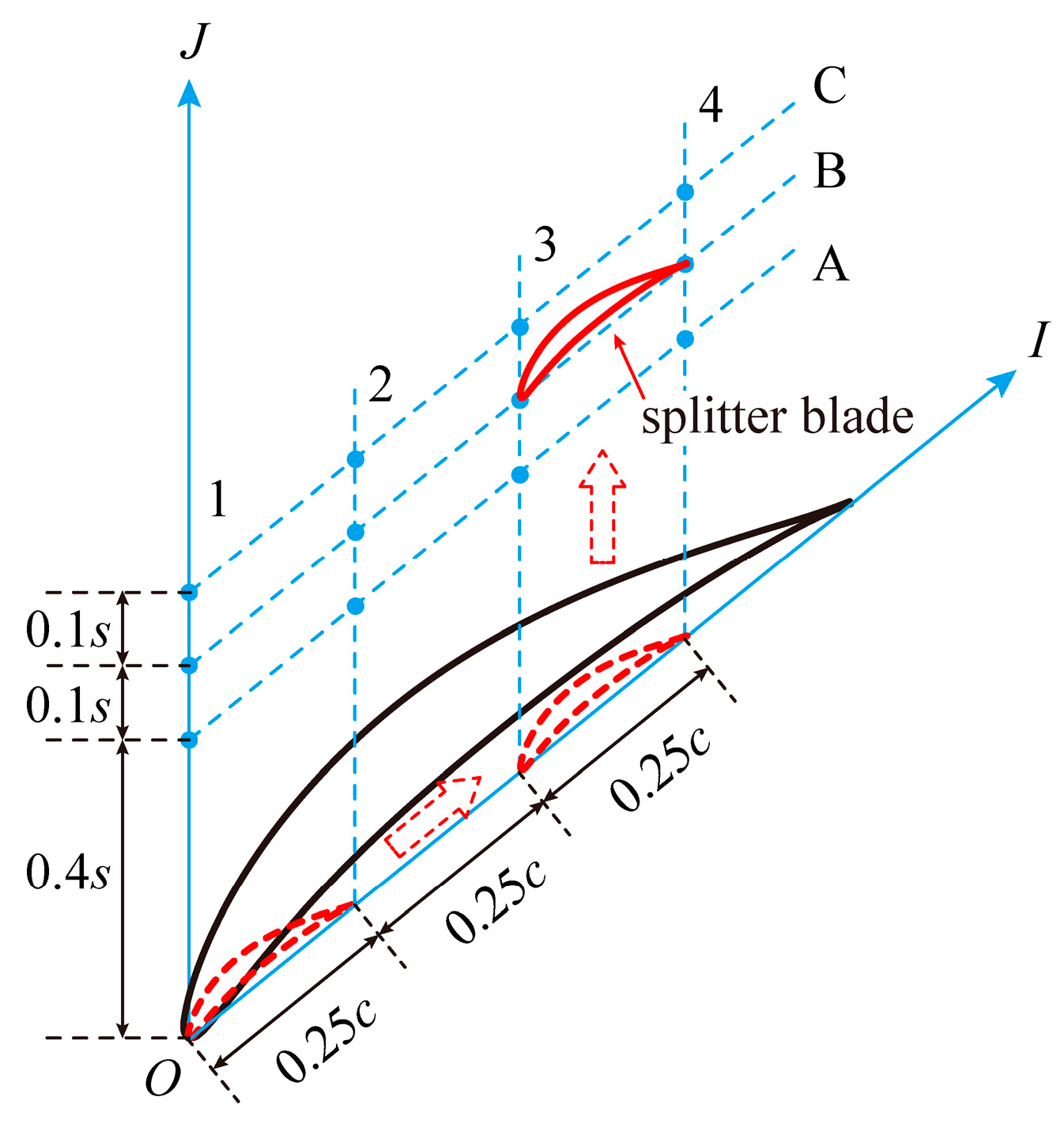
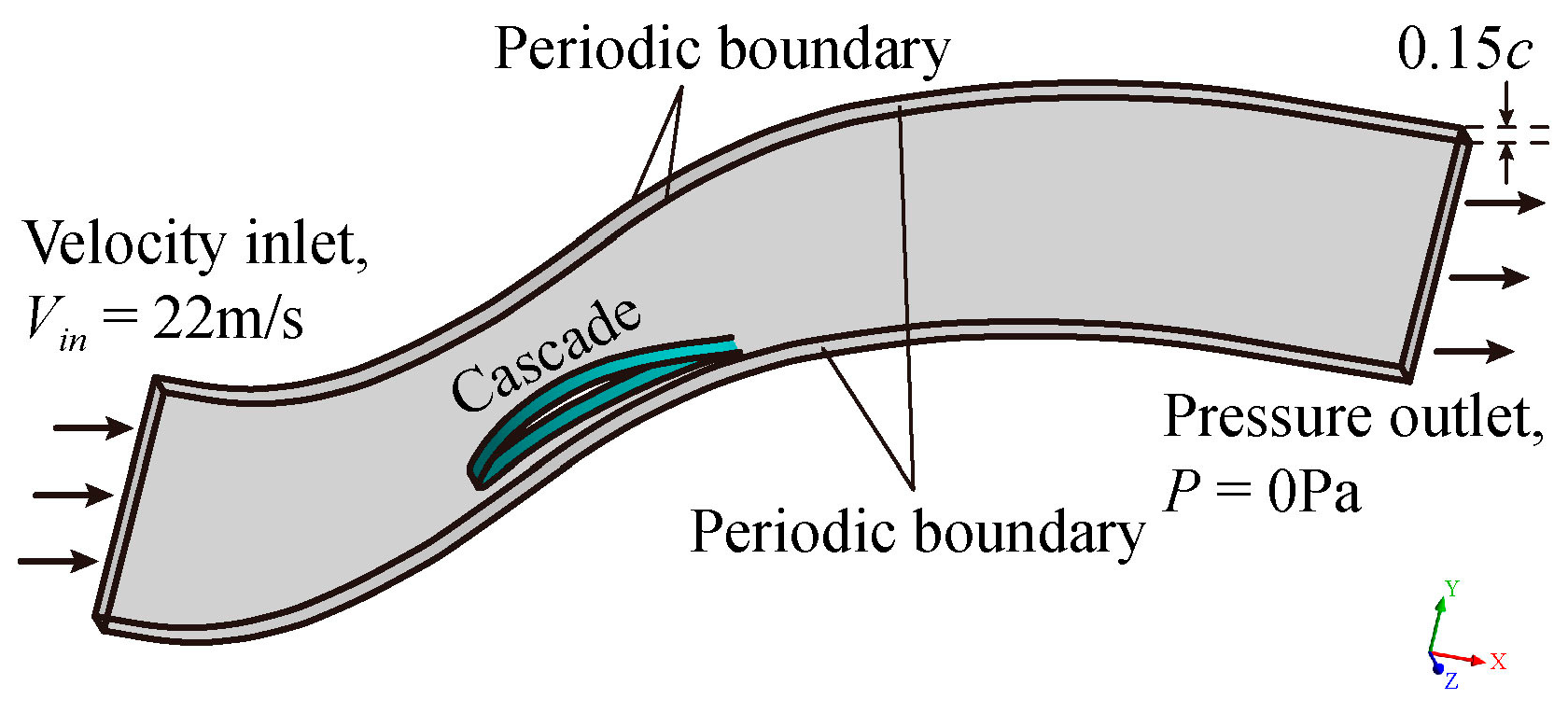
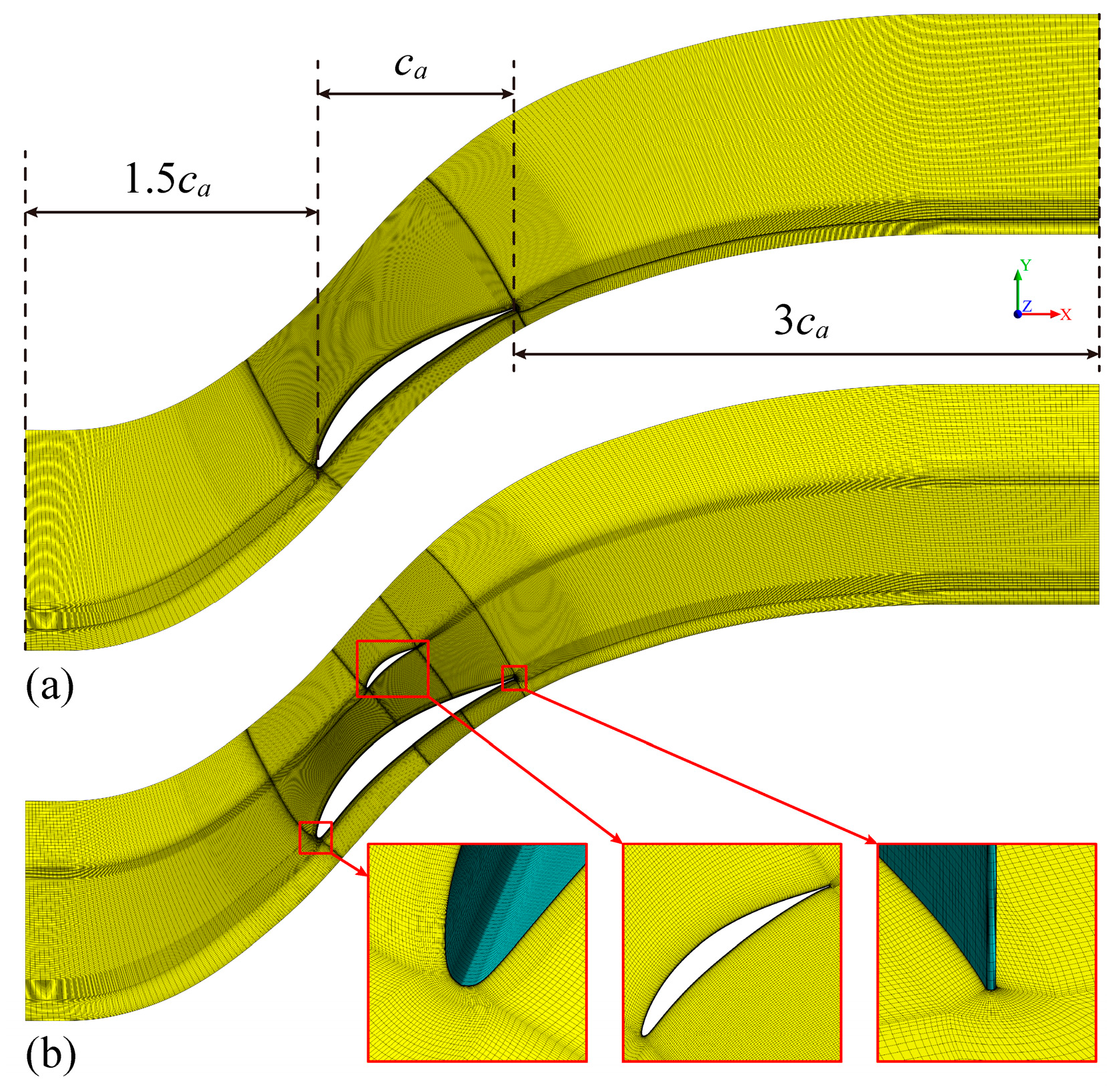






| Parameter | Value |
|---|---|
| Chord c/mm | 160 |
| Camber angle φ/(°) | 45 |
| Stagger angle γ/(°) | 39 |
| Pitch spacing s/mm | 140 |
| Solidity c/s | 1.143 |
| Blade span h/mm | 127 |
| Aspect ratio h/c | 0.794 |
| Incidence angle i/(°) | 0~12 |
| Attack angle α/(°) | 16~28 |
| Design inflow angle β1/(°) | 55 |
| Design outflow angle β2/(°) | 10 |
| Ma/(-) | 0.065 |
| (I/c, J/s) | A | B | C |
|---|---|---|---|
| 1 | (0, 0.4) | (0, 0.5) | (0, 0.6) |
| 2 | (0.25, 0.4) | (0.25, 0.5) | (0.25, 0.6) |
| 3 | (0.5, 0.4) | (0.5, 0.5) | (0.5, 0.6) |
| 4 | (0.75, 0.4) | (0.75, 0.5) | (0.75, 0.6) |
| Case | Grid Quantity (×106) | Number of Nodes (Chordwise) | Number of Nodes (Normal) | Number of Nodes (Spanwise) |
|---|---|---|---|---|
| Base case | 8.13 | 634 | 213 | 55 |
| B3 | 9.60 | 678 | 236 | 55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Wang, J.; Jiang, B.; Zhou, H.; Yang, W.; Ling, J. Large-Eddy Simulation of Flow Separation Control in Low-Speed Diffuser Cascade with Splitter Blades. Processes 2023, 11, 3249. https://doi.org/10.3390/pr11113249
Liang Z, Wang J, Jiang B, Zhou H, Yang W, Ling J. Large-Eddy Simulation of Flow Separation Control in Low-Speed Diffuser Cascade with Splitter Blades. Processes. 2023; 11(11):3249. https://doi.org/10.3390/pr11113249
Chicago/Turabian StyleLiang, Zhong, Jun Wang, Boyan Jiang, Hao Zhou, Weigang Yang, and Jieda Ling. 2023. "Large-Eddy Simulation of Flow Separation Control in Low-Speed Diffuser Cascade with Splitter Blades" Processes 11, no. 11: 3249. https://doi.org/10.3390/pr11113249
APA StyleLiang, Z., Wang, J., Jiang, B., Zhou, H., Yang, W., & Ling, J. (2023). Large-Eddy Simulation of Flow Separation Control in Low-Speed Diffuser Cascade with Splitter Blades. Processes, 11(11), 3249. https://doi.org/10.3390/pr11113249






