1. Introduction
Formulated products are important across several economic sectors (e.g., the food, cosmetics and personal care, pharmaceutical, and agrochemical sectors), and their design is well recognized as one of the important topics within the broader field of chemical product design [
1,
2,
3] that still poses several open problems and needs more systematic methodologies. One of the key hurdles in this regard is the lack of reliable quantitative property models relating product composition and microstructure to physico-chemical properties valued by customers [
1,
4,
5,
6,
7]. This hinders a systematic search across the design space (ingredients, their amounts, and manufacturing process), such as the one that is possible across a molecular domain defined by fundamental units (often groups of atoms), known as computer-aided molecular design (CAMD) [
8,
9,
10]. It is therefore important to equate how other less structured knowledge, in the form of heuristic rules (e.g., typical combinations of ingredients and their amounts) and experimental databases (regarding pure ingredients and previous successful formulations), can be integrated with available property models.
Zhang et al. [
11] proposed such a framework but without systematically integrating property models and heuristic-based procedures, which may lead to suboptimal solutions (for instance, designing a solvent mixture (small molecules) using CAMD tools and then, on top of this, selecting an adequate surfactant (larger molecules) using heuristic rules). Later, we proposed a fully integrated approach [
12] that uses propositional logic to convert heuristic rules into algebraic constraints, which are then incorporated side by side with quantitative property models in a single mixed-integer optimization formulation. The method is valid for formulations with any number
of ingredients to be chosen from a list of
possible ingredients (
). Yet, the overall product model (property models + heuristics) is often uncertain and may be even incomplete, only describing a subset of the important performance–composition relationships. Hundreds or thousands of alternative product formulations may therefore comply with such incomplete model. In other words, the feasible design space, although reduced by the available property models and heuristic rules, is still very large, making it difficult to identify what smaller set of formulations should proceed for testing and refinement.
In this study, we extend the method to incorporate the selection of a relatively small set of the most dissimilar formulations taken from a potentially large feasible design space. Dissimilarity is used as a selection criterion since one wants to determine a first exploratory plan of experiments (herein, “dissimilarity” corresponds to “space filling” in classical Design of Experiments (DoE) methods). For now, we adopt a simple measure of dissimilarity solely based on the number of ingredients shared by a set of alternative formulations, independently of ingredient concentration. To calculate such a measure, we represent a set of alternatives as a bipartite graph and use graph partitioning tools to evaluate the number of external edges. These are edges whose removal transforms the original graph into a set of disconnected subgraphs, with each one representing an alternative product formulation. The number of external edges is then the adopted measure of similarity (the higher the number of external edges, the more similar is the set of formulations). Then, the overall problem is to find the graph with the fewest external edges within the feasible design space. This will be formulated as a single mixed-integer optimization problem.
In a complete DoE programme, results from a first exploratory plan should be fed back to the front of the process and used to improve the product model. A new set of experiments may then be generated, and the process is repeated until a certain level of knowledge/optimality is attained (see, e.g., [
13] for a review on adaptive DoE using Bayesian optimization). In this work, we only focus on generating the first set of experimental points, given the initial available product model. Herein, the overall process is not discussed, nor is the way the additional experimental information is fed back to the product model.
The design of space filling sets for product formulation (with
ingredients chosen from a pool of
available ingredients) is still considered a challenging problem since the set is generated explicitly in the space
; thus, set size increases exponentially with
. The problem is even more complicated if one wants to investigate different concentrations of ingredients [
14]. For instance, with
and
, which is a common problem size in product formulation, a full factorial design has
million possible formulations. In our method, this dimensionality problem is partially avoided since implicit enumeration is used when solving the mixed-integer optimization problem and the search space reduced by available product models. A thorough comparison between efficient space filling methods (e.g., sampling based on low-discrepancy sequences) and our methodology (which may be seen as an implicit space filling design that is restricted by available product models) is still yet to be performed.
Graphs have long been used in chemistry and chemical engineering and for different purposes (molecular modelling, chemical reaction networks, heat exchanger networks, process synthesis) [
15,
16]. As far as we know, this work is the first of its kind to use graphs to represent a set of alternative product formulations, or, more simply, to represent different combinations of
ingredients taken from a pool of
available ingredients.
This paper is an extended version of a shorter paper presented at ESCAPE 29 [
17], including new aspects such as the simultaneous handling of dissimilarity of alternatives and an overall product design objective. The remainder of this paper is organized as follows. First, the problem of generating alternative formulations within a feasible design space is formulated (
Section 2). Then, the graph (and matrix) representation of those alternatives is presented (
Section 3). Next, the chore problem of generating dissimilar formulations is formulated (
Section 4). Finally, a cosmetic emulsion example is provided (
Section 5).
2. Generation of Alternative Product Formulations
Let be an ordered set containing all available ingredients from which a subset is to be selected to make part of the product formulation. Then, any product formulation may be described by a vector of binary variables (codifying the presence or absence of an ingredient) and a corresponding vector of mass fractions. Both and are ordered vectors with elements in the same order of that in set .
Let
be the vector of product performance metrics with target values
, meaning that product quality is evaluated in terms of the deviation of
from the target
. Property models are any relationship between metrics
and product composition (herein represented by the following set of equations:
). Less structured knowledge is often available in the form of heuristic rules for product formulation, which may be simple rules regarding what components should be selected and in what amount for a given desired effect or eventually more complex rules involving logical conditions. In any case, these heuristic rules can be modelled using propositional logic and additional binary variables
[
12], resulting in a set of (often linear) algebraic restrictions. Let
represent these heurist-related restrictions and other problem-specific restrictions. Finally, let
be an objective function to be minimized, accounting for both product quality and cost.
The problem of optimal product formulation may then be stated as the following optimization problem, labelled as
Problem (P1):
Due to model incompleteness and uncertainties, one wants to find not a single “optimal” solution but instead an ordered set
of solutions with increasing value of
. This may be obtained by successively solving (P1) to global optimality and imposing cuts in vector
to prohibit previous solutions [
18]. However, the set
thus generated may include very similar solutions, differing for instance in the existence of only one component. Moreover, it is not certain what should be the size of this set so that significantly different alternatives are captured. In the next section, a graph (and matrix) representation of any set of alternative formulations is proposed, and then, in
Section 4, a graph partitioning technique is used to expand formulation (P1) to generate a set
of formulations with maximum (or close to maximum) dissimilarity.
4. Generation of Sets of Dissimilar Product Formulations
Let be a set of product formulations represented by a 0–1 matrix , as defined above. The problem of partitioning in clusters may be stated as follows: “find row and column permutations of in order to obtain diagonal blocks and minimizing the number of external elements “1” outside the diagonal blocks”.
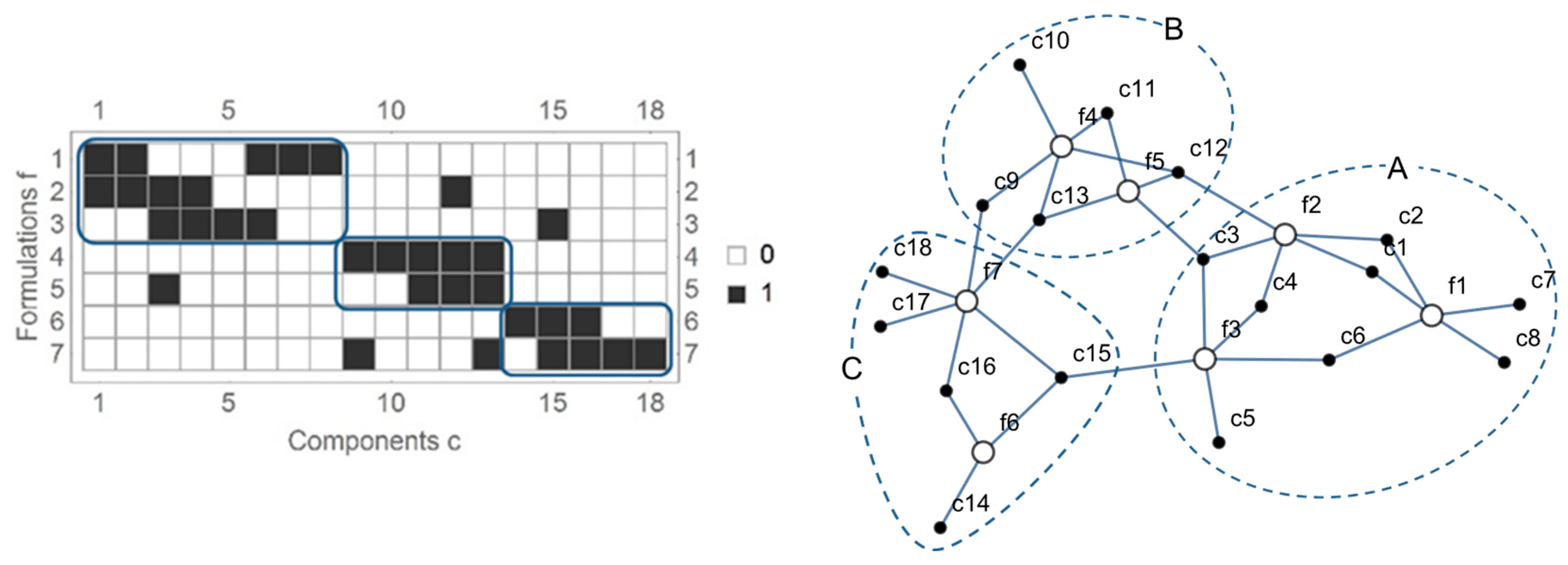
The matrix on the left side of
Figure 1 is an example of the result of such matrix rearrangement, with three diagonal blocks corresponding to three identified clusters, as well as five external elements outside the diagonal blocks. The second cluster, for instance, contains formulations
and
and components
to
. Component
does belong to formulation
but is an external element since it does not belong to the second cluster. In general, each external element corresponds to a component that is shared or, more precisely, to a component from one cluster that is used in a formulation belonging to a second cluster. The number of external elements is thus a measure of similarity between clusters.
The right side of
Figure 1 shows the same clustering but in graph format. The external elements of matrix
here correspond to external edges, which are those connecting vertices located in different clusters. External edges are also designated by cut edges, since their removal decomposes the graph into
disconnected subgraphs. For this reason, the set of external edges is designated by an edge separator.
Using graph language, the above-stated problem of partitioning is as follows: “find the minimum number of edges whose removal decomposes the bipartite graph into disconnected subgraphs (also designated as partitions or clusters)”. In the graph literature, this is known as the problem of graph partitioning by edge separator (GPES).
Sparse matrix rearrangement is a less studied problem than graph partitioning. In addition, the former is often solved by first translating the matrix into an equivalent graph and then applying graph partitioning methods [
19]. Therefore, graph partitioning is the technique used in this work to find dissimilar formulations, although the matrix representation is perhaps clearer and thus will be used to present results.
The problem of graph partitioning is an NP-complete combinatorial optimization problem that has been well studied in multiple contexts, including parallel computing, sparse matrix computations, integrated circuit design, biological and social networks, and data mining.
For small graphs, exact solutions of the graph partitioning problem can be obtained using integer programming. Above some hundreds of vertices, computational time becomes prohibitive; thus, it is preferable to use heuristic algorithms. There are several of these available, each with different performances in terms of computational time versus quality of solutions (multilevel algorithms are perhaps the most well known [
20,
21,
22]; Markov cluster algorithms, based on random walks in graphs, are also an interesting alternative [
23,
24]). In the case studied here, the number of vertices is at most
, which is a modest graph size that can, in principle, be easily handled by integer programming. This is therefore the technique we will use here, specifically the standard 0–1 formulation of Boulle [
25], transposed to the particular (and simpler) case of a bipartite graph.
It is now time to pose our central problem: “given a set of available components, find dissimilar formulations obeying to the product design restrictions of the above-listed Problem (P1) ( and )”. In graph language, this is the problem of: (i) constructing the bipartite graph , with edges still to be decided, and (ii) then partitioning the graph via edge separator into clusters, with each cluster having one and only one formulation (). Two sets of binary variables are thus needed, and , for all and all . In the first case, if component is chosen to be in formulation , while in the second case, if component belongs to cluster (but not necessarily to formulation ).
The total number of edges is thus
, and the number of internal edges is
, with
(in
Figure 1,
is an example of an internal edge). The number of external edges, which is the adopted measure of similarity, is
. Then, the graph construction and partition problem to find the
most dissimilar formulations is as follows:
The components of Restriction (5) are a linear formulation of ; Equation (6) imposes that each component belongs to only one cluster; and the components of Equation (7) are anti-degeneracy constraints ( must belong to cluster , must belong either to or to , and, in general, must belong to one of the first th clusters). Although are binary variables, they may be treated as continuous, given Restriction (5). The total number of binary variables ( and ) is therefore 2.
For a graph with edges, is an absolute measure of the partitioning quality and equivalently of the similarity between formulations. When comparing solutions for graphs of different dimensions, the fraction of external edges should be used instead: .
In addition to the dissimilarity criterion (Equations (4)–(8) above), all generated product formulations must obey to the design restrictions of Problem (P1), which are now written as follows:
Here, mass fractions (of each component in formulation ) are continuous variables, and are additional binary variables used to describe heuristic rules. Therefore, the most dissimilar formulations adhering to design restrictions and and without considering the design objective are the solutions of Equations (4)–(10) (from now on referred to as Problem (P2)). If and are linear functions, Problem (P2) is a MILP problem.
In order to include objective
, a multiobjective approach is needed—for instance, defining a global objective as a weighted sum of
and
(or more precisely, a measure of
evaluated over
, such as the mean value of
). Due to the combinatorial nature of Problem (P2), there may be quite a few solutions for the same minimum value of
(herein referred to as
). One may then first solve Problem (P2) to find
and, in a second stage, solve the following problem—
Problem (P3)—where the mean value of the design objective (or other appropriate measure) is minimized subject to
:
This way, one can find the set of formulations that are simultaneously the most dissimilar and the optimal ones in terms of a given design objective. If , , and are linear functions, Problem (P3) is a MILP problem.
If the solution of Problem (P3) results in product formulations having unsatisfactory values of the design objective , Restriction (12) may be relaxed, thus allowing for the generation of less dissimilar formulations but a better average performance (lower mean value of ). Successive relaxations of Restriction (12) will produce a Pareto curve of the two competing objectives ( versus ).
5. Example of a Cosmetic Emulsion
The above-proposed optimization tools are now applied to an example of a cosmetic emulsion that has already been explored in [
12]. The problem is to formulate a rinse-off hair conditioner, which is an o/w emulsion, selecting ingredients from a set of 32 possible ingredients organized in 6 subsets: emollients of type
(
to
), emollients of type
(
to
), emollients of type
(
to
), fatty alcohols (
), thickening polymers (
), and cationic surfactants (
). The design variables are vectors
(choice of ingredients) and
(mass fractions), both with dimension 32. The formulation also includes five mandatory ingredients (water, glycerol, disodium EDTA, propylparaben, and perfume) in fixed amounts (except for water, whose mass fraction is such that mass fractions of all components sum up to 1).
The available product model is presented in
Table 1, including design variables, product performance specifications, property models, and heuristic rules. The model is incomplete, not covering all product attributes valued by consumers nor their interactions [
26]. Only three product performance metrics are fully quantified with models estimating them as a function of product composition: initial viscosity (
), final viscosity (
), and greasiness value (
). These models have been validated previously [
12] (in the case of
and
, validation included the case of heuristic 3.3.; in the case of
, validation was partial).
Given model incompleteness and uncertainty, the goal is to find a small set of alternative formulations to proceed to experimental testing. These alternatives are thus equated using relatively loose specifications for the three quantitative metrics: , , and .
5.1. Modelling of Heuristic Rules
The simplest heuristic rules are recommended or regulatory limits for a particular ingredient , which are easily modelled as linear constraints of the type . If ingredient is chosen (), then the desired limits and are imposed. Otherwise, if ingredient is not chosen (), then constraint reduces to . If no heuristic limits are known, one simply writes .
Heuristics expressed as logical expressions may also be translated to linear algebraic restrictions using additional binary variables and propositional logic [
12], as is the case with Heuristics 3.2 and 3.3, which are modelled as follows.
Heuristic 3.2. Let
and
(no thickening polymers are used). Then, the logical condition to be modelled is as follows:
The right-hand side of the implication is equivalent to the following:
The implication may then be written as follows: . This is modelled by the algebraic constraint , where is a non-attainable upper bound for (in this case, is an adequate value).
Finally, the logical equivalence
may be modelled as the following set of linear constraints:
Heuristic 3.3. In order to model Heuristic 3.3, the viscosity model has to be reformulated in such a way that if
viscosity limits are obeyed. Let
and
. Then, the two following restrictions can describe both the viscosity model,
, and Heuristic 3.3:
If
, the first restriction reduces to
and the second restriction reduces to
. This last one is non-active if
is a sufficiently large constant. On the other hand, if
, the first restriction is non-active (with
being a sufficiently low constant) and the second restriction reduces to
, with
being any value between
and
. Hence, viscosity
is “forced” to be within the specifications stated by Heuristic 3.3.
A similar formulation is required for the viscosity
:
with constants
,
, and
having similar meanings. The following numerical values were adopted for the six constants:
,
,
,
,
,
.
5.2. Sets of Dissimilar Alternative Formulations
Back to the product model as a whole, it generally consists of a set of linear equations and inequations that correspond to the generic design restrictions
and
in Problem (P1) (see
Section 2). One then formulates and solves Problems (P1), (P2), and (P3), which were presented in
Section 2 and
Section 4 and are now being applied to this particular case of a hair conditioner. All the problems are MILP problems, and all of them were solved using GAMS/CPLEX [
35] on a laptop with an Intel
® Core™ i7-1065G7 processor.
Problem (P1) is formulated with
as the cost of the formulation (excluding fixed ingredients and processing costs). Binary cuts are used to generate a rank of 50 formulations with increasing cost. These 50 alternative formulations use 15 different components and have a cost ranging between 0.884 and 0.952 USD/kg. This set is clustered using the heuristic multilevel algorithm hMeTiS, a publicly available tool [
21], with a CPU time below 1 s. The result for three clusters (and a minimum of three components per cluster) is poor, with almost half of the edges being external edges (
). The quality of the partitioning is even worse with a higher number of clusters. One then concludes that significantly different subsets of alternative formulations cannot be found within this set
of 50 formulations. This means that
does not have enough diversity in terms of formulations using significantly different sets of components; thus, it is a relatively poor set from which to extract a small number of different alternatives to test.
Next, Problem (P2) is solved for different input values of
, resulting in each case in a set of
formulations with maximum dissimilarity. Afterwards, Problem (P3) is solved resulting in
formulations that are simultaneously the most dissimilar and the ones with the lowest average cost. In all cases, the average cost is not considered to be excessive, and as such, the goal of maximum dissimilarity is not relaxed. Results are shown in
Figure 2 and
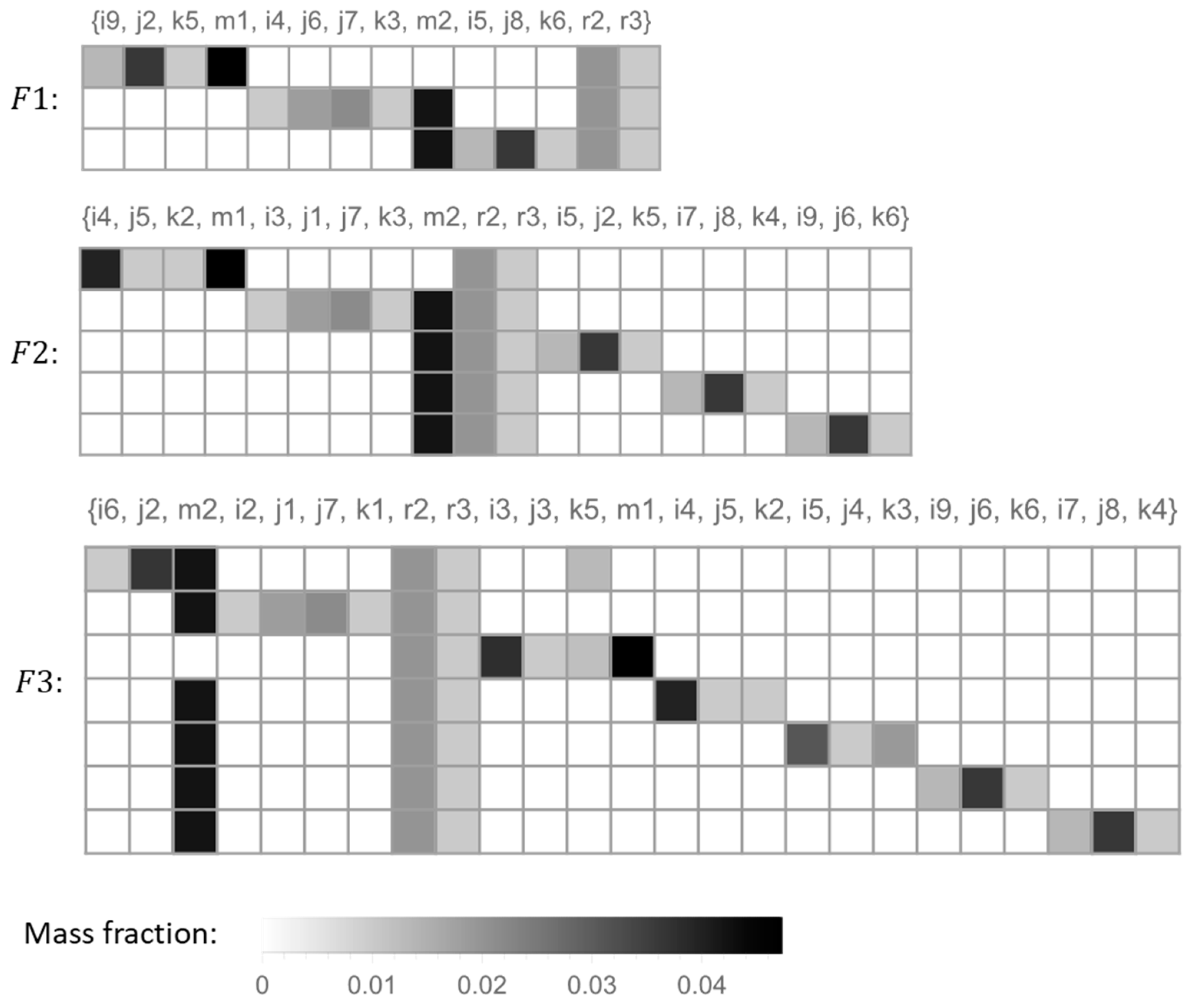
Table 3 below. In
Figure 2, each set of formulations is represented by a matrix, and the squares were coloured using a grayscale according to the mass fraction of the selected ingredients.
With
one obtains set
, which uses 14 different components and has a total of 19 edges (non-zero elements in the matrix representation). Out of these 14 different components, only 5 are external edges—corresponding to components
,
, and
—that are used in more than one of the three formulations. The fraction of external edges is thus
= 5/19 = 0.263. If the budget for experimental tests allows for, at most, three candidate formulations, then set
is a good plan of experiments, with both maximum dissimilarity between experimental points and minimum average cost (given the available knowledge, expressed in the form of the product model in
Table 1).
For higher values of
, one obtains sets of formulations that use more components, have a lower level of dissimilarity (higher values of
), and have a higher average cost. Examples of these types of sets are sets
and
(also shown in
Figure 2), which have 5 and 7 formulations, respectively. These sets clearly cover a larger design space that includes new and more expensive ingredients. In fact, in order to find a larger number of dissimilar formulations, the algorithm is forced to construct formulations with more ingredients, also including more expensive ones.
Regarding computational time, Problem (P2) is solved in less than 0.3 s in all cases, while the time to solve Problem (P3) increases substantially as increases. This indicates that, for large values of , there is room to test alternative graph partitioning algorithms (both classical multilevel algorithms and Markov cluster algorithms), which are faster than integer programming (but they do not guarantee global optimality). A comparison between these heuristic partitioning methods and the approach adopted for this paper (MILP Problems P2 and P3) that includes the trade-off between CPU time and quality of partitioning is still yet to be performed. Furthermore, there is still a previous problem to solve, which is how to integrate product design restrictions (Equations (9) and (10)) with those efficient graph partitioning algorithms. Using integer programming, this integration is straightforward and was applied in Problems (P2) and (P3).
In the solutions presented thus far (sets
,
, and
), no thickening polymers were selected; instead, the cheaper solution of using fatty alcohols in excess was adopted, in accordance with Heuristic 3.2 of
Table 1. Still, one may want to deliberately include this alternative in the experimental set. To do so, one only has to solve Problems (P2) and (P3) with explicit restrictions on the binary variables
, which control this alternative. With
and the restriction
, at least two of the generated formulations will use a thickening polymer. The solution thus obtained (not shown in
Figure 2) has the same number of external edges as that of set
(
) and uses the same 25 ingredients of set
plus polymers
and
(separately in two of the seven alternative formulations). The average cost increases from 1.36 to 1.46 EUR/kg.