Research on Pressure Control of an Electro-Hydraulic Servo System Based on Sliding-Mode Variable-Structure Direct Torque Control
Abstract
1. Introduction
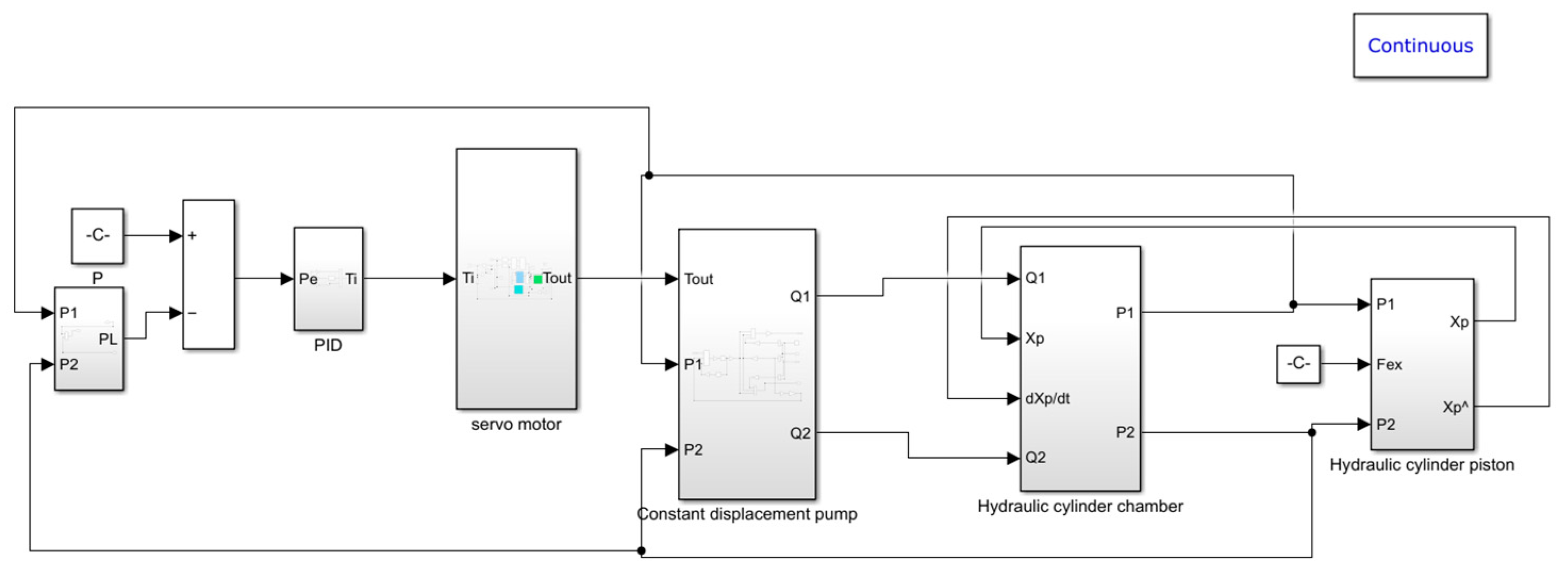
2. Principle of the DDVC Electro-Hydraulic Servo System
3. Mathematical Model of the DDVC Electro-Hydraulic Servo System
3.1. Mathematical Model of the Servo Motor
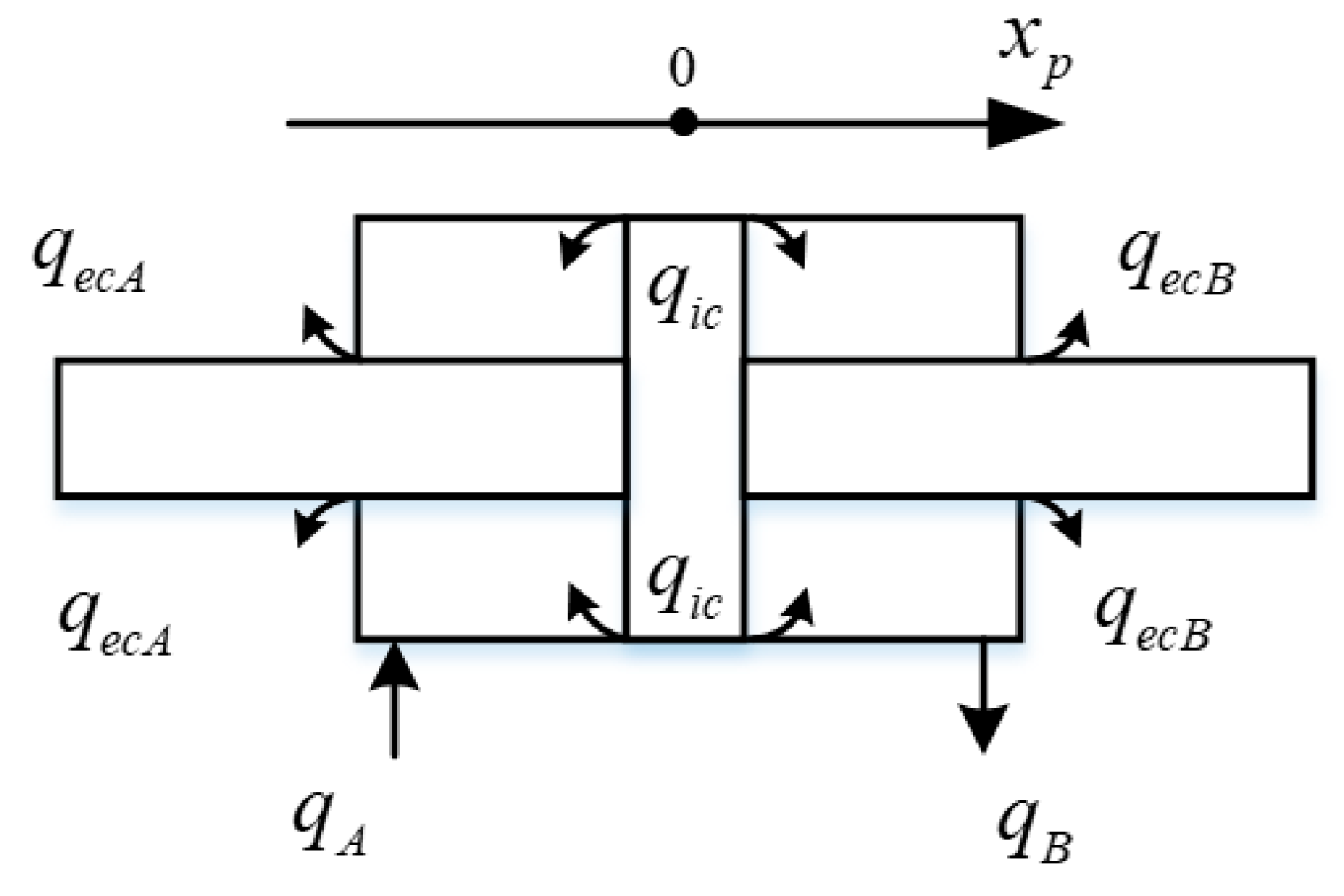
3.2. Mathematical Model of the Hydraulic System
3.2.1. Flow Equation of the Constant-Displacement Pump
3.2.2. Flow Continuity Equation of the Hydraulic Cylinder
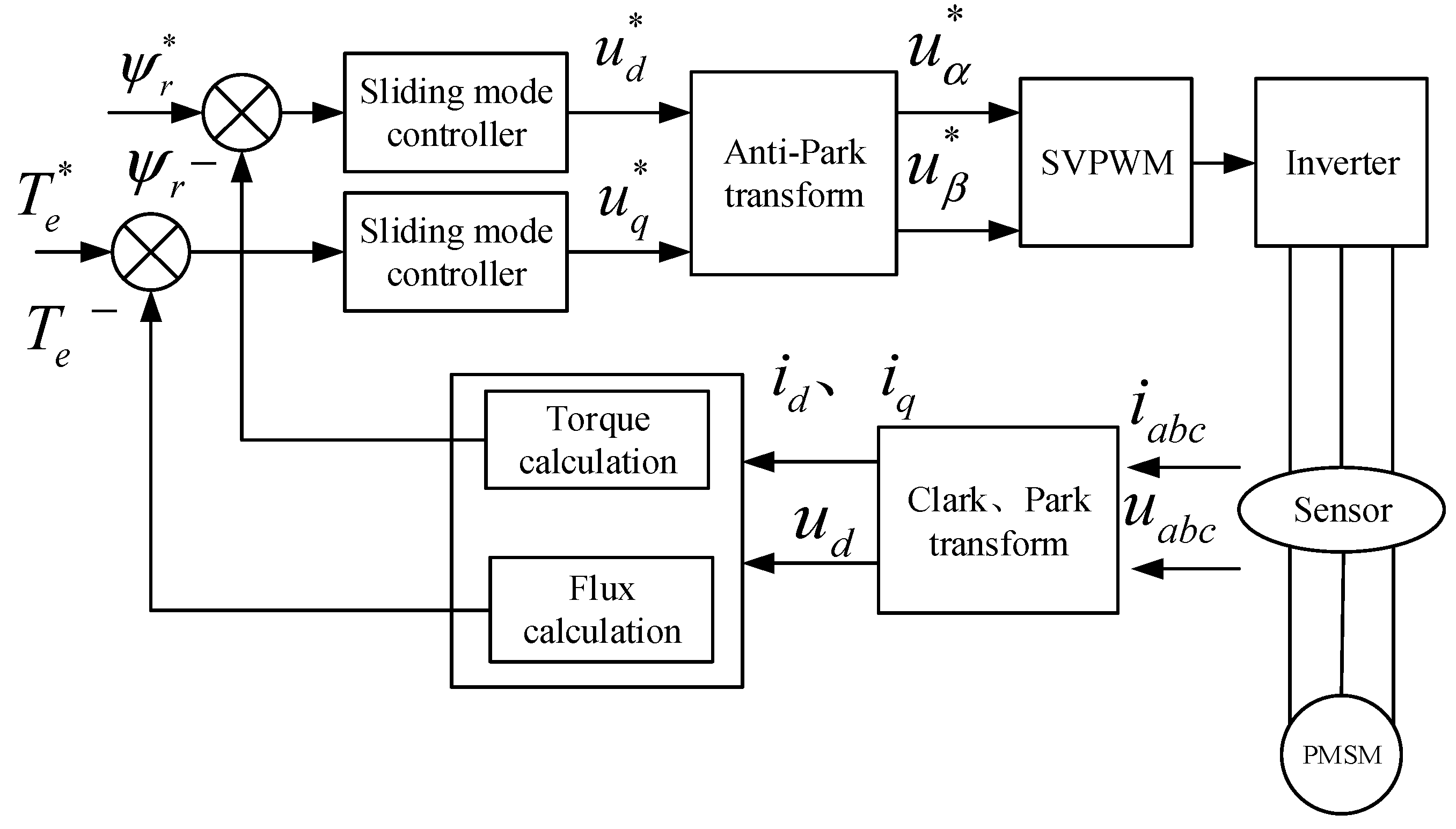
4. The Motor Direct Torque Control Algorithm
5. Direct Torque Control of Servo Motor Based on Sliding-Mode Control
5.1. Space Vector Pulse-Width Modulation
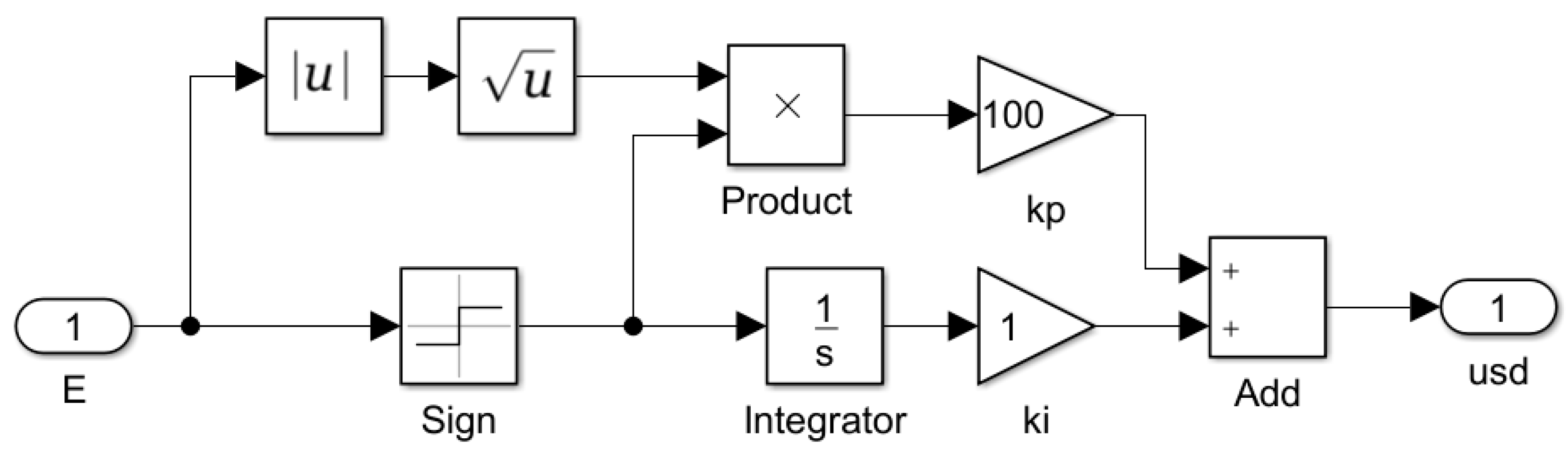
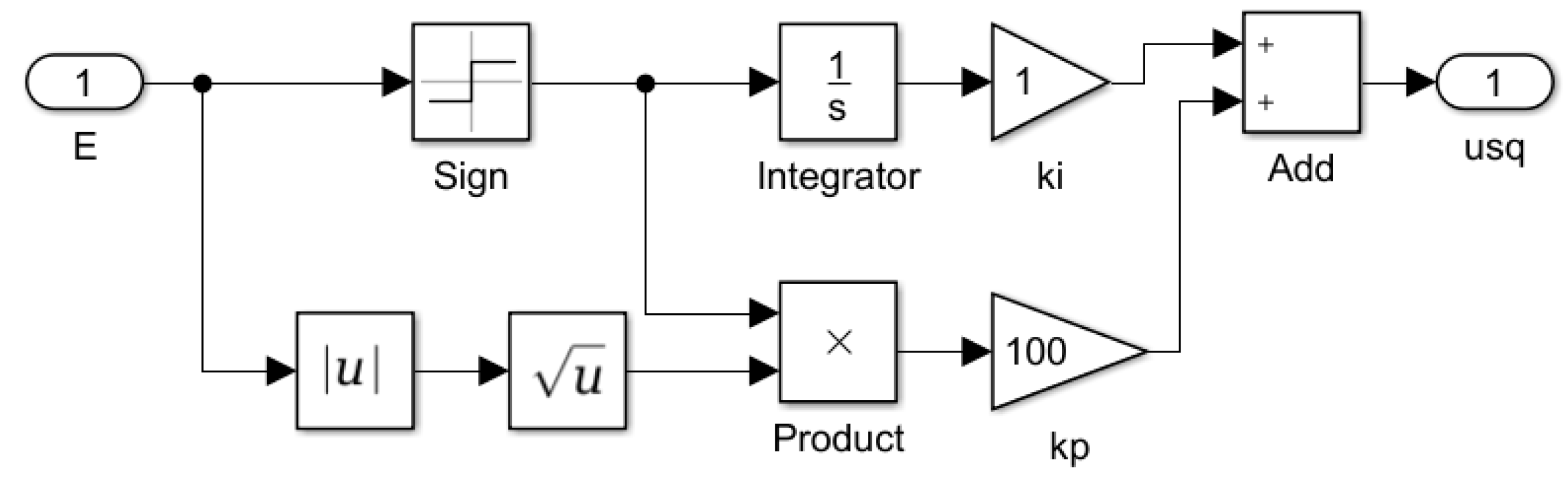
5.2. Sliding-Mode Controller Design
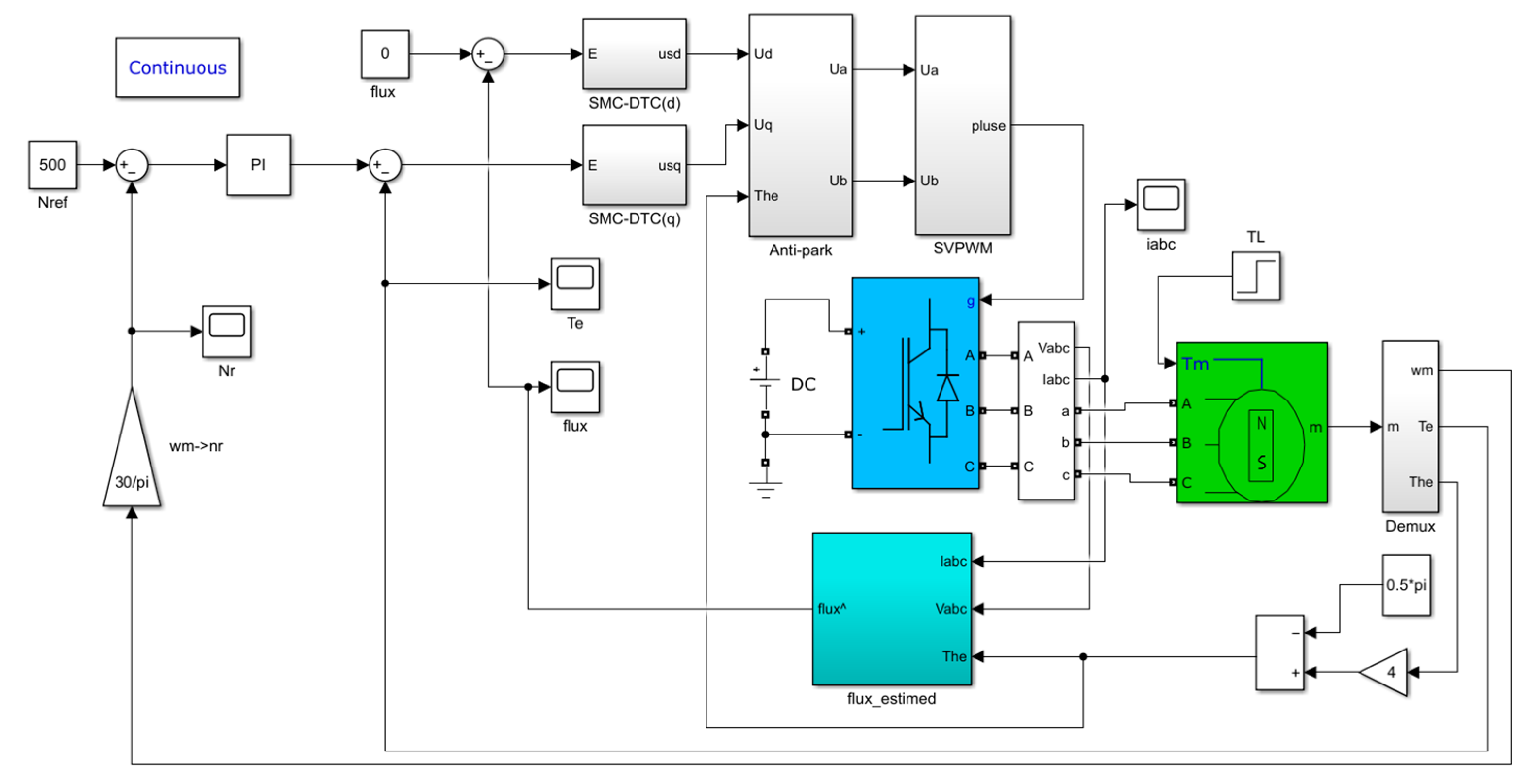
6. Simulation Analysis
6.1. Building the Simulation Model
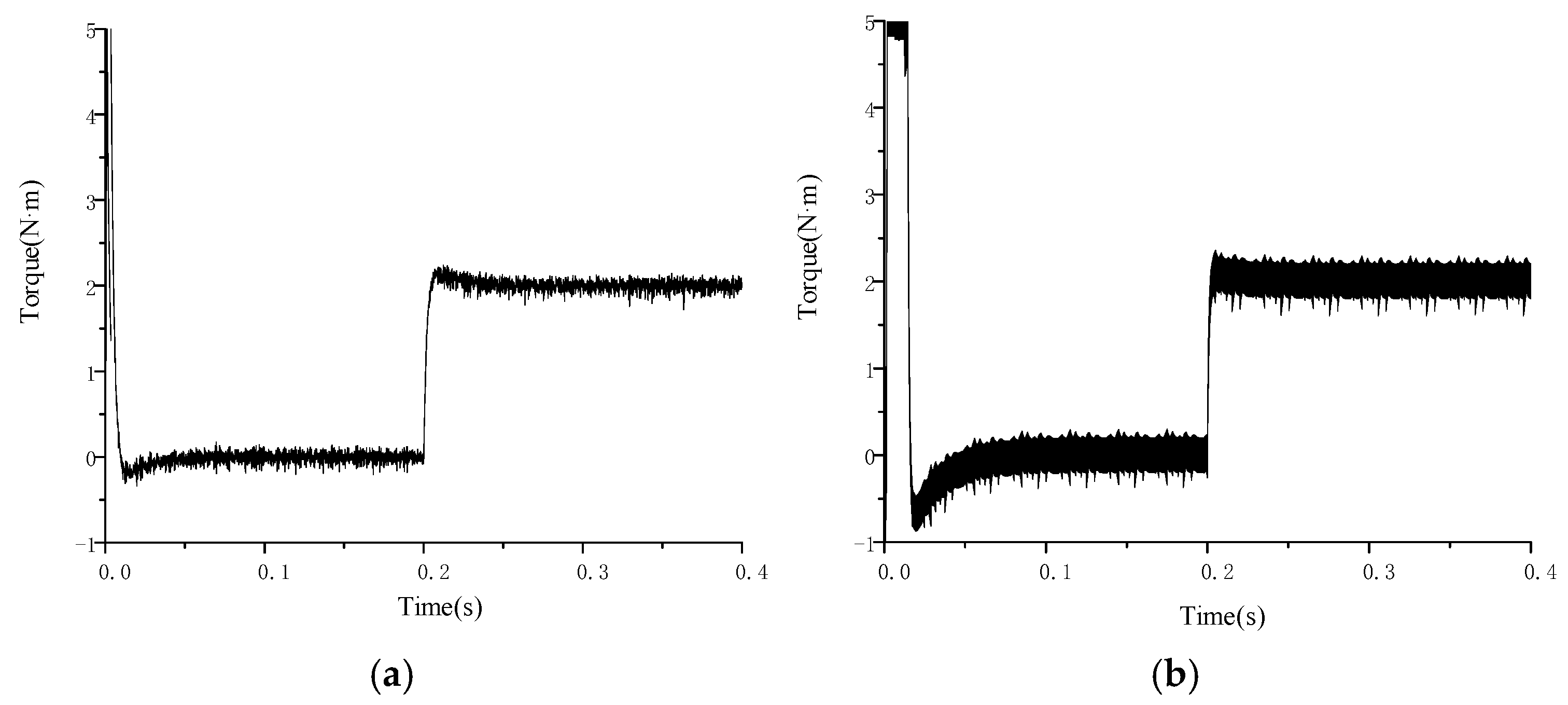
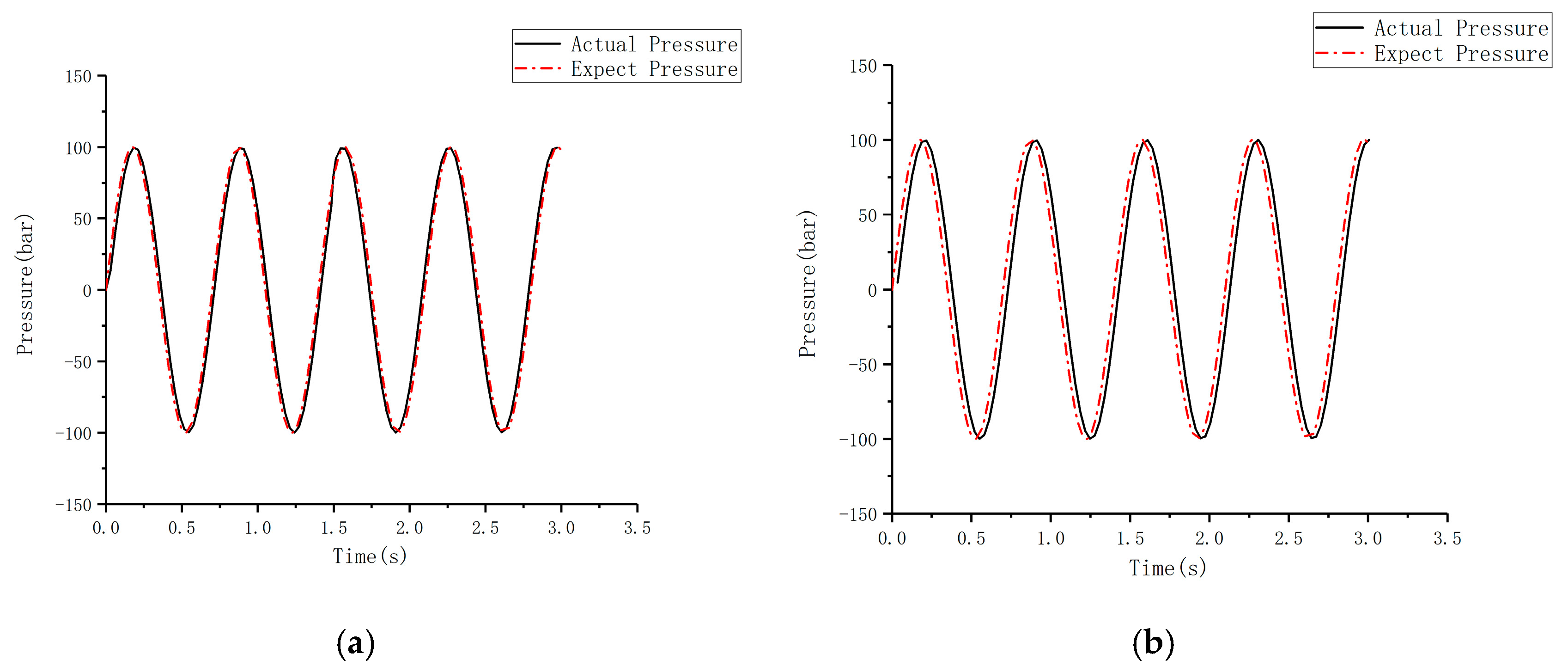
6.2. Analysis of Simulation Results
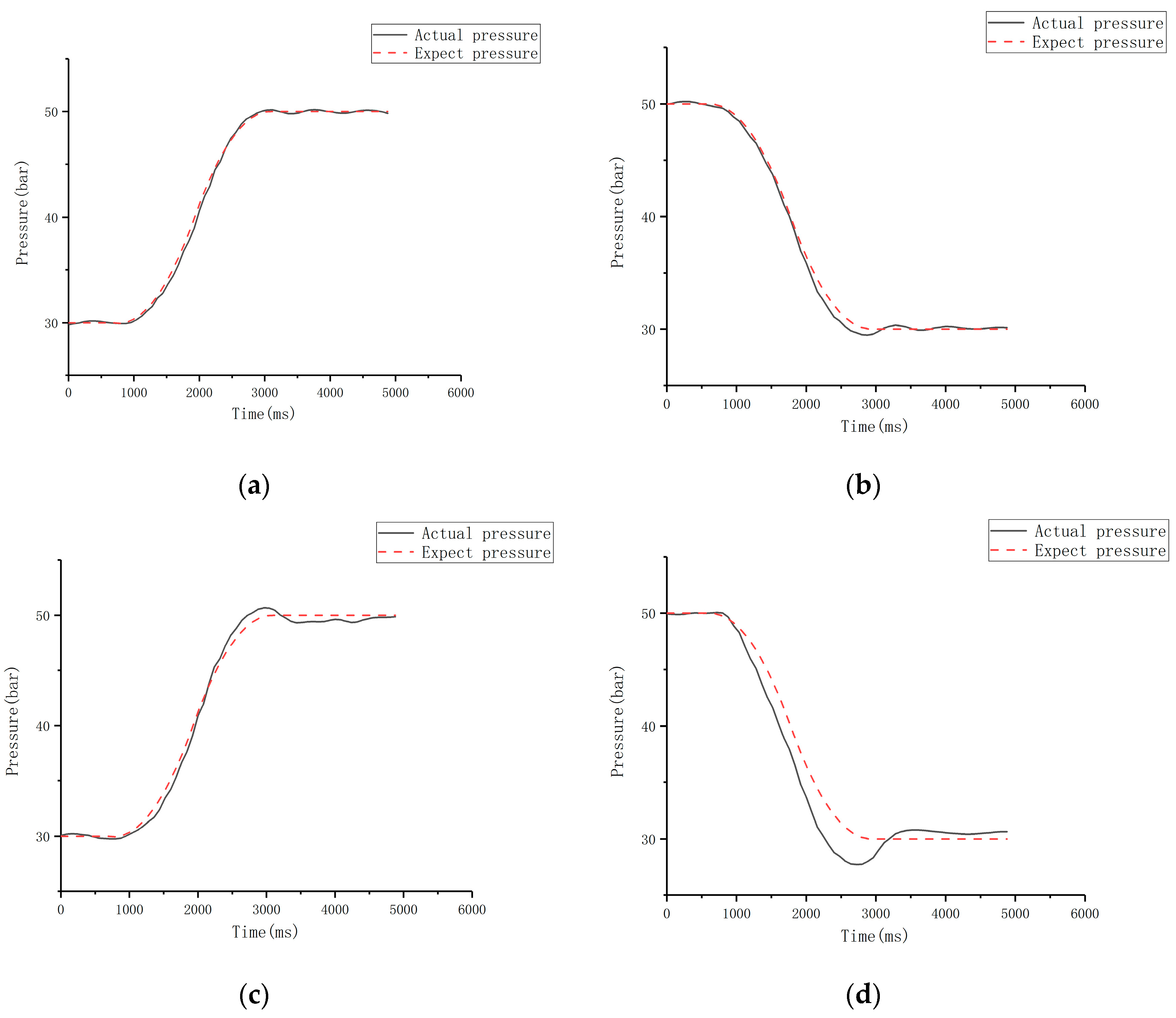
6.3. Experimental Content and Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, B.; Zhu, Q.; Yao, J.; Zhang, J.; Huang, Z.; Jin, Z.; Wang, X. Design, Mathematical Modelling and Force Control for Electro-Hydraulic Servo System with Pump-Valve Compound Drive. IEEE Access 2020, 8, 171988–172005. [Google Scholar]
- Zhao, P. Research on Position Control of Transferable Vane Electro-Hydraulic Servo Closed Pump Control System. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2020. [Google Scholar]
- Yao, B. Study on Thermal Balance of Direct-Drive Volumetric Control Electro-Hydraulic Servo System. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2020. [Google Scholar]
- Helbig, A. Injection moulding machine with electric-hydrostatic drives. In Proceedings of the 3rd International Fluid Power Conference (3. IFK), Aachen, Germany, 5–6 March 2002; pp. 67–82. [Google Scholar]
- Sedrak, D. Closed-loop electronic valuing and the application of variable voltage variable frequency in hydraulics. Elev. World 1999, 47, 66–72. [Google Scholar]
- Lee, S.R.; Hong, Y.S. A Dual EHA System for the Improvement of Position Control Performance via Active Load Compensation. Int. J. Precis. Eng. Manuf. 2017, 18, 937–944. [Google Scholar] [CrossRef]
- Ahn, K.K.; Nam, C.; Jin, M.L. Adaptive Backstepping Control of an Electro-Hydraulic Actuator. IEEE/ASME Trans. Mechatron. 2014, 19, 987–995. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Qu, X.; Zhang, Z. Robust feedback linearization control of electro-hydraulic position servo system. Mach. Tool Hydraul. 2016, 44, 148–152. [Google Scholar]
- Han, J. Development and application of electro-hydraulic servo system. Mach. Tool Hydraul. 2012, 40, 15–18. [Google Scholar]
- Liu, D. Analysis and Compensation Method for Position and Force Control Characteristics of Electrohydrostatic System. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2020. [Google Scholar]
- Ba, D.X.; Ahn, K.K.; Truong, D.Q.; Park, H.G. Integrated Model-based Backstepping Control for an Electro-Hydraulic System. Int. J. Precis. Eng. Manuf. 2016, 17, 565–577. [Google Scholar]
- Hoang, Q.D.; Lee, S.G.; Dugarjavn, B. Super-Twisting Observer-Based Integral Sliding Mode Control for Tracking the Rapid Acceleration of a Pison in a Hybrid Electro-Hydraulic and Pneumatic System. Asian J. Control. 2019, 21, 483–498. [Google Scholar]
- Luo, G.; Görges, D. Modeling and Adaptive Robust Force Control of a Pump-Controlled Electro-Hydraulic Actuator for an Active Suspension System. In Proceedings of the IEEE Conference on Control Technology and Applications (CCTA), Hong Kong, China, 19–21 August 2019; pp. 592–597. [Google Scholar]
- Helian, B.; Chen, Z.; Yao, B. Precision Motion Control of a Servo Motor-Pump Direct Drive Electro-hydraulic System with a Nonlinear Pump Flow Mapping. IEEE Trans. Ind. Electron. 2019, 67, 8638–8648. [Google Scholar]
- Zhang, Z.; Li, H.; Zhu, D. EHA feedback linearization optimal sliding mode surface double fuzzy sliding mode control. J. Beijing Univ. Aeronaut. Astronaut. 2016, 42, 1398–1405. [Google Scholar]
- Kou, F.; Du, J.; Wang, Z.; Li, D.; Xu, J. Nonlinear modeling and coordinate optimization of a semi-active energy regenerative suspension with an electro-hydraulic actuator. Algorithms 2018, 11, 12. [Google Scholar] [CrossRef]
- Zhao, S.; Gao, L.; Bin, Y. Multi-variable coupled mechanism and kinetic energy stiffness analysis method for a mechanical-electrical hydraulic system. Vib. Shock. 2018, 37, 27–33. [Google Scholar]
- He, D.; Wang, T.; Xie, J.; Ren, Z.; Liu, Y. An analysis on parametrically excited nonlinear vertical vibration of a roller system in corrugated rolling mills. Vib. Shock. 2019, 38, 164–171. [Google Scholar]
- Jiang, J.; Ge, Z.; Yang, C.; Liang, H. Differentiator-based discrete variable structure controller for direct drive electro-hydraulic servo system. J. Jilin Univ. 2018, 48, 1492–1499. [Google Scholar]
- Chen, G.; Jia, P.; Yan, G.; Liu, H.; Chen, W.; Jia, C.; Ai, C. Research on Feedback-Linearized Sliding Mode Control of Direct-Drive Volume Control Electro-Hydraulic Servo System. Processes 2021, 9, 1676. [Google Scholar] [CrossRef]



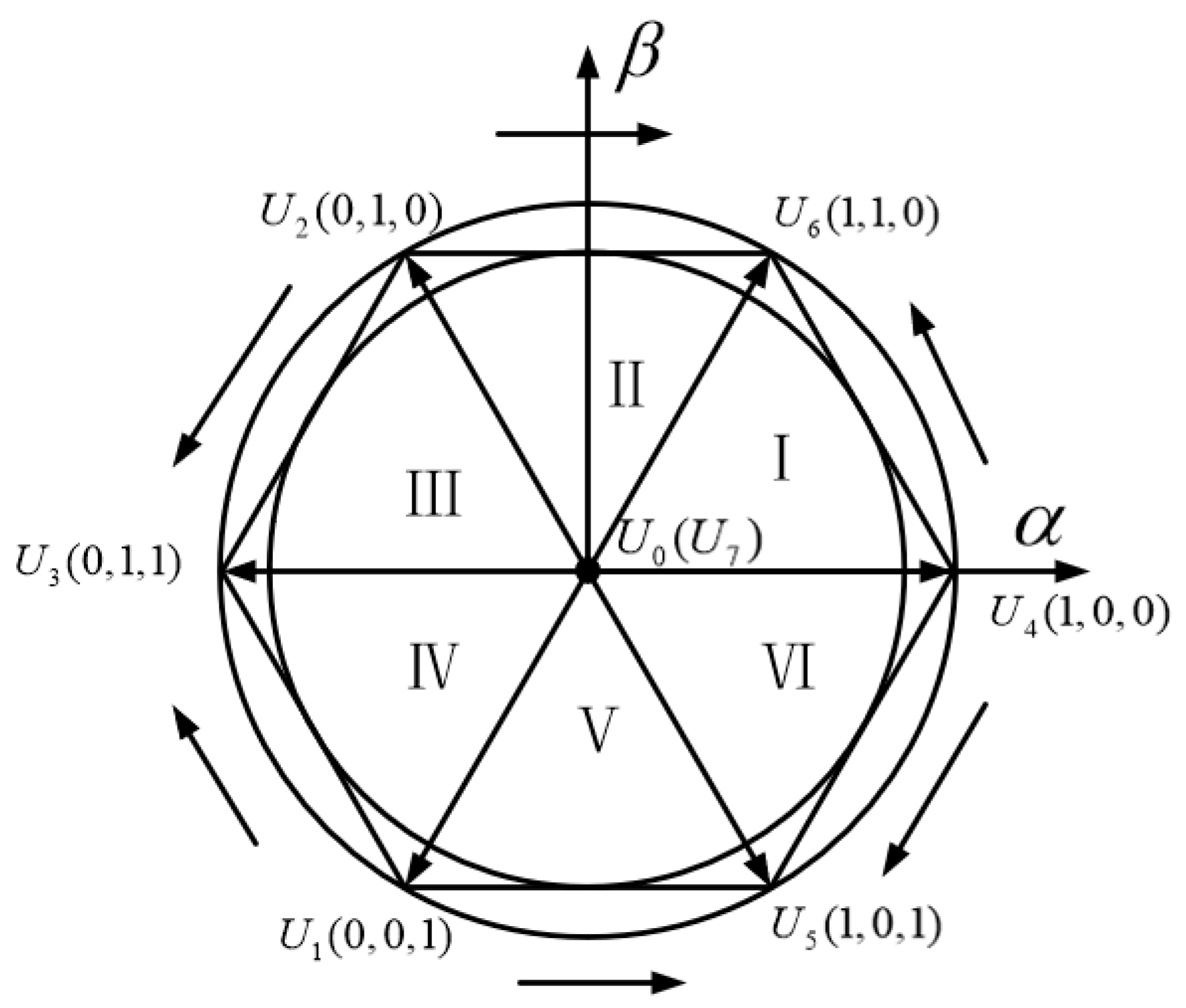







| N | Sector |
|---|---|
| 3 | I |
| 1 | II |
| 5 | III |
| 4 | IV |
| 6 | V |
| 2 | VI |
| N | T4 | T6 | T0 |
|---|---|---|---|
| 1 | Z | Y | T0 = (TS − T4 − T6)/2 |
| 2 | Y | −X | |
| 3 | −Z | X | |
| 4 | −X | Z | |
| 5 | X | −Y | |
| 6 | −Y | −Z |
| N | Tcm1 | Tcm2 | Tcm3 |
|---|---|---|---|
| 1 | Tb | Ta | Tc |
| 2 | Ta | Tc | Tb |
| 3 | Ta | Tb | Tc |
| 4 | Tc | Tb | Ta |
| 5 | Tc | Ta | Tb |
| 6 | Tb | Tc | Ta |
| Symbol | Physical Significance | Set Value |
|---|---|---|
| [(m3/s)/Pa] | Leakage coefficient of pump | 3 × 10−13 |
| [(m3/s)/Pa] | External leakage coefficient of pump | 3 × 10−13 |
| [L/r] | Pump delivery | 0.008 |
| [(m3/s)/Pa] | Leakage coefficient of hydraulic cylinder | 3 × 10−13 |
| [(m3/s)/Pa] | External leakage coefficient of hydraulic cylinder | 3 × 10−13 |
| [N/(m/s)] | Viscous damping coefficient | 150 |
| [N] | Maximum static friction | 25 |
| [N] | Coulomb friction | 15 |
| [mL] | One-side initial volume of hydraulic cylinder | 450 |
| [N/m2] | Oil elastic modulus | 6.5 × 10−8 |
| [cm2] | Effective area of piston | 71 |
| [kg·m2] | Moment of inertia on the axis of rotation | 2.65 × 10−4 |
| Motor damping coefficient | 7.2 × 10−5 | |
| [kg] | Converted load mass | 500 |
| Symbol | Physical Significance | Value |
|---|---|---|
| [(m3/s)/Pa] | Leakage coefficient of pump | 1 × 10−13 |
| [(m3/s)/Pa] | External leakage coefficient of pump | 1 × 10−13 |
| [mL/r] | Pump delivery | 0.8 |
| [kW] | Pump rated power | 1 |
| [Mpa] | Maximum operating pressure of pump | 21 |
| [(m3/s)/Pa] | Leakage coefficient of hydraulic cylinder | 1 × 10−13 |
| [N/(m/s)] | Piston damping coefficient | 150 |
| Gas polytropic index | 1.3 | |
| [N] | Sliding static friction | 25 |
| [N] | Sliding coulomb friction | 15 |
| [mL] | One-side initial volume of hydraulic cylinder | 450 |
| [N/m2] | Oil elastic modulus | 6.5 × 10−8 |
| [cm2] | Effective area of piston | 71 |
| [Kg] | Converted load mass | 2000 |
| [mL] | Initial gas volume of accumulator | 200 |
| [Mpa] | Initial pressure of accumulator | 3 |
| [mL] | Initial oil volume of accumulator | 200 |
| [V] | Rated voltage of servo motor | 220 |
| [kW] | Rated power of servo motor | 1 |
| [r/min] | Rated speed of servo motor | 3000 |
| [kg m2] | Servo motor moment of inertia | 2.65 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Wang, Z.; Jia, P.; Yan, G.; Zhang, T.; Jia, C.; Chen, G. Research on Pressure Control of an Electro-Hydraulic Servo System Based on Sliding-Mode Variable-Structure Direct Torque Control. Processes 2023, 11, 92. https://doi.org/10.3390/pr11010092
Liu R, Wang Z, Jia P, Yan G, Zhang T, Jia C, Chen G. Research on Pressure Control of an Electro-Hydraulic Servo System Based on Sliding-Mode Variable-Structure Direct Torque Control. Processes. 2023; 11(1):92. https://doi.org/10.3390/pr11010092
Chicago/Turabian StyleLiu, Rongsheng, Zekai Wang, Pengshuo Jia, Guishan Yan, Tiangui Zhang, Chunyu Jia, and Gexin Chen. 2023. "Research on Pressure Control of an Electro-Hydraulic Servo System Based on Sliding-Mode Variable-Structure Direct Torque Control" Processes 11, no. 1: 92. https://doi.org/10.3390/pr11010092
APA StyleLiu, R., Wang, Z., Jia, P., Yan, G., Zhang, T., Jia, C., & Chen, G. (2023). Research on Pressure Control of an Electro-Hydraulic Servo System Based on Sliding-Mode Variable-Structure Direct Torque Control. Processes, 11(1), 92. https://doi.org/10.3390/pr11010092





