Designing Dispatching Rules via Novel Genetic Programming with Feature Selection in Dynamic Job-Shop Scheduling
Abstract
1. Introduction
- (1)
- Most feature selection methods assess the effect of each terminal by the frequency with which it occurs in the best-evolved rules. The main shortcoming of this technique is that the results may be biased towards irrelevant features because of the occurrence of redundant features.
- (2)
- Obtaining a diverse set of excellent individuals is a challenging task and is considered a key factor in achieving high accuracy in feature selection. Although the niching-based GP feature selection method has been proven to be an effective algorithm, it is still difficult and complex to determine the parameter of the niche.
- (3)
- The proposed feature selection approaches for DJSS are usually based on the mode of offline selection mechanisms or a checkpoint to obtain relative terminal sets. This offline approach not only requires a significant expenditure of time and code effort but may also waste some of the excellent individual structures that have been generated during the feature selection process.
- (4)
- The enhancement of the solution quality of dispatching rules in different job shop scenarios is not taken into account by current techniques, which primarily concentrate on rule interpretability via the feature selection process.
- (1)
- Develop a three-stage GP framework to utilize the information of both the selected features and the promising diverse individuals in the feature selection process.
- (2)
- Propose a novel GP method, GP via dynamic diversity management, with a feature selection mechanism to acquire compact, interpretable, and high-quality rules for DJSS automatically. In this strategy, the level of population diversity is related to the stopping criterion and the time elapsed to gradually adjust the search space of the algorithm from exploration to exploitation.
- (3)
- Verify the effectiveness of the proposed approach compared to the three GP-based algorithms and 20 benchmark rules from the existing literature under mean tardiness, mean weighted tardiness, and mean flowtime objectives, respectively.
2. Background
2.1. Problem Definitions for DJSS
2.2. Related Work
3. Proposed Methods
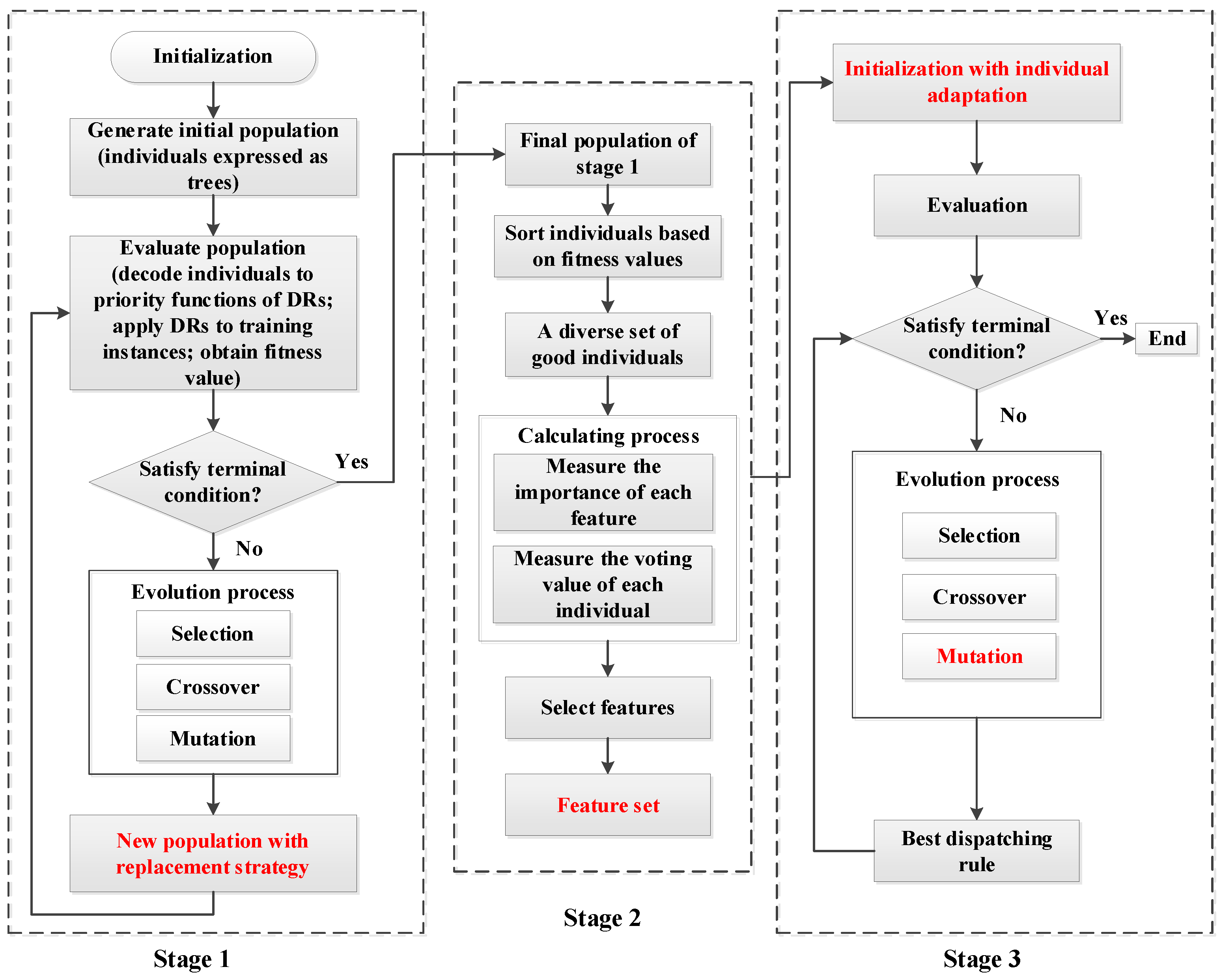
3.1. Framework of the Proposed Approach
3.2. A Novel GP Method
- (1)
- The replacement strategy: The pseudocode of the proposed replacement strategy in GP is described in Algorithm 1. The algorithm aims to select the number of desired survivors to create a new population for the next generation. Initially, the current population and offspring are added to create a set of candidates . Since the fitness in this article is to be reduced, the smallest candidate is chosen and removed from the present candidates and utilized to create a new population. A threshold value is then computed for penalizing the candidates in subsequent steps (line 4). After the previous initial steps, the survivors are chosen from the candidate set to create the new population through iterations (see lines 5–15). The algorithm categorizes the candidates into the penalized set () and the non-penalized set () at each iteration (line 6). To be specific, any candidate with a distance to the nearest survivor below the threshold , is classified as a penalty candidate or else as a non-penalized candidate. If there are non-penalized candidates, a multi-objective method that considers fitness and simplicity is used to choose randomly dominated candidates, while penalized candidates are disregarded. If there are non-penalized candidates, a multi-objective selection procedure that takes into account fitness and simplicity is applied to select randomly dominated candidates, with penalized individuals being overlooked (lines 7–9). Otherwise, if all candidates are penalized, the algorithm will choose the farthest (line 11). It may imply that the population diversity is too limited under this condition; thus, it seems more promising to select the individual with the farthest distance. Lastly, the selected candidate is removed from the candidates set and incorporated into the new population.
Input: A current population , offspring , number of survivors , elapsed iterations , termination criterion , initial distance threshold Output: New Population 1 ; 2 ; 3 ; 4 ; 5 while do 6 categorize-individuals ; 7 if then
8 non-dominated-set9 random-sampling 10 else 11 farthest 12 end
13
14
15 end
16 return
- (2)
- Phenotypic Characterization of Dispatching Rules: The minimum required distance function used in Algorithm 1 to establish the threshold value, which is then utilized to distinguish between individuals who are penalized and those who are not. The threshold is a dynamic value that decreases linearly during the evolution process. This indicates that more closely related individuals are accepted as the iteration goes on, gradually moving the focus away from exploration and toward exploitation. In this way, the dynamic threshold automatically focuses the search toward the most promising areas in the final stage of the optimization.
| Algorithm 2. Compute the phenotypic characterizationof dispatching rule. |
| Input: the dispatching rule to be characterized, the reference rule , set of decision situations . |
| Output: decision vector . |
| 1 for do; |
| 2 ; for each decision situation |
| 3 ; determine ranks, highest priority gets rank 1 |
| 4 ; |
| 5 |
| 6 |
| 7 end for 8 return |
3.3. Feature Selection
| Algorithm 3. Feature Selection process. |
| Input: A set of good and diverse individuals . |
| Output: The selected feature set F. |
| ; |
| do |
| do |
| by Equation (4); |
| by Equations (5)–(7) |
| then |
| 7 |
| 8 end 9 end |
| 10 if then 11 ; 12 end 13 end 14 return F |
3.4. Individual Adaptation Strategy
4. Experimental Design
4.1. Discrete Event Simulation Model
4.2. Algorithm Parameters
4.3. Comparison Design
5. Results and Discussion
5.1. Training Performance
5.2. Test Performance
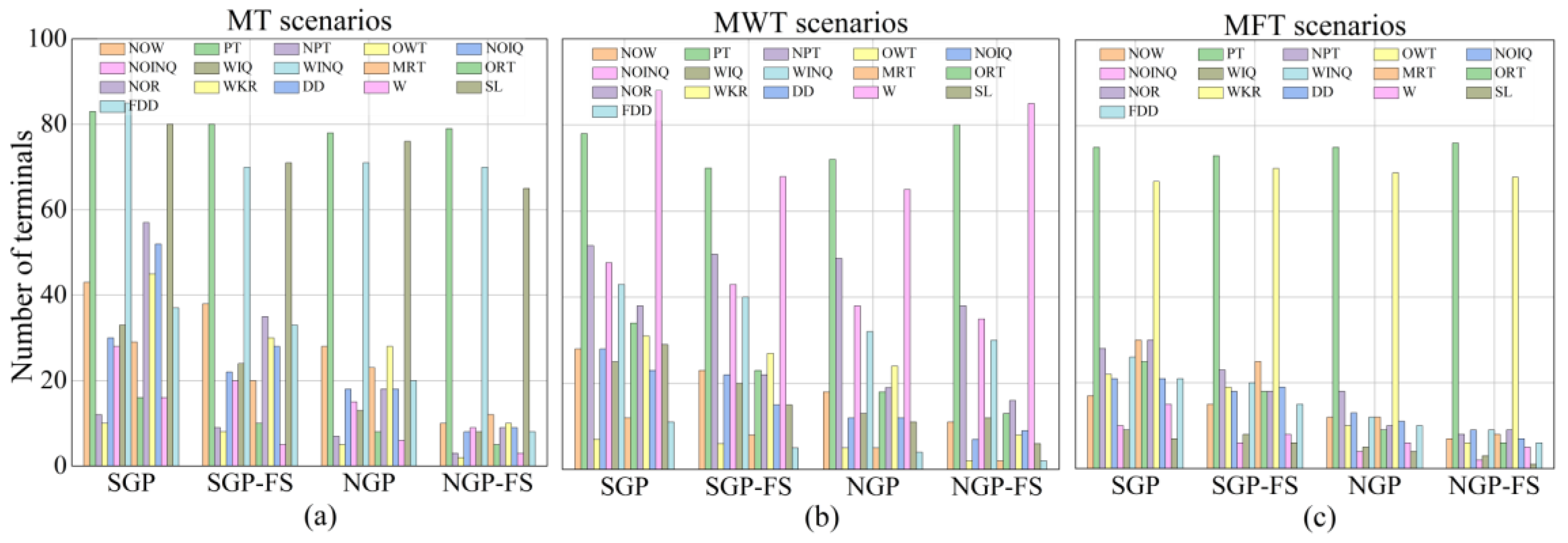
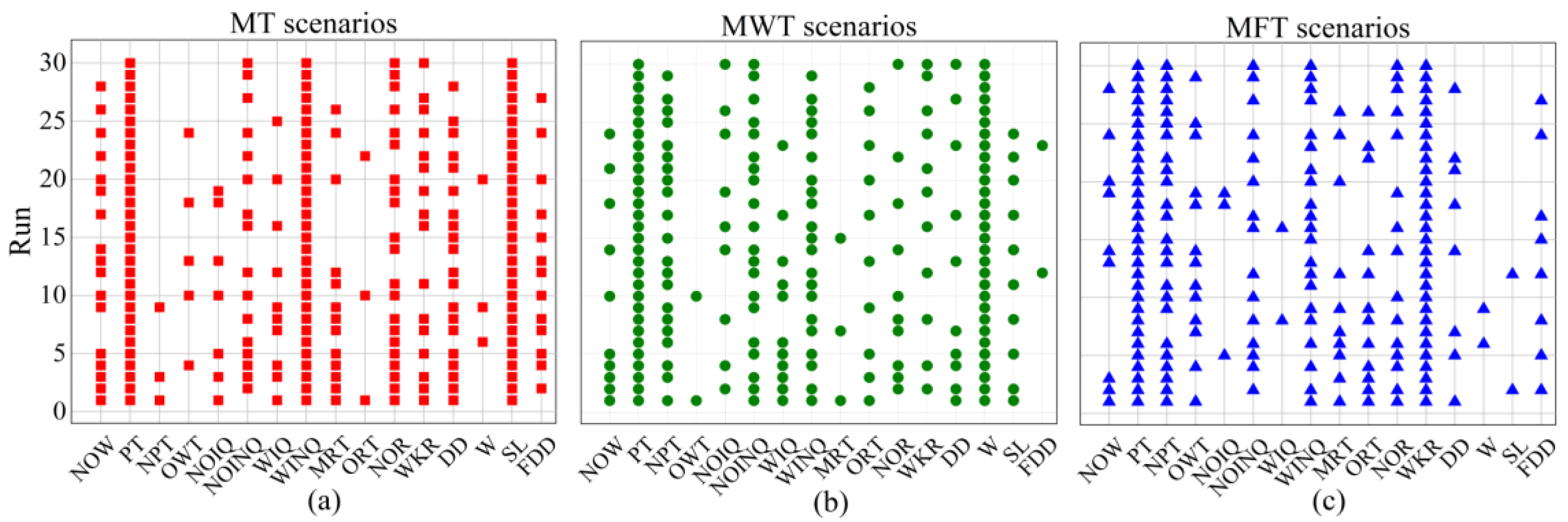
5.3. Unique Feature Analysis
6. Further Analyses
6.1. Feature Analyses
6.2. Rule Analysis
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Branke, J.; Nguyen, S.; Pickardt, C.W.; Zhang, M. Automated design of production scheduling heuristics: A review. IEEE Trans. Evol. Comput. 2016, 20, 110–124. [Google Scholar] [CrossRef]
- Zhang, F.; Nguyen, S.; Mei, Y.; Zhang, M. Genetic Programming for Production Scheduling; Springer: Singapore, 2021. [Google Scholar]
- Xiong, H.; Shi, S.; Ren, D.; Hu, J. A survey of job shop scheduling problem: The types and models. Comput. Oper. Res. 2022, 142, 105731. [Google Scholar] [CrossRef]
- Kim, J.G.; Jun, H.B.; Bang, J.Y.; Shin, J.H.; Choi, S.H. Minimizing tardiness penalty costs in job shop scheduling under maximum allowable tardiness. Processes 2020, 8, 1398. [Google Scholar] [CrossRef]
- Ghasemi, A.; Ashoori, A.; Heavey, C. Evolutionary learning based simulation optimization for stochastic job shop scheduling problems. Appl. Soft Comput. 2021, 106, 107309. [Google Scholar] [CrossRef]
- Shady, S.; Kaihara, T.; Fujii, N.; Kokuryo, D. Automatic design of dispatching rules with genetic programming for dynamic job shop scheduling. IFIP Adv. Inf. Commun. Technol. 2020, 591, 399–407. [Google Scholar]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Braune, R.; Benda, F.; Doerner, K.F.; Hartl, R.F. A genetic programming learning approach to generate dispatching rules for flexible shop scheduling problems. Int. J. Prod. Econ. 2022, 243, 108342. [Google Scholar] [CrossRef]
- Luo, J.; Vanhoucke, M.; Coelho, J.; Guo, W. An efficient genetic programming approach to design priority rules for resource-constrained project scheduling problem. Expert Syst. Appl. 2022, 198, 116753. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, X.; Wang, W.; Wu, J. A Genetic Programming-Based Iterative Approach for the Integrated Process Planning and Scheduling Problem. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2566–2580. [Google Scholar] [CrossRef]
- Lara-Cárdenas, E.; Sánchez-Díaz, X.; Amaya, I.; Cruz-Duarte, J.M.; Ortiz-Bayliss, J.C. A genetic programming framework for heuristic generation for the job-shop scheduling problem. Adv. Soft Comput. 2020, 12468, 284–295. [Google Scholar]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Importance-Aware Genetic Programming for Automated Scheduling Heuristics Learning in Dynamic Flexible Job Shop Scheduling. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Dortmund, Germany, 10–14 September 2022; pp. 48–62. [Google Scholar]
- Omuya, E.O.; Okeyo, G.O.; Kimwele, M.W. Feature selection for classification using principal component analysis and information gain. Expert Syst. Appl. 2021, 174, 114765. [Google Scholar] [CrossRef]
- Salimpour, S.; Kalbkhani, H.; Seyyedi, S.; Solouk, V. Stockwell transform and semi-supervised feature selection from deep features for classification of BCI signals. Sci. Rep. 2022, 12, 11773. [Google Scholar] [CrossRef]
- Song, X.F.; Zhang, Y.; Gong, D.W.; Gao, X.Z. A fast hybrid feature selection based on correlation-guided clustering and particle swarm optimization for high-dimensional data. IEEE Trans. Cybern. 2021, 52, 9573–9586. [Google Scholar] [CrossRef]
- Vandana, C.P.; Chikkamannur, A.A. Feature selection: An empirical study. Int. J. Eng. Trends Technol. 2021, 69, 165–170. [Google Scholar]
- Friedlander, A.; Neshatian, K.; Zhang, M. Meta-learning and feature ranking using genetic programming for classification: Variable terminal weighting. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 941–948. [Google Scholar]
- Mei, Y.; Zhang, M.; Nyugen, S. Feature selection in evolving job shop dispatching rules with genetic programming. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016; pp. 365–372. [Google Scholar]
- Mei, Y.; Nguyen, S.; Xue, B.; Zhang, M. An Efficient Feature Selection Algorithm for Evolving Job Shop Scheduling Rules with Genetic Programming. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 339–353. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M. Evolving scheduling heuristics via genetic programming with feature selection in dynamic flexible job-shop scheduling. IEEE Trans. Cybern. 2020, 51, 1797–1811. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Yan, Y.; Ji, L. Research on control strategy and policy optimal scheduling based on an improved genetic algorithm. Neural Comput. Appl. 2022, 34, 9485–9497. [Google Scholar] [CrossRef]
- Zeiträg, Y.; Figueira, J.R.; Horta, N.; Neves, R. Surrogate-assisted automatic evolving of dispatching rules for multi-objective dynamic job shop scheduling using genetic programming. Expert Syst. Appl. 2022, 209, 118194. [Google Scholar] [CrossRef]
- Rafsanjani, M.K.; Riyahi, M. A new hybrid genetic algorithm for job shop scheduling problem. Int. J. Adv. Intell. Paradig. 2020, 16, 157–171. [Google Scholar] [CrossRef]
- Lee, J.; Perkins, D. A simulated annealing algorithm with a dual perturbation method for clustering. Pattern Recognit. 2021, 112, 107713. [Google Scholar] [CrossRef]
- Yi, N.; Xu, J.; Yan, L.; Huang, L. Task optimization and scheduling of distributed cyber–physical system based on improved ant colony algorithm. Future Gener. Comput. Syst. 2020, 109, 134–148. [Google Scholar] [CrossRef]
- Shady, S.; Kaihara, T.; Fujii, N.; Kokuryo, D. A hyper-heuristic framework using GP for dynamic job shop scheduling problem. In Proceedings of the 64th Annual Conference of the Institute of Systems, Control and Information Engineers, Kobe, Japan, 20–22 May 2020; pp. 248–252. [Google Scholar]
- Liu, L.; Shi, L. Automatic Design of Efficient Heuristics for Two-Stage Hybrid Flow Shop Scheduling. Symmetry 2022, 14, 632. [Google Scholar] [CrossRef]
- Branke, J.; Hildebrandt, T.; Scholz-Reiter, B. Hyper-heuristic evolution of dispatching rules: A comparison of rule representations. Evol. Comput. 2015, 23, 249–277. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, S.; Mei, Y.; Zhang, M. Genetic programming for production scheduling: A survey with a unified framework. Complex Intell. Syst. 2017, 3, 41–66. [Google Scholar] [CrossRef]
- Shady, S.; Kaihara, T.; Fujii, N.; Kokuryo, D. Evolving Dispatching Rules Using Genetic Programming for Multi-objective Dynamic Job Shop Scheduling with Machine Breakdowns. Procedia CIRP 2021, 104, 411–416. [Google Scholar] [CrossRef]
- Wen, X.; Lian, X.; Qian, Y.; Zhang, Y.; Wang, H.; Li, H. Dynamic scheduling method for integrated process planning and scheduling problem with machine fault. Robot. Comput. Integr. Manuf. 2022, 77, 102334. [Google Scholar] [CrossRef]
- Burdett, R.L.; Corry, P.; Eustace, C.; Smith, S. Scheduling pre-emptible tasks with flexible resourcing options and auxiliary resource requirements. Comput. Ind. Eng. 2021, 151, 106939. [Google Scholar] [CrossRef]
- Park, J.; Mei, Y.; Nguyen, S.; Chen, G.; Zhang, M. An investigation of ensemble combination schemes for genetic programming based hyper-heuristic approaches to dynamic job shop scheduling. Appl. Soft Comput. 2018, 63, 72–86. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, J.J.; Huang, Z. Automatic design of scheduling policies for dynamic flexible job shop scheduling via surrogate-assisted cooperative co-evolution genetic programming. Int. J. Prod. Res. 2020, 58, 561–2580. [Google Scholar] [CrossRef]
- Nguyen, S.; Mei, Y.; Xue, B.; Zhang, M. A hybrid genetic programming algorithm for automated design of dispatching rules. Evol. Comput. 2019, 27, 467–496. [Google Scholar] [CrossRef]
- Shady, S.; Kaihara, T.; Fujii, N.; Kokuryo, D. A novel feature selection for evolving compact dispatching rules using genetic programming for dynamic job shop scheduling. Int. J. Prod. Res. 2022, 60, 4025–4048. [Google Scholar] [CrossRef]
- Shady, S.; Kaihara, T.; Fujii, N.; Kokuryo, D. Feature selection approach for evolving reactive scheduling policies for dynamic job shop scheduling problem using gene expression programming. Int. J. Prod. Res. 2022, 60, 1–24. [Google Scholar] [CrossRef]
- Panda, S.; Mei, Y.; Zhang, M. Simplifying Dispatching Rules in Genetic Programming for Dynamic Job Shop Scheduling. In Proceedings of the European Conference on Evolutionary Computation in Combinatorial Optimization, Madrid, Spain, 20–22 April 2022; pp. 95–110. [Google Scholar]
- Huang, Z.; Zhang, F.; Mei, Y.; Zhang, M. An Investigation of Multitask Linear Genetic Programming for Dynamic Job Shop Scheduling. In Proceedings of the European Conference on Genetic Programming (Part of EvoStar), Madrid, Spain, 20–22 April 2022; pp. 162–178. [Google Scholar]
- Fan, H.; Xiong, H.; Goh, M. Genetic programming-based hyper-heuristic approach for solving dynamic job shop scheduling problem with extended technical precedence constraints. Comput. Oper. Res. 2021, 134, 105401. [Google Scholar] [CrossRef]
- Chen, Q.; Xue, B.; Zhang, M. Preserving population diversity based on transformed semantics in genetic programming for symbolic regression. IEEE Trans. Evol. Comput. 2020, 25, 433–447. [Google Scholar] [CrossRef]
- Rueda, R.; Cuéllar, M.P.; Ruíz LG, B.; Pegalajar, M.C. A similarity measure for Straight Line Programs and its application to control diversity in Genetic Programming. Expert Syst. Appl. 2022, 194, 116415. [Google Scholar] [CrossRef]
- Nieto-Fuentes, R.; Segura, C. GP-DMD: A genetic programming variant with dynamic management of diversity. Genet. Program. Evolvable Mach. 2022, 23, 279–304. [Google Scholar] [CrossRef]
- Zhang, F.; Mei, Y.; Nguyen, S.; Zhang, M.; Tan, K.C. Surrogate-assisted evolutionary multitask genetic programming for dynamic flexible job shop scheduling. IEEE Trans. Evol. Comput. 2021, 25, 651–665. [Google Scholar] [CrossRef]
- Ferreira, C.; Figueira, G.; Amorim, P. Effective and interpretable dispatching rules for dynamic job shops via guided empirical learning. Omega 2022, 111, 102643. [Google Scholar] [CrossRef]
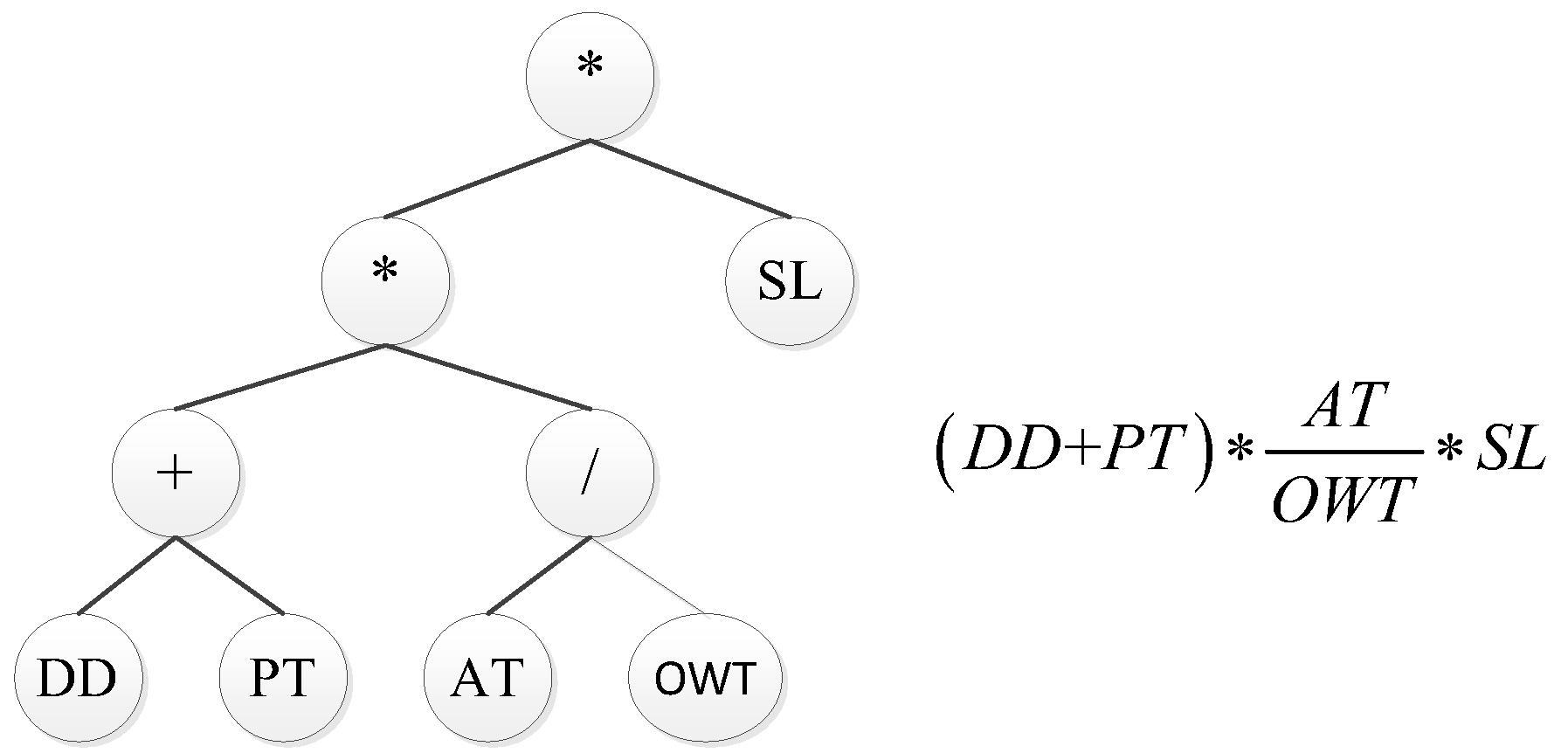

| Parameter | Description | Training | Test |
|---|---|---|---|
| Mean processing time | 25, 50 | 25, 50, 100 | |
| Due dates tightness factor | 3, 5, 7 | 2, 4, 6 | |
| Shop utilization level | 85, 90, 95 | 80, 90, 99, | |
| Scenariosreplications | 181 | 27 | |
| Objectives functions: MT, MWT, MFT, | |||
| Node Name | Description |
|---|---|
| NOW | The current time |
| PT | Processing time of the operation |
| NPT | Processing time of the next operation |
| OWT | The waiting time of the operation |
| NOIQ | Number of operations in the current queue |
| NOINQ | Number of operations in the next queue |
| WIQ | Work in the current queue |
| WINQ | Work in the next queue |
| MRT | Ready time of the machine |
| ORT | Ready time of the operation |
| NOR | Number of operations remaining |
| WKR | Work remaining (including the current operation) |
| DD | Due date of the job |
| W | Weight of the job |
| SL | Slack time of the job |
| FDD | Flow due date of the operation |
| Function set | +,−,×,/, max, min |
| Parameter | Value |
|---|---|
| Initialization | Ramped-half-and-half |
| Population size | 450 |
| Maximal depth | 8 |
| Crossover/Mutation rate | 90%/20% |
| Selection | Tournament selection (size = 5) |
| Number of generations in stage 1 and stage 3 | 50/50 |
| Terminal/non-terminal selection rate | 10%/90% |
| Benchmark Rules | Descriptions |
|---|---|
| SPT | Shortest processing time |
| EDD | Earliest due date |
| FDD | Earliest flow due date |
| LPT | Longest processing time |
| FIFO | First in, first out |
| LILO | Last in, last out |
| CR | Critical ratio |
| RR | Raghu and Rajendran |
| MDD | Modified due date |
| SL | Slack |
| WATC | Weighted apparent tardiness cost |
| COVERT | Cost over time |
| PW | Process waiting time |
| NPT | Next processing time |
| WINQ | Work in next queue |
| PT+WINQ | Processing time+WINQ |
| 2PT+WINQ+NPT | Double processing time+WINQ+NPT |
| PT+WINQ+SL | Processing time+WINQ+SL |
| SPT+PW+FDD | Processing time+PW+FDD |
| 2PT+WINQ+NPT+WSL | 2Processing time+WINQ+NPT+waiting slack |
| Measures | Obj | SGP | SGP-FS | NGP | NGP-FS |
|---|---|---|---|---|---|
| Percentage deviation | MT | 115.78 ± 5.21 | 106.21 ± 12.37 | 126.92 ± 4.25 | 141.58 ± 3.69 (+,+,+) |
| MWT | 131.57 ± 15.23 | 128.18 ± 21.28 | 145.46 ± 12.77 | 162.33 ± 10.97 (+,+,+) | |
| MFT | 78.03 ± 2.91 | 66.14 ± 5.24 | 111.24 ± 3.61 | 119.57 ± 3.58 (+,+,+) | |
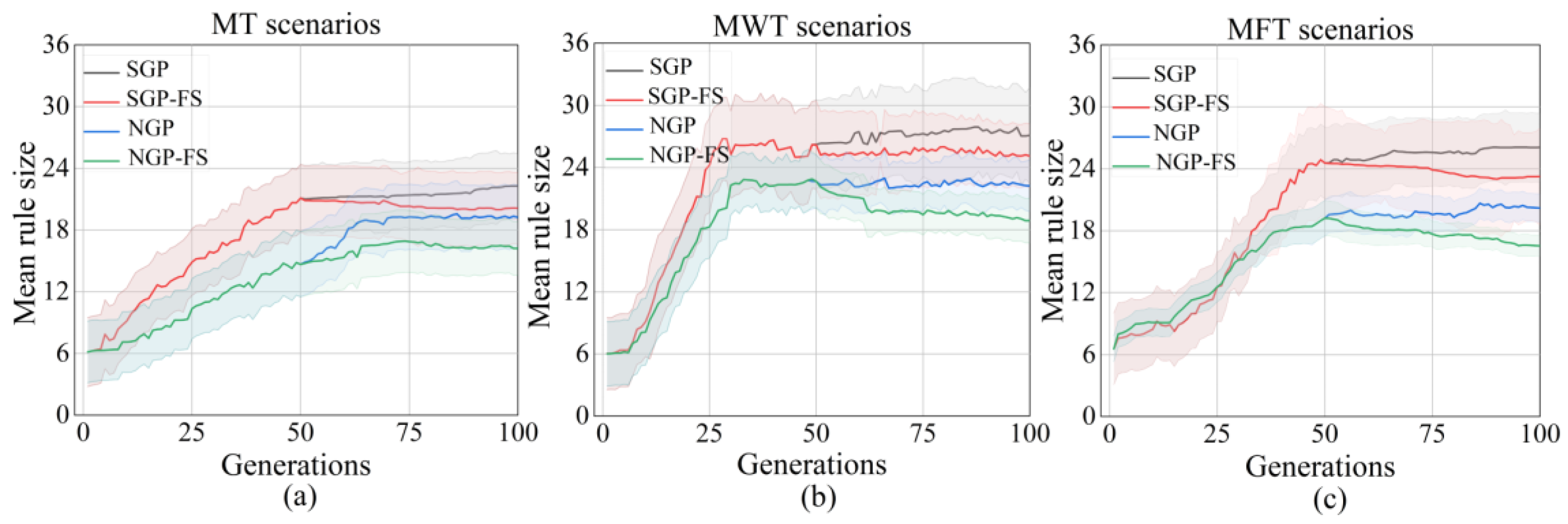
| Mean rule size | MT | 25.23 ± 3.35 | 20.85 ± 3.57 | 19.23 ± 3.15 | 17.26 ± 2.67 (+,+,+) |
| MWT | 27.19 ± 4.36 | 25.85 ± 3.49 | 22.23 ± 3.08 | 18.56 ± 2.78 (+,+,+) | |
| MFT | 26.15 ± 3.46 | 21.36 ± 3.81 | 18.23 ± 1.79 | 14.63 ± 1.26 (+,+,+) | |
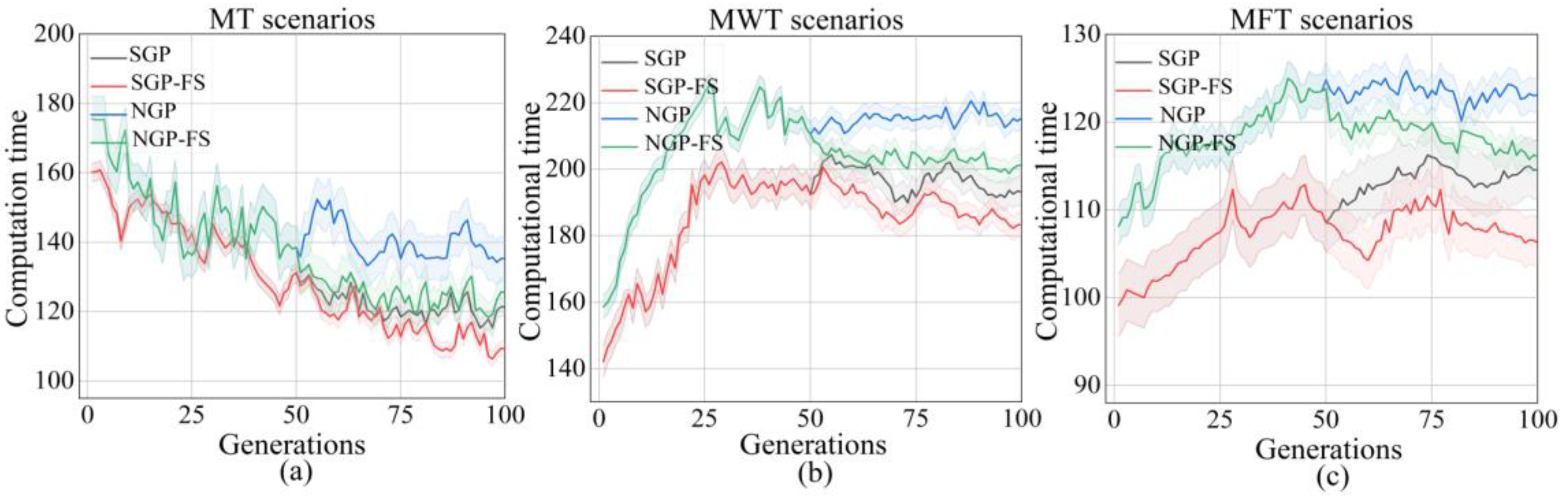
| Computational time | MT | 131.83 ± 2.67 | 125.66 ± 1.95 | 145.04 ± 6.77 | 132.64 ± 3.14 (+,=,+) |
| MWT | 189.43 ± 4.73 | 180.14 ± 3.91 | 210.18 ± 3.36 | 195.26 ± 3.44 (+,=,+) | |
| MFT | 113.83 ± 3.67 | 110.66 ± 3.95 | 120.04 ± 1.97 | 114.64 ± 2.11 (+,=,+) |
| Scenarios | RBR | SGP | SGP-FS | NGP | NGP-FS |
|---|---|---|---|---|---|
| (20, 2, 80%) | 56.34 ± 9.97 (PT+WINQ) | 51.78 ± 5.35 | 54.86 ± 2.43 | 48.54 ± 5.69 | 44.88 ± 3.62 (+, +, +, +) |
| (20, 2, 90%) | 148.12 ± 17.45 (PT+WINQ) | 135.84 ± 7.81 | 142.58 ± 4.14 | 128.77 ± 15.46 | 121.56 ± 16.83 (+, +, +, +) |
| (20, 2, 99%) | 204.33 ± 22.01 (PT+WINQ) | 195.36 ± 12.13 | 201.61 ± 18.56 | 145.85 ± 15.27 | 88.60 ± 6.99 (+, +, +, +) |
| (20, 4, 80%) | 87.64 ± 11.79 (PT+WINQ) | 88.67 ± 6.35 | 92.15 ± 9.25 | 86.84 ± 8.49 | 82.93 ± 7.15 (+, +, +, +) |
| (20, 4, 90%) | 120.62 ± 18.19 (2PT+NPT+WINQ) | 121.28 ± 7.59 | 125.69 ± 8.82 | 115.98 ± 17.71 | 116.32 ± 18.56 (+, +, +, =) |
| (20, 4, 99%) | 329.25 ± 16.38 (PT+WINQ) | 322.13 ± 2.3 | 338.15 ± 27.43 | 313.58 ± 20.98 | 314.25 ± 17.92 (+, +, +, =) |
| (20, 6, 80%) | 30.72 ± 19.97 (COVERT) | 22.15 ± 9.92 | 28.60 ± 6.91 | 20.45 ± 15.37 | 16.85 ± 17.92 (+, +, +, +) |
| (20, 6, 90%) | 91.99 ± 14.56 (COVERT) | 90.33 ± 11.01 | 92.15 ± 10.27 | 87.67 ± 15.09 | 85.44 ± 12.63 (+, +, +, =) |
| (20, 6, 99%) | 409.14 ± 25.32(RR) | 409.52 ± 15.55 | 411.24 ± 18.48 | 405.79 ± 12.17 | 400.81 ± 10.84 (+, +, +, +) |
| (50, 2, 80%) | 84.48 ± 21.63 (PT+WINQ) | 83.95 ± 5.69 | 85.89 ± 4.16 | 78.22 ± 7.15 | 75.47 ± 5.89 (+, +, +, +) |
| (50, 2, 90%) | 71.51 ± 14.99 (PT+WINQ) | 69.17 ± 5.88 | 72.29 ± 7.25 | 69.19 ± 3.84 | 65.18 ± 2.97 (+, +, +, +) |
| (50, 2, 99%) | 246.77 ± 62.59 (2PT+NPT+WINQ) | 233.06 ± 19.42 | 255.47 ± 51.92 | 185.12 ± 17.59 | 135.29 ± 18.64 (+, +, +, +) |
| (50, 4, 80%) | 48.98 ± 11.04 (2PT+NPT+WINQ) | 48.61 ± 2.95 | 52.17 ± 8.32 | 38.1 ± 4.09 | 35.74 ± 4.14 (+, +, +, +) |
| (50, 4, 90%) | 303.6 ± 45.68 (COVERT) | 299.65 ± 28.79 | 310.55 ± 35.07 | 287.35 ± 21.22 | 285.16 ± 18.87 (+, +, +, =) |
| (50, 4, 99%) | 57.97 ± 21.25 (SL/RO) | 55.15 ± 9.63 | 65.84 ± 10.16 | 50.63 ± 8.25 | 45.23 ± 9.12 (+, +, +, +) |
| (50, 6, 80%) | 148.89 ± 32.45 (PT+WINQ) | 145.52 ± 15.06 | 156.29 ± 11.81 | 142.87 ± 10.93 | 137.65 ± 16.34 (+, +, +, +) |
| (50, 6, 90%) | 67.11 ± 14.38 (SL/RO) | 68.29 ± 14.43 | 72.37 ± 11.67 | 60.25 ± 12.29 | 54.15 ± 14.15 (+, +, +, +) |
| (50, 6, 99%) | 75.95 ± 14.38 (COVERT) | 74.17 ± 8.88 | 82.16 ± 9.13 | 69.15 ± 7.08 | 64.25 ± 6.89 (+, +, +, +) |
| (100, 2, 80%) | 51.67 ± 7.19 (2PT+NPT+WINQ) | 48.97 ± 5.86 | 53.79 ± 5.39 | 31.18 ± 4.61 | 25.16 ± 3.74 (+, +, +, +) |
| (100, 2, 90%) | 141.25 ± 26.94 (PT+WINQ) | 138.15 ± 17.13 | 145.17 ± 16.99 | 126.48 ± 18.79 | 117.26 ± 17.52 (+, +, +, +) |
| (100, 2, 99%) | 147.37 ± 24.86 (2PT+NPT+WINQ) | 142.38 ± 15.79 | 152.49 ± 28.01 | 105.69 ± 14.21 | 73.45 ± 15.13 (+, +, +, +) |
| (100, 4, 80%) | 30.64 ± 25.71 (PT+WINQ) | 29.32 ± 2.67 | 35.14 ± 9.59 | 22.37 ± 5.89 | 15.57 ± 3.67 (+, +, +, +) |
| (100, 4, 90%) | 242.83 ± 33.71 (COVERT) | 240.18 ± 27.06 | 251.29 ± 28.17 | 229.16 ± 22.40 | 225.84 ± 21.28 (+, +, +, +) |
| (100, 4, 99%) | 301.55 ± 41.79 (PT+WINQ) | 283.67 ± 15.47 | 302.47 ± 24.09 | 162.28 ± 17.13 | 156.42 ± 16.67 (+, +, +, +) |
| (100, 6, 80%) | 227.26 ± 48.99 (COVERT) | 222.81 ± 28.16 | 232.71 ± 38.30 | 211.06 ± 32.95 | 198.08 ± 34.56 (+, +, +, +) |
| (100, 6, 90%) | 198.05 ± 76.56 (COVERT) | 195.78 ± 15.20 | 215.48 ± 26.38 | 187.26 ± 18.81 | 181.47 ± 21.28 (+, +, +, +) |
| (100, 6, 99%) | 42.54 ± 27.48 (COVERT) | 37.85 ± 4.73 | 49.92 ± 13.65 | 34.91 ± 8.29 | 32.45 ± 7.59 (+, +, +, +) |
| Scenarios | RBR | SGP | SGP-FS | NGP | NGP-FS |
|---|---|---|---|---|---|
| (20, 2, 80%) | 1583.27 ± 85.48 (WATC) | 1526.94 ± 87.61 | 1694.65 ± 121.26 | 1489 ± 99.34 | 1146.48 ± 71.27 (+, +, +, +) |
| (20, 2, 90%) | 1889.42 ± 78.99 (WATC) | 1874.36 ± 88.34 | 1983.19 ± 112.75 | 1764.22 ± 95.57 | 1609.45 ± 57.31 (+, +, +, +) |
| (20, 2, 99%) | 1914.32 ± 78.31 (WATC) | 1904.53 ± 85.14 | 1935.96 ± 103.67 | 1837.29 ± 95.28 | 1615.84 ± 13.07 (+, +, +, +) |
| (20, 4, 80%) | 2187.37 ± 35.98 (PT+WINQ) | 2199.39 ± 38.73 | 2213.47 ± 45.31 | 2116.48 ± 35.16 | 1959.24 ± 46.63 (+, +, +, +) |
| (20, 4, 90%) | 2796.24 ± 19.58 (2PT+NPT+WINQ) | 2834.07 ± 22.15 | 2867.89 ± 24.14 | 2791.34 ± 20.36 | 2579.85 ± 27.61 (+, +, +, +) |
| (20, 4, 99%) | 948.76 ± 27.48 (PT+WINQ) | 951.93 ± 21.95 | 995.15 ± 26.31 | 927.64 ± 35.18 | 785.34 ± 26.18 (+, +, +, +) |
| (20, 6, 80%) | 1489.76 ± 23.79 (COVERT) | 1507.38 ± 27.13 | 1535.07 ± 38.95 | 1465.67 ± 25.37 | 1237.85 ± 17.92 (+, +, +, +) |
| (20, 6, 90%) | 3637.95 ± 48.99 (COVERT) | 3625.11 ± 55.38 | 3637.59 ± 65.57 | 3512.48 ± 79.05 | 3258.24 ± 68.79 (+, +, +, +) |
| (20, 6, 99%) | 1796.61 ± 16.47(RR) | 1783.29 ± 11.23 | 1899.82 ± 17.89 | 1727.33 ± 9.34 | 1432.11 ± 7.95 (+, +, +, +) |
| (50, 2, 80%) | 1484.68 ± 16.87 (PT+WINQ) | 1413.21 ± 15.06 | 1485.29 ± 24.61 | 1378.52 ± 17.65 | 957.39 ± 15.24 (+, +, +, +) |
| (50, 2, 90%) | 1768.52 ± 24.19 (PT+WINQ) | 1769.37 ± 25.48 | 1872.94 ± 47.58 | 1699.31 ± 23.57 | 1575.28 ± 12.96 (+, +, +, +) |
| (50, 2, 99%) | 2395.77 ± 18.59 (2PT+NPT+WINQ) | 2395.56 ± 39.71 | 2428.27 ± 41.82 | 2385.52 ± 27.65 | 1835.56 ± 19.24 (+, +, +, +) |
| (50, 4, 80%) | 1548.98 ± 21.44 (2PT+NPT+WINQ) | 1597.61 ± 22.64 | 1682.17 ± 28.26 | 1538.1 ± 24.19 | 1335.64 ± 24.24 (+, +, +, +) |
| (50, 4, 90%) | 1524.67 ± 32.78 (COVERT) | 1529.53 ± 38.79 | 1580.28 ± 35.17 | 1487.55 ± 31.72 | 1285.47 ± 28.87 (+, +, +, +) |
| (50, 4, 99%) | 1256.97 ± 19.34 (SL/RO) | 1255.15 ± 19.63 | 1267.74 ± 21.26 | 1150.67 ± 18.25 | 945.73 ± 19.32 (+, +, +, +) |
| (50, 6, 80%) | 1643.89 ± 12.35 (PT+WINQ) | 1605.12 ± 15.27 | 1658.29 ± 18.58 | 1599.28 ± 13.83 | 1137.45 ± 15.62 (+, +, +, +) |
| (50, 6, 90%) | 1667.31 ± 34.38 (SL/RO) | 1660.37 ± 34.83 | 1665.37 ± 32.67 | 1560.25 ± 22.69 | 1454.15 ± 24.35 (+, +, +, +) |
| (50, 6, 99%) | 972.59 ± 14.83 (COVERT) | 989.37 ± 15.28 | 1082.16 ± 11.13 | 969.45 ± 6.27 | 689.25 ± 8.89 (+, +, +, +) |
| (100, 2, 80%) | 1651.37 ± 17.28 (2PT+NPT+WINQ) | 1648.26 ± 15.39 | 1686.81 ± 15.29 | 1531.48 ± 24.61 | 1225.86 ± 23.84 (+, +, +, +) |
| (100, 2, 90%) | 1526.75 ± 26.18 (PT+WINQ) | 1518.15 ± 27.13 | 1545.27 ± 26.99 | 1326.34 ± 28.81 | 1117.26 ± 27.52 (+, +, +, +) |
| (100, 2, 99%) | 1466.67 ± 14.96 (2PT+NPT+WINQ) | 1452.68 ± 17.89 | 1487.59 ± 18.21 | 1385.71 ± 14.21 | 983.65 ± 9.13 (+, +, +, +) |
| (100, 4, 80%) | 2030.64 ± 25.61 (PT+WINQ) | 2029.32 ± 22.35 | 2135.74 ± 29.59 | 1982.77 ± 25.15 | 1715.57 ± 23.67 (+, +, +, +) |
| (100, 4, 90%) | 2442.83 ± 53.92 (COVERT) | 2483.58 ± 57.06 | 2541.29 ± 58.47 | 2429.56 ± 42.47 | 2285.95 ± 41.18 (+, +, +, +) |
| (100, 4, 99%) | 2519.55 ± 33.37 (PT+WINQ) | 2513.17 ± 35.28 | 2598.37 ± 34.29 | 2409.78 ± 37.53 | 2156.42 ± 36.87 (+, +, +, +) |
| (100, 6, 80%) | 927.16 ± 16.05 (COVERT) | 928.81 ± 18.26 | 999.87 ± 18.27 | 911.26 ± 12.96 | 618.48 ± 14.36 (+, +, +, +) |
| (100, 6, 90%) | 1798.25 ± 27.17 (COVERT) | 1795.78 ± 25.19 | 1815.48 ± 27.38 | 1687.26 ± 19.71 | 1481.47 ± 11.28 (+, +, +, +) |
| (100, 6, 99%) | 2022.54 ± 37.56 (COVERT) | 2017.85 ± 34.73 | 2249.92 ± 33.74 | 1934.91 ± 28.29 | 1632.55 ± 17.29 (+, +, +, +) |
| Scenarios | RBR | SGP | SGP-FS | NGP | NGP-FS |
|---|---|---|---|---|---|
| (20, 2, 80%) | 311.21 ± 9.45 (PT+WINQ) | 305.74 ± 3.07 | 309.27 ± 3.14 | 301.35 ± 2.37 | 285.56 ± 1.84 (+, +, +, +) |
| (20, 2, 90%) | 341.89 ± 11.17 (PT+WINQ) | 336.68 ± 4.69 | 339.56 ± 5.27 | 331.63 ± 4.21 | 321.18 ± 2.12 (+, +, +, +) |
| (20, 2, 99%) | 377.33 ± 12.01 (PT+WINQ) | 375.68 ± 5.24 | 371.61 ± 5.49 | 365.27 ± 4.78 | 338.25 ± 4.38 (+, +, +, +) |
| (20, 4, 80%) | 294.64 ± 8.19 (2PT+NPT+WINQ | 288.67 ± 5.67 | 292.25 ± 5.16 | 286.63 ± 3.48 | 281.83 ± 3.27 (+, +, +, +) |
| (20, 4, 90%) | 331.62 ± 10.86 (PT+WINQ) | 324.18 ± 5.32 | 327.69 ± 8.91 | 321.37 ± 7.65 | 315.42 ± 7.78 (+, +, +, +) |
| (20, 4, 99%) | 398.75 ± 15.38 (PT+WINQ) | 389.53 ± 7.13 | 394.34 ± 6.13 | 387.26 ± 5.17 | 365.37 ± 4.19 (+, +, +, +) |
| (20, 6, 80%) | 230.52 ± 13.97 (PT+WINQ) | 225.15 ± 4.96 | 228.60 ± 5.18 | 223.75 ± 3.78 | 216.75 ± 3.12 (+, +, +, +) |
| (20, 6, 90%) | 305.79 ± 14.28 (PT+WINQ) | 296.33 ± 11.01 | 301.75 ± 5.37 | 294.67 ± 4.15 | 285.84 ± 2.47 (+, +, +, +) |
| (20, 6, 99%) | 513.84 ± 28.76 (PT+WINQ) | 509.52 ± 6.35 | 511.34 ± 8.48 | 495.67 ± 5.17 | 456.21 ± 4.23 (+, +, +, +) |
| (50, 2, 80%) | 351.28 ± 12.64 (PT+WINQ) | 341.05 ± 5.23 | 347.69 ± 5.99 | 335.12 ± 5.15 | 325.26 ± 4.16 (+, +, +, +) |
| (50, 2, 90%) | 489.72 ± 17.05 (PT+WINQ) | 478.23 ± 3.57 | 485.49 ± 5.25 | 473.19 ± 2.74 | 465.38 ± 1.97 (+, +, +, +) |
| (50, 2, 99%) | 595.27 ± 37.23 (2PT+NPT+WINQ) | 587.36 ± 4.89 | 591.21 ± 4.12 | 585.12 ± 3.37 | 535.18 ± 2.37 (+, +, +, +) |
| (50, 4, 80%) | 407.98 ± 45.24 (2PT+NPT+WINQ) | 398.26 ± 4.95 | 405.23 ± 4.17 | 395.15 ± 3.94 | 386.69 ± 3.81 (+, +, +, +) |
| (50, 4, 90%) | 431.16 ± 48.28 (PT+WINQ) | 425.15 ± 3.79 | 428.15 ± 5.08 | 421.67 ± 3.88 | 412.66 ± 3.79 (+, +, +, +) |
| (50, 4, 99%) | 617.57 ± 59.25 (PT+WINQ) | 604.27 ± 9.73 | 615.24 ± 10.16 | 591.23 ± 7.13 | 525.73 ± 6.12 (+, +, +, +) |
| (50, 6, 80%) | 358.19 ± 13.79 (PT+WINQ) | 348.12 ± 6.06 | 356.29 ± 8.81 | 345.81 ± 5.92 | 337.25 ± 5.14 (+, +, +, +) |
| (50, 6, 90%) | 497.11 ± 31.67 (PT+WINQ) | 492.29 ± 14.43 | 496.17 ± 9.23 | 485.36 ± 7.19 | 474.37 ± 6.28 (+, +, +, +) |
| (50, 6, 99%) | 695.05 ± 67.36 (PT+WINQ) | 689.37 ± 6.98 | 693.26 ± 7.27 | 686.35 ± 5.98 | 608.48 ± 5.12 (+, +, +, +) |
| (100, 2, 80%) | 451.27 ± 45.48 (2PT+NPT+WINQ) | 444.21 ± 6.17 | 453.29 ± 6.38 | 436.18 ± 5.62 | 425.86 ± 4.74 (+, +, +, +) |
| (100, 2, 90%) | 641.25 ± 56.74 (PT+WINQ) | 632.15 ± 7.05 | 638.67 ± 7.99 | 626.48 ± 6.73 | 618.36 ± 5.77 (+, +, +, +) |
| (100, 2, 99%) | 832.17 ± 85.86 (2PT+NPT+WINQ) | 812.38 ± 5.99 | 826.19 ± 6.01 | 798.27 ± 5.32 | 713.25 ± 4.84 (+, +, +, +) |
| (100, 4, 80%) | 439.24 ± 48.76 (PT+WINQ) | 429.12 ± 6.67 | 435.24 ± 7.27 | 422.27 ± 6.19 | 415.28 ± 5.16 (+, +, +, +) |
| (100, 4, 90%) | 553.83 ± 62.71 (2PT+NPT+WINQ) | 546.18 ± 7.08 | 551.29 ± 8.23 | 539.26 ± 7.12 | 527.34 ± 6.18 (+, +, +, +) |
| (100, 4, 99%) | 815.75 ± 91.87 (PT+WINQ) | 808.27 ± 9.26 | 812.47 ± 10.09 | 804.28 ± 9.58 | 756.12 ± 8.12 (+, +, +, +) |
| (100, 6, 80%) | 537.26 ± 76.19 (PT+WINQ) | 528.71 ± 8.09 | 532.61 ± 8.31 | 521.76 ± 7.25 | 498.58 ± 6.76 (+, +, +, +) |
| (100, 6, 90%) | 668.25 ± 87.56 (PT+WINQ) | 661.78 ± 15.20 | 665.48 ± 26.38 | 657.26 ± 8.19 | 625.17 ± 7.13 (+, +, +, +) |
| (100, 6, 99%) | 852.54 ± 101.27 (PT+WINQ) | 836.75 ± 7.93 | 849.92 ± 8.15 | 824.11 ± 7.72 | 759.25 ± 6.19 (+, +, +, +) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sitahong, A.; Yuan, Y.; Li, M.; Ma, J.; Ba, Z.; Lu, Y. Designing Dispatching Rules via Novel Genetic Programming with Feature Selection in Dynamic Job-Shop Scheduling. Processes 2023, 11, 65. https://doi.org/10.3390/pr11010065
Sitahong A, Yuan Y, Li M, Ma J, Ba Z, Lu Y. Designing Dispatching Rules via Novel Genetic Programming with Feature Selection in Dynamic Job-Shop Scheduling. Processes. 2023; 11(1):65. https://doi.org/10.3390/pr11010065
Chicago/Turabian StyleSitahong, Adilanmu, Yiping Yuan, Ming Li, Junyan Ma, Zhiyong Ba, and Yongxin Lu. 2023. "Designing Dispatching Rules via Novel Genetic Programming with Feature Selection in Dynamic Job-Shop Scheduling" Processes 11, no. 1: 65. https://doi.org/10.3390/pr11010065
APA StyleSitahong, A., Yuan, Y., Li, M., Ma, J., Ba, Z., & Lu, Y. (2023). Designing Dispatching Rules via Novel Genetic Programming with Feature Selection in Dynamic Job-Shop Scheduling. Processes, 11(1), 65. https://doi.org/10.3390/pr11010065







