Unified Approach for Prediction of the Volumetric Mass Transfer Coefficients in a Homogeneous and Heterogeneous Bubble Column Based on the Non-Corrected Penetration Theory: Case Studies

Abstract

A critical review on the improvement of penetration theory is presented in this work. The volumetric liquid-phase mass transfer coefficients k_La in seven different liquids (1-butanol, 2-propanol, anilin, decalin, nitrobenzene, tetralin, and ethylene glycol) aerated with air in a small bubble column (BC) (inner diameter: 0.095 m) were measured at ambient conditions and further analyzed. It was found that the k_La values can be predicted satisfactorily on the basis of the classical Higbie’s penetration model. The gas–liquid contact time was defined as the ratio of the Sauter-mean bubble diameter to bubble rise velocity. Moreover, the experimental k_La values were well predicted, not only in the homogeneous regime, but also in the transition and heterogeneous regimes. This is a new finding, since to date, it was considered that the penetration theory needs a correction factor for a successful application to any liquid, even in the homogeneous regime. The predictions of the mass transfer coefficients k_La in the above-mentioned seven liquids imply that the mean bubble diameters are always ellipsoidal or spherical, which is the key condition for the applicability (without a correction) of penetration theory. In the presented (in this work) model-based k_La predictions, the Sauter-mean bubble diameters were estimated by means of the reliable correlation of Wilkinson et al., which always predicts a gradually decreasing bubble size at higher gas velocities.

1. Introduction

Bubble column (BC) reactors are frequently used in industry. Especially when it is required to carry out highly exothermic reactions in the liquid phase. They are relatively simple gas–liquid contactors, with complicated hydrodynamics. The mass transfer (MT) between the phases and the mode of operation can play a decisive role in gas–liquid contactors. In the case of chemical reactions, an effective temperature control is required. This is achieved by means of wall heat transfer or internal heat exchangers (inserted rods and coils). Very often (for instance, in the case of certain chlorinations) the mode of heat removal restricts the gas–liquid reactor performance. One of the main advantages of BCs are their excellent heat transfer properties and thus easy temperature control and reasonable interphase MT rates at low energy input [1]. The main disadvantage is the considerable backmixing in both phases, high pressure drop (especially under ambient pressure), and bubble coalescence. In principle, the backmixing can be suppressed by means of certain column modifications, and thus the interphase MT can be improved. Backmixing is detrimental to BC performance. BCs with internals and BCs equipped with multiple needles (as a gas sparger) at the bottom lead to the reduction of the liquid backmixing and thus higher MT coefficients. Many oxidations, chlorinations, hydrogenations, etc. are performed in BCs. These processes belong to the slow reaction-absorption regime [1].

MT investigation in BCs is a very important research topic, since very often the MT time (inverse of the MT coefficient k_La) is the determining factor for the BC operation. The MT is also important for successful reactor scale-up. The design and scale-up of BCs is a difficult task, due to the complicated MT process. The difficult scale-up is also due to the complex interaction and mixing of phases [2], intricate hydrodynamics, and heat transfer in the bubble bed. The volumetric liquid-phase MT coefficient (k_La) is the rate of gas transfer across the gas–liquid interface per unit of driving force (the gas concentration gradient between the liquid and the gas). The k_La coefficient can be seen as the product of two terms: the liquid-phase MT coefficient k_L and the specific interfacial area a. Both terms depend on the density, diffusivity, and surface tension of the liquid and the liquid dynamics. The k_La value is one of the key estimators of reactor performance. According to Han and Al-Dahhan [2] the gas–liquid MT is directly affected by the hydrodynamics, phase mixing, and physical properties. In every mass balance the MT term consists of the liquid phase MT coefficient k_L, the specific gas-liquid interfacial area a and a concentration difference driving force [3]. The steady-state axial dissolved oxygen concentration profiles are also influenced by both the overall gas holdup and the overall k_La value.

There are various methods (steady-state, non-steady state, and transient) for k_La determination. In the steady-state methods, the rates of oxygen uptake in steady-state operation are evaluated, either by measurement of inlet and outlet rates of oxygen or by direct analysis of a compound that reacts with oxygen (for instance, in the sulfite method). The issue with this approach is the fact that the addition of a chemical may change the physicochemical properties of the liquid. In the transient methods, a step-change of the oxygen concentration in the inlet gas stream is generated, and then the response of the dissolved oxygen concentration in the system is followed [4]. Chang et al. [5] have developed a new gassing-in method for k_La measurement. Rubio et al. [3] have also determined the overall k_La coefficient by means of the dynamic gassing-in method. This method is explained in more details in the book of Chisti [6]. The transient method is not very widely used and will not be discussed in this review.

For k_La measurements in BCs, the driving force is usually produced by a dynamic change in the gas or liquid input (pulse or step), by pressurizing the gas phase or by the presence of chemical reactions [2]. In most MT studies in BCs, the dynamic gas absorption or desorption method has been used. In the first method, the nitrogen flow is switched to air or oxygen, whereas in the second case it is vice versa. In these dynamic methods, the measured transient concentration profiles of the introduced gas represent both the extent of gas–liquid MT and the phase mixing [2].

Usually, k_La measurements are performed by means of an oxygen electrode. In principle, this is characterized with a certain lag in its response. This should be short, and a model of the dynamic behavior of the oxygen sensor should be included. Linek et al. [4] developed a variation of this method based on an oxygen sensor, by introducing a step variation of pressure.

The dissolved oxygen concentration can also be measured by means of an optical oxygen probe [7]. This is a sensor operating on the basis of fluorescence extinction by oxygen. In order to achieve an instantaneous sensor response, the fluorophore is usually dissolved in the liquid [7]. This measurement technique is characterized with fast response, stability, and long life. Han and Al-Dahhan [2] used an improved version of this optical sensor developed by Ocean Optics, Inc. (Dunedin, FL, USA). In this approach, the probe constant of the optical oxygen probe is estimated and taken into account.

In general, the recorded oxygen concentration is compared with the predictions of a mathematical model, which includes k_La as a parameter. Then the value of k_La that gives the best fit is chosen. The choice of the best model is crucial. Usually, a complete liquid mixing in the reactor is assumed. However, if this assumption is not correct then there will be a strong deviation in the k_La estimation. The assumption of perfect liquid mixing could be questionable in the case of tall gas–liquid reactors. In principle, if the perfect liquid mixing condition is met, then the location of the oxygen sensor should not be important. Thus, incorrect assumptions about flow characteristics of gas or liquid phases may lead to errors and deviations from the true k_La values. In many cases, the mass transfer coefficient in the vicinity of the gas distributor is higher than the one in the rest of the bubble bed [2,8].

Han and Al-Dahhan [2] presented a correlation for k_La extraction in the case of a continuously stirred tank reactor (CSTR) model. The latter assumes perfect mixing for both phases and constant concentration in the gas phase [2]. When the CSTR model is not applicable, then the one-dimensional axial dispersion model (ADM) for both liquid and gas phases should be applied and then the system of two partial differential equations should be solved. In their model equations, Han and Al-Dahhan [2] assumed a constant axial gas holdup profile, which is justifiable in the case of tall BC reactors. The authors reported that the ADM yielded better fits to the experimental k_La data than the CSTR model. Han and Al-Dahhan [2] measured the k_La values by means of an oxygen-enriched air dynamic method and an optical oxygen probe technique. These authors reached the conclusion that the ADM yielded a better fit to the experimental k_La data than the CSTR model (that gives exponential curves).

The liquid film controlled MT process in BCs depends on the mean bubble diameter, bubble shape, motion, and interface fluctuations [9]. Reactions with interphase MT are frequently performed in BCs. The mean bubble diameter is very close to the equilibrium bubble size, which is primarily dependent on the energy content of the liquid phase [9].

The MT rates from gas bubbles into a continuous phase can be theoretically studied only when the bubbles are spherical and rise rectilinearly. The main MT equation in the classical penetration theory [10] in a dimensionless form reads as follows:

$$\mathrm{Sh}=1.128{\mathrm{Pe}}^{0.5}$$

(1)

According to Miller [9], this equation was developed for liquid in a potential flow with a short interface contact time t_c. Usually the gas–liquid contact time is assumed to be equivalent to the time it takes a bubble to rise one bubble diameter. When both the Sherwood Sh and Peclet Pe numbers are substituted with their definitions, then Equation (1) can be transformed as follows:

$${\mathrm{k}}_{\mathrm{L}}=1.128\sqrt{\frac{{\mathrm{D}}_{\mathrm{L}}}{{\mathrm{t}}_{\mathrm{c}}}}$$

(2)

This is the most important MT correlation in penetration theory. It was strictly developed for rigid spherical bubbles. In BCs, the gas-side resistance to interphase MT is assumed to be negligible.

The gas–liquid contact time t_c is frequently defined as the ratio of Sauter-mean bubble diameter d_s to bubble rise velocity u_b:

$${\mathrm{t}}_{\mathrm{c}}=\frac{{\mathrm{d}}_{\mathrm{s}}}{{\mathrm{u}}_{\mathrm{b}}}$$

(3)

In the original paper of Higbie [10], the contact time t_c is expressed as a ratio of the rate of surface formation to the bubble surface. The same definition was used in Nedeltchev et al. [11]. It is noteworthy that Deckwer [12] defined the contact time in terms of Kolmogorov’s theory of isotropic turbulence. According to that theory, the energy dissipation of the micro eddies is locally isotropic, regardless of the movement of the macro scale eddies. Deckwer [12] defined the contact time as the ratio of the length scale of the micro eddies to their velocity scale. Therefore, in order to calculate the contact time based on this theory, one needs to know only the kinematic viscosity and the energy dissipation rate per unit mass.

Another interesting question is why the coefficient of molecular diffusivity D_L is so important in Equation (2)? Miller [9] argues that there is a continual attachment and detachment of small liquid eddies at the gas–liquid interface. In the period of attachment there is an interchange of solute by means of a molecular diffusion. In the case of large bubbles more surface disturbances occur and the main MT equation needs to be corrected. Miller [9] developed a correction factor (function of the mean bubble diameter), which renders the penetration theory applicable for bubble sizes above 4 mm. The author’s correction factor is a single function of the mean bubble diameter.

The MT coefficients should be measured beyond the equilibrium zone (up to two column diameters above the gas distributor), where the stable mean bubble diameter is established [9]. In the vicinity of the gas distributor, the k_La values are usually higher [2,8], due to the enhanced liquid turbulence. A stable bubble size is achieved when the turbulent fluctuations and surface tension forces are in balance [9].

Calderbank [13] argued that the shapes and paths of larger bubbles are irregular and vary rapidly with time, thus making an exact theoretical treatment impossible. Most of the theoretical MT relations in the literature are derived for bubbles that are symmetrical with respect to their axis in the direction of rise. The other assumption is that both the Peclet Pe and Schmidt Sc numbers are large. According to Calderbank [13], the penetration theory is valid when the thickness of the velocity boundary layer is far less than the equivalent spherical radius of the dissolving body. The thin concentration boundary layer approximation is valid for a Peclet Pe number greater than 100 and a Reynolds Re number greater than 0.1. When the Re number is very large (potential flow), then Equation (1) applies. The Re numbers of oblate spheroid bubbles are very high and the flow is potential. Large bubbles, greater than 18 mm, assume a spherical-cap shape and undergo potential flow. Calderbank [13] proposed that the MT equation for spherical-cap bubbles takes the form Sh = 1.28Pe^0.5, i.e., the MT process is enhanced by the bubble surface deformations. On the other hand, for very small spherical rigid bubbles, the boundary layer theory is applicable.

Once the k_L coefficient is calculated from Equation (2), then the gas–liquid interfacial area can be estimated as follows:

$$\mathrm{a}=6\frac{{\mathsf{\epsilon }}_{\mathrm{g}}}{{\mathrm{d}}_{\mathrm{s}}}$$

(4)

Theoretically, this definition is strictly valid for rigid spherical bubbles. This parameter is most susceptible to changes in operational variables (pressure, temperature, etc.) and fluid properties. A higher gas density results in higher gas holdup, smaller bubble size, and higher MT characteristics (a and k_La). The MT coefficients can be increased by increasing the temperature [7]. Variations in liquid turbulence and initial bubble diameter also affect the interfacial area. The latter can be measured either by chemical methods or by measuring directly both the overall gas holdup and the Sauter-mean bubble diameter d_s and then applying Equation (4). For instance, by means of a four-point optical probe [14]. Jasim et al. [15,16] recorded, by means of a four-point optical probe, several important bubble characteristics: bubble rise velocity, bubble diameter, bubble passage frequency, and interfacial area. In this work the d_s values were estimated by means of the reliable correlation proposed by Wilkinson et al. [17]. The most important empirical correlations for estimation of the overall gas holdup in BCs are listed in

Table 1. Summary of the most important empirical gas holdup correlations.

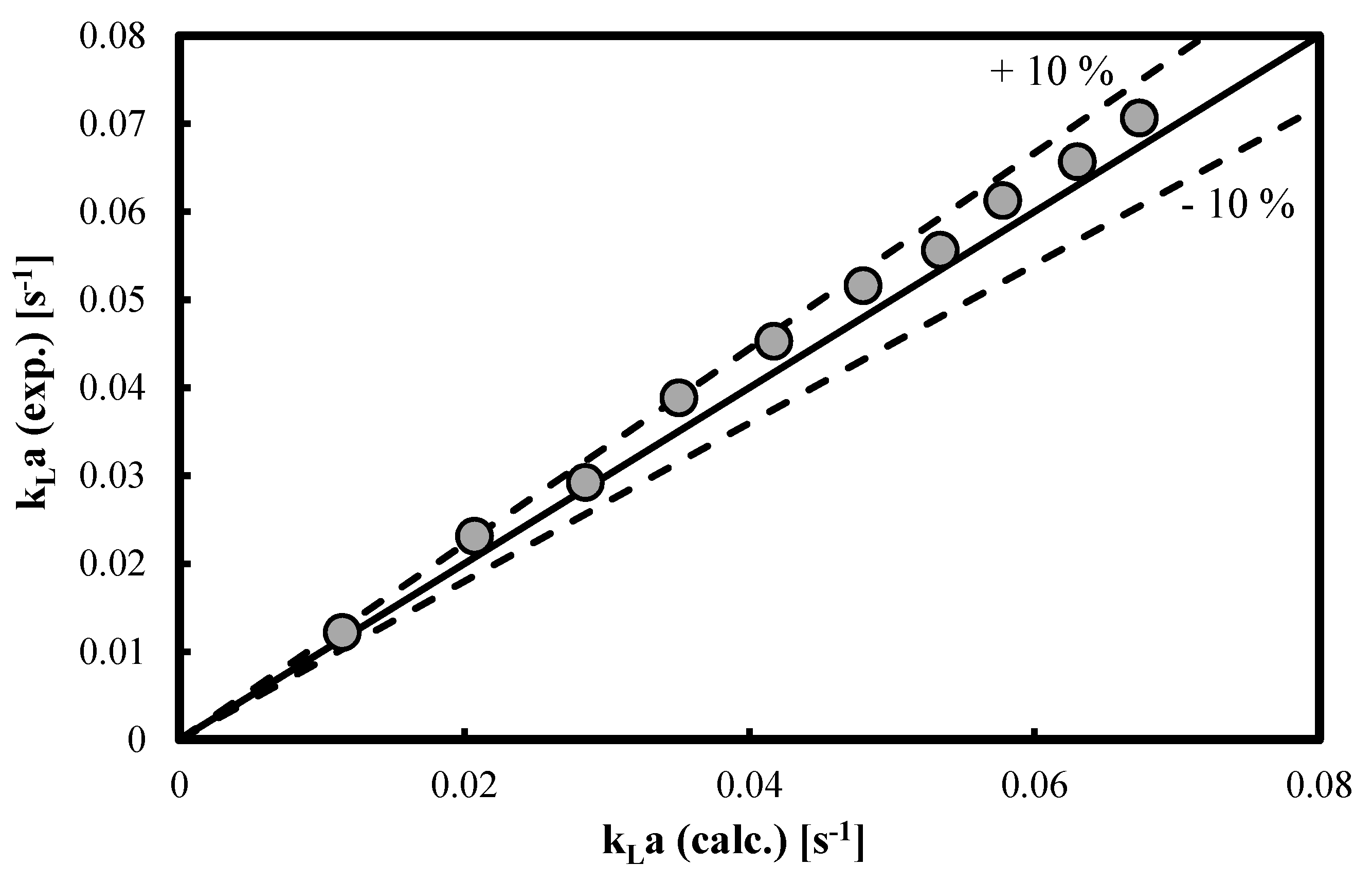
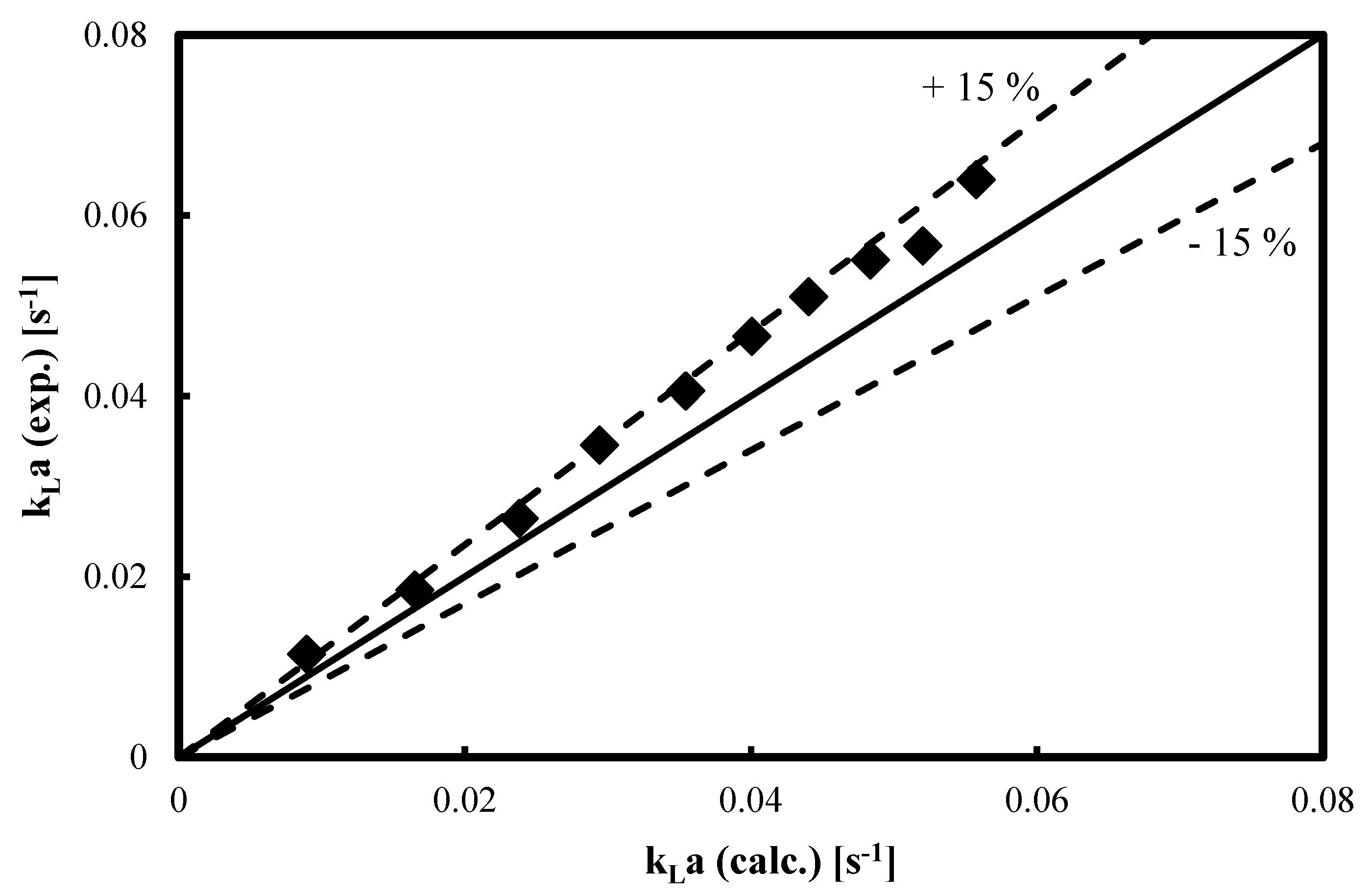
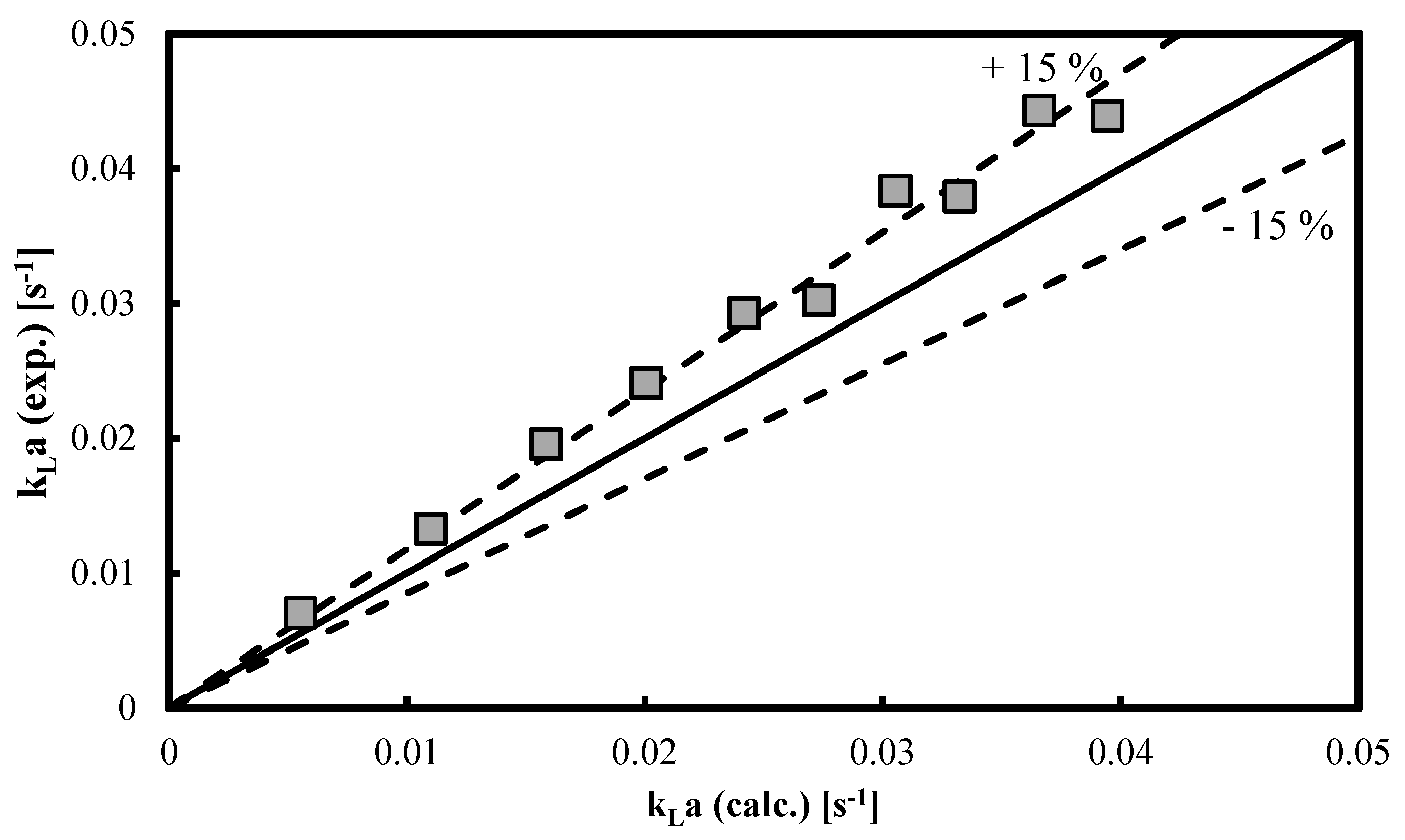
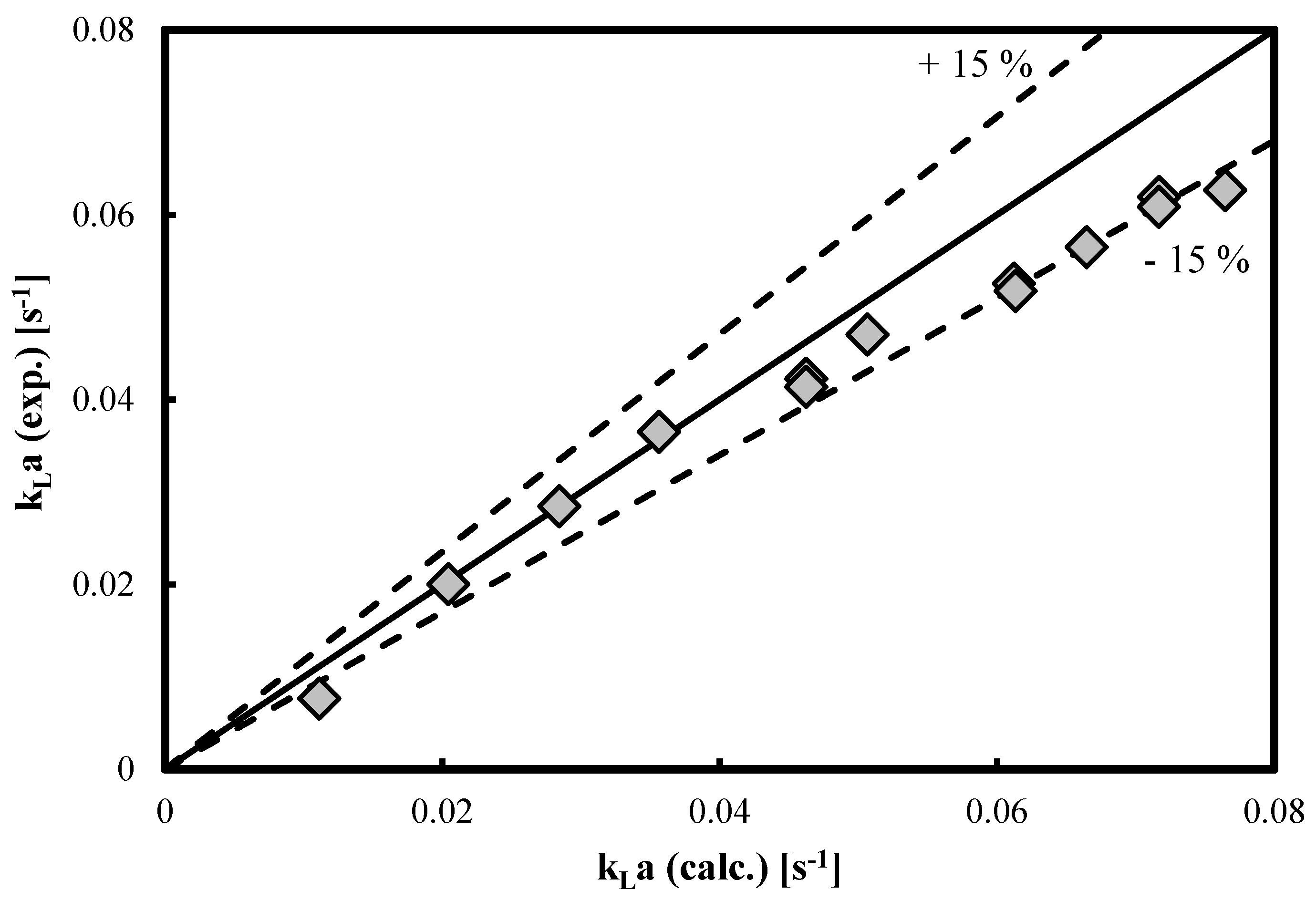
Authors	Empirical Correlation
Jordan and Schumpe [7]	εg/(1 − εg) = a1Eo0.16Ga0.04Fr0.7(1 + 27.0Fr0.52(ρG/ρL)0.58)
Akita and Yoshida [18]	εg/(1 − εg) = 0.2Bo0.125(Ga’)0.083Fr’
Hikita et al. [19]	εg = 0.672f(UgμL/σL)0.578Mo−0.131(ρG/ρL)0.062(μG/μL)0.107 f = 1.0 for electrolyte solutions; f = 100.0414I for 0 < I < 1.0 kg ion/m3; f = 1.1 for I > 1.0 kg ion/m3;
Hammer et al. [20]	εg/(1 − εg) = 0.4(UgμL/σL)0.87Mo−0.27(ρG/ρL)0.17
Idogawa et al. [21]	εg/(1 − εg) = 0.059Ug0.8ρG0.17(σL/72)−0.22exp(-P)
Reilly et al. [22]	εg = 296Ug0.44ρL−0.98ρG0.19σL−0.16 + 0.009
Sotelo et al. [23]	εg = 129(UgμL/σL)0.99Mo−0.123(ρG/ρL)0.187(μG/μL)0.343(ds/Dc)−0.089

.

Deckwer and Schumpe [1] recommended the correlations of Akita and Yoshida [18] and Hikita et al. [19]. The latter is useful for non-electrolyte and salt solutions. In the work of Öztürk et al. [24], these new gas holdup correlations were successfully applied to more than 50 different gas–liquid systems. The most reliable modern correlations for gas holdup prediction take into account the gas density effect. The gas holdup increases with gas density (or operating pressure) due to the shrinkage (reduction) of the bubble diameter [1]. The bubble stability decreases with increasing gas density. Schumpe and Deckwer [25] proposed a reliable correlation for prediction of gas holdups in highly viscous media. Kemoun et al. [26] summarized the most reliable gas holdup correlations.

1.1. Correction Factors of the Penetration Theory

Based on carbon dioxide stripping from an aqueous solution with air, Miller [9] developed the following correction factor:

$${\mathrm{f}}_{\mathrm{c}}=683{\mathrm{d}}_{\mathrm{s}}{}^{1.376}$$

(5)

The statistical deviation between corrected and experimental MT coefficients is ±16.1%. The author argues that the MT process is enhanced by the bubble surface deformations.

Nedeltchev et al. [11] have stressed that the penetration theory is not directly applicable to oblate ellipsoidal bubbles, which are formed in the homogeneous regime of BC operation. The authors introduced a new correction factor, which is a function of the Eötvös number Eo and the dimensionless gas density ratio:

$${\mathrm{f}}_{\mathrm{c}}=0.124{\mathrm{Eo}}^{0.94}{\left(\frac{{\mathsf{\rho }}_{\mathrm{G}}}{1.2}\right)}^{0.15}$$

(6)

Equation (6) has been successfully applied to 18 organic liquids and tap water, as well as 14 different mixtures [11]. k_La values at both ambient and high pressures have been predicted. In total, 263 k_La values were fitted, with an average relative error of 10.4% [11].

The correction factors in Equations (5) and (6) are easy to remember and use. Another correction factor was introduced by Calderbank [13], Lochiel and Calderbank [27,28], and Calderbank et al. [29]. It is a single inversely proportional function of the bubble Reynolds number:

$${\mathrm{f}}_{\mathrm{c}}={\left(1-\frac{2.96}{\sqrt{\mathrm{R}{\mathrm{e}}_{\mathrm{b}}}}\right)}^{0.5}$$

(7)

1.2. Empirical Correlations for k_La Prediction

Many empirical correlations for k_La prediction have been reported in the literature. However, Deckwer and Schumpe [1] argue that the use of empirical correlations is of limited value and that their predictions may lead to errors, especially under industrial conditions. The authors recommend that empirical correlations are applied with caution to new processes. In

Table 2. Summary of the most important empirical k_La correlations.

Authors	Empirical Correlation
Akita and Yoshida [30]	Sh’ = 0.5Sc0.5Ga0.25Eo0.375
Öztürk et al. [24]	Sh = 0.62 Sc0.5Eo0.33Ga0.29Fr0.68(ρG/ρL)0.04
Hikita et al. [31]	kLaUg/g = 14.9f(UgμL/σL)1.76Mo−0.248(μG/μL)0.243Sc−0.604 f = 1 for non-electrolytes;
Jordan and Schumpe [7]	Sh” = b1Sc0.5Bo0.34Ga0.27Fr0.72(1 + 13.2Fr0.37(ρG/ρL)0.49)

are summarized the most frequently used k_La correlations.

Öztürk et al. [24] recommended two reliable empirical correlations for k_La prediction. Akita and Yoshida [30] proposed an empirical correlation, which is applicable to water, glycol, and methanol. Hikita et al. [31] developed a reliable empirical correlation, which predicts the k_La values in sucrose, methanol, and 1-butanol. In the case of electrolytes, the parameter f depends on the ionic strength of the solution. In the work of Deckwer and Schumpe [1] a correlation of Öztürk et al. [24] is also provided. In the case of k_La measurements with non-Newtonian liquids (sucrose, xanthan, and viscoelastic PAA solutions), Suh et al. [32] suggested a dimensionless MT correlation, in which all dimensionless numbers are based on column diameter. In this correlation, the Weissenberg number also participates. The latter expresses the effect of the elastic properties. Jordan and Schumpe [7] reported that the ratio ε_g/k_La tends to be constant at low U_g values.

Kawase et al. [33] proposed a semi-theoretical approach for k_La prediction based on Higbie’s penetration theory [10] and Kolmogorov’s theory of isotropic turbulence. Jordan and Schumpe [7] developed a new correlation for predicting the k_La values measured in organic liquids at high pressures and elevated temperatures.

One of the main goals of this review is to summarize the most important theoretical approaches for predicting the MT coefficients k_L and k_La, as well as the empirical correlations for predicting gas holdups and k_La values. It will also be demonstrated that, in the case of few organic liquids, the classical penetration model can be applied not only to the homogeneous regime but also to the heterogeneous regime of BC operation at ambient conditions.

2. Experimental Setup and Measurement Technique

The liquid concentrations C_L were measured in seven different liquids (1-butanol, 2-propanol, anilin, decalin, nitrobenzene, tetralin, and ethylene glycol) in a small jacketed BC (inner diameter: 0.095 m) equipped with a single tube (3 mm in inner diameter). The organic liquids were aerated with air at ambient pressure and temperature. The clear liquid height was set at 0.85 m. The superficial gas velocity U_g was controlled by means of a mass flow controller and was varied from 0.008 m/s to 0.08 m/s. Before entering the column, the gas passed through a drying tower and a saturator filled with the same liquid and was thermostated to the same temperature (293 ± 1 K) as the BC [24]. The variation of the liquid properties is summarized in

Table 3. Summary of the physicochemical properties of the liquids used.

Liquid	ρL (kg/m3)	μL (Pa s)	σL (N/m)	νL (m2/s)	DL (m2/s)	Sc (−)
Anilin	1022	4.4 × 10−3	43.5 × 10−3	4.31 × 10−6	0.97 × 10−9	4438.44
1-Butanol	809	2.94 × 10−3	24.6 × 10−3	3.63 × 10−6	1.29 × 10−9	2817.14
Decalin	884	2.66 × 10−3	32.5 × 10−3	3.01 × 10−6	1.60 × 10−9	1880.66
Ethyl. glycol	1113	19.94 × 10−3	47.4 × 10−3	17.92 × 10−6	2.60 × 10−10	68,905.94
Nitrobenzene	1203	2.02 × 10−3	38.1 × 10−3	1.68 × 10−6	1.63 × 10−9	1030.14
2-Propanol	785	2.42 × 10−3	21.1 × 10−3	3.08 × 10−6	1.44 × 10−9	2140.84
Tetralin	968	2.18 × 10−3	34.9 × 10−3	2.25 × 10−6	1.58 × 10−9	1425.36

. It is seen that, except for ethylene glycol, the Schmidt numbers Sc varied from 1030.14 to 4438.44. In the case of ethylene glycol the Sc number reached 68,905.94, but it will be demonstrated that the non-corrected penetration theory [10] is still applicable.

The experimental volumetric liquid-phase MT coefficients k_La were measured by means of the dynamic oxygen absorption method. In each measurement, the k_La value was extracted from the following correlation:

$$\ln \left({\mathrm{C}}_{\mathrm{L},\infty }-{\mathrm{C}}_{\mathrm{L}}\right)=-\left(\frac{{\mathrm{k}}_{\mathrm{L}}\mathrm{a}}{{\mathsf{\epsilon }}_{\mathrm{L}}}\right)+\mathrm{const}$$

(8)

Öztürk et al. [24] argued that the k_La definition in Equation (8) refers to the dispersion volume. The ratio k_La/ε_L is called the volumetric liquid-phase MT coefficient referring to liquid volume [1]. The electrode reading C_L in arbitrary units can be used, and the response time need not be considered if the initial part (up to 50%) of the concentration change is neglected [24]. The k_La values agreed well with the results of more sophisticated approaches that considered the time constant, or with the results of independent measurements using a steady-state method [2].

The oxygen fugacity in the liquids (investigated in this work) was measured with a polarographic oxygen electrode (WTW-EO 90) inserted horizontally at half the dispersion height. The electrode response time was less than 3 s in most organic liquids [24]. For absorption runs, oxygen was desorbed by sparging nitrogen. After disengagement of all nitrogen bubbles, a pre-adjusted air flow was fed by switching two magnet valves, and an increase in oxygen fugacity was recorded.

3. Results and Discussion

The successful prediction of k_La values by means of a correction factor in various organic liquids aerated under homogeneous conditions has been described exhaustively in Nedeltchev et al. [11]. In this work, it will be demonstrated that there are special cases (seven organic liquids) in which no correction factor is needed and that the k_La values are predictable in both homogeneous and heterogeneous flow regimes based on the same definition (Equation (3)) as for the gas–liquid contact time.

3.1. k_La Predictions in Alcohols

Figure 1 shows that the k_La values in the system air-2-propanol can be predicted reasonably well (within ±10%), not only in the homogeneous regime, but also in the heterogeneous regime. The k_La values shown in Figure 1 cover the U_g range from 0.008 m/s to 0.079 m/s.

When Equation (3) is used for the estimation of the contact time, then the average relative error (ARE) is 6.13%. On the other hand, when the contact time’s definition in Nedeltchev et al. [11] is used, then the ARE slightly increases up to 9.29%.

Figure 2 shows that the k_La predictions in the system air-1-butanol look very similar to the ones in the system air-2-propanol (see Figure 1). This is not surprising, since both types of alcohol belong to the same group of alcohols. Most of the k_La predictions lie on the +15% error limit. Again, when Equation (3) is used for the contact time, then the ARE is 13.12%. On the other hand, when the contact time’s definition in Nedeltchev et al. [11] is applied, then the ARE slightly increases up to 17.04%.

3.2. k_La Predictions in Other Organic Liquids

The volumetric liquid-phase MT coefficients k_La measured in the system air-nitrobenzene (BC: D_c = 0.095 m) could be well predicted on the basis of the classical penetration model. Figure 3 shows that all k_La values (up to U_g = 0.074 m/s) fit within ±10%. When Equation (3) is used for the contact time, then the ARE is 5.15%. On the other hand, when the contact time’s definition in Nedeltchev et al. [11] is applied, then the ARE slightly increases up to 6.22%.

It is worth mentioning that the boundaries of the main transition regimes are clearly identifiable in Figure 3. Up to k_La (calc.) = 0.0383 s⁻¹, a linear increase of the MT coefficients is observed. This k_La value corresponds to U_g = 0.0296 m/s, which critical gas velocity identifies the end of the homogeneous flow regime. At k_La (calc.) = 0.0531 s⁻¹, there is another change in the rate of increase of the MT coefficients. This identifies the onset of the heterogeneous flow regime.

In the case of an aeration of anilin in a small BC, the k_La values are lower. Figure 4 shows that the k_La values do not exceed 0.05 s⁻¹. They cover the U_g range of 0.007–0.074 m/s. Figure 4 exhibits that the predicted k_La values deviated within 15% from the experimental MT coefficients. When Equation (3) is used for the contact time, then the ARE is 16.24%. On the other hand, when the contact time’s definition in Nedeltchev et al. [11] is used, then the ARE slightly increases up to 19.22%.

The MT coefficients k_La in a BC operated with an air-decalin system can also be predicted reasonably well. Figure 5 shows that the k_La predictions in the U_g range of 0.046–0.076 m/s start to approach the −15% error limit but these predictions are still considered acceptable. When Equation (3) is used for the contact time, then the ARE is 14.35%. On the other hand, when the contact time’s definition in Nedeltchev et al. [11] is used, then the ARE slightly decreases, down to 11.84%. Thus, in this particular case, the alternative definition of the contact time is recommendable.

It is worth noting that at k_La (calc.) = 0.0356 s⁻¹ the rate of k_La increase changes and this corresponds to a transitional gas velocity of 0.0305 m/s, which marks the end of the homogeneous flow regime.

The MT coefficients k_La in a BC operated with an air-tetralin system (see Figure 6) can also be predicted reasonably well (±10%). When Equation (3) is used for the contact time, then the ARE is 7.41%. On the other hand, when the contact time’s definition in Nedeltchev et al. [11] is applied, then the ARE slightly decreases down to 6.37%. Thus, in this particular case, the alternative definition of the contact time is recommendable.

In addition, two main transition velocities can be identified. Figure 6 shows that at k_La (calc.) = 0.0405 s⁻¹ the rate of k_La increase changes. This corresponds to a transitional gas velocity of 0.0302 m/s. The second change of the rate of increase of k_La occurs at 0.0586 s⁻¹, which means that U_g = 0.0454 m/s is identifiable as the onset of the heterogeneous flow regime.

Figure 7 shows that the k_La values can also be well predicted in a highly viscous liquid such as ethylene glycol. Up to U_g = 0.0587 m/s, the k_La values can be predicted reasonably well (within ±15%). The highest two k_La values fall outside the error limits and they correspond to highly turbulent conditions. At k_La = 0.0063 s⁻¹ the rate of k_La increase changes. This point identifies the end of the homogeneous regime, which occurs at U_g = 0.0367 m/s. When Equation (3) is used for estimation of the contact time, then the ARE is 9.27%. On the other hand, when the contact time’s definition in Nedeltchev et al. [11] is used, then the ARE increases up to 17.40%. Obviously, in this particular case the ratio of Sauter-mean bubble diameter to bubble rise velocity better represents the gas–liquid contact time. In addition, the correlation of Nedeltchev et al. [11] was not derived on the basis of ethylene glycol.

In

Table 4. Summary of the values of several important dimensionless numbers in the liquids used.

Liquid	ds (m)	Reb (−)	Mo (−)	Ta (−)	Eo (−)
Anilin	5.15–5.39 × 10−3	244.3–257.2	4.371 × 10−8	4.96–5.22	6.16–6.76
1-Butanol	4.29–4.49 × 10−3	267.5–281.5	6.392 × 10−8	5.92–6.24	6.07–6.65
Decalin	4.30–4.50 × 10−3	284.4–298.8	1.769 × 10−8	4.69–4.93	5.37–5.89
Ethyl. glycol	7.11–7.45 × 10−3	85.9–91.0	1.308 × 10−5	6.47–6.86	11.75–12.89
Nitrobenzene	3.85–4.03 × 10−3	431.2–452.5	2.455 × 10−9	4.51–4.73	4.64–5.09
2-Propanol	3.97–4.14 × 10−3	232.8–244.8	4.563 × 10−8	4.77–5.02	5.75–6.14
Tetralin	4.19–4.39 × 10−3	361.6–379.6	5.384 × 10−9	4.53–4.76	4.83–5.29

are provided the values of the most important dimensionless numbers in the seven liquids used. The bubble shape is determined based on the Tadaki number Ta [34]. For Tadaki values between 2 and 6, the bubbles have an oblate ellipsoidal shape. Table 4 shows that the Ta numbers for all liquids (except for ethylene glycol) are below 6. In the case of ethylene glycol, the Ta values are slightly higher than 6 and probably this small deviation renders the classical penetration theory still applicable.

The current review article provides additional knowledge to the results reported in the other well-known reviews on BCs published by Deckwer and Schumpe [1], Schügerl et al. [35], Shah et al. [36] and Leonard et al. [37].

4. Conclusions

In this review work, the key correlations for the application of the penetration theory are provided. It has been demonstrated that Higbie’s penetration model can be successfully applied for prediction of the MT coefficients k_La, not only in the homogeneous regime, but also in transition and heterogeneous regimes. Various liquids were used, but only in the case of seven of them (1-butanol, 2-propanol, anilin, decalin, nitrobenzene, tetralin and ethylene glycol) were the k_La values successfully predicted at all gas velocities tested. In this work, how to estimate correctly the gas–liquid contact time and how to calculate the Sauter-mean bubble diameter have also been demonstrated. A comparison of the k_La values based on two different definitions of the gas–liquid contact time has also been performed.

As future work, more organic liquids and electrolytes should be included in this investigation and the ranges of the physicochemical properties for which the penetration theory is generally applicable (in all flow regimes) should be specified. Additional definitions of the gas–liquid contact time should be proposed and tested.