Metallic B2C3P Monolayer as Li-Ion Battery Materials: A First-Principles Study
Abstract
:1. Introduction
2. Computational Methods
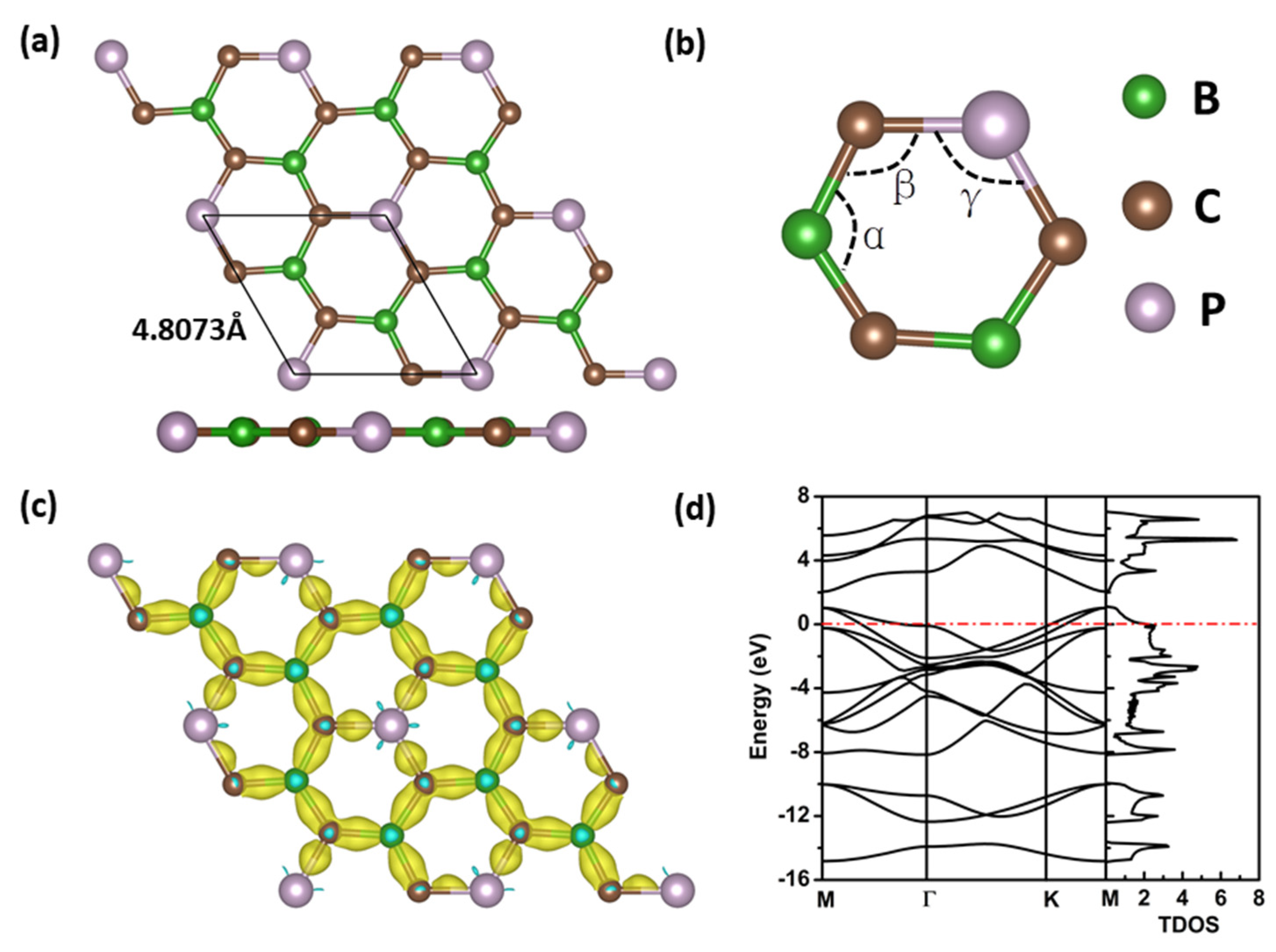
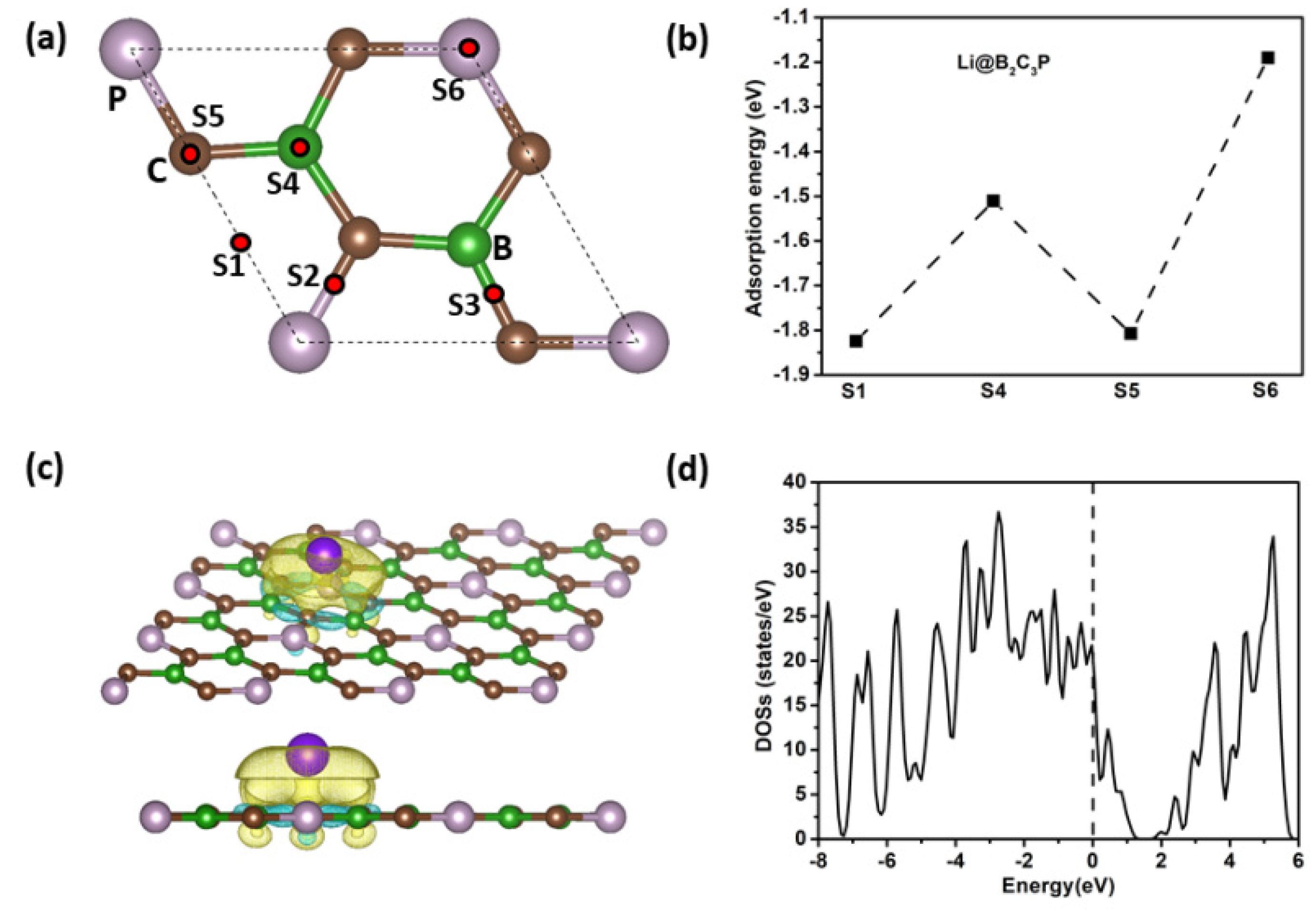
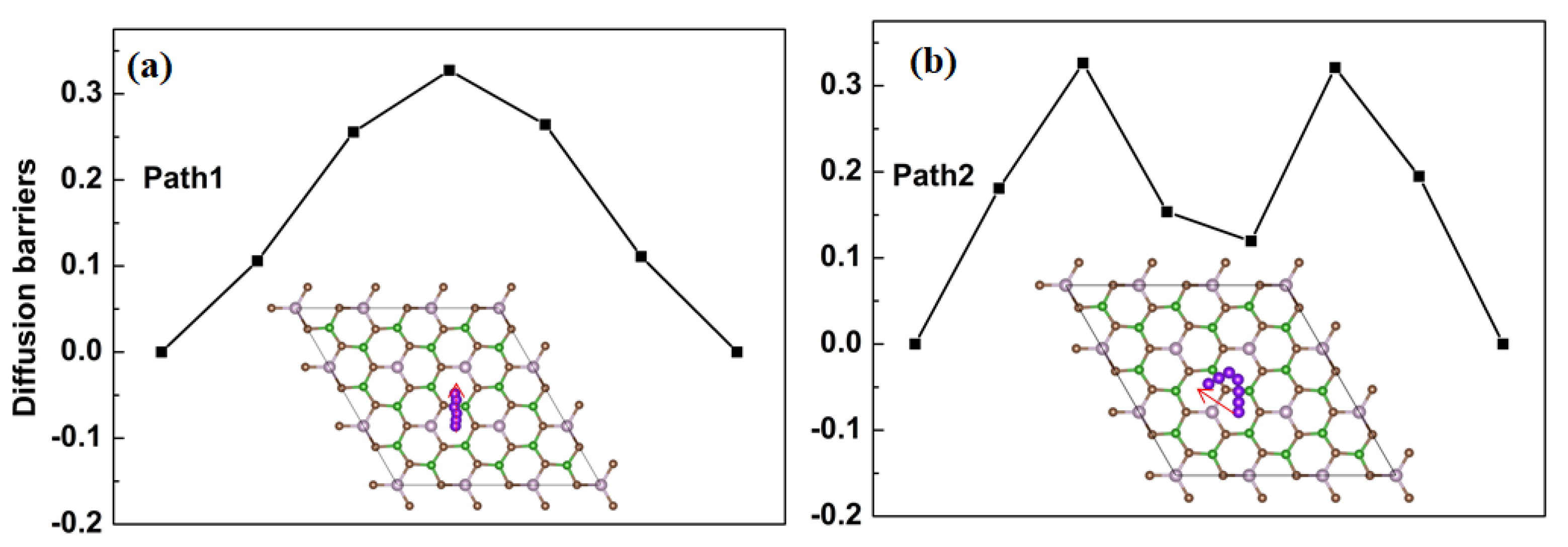
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, K. Recent progress on graphene-analogous 2D nanomaterials: Properties, modeling and applications. Prog. Mater. Sci. 2019, 100, 99–169. [Google Scholar] [CrossRef]
- Yorulmaz, U.; Demiroğlu, İ.; Çakir, D.; Gülseren, O.; Sevik, C. A systematical ab-initio review of promising 2D MXene monolayers towards Li-ion battery applications. J. Phys. Energy 2020, 2, 032006. [Google Scholar] [CrossRef]
- Feng, B.; Ding, Z.; Meng, S.; Yao, Y.; He, X.; Cheng, P.; Chen, L.; Wu, K. Evidence of Silicene in Honeycomb Structures of Silicon on Ag(111). Nano Lett. 2012, 12, 3507–3511. [Google Scholar] [CrossRef]
- Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Silicene: Compelling Experimental Evidence for Graphenelike Two-Dimensional Silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef] [PubMed]
- Mannix, A.J.; Zhou, X.F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes, anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513. [Google Scholar] [CrossRef] [PubMed]
- Feng, B.; Zhang, J.; Zhong, Q.; Li, W.; Li, S.; Li, H.; Cheng, P.; Meng, S.; Chen, L.; Wu, K. Experimental Realization of Two-Dimensional Boron Sheets. Nat. Chem. 2016, 8, 563. [Google Scholar] [CrossRef]
- Li, W.; Kong, L.; Chen, C.; Gou, J.; Sheng, S.; Zhang, W.; Li, H.; Chen, L.; Cheng, P.; Wu, K. Experimental realization of honeycomb borophene. Sci. Bull. 2018, 63, 282–286. [Google Scholar] [CrossRef]
- Lu, W.; Nan, H.; Hong, J.; Chen, Y.; Zhu, C.; Liang, Z.; Ma, X.; Ni, Z.; Jin, C.; Zhang, Z. Plasma-Assisted Fabrication of Monolayer Phosphorene and Its Raman Characterization. Nano Res. 2014, 7, 853–859. [Google Scholar] [CrossRef]
- Yasaei, P.; Kumar, B.; Foroozan, T.; Wang, C.; Salehkgihojin, A. High-Quality Black Phosphorus Atomic Layers by Liquid-Phase Exfoliation. Adv. Mater. 2015, 27, 1887–1892. [Google Scholar] [CrossRef] [PubMed]
- Brent, J.R.; Savjani, N.; Lewis, E.A.; Haigh, S.J.; Lewis, D.J.; Brien, P.O.; Brien, P.O. Production of Few-Layer Phosphorene by Liquid Exfoliation of Black Phosphorus. Chem. Commun. 2014, 50, 13338–13341. [Google Scholar] [CrossRef]
- Coleman, J.; Lotya, N.M.; O’Neill, A.; Bergin, S.D.; King, P.J.; Khan, U.; Young, K.; Gaucher, A.; De, S.; Smith, R.J.; et al. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 2011, 331, 568–571. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef]
- Li, S.; Ci, L.; Lu, H.; Sorokin, P.B.; Jin, C.; Jie, N.; Kvashnin, A.G.; Kvashnin, D.G.; Jun, L.; Boris, I.Y.; et al. Large scale growth and characterization of atomic hexagonal boron nitride layers. Nano Lett. 2010, 10, 3209–3215. [Google Scholar] [CrossRef]
- Li, L.K.; Yu, Y.J.; Ye, G.J.; Ge, Q.Q.; Ou, X.D.; Wu, H.; Feng, D.L.; Chen, X.H.; Zhang, Y.B. Black phosphorus Field-Effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Kang, W.; Xue, J. The potential application of phosphorene as an anode material in Li-ion batteries. J. Mater. Chem. A 2014, 2, 19046–19052. [Google Scholar] [CrossRef]
- Kulish, V.V.; Malyi, O.I.; Persson, C.; Wu, P. Phosphorene as an anode material for Na-ion batteries: A first-principles study. Phys. Chem. Chem. Phys. 2015, 17, 13921–13928. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Wang, Y. Geometric and Electronic Structures of Two-Dimensional SiC3 Compound. J. Phys. Chem. C 2014, 118, 4509–4515. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, S.; Guo, Y.; Wang, Q. TiC2: A new two-dimensional sheet beyond MXenes. Nanoscale 2016, 8, 233. [Google Scholar] [CrossRef] [PubMed]
- Jing, Y.; Mam, Y.; Li, Y.; Heine, T. GeP3: A Small Indirect Band Gap 2D Crystal with High Carrier Mobility and Strong Interlayer Quantum Confinement. Nano Lett. 2017, 17, 1833–1838. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Meng, F.; Wang, H.; Wang, H.; Ni, Y. Novel two-dimensional semiconductor SnP3: High stability, tunable bandgaps and high carrier mobility explored using first-principles calculations. J. Mater. Chem. A 2018, 6, 11890–11897. [Google Scholar] [CrossRef]
- Lu, N.; Zhuo, Z.; Guo, H.; Wu, P.; Fa, W.; Wu, X.; Zeng, X.C. CaP3: A New Two-Dimensional Functional Material with Desirable Band Gap and Ultrahigh Carrier Mobility. J. Phys. Chem. Lett. 2018, 9, 1728–1733. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Zhao, Z.; Sun, Y.; Bergara, A.; Lin, J.; Zhang, S.; Xu, H.; Zhang, L.; Yang, G.; Liu, Y. Two-Dimensional PC6 with Direct Band Gap and Anisotropic Carrier Mobility. J. Am. Chem. Soc. 2019, 141, 1599–1605. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.X.; Pandey, R.; Karna, S.P. Carbon Phosphide Monolayer with Superior Carrie Mobility. Nanoscale 2016, 8, 8819–8825. [Google Scholar] [CrossRef]
- Zhou, W.; Guo, Y.; Shen, Y.; Wang, Q.; Jena, P. Imidazole-graphyne: A new 2D carbon nitride with a direct bandgap and strong IR refraction. Phys. Chem. Chem. Phys. 2020, 23, 10274. [Google Scholar] [CrossRef] [PubMed]
- Kistanov, A.A.; Shcherbinin, S.A.; Ustiuzhanina, S.V.; Huttula, M.; Prezhdo, O.V. First-Principles Prediction of Two-Dimensional B3C2P3 and B2C4P2: Structural Stability, Fundamental Properties, and Renewable Energy Applications. J. Phys. Chem. Lett. 2021, 12, 3436–3442. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Guo, J.; Li, L.; Dai, T. Structural and electronic properties of predicting two-dimensional BC2P and BC3P3 monolayers by the global optimization method. Chem.Phy.Lett. 2019, 726, 69–76. [Google Scholar] [CrossRef]
- Tang, M.; Wang, C.; Schwingenschlögl, U.; Yang, G. BC6P Monolayer: Isostructural and Isoelectronic Analogues of Graphene with Desirable Properties for K-Ion Batteries. Chem. Mater. 2021, 33, 9262–9269. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 82, 094116. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter. 2009, 21, 395502. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.; Tang, G.; Geng, W. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Fan, D.; Lu, S.H.; Guo, Y.D.; Hu, X.J. Two-dimensional stoichiometric boron carbides with unexpected chemical bonding and promising electronic properties. J. Mater. Chem. C 2018, 6, 1651. [Google Scholar] [CrossRef]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based bader analysis algorithm without latticebias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Zhang, H.; Shao, H.Z.; Xu, Y.F.; Zhang, R.J.; Zhu, H.Y. The electronic, optical, and thermodynamic properties of borophene from first-principles calculations. J. Mater. Chem. C 2016, 4, 3592–3598. [Google Scholar] [CrossRef] [Green Version]
- Drummond, N.; Zólyomi, V.; Fal’Ko, V. Electrically tunable band gap in silicone. Phys. Rev. B 2012, 85, 075423. [Google Scholar] [CrossRef]
- Guan, J.; Zhu, Z.; Tománek, D. Phase Coexistence and Metal-Insulator Transition in Few-Layer Phosphorene: A Computational Study. Phys. Rev. Lett. 2014, 113, 046804. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.F.; Zheng, W.T.; Kuo, J.L. Adsorption and diffusion of Li on pristine and defective grapheme. ACS. Appl. Mater. Interfaces 2012, 4, 2432–2438. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.J.; Du, C.F.; Xue, Y.Q.; Tan, X.Y.; Kang, J.Z.; Gao, Y.; Yu, H.; Yan, Q.Y. MXenes as a versatile platform for reactive surface modification and superior sodium-ion storages. Exploration 2021, 1, 20210024. [Google Scholar] [CrossRef]
- Shi, R.J.; Jiao, S.L.; Yue, Q.Q.; Gu, G.Q.; Zhang, K.; Zhao, Y. Challenges and advances of organic electrode materials for sustainable secondary batteries. Exploration 2022, 2, 0220066. [Google Scholar] [CrossRef]
- Ni, L.; Xu, G.J.; Li, C.C.; Cui, G.L. Electrolyte formulation strategies for potassium-based batteries. Exploration 2022, 2, 20210239. [Google Scholar] [CrossRef]
- Wang, L.; Liu, T.F.; Wu, T.P.; Lu, J. Exploring new battery knowledge by advanced characterizing technologies. Exploration 2021, 1, 20210130. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, B.W. Room temperature liquid metals for flexible alkali metal-chalcogen batteries. Exploration 2022, 20210182. [Google Scholar] [CrossRef]
- Dong, Y.; Wei, W.; Lv, X.; Huang, B.; Dai, Y. Semimetallic Si3C as a high capacity anode material for advanced lithium ion batteries. Appl. Surf. Sci. 2019, 479, 519–524. [Google Scholar] [CrossRef]
- Persson, K.; Sethuraman, V.A.; Hardwick, L.J.; Hinuma, Y.; Meng, Y.S.; Van Der Ven, A.; Srinivasan, V.; Kostecki, R.; Ceder, G. Lithium diffusion in graphitic carbon. J. Phys. Chem. Lett. 2010, 1, 1176–1180. [Google Scholar] [CrossRef] [Green Version]
- Yuan, G.; Bo, T.; Qi, X.; Liu, P.; Huang, Z.; Wang, B. Monolayer Zr2B2: A promising two-dimensional anode material for Li-ion batteries. Appl. Surf. Sci. 2019, 480, 448–453. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Bo, T.; Zhu, X.; Wang, Z.; Wu, J.; Li, Y.; Wang, B.T. Two-dimensional tetragonal Ti2BN: A novel potential anode material for Li-ion batteries. Appl. Surf. Sci. 2020, 513, 145821. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Wang, Z.; Cheng, J.; Pu, C. Metallic B2C3P Monolayer as Li-Ion Battery Materials: A First-Principles Study. Processes 2022, 10, 1809. https://doi.org/10.3390/pr10091809
Zhou D, Wang Z, Cheng J, Pu C. Metallic B2C3P Monolayer as Li-Ion Battery Materials: A First-Principles Study. Processes. 2022; 10(9):1809. https://doi.org/10.3390/pr10091809
Chicago/Turabian StyleZhou, Dawei, Zhuo Wang, Jinbing Cheng, and Chunying Pu. 2022. "Metallic B2C3P Monolayer as Li-Ion Battery Materials: A First-Principles Study" Processes 10, no. 9: 1809. https://doi.org/10.3390/pr10091809
APA StyleZhou, D., Wang, Z., Cheng, J., & Pu, C. (2022). Metallic B2C3P Monolayer as Li-Ion Battery Materials: A First-Principles Study. Processes, 10(9), 1809. https://doi.org/10.3390/pr10091809





