Entropy Flow Analysis of Thermal Transmission Process in Integrated Energy System Part II: Comparative Case Study
Abstract
:1. Introduction
2. Theoretical Approach of Entropy Analysis
2.1. Entropy Analysis and Distribution Parameter Model
2.2. Improved Lumped Parameter Model
3. Energy Quality Analysis of Heating Network
4. Case Study and Discussion
4.1. Case I: Bali 32-Node Heat Grid
4.1.1. Case Description
4.1.2. Case Calculation Results
4.1.3. Entropy Analysis and Discussion
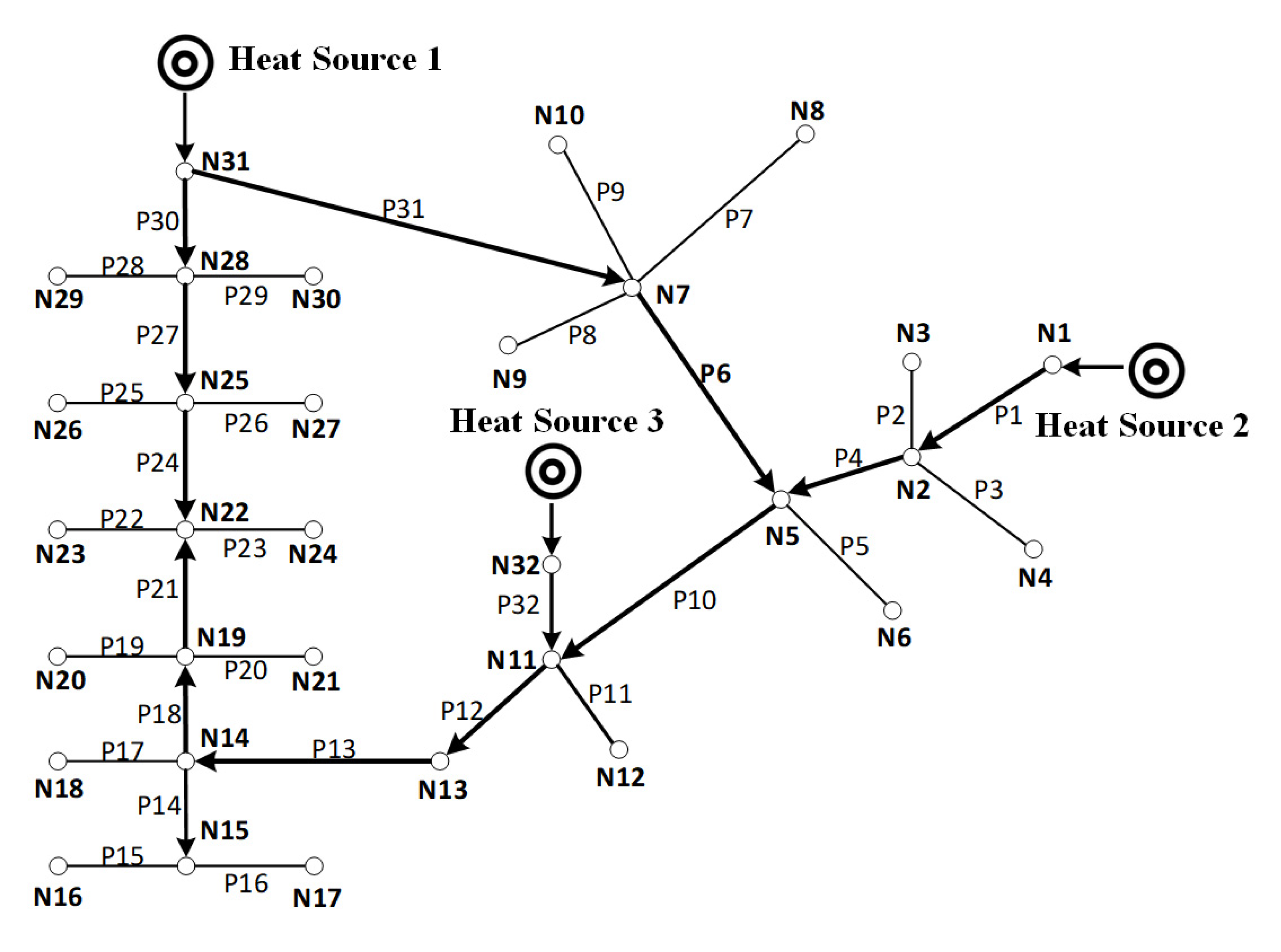
4.2. Case II: China 41-Node Heat Network
4.2.1. Case Description
4.2.2. Case Calculation Results
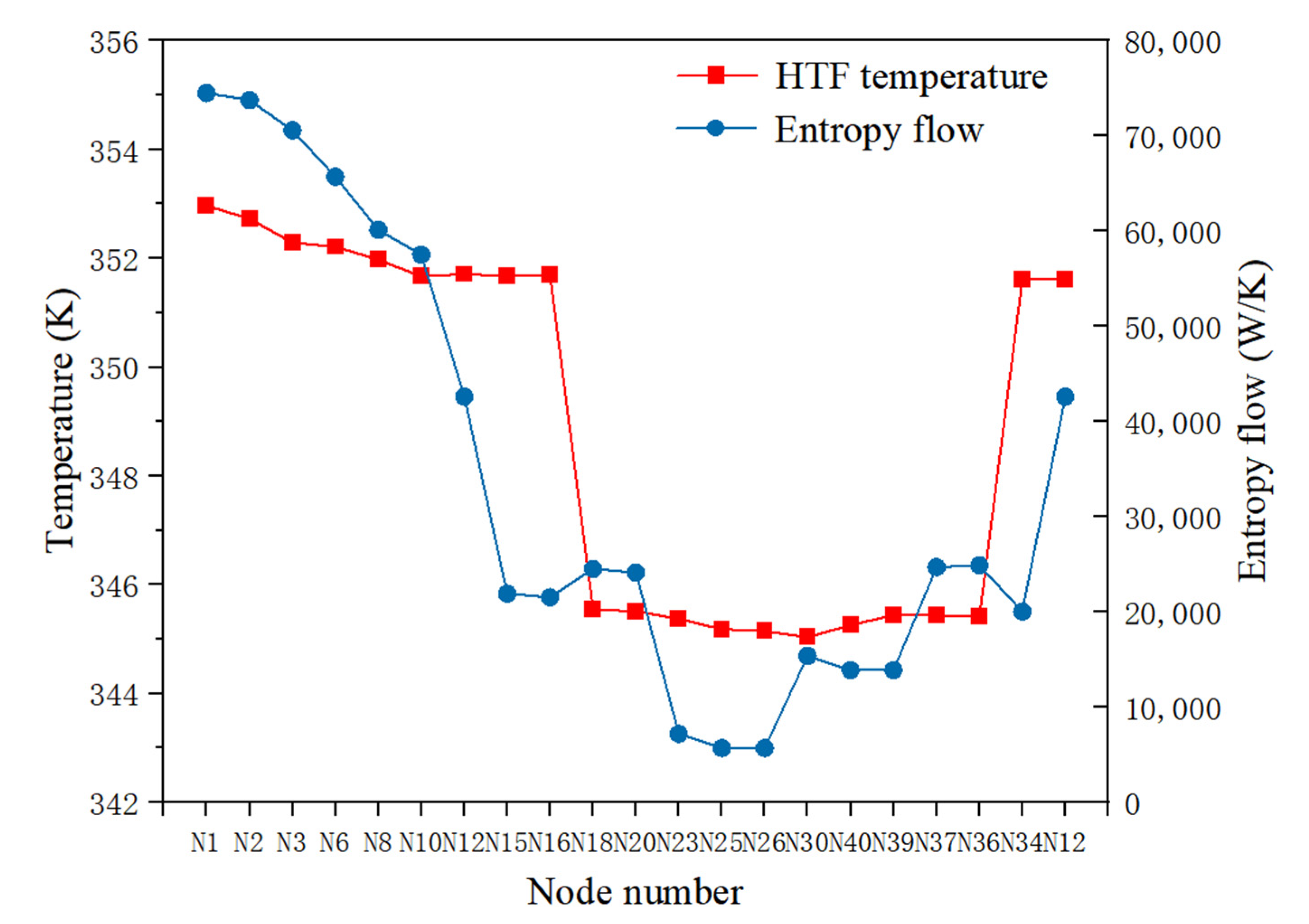
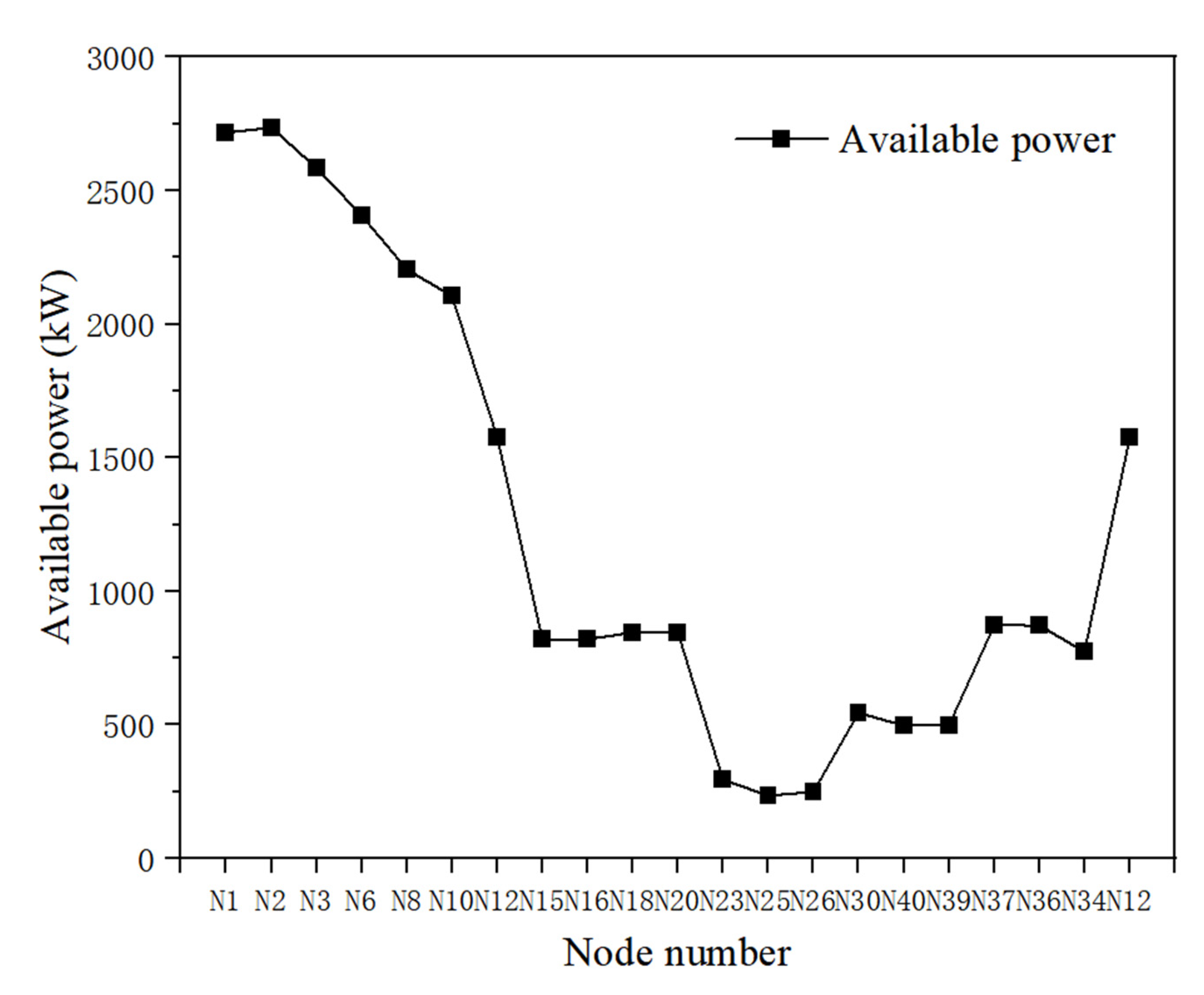
4.2.3. Entropy Analysis
5. Conclusions
- (1)
- An innovative analytical method based on entropy flow was derived on the basis of theory developed in Part I, which can effectively assess the quantity and quality of thermal transport. It is used to study the cases combined with the lumped parameter model, and the achieved evaluation results for thermal parameters and processes are in good agreement with the energy quality theory of the heating network in both cases adopted in this paper.
- (2)
- In both cases, it can be intuitively seen that the entropy flow change of each node is different from the temperature, which is related to the energy quality and consistent with the change trend of the available power. This reflects the flow information of the pipe network node and the change of the energy quality. As the heat dissipates into the environment, the available thermal power decreases and the energy quality declines gradually. Although Case II based on China 41-node heating network is a relatively larger scale heating supply system than Case I based on Bali 32-node heating grid, the consistent results for both show the effectiveness of the proposed calculation method in this part.
- (3)
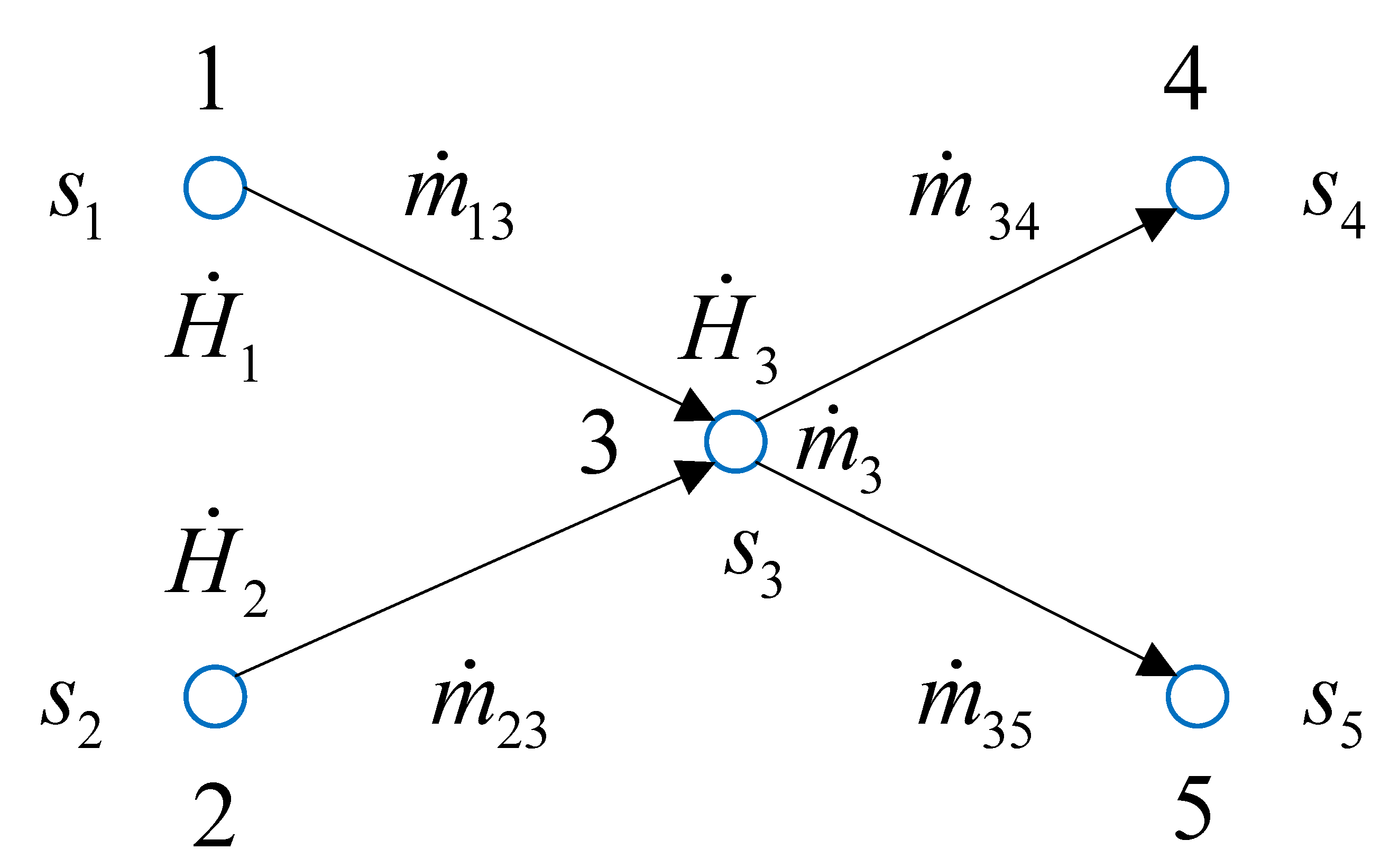
- The comparative case study shows that the variation trend of entropy flow at each node is consistent with the variation of available power but is independent of temperature. Compared with the algebraic sum of the branch entropy flow, the node entropy flow increases, which reflects the entropy generation phenomenon in the mixing process. The change in available power is the opposite. This means that irreversible entropy generation at nodes leads to a loss of available thermal power. Therefore, it is more accurate to describe the dynamic heat conduction process on the entropy scale.
Author Contributions
Funding
Conflicts of Interest
References
- Duquette, J.; Rowe, A.; Wild, P. Thermal performance of a steady state physical pipe model for simulating district heating grids with variable flow. Appl. Energy 2016, 178, 383–393. [Google Scholar] [CrossRef]
- Wu, J.Z.; Yan, J.Y.; Jia, H.J.; Hatziargyriou, N.; Djilali, N.; Sun, H.B. Integrated Energy Systems. Appl. Energy 2016, 167, 155–157. [Google Scholar] [CrossRef]
- Bagherian, M.A.; Mehranzamir, K. A comprehensive review on renewable energy integration for combined heat and power production. Energy Convers. Manag. 2020, 224, 113454. [Google Scholar] [CrossRef]
- Leontaris, G.K.; Tracas, N.D. Unified models at intermediate energy scales and Kaluza-Klein excitations. Phys. Lett. B 1999, 470, 84–89. [Google Scholar] [CrossRef]
- Li, J.Y.; Li, D.X.; Zheng, Y.F.; Yao, Y.P.; Tang, Y.S. Unified modeling of regionally integrated energy system and application to optimization. Int. J. Elec. Power 2022, 134, 107377. [Google Scholar] [CrossRef]
- Weedy, B.M. The Analogy between Thermal and Electrical Quantities. Electr. Pow. Syst. Res. 1988, 15, 197–201. [Google Scholar] [CrossRef]
- Capizzi, G.; Lo Sciuto, G.; Cammarata, G.; Cammarata, M. Thermal transients simulations of a building by a dynamic model based on thermal-electrical analogy: Evaluation and implementation issue. Appl. Energy 2017, 199, 323–334. [Google Scholar] [CrossRef]
- Hao, L.; Xu, F.; Chen, Q.; Wei, M.S.; Chen, L.; Min, Y. A thermal-electrical analogy transient model of district heating pipelines for integrated analysis of thermal and power systems. Appl. Therm. Eng. 2018, 139, 213–221. [Google Scholar] [CrossRef]
- Palsson, H.; Larsen, H.V.; Ravn, H.F.; Bohm, B.; Zhou, J. Equivalent Models of District Heating Systems. 1999. Available online: https://www.researchgate.net/publication/256732635 (accessed on 1 July 2022).
- Sun, Q.Y.; Dong, Q.Y.; You, S.; Li, Z.B.; Wang, R. A unified energy flow analysis considering initial guesses in complex multi-energy carrier systems. Energy 2020, 213, 118812. [Google Scholar] [CrossRef]
- Tian, H.; Zhao, H.R.; Liu, C.Y.; Chen, J.; Wu, Q.W.; Terzija, V. A dual-driven linear modeling approach for multiple energy flow calculation in electricity-heat system. Appl. Energy 2022, 314, 118872. [Google Scholar] [CrossRef]
- Chen, Q.; Guo, Z.Y. Entransy Theory and Its Application to Heat Transfer Analyses in Porous Media. Int. J. Nonlinear Sci. Num. 2010, 11, 11–22. [Google Scholar] [CrossRef]
- Chen, Q. Entransy dissipation-based thermal resistance method for heat exchanger performance design and optimization. Int. J. Heat Mass Transf. 2013, 60, 156–162. [Google Scholar] [CrossRef]
- Chen, Q.; Liang, X.G.; Guo, Z.Y. Entransy theory for the optimization of heat transfer—A review and update. Int. J. Heat Mass Transf. 2013, 63, 65–81. [Google Scholar] [CrossRef]
- Chen, Q.; Guo, Z.Y.; Liang, X.G. Closure to “Discussion of ‘Entransy is Now Clear”. J. Heat Transf. 2014, 136, 095502. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal entransy dissipation rate minimization of a rectangular body with nonuniform heat generation. Sci. China Technol. Sci. 2016, 59, 1352–1359. [Google Scholar] [CrossRef]
- Martinez-Mares, A.; Fuerte-Esquivel, C.R. A Unified Gas and Power Flow Analysis in Natural Gas and Electricity Coupled Networks. IEEE Trans. Power Syst. 2012, 27, 2156–2166. [Google Scholar] [CrossRef]
- Chen, L.G.; Xiao, Q.H.; Feng, H.J. Constructal Optimizations for Heat and Mass Transfers Based on the Entransy Dissipation Extremum Principle, Performed at the Naval University of Engineering; a Review. Entropy 2018, 20, 74. [Google Scholar] [CrossRef]
- Chen, Q.; Fu, R.H.; Xu, Y.C. Electrical circuit analogy for heat transfer analysis and optimization in heat exchanger networks. Appl. Energy 2015, 139, 81–92. [Google Scholar] [CrossRef]
- Lan, T.; Strunz, K. Modeling of the Enthalpy Transfer Using Electric Circuit Equivalents: Theory and Application to Transients of Multi-Carrier Energy Systems. IEEE Trans. Energy Convers. 2019, 34, 1720–1730. [Google Scholar] [CrossRef]
- Chen, B.B.; Sun, H.B.; Yin, G.X.; Wu, W.C.; Guo, Q.L.; Chen, Y.W.; Pan, Z.G.; Wang, B. Energy circuit theory of integrated energy system analysis (II): Hydraulic circuit and thermal circuit. Proc. CSEE 2020, 40, 2133–2142, 2393. (In Chinese) [Google Scholar]
- Zhang, W.Y.; Chui, S.T. A generalized equivalent circuit theory for the electric and magnetic resonances of metallic wire networks. J. Appl. Phys. 2009, 105, 113121. [Google Scholar] [CrossRef]
- Wu, G.F.; Huang, F.Q.S.; Gu, Z.T. A more in-depth understanding of entropy by drawing analogy between thermodynamics and electricity. J. Univ. Shanghai Sci. Technol. 2019, 41, 307–312. [Google Scholar]
- Chen, H.Y.; Wen, J.Z.; Wang, Z.Y.; Yang, X. Transfer laws and equations of energy networks. J. Xi’an Jiaotong Univ. 2014, 48, 66–76. [Google Scholar]
- Chen, H.Y.; Ming, L.I.; Qiu, M.; Hailin, G.E.; Huang, L. Modeling and analysis of time-varying energy network. Sci. Sin. Technol. 2019, 49, 243–254. [Google Scholar] [CrossRef]
- Yang, J.W.; Zhang, N.; Kang, C.Q. Analysis Theory of Generalized Electric Circuit for Multi-energy Networks-Part One Branch Model. Autom. Electr. Power Syst. 2020, 44, 21–32. [Google Scholar]
- Bejan, A. The equivalence of maximum power and minimum entropy generation rate in the optimization of power plants. ASME J. Energy Resour. Technol. 1996, 118, 98–101. [Google Scholar] [CrossRef]
- British Standards Institution. District Heating and District Cooling Pipe Systems; Terms and definitions, 1 online resource (26 pages); British Standards Institution: London, UK, 2019. [Google Scholar]
- Yang, J.W.; Zhang, N.; Botterud, A.; Kang, C.Q. On An Equivalent Representation of the Dynamics in District Heating Networks for Combined Electricity-Heat Operation. IEEE Trans. Power Syst. 2020, 35, 560–570. [Google Scholar] [CrossRef]



| Pipe Number | Mass Flow/ (kg/s) | Pipe Length/ (m) | Pipe Diameter/ (mm) | Heat Loss Coefficient/ (W/m K) | Outlet Temperature/ (K) | Outlet Entropy Flow/ (W/K) |
|---|---|---|---|---|---|---|
| P1 | 4.79 | 362.84 | 4640.96 | 0.321 | 352.62 | 4639.92 |
| P2 | 0.45 | 362.04 | 432.62 | 0.210 | 351.81 | 431.58 |
| P3 | 0.61 | 362.53 | 585.75 | 0.210 | 352.25 | 584.70 |
| P4 | 3.74 | 362.75 | 3612.19 | 0.327 | 352.51 | 3611.15 |
| P5 | 0.74 | 357.65 | 672.36 | 0.189 | 347.47 | 671.34 |
| P6 | 0.88 | 342.02 | 633.06 | 0.236 | 331.82 | 632.02 |
| P7 | 1.30 | 342.47 | 944.77 | 0.210 | 332.26 | 943.73 |
| P8 | 0.65 | 342.41 | 472.68 | 0.210 | 332.23 | 471.63 |
| P9 | 0.66 | 341.82 | 475.75 | 0.210 | 331.49 | 474.72 |
| P10 | 3.87 | 358.57 | 3557.63 | 0.327 | 348.42 | 3556.58 |
| P11 | 1.64 | 352.52 | 1391.82 | 0.210 | 342.26 | 1390.77 |
| P12 | 4.48 | 352.57 | 3792.69 | 0.327 | 342.39 | 3791.64 |
| P13 | 4.48 | 352.44 | 3785.78 | 0.278 | 342.11 | 3784.73 |
| P14 | 1.60 | 352.35 | 1351.91 | 0.219 | 342.03 | 1350.87 |
| P15 | 0.80 | 351.93 | 671.00 | 0.189 | 341.60 | 669.95 |
| P16 | 0.80 | 351.86 | 672.21 | 0.189 | 341.71 | 671.17 |
| P17 | 0.54 | 351.71 | 448.71 | 0.189 | 341.54 | 447.66 |
| P18 | 2.34 | 352.36 | 1976.53 | 0.278 | 342.20 | 1975.49 |
| P19 | 0.54 | 351.64 | 449.10 | 0.189 | 341.48 | 448.07 |
| P20 | 0.54 | 351.64 | 449.17 | 0.189 | 341.40 | 448.13 |
| P21 | 1.27 | 352.24 | 1067.20 | 0.236 | 342.02 | 1066.16 |
| P22 | 0.71 | 350.48 | 583.91 | 0.189 | 340.30 | 582.88 |
| P23 | 0.71 | 350.59 | 583.14 | 0.189 | 340.25 | 582.10 |
| P24 | 0.15 | 341.89 | 109.57 | 0.236 | 331.57 | 108.54 |
| P25 | 0.65 | 342.41 | 472.66 | 0.189 | 332.20 | 471.62 |
| P26 | 0.65 | 342.46 | 472.39 | 0.189 | 332.23 | 471.35 |
| P27 | 1.46 | 342.93 | 1064.37 | 0.210 | 332.61 | 1063.33 |
| P28 | 0.65 | 342.68 | 471.30 | 0.189 | 332.43 | 470.25 |
| P29 | 0.65 | 342.64 | 471.44 | 0.189 | 332.34 | 470.40 |
| P30 | 2.75 | 343.04 | 2015.22 | 0.321 | 332.82 | 2014.17 |
| P31 | 3.50 | 342.84 | 2552.64 | 0.321 | 332.60 | 2551.61 |
| P32 | 2.25 | 342.77 | 1636.94 | 0.321 | 332.55 | 1635.91 |
| Pipe Network Node | Node Branch | Before Confluence (Branch) | After Confluence (Node) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Branch Total Entropy Flow (W/K) | Total Available Power of Branch (W) | Total Branch Heat (W) | Node Entropy Flow (W/K) | Node Available Power (W) | Node Heat (W) | ||||
| N5 | P4, P6 | 4239.25 | 139,130.78 | 1,299,398.82 | 4204.36 | 137,323.62 | 1,299,398.82 | ||
| N11 | P32, P10 | 5193.57 | 153,131.47 | 1,560,946.33 | 5201.60 | 155,241.58 | 1,560,946.33 | ||
| N22 | P21, P24 | 1138.77 | 28,926.54 | 315,013.16 | 1139.02 | 28,416.96 | 315,013.16 | ||
| Pipe Number | Mass Flow/ (kg/s) | Pipe Length/ (m) | Pipe Diameter/ (mm) | Heat Loss Coefficient/ (W/m K) | Outlet Temperature/ (K) | Outlet Entropy Flow/ (W/K) |
|---|---|---|---|---|---|---|
| P1 | 76.26 | 5328.00 | 1200 | 0.20887 | 352.68 | 73,903.07 |
| P2 | 3.37 | 5650.00 | 500 | 0.20898 | 346.67 | 3124.86 |
| P3 | 72.90 | 7664.00 | 1100 | 0.20878 | 352.16 | 70,314.53 |
| P4 | 3.20 | 1461.00 | 400 | 0.20888 | 350.22 | 3115.92 |
| P5 | 1.40 | 1099.00 | 700 | 0.20884 | 349.33 | 1396.46 |
| P6 | 68.31 | 2588.00 | 1100 | 0.20879 | 352.04 | 65,786.65 |
| P7 | 5.82 | 2357.00 | 1100 | 0.20883 | 350.65 | 5595.91 |
| P8 | 62.49 | 1793.00 | 1100 | 0.20880 | 351.92 | 60,115.09 |
| P9 | 2.64 | 405.00 | 350 | 0.20881 | 351.41 | 2623.74 |
| P10 | 59.84 | 4514.76 | 1100 | 0.20880 | 351.71 | 57,383.01 |
| P11 | 15.40 | 532.00 | 250 | 0.20889 | 351.58 | 14,822.13 |
| P12 | 44.44 | 967.00 | 600 | 0.20881 | 351.64 | 42,599.03 |
| P13 | 0.78 | 85.00 | 600 | 0.21014 | 351.16 | 845.09 |
| P14 | 1.56 | 97.00 | 600 | 0.21016 | 351.40 | 1588.42 |
| P15 | 21.08 | 36.00 | 600 | 0.21025 | 351.64 | 20,262.31 |
| P16 | 22.70 | 244.10 | 600 | 0.21014 | 351.66 | 21,814.40 |
| P17 | 4.07 | 144.00 | 300 | 0.21015 | 351.41 | 3990.23 |
| P18 | 18.63 | 781.50 | 600 | 0.21015 | 351.38 | 17,887.94 |
| P19 | 8.93 | 175.00 | 1000 | 0.21011 | 332.76 | 6641.28 |
| P20 | 27.55 | 388.00 | 900 | 0.21010 | 345.34 | 24,447.43 |
| P21 | 15.88 | 92.00 | 350 | 0.21011 | 345.41 | 14,126.30 |
| P22 | 3.69 | 115.00 | 350 | 0.21011 | 345.27 | 3357.47 |
| P23 | 7.99 | 228.45 | 1000 | 0.21010 | 345.23 | 7150.14 |
| P24 | 1.38 | 204.00 | 250 | 0.21011 | 344.82 | 1307.08 |
| P25 | 6.61 | 419.20 | 1000 | 0.21010 | 345.14 | 5919.76 |
| P26 | 6.61 | 109.00 | 1200 | 0.21010 | 345.01 | 5915.23 |
| P27 | 0.78 | 225.14 | 250 | 0.21012 | 344.05 | 781.91 |
| P28 | 0.79 | 145.00 | 200 | 0.21011 | 344.32 | 791.48 |
| P29 | 3.07 | 813.20 | 200 | 0.21025 | 344.17 | 2773.02 |
| P30 | 1.96 | 334.00 | 1200 | 0.21010 | 344.43 | 1812.31 |
| P31 | 17.66 | 816.80 | 1200 | 0.2101 | 344.93 | 15,614.83 |
| P32 | 14.37 | 491.00 | 500 | 0.21011 | 344.84 | 12,705.33 |
| P33 | 3.29 | 415.50 | 1100 | 0.21009 | 354.74 | 2872.43 |
| P34 | 21.00 | 51.00 | 600 | 0.21014 | 361.89 | 20,093.27 |
| P35 | 1.64 | 52.00 | 90 | 0.21014 | 361.77 | 1563.35 |
| P36 | 19.36 | 1445.38 | 900 | 0.21013 | 361.61 | 18,466.90 |
| P37 | 8.91 | 1486.53 | 1000 | 0.21012 | 342.69 | 6490.05 |
| P38 | 28.28 | 94.00 | 600 | 0.21012 | 355.64 | 24,989.97 |
| P39 | 12.57 | 250.00 | 500 | 0.21012 | 355.57 | 11,101.94 |
| P40 | 15.70 | 329.00 | 500 | 0.21012 | 355.57 | 13,864.95 |
| P41 | 15.70 | 90.00 | 500 | 0.21012 | 355.55 | 13,861.37 |
| P42 | 15.70 | 694.50 | 500 | 0.21014 | 355.40 | 13,833.73 |
| Pipe Network Node | Node Branch | Before Confluence (Branch) | After Confluence (Node) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Branch Total Entropy Flow (W/K) | Total Available Power of Branch (kW) | Total Branch Heat (kW) | Node Entropy Flow (W/K) | Node Available Power (kW) | Node Heat (kW) | ||||
| N15 | P15, P35 | 20,714.62 | 825.45 | 7515.36 | 21,901.92 | 819.05 | 7515.36 | ||
| N18 | P18, P19 | 24,237.23 | 854.58 | 8716.71 | 24,513.13 | 845.56 | 8716.71 | ||
| N30 | P30, P42 | 15,376.39 | 551.03 | 5483.22 | 15,376.36 | 543.69 | 5483.22 | ||
| N36 | P36, P37 | 24,876.91 | 876.53 | 8115.87 | 24,886.45 | 871.82 | 8115.87 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Wang, J.; Zhao, H.; Yu, Z.; Han, J.; Chen, J.; Liu, C. Entropy Flow Analysis of Thermal Transmission Process in Integrated Energy System Part II: Comparative Case Study. Processes 2022, 10, 1719. https://doi.org/10.3390/pr10091719
Chen C, Wang J, Zhao H, Yu Z, Han J, Chen J, Liu C. Entropy Flow Analysis of Thermal Transmission Process in Integrated Energy System Part II: Comparative Case Study. Processes. 2022; 10(9):1719. https://doi.org/10.3390/pr10091719
Chicago/Turabian StyleChen, Changnian, Junjie Wang, Haoran Zhao, Zeting Yu, Jitian Han, Jian Chen, and Chunyang Liu. 2022. "Entropy Flow Analysis of Thermal Transmission Process in Integrated Energy System Part II: Comparative Case Study" Processes 10, no. 9: 1719. https://doi.org/10.3390/pr10091719
APA StyleChen, C., Wang, J., Zhao, H., Yu, Z., Han, J., Chen, J., & Liu, C. (2022). Entropy Flow Analysis of Thermal Transmission Process in Integrated Energy System Part II: Comparative Case Study. Processes, 10(9), 1719. https://doi.org/10.3390/pr10091719







