Abstract
Dispersed bubbly flow is important to understand when working in a wide variety of hydrodynamic engineering areas; the main objective of this work is to numerically study bubble-induced instability. Surface tension and bubble-induced turbulence effects are considered with the momentum and k-ω transport equations. Steady dispersed bubbly flow is generated at the inlet surface using time-step and user-defined functions. In order to track the interface between the liquid and gas phases, the volume of fraction method is used. Several calculation conditions are considered in order to determine the effects of bubble diameter, bubble distribution, bubble velocity and bubble density on flow instability and void fraction. The void fraction of the domain is set to no more than 0.5% under different bubbly (micro/small) flow conditions; and the order of magnitude of the Reynolds number is 106. Results from the simulation indicate that velocity fluctuation induced by bubble swarm increases with increasing bubble diameter. Bubble density and bubble distribution seem to have a complex influence on flow instability. Bubble-induced turbulence results indicate that small bubbles produce a significant disturbance near the boundary region of bubble swarm; this indicates that induced bubble swarm has a potential capability of enhancing heat and mass transfer in the velocity boundary layer. Results from this study are useful for two-phase flow, bubble floatation and other hydrodynamic engineering applications.
1. Introduction
Gas–liquid bubbly flow is commonly observed in fluid machinery and various engineering applications to date [1,2,3,4], such as bubble floating devices and other equipment used for multiphase transportation that focus on the cavitation phenomenon. This is not the case when a steady flow can be used in the analysis of an impeller or some other hydrodynamic system [5]. In most cases, the bubbles that disperse in the continuous water phase vary widely in distribution, shape and size, which is known as the bubbly flow. Due to the abundant number of small bubbles, the flow mechanism of two-phase flow is much more complicated than that found in single-phase flow and includes the effects of: discontinuity of properties at the phase interface [6]; bubble merge and annihilate [7,8]; forces acting on the gas–liquid interface [9,10]; flow instability [11,12]; and bubble-induced turbulence [13,14].
Previous studies evaluated bubbly flow characteristics of void fraction, bubble distribution, phase interaction and the effect of multi-physics coupling using experimental methods or numerical simulation. Li [15] conducted a theoretical analysis to present potential fluctuations at the interfaces between vapor flow and liquid flow based on the equation of continuity. Potential fluctuation has oscillatory wave behaviors along three spatial dimensions and one temporal dimension. The analysis is supported by visualizing flow regimes and measuring heat transfer coefficients during two-phase flow in a smooth tube and a three-dimensional hierarchical tube to address the physical mechanism for two-phase flow patterns. Experimental measurement is a robust but reliable method to obtain flow field parameters and analyze bubble-induced instability. Many previous experimental studies were focused on measuring void fraction [16,17,18], liquid turbulence [19,20,21], time-mean velocity [22] and Reynolds stress [19,21] of bubbly flow in small confined circular or rectangular channels. Zhou et al. [19] studied the local liquid turbulence data in air–water flow, for a wide void fraction range by utilizing the particle image velocimetry (PIV) and planar laser-induced fluorescence (PLIF) methods. Domnick and Durst [22] studied the effects of bubble size, velocity and concentration on vertically flashing flow behind a constriction; they found that most bubbles occurred at a location with low static pressure. This produced a strong disturbance interaction between bubble growth and the main flow going downstream. Bubbly flow always shows up in boiling systems; bubble parameters (velocity, distribution density, size, void fraction and surface tension) have a significant influence on the flow field and also have complex impacts on the heat and mass transfer process [16,23]. Bubble dynamics and the induced turbulence are fundamental to understand quantity transportation in bubbly flow.
Numerical simulation (when compared with experimental methods) is a relatively cost-effective approach that is used to study bubbly flow mechanics. CFD is a powerful tool that is used in order to investigate flow field parameters [24]. Guan et al. [25] proposed a new drag model (the Local-Dual-Bubble-Size model) using the Energy-Minimization Multi-Scale approach and determined that the Local-Dual-Bubble-Size model produced good agreement with experimental data. Turbulence was produced by bubble mechanics including bubble deformation, bubble collision and forces acting on the bubble or gas–liquid interface (including buoyancy force, drag force, stress and drag force). It is difficult to experimentally study the effect of a single factor on the liquid turbulence; however, numerical simulation is an excellent method in order to determine the effect of a single factor. Feng and Bolotnov [26] evaluated the interaction between a single bubble and homogeneous turbulent flow using the direct numerical simulation (DNS) method; the effects of bubble deformability, turbulent intensity and slip velocity on liquid turbulence were investigated. Their results indicate that bubbles with large deformation produce large turbulence intensity enhancements. Yang et al. [27] numerically studied bubbly flow characteristics (for a bubble size range of 10~100 um) produced during a dissolved air flotation process. Zhou et al. [14] concluded that the bubbles enhance the liquid turbulence at a low void fraction and low inlet velocities; however, at high inlet velocities and high void fractions, bubbles reduce the liquid turbulence. Kawamura and Kodama [28] developed a new computational model in order to obtain the turbulence information in the vicinity of the gas–liquid interface induced by bubbles of different velocity and size. Chahine [29] numerically studied cavitation inception and development; they provide an estimate of the effect of air bubbles on the drag and lift for a lifting surface. Single bubble dynamics is a fundamental theory for understanding the effect of bubble cluster on liquid flow and energy transportation. Yi et al. [30] evaluated the effect of gravity on bubble dynamics and energy transportation in flow boiling processes. They indicated that low-gravity conditions reduced bubble formation and departure time; and the bubble departure radius is smaller than that found for standard-gravity conditions.
Although numerical simulation is a convenient method to study bubble dynamics and energy transport characteristics, it is difficult to model two-phase bubbly flow (taking into account phase interactions and the various effects for each bubble parameter). Bahreini et al. [31] used the coupled level set and volume of fraction (CLSVOF) method combined with open-source code (independently developed) in order to investigate the condensation behavior of single and multiple bubbles in sub-cooled flow boiling. Cédric et al. [32] showed that the choice of third-order numerical schemes for turbulent bubbly flow may result in significant errors; this is the result of using less stringent numerical definitions (i.e., solution scheme of unsteady and convective terms). By comparing several existing turbulent models, they recommended the RNG k-ε model for turbulent bubbly flow because the RNG k-ε model produces a better depiction of the turbulent dissipation rate and turbulent viscosity, but they did not discuss the k-omega model for dispersed bubble flow.
Bubbly flow is a complex phenomenon when compared with single-phase flow; the main subject of this research is to study the flow instability of a swarm flow of bubbles with different diameters, bubble generation frequency, bubble distribution and velocity in a two-dimensional contraction section. The author’s previous work indicated that the k-ω model has a better convergence and stability for multiphase flow. Thus, by using the volume of fraction method the gas–liquid interface was tracked and the standard k-ω turbulent model was applied to calculate the flow field. The surface tension effect was also considered and added in the momentum equation as a source term. As marked in Figure 1a, four points located at (1.5, 0.5), (1.5, 0.75), (1.5, 0.95) and (1.5, 1.2) were added using as velocity and void fraction probes in order to acquire the simultaneous flow information. To eliminate the reversed flow effect, a 0.4 m long extension was added at the outlet surface of the geometry model. The averaged surface velocity at x = 1.5 and for a volume fraction of the outlet surface was also calculated for a flow instability analysis. Finally, an experimental validation was conducted in a water tunnel to verify the simulation accuracy.
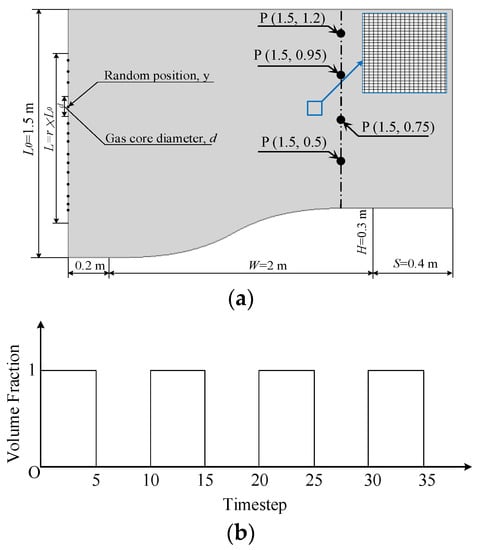
Figure 1.
Calculation model for CFD simulations. (a) Mesh and geometric parameters of the CFD model; (b) time-dependent control function of the bubble volume fraction.
2. Numerical Methodology
2.1. Computational Conditions
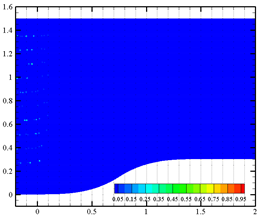
The computational domain shown in Figure 1 is a contraction section, with bi-cubic curve on the bottom surface. Geometry (height of 1.5 m and width of 2 m) and bubble generation region at the inlet surface are shown in Figure 1a. In order to reduce the inlet and outlet effect on the flow field, a 0.2 m and a 0.4 m extension was added to the inlet and outlet surface, respectively. The bubble generation region, L0 is limited at the central region of the inlet surface; the region factor, r is changed from 0.4 to 0.8 for different calculation cases (this determines the bubbly flow region along the mainstream). Note that bubble flow is always generated in a stream with no regularity, the divided positions (DIV = 10, 20, 40) of the bubble cores are within the bubble generation region and are generated by using a random function. The bubble diameter is controlled by adjusting the length of the gas core diameter, d, as displayed in Figure 1a; and the gas charging time, dt is kept the same (5 time-steps for all cases) for each bubble core after the random function is applied. As Figure 1b shows, the volume fraction of each bubble generation region is defined by a periodic function. In each period, the volume fraction of each bubble core region in the inlet surface is set as unity for the initial 5 time-steps; and set to zero for the latter 5 time-steps.
Figure 1a shows the inlet velocity boundary condition for constant temperature (Tc = 300 K) and pressure (Pc = 101.15 kPa). In developing the calculation model, the following conditions are considered: size of the small bubbles (treated as rigid bubbles); the incompressible ideal gas model is selected for the air density model; outflow boundary condition is then applied at the outlet surface; no slip condition is applied on both the top and bottom wall surfaces. Variables to study the flow instability characteristics of turbulent bubbly flow conditions include: inlet velocity, bubble generation region, bubble density and gas core diameter (resulting in different bubble diameter). Table 1 summarizes the calculation cases considered in this study and the detailed parameters for each simulation case are also listed.

Table 1.
Calculating cases under different simulation conditions.
2.2. Governing Equations
Gas–liquid bubbly flow was treated as incompressible flow for each case due to the incompressibility of the water flow and low velocity of the small/micro-size gas bubbles. The liquid water phase was selected as the primary phase and the bubble phase was treated as secondary phase. The VOF model tracked the movement of the volume and found the interface in an indirect way; this was used to model the bubbly flow and capture the phase interface in this study. FLUENT 17.2 was used to solve the governing equations of gas–liquid bubbly flow. Considering the water insolubility of air-bubbles, two-phase mass transfer was neglected at the phase interface. The continuity equation is given as,
Momentum equation solved throughout the domain is given as,
The void fraction of each cell is independent. The interface between the liquid-phase and gas phase can be determined by solving the void fraction transport equation as shown in Equation (3):
Then, the void fraction of the water phase is computed based on the following:
Note that the resulting velocity field is shared by both the water and gas phases; density and viscosity is independent for each cell. For the transport equations, Equations (1)–(4), the properties of each control volume are calculated by,
Phase interaction produced by surface tension and drag force was included as a source term in the momentum equation, Equation (2); the interphase force term, , is defined by Equation (7a). The continuum surface force (CSF) model proposed by Brackbill et al. [33] was adopted in this simulation, and the corresponding volume force term in Equation (2), , is defined as Equation (7b) with the drag force model discussed in Section 3.3.
Curvature, of the gas–liquid interface is calculated in terms of the divergence of the unit normal as shown in Equation (8):
The standard k-ω model is used for both the water and gas phases. Turbulence kinetic energy, k, and the specific dissipation rate, ω, can be calculated by solving the transport equations given in Equations (9) and (10):
where generation of turbulence kinetic energy, , due to the mean velocity gradient, and represents the generation of specific dissipation rate; and are the dissipation of k and ω due to turbulence, respectively; and are source terms of k and ω related to the interphase interactions. Effective diffusivity () for turbulence kinetic energy and the specific dissipation rate are determined by Equations (11a) and (11b):
where and are the turbulent Prandtl numbers for k and ω, respectively.
All flow cases of this study are under high Reynolds number (>105), and the turbulent viscosity, , can be calculated by combining k and ω as shown in Equation (12).
2.3. Solution Method
Gradients were evaluated by applying the Green–Gauss node method to ensure second-order spatial accuracy. Momentum (k and ω) transport equations were solved by using the SIMPLEC scheme to improve calculation convergence. PRESTO! and the Geo-Reconstruct scheme was adopted for the spatial discretization of pressure and volume. The transient term was discretized with a first-order implicit scheme; other terms in this model were discretized by using a second-order upwind method. Numerical results, including flow instability, void fraction, turbulence kinetic energy and bubble distribution, were recorded for each case.
3. Results and Discussion
Bubble-induced velocity fluctuation, turbulent characteristics and void fraction effects have been studied and discussed in this section. A set of parametric simulations on flow instability were performed with the calculating parameters for each case presented in Table 1. Velocity fluctuation was predicted by numerical simulation and compared with experimental measurements for bubbly flow. The numerical data were evaluated with Tecplot 360EX and the data graphs were plotted by using the software of Origin 8.2. Effects of bubble diameter, velocity, void fraction and bubble distribution on bubbly flow instability were discussed.
3.1. Comparison with Experimental Results
Figure 2 shows the measured instantaneous velocity results obtained by using an immersion hot film meter (dP100-1) in a water tunnel; these values are compared to CFD velocity predictions produced using by the same conditions. The velocity probe was installed in a bracket (as shown in Figure 2a) with data acquisition line at a point that was set 0.3 m in front of the bracket in order to eliminate any downstream effects that may have been caused by the supporting device. The hot film probe for water used (shown in Figure 2b) has an accuracy of ±0.2% of the full scale, 0~14 m s−1. Note that the discrepancies of bubble generation between numerical algorithm and the bubble-sowing device of the test system cannot be eliminated; both the filtering process of the experimental data acquisition system and the measurement accuracy of the hot film resulted in a velocity fluctuation difference between the experiment and the simulation. The calculated velocity using the CFD simulation yielded an amplitude of approximately 0.5% of the average velocity and for the hot film probe measurement it was 0.19%. Experimental time-averaged velocity values showed an acceptable consistent with CFD simulation results (See in Figure 2c); this indicates that the simulation model and the bubble generation method are reliable.
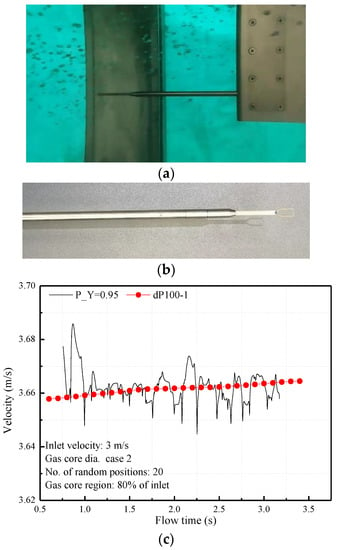
Figure 2.
Comparison of experimental data with simulation results: (a) test section of experimental apparatus, (b) hot film meter for water measurement, and (c) comparison of instantaneous velocity results (CFD simulation and experiment results).
3.2. Effect of Bubble Parameters on Flow Instability
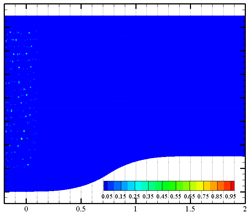
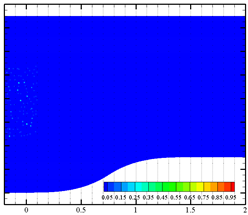
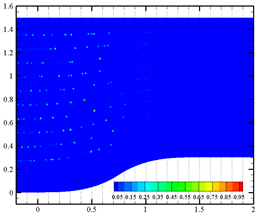
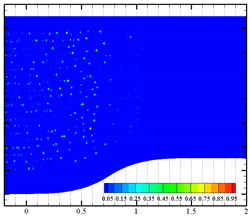
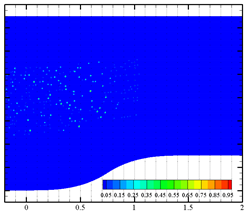
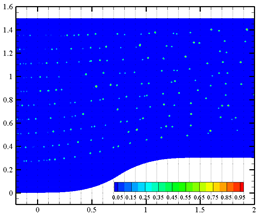
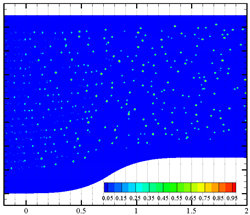
Effects of bubble cluster parameters (i.e., bubble diameter, bubble density, bubble distribution and bubble velocity) on liquid-phase velocity fluctuation are discussed in detail in this section. Nine different inlet boundary conditions were applied at the inlet surface with user-defined functions (UDFs). Four data-collecting probes (shown in Figure 1a) were set at coordinates of (1.5, 0.5), (1.5, 0.75), (1.5, 0.95) and (1.5, 1.2), respectively. Instantaneous velocity measurements from these probes and a surface-averaged velocity (at x = 1.5) were recorded every 20 time-steps. Fixed time-step size of 1 ms was used for all simulation cases. For case 1, case 3 and case 9, the sequence charts of the distribution of the dispersed bubble and void fraction are presented in Table 2. Bubble coalescence and bubble breaking-up phenomena are not observed. Thus, the bubble deformation in water is the main factor affecting the liquid velocity.

Table 2.
Phase distribution in the contraction section under three different flow parameters.
Figure 3 presents the results of velocity fluctuation caused by variation in bubble size. Calculated air bubble diameter for each case is listed in Table 1. All bubbles are regulated at the y-coordinate from 0.15 to 1.35; all other bubble parameters and flow variables are kept the same. Bubble diameters for Figure 3a, Figure 3b,c are 2.76, 3.91 and 5.53 mm, respectively. For fully developed flow (time > 1.5 s) the mean magnitude of the liquid velocity fluctuation (as shown in Figure 4) is 2.01% (diameter 2.76 mm), 2.44% (diameter 3.91 mm) and 4.84% (diameter 5.53 mm), indicating that the intensity of the disturbance in dispersed bubbly flow increases with increasing bubble diameter. For all three cases, the magnitude of velocity fluctuation at (1.5, 0.5) and (1.5, 1.2) is obviously larger than the other two locations; this is mainly explained by the fact that bubbles are absence in the vicinity of the wall region offsetting the liquid–bubble interaction.
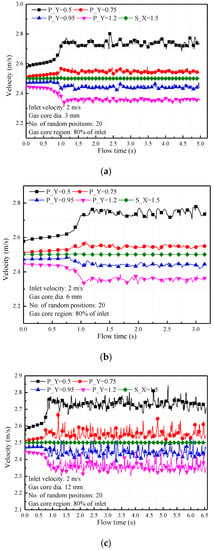
Figure 3.
Instantaneous velocity at four locations [(1.5, 0.5), (1.5, 0.75), (1.5, 0.95), and (1.5, 1.2)] and an average surface velocity measured at x = 1.5 m. Effects of bubble diameter on bubble–liquid flow velocity fluctuation, with gas charging length, d, of (a) 3, (b) 6, and (c) 12 mm, and the corresponding generated bubble size was 2.76, 3.91 and 5.53 mm, respectively.
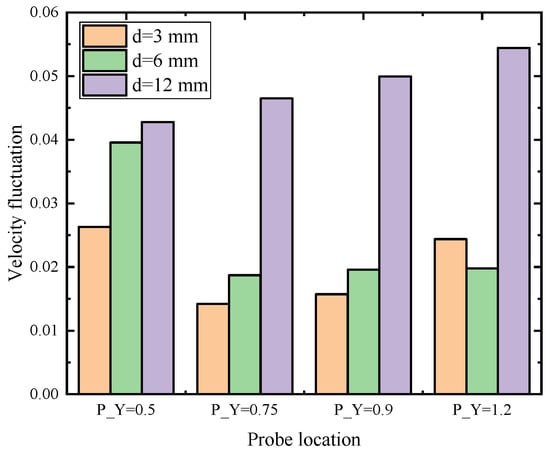
Figure 4.
Magnitude of velocity fluctuation with different gas charging length: d1 = 3, d2 = 6 and d3 = 12 mm, resulting bubble diameter of 2.76, 3.91 and 5.53 mm, respectively.
Figure 5 illustrates the effect of bubble density on the liquid velocity fluctuation. To avoid bubble coalescence and maintain dispersed bubble distribution, three types of bubble distribution (DIV = 10, DIV = 20 and DIV = 40) are selected for the simulation. The bubble generation region (L), bubble diameter and inlet velocity are kept constant; cases varied in the gas core number (DIV). Sparsely distributed bubbles seem to have a larger impact on liquid velocity and the bubble cluster produces a more stable velocity; this is illustrated in the instantaneous velocity results [see Figure 5a–d] at several locations. In Figure 6, bubbly flow with sparse bubbles (low density) is shown to have a larger liquid fluctuation than is found with a high-density of dispersed bubbles. Additionally, the central zone produces a better distribution than is found in the transition region between bubble cluster and liquid flow.
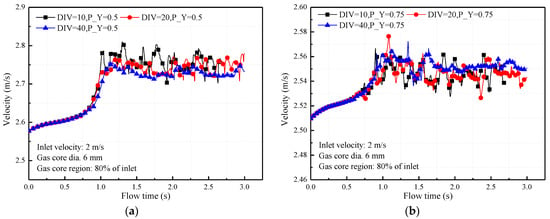
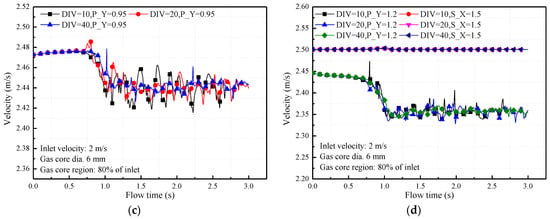
Figure 5.
Effect of bubble density on bubble–liquid flow instability with random bubble infused positions (DIV of 10, 20 and 40). Surface-averaged velocity of bubble–liquid flow was monitored at (x, y) coordinates of (a) (1.5, 0.5) for P_Y = 0.5; (b) (1.5, 0.75) for P_Y = 0.75; (c) (1.5, 0.95) for P_Y = 0.95; (d) (1.5, 1.2) for P_Y = 1.2 and S_X = 1.5.
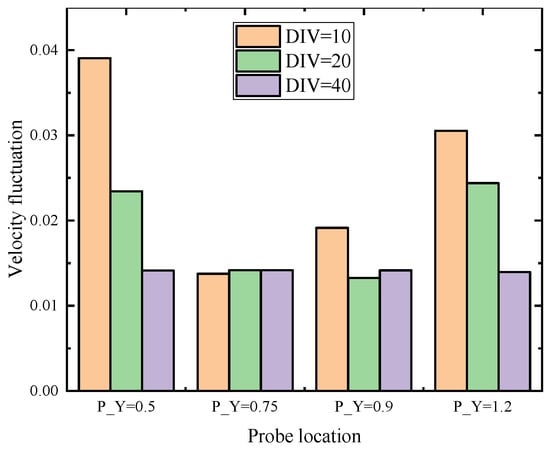
Figure 6.
Magnitude of velocity fluctuation under different bubble density which is characterized by dividing bubbly flow region (inlet surface) into different random positions: DIV = 10, DIV = 20 and DIV = 40, respectively.
To better understand this issue, the bubbly flow region is varied by changing the boundary of the bubble cluster and the bubble region length is defined by using a distribution factor, r = L/L0. Consider r = 0.4, points (1.5, 0.5) and (1.5, 1.2) are located out of the bottom boundary of the bubble cluster at the contraction outlet (see Table 2). For r = 0.6, point (1.5, 0.5) is near the bubble cluster and at point (1.5, 1.2) is located at the boundary region. For r = 0.8, all points are located in the bubbly flow region. Note that the bubble density is maintained at DIV = 20 for each case. As can be seen in the simulation results (see Figure 7 and Figure 8) for locations located out of the bubbly flow region, small velocity fluctuations were detected for simulation conditions at r = 0.4 and r = 0.6; for locations in the bubble cluster, much higher velocity fluctuations are found. It can be concluded that the transition region produces a higher velocity fluctuation than that in a pure liquid region or in the fully developed bubbly flow region. This indicates that the manipulated bubbly flow can be utilized to enhance the flow mixing strength in the vicinity of the boundary region.
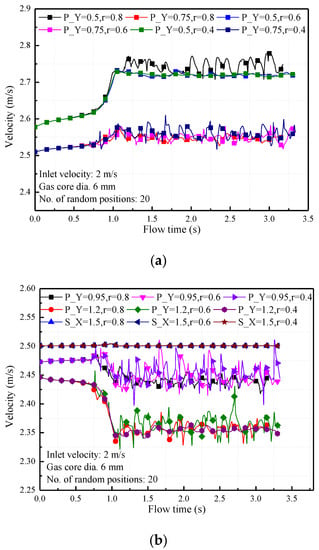
Figure 7.
Comparison of velocity fluctuation of the gas–liquid bubbly flow for different central distribution factors, r with given values of 0.4, 0.6 and 0.8. Data were monitored at (x, y) coordinate of (a) (1.5, 0.5) for P_Y = 0.5 and (1.5, 0.75) for P_Y = 0.75, (b) (1.5, 0.95) for P_Y = 0.95, (1.5, 1.2) for P_Y = 1.2, and S_X = 1.5 presents the surface-averaged velocity of bubble–liquid flow.
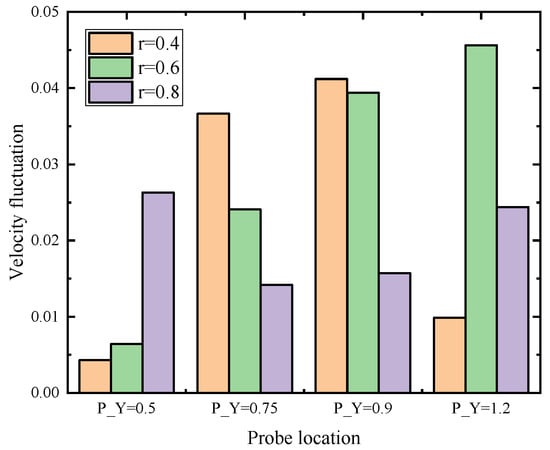
Figure 8.
Magnitude of velocity fluctuation under different bubble distribution, which means bubble swarm is limited with different spatial concentration characterized by distribution factor, r = L/L0.
The effect of bubble velocity on bubbly flow instability is shown in Figure 9 and Figure 10. Simulation results reveal that the fluctuation of liquid velocity increases with decreasing bubble velocity. Buoyance force acting on the bubbles dominate the bubble motion and it leads to an intense turbulent mixing throughout the bubbly flow region. Convection in the vicinity of each bubble also results in a strong liquid velocity fluctuation for the low bubble velocity case. The change in the direction of velocity near the gas–liquid interface during the bubble rising driven by the buoyancy lift is the main reason that produces the local flow disturbance. At higher-velocity conditions, bubble-induced fluctuation decreases remarkably due to the fact that the drag force becomes the dominant force driving the bubble forward.
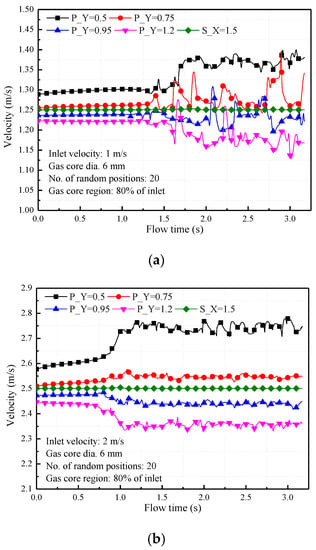
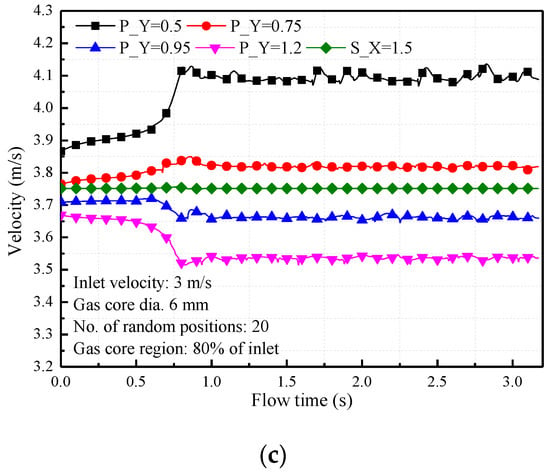
Figure 9.
Effect of the inlet gas–liquid bubbly velocity on flow instability for various inlet velocities: (a) inlet velocity, v = 1 m s−1; (b) inlet velocity, v = 2 m s−1; (c) inlet velocity, v = 3 m s−1.
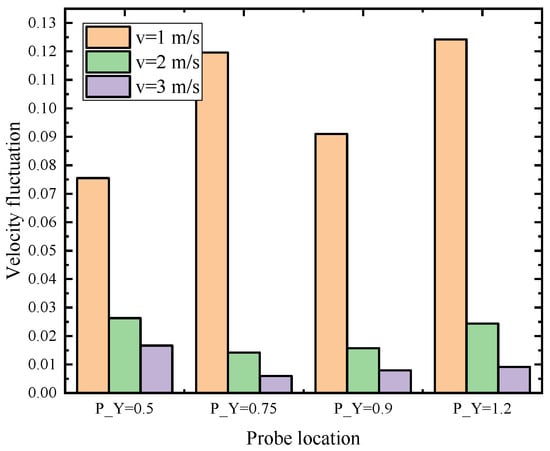
Figure 10.
Magnitude of velocity fluctuation under different initial bubble velocity.
Bubble diameter, bubble density, bubble distribution and bubble velocity have a significant influence on liquid velocity fluctuation. For dispersed bubbly flow, the bubble interactions can be neglected; however, bubble deformation and the forces that act on the bubble are the principal factors that affect the flow field in the vicinity of each bubble. The following sections provide an in-depth understanding of bubble-induced velocity instability.
3.3. Bubble-Induced Turbulence
As previously discussed, turbulence kinetic energy generated from the relative motion between the liquid-phase and the dispersed bubbles is related to the forces acting on the bubble (i.e., buoyancy lift, inertia force and drag force) and is included in the transport equation as a source term. The interphase force models included in these simulation cases are included by using UDFs. Additionally, surface tension and drag force are considered as source terms added to the transport equation. Drag force acting on the bubbles is the dominant force at high Reynolds number flow; this might be orders of magnitude larger than other forces. The drag force model (as showed in Equation (12)) proposed by Ishii and Zuber [34] is adopted as a result of its feasibility to handle dispersed sphere bubbly flow.
Figure 11a–i show the relations of predicted turbulence kinetic energy and void fraction at location (1.5, 0.75) for all the cases (conditions detailed in Table 1). The instantaneous void fraction is plotted to demonstrate a clear understanding of bubble effect on liquid velocity. For the void fraction curve, each peak value indicates a bubble or bubble boundary flows that passes the probe. It is obvious that for each case, turbulence kinetic energy reaches a peak value when the local void fraction increases. Note that bubbly flow with higher bubble density or larger bubble size has a higher probability to affect the void fraction at the data point; this indicates a stronger turbulence and velocity fluctuation (as shown in case 3, case 8 and case 9). Similar results are also reported by Erdogan et al. [35] and Shu et al. [36]. Additionally, another phenomenon is shown; turbulence kinetic energy increases while the void fraction remains zero. This type of turbulence increase is mainly induced by the turbulence diffusion when the dispersed bubbles flow through/near the probe location.
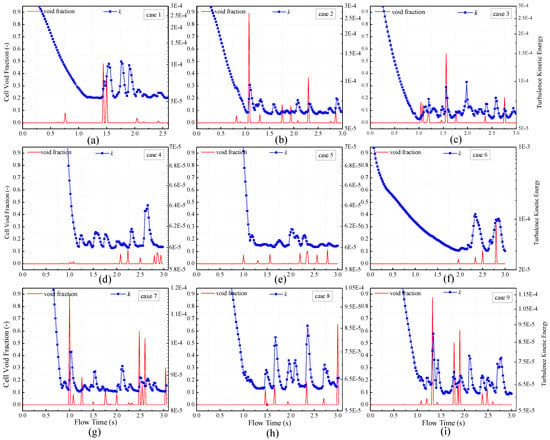
Figure 11.
Bubble effect on turbulence kinetic energy under different dispersed bubble flow conditions (Cases 1–9), seen in Table 1.
3.4. Bulk Void Fraction
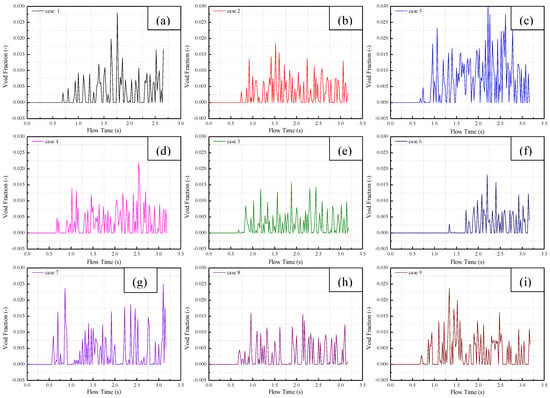
Figure 12a–i shows void fraction (averaged) values at the outlet surface for different dispersed bubbly flow parameters. It is shown that the void fraction fluctuated acutely with time and the peak value is always smaller than 2.5% (except for case 1 and case 3); indicating that bubbly flow (with large bubble diameter) has a relatively large void fraction. It is noted that bubble positions at the inlet surface are located randomly and the bubbles are generated synchronously. Thus, the fluctuation of void fraction (surface averaged) is mainly caused by the fact that some bubbles merged at the stage of bubble generation because the close bubble core is generated; additionally, the bubble distribution is redistributed to flow through the contracting section. It is reasonable to propose that the flow with tiny dispersed bubbles can have a considerable disturbance effect; this is important to understand when enhancing heat and mass transfer near the surface wall or in the boundary layer.
As indicated in Figure 11, the existence of bubble and bubble parameters can have a significant influence on flow instability. Therefore, the void fraction of the domain is an important variable to understand. Figure 13 presents the result of the volume averaged void fraction for various cases that have been simulated. In all cases, the bulk void fraction increases with flow time and levels out as the balance between bubbles generated at inlet and bubbles exiting the outlet is achieved. For Cases 1, 2 and 5, the number of the bubble core is set as a variable; Cases 2, 3 and 4 have different bubble diameters. It can be concluded that the bulk void fraction increases with increasing bubble number and bubble diameter; additionally, velocity and the bubble generation region have a small effect on the bulk void fraction. As Figure 13 shows, the bulk void fraction of the calculating domain is smaller than 0.5%; except for case 3 which has a maximum bubble diameter of 5.53 mm. Unlike the results of the surface-averaged void fraction shown in Figure 12, the bulk void fraction of the domain reaches a relatively steady condition after steady bubbly flow is achieved.
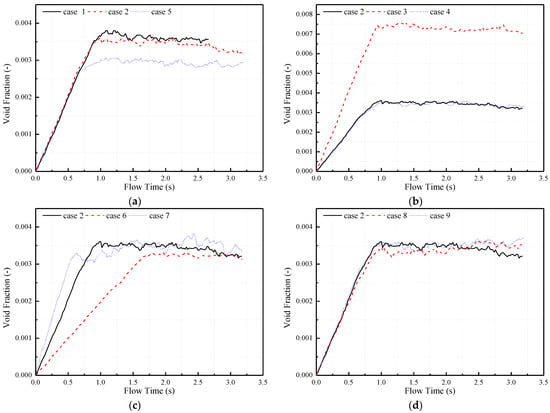
Figure 13.
Effect of gas–liquid bubbly flow parameters on domain void fraction: (a) bubble density, (b) bubble diameter, (c) inlet velocity, and (d) bubble distribution.
4. Conclusions
A comprehensive study on bubble-induced flow instability for dispersed bubbly flow was performed; this is important to understand for various hydrodynamic applications (i.e., bubble floatation, flow drag reduction and two-phase flow, etc.). This was studied by introducing the bubble generation function as a boundary condition; surface tension and the bubble-induced turbulence were implemented in the simulation model by using user-defined functions. This model allowed the effects of the bubble generation region, bubble distribution, bubble velocity and bubble diameter of bubbly flow instability to be evaluated and understood. Based on the performed simulations, the following conclusions can be obtained.
- (1)
- The presence of bubbles dramatically influences the velocity field and turbulence kinetic energy. The magnitude of velocity fluctuation increases with increasing bubble diameter; this is especially important for low-velocity flow conditions.
- (2)
- For bubble swarm with a concentrated distribution, velocity fluctuation is much higher in the central zone when compared to in the boundary region. However, when considering bubble swarm with sparse distribution, a contrary phenomenon is observed.
- (3)
- Bubble-induced turbulence disturbs the velocity boundary layer near the boundary wall; this will potentially result in enhancing heat and mass transfer by introducing overheating micro-bubbles.
- (4)
- An analysis was performed on dispersed bubbly flow and this is helpful in understanding bubble floatation, which is important in various engineering applications. Foundations in this work can be used as guidance and extended for the design of drag-reduction characteristics of submerged moving objects under dispersed, small/micro, bubbly flow conditions.
Author Contributions
J.C., methodology, experiment, and writing—original manuscript. W.L., validation and writing—review and editing. C.F., funding acquisition and supervision. J.Z., formal analysis. D.J.K., writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China, grant number [52106215, 52106097].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The computing resource and experimental instruments were supported by the National Science Foundation of China [52106215, 52106097].
Conflicts of Interest
The authors do not have any actual and potential conflict of interest with works and organizations described in this paper.
Nomenclature
| Cd | drag coefficient |
| DIV | number of bubble cores |
| d | gas core diameter, m |
| g | gravity acceleration, m s−2 |
| k | turbulence kinetic energy, m2 s−2 |
| L0 | length scale of inlet, m |
| L | length scale of bubble region, m |
| p | pressure, Pa |
| Pr | Prandtl number |
| r | region factor, r = L/L0 |
| Re | Reynolds number |
| T | temperature, K |
| t | Solution time, s |
| v | averaged velocity, m s−1 |
| vg | gas phase velocity, m s−1 |
| Greek symbols | |
| αg | volume fraction of gas phase |
| αw | volume fraction of water phase |
| μ | viscosity, Pa s |
| μt | turbulent viscosity, Pa s |
| ρ | mean density, kg m−3 |
| ω | specific dissipation rate |
| κ | curvature, m−1 |
| ∇ | partial differential operator |
| Γ | effective diffusivity |
| Subscripts | |
| csf | continuum surface force model |
| drag | drag force |
| w | water phase |
| g | gas phase |
References
- Tahir, W.; Althobaiti, N.; Kousar, N.; Alhazmi, S.E.; Bilal, S.; Riaz, A. Effects of Homogeneous-Heterogeneous Reactions on Maxwell Ferrofluid in the Presence of Magnetic Dipole Along a Stretching Surface: A Numerical Approach. Math. Probl. Eng. 2022, 8, 4148401. [Google Scholar] [CrossRef]
- Chen, P.; Cui, B.; Li, J.; Zheng, J.; Zhao, Y. Particle Erosion under Multiphase Bubble Flow in Horizontal-Vertical-Upward Elbows. Powder Technol. 2022, 397, 117002. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Malik, F.; Khan, L.; Ghaffari, A.; Riaz, A.; Nisar, K. Sooppy Impact of Induced Magnetic Field on Thermal Enhancement in Gravity Driven Fe3O4 Ferrofluid Flow through Vertical Non-Isothermal Surface. Results Phys. 2020, 19, 103472. [Google Scholar] [CrossRef]
- Ijaz, N.; Riaz, A.; Zeeshan, A.; Ellahi, R.; Sait, S.M. Buoyancy Driven Flow with Gas-Liquid Coatings of Peristaltic Bubbly Flow in Elastic Walls. Coatings 2020, 10, 115. [Google Scholar] [CrossRef] [Green Version]
- Cheng, F.; Ji, W.; Qian, C.; Xu, J. Cavitation bubbles dynamics and cavitation erosion in water jet. Results Phys. 2018, 9, 1585–1593. [Google Scholar] [CrossRef]
- Oliveira, W.D.; Paula, I.D.; Martins, F.; Farias, P.; Azevedo, L. Bubble characterization in horizontal air–water intermittent flow. Int. J. Multiph. Flow 2015, 69, 18–30. [Google Scholar] [CrossRef]
- Orvalho, S.; Ruzicka, M.C.; Olivieri, G.; Marzocchella, A. Bubble coalescence: Effect of bubble approach velocity and liquid viscosity. Chem. Eng. Sci. 2015, 134, 205–216. [Google Scholar] [CrossRef]
- Sohn, S.; Baek, S. Bubble merger and scaling law of the Rayleigh–Taylor instability with surface tension. Phys. Lett. A 2017, 16, 3812–3817. [Google Scholar] [CrossRef]
- Sanada, T.; Sugihara, K.; Shirota, M.; Watanabe, M. Motion and drag of a single bubble in super-purified water. Fluid Dyn. Res. 2008, 40, 534–545. [Google Scholar] [CrossRef]
- Pang, M.; Wei, J.; Bo, Y.; Kawaguchi, Y. Numerical Investigation on Turbulence and Bubbles Distribution in Bubbly Flow under Normal Gravity and Microgravity Conditions. Microgravity Sci. Technol. 2010, 22, 283–294. [Google Scholar] [CrossRef]
- Chen, T.; Mu, Z.; Huang, B.; Zhang, M.; Wang, G. Dynamic Instability Analysis of Cavitating Flow with Liquid Nitrogen in a Converging–Diverging Nozzle. Appl. Therm. Eng. 2021, 192, 116870. [Google Scholar] [CrossRef]
- Li, G.B.; Wang, Y.R.; Xiao, L.M. Instability of an annular liquid sheet exposed to compressible gas flows. Int. J. Multiph. Flow 2019, 119, 72–83. [Google Scholar] [CrossRef]
- Yang, M.; Lian, C.Y.; Fan, L.S.; Lee, D.J. On the second-order moment turbulence model for simulating a bubble column. Chem. Eng. Sci. 2002, 57, 3269–3281. [Google Scholar]
- Zhou, L.; Li, R.; Du, R. Numerical simulation of the effect of void fraction and inlet velocity on two-phase turbulence in bubble-liquid flows. Acta Mech. Sin. 2006, 22, 425–432. [Google Scholar] [CrossRef]
- Li, W. Two-phase heat transfer correlations in three-dimensional hierarchical tube. Int. J. Heat Mass Transf. 2022, 191, 122827. [Google Scholar] [CrossRef]
- Kawahara, A.; Sadatomi, M.; Nei, K.; Matsuo, H. Experimental study on bubble velocity, void fraction and pressure drop for gas—Liquid two-phase flow in a circular microchannel. Int. J. Heat Fluid Flow 2009, 30, 831–841. [Google Scholar] [CrossRef]
- Peters, F.; Els, C. An experimental study on slow and fast bubbles in tap water. Chem. Eng. Sci. 2012, 82, 194–199. [Google Scholar] [CrossRef]
- Ji, H.; Chang, Y.; Huang, Z.; Wang, B.; Li, H. A new contactless impedance sensor for void fraction measurement of gas—Liquid two-phase flow. Meas. Sci. Technol. 2016, 27, 124001. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, X.; Liu, Y. Liquid-phase turbulence measurements in air-water two-phase flows over a wide range of void fractions. Nucl. Eng. Des. 2016, 310, 534–543. [Google Scholar] [CrossRef]
- Rivera, Y.; Muoz-Cobo, J.L.; Cuadros, J.L.; Berna, C.; Escrivá, A. Experimental study of the effects produced by the changes of the liquid and gas superficial velocities and the surface tension on the interfacial waves and the film thickness in annular concurrent upward vertical flows. Exp. Therm. Fluid Sci. 2021, 120, 110224. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Wang, L.; Mao, H.; Ma, Y.; Xie, F. Experimental investigation on two-phase flow instabilities in long-distance transportation of liquid oxygen. Cryogenics 2019, 102, 56–64. [Google Scholar] [CrossRef]
- Domnick, J.; Durst, F. Measurement of bubble size, velocity and concentration in flashing flow behind a sudden constriction. Int. J. Multiph. Flow 1995, 21, 1047–1062. [Google Scholar] [CrossRef]
- Al-Yahia, O.S.; Yoon, H.J.; Jo, D. Experimental study of bubble flow behavior during flow instability under uniform and non-uniform transverse heat distribution. Nucl. Eng. Technol. 2020, 52, 2771–2788. [Google Scholar] [CrossRef]
- Sokolichin, A.; Eigenberger, G. Applicability of the standard κ-ε turbulence model to the dynamic simulation of bubble columns: Part I. Detailed numerical simulations. Chem. Eng. Sci. 1999, 54, 2273–2284. [Google Scholar] [CrossRef]
- Xgab, C.; Ning, Y. CFD simulation of bubble column hydrodynamics with a novel drag model based on EMMS approach—ScienceDirect. Chem. Eng. Sci. 2021, 243, 116758. [Google Scholar]
- Feng, J.; Bolotnov, I.A. Evaluation of bubble-induced turbulence using direct numerical simulation. Int. J. Multiph. Flow 2017, 93, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Pozo, D.; Torfs, E.; Rehman, U.; Nopens, I. Numerical simulation on the effects of bubble size and internal structure on flow behavior in a DAF tank: A comparative study of CFD and CFD-PBM approach. Chem. Eng. J. Adv. 2021, 7, 100131. [Google Scholar] [CrossRef]
- Kawamura, T.; Kodama, Y. Numerical simulation method to resolve interactions between bubbles and turbulence. Int. J. Heat Fluid Flow 2002, 23, 627–638. [Google Scholar] [CrossRef]
- Chahine, G.L. Numerical simulation of bubble flow interactions. J. Hydrodyn. Ser. B 2009, 21, 316–332. [Google Scholar] [CrossRef]
- Yi, T.; Chu, X.; Wang, B.; Wu, J.; Yang, G. Numerical simulation of single bubble evolution in low gravity with fluctuation. Int. Commun. Heat Mass Transf. 2022, 130, 105828. [Google Scholar] [CrossRef]
- Bahreini, M.; Derakhshandeh, J.F.; Ramiar, A.; Dabirian, E. Numerical study on multiple bubbles condensation in subcooled boiling flow based on CLSVOF method—ScienceDirect. Int. J. Therm. Sci. 2021, 170, 107121. [Google Scholar] [CrossRef]
- Laborde-Boutet, C.; Larachi, F.; Dromard, N.; Delsart, O.; Schweich, D. CFD simulation of bubble column flows: Investigations on turbulence models in RANS approach. Chem. Eng. Sci. 2009, 64, 4399–4413. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 2010, 25, 638–651. [Google Scholar] [CrossRef]
- Erdogan, S.; Schulenberg, T.; Deutschmann, O.; Wörner, M. Evaluation of models for bubble-induced turbulence by DNS and utilization in two-fluid model computations of an industrial pilot-scale bubble column. Chem. Eng. Res. Des. 2021, 175, 283–295. [Google Scholar] [CrossRef]
- Shu, S.; Bahraoui, N.E.; Bertrand, F.; Chaouki, J. A bubble-induced turbulence model for gas-liquid bubbly flows in airlift columns, pipes and bubble columns. Chem. Eng. Sci. 2020, 6, 227–238. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).