Active and Passive Defense Strategies of Cyber-Physical Power System against Cyber Attacks Considering Node Vulnerability
Abstract
:1. Introduction
1.1. Vulnerability Assessment
1.2. Defense Strategy
2. Vulnerability Analysis
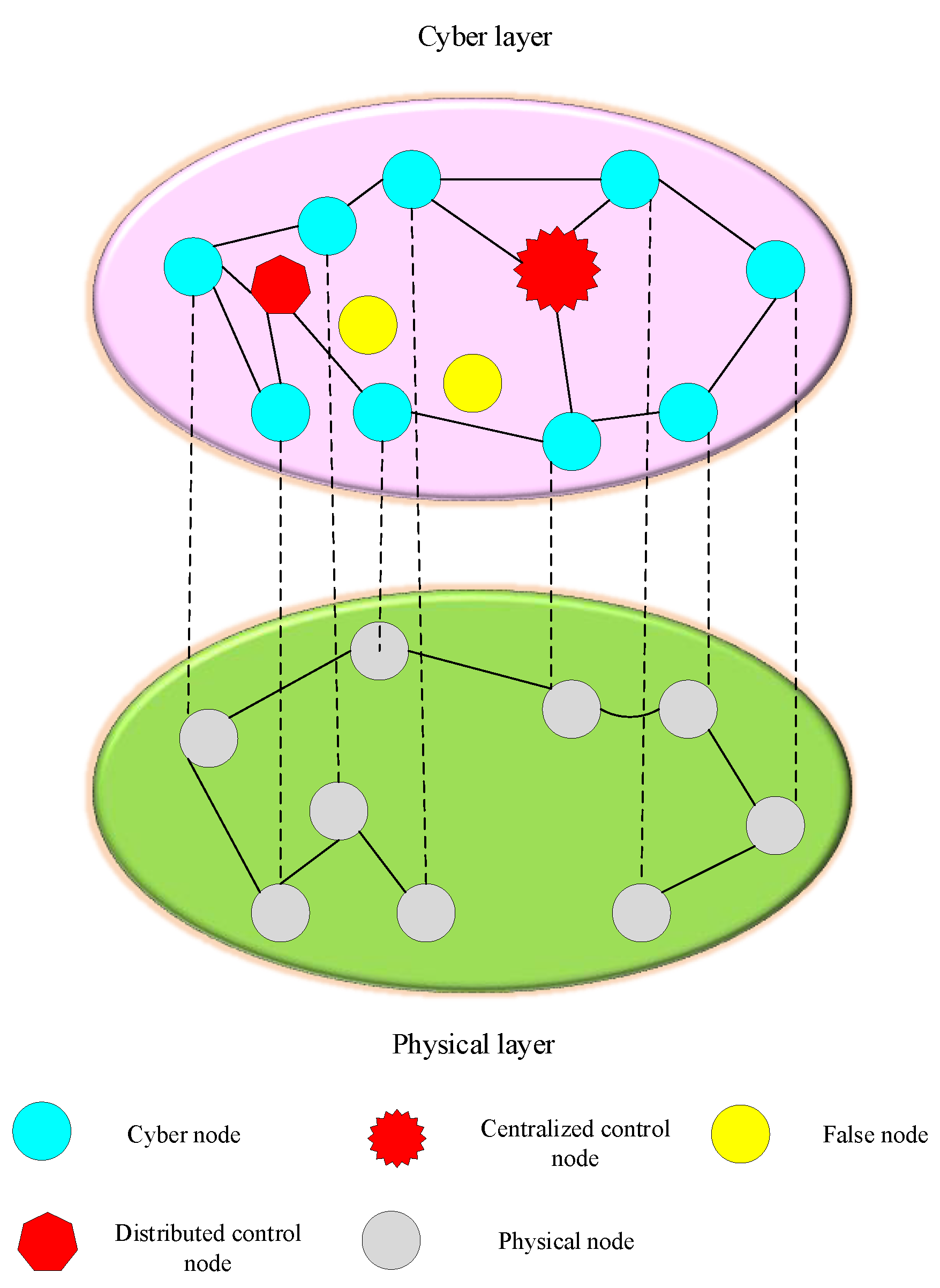
2.1. Cyber Physical System Model
- •
- Degree distribution
- •
- Clustering coefficient
- •
- Modular Q
2.2. Phisical Characteristic Index
2.3. Topology Structure Index
2.4. Comprehensive Vulnerability Index
3. Active and Passive Defense Strategies
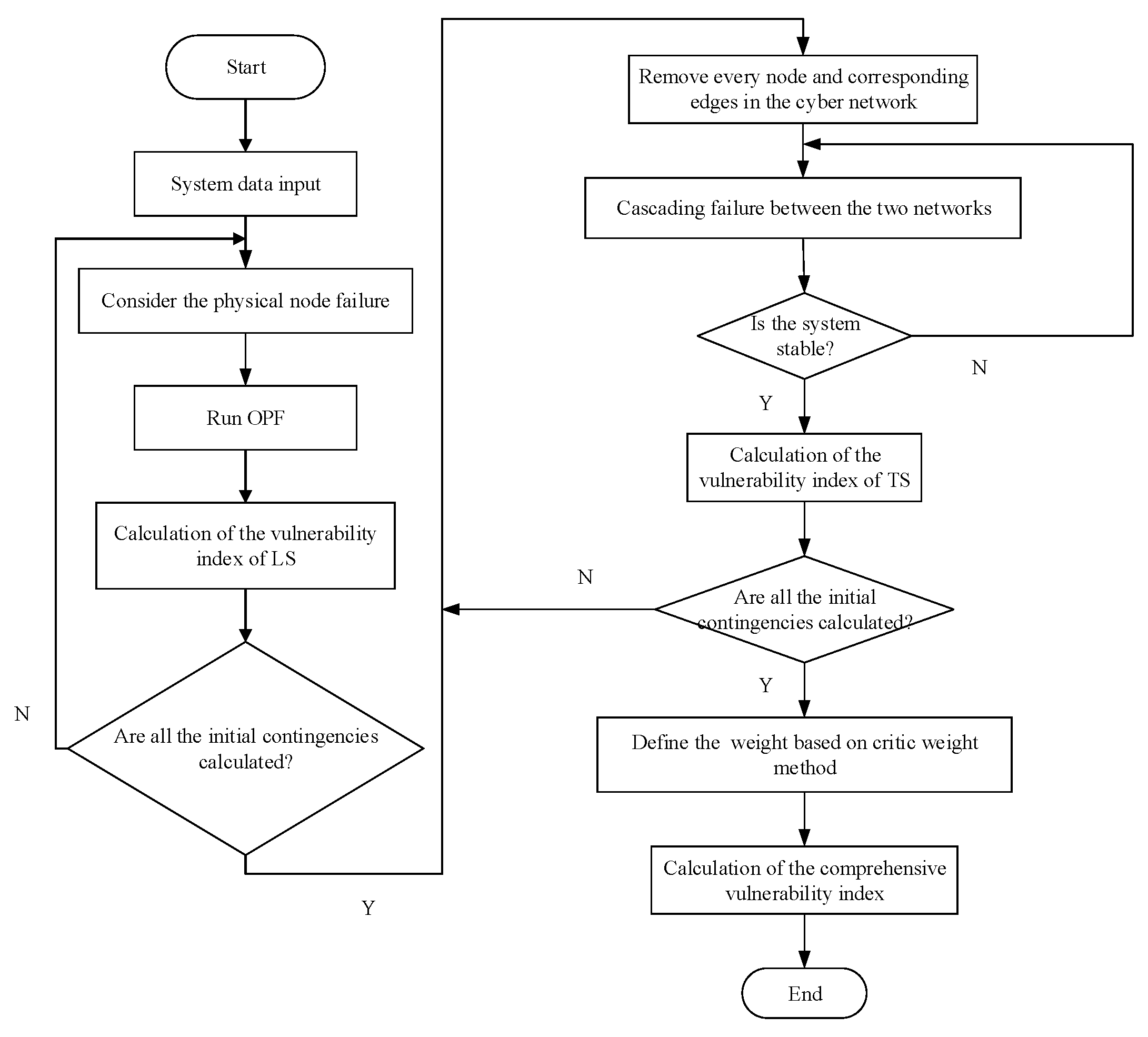
3.1. Active Defense Strategy Based on Vulnerability Assessment
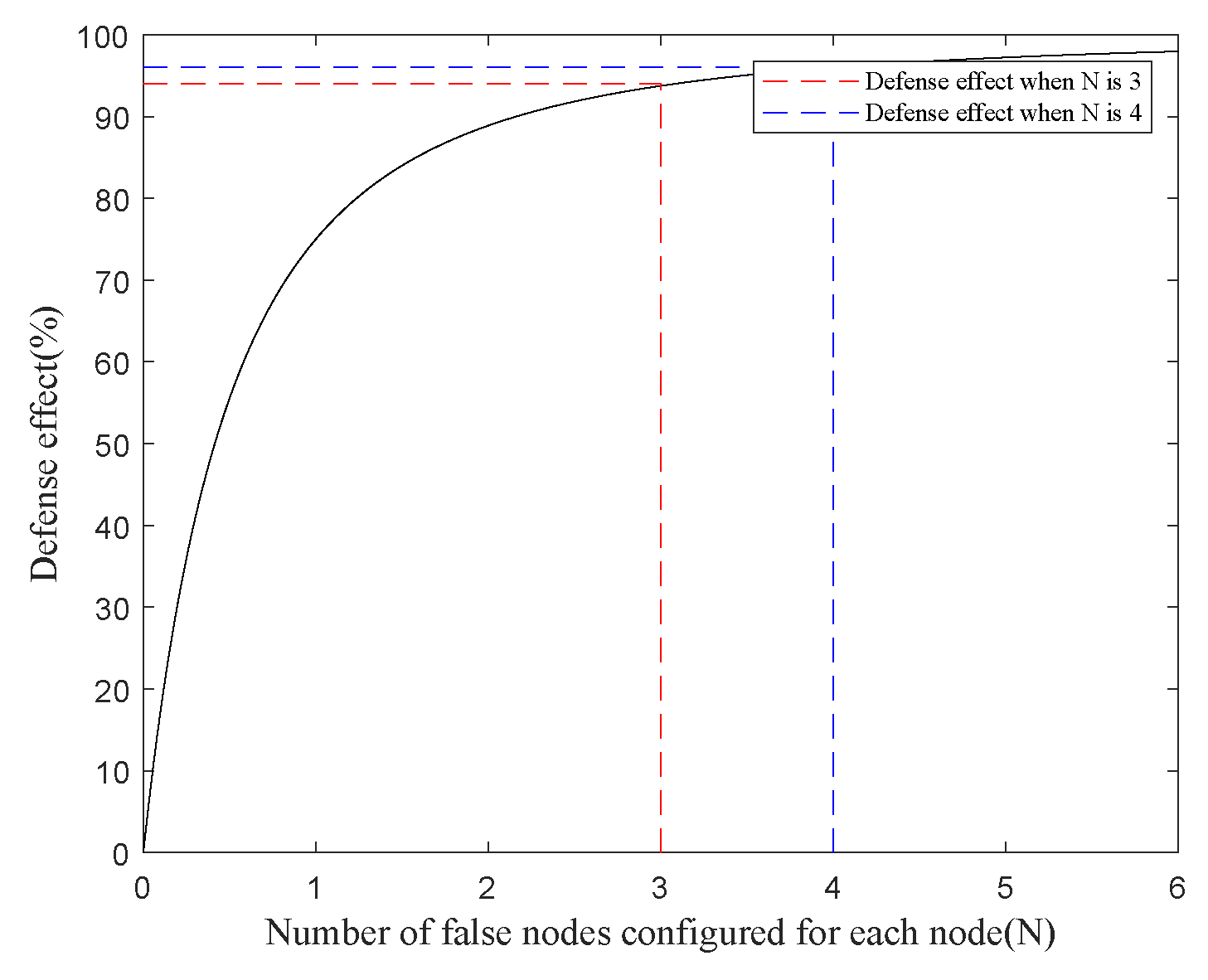
3.2. Passive Defense Strategy
4. Case Study and Discussion
4.1. Scale-Free (SF) Network
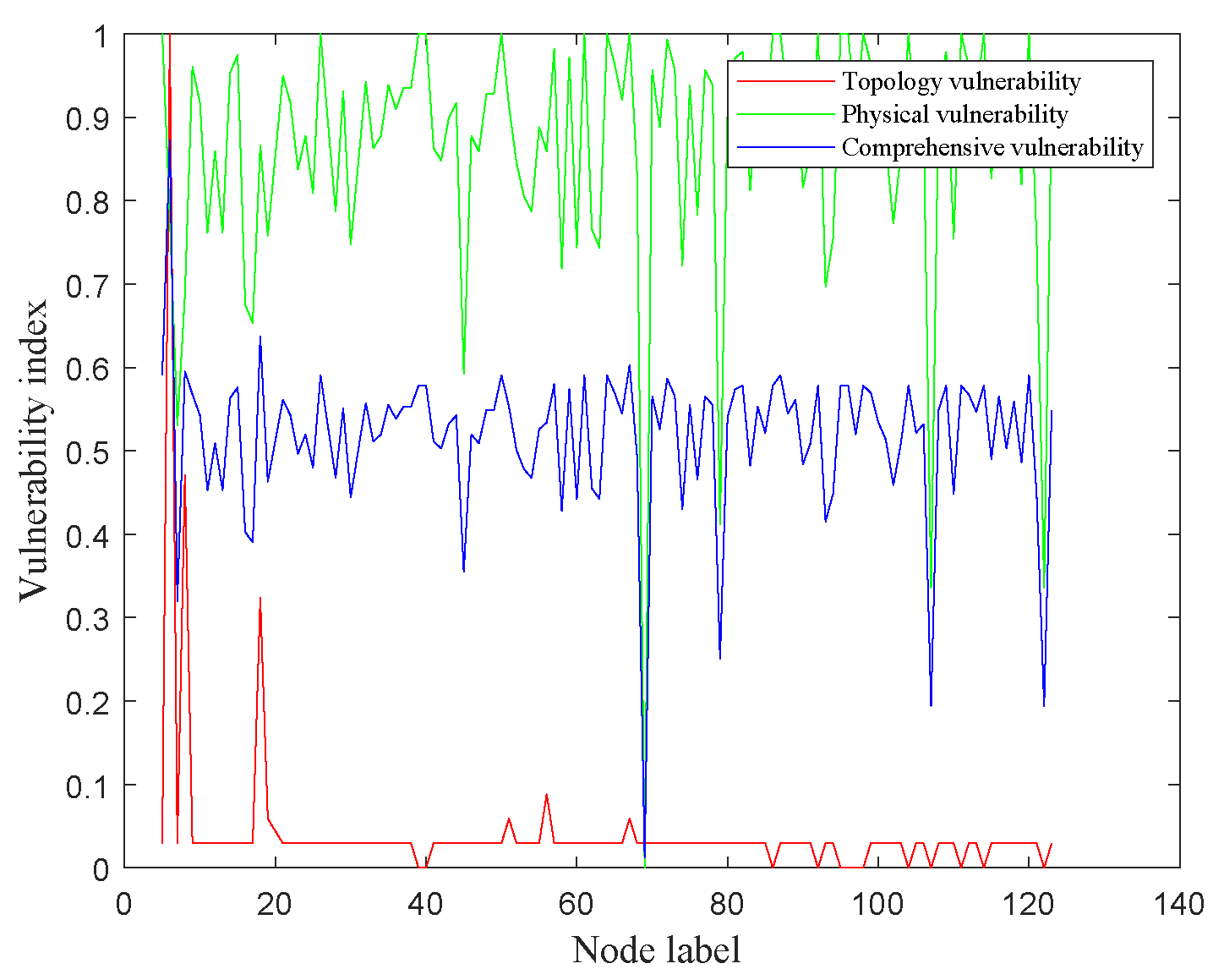
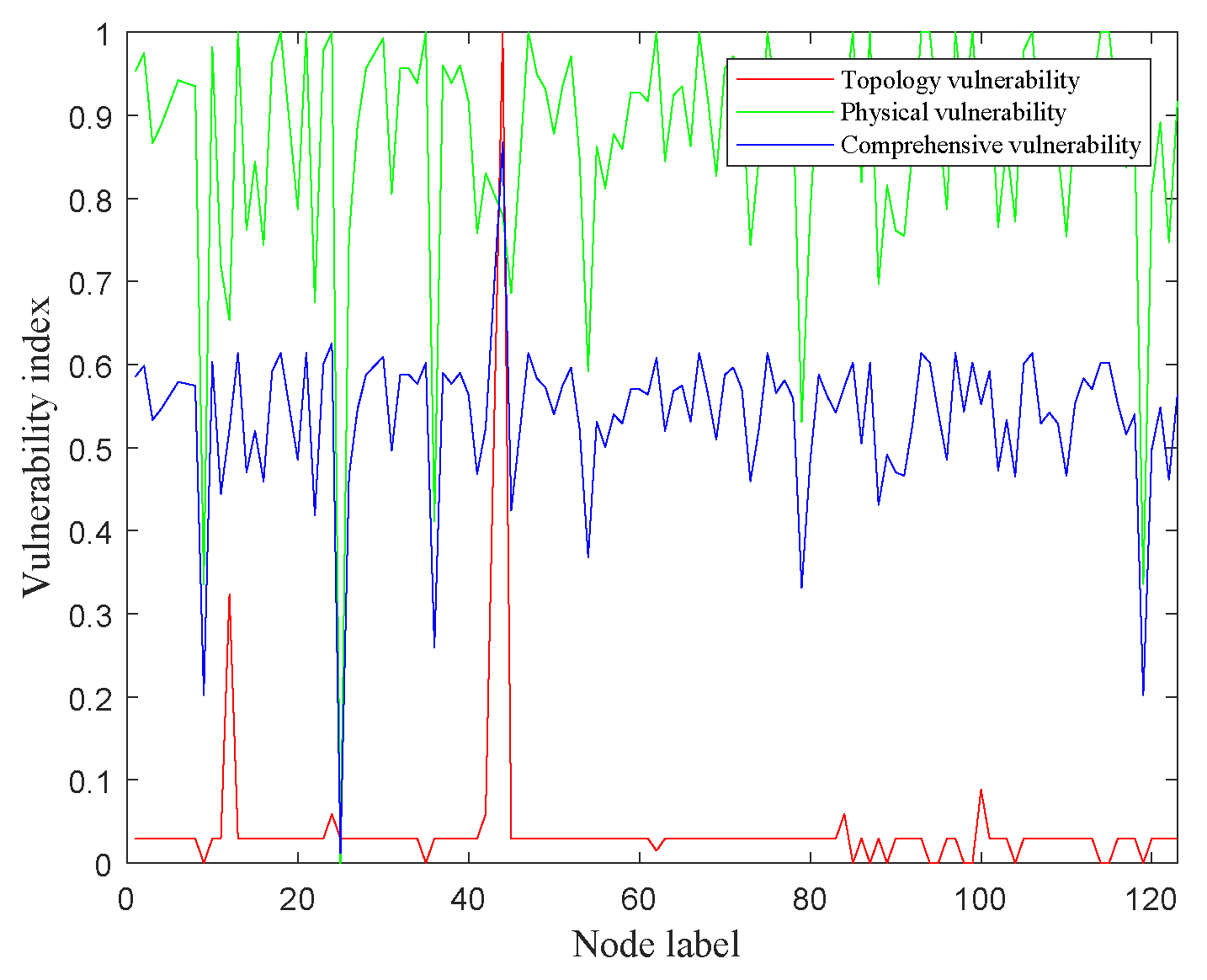
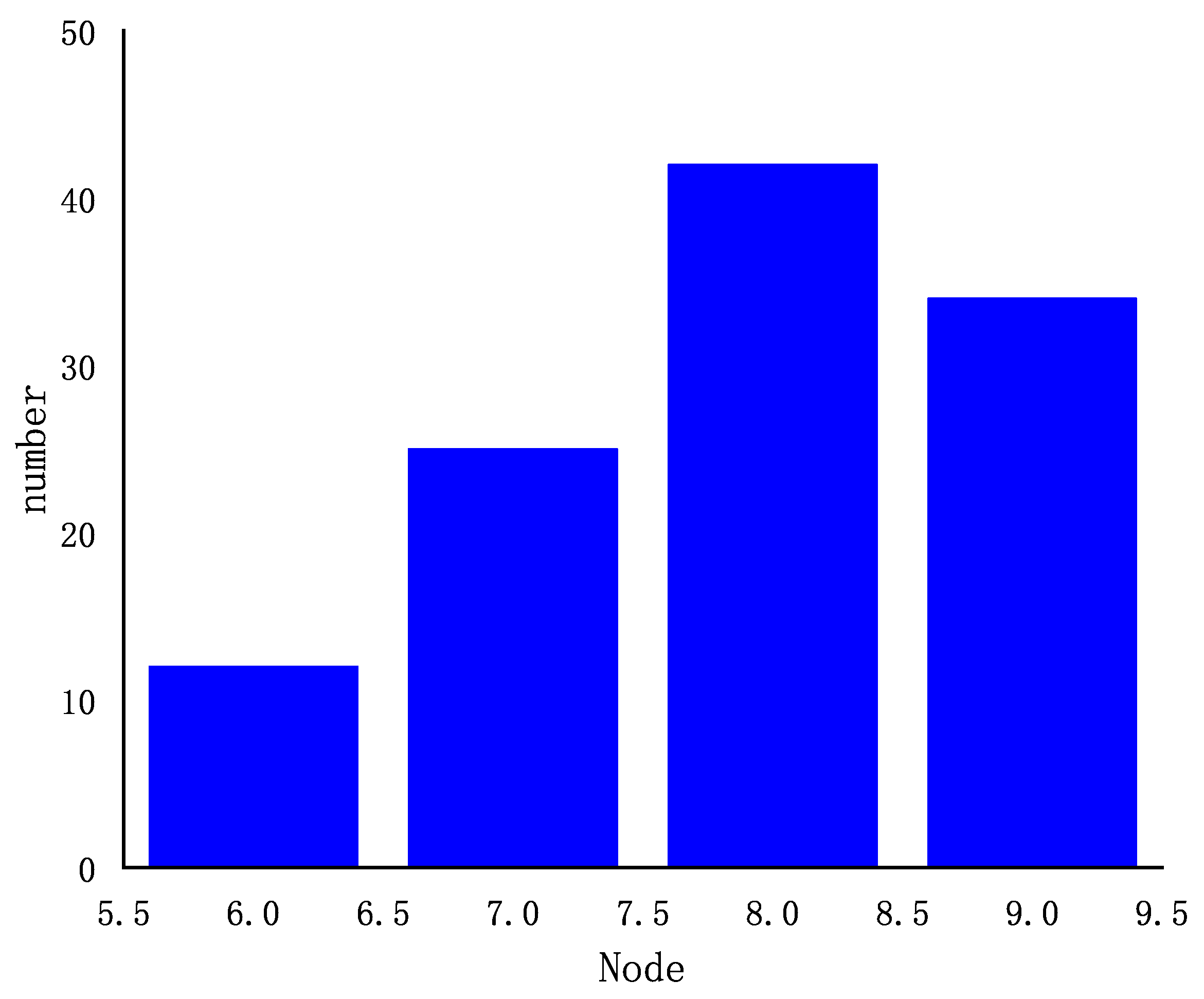
4.1.1. Result 1: Vulnerability Assessment and Deploying False Nodes Based on the Comprehensive Vulnerability Index
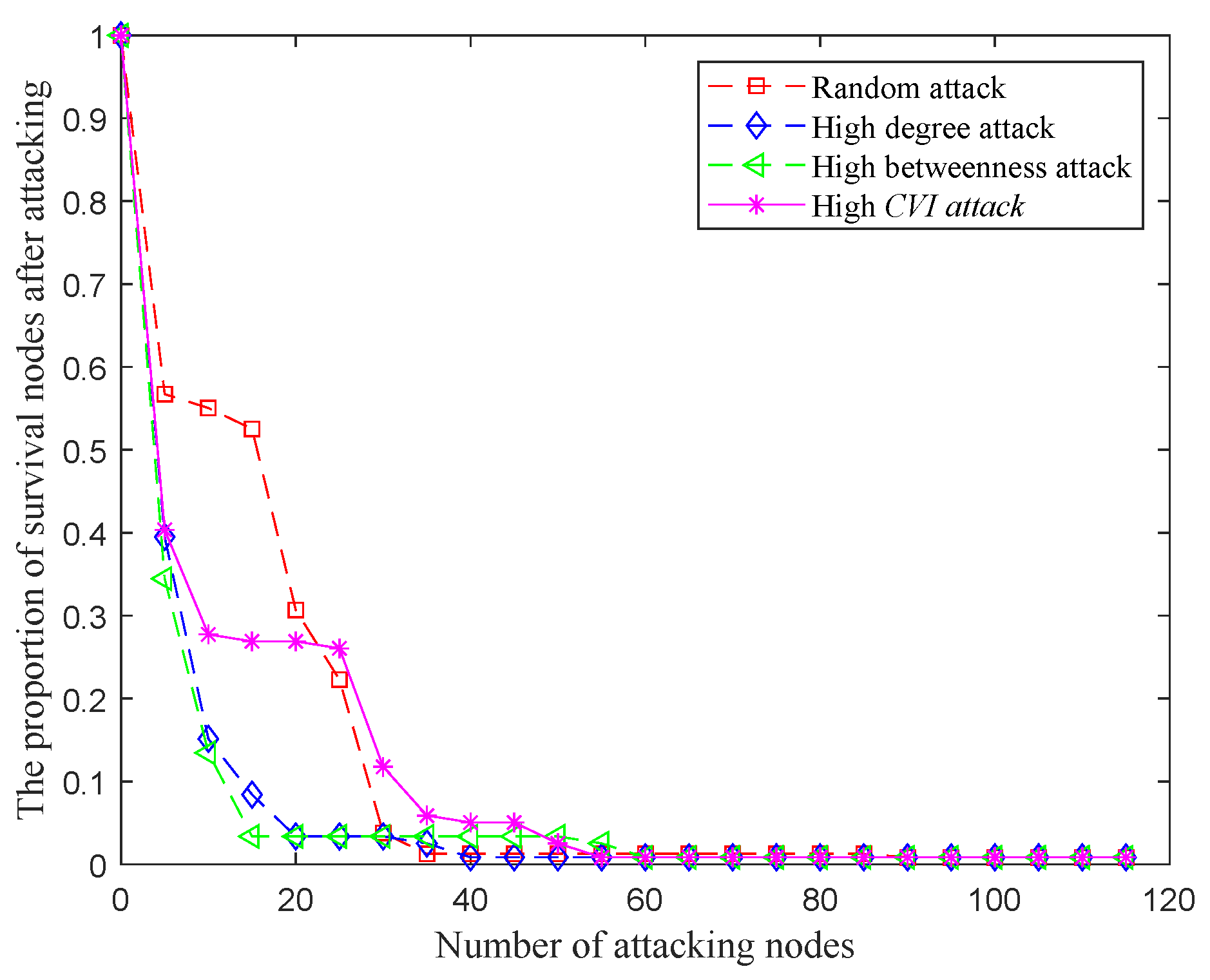
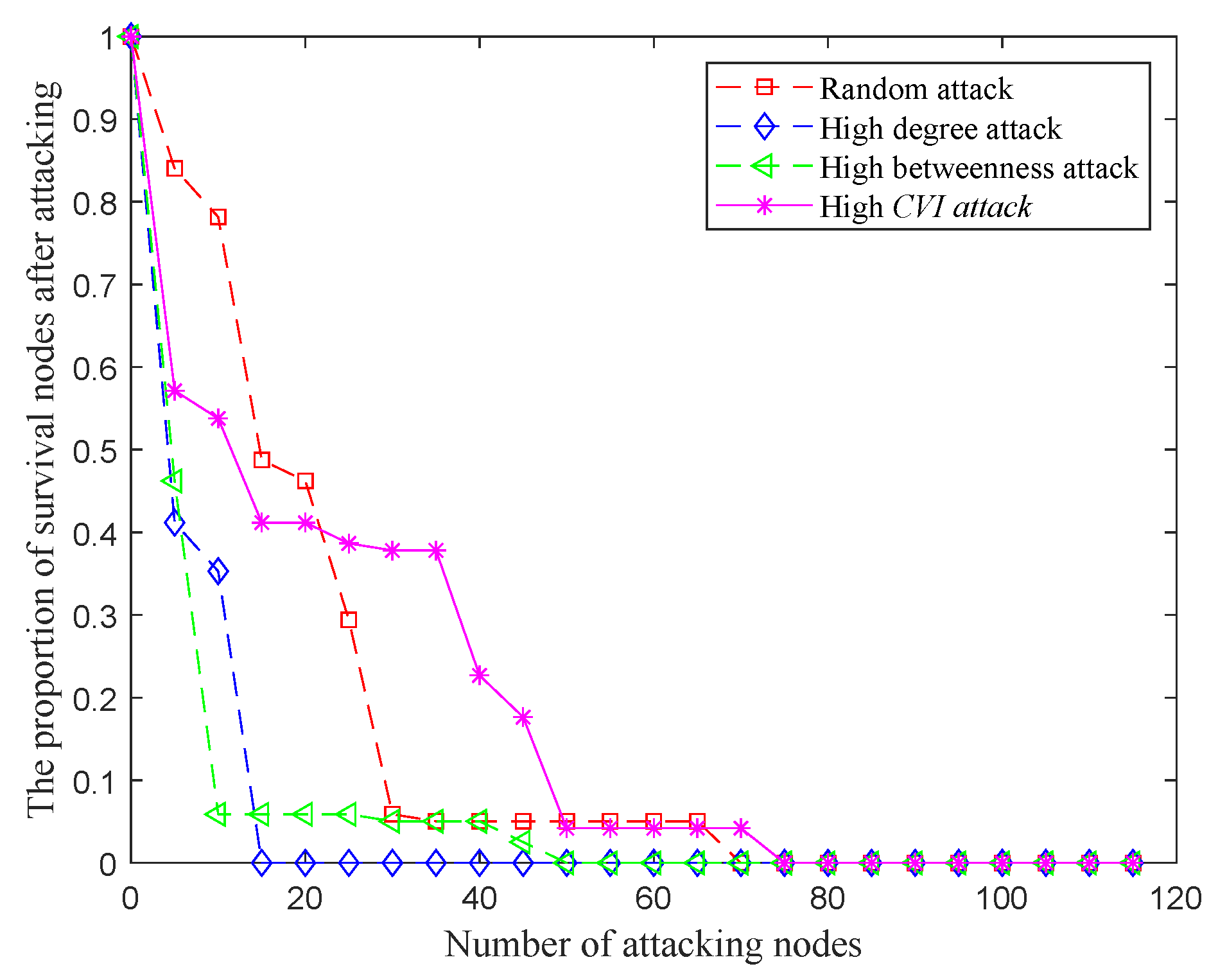
4.1.2. Nodes Survived under Different Types of Attacks
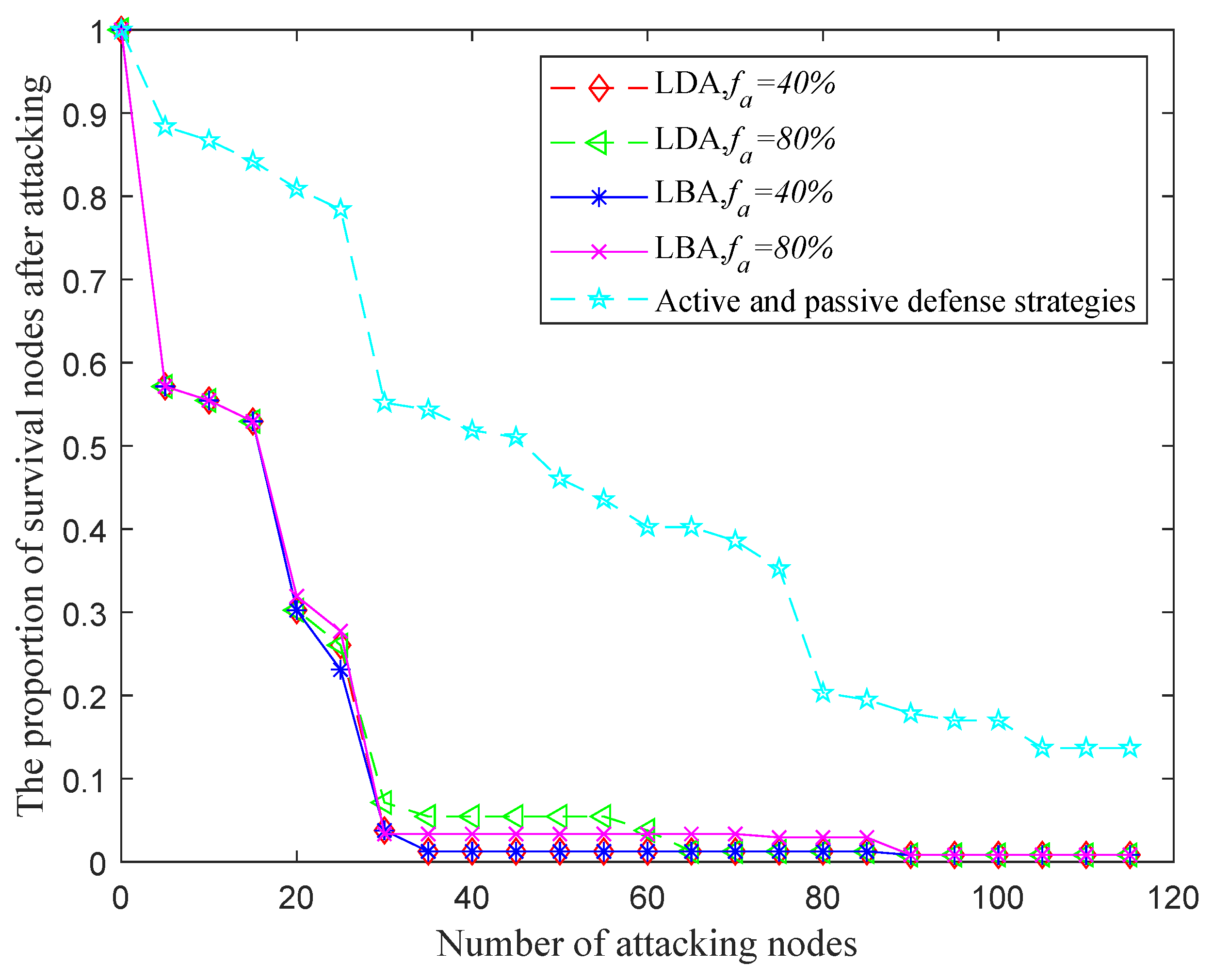
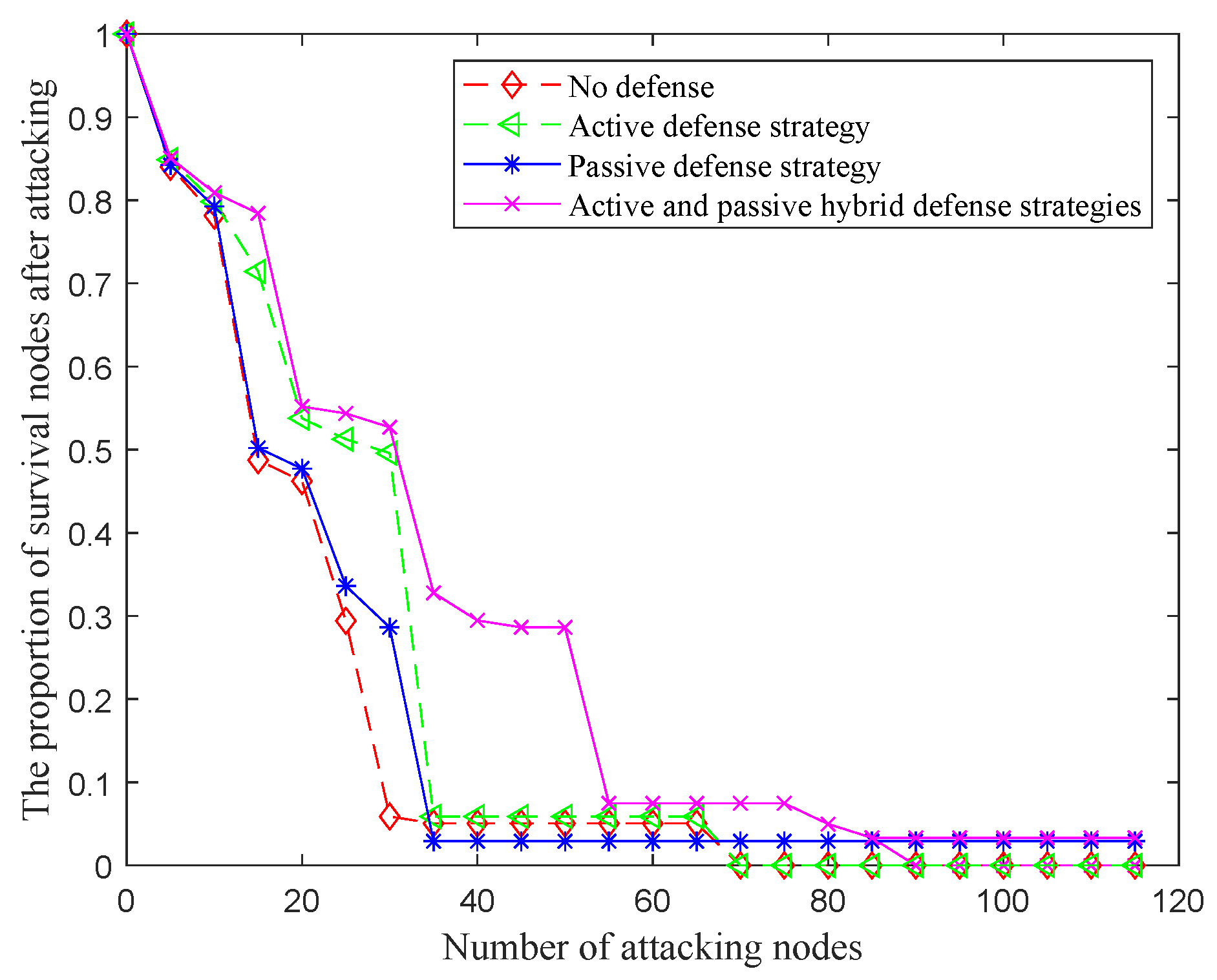
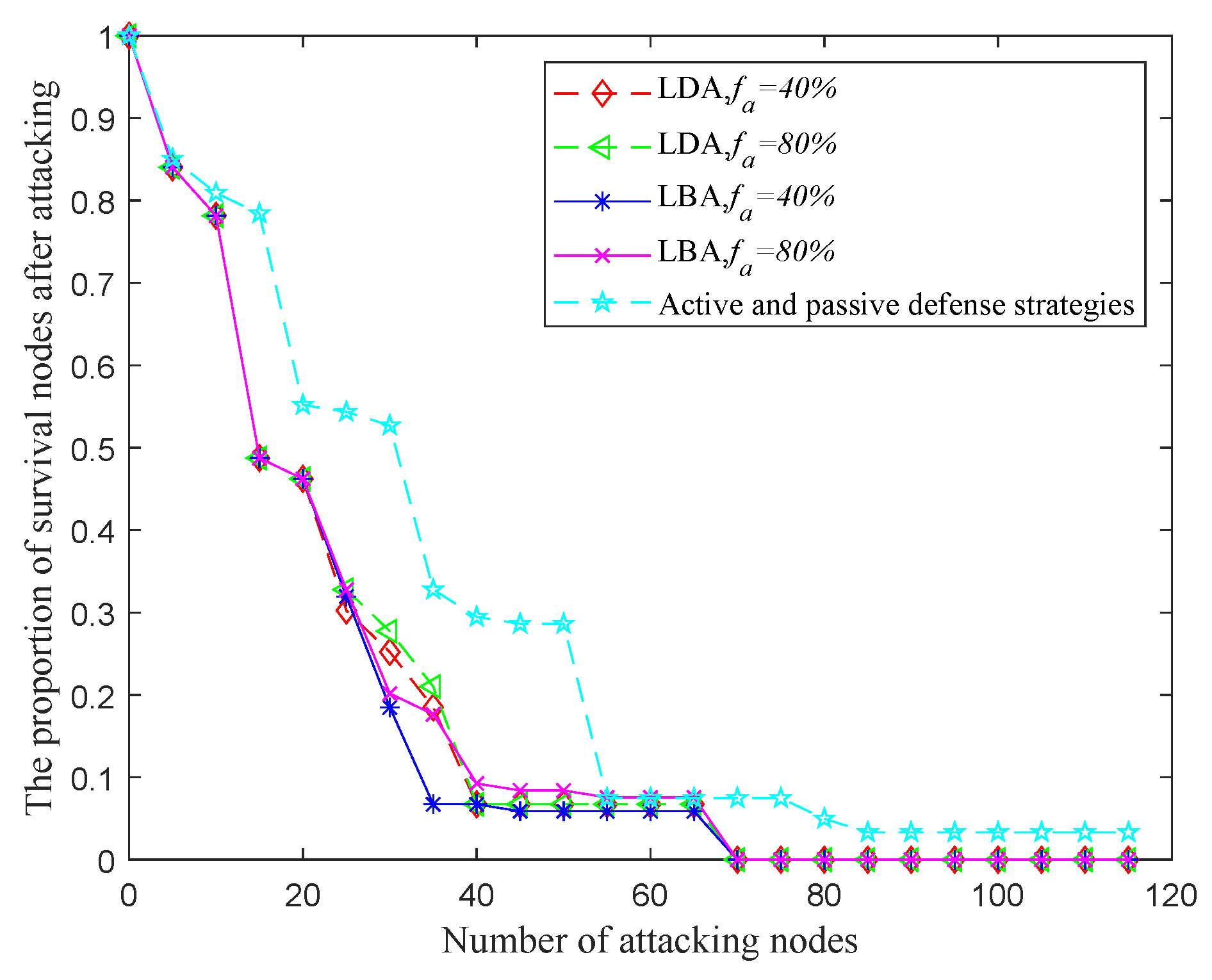
4.1.3. The Effect of the Active and Passive Hybrid Stategies
- •
- Low Degree Nodes Link Addition (LDA): At each step, the node degree of the network is calculated and two nodes with the lowest degree are added with an edge. Repeat the algorithm until the specified number of added edges is reached.
- •
- Low Betweenness Nodes Link Addition (LBA): At each step, the node betweenness of the network is calculated and two nodes with the lowest betweenness are added with an edge. Repeat the algorithm until the specified number of added edges is reached.
4.2. Small World (SW) Network
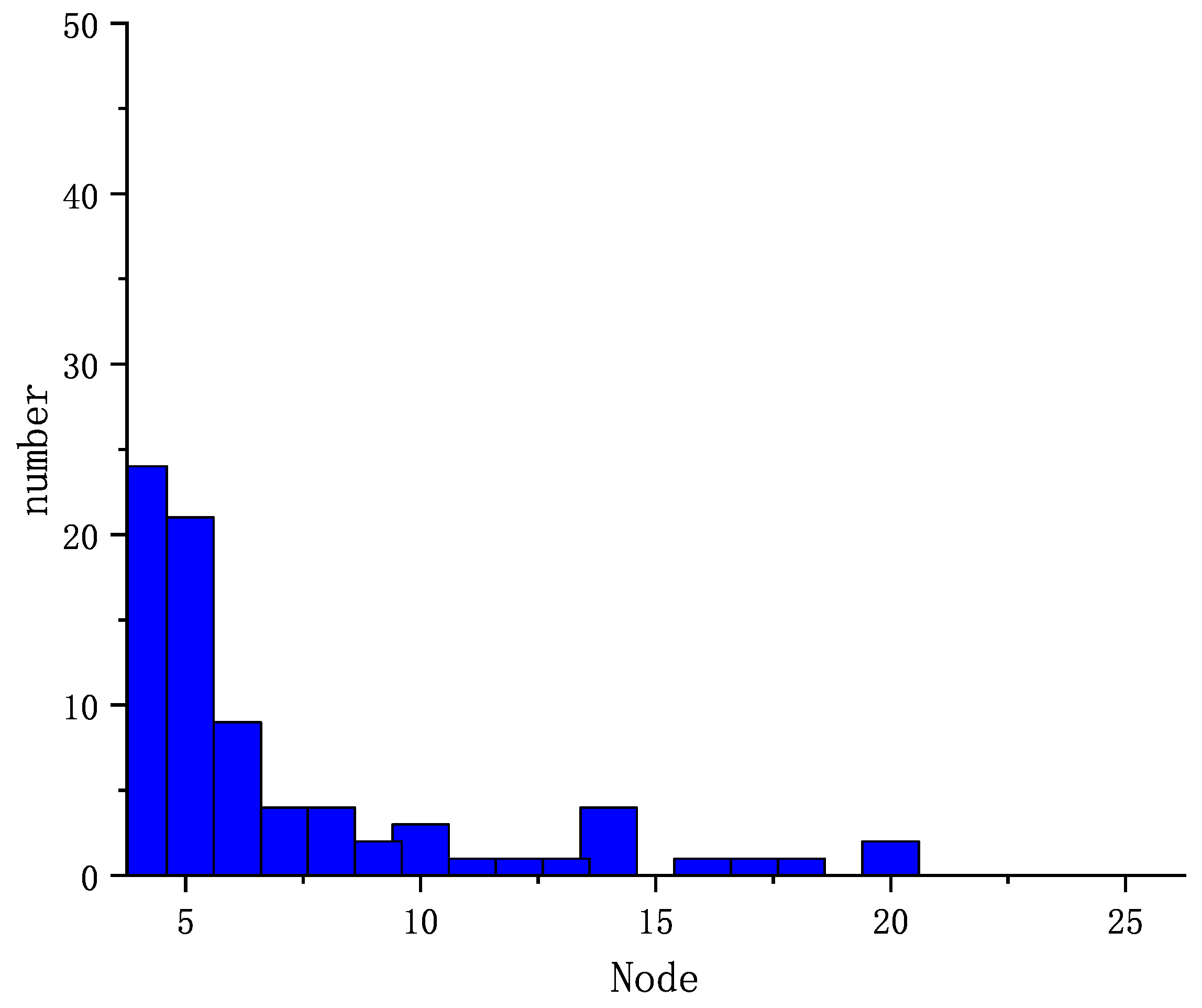
4.2.1. Result 1: Vulnerability Assessment and Deploying False Nodes Based on the Comprehensive Vulnerability Index
4.2.2. Nodes Survived under Different Types of Attacks
4.2.3. The Effect of the Active and Passive Stategies
4.3. Comparision and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zonouz, S.; Rogers, K.M.; Berthier, R.; Bobba, R.B.; Sanders, W.H.; Overbye, T.J. SCPSE: Security-Oriented Cyber-Physical State Estimation for Power Grid Critical Infrastructures. IEEE Trans. Smart Grid 2012, 3, 1790–1799. [Google Scholar] [CrossRef]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos 2007, 17, 967–979. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Yan, Z.M.; Chen, K.J.; Sun, J.W.; Xu, Y.; Liu, Y. Vulnerability Assessment of Deep Reinforcement Learning Models for Power System Topology Optimization. IEEE Trans. Smart Grid 2021, 12, 3613–3623. [Google Scholar] [CrossRef]
- Gao, X.L.; Pu, C.L.; Li, L.B. Vulnerability Assessment of Power Grids Against Cost-Constrained Hybrid Attacks. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1477–1481. [Google Scholar] [CrossRef]
- Venkataramanan, V.; Hahn, A.; Srivastava, A. CP-SAM: Cyber-Physical Security Assessment Metric for Monitoring Microgrid Resiliency. IEEE Trans. Smart Grid 2020, 11, 1055–1065. [Google Scholar] [CrossRef]
- Liu, N.A.; Hu, X.J.; Ma, L.; Yu, X.H. Vulnerability Assessment for Coupled Network Consisting of Power Grid and EV Traffic Network. IEEE Trans. Smart Grid 2022, 13, 589–598. [Google Scholar] [CrossRef]
- Ding, K.; Qian, Y.M.; Wang, Y.; Hu, P.; Wang, B. A Data-Driven Vulnerability Evaluation Method in Grid Edge Based on Random Matrix Theory Indicators. IEEE Access 2020, 8, 26495–26504. [Google Scholar] [CrossRef]
- Ibrahim, M.; Alsheikh, A. Automatic Hybrid Attack Graph (AHAG) Generation for Complex Engineering Systems. Processes 2019, 7, 787. [Google Scholar] [CrossRef] [Green Version]
- Ni, Z.; Paul, S. A Multistage Game in Smart Grid Security: A Reinforcement Learning Solution. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2684–2695. [Google Scholar] [CrossRef]
- Venkataramanan, V.; Srivastava, A.; Hahn, A. Cp-tram: Cyber-physical transmission resiliency assessment metric. IEEE Trans. Smart Grid 2020, 11, 5114–5123. [Google Scholar] [CrossRef]
- Hu, P.; Lee, L. Community-Based Link-Addition Strategies for Mitigating Cascading Failures in Modern Power Systems. Processes 2020, 8, 126. [Google Scholar] [CrossRef] [Green Version]
- Yagan, O.; Qian, D.J.; Zhang, J.S.; Cochran, D. Optimal Allocation of Interconnecting Links in Cyber-Physical Systems: Interdependence, Cascading Failures and Robustness. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1708–1720. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Wang, C.; Stojmenovic, M.; Nayak, A. Characterization of cascading failures in interdependent cyber-physical systems. IEEE Trans. Comput. 2015, 64, 2158–2168. [Google Scholar] [CrossRef]
- Ji, X.; Wang, B.; Liu, D.C.; Dong, Z.Y.; Chen, G.; Zhu, Z.S.; Zhu, X.D.; Wang, X.T. Will electrical cyber-physical interdependent networks undergo firstorder transition under random attacks? Phys. A Stat. Mech. Appl. 2016, 460, 235–245. [Google Scholar] [CrossRef]
- Wang, K.; Du, M.; Maharjan, S.; Sun, Y.F. Strategic Honeypot Game Model for Distributed Denial of Service Attacks in the Smart Grid. IEEE Trans. Smart Grid 2017, 8, 2474–2482. [Google Scholar] [CrossRef]
- Zhou, H.F.; Wu, C.M.; Jiang, M.; Zhou, B.Y.; Gao, W.; Pan, T.T.; Huang, M. Evolving defense mechanism for future network security. IEEE Commun. Mag. 2015, 53, 45–51. [Google Scholar] [CrossRef]
- Ni, M.; Li, M.L.; Li, J.; Wu, Y.J.; Wang, Q. Concept and Research Framework for Coordinated Situation Awareness and Active Defense of Cyber-physical Power Systems Against Cyber-attacks. Mod. Power Syst. Clean Energy 2021, 9, 477–484. [Google Scholar] [CrossRef]
- Farraj, A.; Hammad, E.; Kundur, D. A Distributed Control Paradigm for Smart Grid to Address Attacks on Data Integrity and Availability. IEEE Trans. Signal Inf. Process. Over Netw. 2017, 4, 70–81. [Google Scholar] [CrossRef]
- Di Muro, M.A.; La Rocca, C.E.; Stanley, H.E.; Havlin, S.; Braunstein, L.A. Recovery of Interdependent Networks. Sci. Rep. 2016, 6, 22834. [Google Scholar] [CrossRef]
- La Rocca, C.E.; Stanley, H.E.; Braunstein, L.A. Strategy for for stopping failure cascades in interdependent networks. Phys. Stat. Mech. Appl. 2018, 508, 577–583. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Liu, X. An Overview on Fault Diagnosis, Prognosis and Resilient Control for Wind Turbine Systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Parshani, R.; Rozenblat, C.; Ietri, D.; Ducruet, C.; Havlin, S. Intersimilarity between coupled networks. Europhys. Lett 2010, 92, 68002. [Google Scholar] [CrossRef] [Green Version]
- Levitin, G.; Hausken, K.; Ben Haim, H. False Targets in Defending Systems against Two Sequential Attacks. Mil. Oper. Res. J. Mil. Oper. Res. Soc. 2014, 19, 19–35. [Google Scholar] [CrossRef]
- Barabási, A.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 186–197. [Google Scholar] [CrossRef] [Green Version]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ’small-world’networks. Nature 2011, 393, 301–303. [Google Scholar]


| , | The initial condition of physical network and cyber network (not suffering attacks) |
| M, N | The scale of physical network and cyber network |
| , | The giant connected components in and (the survival nodes at stage i + 1) |
| , | The sets of remaining nodes in and which have supporting interlinks at stage i |
| , | The fractions corresponding to retaining the interlink , |
| , | The fractions corresponding to giant connected components , |
| F(X) components by the matrix X | The function of solving the giant connected |
| Network | C | P |
|---|---|---|
| Stage 1 | M | |
| Stage 2 | ||
| Stage 3 | ||
| Stage 4 | ||
| … | … | … |
| Stage i | ||
| Stage i + 1 |
| Node | Physical Index | Topology Index | CVI | Node | Physical Index | Topology Index | CVI |
|---|---|---|---|---|---|---|---|
| 6 | 0.779783 | 1 | 0.872693 | 120 | 1 | 0.029412 | 0.590509 |
| 18 | 0.866426 | 0.323529 | 0.637378 | 72 | 0.99278 | 0.029412 | 0.586335 |
| 67 | 1 | 0.058824 | 0.602918 | 57 | 0.981949 | 0.029412 | 0.580074 |
| 8 | 0.685921 | 0.470588 | 0.595072 | 39 | 1 | 0 | 0.5781 |
| 5 | 1 | 0.029412 | 0.590509 | 40 | 1 | 0 | 0.5781 |
| 26 | 1 | 0.029412 | 0.590509 | 86 | 1 | 0 | 0.5781 |
| 50 | 1 | 0.029412 | 0.590509 | 92 | 1 | 0 | 0.5781 |
| 61 | 1 | 0.029412 | 0.590509 | 95 | 1 | 0 | 0.5781 |
| 64 | 1 | 0.029412 | 0.590509 | 96 | 1 | 0 | 0.5781 |
| 87 | 1 | 0.029412 | 0.590509 | 98 | 1 | 0 | 0.5781 |
| Type | Random Attack | High Degree Attack | High Betweeness Attack | High CVI Attack |
|---|---|---|---|---|
| Threshold | 35 | 20 | 15 | 40 |
| Different Situations | Attacking Nodes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
| No defense | 0.5504 | 0.3067 | 0.0378 | 0.0126 | 0.0126 | 0.0126 | 0.0126 | 0.0126 | 0.0084 | 0.0084 |
| Active defense | 0.5588 | 0.5 | 0.2143 | 0.2143 | 0.1555 | 0.1471 | 0.1303 | 0.1050 | 0.0630 | 0.0630 |
| Passive defense | 0.8672 | 0.6763 | 0.3527 | 0.2946 | 0.2780 | 0.2282 | 0.2199 | 0.1037 | 0.0996 | 0.0830 |
| Active and passive hybrid defense | 0.8672 | 0.8091 | 0.5519 | 0.5187 | 0.4606 | 0.4025 | 0.3859 | 0.2033 | 0.1784 | 0.1701 |
| Node | Physical Index | Topology Index | CVI | Node | Physical Index | Topology Index | CVI |
|---|---|---|---|---|---|---|---|
| 44 | 0.779783 | 1 | 0.867408 | 30 | 0.99278 | 0.029412 | 0.609456 |
| 3 | 0.866426 | 0.323524 | 0.650407 | 10 | 0.981949 | 0.029412 | 0.602935 |
| 24 | 1 | 0.058824 | 0.625506 | 35 | 1 | 0 | 0.6021 |
| 13 | 1 | 0.029412 | 0.613803 | 67 | 1 | 0 | 0.6021 |
| 18 | 1 | 0.029412 | 0.613803 | 85 | 1 | 0 | 0.6021 |
| 21 | 1 | 0.029412 | 0.613803 | 93 | 1 | 0 | 0.6021 |
| 47 | 1 | 0.029412 | 0.613803 | 94 | 1 | 0 | 0.6021 |
| 62 | 1 | 0.029412 | 0.613803 | 97 | 1 | 0 | 0.6021 |
| 75 | 1 | 0.029412 | 0.613803 | 99 | 1 | 0 | 0.6021 |
| 87 | 1 | 0.029412 | 0.613803 | 106 | 1 | 0 | 0.6021 |
| Different Situations | Attacking Nodes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
| No defense | 0.7815 | 0.4622 | 0.0588 | 0.0504 | 0.0504 | 0.0504 | 0 | 0 | 0 | 0 |
| Active defense | 0.7983 | 0.5378 | 0.4958 | 0.0588 | 0.0588 | 0.0588 | 0 | 0 | 0 | 0 |
| Passive defense | 0.7925 | 0.4772 | 0.2863 | 0.029 | 0.029 | 0.029 | 0.029 | 0.029 | 0.029 | 0.029 |
| Active and passive hybrid defense | 0.8091 | 0.5519 | 0.5270 | 0.2946 | 0.2863 | 0.0747 | 0.0747 | 0.0498 | 0.0332 | 0.0332 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Z.; Shi, H.; Wang, Y.; Yin, G.; Abu-Siada, A. Active and Passive Defense Strategies of Cyber-Physical Power System against Cyber Attacks Considering Node Vulnerability. Processes 2022, 10, 1351. https://doi.org/10.3390/pr10071351
Qu Z, Shi H, Wang Y, Yin G, Abu-Siada A. Active and Passive Defense Strategies of Cyber-Physical Power System against Cyber Attacks Considering Node Vulnerability. Processes. 2022; 10(7):1351. https://doi.org/10.3390/pr10071351
Chicago/Turabian StyleQu, Zhengwei, Hualiang Shi, Yunjing Wang, Guiliang Yin, and Ahmed Abu-Siada. 2022. "Active and Passive Defense Strategies of Cyber-Physical Power System against Cyber Attacks Considering Node Vulnerability" Processes 10, no. 7: 1351. https://doi.org/10.3390/pr10071351
APA StyleQu, Z., Shi, H., Wang, Y., Yin, G., & Abu-Siada, A. (2022). Active and Passive Defense Strategies of Cyber-Physical Power System against Cyber Attacks Considering Node Vulnerability. Processes, 10(7), 1351. https://doi.org/10.3390/pr10071351







