Abstract
Shale oil is one of the world’s most important strategic energy reserves. The microscopic kerogen and matrix structure plays an important role in fluid flow and diffusion processes. The oil flow time in the shale reservoir is determined by the pore spatial scale. An accurate shale reservoir flow model must consider these factors. In this research, fluid flow, Fick’s diffusion in consideration of the time delay effect, desorption, as well as the absorption are considered using the molecular momentum correlation and the partial pressure law of the components. The effect of the above-mentioned factors on the time scale contribution of the well rate is discussed. The spatial distribution diagram of the time scale is constructed and analyzed. The results show that the production process is composed of five periods. The time delay effect is reflected by fluctuations in the production at periods 1–3. The time scale corresponds to different mediums. The oil mainly flows through the outer boundary of the stimulated region through surface diffusion. The time scale spatial distribution diagram also shows that the oil flows into the endpoint of the hydraulic fracture at an early stage. Moreover, the outer boundary needs a longer time to be exploited. The proposed model improves the simulation of shale oil flow, and therefore, would be favorable in designing a more suitable working system.
1. Introduction
As the shale oil revolution advances, the research on shale oil has become hot due to its economics, clean nature and strategic energy reserves in China. Despite high geological storage, during the production of a shale reservoir, the wellbore pressure decreases sharply. In order to alleviate the drop in pressure, hydraulic fracture is used as one of the economic and effective methods for oil production from shale reservoirs. After fracture, multiple spatial and time scales exist in the tight reservoir, such as kerogen (nm), inorganic matrix (nm and μm), natural fracture (μm and mm) and hydraulic fracture (mm and cm). Additionally, the production system should be changed at the beginning or end of the mass transfer in the above media. Therefore, the fluid flow models in conventional reservoirs could not precisely describe the shale oil diffusion and mass transfer time, which was mainly attributed to the diffusion of crude oil inside the kerogen. The kerogen pore microstructure also exerts an influence on the mass transfer of shale oil. Consequently, it is necessary to upscale the microstructure of the shale reservoir.
Furthermore, the organic pores are hydrophobic and have small size. The Fick’s diffusion and surface diffusion take place more easily than the oil flow [1,2]. Since the pores are tortuous, the multiple time and space scale theory needs to be considered in the diffusion. The diffusion model inside the kerogen has been established in some previous works using the multiscale flow theory. However, the Fick’s diffusion and surface diffusion are incorporated as one medium. Zhang Shaojie [3] and Cui Jiangfeng [4] investigated the effect of oil components on the diffusion and coupling between the inorganic pore and the kerogen pore. However, the surface diffusion of the absorption layer and the fractal structure in the kerogen pore were ignored. Zhang Wei [5] and Sui Hongguang [6] used molecular simulations and introduced an absorption layer in the diffusion model of shale oil. The results showed that the water flow was impeded by the absorption layer. The oil diffusion followed an isotropic path. The absorption was upscaled by apparent viscosity and density. Based on the reservoir spatial scale, Sui Tien Dung Le [7], Su Yuliang [8] and Wang Zijie [9] introduced apparent permeability into the black oil model. However, in the works mentioned above, the absorption layer was difficult to be considered. Feng Qihong [10] presented the absorption layer in the kerogen pore, matrix pore and natural fracture by the slippage effect. The effect of pore shape and slippage on the apparent permeability was investigated. Zhang Tao [11] and Wang Sen [12] proposed multiple absorption layer models using molecular simulation. The slippage was caused by surface diffusion. The oil diffusion inside the kerogen was upscaled using the Navier–Stokes equation under cylindrical coordinates. However, the absorption and desorption velocities were different from each other. The phenomenon was difficult to be considered in the works mentioned above. The dynamic coupling was introduced in only a handful of shale gas flow models [13,14,15] rather than the shale oil flow models. Zhu [16] introduced dynamic coupling into the laminated mass transfer model in shale reservoirs. Cao [17] investigated the absorption and desorption of different components. The influence of TOC value and fluid characteristics on the mass transfer of shale oil was also addressed. However, the dynamic coupling was not introduced into the mass transfer between the kerogen, the matrix and the natural fractures. The mass transfer mechanism between the matrix and the natural fracture was different from the mechanism inside the kerogen.
The multiphase flow in the fracture and inorganic pore exerted a significant impact on each other. Xue [18] investigated the effect of temperature and coalbed gas flow on water loss in coal seam. The change in mass transfer rate to the fracture network lagged behind the decline in gas’s diffusion coefficient. Zhang [19] introduced deformation of pores into the coal gas and water double flow model. The deformation was caused by the gas desorption and absorption. The deformation may decrease the diffusion coefficient of the organic pore and led to the anisotropy of permeability [20]. In the shale reservoirs, the two phase flow model in fracture network [21] was mainly used to describe the deformation of porous medium, degassing and the condensation of fluid. Sherafati [22] investigated the impact of capillary pressure on the Fick’s diffusion, imbibition, degassing and the condensation in shale reservoir. The gas is confined in the nanopores, which promotes the impact. In order to improve the effect of the system, the shale oil mass transit and diffusion time should be predicted.
The shale oil mass transit and diffusion time in kerogen is different from that in the inorganic matrix, whereas the phenomenon is known as the multiple temporal scale. The shale oil flows faster in the fracture network, and slowly in the inorganic pore, whereas it is extremely hard for oil to flow inside the kerogen. Bernard [23] introduced the multitemporal scale theory in 1964. The value of the temporal scale was derived by Sarlet [24] using the perturb theory in 1977. Li [25,26] first analyzed the shale gas flow temporal scale using empirical correlations. In Li’s works [25,26], the definition of temporal scales is not provided. Moreover, in some previous works [27,28,29], more attention has been given to multiple spatial scale than the temporal scale. The well rate and pressure field are derived at each time point. The variation in wellbore pressure and rate with time has not been investigated. Therefore, not much progress could be made when evaluating the impact of pore microstructure on the flow of shale oil. Under an improper shale reservoir development system, the effective porosity declines, and the fluid is condensed or degassed. There is not enough time for a slow mass transfer process for the shale oil, such as desorption, absorption, Fick’s diffusion and surface diffusion on the kerogen. In addition, for the case with multiple adsorbed layers of shale oil and organic pores with a spatial scale of nanometers, the molecular momentum exchange between the layers and the pore wall occurs more easily. Meanwhile, the Fick’s diffusion coefficient decreases [30,31]. Due to these reasons, the shale reservoir could not be exploited efficiently, especially the oil in the kerogen.
In the current paper, a shale oil flow model is addressed, which accounts for Fick’s diffusion, dynamic crossflow, dynamitic coupling and time delay effect. Furthermore, based upon the well rate from a previous study, the time scale is investigated. The temporal scale ti is defined as the time for the shale oil diffusion and transfer along the porous medium. The pressure field is divided into several parts. Different parts correspond to different regions. The changing amplitude of each part is the time scale contribution αi. Based on the peak value of αi, the main factor that influences the mass transfer is identified. The development system is optimized based on this factor. Afterward, a field study for the validation of the addressed model is conducted. The effect of the size, porosity, permeability and Fick’s diffusion coefficient of unstimulated region on the shale oil flow temporal scale contribution is discussed. Lastly, the spatial distribution of time scales is evaluated to reveal the coupling between the spatial and temporal scales. The results from the study would be helpful in selecting a more effective working system for developing shale reservoirs.
2. Shale Oil Flow Model
2.1. Physical Model
The model assumed for shale oil mass transit was divided into three regions [8], as demonstrated in Figure 1. Region 1 was the hydraulic fracture, Region 2 was the stimulated reservoir region, and Region 3 was the unstimulated reservoir region. The boundary of the shale reservoir was impervious except for the crossover point of the wellbore and artificial fracture. The y (m) axis extended along the direction of wellbore, while the x (m) axis extended along the direction of hydraulic fracture. The model size along the y axis was represented by ye (m), while that parallel to the x direction was represented by xe (m). Moreover, the boundary beside the wellbore and artificial fracture was the inner boundary, whereas the other boundary was the outer boundary. The artificial fracture had a length of lf (m) and a width of w (m). The size parallel to the y axis of the Stimulated Region was xs (m). The reservoir pressure is represented by p0 (Pa), while the wellbore pressure is given by pw (Pa).
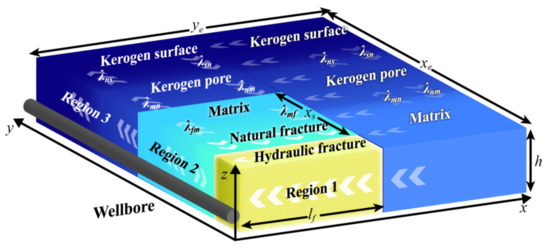
Figure 1.
Schematic of the physical model of shale oil flow.
2.2. Coupling between the Fick’s Diffusion in Kerogen and the Fluid Flow in the Matrix
The cross flow coefficients, σsn (s−1·Pa−1) and σns (s−1·Pa−1) between the kerogen surface and the organic pore depend on the dynamic absorption and desorption effect of shale oil component [13,14,15]. In addition, the cross flow coefficients, σmn (s−1·Pa−1), σnm (s−1·Pa−1), σmf (s−1·Pa−1), and σfm (s−1·Pa−1) between the natural fracture network and the organic and inorganic pores in the matrix depend on the microstructure of the matrix and the size and the shape of the fracture network. In short, different microstructures of porous media in the shale reservoir, and the absorption, diffusion and desorption on the kerogen were upscaled as different values of cross flow coefficients, which is known as dynamic coupling.
As shown in Figure 2, taking the direction of the Fick’s diffusion as the natural coordinate, the matrix throat was turned into a column using the coordinate transformation. The underside was in contact with the kerogen pore. The contact surface Sns was a circle with the radius Rns (m) and spherical angle 2θn. The oil flowed out of Sns through its normal direction, where rns (m) is the radius of the contact surface.
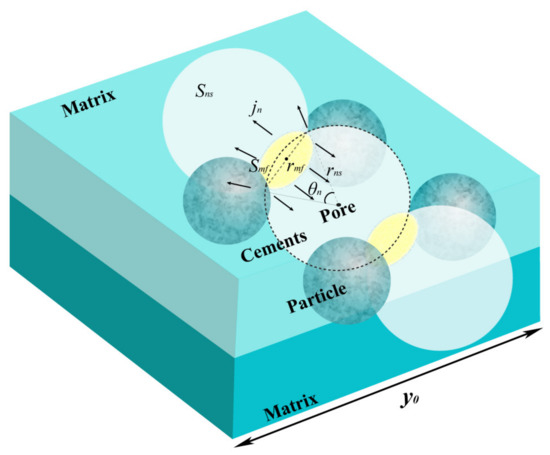
Figure 2.
Schematic of the matrix and kerogen pore.
For simplification, the shale oil was assumed to possess only one component. Additionally, the compression factor, Z, was the ratio of component’s actual volume to the volume when the component turned into an ideal gas. In other words, the Dalton’s partial pressure law was suitable for the oil component when the law was modified by Z. Based on the partial pressure law, the crossflow from kerogen to the matrix is given by Equation (1).
where cn (mol/m3) is the oil component concentration in the kerogen pore, nϕ (1/m2) is the number of kerogen pores adhering to a unit inorganic matrix surface, Vϕ (m3) and Vo (m3) are the organic pore and oil component volumes, respectively, pn (Pa) is the pressure in the kerogen, C (Pa−1) is the fluid compressibility, (mol/m2/s) is the diffusion flux from kerogen to the matrix, and μ (Pa·s) is the viscosity. The momentum balance is given by Equation (2).
where is the gradient operator under natural coordinates, is the gradient operator under real coordinates, M (kg/mol) is the molecular mass of the shale oil, t (s) is the diffusion time, and B (s/m) is the migration rate of shale oil component, which represents the molecular momentum exchange time per unit distance.
As the absorbed layer, the boundary condition is given by Equation (3).
where h (m) is the reservoir thickness. The initial condition is given by Equation (4).
Based on a previous study [32], the diffusion flux in the kerogen, , at the time point t is affected by between the time points t and 0, and is given by Equation (5).
where Θ is the effect of the between the time points t and 0 on Fick’s diffusion at a later time. The boundary condition is given by Equation (6).
The initial condition is given by Equation (7).
where Ψ is the solution of Equation (8), which presents the effect of concentration gradient on the spatial distribution of at the time point u. In other words, is generated by the concentration gradient.
The boundary condition is given by Equation (9).
The value of Ψ is obtained using Equations (8)–(10).
The solution of Equations (8)–(10) is given by Equation (11) [32].
where fns is the function of spherical angle θ. In order to obtain the value of , the natural coordinate in Equations (5) and (8) is turned into the real coordinate (see Equation (12)).
where I is the transformation coefficient from natural coordinate to real coordinate. The more tortuous the kerogen pore, the larger the value of I. Moreover, is given by Equation (13) [32].
where τ (s) is the lagged time of the mass transfer between the kerogen pore and the inorganic matrix, which presents the decay time of Θ. It is larger when B is larger or the pore is tortuous. The lagged time is shorter when the diffusion is approximated to traditional Fick’s diffusion. Substituting Equation (13) into Equation (3), the cross-flow from kerogen to matrix, qnm (mol/(m3·s)), is derived and given by Equation (14).
where the microstructure of kerogen pore is presented by H(0). For t = 0, Equation (15) is obtained.
The mass transfer coefficient between the kerogen pore and the inorganic matrix, σnm (Pa −1·s−1) is given by Equation (16).
The cross-flow continuous equation from the matrix to the kerogen is represented by Equation (17).
The solution of Equation (2) is given by Equation (18) [32].
where wm (m) is the matrix throat length, cm (mol/m3) is the shale oil component concentration in the inorganic matrix, and (mol/m2/s) is the diffusion flux from matrix to the kerogen. The mass transfer rate, qmn (mol/(m3·s)), between the kerogen pore and the inorganic matrix is given by Equation (19).
where
The cross-flow coefficient from matrix to kerogen, σmn (Pa −1·s−1), is given by Equation (21).
2.3. Shale Oil Flow Model in Region 1
The shale oil was assumed to flow into the wellbore at a constant production rate Q (m3/s). Moreover, the coupling between Regions 1 and 2 conformed to non-equilibrium effect.
The gas flow equation inside the finite conduction hydraulic fracture is given by Equation (22).
where klf (m2) and ϕlf are the permeability and porosity of the hydraulic fracture, and plf (Pa) is the hydraulic fracture pressure.
2.4. Shale Oil Flow Model in Region 2
There is surface diffusion in the organic pore, Fick’s diffusion in the organic pore, shale oil flow in the inorganic pore, and shale oil flow in the fracture network in the stimulated reservoir region. The partial pressure of oil component is given by Equation (23).
where Dn (m) and Ds (m) are the Fick’s and surface diffusion coefficients, respectively, λns (s−1) and λsn (s−1) are the absorption and desorption coefficients of the organic pore surface, respectively, and pm (Pa) and ps (Pa) are the pressures in the inorganic pore and on the organic pore surface, respectively.
Due to the tortuous nature of pore and the spatial variable profile, the molecular momentum often changes with time, and gives a normal stress to the pore wall. The molecular intertance is considered in this work. The concentration gradient not only drives the diffusion, but also balances the stress. The time lag effect is considered into Fick’s diffusion [32,33]. In other words, the Fick’s diffusion at time t is affected by the concentration gradient between the time points t and 0 and is described by Volterra equation [34,35,36,37,38], instead of the traditional steady Fick’s law. However, Fick’s diffusion considering the time lag effect has not been investigated at present. The flow rate in the kerogen, qn (mol/(m3·s)), is given by Equation (24).
where τ (s) is the lagged time of the Fick’s diffusion in the kerogen, and (mol/m2/s) is the diffusion flux. The solution of Equation (2) is given by Equation (25).
Substituting Equation (25) into Equations (24) and (26) is obtained.
When t = 0
where H(0) presents the shape of the Fick’s diffusion profile. The tortuous pore is upscaled as the time lag effect. The Fick’s diffusion coefficient Dn (m) is given by Equation (28).
The continuous equation of the kerogen block is given by Equation (29).
Based on a previous study [32] and substituting Equation (26) into Equation (29), Fick’s diffusion model considering time lag effect is given by Equation (30).
The flow model in Region 2 is represented by Equation (31).
where ϕf and kf (m2) are the porosity and permeability of the natural fracture network, respectively, and ϕm and km (m2) are the porosity and permeability of the inorganic pore, respectively.
2.5. Shale Oil Flow Model in Region 3
There is surface diffusion in the organic pore, Fick’s diffusion in the organic pore, and fluid flow in the inorganic pore in the unstimulated reservoir region. The values of the permeability in the natural fracture network and the inorganic matrix, the porosity in the natural fracture network and the inorganic matrix, the Fick’s diffusion coefficient in the organic pore are less than the corresponding values in Region 2. The model is given by Equation (32).
2.6. Definition and the Estimation of Temporal Scale
The temporal scale in this manuscript is defined as the time for the shale oil diffusion and transfer through a unit porous medium volume. Based on Equations (1) and (31), the time scale ti corresponding to Darcy flow inside the natural fracture network is given by Equation (33).
The one corresponding to Fick’s diffusion inside the organic pore is represented by Equation (34).
The one corresponding to shale oil desorption from organic pore surface is given by Equation (35).
Based on Equations (33)–(35), the range of time scales in correspondence with different mass transfer processes is estimated during the time scale analysis of the case study given below.
3. Case Study
3.1. Comparison with Eagle Ford Oilfield Production
The shale oil transfer and diffusion model validation was conducted by comparing the results from the addressed time scale analysis with the well production obtained from the Eagle Ford oilfield [21] in the United States. The model parameters are based on a previous study [8] and are presented in Table 1.

Table 1.
Parameters of shale reservoirs [13,21,39] obtained from the Eagle Ford oilfield.
Figure 3a shows that the results from the time scale analysis are in good agreement with the oilfield production rate. The error is mainly attributed to the linear diffusion and flow assumption.
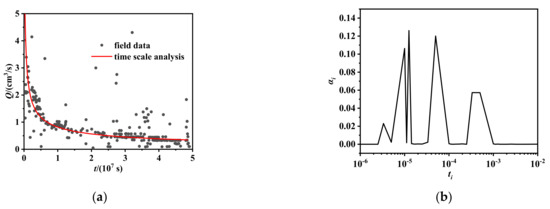
Figure 3.
Comparison between the results of the temporal scale analysis and the field data. (a) Dimensionless well rate. (b) Time scale distribution.
Figure 3b shows the time scale distribution. The small peak around the time scale 4 × 10−6 corresponded to the hydraulic fracture. The peak around the temporal scale 2 × 10−5 corresponded to the shale oil flow along the hydraulic fracture. A small valley existed on the right-hand side of the peak, which was due to the sharp decline of permeability at the boundary of Region 2. The peak around the time scale 8 × 10−5 corresponded to the matrix and kerogen. The peaks were higher since more fluid flowed out of Region 2. The peak around the time scale 4 × 10−4 corresponded to Region 3. Since more oil flowed from Region 3, the peak was wider.
3.2. Effect of the Size of the Unstimulated Region on the Shale Oil Flow
The well rate under different xs is shown in Figure 4. First, the production mainly included four stages. During Stage 1, the oil mainly flowed from the hydraulic and natural fracture network into the wellbore. Therefore, the production rate decreased slowly. Stage 1 was quite short. During Stage 2, the pressure propagated to the intersection between the stimulated and unstimulated regions, while the intersection performed as a fault. The well rate decreased sharply. During Stage 3, the oil flowed from the kerogen pore to the inorganic matrix and natural fracture. More oil flowed through the boundary of Region 2. The production declined more slowly than Stage 2. However, Stage 3 was quite short. Afterwards, more oil diffused and desorbed inside the kerogen. At Stage 4, the well rate decreased more rapidly. Eventually, the oil concentration in the kerogen decreased with time. The diffusion turned slow. At Stage 5, the well rate decreased even more rapidly than Stage 4.
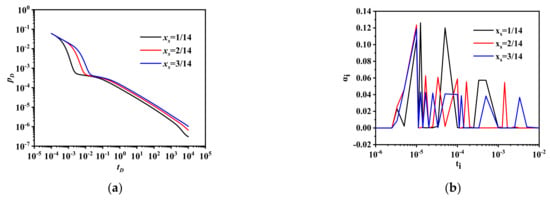
Figure 4.
Effect of xs on well rate. (a) Dimensionless well rate. (b) Time scale distribution.
For longer xs, the fluid flowed through a longer Region 2, which is why Stage 1 was longer. At Stage 2, the production rate was also higher. Due to longer intersection between the stimulated and unstimulated regions, Stage 2 was shorter. During Stage 3, the production was as high as the case with shorter xs. Region 3 was smaller. Therefore, Stage 3 was shorter. The oil in the kerogen flowed more easily to the wellbore. The production rate in Stage 4 was higher. Meanwhile, desorption happened more easily than the surface diffusion. More gas entered the kerogen pore. Due to this reason, during Stage 5, the production rate decreased more slowly.
For the case when xs = 2/14, due to the longer Region 2, the peak around the time scale 10−5 was higher and wider. In Region 2, the cross-flow was easier than the fluid flow through the outer boundary of Region 2. Less fluid flowed out of Region 3. More smaller peaks and valleys appeared on the right-hand side of the high peak. The valleys corresponded to the intersection between the stimulated and unstimulated regions. While the small peaks corresponded to the cross-flow in Region 2, the pressure at the intersection became lower. Additionally, the peaks corresponding to Region 3 became narrower and shifted leftwards. More oil in the matrix and kerogen flowed into Region 2. The peak around the time scale 8 × 10−5 was higher on its right. Another peak appeared on the right-hand side of the time scale 4 × 10−4 and corresponded to the desorption of oil. The peak was higher than the case with the smaller region. For the case when xs = 3/14, the peak near the temporal scale 0.005 corresponded to the desorption of oil in Region 3. The valley between the two peaks indicated the low surface diffusion rate in organic pore. Moreover, the peaks corresponded to the natural fracture network and connected with each other.
3.3. Effect of Unstimulated Region’s Porosity, Diffusion Coefficient and Permeability on Shale Oil Flow
The well rate under different diffusion coefficient, porosity and permeability of the unstimulated region is shown in Figure 5. The larger the diffusion coefficient and permeability of the unstimulated region, the easier for the fluid in Region 3 to flow out, which is why during Stage 2, the drop in the production rate was smaller. At Stage 3, Region 2 continued to receive more fluid. The production rate decreased a little. Since less oil remained in Region 3 at the start of Stage 4, the production rate decreased as fast as in the case with the smaller diffusion coefficient and permeability of the unstimulated region. The oil in the kerogen was more easily desorbed than the surface diffusion. Therefore, during Stage 5, the production rate decreased more slowly.
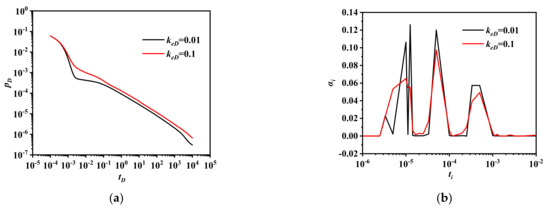
Figure 5.
Effect of diffusion coefficient, porosity and permeability of the unstimulated region on well rate. (a) Dimensionless well rate. (b) Time scale distribution.
The peaks corresponding to the natural fracture network and the artificial fracture connected with each other. Since the oil concentration in the hydraulic fracture was maintained at a certain level, the left-hand side of the peak was higher. The fluid supply from Region 3 took a larger proportion of the well rate than the cross-flow. Therefore, the right-hand side of the peak was also higher. Moreover, the valley near the temporal scale 10−5 vanished. Additionally, the peaks on the right-hand side of the temporal scale 2 × 10−5 were lower. In the inorganic matrix and organic pore, fluid flow and diffusion through the boundary of region 2 were easier than the case with tighter Region 3. The left-hand side of the peaks corresponding to Region 3, the matrix and the kerogen were less steep. Moreover, the peak around the time scale 8 × 10−4 was higher on the right-hand side, which indicates that the kerogen in Region 3 was exploited.
3.4. Effect of the Lagged Time on Shale Oil Flow
The well rate under different lagged times is presented in Figure 6. When the time delay effect was taken into account, the flow route inside the hydraulic fracture was longer. The mass transfer time of shale oil to the wellbore is longer. Therefore, the well rate increased a little with the progression of time during Stage 1, while it decreased with the lagged time. Moreover, the pore wall exerted a normal stress onto the fluid flow. The stress direction changed along the fracture. Afterwards, the pressure propagated throughout the hydraulic fracture. The stage was longer in the case with the longer lagged time. The well rate fluctuated instead of declining rapidly during Stage 2 and later in Stage 1, which was due to the tortuous natural fracture. During the rising period, the stress direction was along the inner boundary. During the declining period, the fluid flowed through the outer boundary of Region 2. The flow velocity decreased, while the stress direction pointed to Region 3. More oil remained beside the boundary instead of flowing to the wellbore. However, for shorter lagged time, the normal stress on the cross-flow channel was smaller. At the end of Stage 2, the production decreased with the lagged time. Furthermore, under the effect of Stages 2 and 1, the well rate rapidly increased again. As the effect decayed, the production curve coincided with the case without the effect of time lag. More importantly, no effect was exerted on the time scale distribution by the time lag effect.
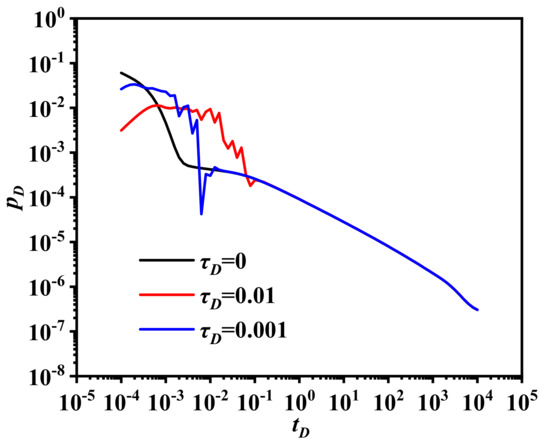
Figure 6.
Effect of lagged time on well rate.
4. Spatial Distribution of Time Scale
Figure 7 shows the contribution distribution of time scale 4 × 10−6. Only the hydraulic fracture and natural fracture were affected by the temporal scale. The shale oil flowed through the artificial fracture more easily. The oil component concentration in the end point of the hydraulic fracture could easily be maintained due to flow from Region 3 than the area beside the wellbore. In addition, the outer boundary of Region 2 performed as a fault. Therefore, the contribution was higher in the area far from the wellbore and lower beside the wellbore.
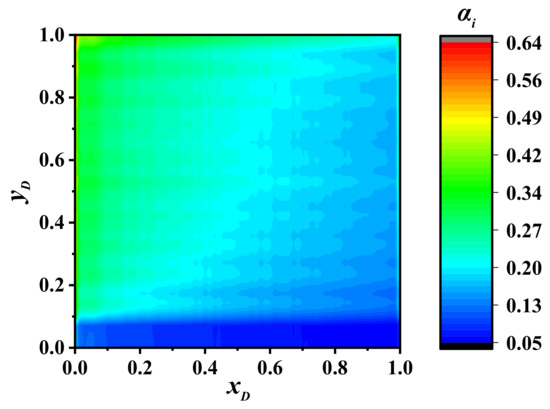
Figure 7.
Spatial distribution of time scale 4 × 10−6 contribution in the natural fracture.
Figure 8 shows the contribution distribution of time scale 2 × 10−5. Due to low oil concentration in the hydraulic fracture, more fluid flowed from Region 3 into the hydraulic fracture than from the natural fracture network. The time scale contribution was lower. In the intersection between the stimulated and unstimulated regions, the transfer rate was mainly composed of the fluid flow out of the natural fracture. The contribution was higher in the area far from the wellbore and lower beside the wellbore. However, far from the hydraulic fracture, the oil flowed from the matrix to the natural fracture. Consequently, the temporal scale distribution stripe was along the hydraulic fracture. In the inorganic pore, the contribution in Region 3 was larger than the one beside the wellbore. Additionally, the fluid in the left-hand side of Region 3 flowed to Region 2. Therefore, the contribution in the left-hand side of Region 3 was higher. In the area 0 < xD < 0.05, since the oil mainly flowed in the direction parallel to the wellbore, the drainage area was as strip parallel to the wellbore. Meanwhile, the time scale contribution was higher. The area with low time scale contribution penetrated the area 0 < xD < 0.05. The time scale contribution distribution in the kerogen was similar to the matrix. However, since the pressure propagated into the kerogen later than to the matrix, the contribution was lower than the matrix. The strip with high time scale contribution was narrower than in the matrix. The fluid flow in the matrix exerted little effect to the kerogen surface.
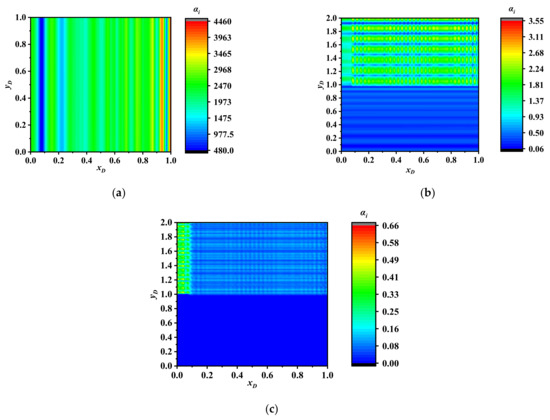
Figure 8.
Spatial distribution of time scale 2 × 10−5 contribution. (a) Natural fracture. (b) Matrix. (c) Kerogen pore.
Figure 9 shows the contribution distribution of time scale 8 × 10−5. In the area beside the hydraulic fracture, since there was low oil concentration in the natural fracture, more shale oil flowed out of the inorganic matrix and organic kerogen. The temporal scale contribution was higher than the area far from the hydraulic fracture. However, more oil entered the natural fracture network due to the dynamic coupling and the Fick’s diffusion rather than the mass transfer inside the natural fracture network. Some of the desorbed oil entered Region 2 through surface diffusion. The contribution was higher at the outer boundary of Region 2. However, the contribution was lower than that beside the hydraulic fracture. In the area 0 < xD < 0.05 and 1 < yD < 2, since the oil in the matrix entered the end point of hydraulic fracture rather than the oil in the area xD = 0.05, the time scale contribution was higher. In the kerogen pore or the area far from the wellbore, the area with larger contribution was narrower. The oil flow beside the outer boundary of Region 3 was quite difficult. The time scale contribution in the matrix and kerogen was lower. However, in the area 0.05 < xD < 1 and 0 < yD < 1, Fick’s diffusion in organic pore occurred later than the mass transfer in the inorganic pore. Therefore, the temporal scale contribution was higher. The contribution in the area xD = 0.7 was lower, which corresponded to the dynamic coupling between the kerogen and the inorganic pore. The oil in inorganic pore reached the natural fracture network earlier than the one in the kerogen. The diffusion in the area 0.1 < xD < 0.7 was mainly affected by the matrix, while the diffusion in the area xD > 0.7 was mainly affected by the kerogen. On the kerogen surface, more oil was desorbed, and the surface diffusion coefficients in Regions 2 and 3 were equal to each other, which promoted the surface diffusion. Therefore, the contribution in Region 3 was larger. In the area 0.05 < xD < 1 and 0 < yD < 1, the oil concentration was lower, while the surface diffusion was parallel to the wellbore. The area with higher contribution of time scale 8 × 10−5 was distributed as strips.
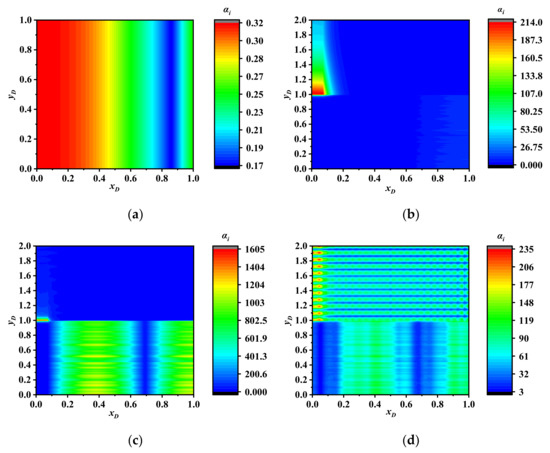
Figure 9.
Spatial distribution of time scale 8 × 10−5 contribution. (a) Natural fracture. (b) Matrix. (c) Kerogen pore. (d) Kerogen surface.
Figure 10 shows the contribution distribution of time scale 8 × 10−4. Beside the wellbore, the oil flowed through a longer distance from Region 3. In the area beside the hydraulic fracture, the time scale contribution was lower. Most of the oil supply to the natural fracture was from Region 3 at the intersection between the stimulated and unstimulated regions. The temporal scale contribution was higher far from the hydraulic fracture. Most of the fluid inside the matrix and kerogen flowed through Region 3. The time scale contribution was higher in the matrix and kerogen. Additionally, in the left-hand side of Region 3, more fluid flowed to the hydraulic fracture, and therefore, the contribution was higher. However, more oil remained in the right-hand side of Region 3 and flowed through the direction parallel to the hydraulic fracture. The time scale contribution was consequently high. In the area yD = 1, the oil diffusion into Region 2 was more evident than the cross-flow, and therefore, the area with low contribution was narrower.
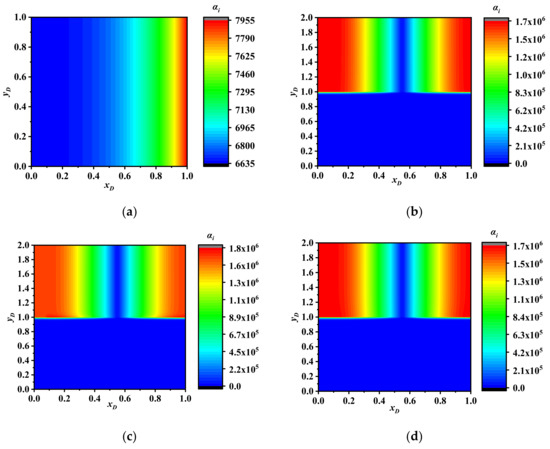
Figure 10.
Spatial distribution of time scale 8 × 10−4 contribution. (a) Natural fracture. (b) Matrix. (c) Kerogen pore. (d) Kerogen surface.
5. Conclusions
In this work, the microscopic structure of the shale reservoir was analyzed in terms of the time delay effect, Fick’s diffusion and the dynamic coupling. The spatial distribution of the time scale was researched for the first time to reveal the coupling between the time scale and spatial scale. Based on the results, the following conclusions are drawn.
- (1)
- The production was composed of five stages. Stage 1 was prolonged, while Stage 3 was shortened in the case with a larger stimulated region and time lag effect. The well rate in Stage 5 was lower when the unstimulated region had a lower diffusion coefficient, permeability, porosity or a larger size. The time lag effect reflected the production fluctuation during Stages 1–3.
- (2)
- The larger time scale had a larger contribution in the kerogen and unstimulated region, while the smaller time scale had a larger contribution in the natural fracture and stimulated region. In short, the time scale corresponded to different mediums. The oil mainly flowed through the outer boundary of the stimulated region through surface diffusion. The time scale spatial distribution diagram also showed that the oil flowed into the end point of the hydraulic fracture at an early time. Moreover, the outer boundary needed a longer time to be exploited.
- (3)
- In the time scale contribution diagram, the left-hand side peaks corresponded to the natural and hydraulic fracture network, whereas the right-hand side peaks corresponded to the unstimulated region and the surface of the kerogen pore. In the case with a tight and larger unstimulated region, small valleys existed on the left of the time scale distribution diagram, while the peaks at the right of the diagram were higher. In the case with the larger stimulated region, both the surface diffusion and the desorption of oil were promoted, and therefore, the well rate was enhanced.
Author Contributions
Data curation, M.L.; Funding acquisition, Y.S.; Writing, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Science Foundation, China (grant nos.: 52104058, and 51974348), Post-doctoral Self Innovative Project (grant no.: 20CX06094A), the Qingdao Post-doctoral Application Research Project (grant no.: qdyy20200066), and the Guizhou Science and Technology Project (grant no.: (2020)2Y028).
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Written informed consent has been obtained from the patients to publish this paper.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Symbol | Definition |
| B | Migration rate of shale oil component, s/m |
| c | Concentration, mol/m3 |
| C | Gas compressibility coefficient, Pa−1 |
| D | Diffusion coefficient, m2/s |
| h | Reservoir height, m |
| k | Permeability, m2 |
| J | Diffusion flux, mol/m3/s |
| M | Molecular mass |
| n | Number |
| p | Pressure, Pa |
| q | Mass transfer rate, m3/s |
| Q | Production, m3/s |
| R | Conventional gas constant |
| T | Temperature |
| t | Time, s |
| tj | Temporal scale |
| w | Width, m |
| x | Length along the hydraulic fracture, m |
| y | Length along the wellbore, m |
| Z | Compression factor |
| Greek letters | |
| αi | Contribution of each temporal scale |
| μ | Viscosity, Pa·s |
| σ | Transfer coefficient, s−1·Pa−1 |
| θ | Angle, ° |
| ϕ | Porosity |
| Subscripts | |
| 0 | Shale reservoir |
| D | Dimensionless |
| e | Model size |
| f | Natural fracture |
| fm | From the natural fracture to the matrix |
| i | The index of temporal scales |
| lf | Hydraulic fracture |
| m | Matrix |
| mf | From the matrix to the natural fracture |
| o | Oil |
| s | Stimulated region |
| w | Wellbore |
| ϕ | Pore |
References
- Liu, J.; Yang, Y.; Sun, S.; Yao, J.; Kou, J. Flow behaviors of shale oil in kerogen slit by molecular dynamics simulation. Chem. Eng. J. 2022, 434, 134–682. [Google Scholar] [CrossRef]
- Fakher, S.; Elgahawy, Y.; Abdelaal, H.; Imqam, A. What are the dominant flow regimes during carbon dioxide propagation in shale reservoirs’ matrix, natural fractures and hydraulic fractures? In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 10 April 2021. [Google Scholar]
- Zhang, S.; Li, Y.; Pu, H. Studies of the storage and transport of water and oil in organic-rich shale using vacuum imbibition method. Fuel 2020, 266, 117–196. [Google Scholar] [CrossRef]
- Cui, J. Oil transport in shale nanopores and micro-fractures: Modeling and analysis. J. Pet. Sci. Eng. 2019, 178, 640–648. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, Q.; Wang, S.; Xing, X. Oil diffusion in shale nanopores: Insight ofmolecular dynamics simulation. J. Mol. Liq. 2019, 290, 111–183. [Google Scholar] [CrossRef]
- Sui, H.; Zhang, F.; Wang, Z.; Wang, D.; Wang, Y. Molecular simulations of oil adsorption and transport behavior in inorganic shale. J. Mol. Liq. 2020, 305, 112–745. [Google Scholar] [CrossRef]
- Le, T.D.; Murad, M.A. A new multiscale model for flow and transport in unconventional shale oil reservoirs. Appl. Math. Model. 2018, 64, 453–479. [Google Scholar] [CrossRef]
- Su, Y.; Lu, M.; Li, M.; Zhang, Q.; Wang, W.; Dong, M. Numerical simulation of shale oil coupled flow in multi-pore media. Oil Gas Geol. 2019, 40, 651–660. [Google Scholar]
- Wang, Z.; Fan, W.; Sun, H.; Yao, J.; Zhu, G.; Zhang, L.; Yang, Y. Multiscale flow simulation of shale oil considering hydro-thermal process. Appl. Therm. Eng. 2020, 177, 115–428. [Google Scholar] [CrossRef]
- Feng, Q.; Xua, S.; Wang, S.; Li, Y.; Gao, F.; Xu, Y. Apparent permeability model for shale oil with multiple mechanisms. J. Pet. Sci. Eng. 2019, 175, 814–827. [Google Scholar] [CrossRef]
- Wang, S.; Javadpour, F.; Feng, Q. Fast mass transport of oil and supercritical carbon dioxide through organic nanopores in shale. Fuel 2016, 181, 741–758. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.; Yin, Y.; He, M.; Liu, Q.; Huang, L.; Shi, J. The transport behaviors of oil in nanopores and nanoporous media of shale. Fuel 2019, 242, 305–315. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J.; Dong, M.; Wang, J.; Li, Y.; Gong, H.; Sang, Q. A model of dynamic adsorption-diffusion for modeling gas transport and storage in shale. Fuel 2016, 173, 115–128. [Google Scholar] [CrossRef]
- Yuan, W.; Pan, Z.; Li, X.; Yang, Y.; Zhao, C.; Connell, L.D.; Li, S.; He, J. Experimental study and modelling of methane adsorption and diffusion in shale. Fuel 2014, 7, 509–519. [Google Scholar] [CrossRef]
- Singh, H.; Cai, J. A mechanistic model for multi-scale sorption dynamics in shale. Fuel 2018, 234, 996–1014. [Google Scholar] [CrossRef]
- Zhu, C.; Sheng, J.J.; Ettehadtavakkol, A.; Li, Y.; Dong, M. Numerical and experimental study of oil transfer in laminated shale. Int. J. Coal Geol. 2020, 217, 103–365. [Google Scholar] [CrossRef]
- Cao, Y.; Yan, B.; Alfi, M.; Killough, J.E. A novel compositional model of simulating fluid flow in shale reservoirs—Some priliminary tests and results. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 15 September 2015. [Google Scholar]
- Xue, Y.; Liu, J.; Liang, X.; Wang, S.; Ma, Z. Ecological risk assessment of soil and water loss by thermal enhanced methane recovery: Numerical study using two-phase flow simulation. J. Clean. Prod. 2022, 334, 130–183. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Elsworth, D. How sorption-induced matrix deformation affects gas flow in coal seams: A new FE model. Int. J. Rock Mech. Min. Sci. 2008, 45, 1226–1236. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Elsworth, D.; Miao, X.; Mao, X. Linking gas-sorption induced changes in coal permeability to directional strains through a modulus reduction ratio. Int. J. Coal Geol. 2010, 83, 21–30. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, L.; Huang, S.; Bai, Y.; Jia, P.; Wang, S.; Xu, B.; Chen, L. An approximate semianalytical method for two-phase flow analysis of liquid-rich shale gas and tight light-oil wells. J. Pet. Sci. Eng. 2019, 176, 562–572. [Google Scholar] [CrossRef]
- Sherafati, M.; Jessen, K. Modeling and simulation of mass transfer and equilibrium in tight oil formations. In Proceedings of the Unconventional Resources Technology Conference, Austin, TX, USA, 24 July 2017. [Google Scholar]
- Ericson, D.B.; Ewing, M.; Wollin, G. The Pleistocene epoch in deep-sea sediments. A complete time scale dates the beginning of the first ice age at about 112 million years ago. Deep Sea Res. Oceanogr. 1964, 12, 723–732. [Google Scholar]
- Sarlet, W. On a common derivation of the averaging method and the two-timescale method. Celest. Mech. 1977, 17, 299–311. [Google Scholar] [CrossRef]
- Qiangui, L.; Yili, K.; Jian, Y.; Hao, Z.; Lijun, Y. Study on temporal scales of mass transfer processes in developing tight sandstone gas reservoirs. Nat. Gas Geosci. 2007, 18, 149–153. (In Chinese) [Google Scholar]
- Qiangui, L.; Yili, K.; Pingya, L. Multi-scale effect in tight sandstone gas reservoir and production mechanism. Nat. Gas Ind. 2006, 26, 111–113. [Google Scholar]
- Zhang, Q.; Su, Y.; Wang, W.; Lu, M.; Sheng, G. Apparent permeability for liquid transport in nanopores of shale reservoirs: Coupling flow enhancement and near wall flow. Int. J. Heat Mass Transf. 2017, 115, 224–234. [Google Scholar] [CrossRef]
- He, Y.; Cheng, J.; Dou, X.; Wang, X. Research on shale gas transportation and apparent permeability in nanopores. J. Nat. Gas Sci. Eng. 2017, 38, 450–457. [Google Scholar] [CrossRef]
- Singh, H.; Javadpour, F. Langmuir slip-Langmuir sorption permeability model of shale. Fuel 2016, 164, 28–37. [Google Scholar] [CrossRef]
- Yildirim, A.; Öner, M.D.; Bayram, M. Fitting Fick’s model to analyze water diffusion into chickpeas during soaking with ultrasound treatment. J. Food Eng. 2011, 104, 134–142. [Google Scholar] [CrossRef]
- Higgoda, U.A.; Kankanamge, C.J.; Hellmann, R.; Koller, T.M.; Fröba, A.P. Fick diffusion coefficients of binary fluid mixtures consisting of methane, carbon dioxide, and propane via molecular dynamics simulations based on simplified pair-specific ab initio-derived force fields. Fluid Phase Equilibria 2019, 502, 112–257. [Google Scholar] [CrossRef]
- Galdi, G.P.; Pileckas, K.; Silvestre, A.L. On the unsteady Poiseuille flow in a pipe. Z. Angew. Math. Phys. 2007, 58, 994–1007. [Google Scholar] [CrossRef]
- Barbeiro, S.; Bardeji, S.G.; Ferreira, J.A. Laplace transform—Finite element method for non Fickian flows. Comput. Methods Appl. Mech. Eng. 2013, 261, 16–23. [Google Scholar] [CrossRef][Green Version]
- Branco, J.R.; Ferreira, J.A.; Oliveira, P. Numerical methods for the generalized Fisher–Kolmogorov–Petrovskii–Piskunov equation. Appl. Numer. Math. 2007, 88, 89–102. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Oliveira, P. Memory effects and random walks in reaction-transport systems. Appl. Anal. 2007, 86, 99–118. [Google Scholar] [CrossRef]
- Xie, J.; Huanga, Q.; Zhao, F. Numerical solution of nonlinear Volterra–Fredholm–Hammerstein integral equations in two-dimensional spaces based on Block Pulse functions. J. Comput. Appl. Math. 2017, 317, 565–572. [Google Scholar] [CrossRef]
- Bazm, S. Bernoulli polynomials for the numerical solution of some classes of linear and nonlinear integral equations. J. Comput. Appl. Math. 2015, 275, 44–60. [Google Scholar] [CrossRef]
- Cardone, A.; Conte, D. Multistep collocation methods for Volterra integro-differential equations. Appl. Math. Comput. 2013, 221, 770–785. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Wang, W.; Liu, J.; Lu, M.; Zhang, Q.; Ren, L. A multiple porosity media model for multi-fractured horizontal wells in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2015, 27, 1562–1573. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).