Adaptive Control of Advanced G-L Fuzzy Systems with Several Uncertain Terms in Membership-Matrices
Abstract
:1. Introduction
2. Materials and Methods
2.1. GLT Fuzzy-Model Theory
2.2. Adaptive Control Scheme
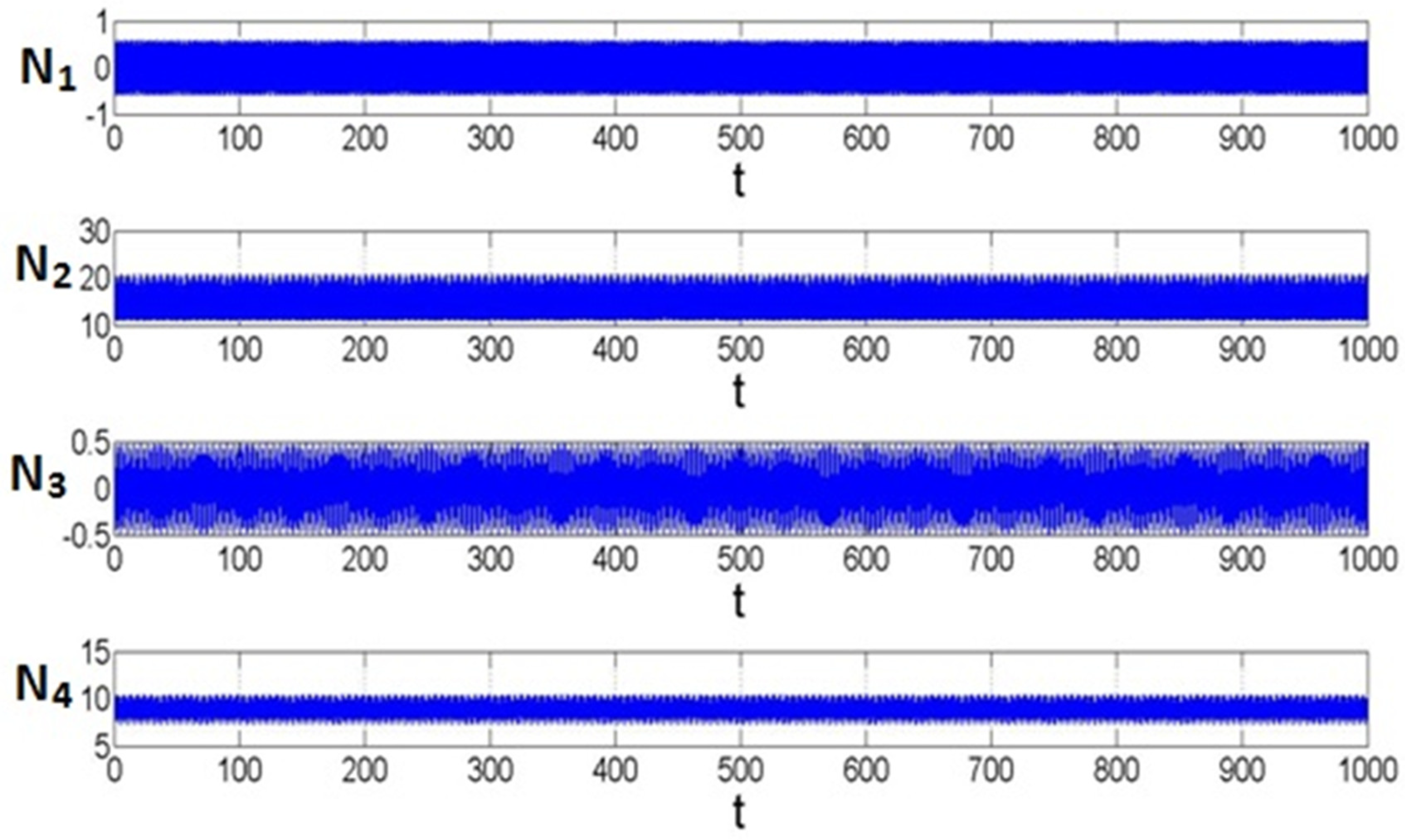
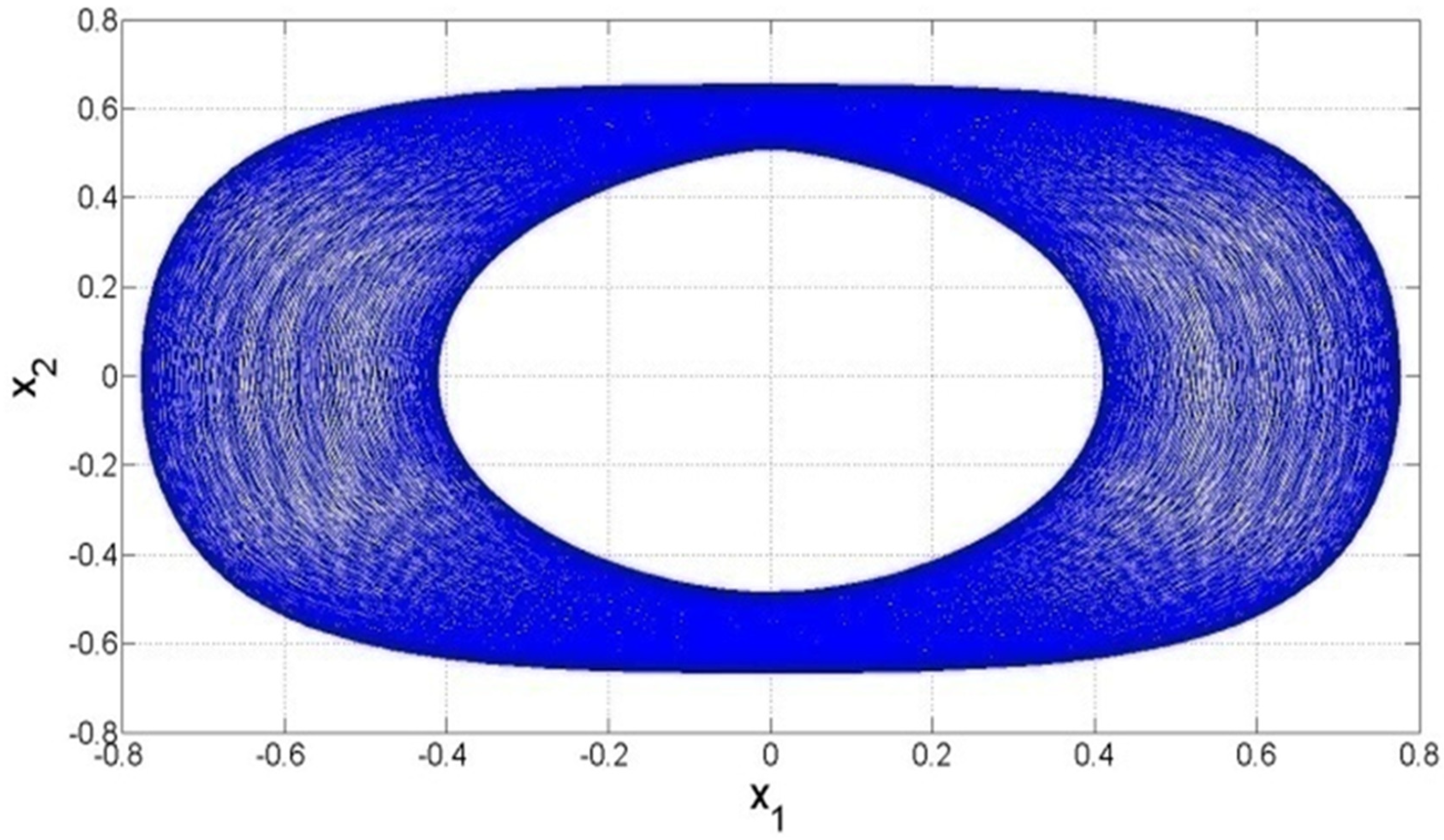
3. Simulation Results and Discussion
Fuzzy Adaptive Control of GLT Systems
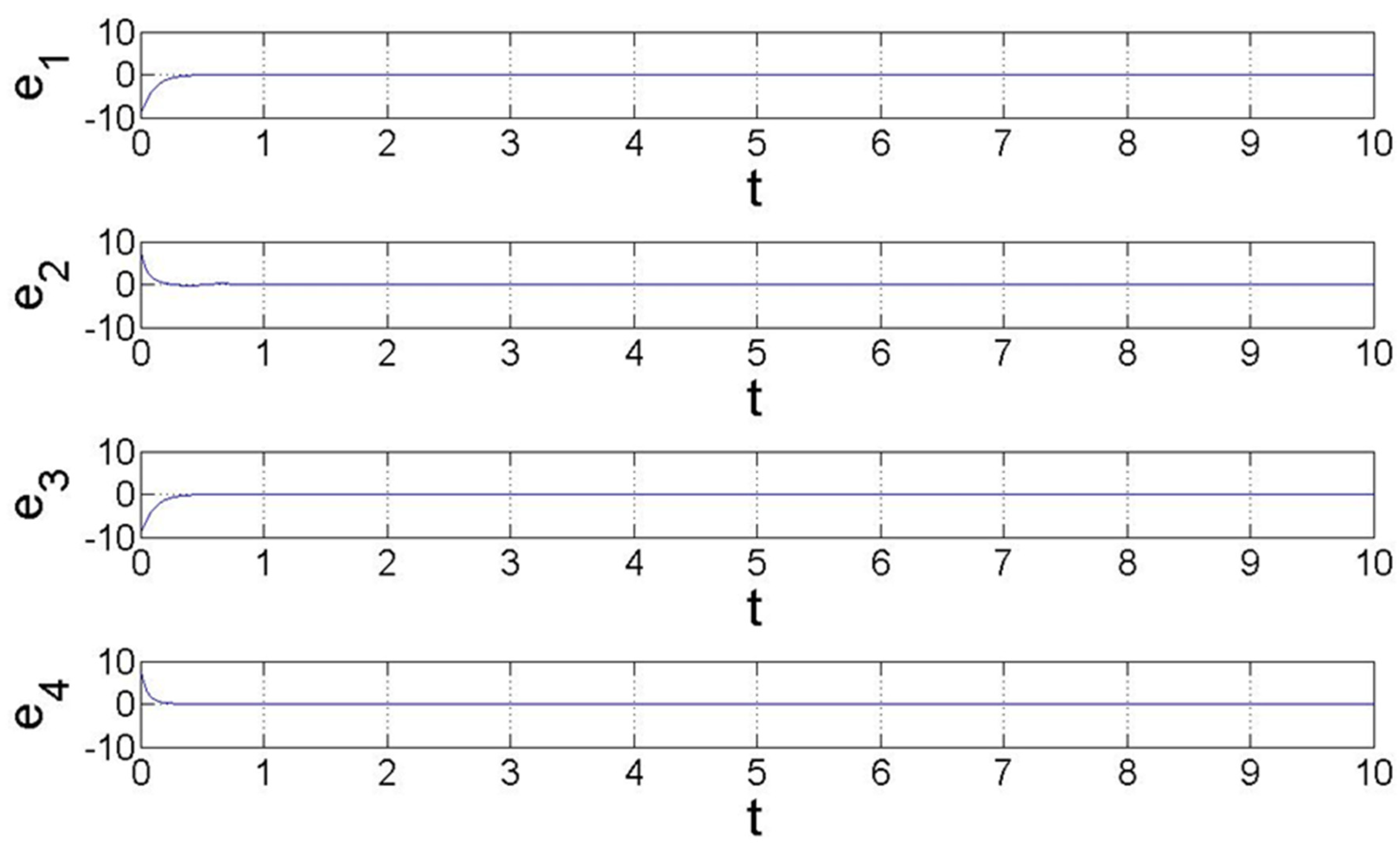
- CASE I: Parameter b3 is unknown
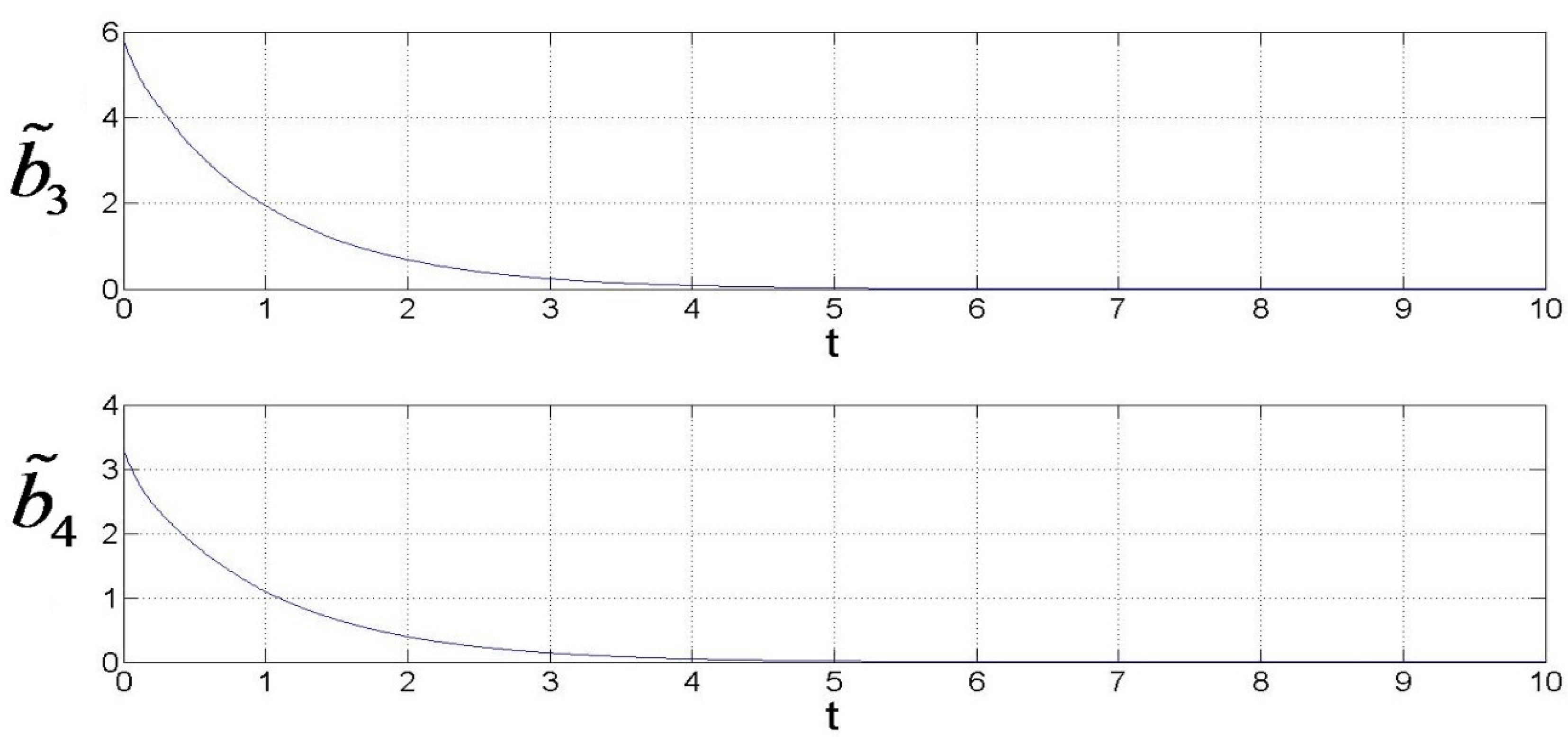
- CASE II: Parameters b3 and b4 are unknown
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy logic. Computer 1988, 21, 83–93. [Google Scholar] [CrossRef]
- Liu, B.; Han, Y.; Jiang, F.; Su, H.; Zou, J. Group controllability of discrete-time multi-agent systems. J. Franklin. Inst. 2016, 353, 3524–3559. [Google Scholar] [CrossRef]
- Khoshdast, H.; Soflaeian, A.; Shojaei, V. Coupled fuzzy logic and experimental design application for simulation of a coal classifier in an industrial environment. Physicochem. Probl. Miner. Processing 2019, 55, 504–515. [Google Scholar]
- Wang, X.-L.; Yang, G.-H.; Li, X.-J. Fault detection filter design with varying gains for multi-delay uncertain systems. J. Franklin. Inst. 2016, 353, 3699–3721. [Google Scholar] [CrossRef]
- Huang, S.-J.; Yang, G.-H.J. Fault estimation for a class of linear parameter varying systems with markovian jumps. J. Franklin. Inst. 2016, 353, 4680–4700. [Google Scholar] [CrossRef]
- He, S.; Liu, F.J. Resilient fault detection observer design of fuzzy markovian jumping systems with mode-dependent time-varying delays. J. Franklin. Inst. 2016, 353, 2943–2965. [Google Scholar] [CrossRef]
- Heydari, G.; Vali, M.; Gharaveisi, A.A. Chaotic time series prediction via artificial neural square fuzzy inference system. Expert Syst. Appl. 2016, 55, 461–468. [Google Scholar] [CrossRef]
- Dash, R.; Dash, P.J. Efficient stock price prediction using a self evolving recurrent neuro-fuzzy inference system optimized through a modified differential harmony search technique. Expert Syst. Appl. 2016, 52, 75–90. [Google Scholar] [CrossRef]
- Sosnowski, M.; Krzywanski, J.; Scurek, R. A Fuzzy Logic Approach for the Reduction of Mesh-Induced Error in CFD Analysis: A Case Study of an Impinging Jet. Entropy 2019, 21, 1047. [Google Scholar] [CrossRef] [Green Version]
- Krzywanski, J. Heat Transfer Performance in a Superheater of an Industrial CFBC Using Fuzzy Logic-Based Methods. Entropy 2019, 21, 919. [Google Scholar] [CrossRef] [Green Version]
- Akbar, H.; Özlem, M.T.; Güldal, G.; Reza, V.B. Development of a fuzzy logic based model to elucidate the effect of FSW parameters on the ultimate tensile strength and elongation of pure copper joints. J. Manuf. Process. 2020, 53, 250–259. [Google Scholar]
- Thillaigovindan, N.; Shanthi, S.A.; Naidu, J.V. A better score function for multiple criteria decision making in fuzzy environment with criteria choice under risk. Expert Syst. Appl. 2016, 59, 78–85. [Google Scholar] [CrossRef]
- Li, S.-Y.; Ge, Z.-M. Generalized synchronization of chaotic systems with different orders by fuzzy logic constant controller. Expert Syst. Appl. 2011, 38, 2302–2310. [Google Scholar] [CrossRef]
- Li, S.-Y. Chaos control of new mathieu–van der pol systems by fuzzy logic constant controllers. Appl. Soft Comput. 2011, 11, 4474–4487. [Google Scholar] [CrossRef]
- Dong, G.; Ren, H.; Yao, D.; Li, H.; Lu, R. Prescribed Performance Consensus Fuzzy Control of Multiagent Systems With Nonaffine Nonlinear Faults. IEEE Trans. Fuzzy Syst. 2021, 29, 3936–3946. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, W.; Ma, H.; Li, H. Event-Triggered Fuzzy Adaptive Containment Control for Nonlinear Multiagent Systems With Unknown Bouc–Wen Hysteresis Input. IEEE Trans. Fuzzy Syst. 2021, 29, 731–741. [Google Scholar] [CrossRef]
- Li, H.; Wu, Y.; Chen, M. Adaptive Fault-Tolerant Tracking Control for Discrete-Time Multiagent Systems via Reinforcement Learning Algorithm. IEEE Trans. Cybern. 2021, 51, 1163–1174. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Lam, H.-K.; Zhou, Q.; Du, H. Adaptive sliding mode control for interval type-2 fuzzy systems. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1654–1663. [Google Scholar] [CrossRef]
- Zhang, J.; Tong, S.-C.; Li, Y.-M. Adaptive Fuzzy Finite-Time Output-Feedback Fault-Tolerant Control of Nonstrict-Feedback Systems Against Actuator Faults. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1276–1287. [Google Scholar] [CrossRef]
- Li, K.; Li, Y.; Zong, G. Adaptive Fuzzy Fixed-Time Decentralized Control for Stochastic Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2021, 29, 3428–3440. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, J.; Zhang, Q.; Zhang, D. Dissipative control for t–s fuzzy descriptor systems with actuator saturation and disturbances. J. Frankl. Inst. 2016, 353, 4950–4978. [Google Scholar] [CrossRef]
- Su, X.; Shi, P.; Wu, L.; Basin, M. Reliable filtering with strict dissipativity for ts fuzzy time-delay systems. IEEE Trans. Cybern. 2014, 44, 2470–2483. [Google Scholar] [PubMed]
- Li, S.-Y.; Hernández, M.A.B. Robust synchronization of chaotic systems with novel fuzzy rule-based controllers. Inf. Sci. 2019, 481, 604–615. [Google Scholar] [CrossRef]
- Derakhshan, S.F.; Fatehi, A.; Sharabiany, M.G. Nonmonotonic observer-based fuzzy controller designs for discrete time ts fuzzy systems via LMI. IEEE Trans. Cybern. 2014, 44, 2557–2567. [Google Scholar] [CrossRef]
- Nagamani, G.; Ramasamy, S.J. Dissipativity and passivity analysis for discrete-time t–s fuzzy stochastic neural networks with leakage time-varying delays based on abel lemma approach. J. Frankl. Inst. 2016, 353, 3313–3342. [Google Scholar] [CrossRef]
- Wang, S.; Fei, J. Robust adaptive sliding mode control of mems gyroscope using t–s fuzzy model. Nonlinear Dyn. 2014, 77, 361–371. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, M.; Zhang, Q. Non-fragile static output feedback control for singular t–s fuzzy delay-dependent systems subject to markovian jump and actuator saturation. J. Franklin. Inst. 2016, 353, 2373–2397. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.; Li, Y.; Qi, Z.; Chu, Y. Improvement on stability conditions for continuous-time t–s fuzzy systems. J. Franklin. Inst. 2016, 353, 2218–2236. [Google Scholar] [CrossRef]
- Hsueh, Y.-C.; Su, S.-F.; Chen, M.-C. Decomposed fuzzy systems and their application in direct adaptive fuzzy control. IEEE Trans. Cybern. 2014, 44, 1772–1783. [Google Scholar] [CrossRef]
- Xie, X.-P.; Liu, Z.-W.; Zhu, X.-L. Systems. An efficient approach for reducing the conservatism of lmi-based stability conditions for continuous-time t–s fuzzy systems. Fuzzy Sets Syst. 2015, 263, 71–81. [Google Scholar] [CrossRef]
- Zhang, J.H.; Shi, P.; Xia, Y.Q. Fuzzy delay compensation control for t-s fuzzy systems over network. IEEE Trans. Cybern. 2013, 43, 259–268. [Google Scholar] [CrossRef] [PubMed]
- Jee, S.C.; Lee, H. H−/h∞ fault detection and isolation for nonlinear systems with state delay in t–s form. J. Franklin. Inst. 2016, 353, 2030–2056. [Google Scholar] [CrossRef]
- Song, M.K.; Park, J.B.; Joo, Y.H. Systems. Robust stabilization for uncertain markovian jump fuzzy systems based on free weighting matrix method. Fuzzy Sets Syst. 2015, 277, 81–96. [Google Scholar] [CrossRef]
- Wu, Z.-G.; Shi, P.; Su, H.; Chu, J. Sampled-data fuzzy control of chaotic systems based on a t–s fuzzy model. IEEE Trans. Fuzzy Syst. 2013, 22, 153–163. [Google Scholar] [CrossRef]
- Wu, Z.G.; Shi, P.; Su, H.Y.; Chu, J. Reliable h-infinity control for discrete-time fuzzy systems with infinite-distributed delay. IEEE Trans. Fuzzy Syst. 2012, 20, 22–31. [Google Scholar]
- Li, S.-Y.; Ge, Z.-M. Fuzzy modeling and synchronization of two totally different chaotic systems via novel fuzzy model. IEEE Trans. Syst. Man Cybern. 2011, 41, 1015–1026. [Google Scholar]
- Liu, M.; Zhang, S.; Tang, X.; Fan, Z.; Zheng, S. Optimal H∞ filtering for discrete-time-delayed chaotic systems via a unified model. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; IEEE: Piscataway, NJ, USA; pp. 2553–2560. [Google Scholar]
- Liu, M.; Zhang, S.; Fan, Z.; Zheng, S.; Sheng, W. Exponential h∞ synchronization and state estimation for chaotic systems via a unified model. IEEE Trans. Neural Netw Learn Syst. 2013, 24, 1114–1126. [Google Scholar]
- Hsiao, F.-H. Delay-Dependent Exponential Optimal Synchronization for Nonidentical Chaotic Systems via Neural-Network-Based Approach. In Abstract and Applied Analysis; Hindawi: London, UK, 2013. [Google Scholar]
- Liu, M.; Chen, H.; Zhang, S.; Sheng, W. Automation; Systems. H∞ synchronization of two different discrete-time chaotic systems via a unified model. Int. J. Control. Autom. Syst. 2015, 13, 212–221. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, B.; Qin, J.; Gao, H.; Karimi, H.R. H∞ consensus and synchronization of nonlinear systems based on a novel fuzzy model. IEEE Trans. Cybern. 2013, 43, 2157–2169. [Google Scholar] [CrossRef]
- Wen, S.; Bao, G.; Zeng, Z.; Chen, Y.; Huang, T. Global exponential synchronization of memristor-based recurrent neural networks with time-varying delays. Neural Netw. 2013, 48, 195–203. [Google Scholar] [CrossRef] [PubMed]
- Wen, S.; Zeng, Z.; Huang, T.; Chen, Y. Fuzzy modeling and synchronization of different memristor-based chaotic circuits. Mod. Phys. Lett. 2013, 377, 2016–2021. [Google Scholar] [CrossRef]
- Wen, S.; Zeng, Z.; Huang, T.; Simulation, N. Event-based control for memristive systems. Commun Nonlinear Sci Numer Simul. 2014, 19, 3431–3443. [Google Scholar] [CrossRef]
- Wen, S.; Zeng, Z.; Huang, T.; Zhang, Y. Exponential adaptive lag synchronization of memristive neural networks via fuzzy method and applications in pseudorandom number generators. IEEE Trans. Fuzzy Syst. 2013, 22, 1704–1713. [Google Scholar] [CrossRef]
- Hassan, M.F.J.A.M. A new approach for secure communication using constrained hyperchaotic systems. Appl. Math. Comput. 2014, 246, 711–730. [Google Scholar] [CrossRef]
- Chen, C.-K.; Lin, C.-L.; Lin, S.-L.; Chiang, C.-T. Data encryption and transmission based on personal ecg signals. Sensor Netw Data Commun. 2015, 4, 1–13. [Google Scholar] [CrossRef]
- Li, S.-Y.; Hernández, M.A.B.; Tam, L.-M.; Chen, C.S. A Cloud Image Data Protection Algorithm with Multi-Level Encryption Scheme and Automated-Selection Mechanism. Appl. Sci. 2019, 9, 5146. [Google Scholar] [CrossRef] [Green Version]
- Hassan, M.F. Synchronization of uncertain constrained hyperchaotic systems and chaos-based secure communications via a novel decomposed nonlinear stochastic estimator. Nonlinear Dyn. 2016, 83, 2183–2211. [Google Scholar] [CrossRef]
- Wu, Z.-G.; Shi, P.; Su, H.; Chu, J. Local synchronization of chaotic neural networks with sampled-data and saturating actuators. IEEE Trans. Cybern. 2014, 44, 2635–2645. [Google Scholar]
- Wang, Z.-P.; Wu, H.-N. On fuzzy sampled-data control of chaotic systems via a time-dependent lyapunov functional approach. IEEE Trans. Cybern. 2014, 45, 819–829. [Google Scholar] [CrossRef]
- Yan, S.; Qian, C.; Huang, T. Global asymptotic synchronization of a class of non-linear systems via sampled-data feedback. Trans. Inst. Meas. Control. 2018, 40, 12–21. [Google Scholar] [CrossRef]
- Li, S.-Y.; Yang, C.-H.; Lin, C.-T.; Ko, L.-W.; Chiu, T.-T. Chaotic motions in the real fuzzy electronic circuits. In Abstract and Applied Analysis; Hindawi: London, UK, 2013. [Google Scholar]
- Liu, M.; Chen, H.; Zhang, S.; Fan, Z. Applications. Exponential synchronization of two totally different chaotic systems based on a unified model. Neural Comput Applic. 2014, 25, 1801–1808. [Google Scholar] [CrossRef]
- Li, S.-Y.; Ko, L.-W.; Lin, C.-T.; Tam, L.-M.; Chen, H.-K.; Lao, S.-K. System modeling and synchronization of nonlinear chaotic systems with uncertainty and disturbance by innovative fuzzy modeling strategy. In Proceedings of the 2013 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Hyderabad, India, 7–10 July 2013; pp. 1–5. [Google Scholar]
- Manju, A.; Nigam, M.J. Applications of quantum inspired computational intelligence: A survey. Artif. Intell. Rev. 2014, 42, 79–156. [Google Scholar] [CrossRef]
- Li, S.-Y.; Chen, H.-K.; Tam, L.-M.; Huang, S.-C.; Ge, Z.-M. Pragmatical adaptive synchronization–new fuzzy model of two different and complex chaotic systems by new adaptive control. Inf. Sci. 2014, 277, 458–480. [Google Scholar] [CrossRef]
- Shen, Z.-P.; Yan, R.; Wu, Y.-L. Tracking control of Uncertain Chaotic System. Electro-Opti. Control 2015, 11, 52–55. [Google Scholar]
- Tam, L.-M.; Li, S.-Y. Novel-fuzzy-model based modeling and control of nonlinear chaotic systems with uncertainty. In Proceedings of the 2015 International Conference on Advanced Robotics and Intelligent Systems (ARIS), Taipei, Taiwan, 29–31 May 2015; pp. 1–6. [Google Scholar]
- Li, S.-Y.; Tam, L.-M.; Tsai, S.-E.; Ge, Z.-M. Novel fuzzy modeling and synchronization of chaotic systems with multinonlinear terms by advanced ge-li fuzzy model. IEEE Trans. Cybern. 2015, 46, 2228–2237. [Google Scholar] [CrossRef]
- Egardt, B. Stability of Adaptive Controllers; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Landau, Y.D. Adaptive Control: The Model Reference Approach; Marcel Dekker, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Liu, Y.-J.; Tong, S. Systems. Adaptive fuzzy control for a class of unknown nonlinear dynamical systems. Fuzzy Sets Syst. 2015, 263, 49–70. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Tong, S. Adaptive fuzzy identification and control for a class of nonlinear pure-feedback mimo systems with unknown dead zones. IEEE Trans. Fuzzy Syst. 2014, 23, 1387–1398. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Tong, S.; Li, D.-J.; Gao, Y. Fuzzy adaptive control with state observer for a class of nonlinear discrete-time systems with input constraint. IEEE Trans. Fuzzy Syst. 2015, 24, 1147–1158. [Google Scholar] [CrossRef]
- Tong, S.; Zhang, L.; Li, Y. Observed-based adaptive fuzzy decentralized tracking control for switched uncertain nonlinear large-scale systems with dead zones. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 37–47. [Google Scholar] [CrossRef]
- Chen, C.P.; Liu, Y.-J.; Wen, G.-X. Fuzzy neural network-based adaptive control for a class of uncertain nonlinear stochastic systems. IEEE Trans Cybern. 2013, 44, 583–593. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.-M.; Yu, J.-K.; Chen, Y.-T. Pragmatical asymptotical stability theorem with application to satellite system. Jpn. J. Appl. Phys. 1999, 38, 6178. [Google Scholar] [CrossRef]
- Ge, Z.-M.; Yu, J.-K. Pragmatical asymptotical stability theorems on partial region and for partial variables with applications to gyroscopic systems. J. Mech. 2000, 16, 179–187. [Google Scholar] [CrossRef]
- Fortuna, L.; Porto, D. Quantum-cnn to generate nanoscale chaotic oscillators. Int. J. Bifurc. Chaos 2004, 14, 1085–1089. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.-Y.; Tsai, S.-H.; Chen, C.-S.; Tam, L.-M. Adaptive Control of Advanced G-L Fuzzy Systems with Several Uncertain Terms in Membership-Matrices. Processes 2022, 10, 1043. https://doi.org/10.3390/pr10051043
Li S-Y, Tsai S-H, Chen C-S, Tam L-M. Adaptive Control of Advanced G-L Fuzzy Systems with Several Uncertain Terms in Membership-Matrices. Processes. 2022; 10(5):1043. https://doi.org/10.3390/pr10051043
Chicago/Turabian StyleLi, Shih-Yu, Shun-Hung Tsai, Chin-Sheng Chen, and Lap-Mou Tam. 2022. "Adaptive Control of Advanced G-L Fuzzy Systems with Several Uncertain Terms in Membership-Matrices" Processes 10, no. 5: 1043. https://doi.org/10.3390/pr10051043
APA StyleLi, S.-Y., Tsai, S.-H., Chen, C.-S., & Tam, L.-M. (2022). Adaptive Control of Advanced G-L Fuzzy Systems with Several Uncertain Terms in Membership-Matrices. Processes, 10(5), 1043. https://doi.org/10.3390/pr10051043







