Study on the Damping Dynamics Characteristics of a Viscoelastic Damping Material
Abstract
:1. Introduction
2. Basic Theory of Modal Analysis
3. Experiments
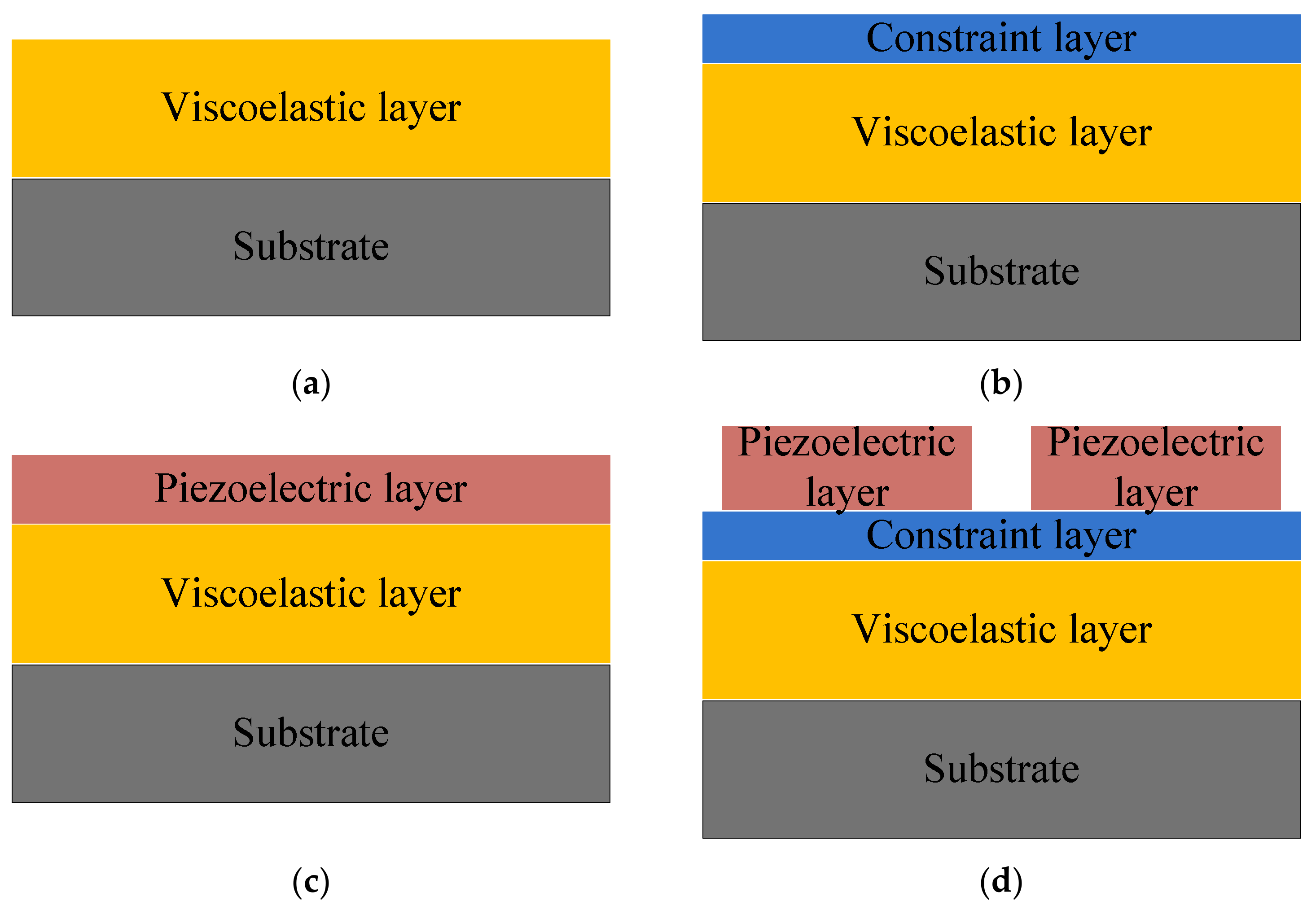
3.1. Experimental Materials
3.2. Experimental Method
3.2.1. DMA Experimental Method
- Fixture mode: Film stretching fixture
- Temperature range: −50 °C~150 °C
- Selected frequency: 1 Hz, 10 Hz, 22 Hz, 50 Hz, 136 Hz
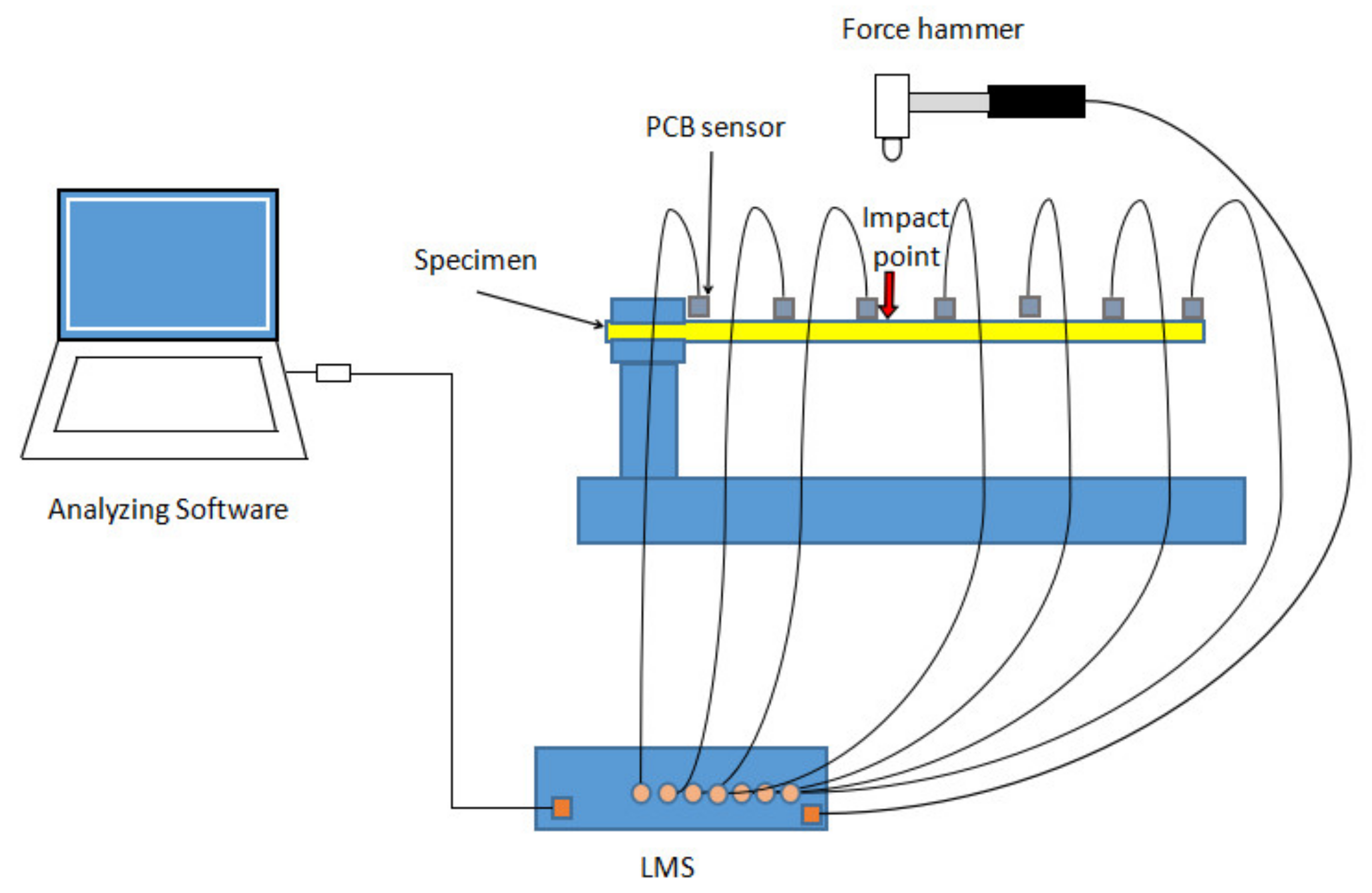
3.2.2. Experimental Modal Analysis
4. Experimental Test Analysis
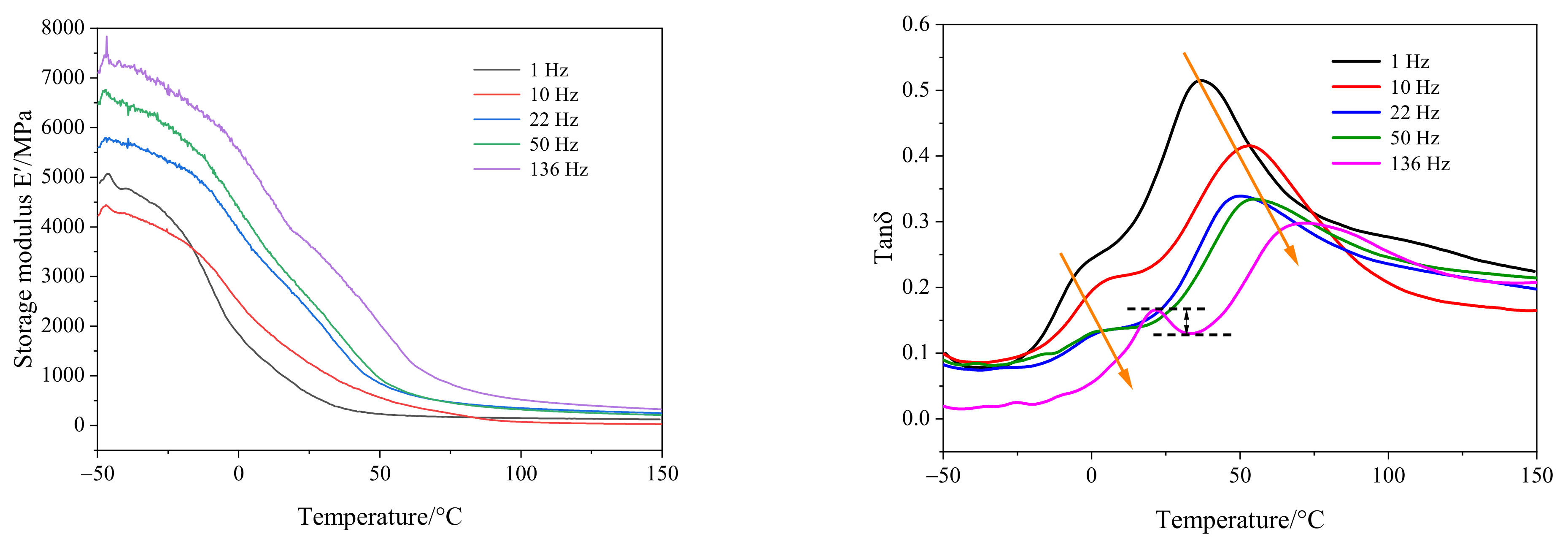
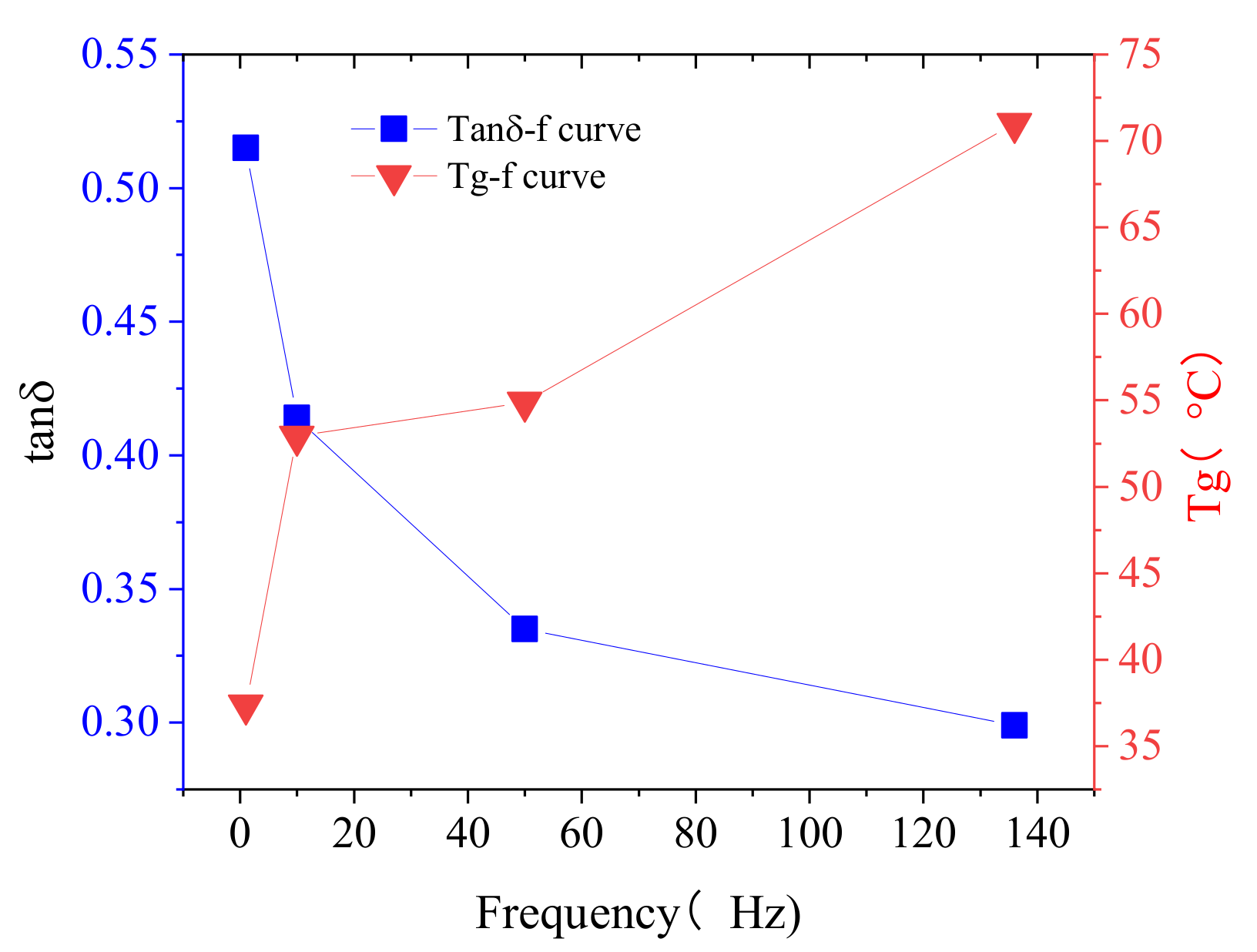
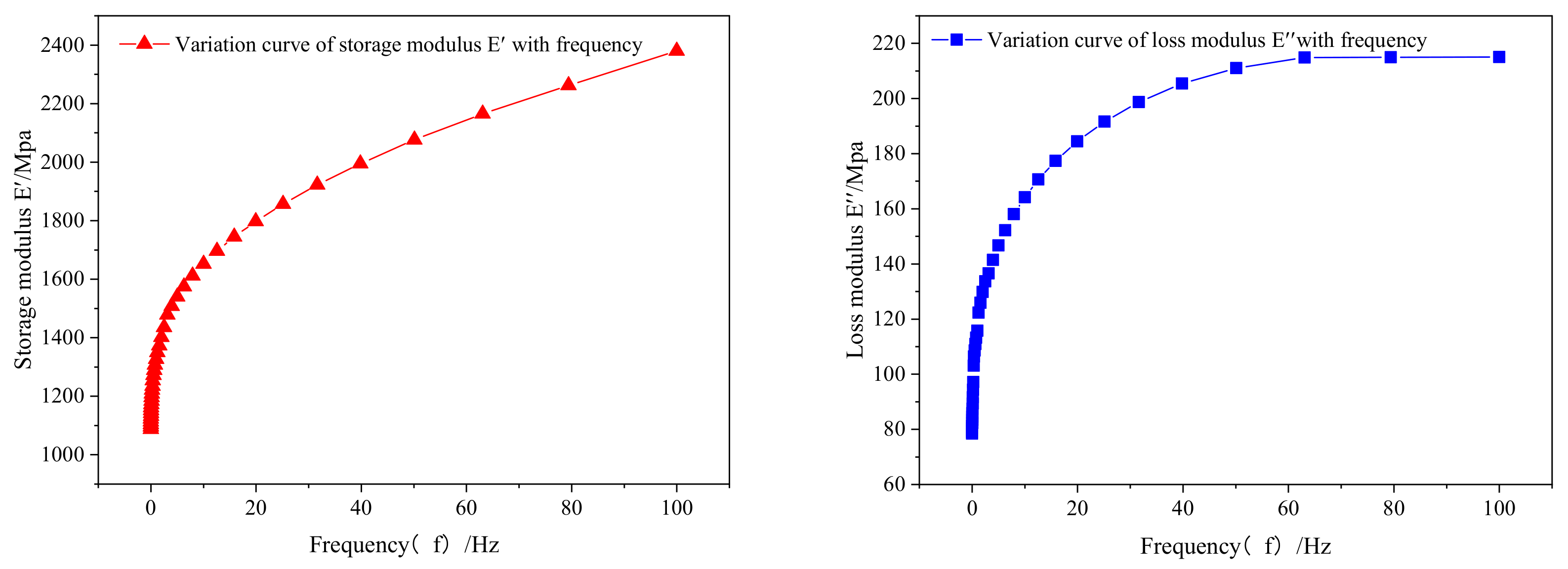
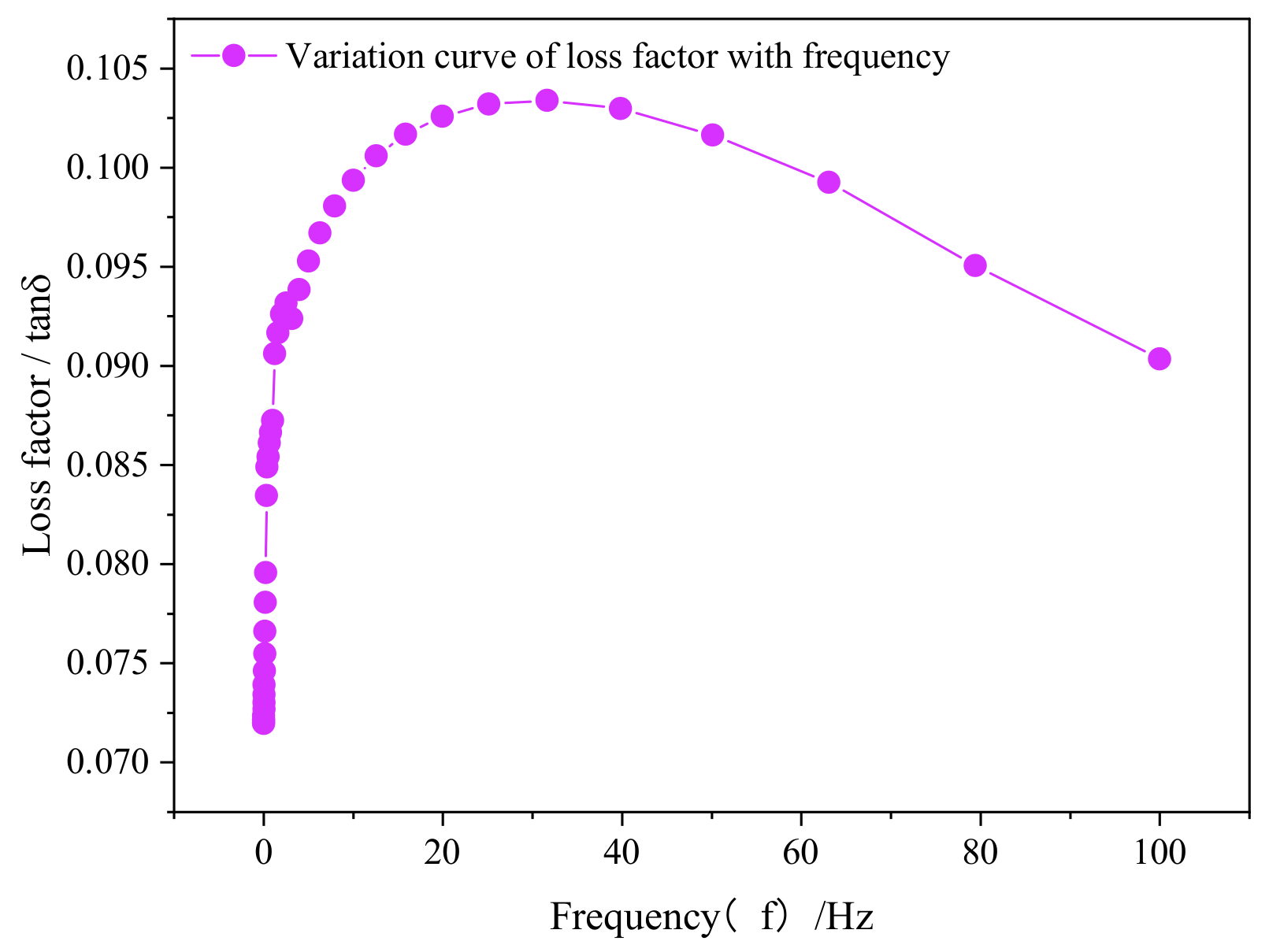
4.1. DMA Test Analysis
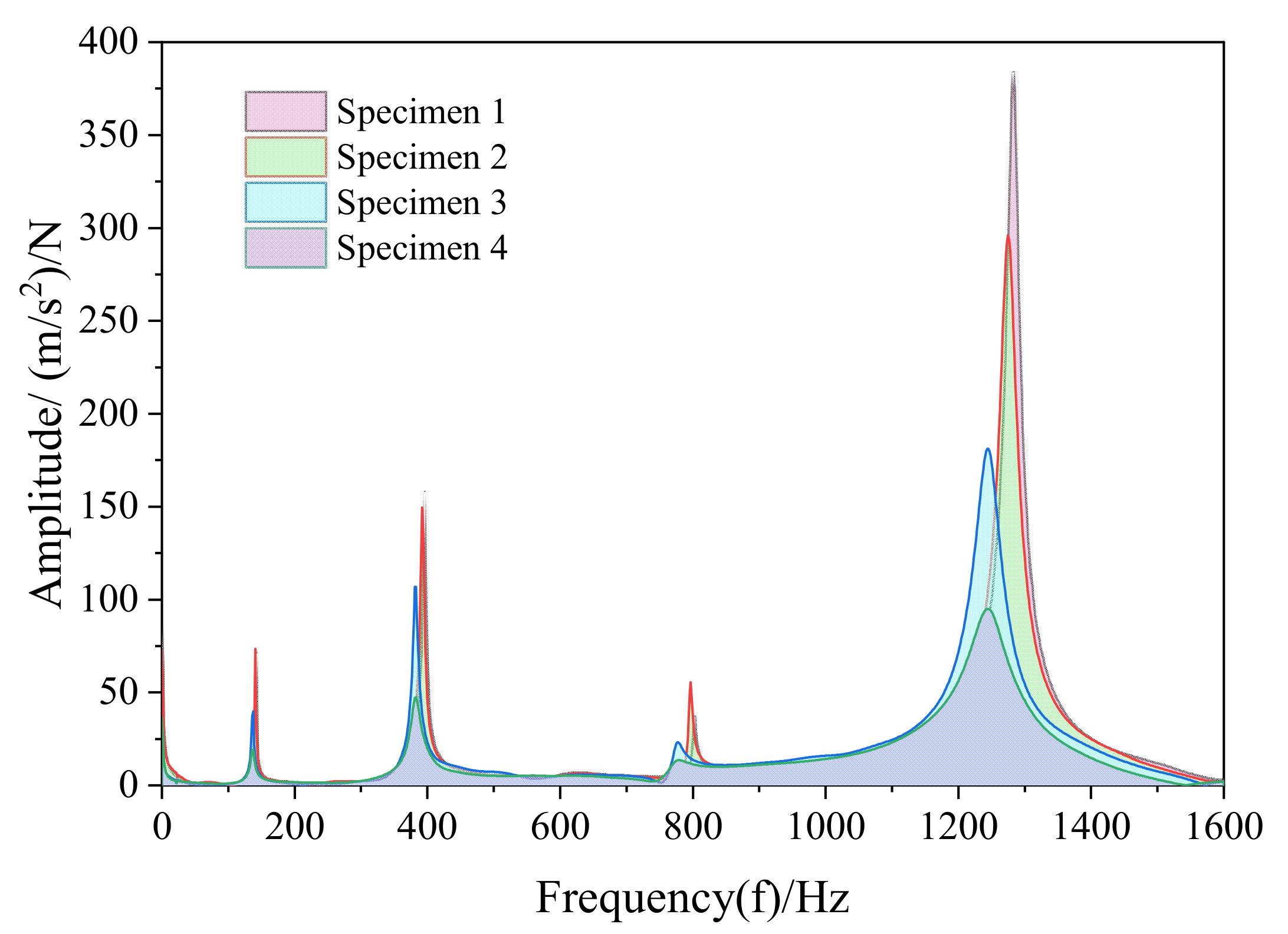
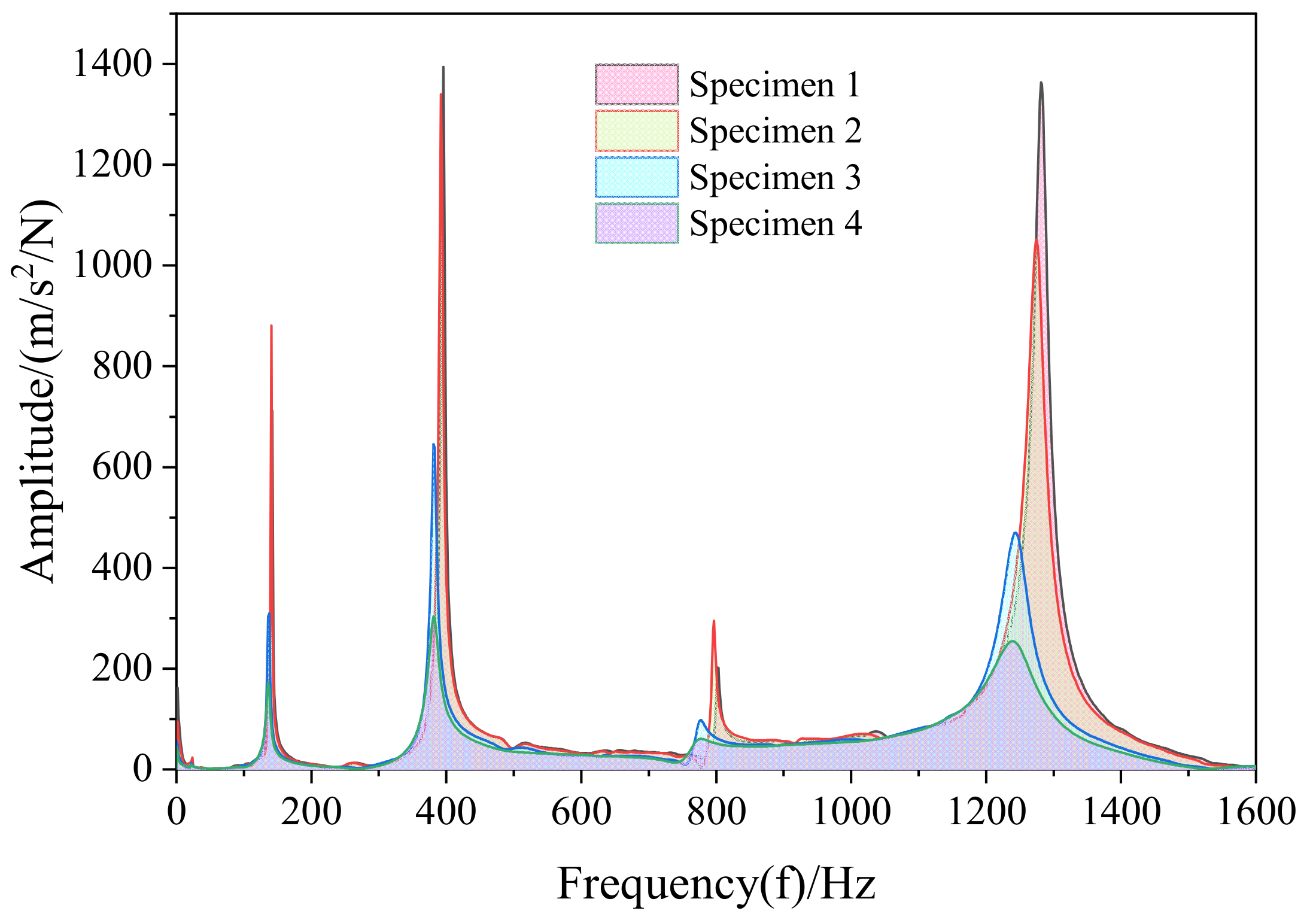
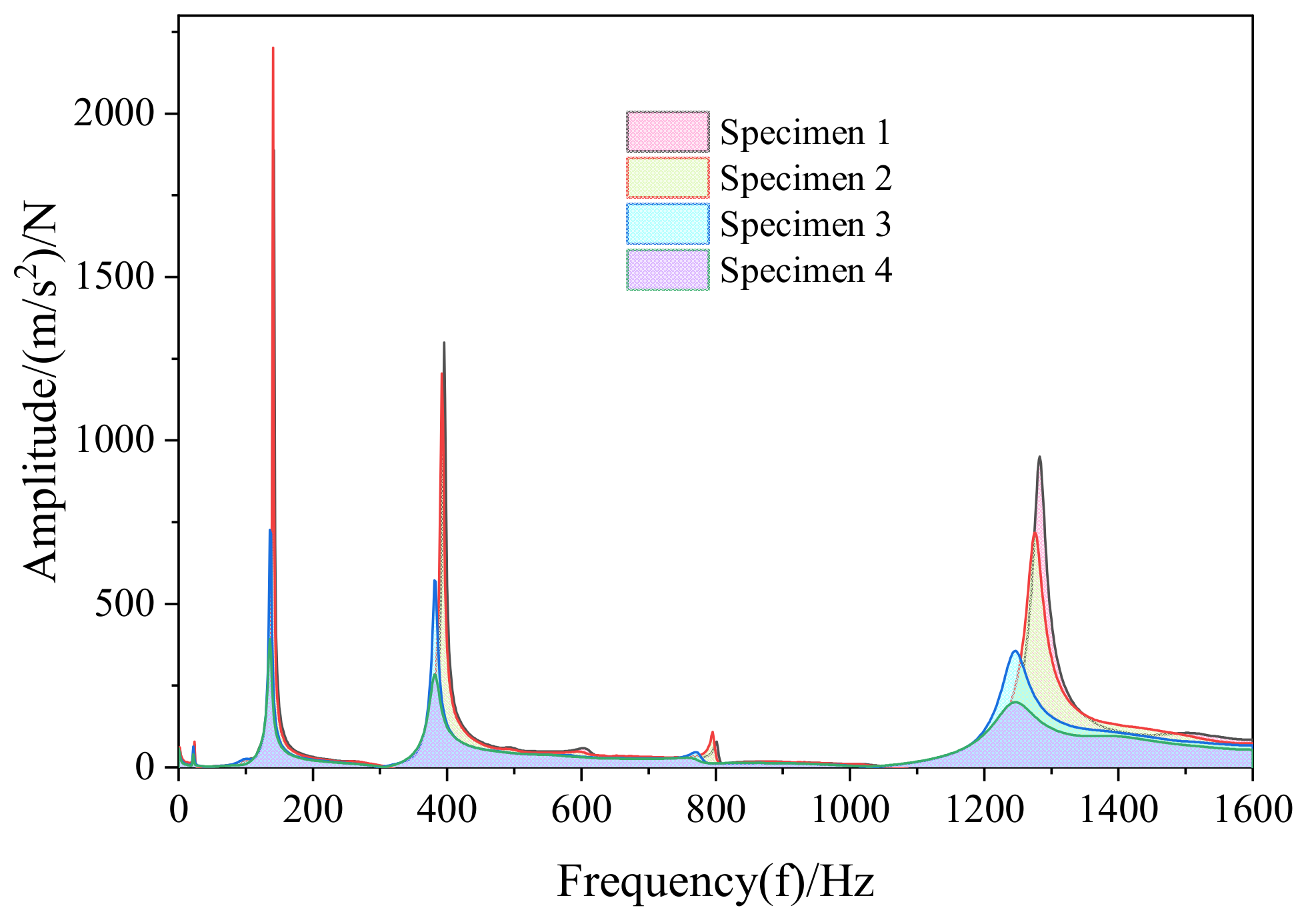
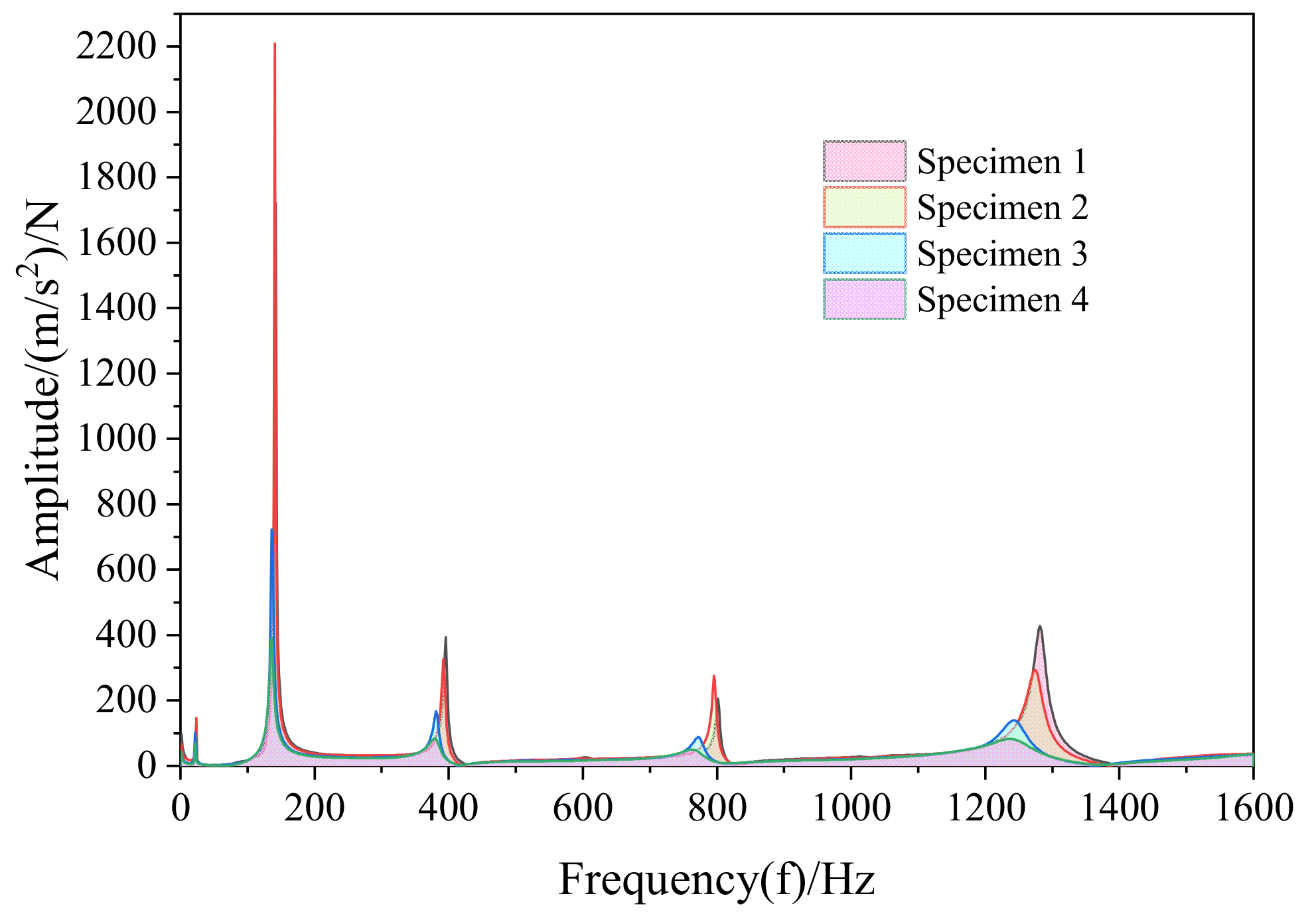
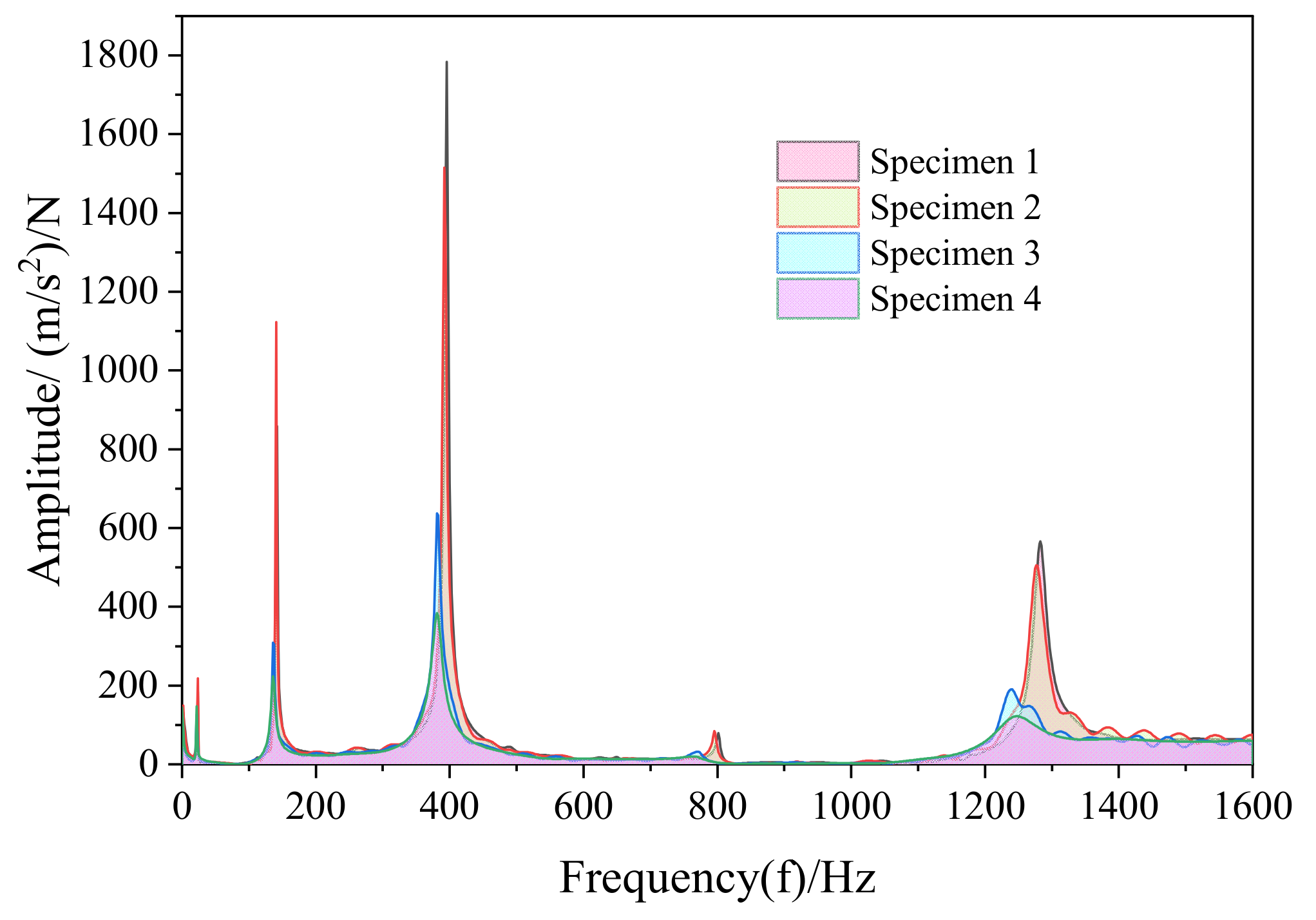
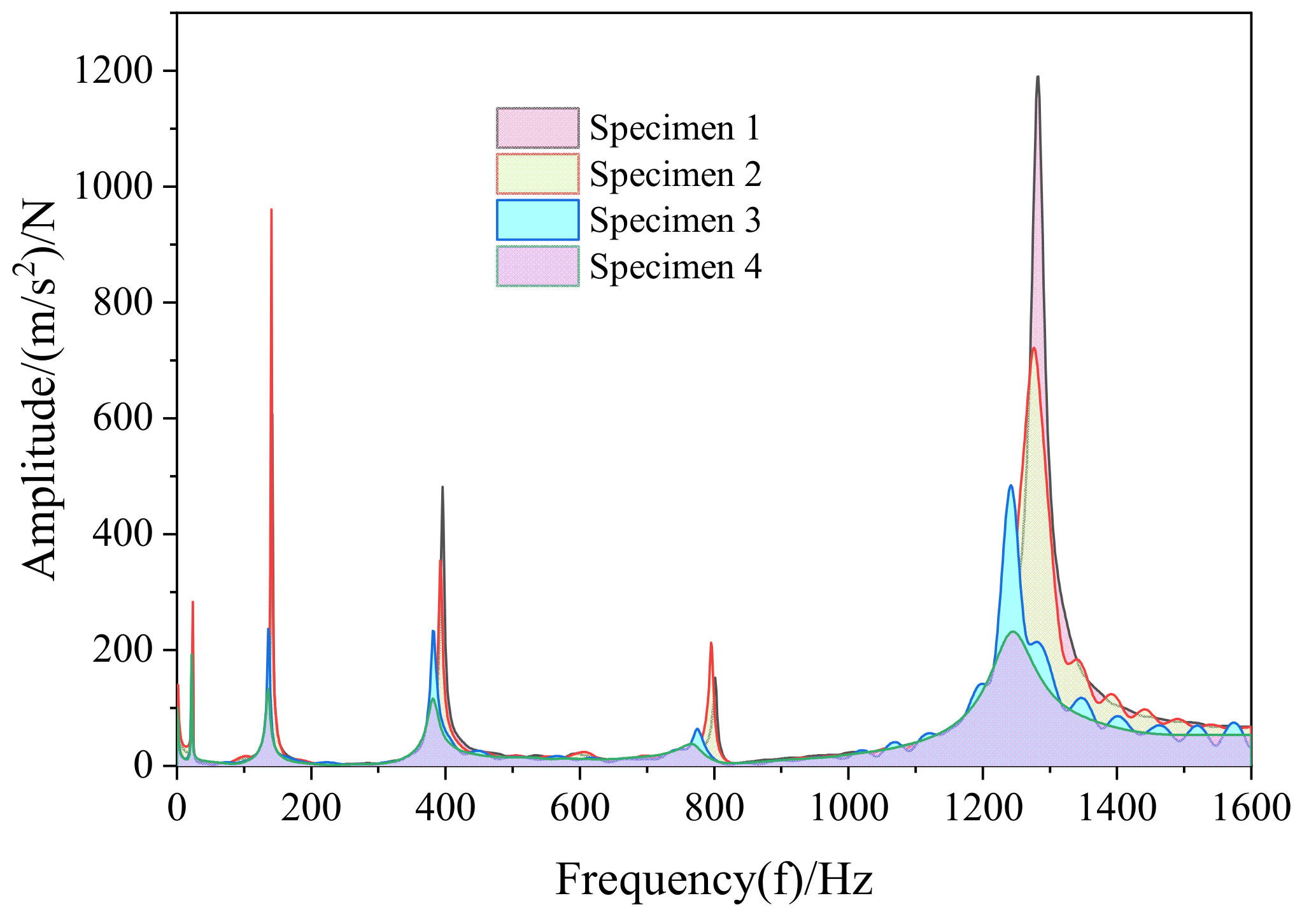
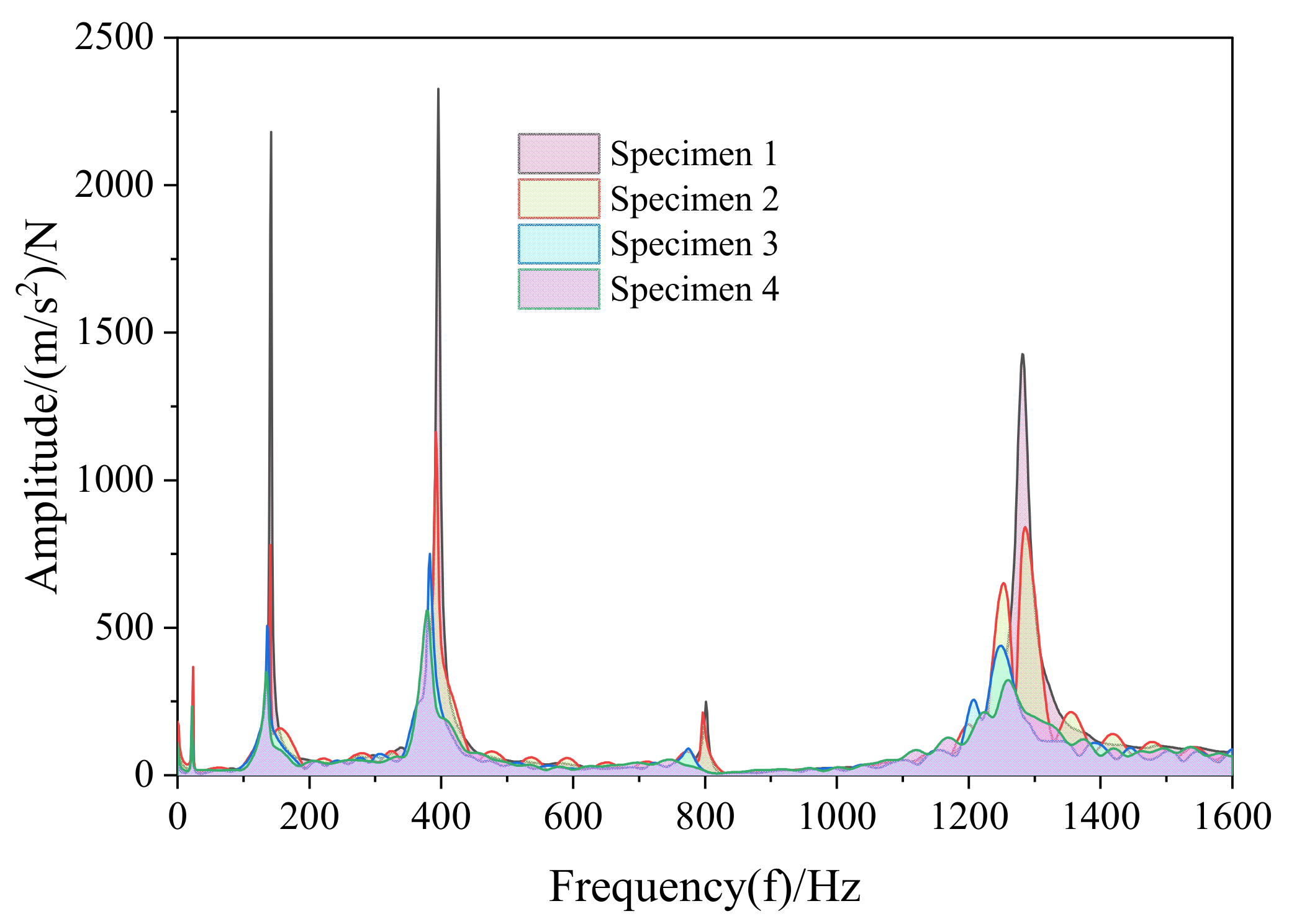
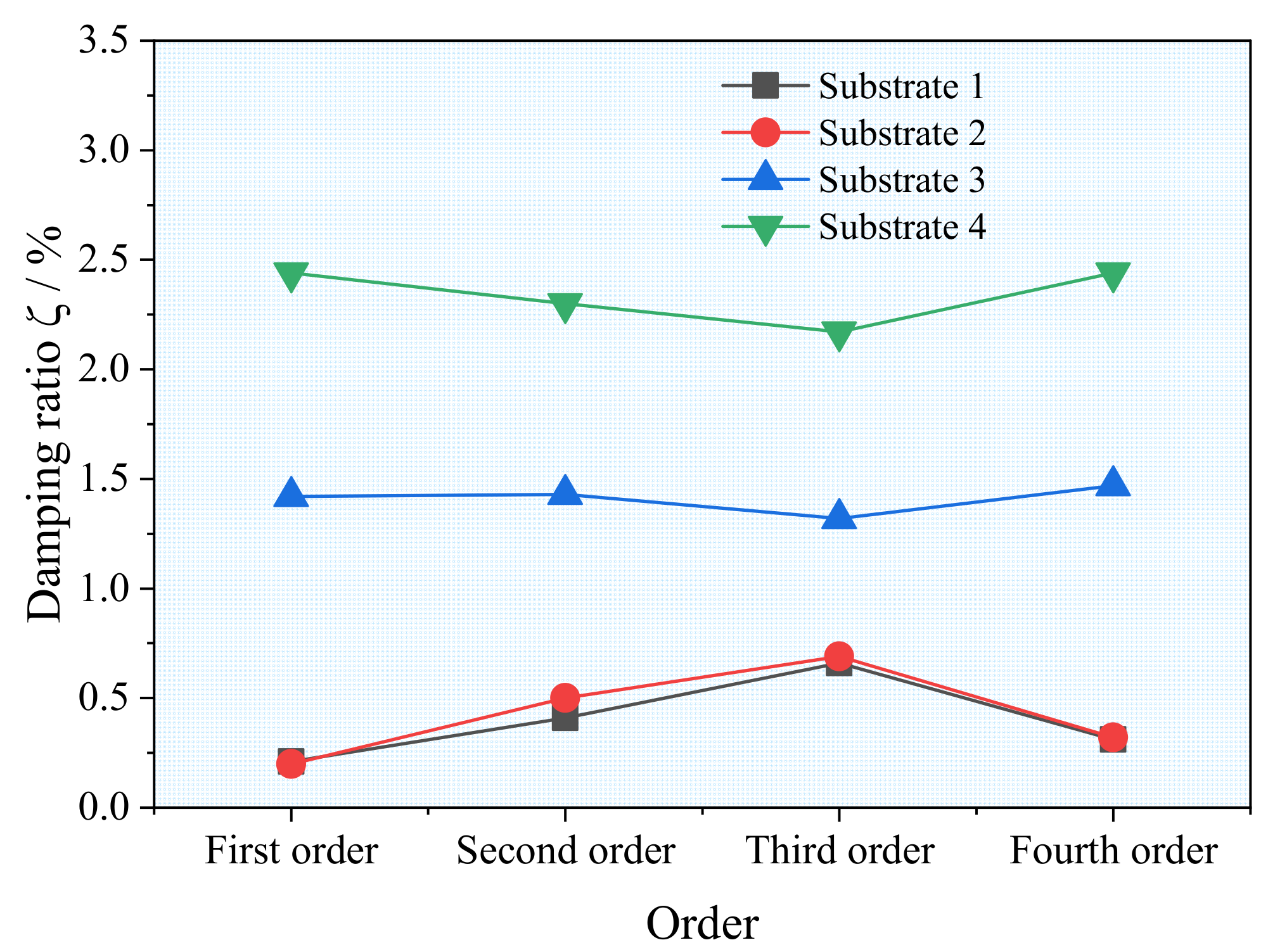
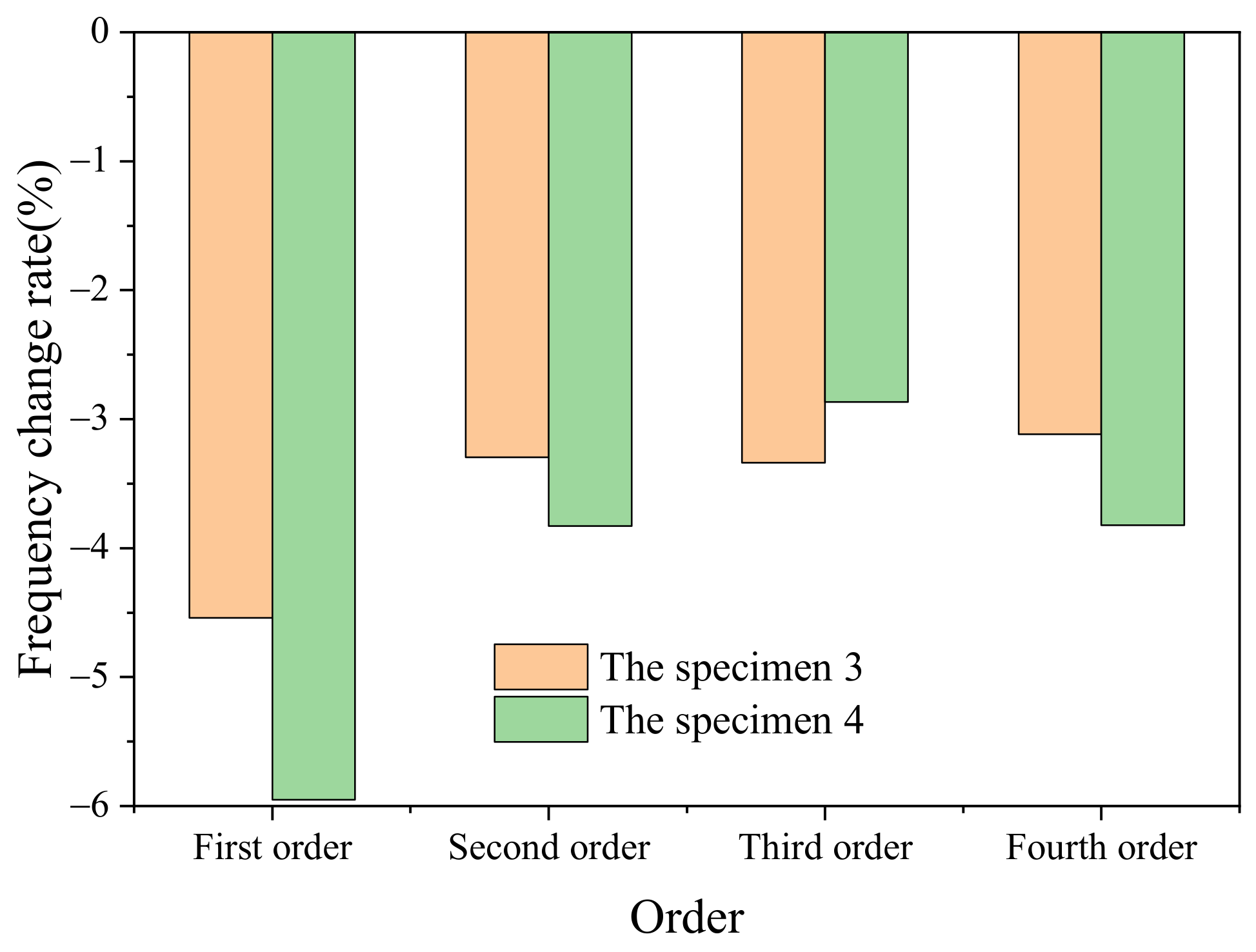
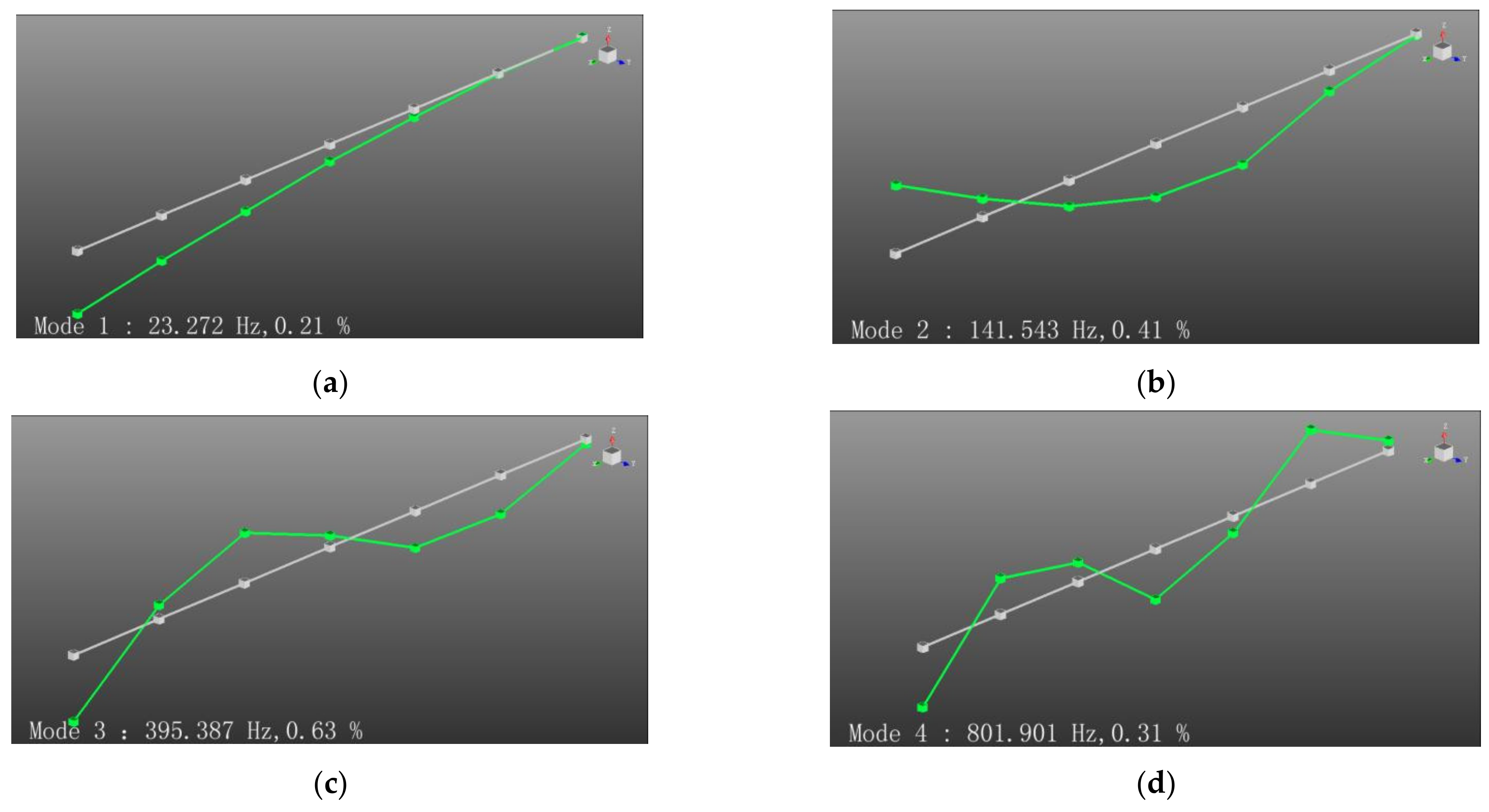
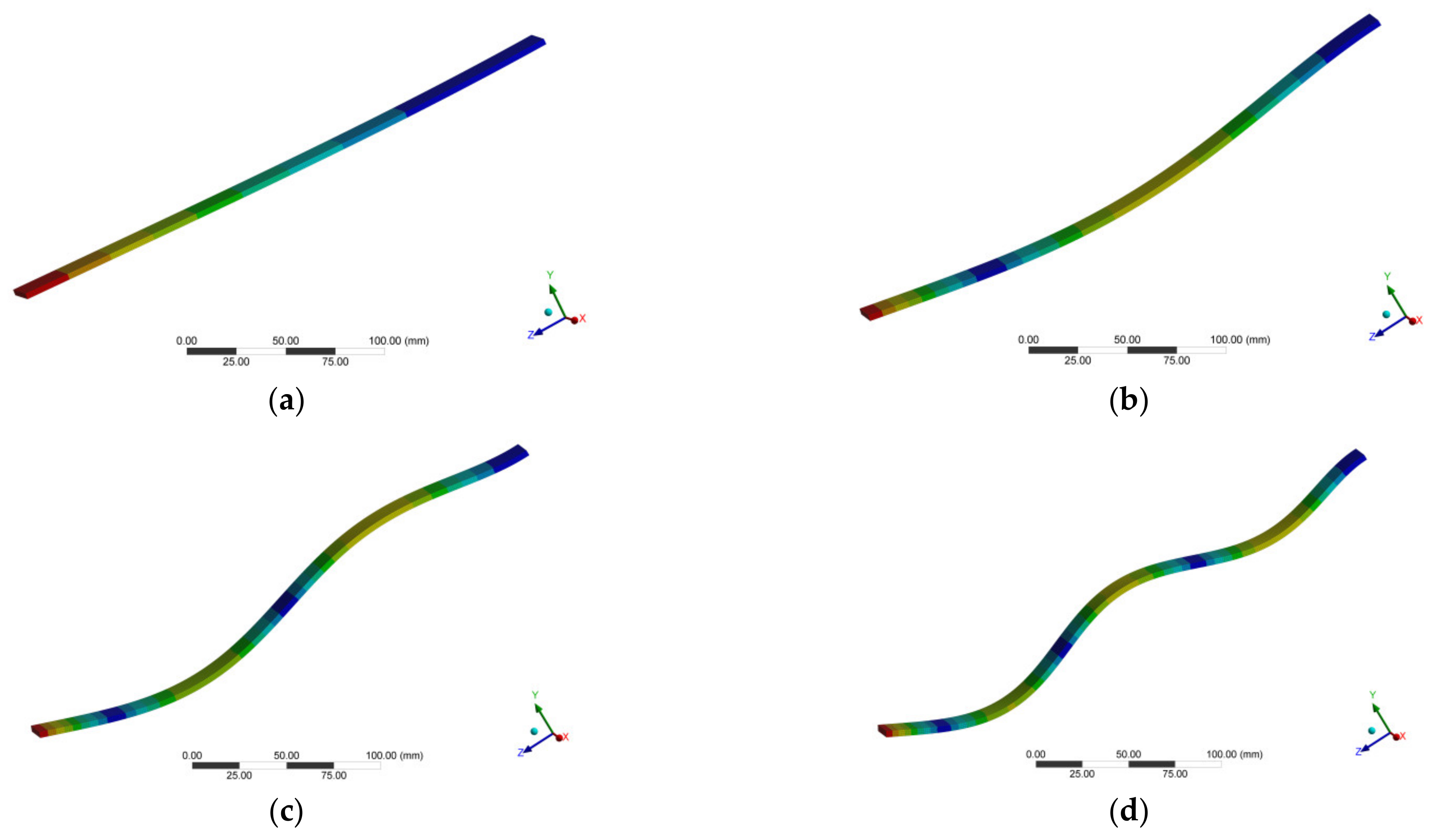
4.2. Modal Test Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yingdong, G.; Chunlong, S.; Haiyan, L.; Shizhen, Z.; Hong, W.; Wenge, W. Research Progress in Organic Polymer Damping Coatings. Paint. Coat. Ind. 2011, 9, 73–76. [Google Scholar]
- Yunfeng, Z. Properties and Application of Advanced Viscoelastic Damping Materials. Aerosp. Mater. Technol. 2009, 39, 1–6. [Google Scholar]
- Gibson, R.F. A review of recent research on mechanics of multifunctional composite materials and structures. Compos. Sci. Technol. 2014, 105, 51–65. [Google Scholar]
- Zhiyuan, W.; Liushuan, Y. Progress of High Damping Foam Metal Metrix Composite. Dev. Appl. Mater. 2004, 19, 38. [Google Scholar]
- Huang, Z.-C.; Qin, Z.-Y.; Chu, F.-L. A review about vibration problems of thin-walled structures with viscoelastic damping layer. J. Vib. Shock. 2014, 33, 105–113. [Google Scholar]
- Fang, Q.-F.; Zhu, Z.-G.; Ge, T.-S. Characterization and Mechanism of High Damping Materials. Physics 2000, 9, 541–545. [Google Scholar]
- Kang, Z.; Zhang, X.P.; Jiang, S.G.; Cheng, G. On topology optimization of damping layer in shell structures under harmonic excitations. Struct. Multidiscip. Optim. 2012, 46, 51–67. [Google Scholar]
- Kim, S.Y.; Chris, K.M.; Kim, I.Y. Optimal damping layout in a shell structure using topology optimization. J. Sound Vib. 2013, 332, 2873–2883. [Google Scholar]
- Yamamoto, T.; Yamada, T.; Izui, K.S.; Nishiwaki, S. Topology optimization of free-layer damping material on a thin panel for maximizing modal loss factors expressed by only real eigenvalues. J. Sound Vib. 2015, 358, 84–96. [Google Scholar]
- Takezawa, A.; Daifuku, M.; Nakano, Y.; Nakagawa, K.; Yamamoto, T.; Katimura, M. Topology optimization of damping material for reducing resonance response based on complex dynamic compliance. J. Sound Vib. 2015, 358, 84–96. [Google Scholar]
- EI-Sabbagh, A.; Baz, A. Topology optimization of unconstrained damping treatments for plates. Eng. Optim. 2014, 46, 1153–1168. [Google Scholar]
- Zhang, X.P.; Kang, Z. Vibration suppression using integrated topology optimization of host structures and damping layers. J. Vib. Control 2016, 22, 66–76. [Google Scholar]
- Yun, K.S.; Youn, S.K. Topology optimization of viscoelastic damping layers for attenuating transient response of shell structures. Finite Elem. Anal. Des. 2018, 141, 154–165. [Google Scholar]
- Yi, Y.M.; Park, S.H.; Youn, S.-K. Asymptotic homogenization of viscoelastic composites with periodic microstructures. Int. J. Solids Struct. 1998, 35, 2039–2055. [Google Scholar]
- Andreassen, E.; Jensen, J.S. Topology optimization of periodic microstructures for enhanced dynamic properties of viscoelastic composite materials. Struct. Multidiscip. Optim. 2014, 49, 695–705. [Google Scholar]
- Chen, W.; Liu, S. Topology optimization of microstructures of viscoelastic damping materials for a prescribed shear modulus. Struct. Multidiscip. Optim. 2014, 50, 287–296. [Google Scholar]
- Li, K. Research on Vibration Reduction Efficiency of Composite High Damping Materials. Space Electron. Technol. 2004, 1, 42–54. [Google Scholar]
- Priyankar, D.; Ray, M.C. Smart damping of large amplitude vibrations of variable thickness laminated composite shells. Thin-Walled Struct. 2018, 127, 710–727. [Google Scholar]
- Sahoo, S.R.; Ray, M.C. Active damping of geometrically nonlinear vibrations of smart composite plates using elliptical SCLD treatment with fractional derivative viscoelastic layer. Eur. J. Mech. A Solids 2019, 78, 103823. [Google Scholar]
- Gupta, A.; Reddy, R.S.; Panda, S.; Kumar, N. Damping treatment of beam with unconstrained/constrained 1-3 smart viscoelastic composite layer. Eur. J. Mech. A Solids 2019, 26, 956–962. [Google Scholar]
- Fu, W.; Wang, C.; Chen, J.; Lai, X.; Li, H. Operational modal analysis of three-dimensional structure based on Laplacian Eigenmaps. Comput. Integr. Manuf. Syst. 2020, 2020, 6348372. [Google Scholar]
- El-Labban, M.; Abdelaziz, M.Y.; Elkhatib, A. Prediction of Mechanical Properties of Nano-Composites Using Vibration Modal Analysis: Application to Aluminum Piston Alloys. Mater. Perform. Charact. 2013, 2, 454–467. [Google Scholar] [CrossRef]
- Chang, K.-C.; Kim, C.-W. Modal-parameter identifification and vibration-based damage detection of a damaged steel truss bridge. Eng. Struct. 2016, 122, 156–173. [Google Scholar] [CrossRef]
- Guan, C.; Zhang, H. Experimental and Theoretical Modal Analysis of Full-Sized Wood Composite Panels Supported on Four Nodes. Materials 2017, 10, 683. [Google Scholar] [CrossRef] [Green Version]
- Mostafa, Y.; Elkhatib, A.; Nassef, M.G.A. Rolling element bearings absolute life prediction using modal analysis. J. Mech. Sci. Technol. 2018, 32, 91–99. [Google Scholar] [CrossRef]
- Qiuhai, L.; Debao, L. Analysis of Experiments in Engineering Vibration; Tsinghua University Press: Beijing, China, 2015. [Google Scholar]
- Fu, Z.; Hua, H. Modal Analysis Theory and Applications; Shanghai Jiaotong University Press: Shanghai, China, 2000. [Google Scholar]
- Zhang, Z. Study on Viscoelastic Damping Material and Constrained Damping Structure Applied in Qingdao Subway Vibration and Noise Reduction; Qingdao Technological University: Qingdao, China, 2014; p. 18. [Google Scholar]



| NO. | Name | Length [mm] | Width [mm] | Thickness [mm] |
|---|---|---|---|---|
| 1 | Sample 1 | 20 | 1.8 | 0.9 |
| 2 | Sample 2 | 20 | 1.85 | 0.8 |
| 3 | Sample 3 | 20 | 4.4 | 0.72 |
| 4 | Sample 4 | 20 | 4.5 | 0.78 |
| 5 | Sample 5 | 20 | 5 | 0.6 |
| NO. | Name | Length [mm] | Thickness [mm] | Width [mm] |
|---|---|---|---|---|
| 1 | Specimen 1 | 300 | 3 | 20 |
| 2 | Specimen 2 | 300 | 3 | 20 |
| 3 | Specimen 3 | 300 | 6 | 20 |
| 4 | Specimen 4 | 300 | 9 | 20 |
| NO. | Name | Model Specifications |
|---|---|---|
| 1 | LMS Test. Lab Modal Testing Advanced | TL-STR.29.2 |
| 2 | ICP® accel., 100 mV/g, 0.5 Hz to 3 kHz, 10–32 side conn | 333B30 |
| 3 | PCB General purpose cable, 30-ft, 10–32 plug to BNC plug | 002C30 |
| 4 | Modally Tuned® Impulse Hammer w/force sensor and tips, 0 to 5 klbf, 1 mV/lbf (0.23 mV/N) | 086D05 |
| 5 | Low-noise, blue, coaxial, Teflon cable, 20-ft, BNC plug to BNC plug | 003D20 |
| 6 | Handheld shaker, 1 g at 159.2 Hz | 394C06 |
| Structural Type | Base Layer [mm] | Damping Layer [mm] | First Natural Frequency [Hz] | Damping Ratio [%] |
|---|---|---|---|---|
| Steel | 3 | / | 23.27 | 0.21 |
| Steel | 3 | / | 23.16 | 0.20 |
| Steel-Damping | 3 | 3 | 22.22 | 1.42 |
| Steel-Damping | 3 | 6 | 21.78 | 2.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Liao, J.; Huang, C.; Yu, H.; Yan, J.; Li, H. Study on the Damping Dynamics Characteristics of a Viscoelastic Damping Material. Processes 2022, 10, 635. https://doi.org/10.3390/pr10040635
Wang F, Liao J, Huang C, Yu H, Yan J, Li H. Study on the Damping Dynamics Characteristics of a Viscoelastic Damping Material. Processes. 2022; 10(4):635. https://doi.org/10.3390/pr10040635
Chicago/Turabian StyleWang, Fei, Jianbin Liao, Chaoming Huang, Hongliang Yu, Jin Yan, and Hanlin Li. 2022. "Study on the Damping Dynamics Characteristics of a Viscoelastic Damping Material" Processes 10, no. 4: 635. https://doi.org/10.3390/pr10040635
APA StyleWang, F., Liao, J., Huang, C., Yu, H., Yan, J., & Li, H. (2022). Study on the Damping Dynamics Characteristics of a Viscoelastic Damping Material. Processes, 10(4), 635. https://doi.org/10.3390/pr10040635






