Abstract
Multi-line overlapping shield tunnels have a complicated layout in the underground space, and the interaction mechanism between tunnels is very complicated. Based on the construction formation of multi-line overlapped shield tunnel with short-distance up- and down-crossing, indoor model tests were conducted to analyze ground settlement (caused by excavation unloading and stratum loss) and the longitudinal deformation law of existing tunnels based on the drainage method, according to the characteristics and control requirements of the short-distance construction of shield tunnels. The results show that as long as the construction strategy of first-down and then-up crossing is adopted, no sudden change in ground settlement would occur. Furthermore, neither the changes in transient settlements nor the final ground settlement would be too large, which is different from the strategy of first-up and then-down crossing; the first-up and then-down crossing strategy generally increases the curvature of the deformation curve of the existing tunnel, and the deformation of the existing tunnel will cause obvious repeated vibrations. This provides theoretical guidance for the design and construction of multi-line overlapped tunnels.
1. Introduction
The construction conditions of shield multi-line overlapping crossings are not rare [1,2]. For example, the double-lane tunnel of Shanghai Metro Line 11 passes through the upper and lower sides of Metro Line 4, which forms a relatively special three-layer four-line overlapping condition. However, the special case of Shanghai Metro Line 2 crosses Line 1 with a minimum net spacing distance of 1.2 m. If a shield is constructed under such conditions of long overlap distance, short net distance and even multi-line overlap, more prominent construction risks may occur and bring greater construction safety hazards. Therefore, it is extremely necessary to study the principle of construction disturbance of short-distance multi-line overlapping shield tunnels (soft soil areas) in a practical and theoretical sense.
Thus far, many scholars have conducted research on the influence of new tunnels on existing tunnels using field measurements, FEM, theoretical analyses and model tests. For example, through the analysis of a large number of tunnel underpasses constructed for the Shenzhen metro, Jin et al. [3] clarified the impact of new tunnel underpasses on the existing tunnels and corresponding influencing factors, and proposed an empirical formula to estimate the settlement of existing tunnels caused by new shield tunnel excavations. Based on the project of the Tohid tunnel crossing, Tehran Metro Line 4, Chakeri et al. [4] used a 3D numerical method to analyze the interaction between the existing and newly built tunnels to guide engineering practices. In addition, for Xi’an Metro Line 1, Kong et al. [5] used a 3D dynamic numerical simulation to analyze the interaction between the CRD method and the tunnel construction of shield method. In order to reveal the influence of the twin tunnels on the close construction of Suzhou Metro Line 4, Liu et al. [6] used a combination of numerical calculations and field monitoring to study the additional stresses and deformation changes of the preceding cavern, caused by the construction conditions of the latter cavern. Lin et al. [7] used a numerical simulation to study the deformation characteristics of the existing tunnel under the new two-hole diagonal tunnel in Changsha, and compared them with field-measured results. Ding et al. [8] used a numerical analysis method to study the effect of new shield tunnel construction on the existing metro, and mainly investigated the effect of the net distance between the two tunnels and the intersection angle of the two tunnels, where Hangzhou Metro Line 4 crosses Line 1. Jin et al. [9] used field monitoring and 3D numerical methods to study the process of two existing metro tunnels in Shenzhen that cross by four dense tunnels, focusing on the settlement of the existing tunnels caused by multiple tunnel underpasses. Based on the engineering example of the close crossing of the 110 kV cable tunnel on Line 9 in Shanghai, Xie et al. [10] used a numerical simulation combined with field monitoring to clarify the impact of new tunnels on existing tunnels, and constructed an automatic monitoring feedback network on a sub-basis to ensure the operational safety of existing tunnels. Relying on a new railroad tunnel project constructed adjacent to an existing tunnel in the Loess Plateau area of Taiyuan, Shanxi, Yuan [11] used empirical assessment methods and 3D numerical simulations to analyze the impact of new tunnel excavations on Loess strata, based on the stability of the adjacent existing tunnel. Based on the shield tunnel construction of the South–North Water Diversion East Canal project in Beijing, Ma et al. [12] used numerical simulation and field monitoring methods to study the impact of shield construction on existing tunnels, and elaborated that the settlement law of existing tunnels was disturbed by the construction of the crossing, and proposed and verified the method of shield tunnel disease remediation. Based on the four-line overlapping tunnel project formed by Nanning Metro Lines 1 and 2 at Chaoyang Square Station, Meng [13] combined practical experience with theoretical analysis, numerical simulation and field monitoring methods to explore the deformation law of tunnel shield construction under the complex spatial relationship of four-line overlapping tunnels, and proposed effective measures to control foundation deformation. Liu [14] used the finite element method to clarify the impact of new box tunnel construction on an existing tunnel in Suzhou. The results showed that the use of effective lubrication is not only beneficial to new tunnel jacking, but also helps control the deformation of existing tunnels that are undermined. Based on the Foshan–Dongguan inter-city railroad shield tunnel in the fully weathered granite stratum through the Guangzhou Metro Line 7 project, Zhang et al. [15] used a combination of field monitoring and 3D dynamic FEM to solve the two major problems of reasonable grouting pressure and existing tunnel deformation control in the actual project. The results showed that a reasonable pressure measure method was adopted to effectively suppress the uplift deformation of the existing tunnel. The FEM method and the field measurement method were specific to particular projects, and the general applicability of the relevant research results has not been verified. In addition, the usefulness of FEM results is highly dependent on the selected intrinsic model and model parameters [16,17], and the generalizability of the research results also needs to be verified.
Theoretical analytical and model test methods have been commonly used to study tunnel interactions in the past. Based on the Timoshenko beam correlation theory on a Kerr foundation, Zhang et al. [18] established an analytical solution for the existing tunnel’s response caused by new tunnel excavation, and the analytical solution was verified, followed by a parametric analysis, which showed that the tunnel’s longitudinal shear stiffness had a significant effect on the existing tunnel’s response. In the context of a shield connection project of the Beijing subway, Tao et al. [19] combined the results of theoretical analysis, numerical simulation and field measurement to investigate the effects of new shield tunnel construction on longitudinal and transverse displacements, additional bending moments and the axial forces of the existing shield tunnel. Based on the new shield tunnel of Line 11, sandwiched between Line 4, in Shanghai, Cai et al. [20] used field monitoring to analyze the deformation pattern of the existing tunnel caused by the construction of the first-downward and then-upward crossing. Based on the improved longitudinal equivalent continuum model, the relationship between the longitudinal deformation curve and the amount of annular joint tension was derived, and the proposed control index for the deformation of existing tunnels caused by multi-level crossings was combined with the industry standard. Although the theoretical analysis method is simple and easily applied, it is inevitable that various assumptions will be added during the derivation of specific theoretical formulas, e.g., many theoretical formulas will include elasticity assumptions, which are obviously unreasonable in the case of new pairs of tunnels that have a large impact on existing tunnels. Choi et al. [21] conducted indoor model tests to study the effects of three factors, namely, the size of the existing tunnel, the center distance between the new and existing tunnels, and the earth pressure coefficient, on the interaction between the two tunnels. Yang et al. [22] used a combination of physical model tests and numerical simulations to study the effects of close-stacked tunnel construction on the deformation and internal forces of existing tunnels, and the results showed that the first-down and then-up tunnel construction sequence was superior to the first-up and then-down construction sequence. Zhang et al. [23] studied existing tunnel and ground deformation under vertical-upward, vertical-downward and up-down, sandwiching existing tunnel conditions in new tunnels using the indoor test method and 3D elasto-plastic FEM method. The results showed that upward penetration construction caused more surface settlement than downward penetration construction. Zhang et al. [24] focused on the effects of shield method construction on large section back-exit tunnels in muddy siltstone strata via numerical simulation and model tests, and proposed an impact range based on a surface settlement criterion. Multi-line stacked soft soil shield tunnels are a complex form of tunnel space arrangement that has emerged with the continuous development of metro construction. For the two typical crossing construction forms of multi-lane stacked shield tunnels, vertical-up and vertical-down, Zhang et al. [25] investigated the effect of new tunneling on the deformation of existing tunnels with the help of indoor model tests.
Therefore, it can be seen that most research has been focused on two-lane overlap construction, while the research concerning multi-lane overlap cases are rare. Compared to two-lane overlapping tunnels, the interaction between multi-lane overlapping tunnels is more complex, and there are no specific standards for their design and construction. Therefore, in this research, similar model tests in a gravity environment are used to study the mechanism of ground disturbance caused by upward- and downward-intersecting multi-lane stacked shield tunnels, with an emphasis on comparing the effect of new double-bored tunnel crossings on existing double-bored tunnels, and the effect this has on ground displacement and surface settlement under different crossing sequences of upward- and downward-first.
2. Model Tests
2.1. Testing Material
2.1.1. Derivation of Similarity Criterion
The purpose of the tests was to study surface settlement and existing tunnel deformation law after shield excavation. Considering that shield construction is a dynamic process, it is difficult to reflect soil properties dynamically and continuously throughout the test, but the dynamic process can be broken down into several segments, and the deformation law generated by each segment can be decomposed, which can be equivalently simplified to the superposition of several static problems. The net size of the model box selected for this model test was 1.40 m × 0.64 m × 1.10 m. Combined with the diameter and depth of the tunnel in the actual project, the final geometric constant determined in the test was 1:40, i.e., the geometric similarity coefficient was Cl = 40. Other similar constants can be derived accordingly as follows: displacement similarity coefficient Cδ = 40, strain similarity coefficient Cε = 1, and the similarity coefficients of stress and the modulus of elasticity are the same. A prototype sand was used as the test fill, and thus the similarity coefficient of gravity was determined to be Cγ = 1. The modulus of elasticity of the polyethylene tube used in the tunnel lining model was about 820 MPa, while the modulus of elasticity of the lining in the actual tunnel project was generally 32.5 GPa after considering the stiffness discount; thus the similarity ratio of stress was also approximated as Cσ = 40.
2.1.2. Test Soil
Generally, the deformation of soil is mainly related to the inertia force, internal friction angle, cohesion, gravity, elastic force and external force of soil particles. In most cases, the elastic force of soil is relatively small, and the effect of the soil deformation rate is also small during the construction process, so these two factors can be ignored. In addition, according to the consensus of the Geotechnical Simulation Committee of the International Society of Geotechnics and Geotechnical Engineering, when the ratio of the model size to the particle size of the model soil is greater than 175, the deformation tendency of the model soil particles and the agglomeration effect of particle movement are less than those of the in situ soil, and this kind of soil can be used as a model test material [26]. In summary, as long as the geometric similarity of the test model is maintained, sand can be used as a model testing material to analyze surface and tunnel deformation caused by excavation and unloading. Therefore, sand with a cohesive force of 5.1 kPa and an internal friction angle of 35.4° was selected for the tests.
2.1.3. Tunnel Model
Plastic is the commonly used tunnel model test material, and the existing tunnel structure in this test was simulated by a polyethylene tube. At the same time, considering the effect of elastic stiffness reduction at the joint of the segment and the difficulty of making the model segment, a thin bolt and thin plastic sheet fixed connection was used at the ring joint; the size of the joint sheet and the connection between segments are shown in Figure 1, where every two segments were connected to each other by six pairs of bolts, the existing tunnel structure was assembled through the seam, and the new tunnel lining was simulated by the PE tube prototype. The lengths of the existing tunnel model and the new tunnel model were 1.4 m and 0.64 m, respectively.
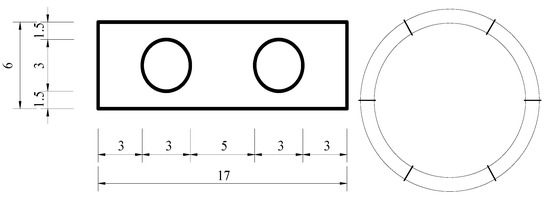
Figure 1.
Size of joint piece and connection of segments.
The segment met the requirements of the geometric similarity ratio and elastic modulus similarity ratio, and the longitudinal bolted joints were mainly seen as springs, and the necessary longitudinal stiffness discount of the prototype tunnel was also considered so that the elastic stiffness coefficient of the completed existing tunnel model joints were able to meet the requirements of the elastic stiffness coefficient similarity ratio. The parameters of the prototype tunnel and the similar model tunnel are shown in Table 1.

Table 1.
Parameters of the prototype tunnel and model tunnel.
2.2. Testing Conditions
In this section, the two crossing construction forms of first-up and then-down, as well as first-down and then-up, were selected. It is also supposed that the net distance between the existing tunnels was 125 mm and the buried depth was 550 mm, and the existing tunnels were crossed from the upper and lower directions, respectively. In addition, there was 100 mm net distance between the existing and newly built tunnels. As shown in Figure 2, the model box was 1400 × 640 × 1100 mm (net size) and the net distance among the tunnels were within 1.5D, which is a complex crossing condition (defined by the Japanese short-distance tunnel construction standard), with D as the tunnel diameter.
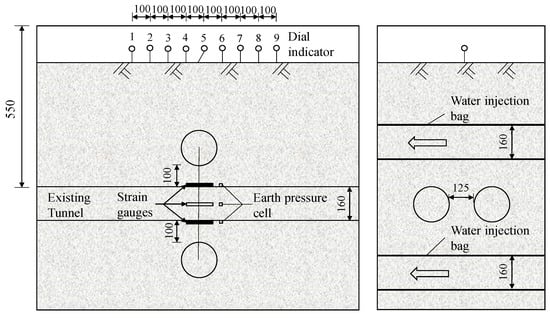
Figure 2.
Complex crossing testing conditions (unit: mm).
2.3. Testing Process
The prefabricated water injection bladder method was used in this study to model ground loss caused by shield excavation, with a 6-ring water injection bladder placed in each newly built tunnel. In addition, a plastic tube (diameter 3 mm) was used to connect the pneumatic connector to the external control valve. The medical infusion set was connected to the outer valve, in which a flowmeter was attached to the valve so as to control the speed of the water flowing in and out of the water injection bag. It should be noted that the unloading during tunnel excavation was realized by the preset and drainage controlling of the water bag, and the water was discharged with a propulsion length of 100 mm and 2 min for each ring. The test process is shown in Figure 3.

Figure 3.
The test process of the multi-line overlapping shield tunnelling for up and under crossing. (a) Buried underpass tunnel; (b) soil layer smoothing; (c) soil compaction; (d) buried existing tunnel; (e) buried upper tunnel; (f) placing displacement meter.
3. Analysis of Test Results
3.1. Analysis of the Surface Settlement
In this research, nine displacement meters were arranged on the ground at equal intervals (100 mm), among which the No. 4, 5, 6, and 7 displacement meters were high-precision laser displacement meters. In the experiment, two conditions of first-up and then-down, and first-down and then-up construction methods were conducted and comprehensively analyzed.
According to Figure 4 and Figure 5, it is obvious that both construction sequences resulted in a similar trend of ground settlements. Since meter No. 5 was set above the newly built tunnel, as a result, the maximum settlement was measured in this position. In addition, the displacement gauges No. 4 and No. 6 were symmetrically arranged in space, so that the changing of the two gauges were the same, and the measured results show that their pattern was almost the same but the values were different, which may be caused by various errors during the test operation. As shown in Figure 4, when the upward and then downward traversing strategy was adopted, the surface settlement caused by excavation unloading and stratigraphic losses during the upward tunnel traversing process was larger than that caused by excavation unloading and stratigraphic losses during the downward tunnel traversing process, which is reflected by the fast-changing displacement curve corresponding to the first 720 s and the slow-changing displacement curve corresponding to the second 720 s. As shown in Figure 5, when the first-down and then-up crossing strategy was used, both the construction of the down-tunnel and the up-tunnel caused larger surface settlement. When the two different crossing strategies of first-up and then-down, and first-down and then-up were adopted, the changes in the surface settlement troughs with the advancement of shield construction are shown in Figure 6 and Figure 7, respectively.
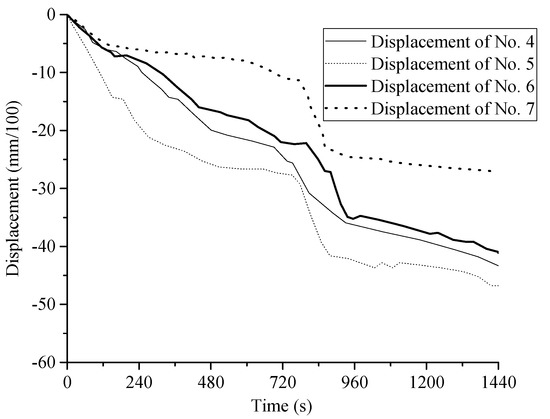
Figure 4.
Relation between ground displacement and time of first-up and then-down crossing.
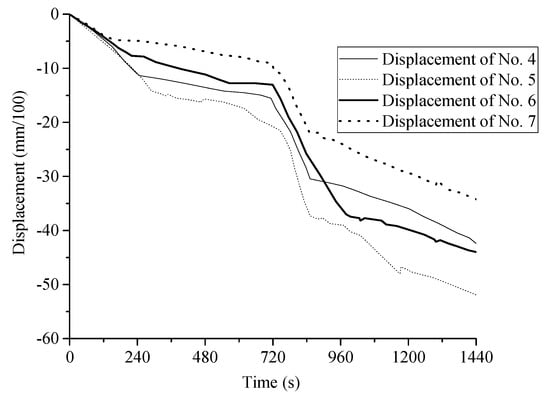
Figure 5.
Relation between ground displacement and time of first-down and then-up crossing.
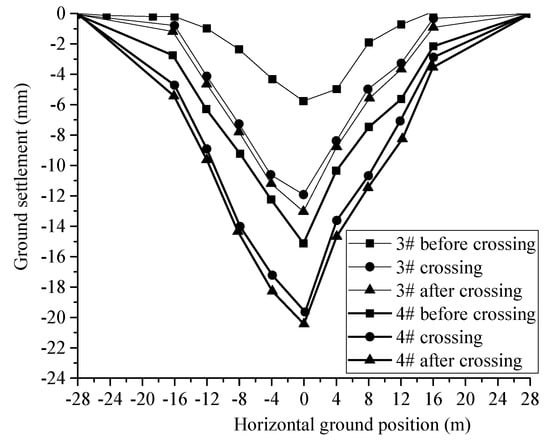
Figure 6.
Horizontal ground settlement under the condition of first-up and then-down crossing.
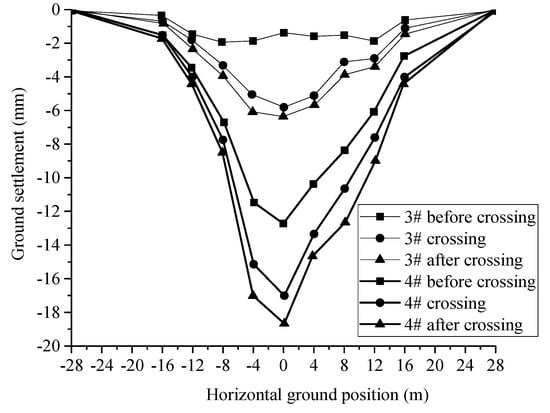
Figure 7.
Horizontal ground settlement under the condition of first-down and then-up crossing.
As shown in Figure 6 and Figure 7, the surface settlement was slightly different between the two crossing sequences, although their difference is very small, with a test value of about 20.1 mm for the first-up and then-down crossing and 19.1 mm for the first-down and then-up crossing; however, the cumulative value of lateral surface settlement at the crossing phase transition boundary and the single change were significantly larger for the first-up and then-down crossing sequence. From the results of displacement changes in each phase of the crossing, the first-down and then-up crossing construction caused uniform changes in surface settlement in each phase, while the first-up and then-down crossing caused abrupt changes in displacement at the beginning of new tunnel construction, which was unfavorable to the protection of surface buildings (structures), and the width of the surface settlement trough was relatively large in the first-down and then-up crossing sequence and the displacement curve changed more gently. Therefore, according to the test results, it is advised that the construction method of first-down and then-up should be preferred. Table 2 shows a comparison of the vertical displacement values of the ground surface under the two crossing sequences.

Table 2.
Comparison of surface displacement under different crossing sequences.
3.2. Analysis of Tunnel Deformation
Figure 8 shows the arrangement of displacement meters, in which displacement meters set in the existing tunnel, No. 1, were numbered from 1 to 6, whereas in the existing tunnel, No. 2, they were numbered from 7 to 12.
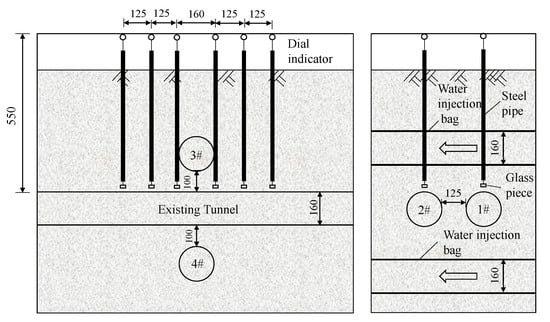
Figure 8.
Arrangement of displacement meters in existing tunnels under mixed crossing (unit: mm).
The relationship between longitudinal deformation of the existing tunnel and time are shown in Figure 9, Figure 10, Figure 11 and Figure 12, in which tunnel displacements under both crossing conditions are experimentally compared.
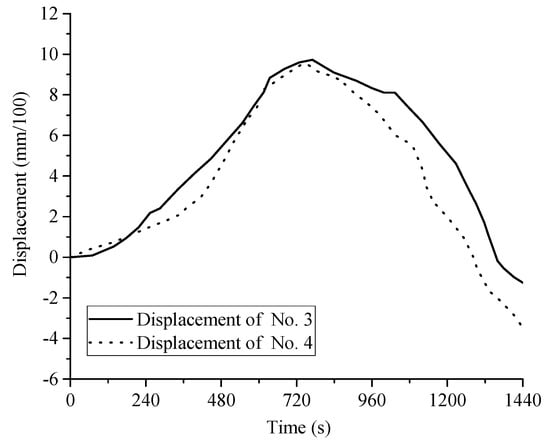
Figure 9.
The relationship between displacement and time for No. 3 and No. 4 displacement meters, under the condition of first-up and then-down crossing.
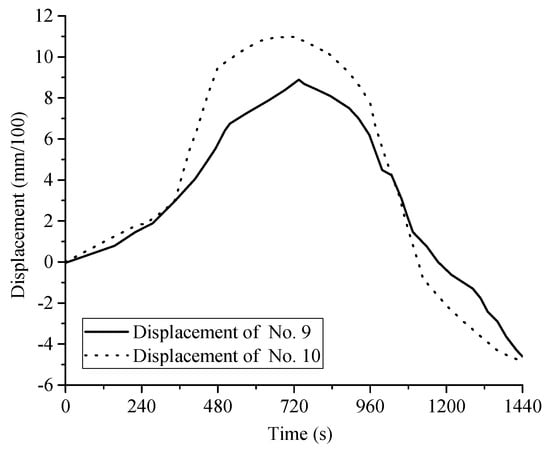
Figure 10.
The relationship between displacement and time for No. 9 and No. 10 displacement meters, under the condition of first-up and then-down crossing.
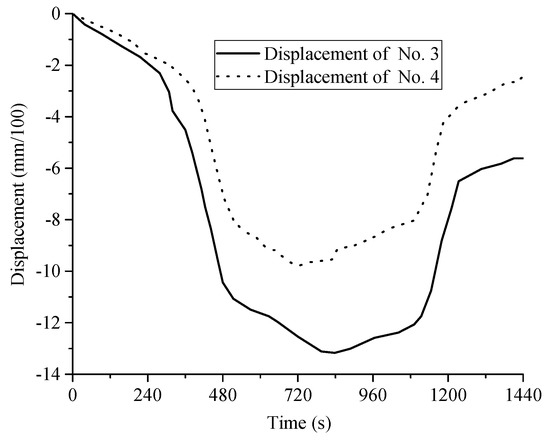
Figure 11.
The relationship between displacement and time for No. 3 and No. 4 displacement meters, under the condition of first-down and then-up crossing.
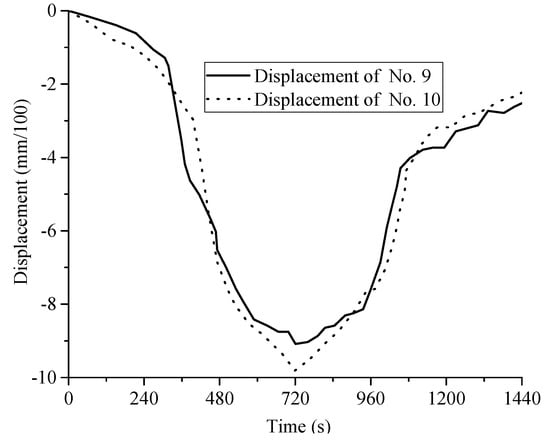
Figure 12.
The relationship between displacement and time for No. 9 and No. 10 displacement meters, under the condition of first-down and then-up crossing.
Since the No. 3 and No. 4 displacement meters were arranged symmetrically, their changing laws should be theoretically identical. According to Figure 9 and Figure 10, it is obvious that the deformation trends of No. 3 and No. 4 were the same, which increase first and then gradually sink. However, their values were different, which was attributed to the uneven drainage of the water injection bag.
In the process of first-up and then-down crossing, the excavation of the upper tunnel, No. 3, caused the existing tunnel to float, in which the impact on the existing tunnel, No. 2, was greater, and thus the magnitude of the change in the displacement gauges of No. 9 and No. 10 were relatively large, and the maximum float value was also larger than the displacement gauges of No. 3 and No. 4. This means that the deformation of the existing tunnel, No. 2, was more significant. During the excavation process of the new tunnel, No. 4, the soil below the existing tunnel was released due to the unloading process, and the existing tunnel sank continuously. It is also notable that the process of the down crossing had a greater impact on the existing tunnel of No. 2, thus the magnitude of the change in the displacements of No. 9 and No. 10 were relatively steep. During the whole crossing process, the maximum uplift of tunnel No. 2 was 0.11 mm, while No. 1 and No. 2 tunnels finally sank after the completion of crossing, and the maximum longitudinal settlement of tunnel No. 2 was about 0.05 mm.
Figure 11 and Figure 12 show that in the first-down and then-up crossing stage, the existing tunnels, No. 1 and No. 2, showed a first-sinking and then-floating deformation trend, and the impact of new tunnel construction on the existing tunnels was greater than the impact of new tunnel construction on the existing tunnels. Therefore, both No. 1 and No. 2 tunnels remained in a sinking state when the crossing was finished. The difference between the displacements of No. 3 and No. 4 was relatively large, which had a little influence on the final conclusion. Moreover, the impact on the existing tunnel, No. 1, was greater in the first-down and then-up crossing method, whose difference was not obvious.
Figure 13 and Figure 14 show the changing curve of tunnel longitudinal deformation caused by tunnel construction progress under two different crossing strategies. As shown in Figure 13a, when the first-up and then-down crossing strategy was adopted, both existing tunnels were uplifted to different degrees during the up-crossing process, while the existing tunnels showed a sinking tendency during down-crossing construction. When the first-up and then-down crossing strategy was adopted, the maximum deformation during the crossing was 3.6 mm for both of the existing tunnels, No. 1 and No. 2, and the final settlement was 2.2 mm and 1.8 mm for No. 1 and No. 2, respectively, with the maximum settlement located in the center of the tunnel.
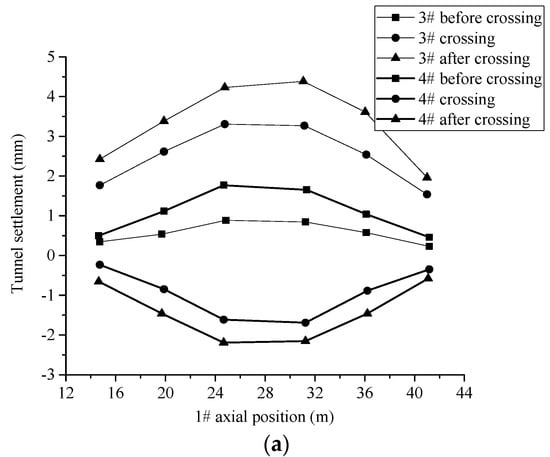
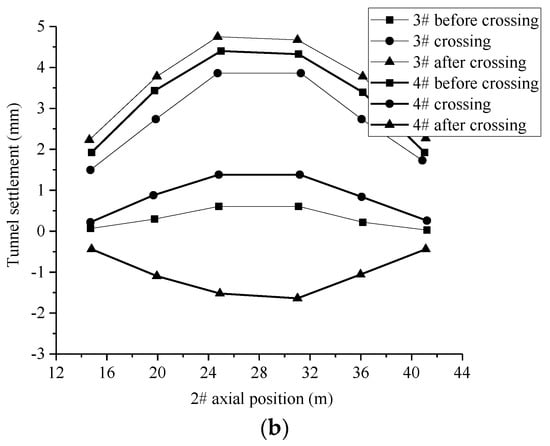
Figure 13.
The longitudinal displacement of the existing tunnels, (a) No. 1 and (b) No. 2, under the condition of first-up and then-down crossing.
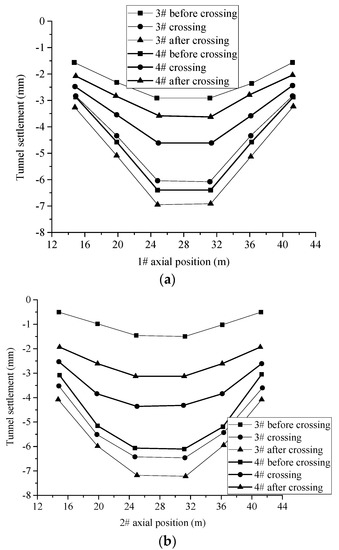
Figure 14.
The longitudinal displacement of the existing tunnels, (a) No. 1 and (b) No. 2, under the condition of first-down and then-up crossing.
According to Figure 14, if the two new tunnels were constructed using the first-down and then-up crossing strategy, the construction of the down-crossing tunnel required an excavation and unloading process, which led to the settlement of both existing tunnels. On the other hand, the construction of the up-crossing tunnel led to the uplift of both existing tunnels, offsetting part of previous settlement, and sinking trend remained. When using the first-down and then-up crossing strategy, the maximum single deformation during the crossing process was 3.7 mm and 3.1 mm for the existing tunnels No. 1 and No. 2, respectively, and the final settlement was 3.2 mm and 4.7 mm for No. 1 and No. 2, with maximum sinkage located in the center of the tunnel.
As shown in Table 3, it can be seen that the maximum single deformation was 3.6 mm and the final settlement was 2.0 mm on average, under the first-up and then-down crossing strategy, while the maximum single deformation was 3.4 mm on average under the first-down and then-up crossing strategy, which was smaller than that with the first-up and then-down crossing strategy. Furthermore, the final settlement was 3.95 mm on average, which was about 98% smaller than that under the first-up and then-down crossing strategy. Obviously, the difference in the maximum single deformation of the existing tunnel due to the two crossing strategies was not significant, but the first-down and then-up crossing strategy resulted in a larger final settlement of the existing tunnel. The deformation of the existing tunnel due to new tunnel construction was asymptotic and the deformation curve did not change significantly. However, the deformation of the existing tunnel due to new tunnel construction was more abrupt and the deformation curve of the existing tunnel was more curvilinear, which affected the current tunnel structure more significantly, resulting in the risk of tunnel leakage.

Table 3.
Longitudinal deformations of existing tunnels under two kinds of crossing methods.
By studying the effects of the two commonly used tunnel crossing strategies on the deformation distribution of the existing tunnels and surface displacement due to construction, it was found that at the same level of construction, the first-down and then-up crossing approach was better for the protection of existing tunnels.
4. Conclusions
An indoor model test was conducted for the excavation process of a multi-lane stacked shield with up- and down-crossing of the existing tunnels. Mechanistically, the effect of the ground loss and the unloading effect on surface settlement and the longitudinal deformation of existing tunnels due to construction under complex conditions of multi-lane stacked tunnels was investigated, and the mainly conclusions are as follows:
(1) For up- and down-crossing forms, there was little difference in the final ground settlement caused by new tunnel construction between the first-up and then-down crossing strategy and the first-down and then-up crossing strategy. The single first-down and then-up crossing construction caused uniform changes in surface settlement at each stage, with relatively large surface settlement trough widths and gentle changes in the displacement curves. On the other hand, the first-up and then-down crossing caused sudden changes in displacement at the beginning of new tunnel construction, which is less favorable for the protection of surface buildings (structures). From the point of view of controlling surface settlement and mitigating building damage, a first-down and then-up crossing strategy should be adopted as a priority.
(2) The maximum single deformation of the existing tunnel due to the tunnel crossing with the first-down and then-up strategy was about 6% smaller than that of the first-up and then-down strategy, and the final settlement of the existing tunnel due to the tunnel crossing with the first-down and then-up strategy was about 98% smaller than that with the first-up and then-down strategy. The deformation of the existing tunnel due to new tunnel construction was asymptotic and deformation did not change significantly. On the other hand, the deformation of the existing tunnel due to new tunnel construction with the first-up and then-down strategy caused a large abrupt change, and there was a larger curvature in the deformation curve of the existing tunnel, which significantly affected the current tunnel structure, and created the possibility of tunnel leakage.
(3) In order to reduce the deformation curvature of the existing tunnel, it is recommended to adopt the first-down and then-up crossing strategy to control surface settlement and mitigate building damage.
Author Contributions
Methodology, writing—original draft preparation, S.L.; software, formal analysis, Y.W.; validation, resources, H.Z.; writing—review and editing, C.S.; supervision, D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors declare that this research was not granted by any funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, W.; Jia, P.; Zhu, L.; Cheng, C.; Han, J.; Chen, Y.; Wang, Z. Analysis of the additional stress and ground settlement induced by the construction of double-O-tube shield tunnels in sandy soils. Appl. Sci. 2019, 9, 1399. [Google Scholar] [CrossRef] [Green Version]
- Han, J.-Y.; Zhao, W.; Jia, P.-J.; Guan, Y.-P.; Chen, Y.; Jiang, B.-F. Risk analysis of the opening of shield-tunnel circumferential joints induced by adjacent deep excavation. J. Perform. Constr. Facil. 2018, 32, 04017123. [Google Scholar] [CrossRef]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Chakeri, H.; Hasanpour, R.; Hindistan, M.A.; Ünver, B. Analysis of interaction between tunnels in soft ground by 3D numerical modeling. Bull. Eng. Geol. Environ. 2011, 70, 439–448. [Google Scholar] [CrossRef]
- Kong, X.X.; Xia, C.C.; Qiu, Y.L.; Zhang, L.Y.; Gong, J.W. Study of construction mechanical behavior of parallel-small spacing metro tunnels excavated by shield method and cross diaphragm (CRD) method in loess region. Rock Soil Mech. 2011, 32, 516–524. [Google Scholar]
- Liu, D.; Zuo, C.; Tang, X.; Ding, S.; Chen, J. Mechanical effects of adjacent metro shield construction of the first hole on the second hole. J. Cent. South Univ. (Sci. Technol.) 2017, 48, 1027–1034. [Google Scholar] [CrossRef]
- Lin, X.-T.; Chen, R.-P.; Wu, H.-N.; Cheng, H. Deformation behaviors of existing tunnels caused by shield tunneling undercrossing with oblique angle. Tunn. Undergr. Space Technol. 2019, 89, 78–90. [Google Scholar] [CrossRef]
- Ding, Z.; Wu, Y.; Zhang, X.; Chen, K. Numerical analysis of impact of soft soil shield tunnel crossing existing subway at close range. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 663–671. [Google Scholar]
- Jin, D.; Yuan, D.; Liu, S.; Li, X.; Luo, W. Performance of existing subway tunnels undercrossed by four closely spaced shield tunnels. J. Perform. Constr. Facil. 2019, 33, 04018099. [Google Scholar] [CrossRef]
- Xie, X.; Tang, G. Effects of curved shield tunnelling adjacent to existing power tunnel. Eur. J. Environ. Civ. Eng. 2018, 22 (Suppl. 1), s164–s178. [Google Scholar] [CrossRef]
- Yuan, S. Analysis of influence of loess tunnel excavation in plateau area on stability of existing adjacent tunnel. Tunn. Constr. 2017, 37, 60–66. [Google Scholar]
- Ma, W.; Peng, H.; Yang, C. Construction parameters control of shield tunnel underneath traversing existing dual shield tunnels. J. Southwest Jiaotong Univ. 2018, 53, 119–127. [Google Scholar]
- Meng, Q. Study on the deformation and control of foundation in shield construction of four-line overlapped tunnel. Chin. J. Undergr. Space Eng. 2019, 15, 911–919, 926. [Google Scholar]
- Liu, W.; Wu, Y.; Zhao, H.; Xu, X.; Miao, L. Deformations of Subway Tunnels Induced by the Overcrossing Jacked Box Tunnels. Symmetry 2021, 13, 1800. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J.; Wu, Y.; Jia, W.; Han, J.; Zhou, L. Analysis of the impact of a double-lane shield going up through a nearby metro tunnel in a fully weathered rock formation. China Civ. Eng. J. 2019, 52, 100–108. [Google Scholar]
- Geng, D.; Dai, N.; Guo, P.; Zhou, S.; Di, H. Implicit numerical integration of highly nonlinear plasticity models. Comput. Geotech. 2021, 132, 103961. [Google Scholar] [CrossRef]
- Geng, D.; Guo, P.; Zhou, S. Implicit numerical integration of an elasto-plastic constitutive model for structured clays. Chin. J. Theor. Appl. Mech. 2018, 50, 78–86. [Google Scholar]
- Zhang, D.M.; Huang, Z.K.; Li, Z.L.; Zong, X.; Zhang, D.M. Analytical solution for the response of an existing tunnel to a new tunnel excavation underneath. Comput. Geotech. 2019, 108, 197–211. [Google Scholar] [CrossRef]
- Tao, L.; Sun, B.; Li, X. Interaction analysis of double holes extremely close approaching parallel shield tunnel construction. Chin. J. Rock Mech. Eng. 2009, 28, 1856–1862. [Google Scholar]
- Cai, W.; Zhang, M.; Wu, H. Analysis of deformation of existing tunnel overlapped by new shield tunnel. J. Shanghai Univ. (Nat. Sci. Ed.) 2016, 22, 813–820. [Google Scholar]
- Choi, J.I.; Lee, S.W. Influence of existing tunnel on mechanical behavior of new tunnel. KSCE J. Civ. Eng. 2010, 14, 773–783. [Google Scholar] [CrossRef]
- Yang, J.; Liu, C.; Chen, Q.; Xie, X. Performance of overlapped shield tunneling through an integrated physical model tests, numerical simulations and real-time field monitoring. Undergr. Space 2017, 2, 45–59. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.; Li, L. Study on construction disturbance mechanism of multi-lane stacked shield tunnel close crossing. Rock Soil Mech. 2017, 38, 1133–1140. [Google Scholar]
- Zhang, J.; Ye, L.; Yan, C.; Yan, B.; Wei, P.; Feng, J. Study on construction influence of shield tunnel of urban rail transit on large-section mining tunnel. Adv. Civ. Eng. 2020, 2020, 6836492. [Google Scholar] [CrossRef]
- Xiaoqing, Z.; Meng, Z.; Yingming, W.; Lei, L.; Youcheng, W. Model test on approaching construction of multi-line overlapped shield tunnelling. J. Shanghai Jiaotong Univ. 2015, 49, 1040–1045. [Google Scholar]
- Sun, J.; Xiao, W. Design on model test of shield tunnel in transparent soil. J. Wuhan Univ. Technol. 2011, 33, 108–112. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).