Abstract
This study evaluates low-temperature district heating (LTDH) networks with different geothermal heat sources under thermo-economic criteria. In particular, the heat and cold supply of modern neighbourhoods are taken into account in a dynamic simulation model built on the modelling language Modelica. Both horizontal and vertical ground heat exchangers (GHE) were investigated in respect to the load profiles of the consumers, depending on dimension as well as location. The selected base case represents a LTDH network near Stuttgart (Germany). The corresponding results of an annual simulation show that a horizontal GHE is suitable for pure heat supply and can reduce costs by up to 12% compared to a vertical system. This economic advantage remains when the cooling demand is considered. Subsequently, a variation of the system location was carried out. It is shown that horizontal GHEs operate more economically in northern regions, whereas vertical ones are more advantageous in regions with increased cooling demand. For both cases, possible savings of between 3.0% and 4.2% resulted from the simulations. The heating-to-cooling demand ratio was used as a first decision criteria to weigh-up between the two systems. Vertical GHEs were more economical than horizontal systems as soon as the ratio dropped below 1.5.
1. Introduction
Within the European Union, the heating and cooling demand of residential buildings accounts for more than 40% of the overall final energy consumption [1,2]. At the same time, renewable energy sources are responsible for only 22% of the whole heating sector. This is in clear contrast to the EU’s ambitious climate targets for 2050. The forecast for the European heating sector illustrates two trends for the coming decades. Firstly, a threefold increase of the cooling sector compared to 2006 values is expected by 2050 [2]. This outlook is confirmed by the 600% increase of cooled floor area between 1990 and 2010 and the expansion of installed space cooling units by 24 times over the same period [3]. Secondly, a reduction in heat demand between 20% and 30% is predicted due to the energy efficiency of new buildings and the refurbishment of the existing building stock [2]. This goes hand in hand with falling temperature levels in modern heating systems. In particular, these developments can be responded to by integrating central low-temperature district heating (LTDH) systems into modern quarters
This work is focused on heating networks that are operated at supply temperatures between 0 and 20 °C. A suitable heat source for such a temperature level is shallow geothermal energy. As it is already commonly used for a large number of buildings, its combination with a central heating grid offers the advantage of reducing the power of the heat source compared to the sum of the individual solutions [4]. In addition to the heating supply, geothermal LTDH systems can be used for passive cooling. Due to the low temperature profile, such networks are particularly suitable for new buildings and renovated existing buildings. Both residential buildings and commercial premises are potential areas of application. In addition to geographical location, building construction is also relevant here. New buildings in particular tend to have an increased cooling demand, which is often not considered. [5]
Here, LTDH networks can play a key role in realising cooling in an environmentally friendly way. In this context, Connolly et al. [6] outlined the importance and potential of these systems for achieving the ambitious climate goals of 2050. Firstly, the systems enable the use of a wider range of renewable energy sources. This leads to the targeted reduction of greenhouse gases without subjecting consumers to the pressure to strongly reduce heating demand. Furthermore, if the use of fossil fuels is unavoidable, heat networks can improve efficiency by approximately 15%. As modern heating and cooling networks are moving into the focus of academic research, a wide range of studies are being carried out, addressing numerous aspects. It is noticeable that, although these LTDH systems are considered to capable of heating and cooling applications, the cooling aspect or the combination of both plays only a minor role in the studies. Furthermore, specific simulations and analysis considering the architecture of the system, its cooling capacity, and its limitations are scarcely available.
Ruesch and Haller [7] investigated the impact of passive cooling of buildings on the regeneration of geothermal bore fields. The authors showed that the heat input from passive cooling only takes up a small contribution to the regeneration of the geothermal heat source, between 6% and 20%. However, the study does not consider the interaction between the shallow geothermal heat source and cooling demand in detail, such as in terms of the temperature profiles within the system. Annual simulations for a LTDH system coupled with an artificial heat source under the consideration of cooling were performed by Bilardo et al. [8]. The study shows the potential of the LTDH systems and supports their possible contribution to the decarbonisation of the heating sector. However, the transferability of these outcomes to the use of geothermal heat sources remains open, as they were not the focus of this work. Wang et al. [9] investigated the cooling potential of a geothermal system for multifamily dwellings in Stockholm (Sweden). This potential was simulated based on a real application for the warmest season of the year. The authors showed that a vertical GHE is able to reduce indoor temperatures by nearly 3 °C. The transferability to a central network and the concrete load profiles of the consumers were not within the focus of this work. Li et al. [10] performed a long-term simulation on ground source heat pumps based on real applications in Changzhou (China). The soil temperature, as well as the heating and cooling capacity of the geothermal system, were investigated for two different multifamily apartment blocks. The study shows that the heating capacity increased over a period of 15 years, whereas the cooling capacity decreased due to increasing temperatures in the system. The transferability of the results to a heating network and the exact load profiles of the consumers were not discussed.
The described literature illustrates open research questions with regard to the interaction of energy systems and geothermal heat sources in the case of simultaneous heating and cooling supply. This combined case will be an increasing phenomenon due to climatic conditions and modern building standards [5]. For this reason, an understanding and assessment of such scenarios is of great interest, reinforced by the range of possible applications. Therefore, this study focused on the following main aspects:
- Holistic simulation of the heating network, consumers, and geothermal heat sources using resilient user profiles;
- Investigation of geothermal heat sources with respect to the heating and cooling capacity;
- Evaluation of these heat sources for various scenarios in terms of thermodynamic and economic aspects.
In this context, a transient model of a geothermal LTDH system was developed in order to simulate the entire energy system considering fluctuating heating and cooling demand during the year. The corresponding load profiles of the consumers were developed for a modern building standard on an annual basis. A vertical and a horizontal ground heat exchanger (GHE) were considered as potential geothermal heat sources. The selected concepts were finally evaluated on thermodynamic and economic parameters. In Section 2, the transient simulation model is described. Furthermore, the development of the load profiles is presented. Section 3 shows the results and discussion for selected cases.
2. Methodology
For the annual simulation of a LTDH system, a dynamic model was developed using the software Dymola [11] in combination with the Modelica-based Buildings library [12]. The design and characteristics of the simulated district network were based on a real application currently under construction in the region of Stuttgart (Germany). This comprises around 650 m of pipes and 41 detached homes as consumers. The annual heat demand is estimated as 350 MWh. A horizontal GHE with 200 kW extraction capacity is used as a heat source for the neighbourhood. In principle, the network offers the possibility to provide cooling. In addition to the mass flow and temperatures in the heating network and the electrical power consumption of the heat pumps, all data required for a thermo-economic evaluation were taken into account. As the main economic parameter, the levelised cost of heat (LCOH) of the entire system was determined. The input and output parameters of the dynamic model are as follows:
Inputs:
- Location and Weather: The weather data used in this model consist of the dry bulb temperature, which is provided by ASHRAE [13] for the investigated region of Stuttgart. In addition, all parameters that characterise the ground of the considered location, such as density, heat capacity, and thermal conductivity are considered;
- Distance: The distance between users is necessary for the calculation of pressure and heat losses or gains within the pipeline;
- Consumers: Each user is described by three thermal demand profiles for heating, cooling, and domestic hot water. Furthermore, the characteristic curves of the heat pump for each load case are implemented.
Outputs:
- Global outputs represent the energy balances that concern the entire network, such as total energy imported or exported from the pipeline and the effect on the geothermal heat source.
- Local outputs show the effects on the consumer, such as electrical power consumption of the heat pump and sufficient supply of the load profiles.
The simulative implementation of the individual model groups such as heat pump, geothermal heat source, and others is described in detail below. Furthermore, the input parameters are characterised and quantified as follows.
2.1. Distribution System
The energy system consisting of the geothermal resource and consumers is connected by a central distribution network. The pipe elements used in this modelling approach are based on a dynamic-hydraulic pipe model developed by van der Heijde et al. [14]. In contrast to the dynamic pipe model included in the Modelica Standard Library (MSL), this model offers the possibility to represent complex thermal network behaviour, including zero mass flow and flow reversal. The model calculates the individual pressure drop of a pipe section depending on the material roughness, as well as the pressure losses due to geodetic elevation differences according to the Darcy–Weisbach equation
with pfric and pgeo being the pressure losses due to friction and geodetic elevation, λpipe the friction factor of the pipe, lpipe the length of the pipe, and di,pipe the inner diameter of the pipe. ρmedium represents the density of the fluid, vpipe the velocity, z the geodetic elevation, and g the gravitational acceleration. These elements characterise the total pressure drop within the pipeline. The properties of the polyethylene pipes such as length and diameter, as well as the thermal and hydraulic properties of the pipes, can be adjusted in the parameters. The assumptions used are shown in Table 1. Due to the very low mass compared to the ground and the heat transfer fluid, the heat capacity of the pipes was neglected in order to reduce the calculation time [15].

Table 1.
Properties of the pipe system.
The heat transfer fluid used in the system is a water-ethylene glycol mixture (brine). The assumed physical properties of the brine at a reference temperature of 10 °C are shown in Table 2.

Table 2.
Physical properties of the used water-ethylene glycol mixture at a reference temperature of 10 °C, own representation according to [16].
In order to simulate the heat losses or gains more accurately, a model of the surrounding soil based on thermal resistors and capacitances was applied. This structure describes the cylindrical heat transfer and thermal storage effect in the soil surrounding the pipe. In contrast to static design methods, dynamic models take into account changing soil temperatures during the year. The annual profile of the undisturbed soil temperature at a specific depth Tsoil is calculated according to Florides et al. [17] and Perpar et al. [18], in accordance with Equation (3)
with Tmean as the mean surface temperature and Tamp as the amplitude of the surface temperature. D describes the depth below the surface and α is the thermal diffusivity of the soil, while tyear and tshift represent the current time and the day of the year with the minimum surface temperature. For the buried pipe, two heat transfer mechanisms are dominant: heat conduction and heat convection. One-dimensional heat conduction after Fourier is taken into account according to Equation (4)
Heat convection is relevant between the fluid and the pipe wall triggered by the movement of fluid particles. A general equation for the heat transfer between a moving fluid and a wall can be written as
The radial heat transfer from the fluid to the outer pipe wall in this model are calculated according to Equation (6)
with λpipe and λsoil as the heat conductivity of the pipe and the soil, and rpipe,outer, rpipe,inner, and rsoil as the radius of the inner pipe, the outer pipe, and the surrounding cylindrical soil cell.
The governing heat transfer mechanism in the soil is heat conduction. Therefore, heat convection and heat radiation are neglected in the soil, and the heat exchange between pipe and soil was only calculated according to heat conduction. In this way, the heat gains as well as heat losses of the pipe system were analysed. Dalla Santa et al. [19] present an extensive collection of data on this subject, specially adapted for near-surface geothermal energy. The chosen parameters for the region of Stuttgart are shown in Table 3.

Table 3.
Physical properties of the soil, own representation according to [19].
2.2. Consumer
The main component for the consumer is the heat pump, which is not modelled as a physical cycle, but by means of real characteristic curves of an existing system by a German manufacturer [20]. This allows a significant reduction of the simulation time without affecting the overall results. The curves used in this approach can be found in Figure 1. The characteristic curves show the heat output at full load, as well as the minimum part load, for different temperature levels. A temperature of 35 °C was used for the provision of room heat, and 55 °C and 65 °C for the provision of domestic hot water. Figure 1b shows the corresponding electrical power consumption of the heat pump. From the imposed load and the brine temperature, the electrical power consumption of the heat pump and the coefficient of performance (COP) is calculated by Equation (7)
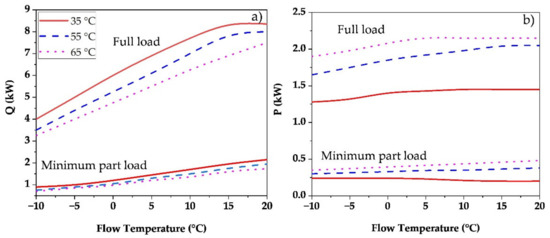
Figure 1.
Characteristic curves of the used heat pump for heating power (a) and electrical consumption (b) according to flow temperature, own representation according to [20].
At the same time, the required amount of heat taken from the grid is calculated. In case of cooling, a passive concept is applied. Therefore, only the power for the circulation pumps on the primary and secondary side is taken into account. As the reference grid is designed as a passive system, the substations contain a pump that represents the circulation pump on the primary side of the heat pump. A schematic visualisation of the consumer substation can be found in Figure 2.
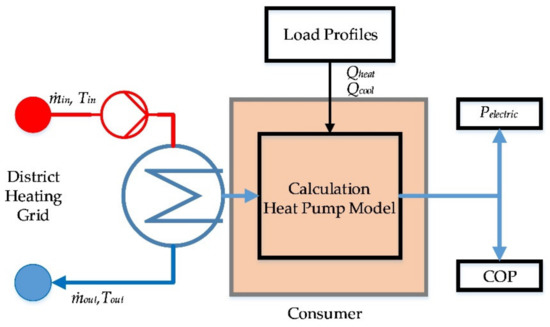
Figure 2.
Scheme of a single consumer unit.
2.3. Load Profiles
Consumer behaviour was implemented by annual load profiles including the heating and cooling demand based on hourly values. As real data is not available, a simulation was conducted to obtain reliable consumer profiles. A schematic illustration of the determination of the load profiles can be found in Figure 3.
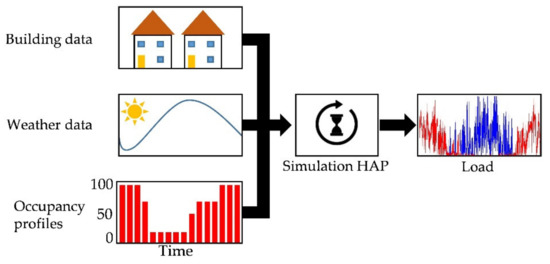
Figure 3.
Schematic illustration of the determination of the load profiles using the Hourly Analysis Program (HAP).
The energy specifications for the buildings were set according the Stuttgart project case. The specifications were derived from the KfW-153 standard and refer to the heat transfer coefficients of the building components [21]. For buildings in accordance with the KfW Efficiency House 55, clearly defined requirements apply to the heat transfer coefficients of the building components. The specifications can be found in Table 4.

Table 4.
Used building components with corresponding maximum thermal transmittance, own representation according to the KfW-153 standard [21].
In addition, the maximum permissible space heating requirement of the buildings is specified with 35 kWh/(m²a). A heated floor area of 150 m² was assumed, whereas a cellar was not taken into account. Furthermore, occupancy profiles were created for the individual rooms, but also for lighting and the use of electronic devices. A corresponding approach for this is provided by Jeong [22]. In addition, comprehensive data on factors influencing the air conditioning of buildings can be found in Polinder et al. [23] and are applied as well.
The calculation of annual load curves was carried out using the software “Hourly Analysis Program (HAP)” from Carrier [24]. This software calculates according to ASHRAE “Residential Cooling and Heating Load Calculations” [13]. The calculated load curves for the reference building can be seen in Figure 4.
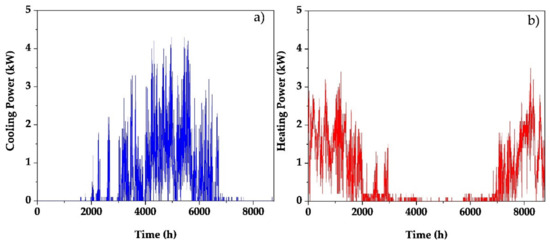
Figure 4.
Calculated heating (a) and cooling (b) load profile according to ASHRAE.
In addition, load profiles for hot domestic water are required. In their study, Santiago et al. [25] present an approach for generating artificial load profiles, which was transferred to the present work. The determined values have also been confirmed by Braas et al. [26].
2.4. Geothermal Heat Sources
One of the central aspects of the investigation is the shallow geothermal heat source. Both a vertical borehole heat exchanger as well as a horizontal heat exchanger were investigated. The performance of any GHE depends largely on the surrounding soil. Studies such as Blum et al. [27] show a median specific heat extraction rate of 48 W/m for a borehole heat exchanger. Horizontal systems are often 10 to 40 W/m, strongly depending on the climatic conditions [28,29]. Each vertical borehole heat exchanger and the surrounding elements were modelled by a resistance-capacitance model, as proposed by Bauer et al. [30] and modified by Laferrière et al. [31]. The modifications allow a free division of the boreholes in the area, as well as the consideration of more precise heat flows within the field. In this work, a double U-Tube is assumed. The temperature response of the ground to heat injection can be calculated using the g-function according to Equation (8), defined by Eskilson [32].
with Tb(t) as the borehole wall temperature, Tg the undisturbed ground temperature, ks the ground thermal conductivity, and H as the borehole length. Nb means the number of boreholes in the field and g(t) represents the g-function. The g-function was calculated according to the finite line source solution, using the method by Cimmino and Bernier [33] and Cimmino [34]. Since this g-function is based on line sources of heat rather than cylinders, the g-function was corrected to consider the cylindrical geometry. As correction factor, the difference between the cylindrical heat source solution and the infinite line source solution according to Equation (9) was applied, as proposed by Li et al. [35].
where, gFLS(t) represents the g-function evaluated for the finite line source solution, gCHS(t) represents the g-function evaluated for the cylindrical geometry, and gILF(t) represents the evaluated solution for the infinite line source. According to Equations (7) and (8), the wall temperature of the borehole for every segment and hence, the heat exchange with the surrounding soil, can be calculated. The physical parameters for the GHE simulation are shown in Table 5.

Table 5.
Physical parameters used for modelling the ground heat exchanger.
In addition, a model was developed for the horizontal heat exchanger. The single pipe model is analogous to the models presented above. The horizontal spacing of the pipes is 0.7 m and the installation depth is 1.5 m. The soil temperature was also calculated according to Equation (3) for the corresponding depth. In contrast to the vertical GHE, a horizontal GHE is strongly affected by changing temperatures on the surface. Therefore, the dry bulb temperature calculated alongside the load profiles was taken into account. The model itself was set up according to the approach of Sangi and Müller [36] and uses a configurable discretisation of the soil cell. The horizontal GHE can be varied in its performance by adding any number of parallel lines.
For simplification, it is assumed that the entire mass of a cell is concentrated in one point. Furthermore, mass transfers such as rain and underground flows through the system boundary and associated heat inputs and outputs are neglected [31,32].
Heat transfer between the soil cell and the wider environment therefore takes place due to the temperature difference between the cell and the far field temperature, which is calculated according to Equation (3).
2.5. Economical Assessment
The economic analysis was based on the guideline VDI 2067 “Economic efficiency of building services systems” [37]. The economic feasibility was calculated in terms of equivalent annual cost (EAC), which represents the annual cost of owning, operating, and maintaining the system components. The EAC was calculated by Equation (10)
with R as the annual revenues, Pi as the annualised capital cost of investment of the specific component I, and OMi as the sum of annual cost for operation and maintenance. Furthermore, Qi means the annual amount of energy used and bi is the cash value factor.
Thereby, the annualised capital cost of investment of the specific system component i is calculated by the following Equation (11)
where P0 means the investment amount of the specific component, q the interest factor, and Tobs the observation period in years. Increases in costs for operating and maintenance, as well as energy, are considered via the cash value factor bi according to Equation (12)
with r being the price change factor, which has to be specified beforehand.
For the final determination of the levelised cost of heat (LCOH) and the levelised cost of cold (LCOC), the EAC are related to the total annual heating and cooling demand according to Equation (13)
The general assumptions regarding the economical assessment can be found in Table 6. It should be noted at this point that no state subsidies are taken into account in the calculations.

Table 6.
Assumptions for the economical assessment.
3. Results
In this chapter, simulation results are presented and discussed. First, a general comparison between the two geothermal heat sources for the region of Stuttgart (Germany) was carried out. Here, both the sole heating case and the combination with cooling were taken into account. The parameters of the original design case are shown in Table 7. Subsequently, the location of the system was varied and the corresponding weather data was implemented. Oslo was chosen as a more northerly region and Bordeaux as a more southerly variation.

Table 7.
Parameters of the original design case.
3.1. Sole Heating Case
In the initial case, a horizontal and a vertical GHE were considered. The total costs for the LTDH network itself amount to around €150,000. Based on the studies by Blum et al. [27], average costs for the borehole heat exchangers of 1050 €/kW are assumed. This means installation costs of €210,000 for the standard case with 200 kW extraction capacity. According to Brennenstuhl et al. [28,38], the horizontal GHE can be assumed with mean costs of around 450 €/kW. This results in installation costs of €90,000 for the standard case. Near-surface geothermal systems in combination with heat pumps are dependent on the opposing effects of investment costs and operating costs. Keeping all other parameters equal, a reduction in the size of the heat source leads to reduced temperatures in the network, which increases the electricity demand of the heat pump.
The overall COP values determined for the sole heating scenario with respect to both geothermal sources are shown in Figure 5a. It can be seen that borehole heat exchangers are advantageous in the cold season and collectors are advantageous in the summer. This is due to the pronounced weather dependency of the collector, which is more dependent on external influences. Therefore, it cools down more in winter than a comparable vertical GHE, but also heats up more in summer. The use of horizontal systems thus leads to a reduced electricity demand of the heat pumps, but increases the demand in winter. For this reason, vertical GHEs have a higher averaged COP over the year than comparable systems with a horizontal collector. However, the savings in electricity cannot compensate for the significantly higher investment costs. It can be found that the horizontal GHE is the more economical option in the design case. The calculated LCOH amounts to 19.8 ct/kWhth when using horizontal systems and 22.3 ct/kWhth in the case of a vertical systems. Accordingly, horizontal systems result in significant savings of around 12%.
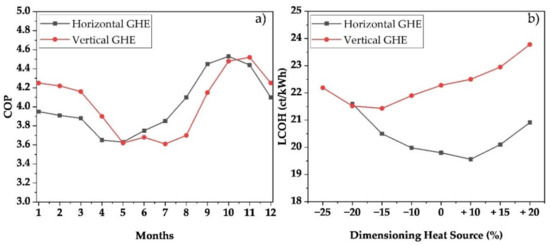
Figure 5.
Overall COP for the design case (a) and LCOH for various dimensioning of the geothermal heat source (b).
In the second step, the dimensioning of the heat source was varied originating from the extraction power of the design case described above. Figure 5b shows the LCOH for the individual consumer, taking all prices into account. The simulation demonstrated that a standard procedure for the dimensioning of GHEs does not lead to the most feasible design under economic aspects. It can be shown that an enlargement of the collector by 10% enables a cost reduction of the LCOH by 1.5%. In the case of a vertical GHE, reducing the system by 15% leads to savings of 3.8%, although the average COP drops by 8.5% due to the decreasing temperature in the distribution system. In this case, increasing the horizontal GHE leads to the minimum cost of all cases evaluated. The main indicators for the standard design and the cost minima are shown in Table 8.

Table 8.
Main indicators for the LCOH calculation.
The optimised dimensioning illustrates the conflict between investment costs and operating costs. A smaller heat source can be realised more cost-effectively, but due to the lower capacity, it leads to reduced flow temperatures and thus to an increased electricity demand of the heat pump. In the case of the horizontal system, a reduction of 25% leads to an undercutting of the permissible minimal supply temperature in winter. For this reason, the case was not considered in more detail.
As shown above, several cost rates for the horizontal collector from Brennenstuhl et al. [28,38] were used in the modelling, which is why the LCOH observed there are compared with the results from the simulation. Brennenstuhl determined a LCOH of 21 ct/kWh in the existing quarter, resulting in a cost deviation of 6%. Due to the high overlap between the simulation and the real grid, this results in a good comparability of the two systems.
The accuracy of the simulated results is also relevant for classification and evaluation. Deviations can occur due to the discretisation of the calculation area into smaller segments [40]. For this reason, the design case was simulated 15 times with identical initial parameters and the influence of the discretisation errors on the overall result was determined. Here, a mean deviation of the LCOH of 1.07% can be determined for systems with a horizontal GHE. When considering a vertical GHE, the mean error of the LCOH is 1.41%. The increased deviation may be due to the higher complexity of the vertical model compared to the horizontal model, as more modelling nodes are used. The error results in an LCOH between 19.59 ct/kWh and 20.01 ct/kWh for the horizontal GHE. For the vertical system, the LCOH is between 21.97 ct/kWh and 22.59 ct/kWh.
3.2. Heating and Cooling Scenario
If only the heat supply is considered, the lowest possible temperature spread between the flow and the heating temperature at the heat pump is favoured. This reduces electricity demand, and thus the operating costs. When passive cooling is considered, new challenges arise. In this case, a low spread is disadvantageous, as it reduces the cooling capacity or even inhibits cooling from reaching a certain point. In this context, a supply temperature in the network of a maximum of 15 °C is assumed to be permissible. At higher temperatures, the temperature gradient is too low to guarantee cooling with respect to the dew point inside the dwelling. Figure 6 shows the flow temperature profiles for both the horizontal collector and the borehole heat exchanger array in the design case. The simulation shows that the horizontal collector (Figure 6b) regularly exceeds the temperature limit for 11 days. On these days, passive cooling of the buildings is not assured. On the other hand, the borehole heat exchanger field can ensure passive cooling even if the area is reduced.
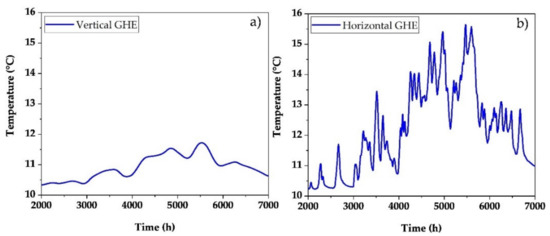
Figure 6.
Flow temperature profiles for a vertical (a) and a horizontal (b) GHE during the cooling season.
LCOH and LCOC for LTDH providing heating and passive cooling were determined. At this point, the calculation differs from the sole heating scenario. The cooling was therefore seen as an additional option and the LCOC were calculated separately. For this purpose, the existing infrastructure of the LTDH was considered. Since heat pumps with additional capabilities cause higher investment costs, a price increase for passive cooling of 20% was assumed. Furthermore, the additional electricity costs of the circulation pumps were taken into account. The calculated LCOH are shown in Figure 7a. It can be seen that a slightly reduced LCOH is associated with the heat input from cooling. As already explained, this is due to the overall improvement in COP and the resulting reduction in electricity demand. Only scenarios that can provide both heating and cooling over the entire year are listed here. For this reason, horizontal GHEs were considered with a dimensioning of +15%. Nevertheless, the economic advantages of horizontal GHEs remain for the case of heating.
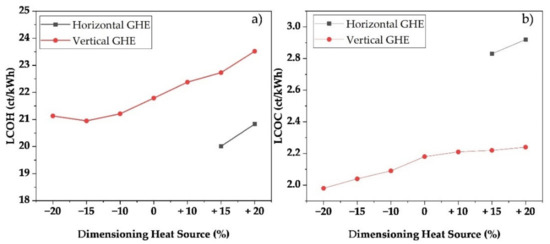
Figure 7.
LCOH (a) and LCOC (b) for various dimensioning of the geothermal heat source.
The simulated LCOC are shown in Figure 7b. Since the costs of the network as well as the heat pumps in general are already fully taken into account in the LCOH, the LCOC are significantly lower. First of all, it can be seen that horizontal GHEs cannot provide reliable cooling in the design case. Only when the collector area is increased by at least 15% does the flow temperature permanently remains below 15 °C during the cooling period. Therefore, scenarios that cannot guarantee cooling are not evaluated. It can be seen that a vertical GHE leads to significantly lower LCOC. This is due to the temperature profile being favourable for cooling. A reduction of the source leads to reduced temperatures in summer, whereas an increase keeps the temperature almost constant at the level of the ground. The temperature profile reduces the mass flow in the pipe system necessary for cooling, and thus the power requirement of the pumps. This reduces the LCOC for vertical systems by around 22% compared to a horizontal collector.
For a precise evaluation, it is necessary to determine equivalent annual cost (EAC). Therefore, the LCOH and the LCOC were offset against the annual demand. The consumer’s heating and cooling requirements remain constant for all cases. The results are shown in Figure 8. It can be seen that the economic advantage of the horizontal GHE remains even when cooling is taken into account. Increasing the horizontal GHE results in a saving of 2.7% per year compared to the economically most feasible vertical system. Nevertheless, it is remarkable that the systems with cost-intensive borehole heat exchangers are also competitive. For these cases, the possible savings in electricity leads to significantly improved economic efficiency in contrast to the pure heating case. Due to the significantly more favourable LCOC of vertical GHEs, the economic efficiency of these systems will increase with increasing cooling volume compared to horizontal GHEs.
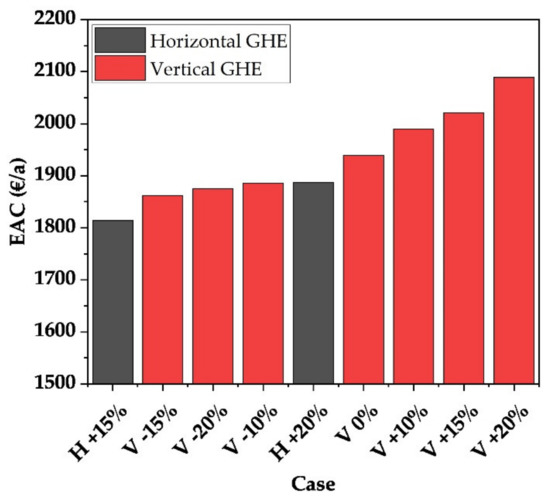
Figure 8.
Total cost for heating and cooling per consumer for each case in the region of Stuttgart.
At the same time, horizontal GHEs offer higher flexibility with regard to changes in heating or cooling demand. The simulations show that they can provide both heating and cooling over a wide range of dimensioning.
3.3. Variation of the Region
In the following, two alternative locations for the heating and cooling system are examined. Weather data from Oslo (Norway) and Bordeaux (France) were used for the calculations. The design parameters and assumptions were kept constant in order to maintain comparability. Only the power of the geothermal heat source for the base case (0%) was adjusted to fulfil the load profiles of the corresponding neighbourhood. The main parameters determined for the systems at the selected locations are shown in Table 9. It is assumed that the demand for domestic hot water remains constant regardless of the region.

Table 9.
Comparison between the three locations.
The results for the calculated LCOH and LCOC for the Oslo location are presented in Figure 9a,b. The increased demand for space heating by around 60% compared to Stuttgart leads to an increased extraction capacity of the geothermal heat sources and therefore to increased investment cost, as is shown above. In general, the specific LCOH is reduced by the overall increase in heat demand, which leads to more economic geothermal heat sources. For the design case, the LCOH can be reduced by 6% in the case of a horizontal GHE. The conducted calculations show that both smaller and a larger dimensioning result in higher cost. For the vertical GHE it is shown that the development of the cost is analogous to the case described above. Smaller dimensioning leads to reduced cost, and again, the reduced investment cost exceeds the additional demand for electricity. Reducing both GHEs by 15% leads to a turning point where the vertical system is slightly more economical than the horizontal collector. This results from the significantly increasing electricity demand for the horizontal GHE due to the sharply falling temperature profile. The specific LCOH is reduced by the overall increase in heat quantity. The specific LCOC is slightly increased because the additional investment costs are allocated to an overall 25% reduction in the amount of cooling. This illustrates that the flat-plate collector, if undersized, reduces the LCOC due to the low temperature profile. As in the case of Stuttgart, an increase in size leads to increased costs due to the rising temperature level. Once again, the vertical GHE shows a nearly constant cost development. Due to the constant temperature profile, the mass flow and therefore the electricity demand of the pumps remain nearly the same. An evaluation of the cases in terms of total annual costs id shown in Figure 10. It can be seen that the horizontal GHE can reduce costs by around 4.3% due to an increased heat demand in combination with a reduced cooling demand. This leads to a cost advantage for the horizontal GHE, which is also reflected in a wider range of advantageous dimensioning. Nevertheless, shifting the region further north may lead to problems as the temperature near the surface drops too far for a horizontal collector.
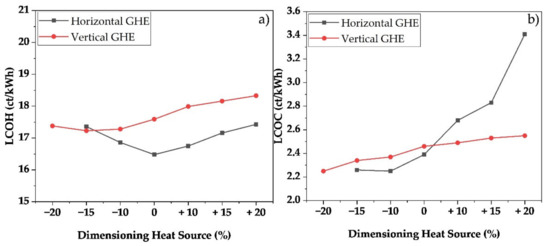
Figure 9.
LCOH (a) and LCOC (b) for various dimensioning of the geothermal heat source for the region of Oslo.
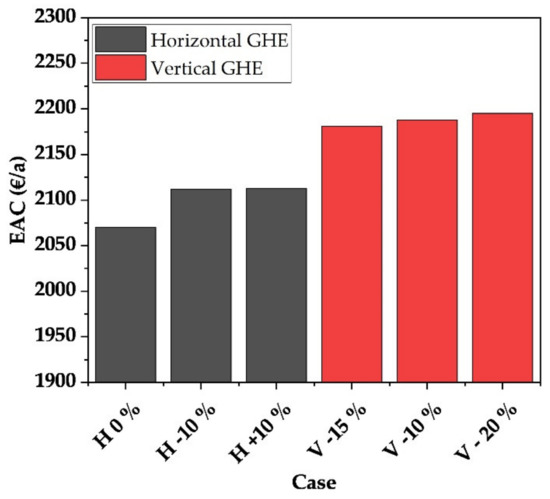
Figure 10.
Total cost for heating and cooling per consumer for each case in the region of Oslo.
The region around Bordeaux has overall milder climatic conditions. Therefore, the heating demand is reduced, whereas the demand for space cooling increases. Once again, only scenarios that can guarantee a constant supply of heating and cooling are presented. The simulated results presented in Figure 11a show similar characteristics as the scenarios above. Due to the higher temperatures in the ground, a horizontal GHE is more economical in the case of heat demand. Furthermore, it can be seen once again that the LCOC (Figure 11b) for the vertical GHE is significantly lower. This is due to the higher temperature in the flat-plate collector, which results from the overall higher ground temperature. Although the LCOH is lower when a horizontal GHE is used, the calculation shows that systems with borehole heat exchangers can be operated more economically when the provision of cooling is taken into account. Figure 12 shows the total costs per year for each customer. Here, it can be seen that the vertical systems are now up to 3% more economical, and are also able to operate over a wide range of dimensions. The horizontal GHEs, on the other hand, lead to higher costs for the customer.
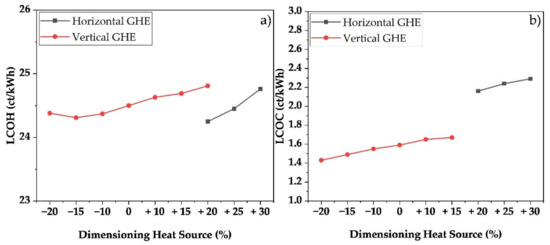
Figure 11.
LCOH (a) and LCOC (b) for various dimensioning of the geothermal heat source for the region of Bordeaux.
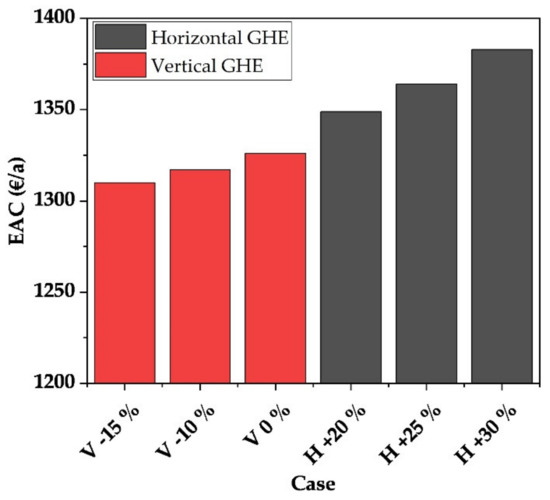
Figure 12.
Total cost for heating and cooling per consumer for each case in the region of Bordeaux.
The evaluation of the results shows that, depending on the scenario, different system configurations emerge as the most economical solution. Due to the low investment costs, horizontal GHEs have a significant advantage, which, however, must be re-evaluated when cooling is taken into account. Here, it is interesting at which point one system outweighs the other. According to the provided simulation results, the heating-to-cooling demand ratio can be applied as a decision criterion by Equation (14)
Accordingly, the Oslo case shows a ratio of 4.0, whereby the horizontal systems are preferred. In Stuttgart, the ratio is 2.2. In this region, horizontal and vertical GHE are almost equal in their economic efficiency, and cooling can only be guaranteed by larger collectors. Nevertheless, collectors are the more economical solution here as well. The region of Bordeaux has a heating-to-cooling demand ratio of 0.8. In this region, vertical GHEs are the more economical systems. An overview of the parameters is shown in Table 10. Studies for the Madrid region are still being considered. In this region, however, the horizontal GHE cannot guarantee passive cooling even with significantly larger dimensions due to the high ground temperatures in summer. For this reason, only vertical GHEs can be used here. Based on the results obtained, there seems to be a tipping point between both geothermal systems depending on the respective loads. Here, regions with a heating-to-cooling demand ratio below 1.5 seem to tend towards vertical systems. In contrast, horizontal GHEs become more economical the larger the RH/C becomes.

Table 10.
Parameters of the three regional cases.
4. Conclusions
In this study, a dynamic model of a district heating network was developed using the Modelica programming language. A complete heating network with 41 consumers and over 600 m of piping was set up. Furthermore, heat pumps and two geothermal heat sources were implemented in the simulation environment and integrated into the overall model. Based on an annual simulation, selected concepts were technically and economically evaluated. Therefore, load profiles for heating and cooling demand of potential consumers were developed and applied to the simulation model. The results show that in case of heating alone, a horizontal collector is preferable compared to borehole heat exchangers, enabling savings of around 12%. The LCOH determined was 19.8 ct/kWh. Error analysis shows a mean error for horizontal GHE of 1.07% and a mean error for vertical GHE of 1.41%. Sensitivity analyses with regard to the dimensioning of the respective geothermal heat source show an optimisation potential regarding the sizing. For example, an increase of 10% of the horizontal GHE leads to a reduction of the LCOH by 1.5%. When passive cooling is taken into account, it can be stated that a horizontal GHE designed for the heating load cannot guarantee passive cooling in general. For example, the limit temperature for passive cooling is exceeded on 11 days in the design case of the horizontal GHE. In contrast, vertical GHEs can ensure cooling over the entire summer period. Nevertheless, even if oversizing is necessary, horizontal systems are the more economical systems and allow annual savings of around 3%.
Depending on the geographical location, it can be recognised that the choice of a suitable geothermal heat source is of great significance. Using climate data from Oslo (Norway), it can be observed that horizontal collectors provide a favourable heat supply. Furthermore, they are able to cover the small amount of cooling during the summer period. The overall costs per year are reduced by 4.1% in contrast to vertical heat exchangers. In the Bordeaux region, vertical systems are the more economical solution, as they can serve the higher cooling demand cheaply. In this case, costs can be reduced by 3% per year.
It can be concluded that vertical GHEs are advantageous in their wide range of applications. They can reliably provide both heat and cold over a wide variation of dimensioning. Nevertheless, their high investment costs represent a significant disadvantage compared to other heat sources. Horizontal GHEs are particularly suitable for the cost-effective provision of heat. When considering the cooling supply, their dimensioning must be planned more carefully, as undersizing can easily occur. The heating-to-cooling demand ratio can be used as a decision indicator for selecting the respective geothermal system. It can be seen that for ratios below around 1.5, vertical GHEs are the more economical option. If, on the other hand, the heating demand predominates, horizontal systems are preferred. For values in the transitional range between 2–1.5, detailed investigations must be carried out with regard to the other boundary parameters such as soil properties, consumer behaviour, etc. In future work, these criteria for the evaluation of the individual scenarios will be determined. These will allow an assessment of the individual cases based on a variable weighting of the factors independent of the system’s location.
Author Contributions
All authors contributed to this work by collaboration. S.K. is the main author of this manuscript. F.H. had the initial idea and assisted in the conceptual design of the study, as well as in the writing of the manuscript. D.B. supervised the whole project. All authors have read and agreed to the published version of the manuscript.
Funding
The funding of the project EWIO by the European Commission in the framework of the “European Regional Development Fund” is gratefully acknowledged. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—491183248. Funded by the Open Access Publishing Fund of the University of Bayreuth.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Corresponding data are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Latin Letters | |
| bi | Cash value factor |
| D | Depth below the surface (surface=0) |
| di,pipe | Inner diameter of the pipe |
| g | g-function |
| gFLS(t) | g-function evaluated for the finite line source solution |
| gCHS(t) | g-function evaluated for the cylindrical geometry |
| gILF(t) | g-function evaluated for the infinite line source solution |
| H | Borehole length |
| ks | Ground thermal conductivity |
| lpipe | Length of the pipe |
| Nb | Number of boreholes in the field |
| OMi | Sum of annual cost for operation and maintenance |
| Pi | Annualised capital cost of investment pf the specific component i |
| P0 | Investment amount of the specific component |
| Pel | Electrical power |
| pfric | Pressure losses due to friction |
| pgeo | Pressure losses due to geodetic elevation |
| Q | Heat flow |
| Qi | Annual amount of energy |
| q | Interest factor |
| R | Annual revenues |
| rpipe,inner | Inner radius of the pipe |
| rpipe,outer | Outer radius of the pipe |
| rsoil | Radius of the cylindrical soil cell |
| Tamp | Amplitude of surface temperature |
| Tb(t) | Borehole wall temperature |
| Tg | Undisturbed ground temperature |
| Tmean | Mean surface temperature (average air temperature). |
| Tsoil | Soil temperature at depth D and Time of year |
| tshift | Day of the year of the minimum surface temperature |
| tyear | Current time |
| vpipe | Velocity within the pipe |
| z | Geodetic elevation |
| Greek Letters | |
| α | Thermal diffusivity of the ground (soil) |
| ρmedium | Density of the fluid |
| λpipe | Friction factor |
| λpipe | Heat conductivity of the pipe |
| λsoil | Heat conductivity of the soil |
| Abbreviations | |
| COP | Coefficient of Performance |
| GHE | Ground Heat Exchanger |
| LCOC | Levelised Cost of Cold |
| LCOH | Levelised Cost of Heat |
| LTDH | Low-temperature district heating |
References
- European technology platform on renewable heating and cooling. In 2020–2030–2050, Common Vision for the Renewable Heating and Cooling Sector in Europe; European Union: Brussels, Belgium, 2011; Available online: https://op.europa.eu/en/publication-detail/-/publication/151b6f88-5bf1-4bad-8c56-cc496552cd54/language-en (accessed on 9 January 2022).
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Pezzutto, S.; Fazeli, R.; de Felice, M.; Sparber, W. Future development of the air-conditioning market in Europe: An outlook until 2020. WIREs Energy Environ. 2016, 5, 649–669. [Google Scholar] [CrossRef]
- Winter, W.; Haslauer, T.; Obernberger, I. Untersuchungen der Gleichzeitigkeit in kleinen und mittleren Nahwärmenetzen. Euroheat Power 2001, 9. Available online: http://www.verenum.ch/Dokumente/2001_Winter-Gleichzeitig.pdf (accessed on 9 January 2022).
- Santamouris, M. Cooling the buildings—Past, present and future. Energy Build. 2016, 128, 617–638. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Werner, S.; Möller, B.; Persson, U.; Boermans, T.; Trier, D.; Østergaard, P.A.; Nielsen, S. Heat Roadmap Europe: Combining district heating with heat savings to decarbonise the EU energy system. Energy Policy 2014, 65, 475–489. [Google Scholar] [CrossRef]
- Ruesch, F.; Haller, M. Potential and limitations of using low-temperature district heating and cooling networks for direct cooling of buildings. Energy Procedia 2017, 122, 1099–1104. [Google Scholar] [CrossRef]
- Bilardo, M.; Sandrone, F.; Zanzottera, G.; Fabrizio, E. Modelling a fifth-generation bidirectional low temperature district heating and cooling (5GDHC) network for nearly Zero Energy District (nZED). Energy Rep. 2021, 13, 193. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Q.; Nourozi, B.; Pieskä, H.; Ploskić, A. Evaluating the cooling potential of a geothermal-assisted ventilation system for multi-family dwellings in the Scandinavian climate. Build. Environ. 2021, 204, 108114. [Google Scholar] [CrossRef]
- Li, S.; Dong, K.; Wang, J.; Zhang, X. Long term coupled simulation for ground source heat pump and underground heat exchangers. Energy Build. 2015, 106, 13–22. [Google Scholar] [CrossRef]
- Dassault Systems. Dymola Systems Engineering. Available online: https://www.3ds.com (accessed on 9 January 2022).
- Wetter, M.; Zuo, W.; Nouidui, T.S.; Pang, X. Modelica Buildings library. J. Build. Perform. Simul. 2014, 7, 253–270. [Google Scholar] [CrossRef]
- ASHRAE. Handbook—Fundamentals: Chapter 17, Residential Cooling and Heating Load Calculations; American Society of Heating, Refrigerating and Air-conditioning Engineers: Atlanta, GA, USA, 2017. [Google Scholar]
- Van der Heijde, B.; Fuchs, M.; Tugores, C.R.; Schweiger, G.; Sartor, K.; Basciotti, D.; Müller, D.; Nytsch-Geusen, C.; Wetter, M.; Helsen, L. Dynamic equation-based thermo-hydraulic pipe model for district heating and cooling systems. Energy Convers. Manag. 2017, 151, 158–169. [Google Scholar] [CrossRef] [Green Version]
- Arce, I.D.H.; López, S.H.; Pérez, S.L.; Rämä, M.; Klobut, K.; Febres, J.A. Models for fast modelling of district heating and cooling networks. Renew. Sustain. Energy Rev. 2018, 82, 1863–1873. [Google Scholar] [CrossRef]
- MEGlobal. Ethylene Glycol Product Guide. Available online: https://www.meglobal.biz/wp-content/uploads/2019/01/Monoethylene-Glycol-MEG-Technical-Product-Brochure-PDF.pdf (accessed on 9 January 2022).
- Florides, G.; Kalogirou, S. Annual ground temperature measurements at various depths. In Proceedings of the 8th REHVA World Congress Clima 2005, Lausanne, Switzerland, 9–12 October 2005. [Google Scholar]
- Perpar, M.; Rek, Z.; Bajric, S.; Zun, I. Soil thermal conductivity prediction for district heating pre-insulated pipeline in operation. Energy 2012, 44, 197–210. [Google Scholar] [CrossRef]
- Santa, G.D.; Galgaro, A.; Sassi, R.; Cultrera, M.; Scotton, P.; Mueller, J.; Bertermann, D.; Mendrinos, D.; Pasquali, R.; Perego, R.; et al. An updated ground thermal properties database for GSHP applications. Geothermics 2020, 85, 101758. [Google Scholar] [CrossRef]
- Alpha Innotec. WZSV-Serie: Betriebsanleitung. 2019. Available online: htttps://www.alpha-innotec.de (accessed on 9 January 2022).
- Kreditanstalt für Wiederaufbau. Anlage zum Merkblatt Energieeffizient Bauen (153); KfW: Frankfurt, Germany, 2016. [Google Scholar]
- Jeong, C.-H.; Lee, J.Y.; Yeo, M.S.; Kim, K.W. Cooling Load Analysis of Residential Buildings for Dehumidification/Sub-Cooling Systems in Radiant Cooling. Sustain. Build. 2007, 1, 505–512. [Google Scholar]
- Polinder, H.; Schweiker, M.; Van der Aa, A. Occupant Behavior and Modeling; Tohoku University: Tohoku, Japan, 2013. [Google Scholar]
- Carrier. Hourly Analysis Program (HAP). Available online: https://www.carrier.com/commercial/en/us/software/hvac-system-design/hourly-analysis-program/ (accessed on 6 December 2021).
- De Santiago, J.; Rodriguez-Villalón, O.; Sicre, B. The generation of domestic hot water load profiles in Swiss residential buildings through statistical predictions. Energy Build. 2017, 141, 341–348. [Google Scholar] [CrossRef] [Green Version]
- Braas, H.; Jordan, U.; Best, I.; Orozaliev, J.; Vajen, K. District heating load profiles for domestic hot water preparation with realistic simultaneity using DHWcalc and TRNSYS. Energy 2020, 201, 117552. [Google Scholar] [CrossRef]
- Blum, P.; Campillo, G.; Kölbel, T. Techno-economic and spatial analysis of vertical ground source heat pump systems in Germany. Energy 2011, 36, 3002–3011. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure. Thermal Use of the Underground—Fundamentals, Approvals, Environmental Aspects (4640). 2010. Available online: https://www.vdi.de/en/home/vdi-standards/details/vdi-4640-blatt-1-thermal-use-of-the-underground-fundamentals-approvals-environmental-aspects (accessed on 9 January 2022).
- Brennenstuhl, M.; Zeh, R.; Otto, R.; Pesch, R.; Stockinger, V.; Pietruschka, D. Report on a Plus-Energy District with Low-Temperature DHC Network, Novel Agrothermal Heat Source, and Applied Demand Response. Appl. Sci. 2019, 9, 5059. [Google Scholar] [CrossRef] [Green Version]
- Bauer, D.; Heidemann, W.; Müller-Steinhagen, H.; Diersch, H.-J.G. Thermal resistance and capacity models for borehole heat exchangers. Int. J. Energy Res. 2011, 35, 312–320. [Google Scholar] [CrossRef]
- Laferrière, A.; Cimmino, M.; Picard, D.; Helsen, L. Development and validation of a full-time-scale semi-analytical model for the short- and long-term simulation of vertical geothermal bore fields. Geothermics 2020, 86, 101788. [Google Scholar] [CrossRef]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes; Lund University: Lund, Sweden, 1987. [Google Scholar]
- Cimmino, M.; Bernier, M. A semi-analytical method to generate g-functions for geothermal bore fields. Int. J. Heat Mass Transf. 2014, 70, 641–650. [Google Scholar] [CrossRef]
- Cimmino, M. Fast calculation of the g -functions of geothermal borehole fields using similarities in the evaluation of the finite line source solution. J. Build. Perform. Simul. 2018, 11, 655–668. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Li, P.; Chan, V.; Lai, A.C.K. Full-scale temperature response function (G-function) for heat transfer by borehole ground heat exchangers (GHEs) from sub-hour to decades. Appl. Energy 2014, 136, 197–205. [Google Scholar] [CrossRef]
- Sangi, R.; Müller, D. Dynamic modelling and simulation of a slinky-coil horizontal ground heat exchanger using Modelica. J. Build. Eng. 2018, 16, 159–168. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure. Economic Efficiency of Building Installations. 2012. Available online: https://www.vdi.de (accessed on 9 January 2022).
- Brennenstuhl, M. Sektorkopplung mit kalter Nahwärme aus Geothermie—intelligenter Energieaustausch am Beispiel einer Plusenergiesiedlung in Wüstenrot, HFT Stuttgart. 2019. Available online: https://docplayer.org/112222856-Waerme-aus-dem-acker-agrothermie-und-kaltwaermenetz.html (accessed on 9 January 2022).
- Strom-Report. Strompreise. 2021. Available online: https://strom-report.de/strompreise/ (accessed on 6 December 2021).
- Roy, C. Review of Discretization Error Estimators in Scientific Computing. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; p. 1, ISBN 978-1-60086-959-4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).