Proactive Maintenance Model Using Reinforcement Learning Algorithm in Rubber Industry
Abstract
:1. Introduction
2. System Description and RL-Based Intelligent Diagnosis
- (a)
- Criticality levels have been introduced in RAM analysis to identify critical levels in curing subsystems.
- (b)
- Identification of critical levels in subsystem helps provide optimal availability and maintainability in curing subsystems.
- (c)
- Criticality levels define the CBM; it is done in this investigation via industrial IoT-connected sensors.
- (d)
- Unplanned maintenance over the long term is made to identify unexpected failures, and maintenance time is derived to predict availability.
- (e)
- To find failure and repair data, curing machine pots are modeled by a Continuous-Time Markov Process (CTMP).
- (f)
- The RLA is trained using a CTMP to analyze the availability of the curing machine.
- (g)
- The CTMP is solved to obtain the steady-state availability of all modules of the curing machine of first-order differential-difference equations.
- (h)
- Using steady-state availability, performance, and quality, the OEE of the curing machine is evaluated.
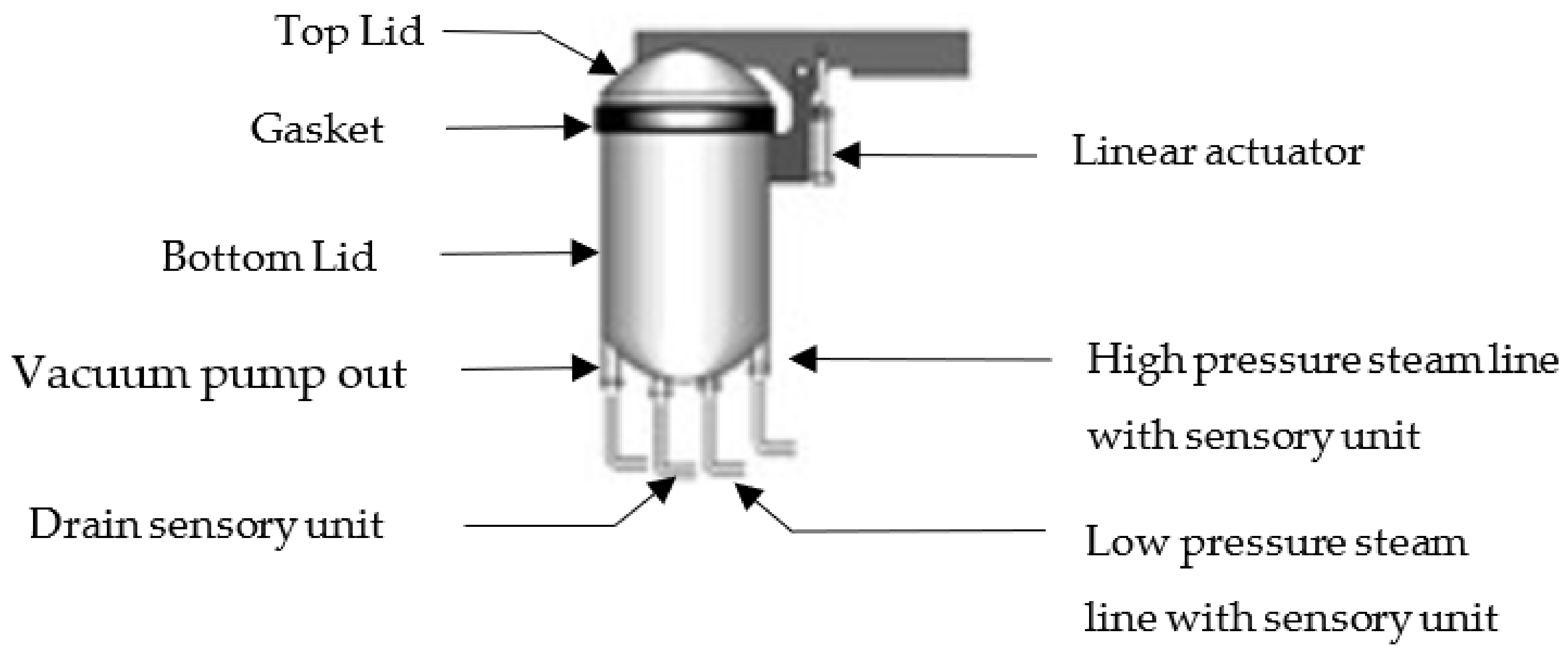
2.1. Criticality Level Analysis in a Curing Machine
2.2. RL-Based Intelligent Diagnosis
3. System Modeling for Overall Equipment Efficiency Analysis
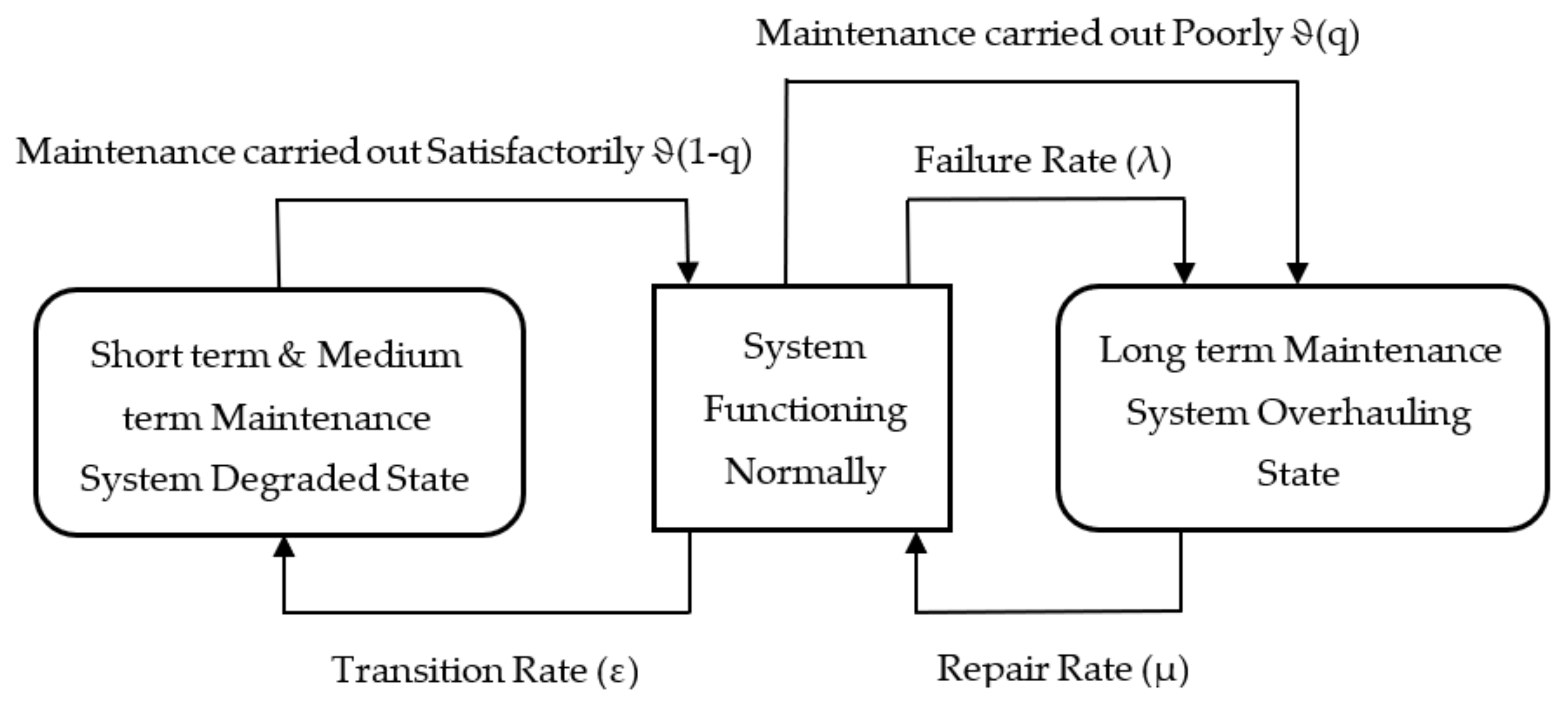
3.1. Reinforcement Learning in the Markov Model
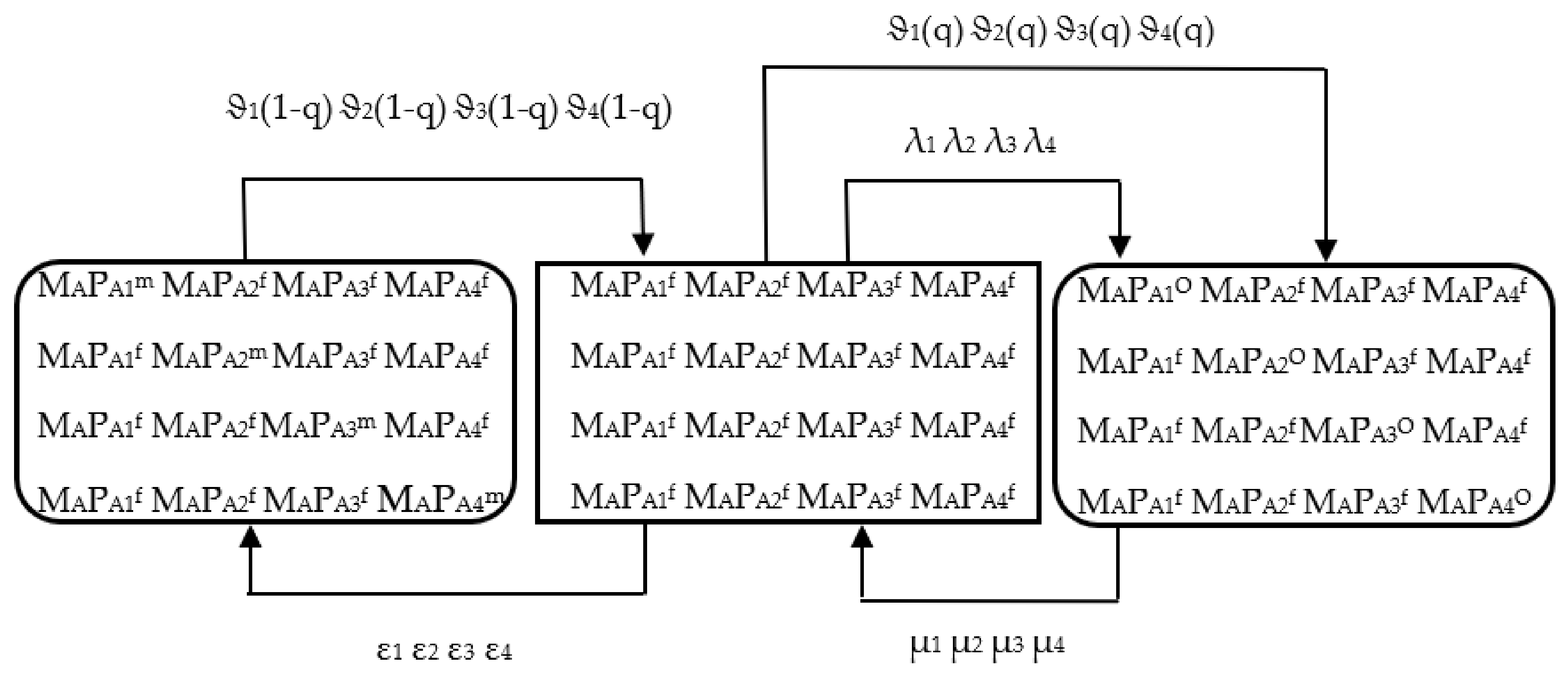
3.2. Mathematical Description for the Estimation of Availability in Scheduled/Unscheduled Maintenance
= 0.998 × 0.9717 × 0.9816
= 0.9519 × 100
= 95.19%
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aly, M.F.; Afefy, I.H.; Abdel-Magied, R.K.; Elhalim, E.K. A comprehensive model of reliability, availability and maintainability (RAM) for industrial systems evaluations. JJMIE 2018, 12, 59–67. [Google Scholar]
- Vulpe, A.; Carausu, A. Stochastic evaluation of availability for subsystems by Markov and semi-Markov models. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; Volume 1. [Google Scholar]
- Gupta, G.; Mishra, R.P.; Jain, P. Reliability analysis and identification of critical components using Markov model. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management IEEM, Singapore, 6–9 December 2015; pp. 777–781. [Google Scholar]
- Wang, L.; Yang, Q.; Tian, Y. Reliability analysis of 6-component star Markov repairable system with spatial dependence. Math. Probl. Eng. 2017, 2017, 9728019. [Google Scholar] [CrossRef]
- Chan, G.K.; Asgarpoor, S. Optimum maintenance policy with Markov processes. Electr. Power Syst. Res. 2006, 76, 452–456. [Google Scholar] [CrossRef]
- El-Damcese, M.A.; Temraz, N.S. Analysis of availability and reliability for repairable parallel systems with different failure rates. Asian J. Inf. Technol. 2010, 9, 231–237. [Google Scholar] [CrossRef] [Green Version]
- Kumar, G.; Jain, V.; Gandhi, O.P. Availability analysis of mechanical systems with condition-based maintenance using semi-Markov and evaluation of optimal condition monitoring interval. J. Ind. Eng. Int. 2018, 14, 119–131. [Google Scholar] [CrossRef]
- Hassani, I.E.; Mazgualdi, C.E.; Masrour, T. Artificial Intelligence and Machine Learning to Predict and Improve Efficiency in Manufacturing Industry. arXiv 2019, arXiv:1901.02256. [Google Scholar]
- Bonada, F.; Echeverria, L.; Domingo, X.; Anzaldi, G. AI for Improving the Overall Equipment Efficiency in Manufacturing Industry. In New Trends in the Use of Artificial Intelligence for the Industry 4.0; BoD—Books on Demand: Hamburg, Germany, 2020. [Google Scholar]
- Chan, S.C.; Fishman, S.; Canny, J.; Korattikara, A.; Guadarrama, S. Measuring the reliability of reinforcement learning algorithms. arXiv 2019, arXiv:1912.05663. [Google Scholar]
- Knowles, M.; Baglee, D.; Wermter, S. Reinforcement learning for scheduling of maintenance. In Proceedings of the International Conference on Innovative Techniques and Applications of Artificial Intelligence, Cambridge, UK, 14–16 December 2010; Springer: London, UK, 2010; pp. 409–422. [Google Scholar]
- Singh, R.; Shah, D.B.; Gohil, A.M.; Shah, M.H. Overall equipment effectiveness (OEE) calculation-Automation through hardware & software development. Procedia Eng. 2013, 51, 579–584. [Google Scholar]
- Tsarouhas, P.H. Overall equipment effectiveness (OEE) evaluation for an automated ice cream production line. Int. J. Prod. Perform. Manag. 2019, 69, 1009–1032. [Google Scholar] [CrossRef]
- Aman, Z.; Ezzine, L.; Moussami, H. Impact of Improving Machines’ Availability Using Stochastic Petri Nets on the Overall Equipment Effectiveness. In Maintenance Management; Intech Open: London, UK, 2020. [Google Scholar]
- Corvaro, F.; Giacchetta, G.; Marchetti, B.; Recanati, M. Reliability, Availability, Maintainability (RAM) study, on reciprocating compressors API 618. Petroleum 2017, 3, 266–272. [Google Scholar] [CrossRef]
- Kumar, R. Availability analysis of thermal power plant boiler air circulation system using Markov approach. Decis. Sci. Lett. 2014, 3, 65–72. [Google Scholar] [CrossRef]
- Artana, K.B.; Ishida, K. Determination of Ship Machinery Performance and Its Maintenance Management Using MARKOV Process Analysis. In WIT Transactions on the Built Environment; WIT Press: Ashurst, UK, 2001. [Google Scholar]
- Fink, O.; Zio, E. Semi-Markov processes with semi-regenerative states for the availability analysis of chemical process plants with storage units. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2013, 227, 279–289. [Google Scholar] [CrossRef] [Green Version]
- Bala, R.J.; Govinda, R.M.; Murthy, C.S. Reliability analysis and failure rate evaluation of load haul dump machines using Weibull distribution analysis. Math. Model. Eng. Probl. 2018, 5, 116–122. [Google Scholar] [CrossRef]
- Ahmadi, S.; Hajihassani, M.; Moosazadeh, S.; Moomivand, H. An Overview of the Reliability Analysis Methods of Tunneling Equipment. Open Constr. Build. Technol. J. 2020, 14, 218–229. [Google Scholar] [CrossRef]
- Fang, Y.; Tao, W.; Tee, K.F. Time-domain multi-state markov model for engine system reliability analysis. Mech. Eng. J. 2016, 3, 16-00084. [Google Scholar] [CrossRef] [Green Version]
- Tsarouhas, P. Reliability, Availability, and Maintainability (RAM) Study of an Ice Cream Industry. Appl. Sci. 2020, 10, 4265. [Google Scholar] [CrossRef]
- Sharma, S.P.; Vishwakarma, Y. Application of Markov process in performance analysis of feeding system of sugar industry. J. Ind. Math. 2014, 2014, 593176. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, T.P.; Soares, F.A.; Vita, R.; Francisco, R.D.P.; Basto, J.P.; Alcalá, S.G. A systematic literature review of machine learning methods applied to predictive maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Dupin, N.; Talbi, E.G. Matheuristics to optimize refueling and maintenance planning of nuclear power plants. J. Heuristics 2021, 27, 63–105. [Google Scholar] [CrossRef]
- Lee, H.; Cha, J.H. New stochastic models for preventive maintenance and maintenance optimization. Eur. J. Oper. Res. 2016, 255, 80–90. [Google Scholar] [CrossRef]
- Vilarinho, S.; Lopes, I.; Oliveira, J.A. Preventive maintenance decisions through maintenance optimization models: A case study. Procedia Manuf. 2017, 11, 1170–1177. [Google Scholar] [CrossRef]
- Gao, X.; Barabady, J.; Markeset, T. Criticality analysis of a production facility using cost importance measures. Int. J. Syst. Assur. Eng. Manag. 2010, 1, 17–23. [Google Scholar] [CrossRef]
- Li, R.; Cheng, Y.; Xu, J.; Li, Y.; Zhao, X.D.S. Research on On-Line Monitoring System of Hydraulic Actuator of Combine Harvester. Processes 2022, 10, 35. [Google Scholar] [CrossRef]
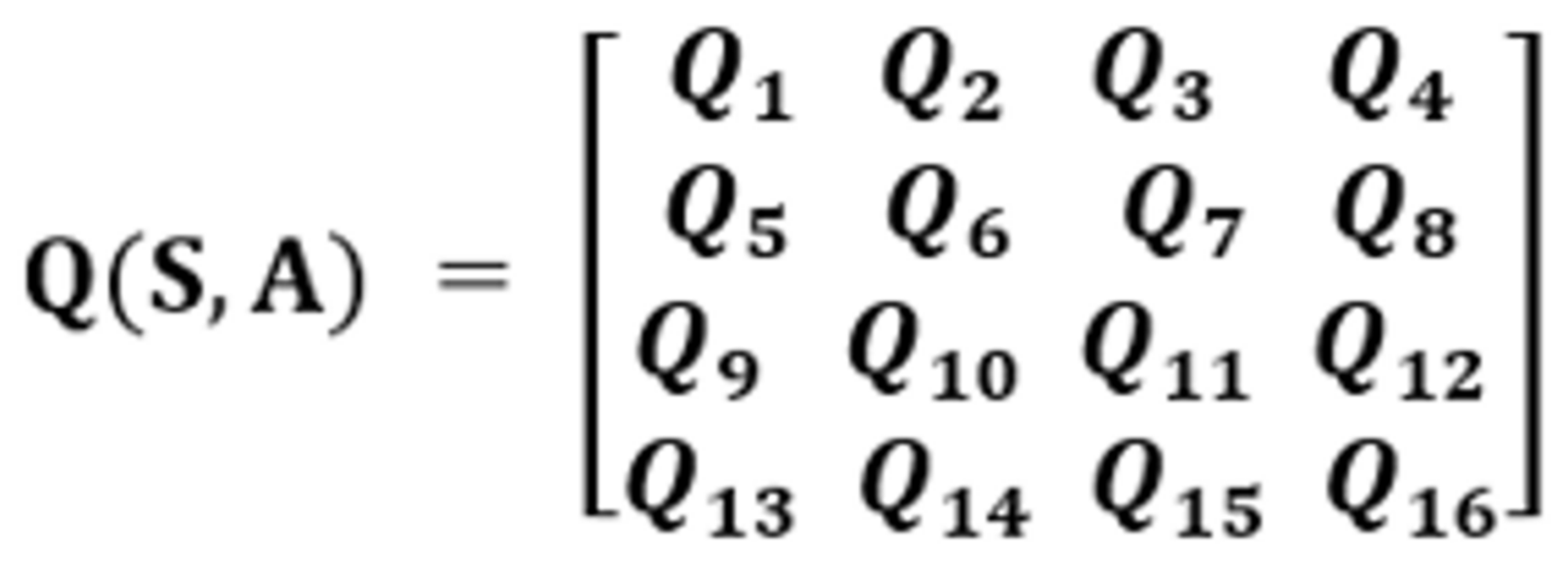


| Module | Pot | Failure Rate | Repair Rate | Transition Rate | Maintenance Rate | ||||
|---|---|---|---|---|---|---|---|---|---|
| Module A | PA1 | λ1 | 0.008 | µ1 | 0.43 | ε1 | 0.01 | ϑ1 | 0.61 |
| PA2 | λ2 | 0.009 | µ2 | 0.51 | ε2 | 0.009 | ϑ2 | 0.59 | |
| PA3 | λ3 | 0.008 | µ3 | 0.49 | ε3 | 0.011 | ϑ3 | 0.65 | |
| PA4 | λ4 | 0.005 | µ4 | 0.55 | ε4 | 0.007 | ϑ4 | 0.62 | |
| Module B | PB1 | λ5 | 0.011 | µ5 | 0.51 | ε5 | 0.008 | ϑ5 | 0.59 |
| PB2 | λ6 | 0.01 | µ6 | 0.48 | ε6 | 0.006 | ϑ6 | 0.59 | |
| PB3 | λ7 | 0.01 | µ7 | 0.45 | ε7 | 0.011 | ϑ7 | 0.63 | |
| PB4 | λ8 | 0.009 | µ8 | 0.49 | ε8 | 0.009 | ϑ8 | 0.62 | |
| Module C | PC1 | λ9 | 0.007 | µ9 | 0.51 | ε9 | 0.008 | ϑ9 | 0.59 |
| PC2 | λ10 | 0.008 | µ10 | 0.55 | ε10 | 0.009 | ϑ10 | 0.63 | |
| PC3 | λ11 | 0.009 | µ11 | 0.6 | ε11 | 0.009 | ϑ11 | 0.62 | |
| PC4 | λ12 | 0.007 | µ12 | 0.59 | ε12 | 0.01 | ϑ12 | 0.58 | |
| Module D | PD1 | λ13 | 0.011 | µ13 | 0.53 | ε13 | 0.011 | ϑ13 | 0.63 |
| PD2 | λ14 | 0.009 | µ14 | 0.48 | ε14 | 0.009 | ϑ14 | 0.61 | |
| PD3 | λ15 | 0.009 | µ15 | 0.49 | ε15 | 0.008 | ϑ15 | 0.59 | |
| PD4 | λ16 | 0.011 | µ16 | 0.53 | ε16 | 0.01 | ϑ16 | 0.6 | |
| MODULE | POT | Overall Equipment Efficiency (OEE) % | |
|---|---|---|---|
| Short- and Medium- Term Maintenance | Long Term Maintenance | ||
| Module A | Pot A1 | 29.56 | 25.86 |
| Module A | Pot A2 | 30.02 | 26.33 |
| Module A | Pot A3 | 29.65 | 25.95 |
| Module A | Pot A4 | 29.56 | 25.86 |
| Module B | Pot B1 | 90.15 | 78.69 |
| Module B | Pot B2 | 90.64 | 79.19 |
| Module B | Pot B3 | 88.56 | 77.11 |
| Module B | Pot B4 | 91.64 | 80.18 |
| Module C | Pot C1 | 45.4 | 39.86 |
| Module C | Pot C2 | 46.15 | 40.6 |
| Module C | Pot C3 | 45.94 | 40.39 |
| Module C | Pot C4 | 44.34 | 38.8 |
| Module D | Pot D1 | 94.39 | 82.57 |
| Module D | Pot D2 | 95.19 | 83.37 |
| Module D | Pot D3 | 94.89 | 83.07 |
| Module D | Pot D4 | 94.59 | 82.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senthil, C.; Sudhakara Pandian, R. Proactive Maintenance Model Using Reinforcement Learning Algorithm in Rubber Industry. Processes 2022, 10, 371. https://doi.org/10.3390/pr10020371
Senthil C, Sudhakara Pandian R. Proactive Maintenance Model Using Reinforcement Learning Algorithm in Rubber Industry. Processes. 2022; 10(2):371. https://doi.org/10.3390/pr10020371
Chicago/Turabian StyleSenthil, Chandran, and Ranjitharamasamy Sudhakara Pandian. 2022. "Proactive Maintenance Model Using Reinforcement Learning Algorithm in Rubber Industry" Processes 10, no. 2: 371. https://doi.org/10.3390/pr10020371
APA StyleSenthil, C., & Sudhakara Pandian, R. (2022). Proactive Maintenance Model Using Reinforcement Learning Algorithm in Rubber Industry. Processes, 10(2), 371. https://doi.org/10.3390/pr10020371






