Abstract
Additives are widely used to enhance the rheological and performance properties of asphalt binder to satisfy the demands of extreme loading and climatic conditions. Meanwhile, adding to the complexity of asphalt binder behaviour that requires more time, effort, and material resources during laboratory work. The purpose of this research was to use Artificial Neural Networks (ANNs) to predict the recovery (R) and nonrecoverable compliance (J) behaviour of asphalt binder based on mechanical test parameters and rheological properties of asphalt binder. A comprehensive experimental database consisting of the results of the frequency sweep and Multiple Stress Creep Recovery (MSCR) test using a dynamic shear rheometer (DSR) at five test temperatures (46 C, 52 C, 58 C, 64 C, and 70 C). Prediction models for R and J of asphalt binder modified with different contents of fly ash, fly ash-based geopolymer, glass powder/fly ash-based geopolymer, and styrene–butadiene styrene (SBS) were developed. The ANNs model was developed using five input parameters (temperature, frequency, storage modulus, loss modulus, and viscosity) and one hidden layer with five neurons. The results pointed out that the hybrid and 4%SBS binders achieved the highest ability to resist extremely heavy traffic and to recover the deformation with 60.1% and 85.5% at 46 C, respectively, compared with the other modified asphalt binders. Excellent R-values for the total data set of 0.937, 0.997, 0.985, and 0.987 for J of unaged binder, J of aged binder, R of unaged binder, and R of aged binder, respectively. Therefore, the ANNs model is appropriate tool to predict the R and J using unaged or aged binders at different temperatures.
1. Introduction
Rutting is a common sign of distress that affects the road network’s serviceability and quality. It is a permanent deformation that occurs in the traffic direction because of unrecoverable strain accumulated by repetitive loads applied to the asphalt pavement [1]. Due to the combined effects of viscoelastic characteristics and shear loads on the hot mix asphalt (HMA) layer, asphalt is highly susceptible to rutting. As the temperature increases, the asphalt binder decreases the ability to elastically recover from deformation, increasing the sensitivity to permanent deformation. In recent decades, there has been attention to modified asphalt binders using different modifiers to enhance the rutting performance. The viscoelastic properties of asphalt binders can be improved by modifying the asphalt binder using different modifiers. Modification, on the other hand, adds to the complexity of binders’ behaviour; thus, substantial laboratory testing is required before field application to establish the best solutions.
The Multiple Stress Creep-Recovery (MSCR) test was developed to measure the binder’s nonlinear reaction and to link that response to rutting in asphalt mixtures [2]. The MSCR test has long been used to predict how polymer-modified asphalt binders may affect creep recovery [3,4,5,6]. In the field of modified and unmodified asphalt binders, the MSCR test is also efficiently conducted and designed to be an indicator of rutting performance [7]. The MSCR test consists of a series of creep and recovery cycles performed at various stress levels. The idea was that by removing shear stress from the creep section, the viscoelastic strain created in the creep component could be recovered, allowing the permanent strain to be separated from the overall strain, which could be used to predict field rutting [8]. The MSCR test was used to determine non-recoverable creep compliance (J) and percent recovery (R). The J had a good correlation with the HMA performance test results and can thus be used to characterise asphalt binders to address HMA rutting characteristics [9]. Tabatabaee and Tabatabaee [10] reported that the J was highly correlated to the compliance measured from unconfined dynamic creep, with R values over 80%. While Dreessen and Gallet [11] noted that the J may be a better choice than G*/sin and/or the softening point, whereby it corresponds better to mix rutting performance as measured by the French rutting test.
Several methods have been developed to predict asphalt pavement performance to eliminate laboratory tests for individual mixes, which are expensive and time-consuming. Using a reliable calibrated model to predict the effects of additives on the behaviour of asphalt binders can significantly reduce operating and testing expenses. Recently, Artificial neural networks (ANNs) have been used in many disciplines of civil engineering, such as water supply engineering [12], pavement materials [13,14] and pavement structure [15]. Plati et al. [15] summarized some advantages that make ANNs a powerful problem-solving tool which could be used to develop complex models through data mining. The ANNs has been used in a variety of pavement applications, such as designing airfield pavement [16,17,18], predicting the rutting performance [19] and the indirect tensile strength [20] of flexible pavement. Also, the ANNs model was used to predict the performance of asphalt mixture modified with recycled asphalt shingles [21], fiber [22], nano-silica [23], SBS [24], glass fiber [25], crushed Boron Waste [26]. Baldo et al. [27] used artificial neural networks to predict the Marshall stability, flow, quotient, and stiffness modulus of asphalt concrete. Seven input parameters with one hidden layer and ten artificial neurons were applied to predict one output. The results indicated that the ANNs model could be used to predict the mechanical properties of asphalt concrete, whereby the developed models were excellent with coefficients of correlation ranging from 0.910 to 0.988. Esfandiarpour and Shalaby [13] performed ANNs to calibrate the creep compliance for different asphalt mixtures at different test temperatures (0 C, −10 C, and −20 C). It was noted that the ANNs model has the highest reliability and is considered an alternative method to predict creep compliance values.
Meanwhile, the complex mechanism of fatigue behaviour under various loading and climate conditions complicated the modelling of the fatigue life of asphalt mixtures using an empirical model [28]. Recently, using ANNs proved to be an effective tool for predicting the fatigue life of asphalt mixtures [29,30]. Xiao et al. [29] investigated the possibility of using ANNs to predict the fatigue life of rubberized asphalt mixtures containing Reclaimed Asphalt Pavement (RAP). The results indicated that the ANNs produced an accurate and precise prediction of fatigue life compared to the traditional statistical methods. Tapkin [30] predicted the fatigue life of asphalt mixtures that contained fly ash as a filler using neural networks. It was noted that ANNs resulted in accurate and precise modelling of fatigue life by utilizing changes in the physical properties of asphalt mixtures. The development of ANNs models to accurately predict HMA fatigue life would result in substantial time and cost savings by reducing laboratory testing.
Additionally, the ANNs model was used to predict the rutting performance of asphalt concrete. Kamboozia et al. [31] studied the possibility of using the viscoelastic parameters and ANNs model to predict the rutting depth of asphalt concrete using a dynamic creep test. The viscoelastic properties were collected from creep diagrams, and an artificial neural network was used to train and develop a rut depth prediction model for asphalt concrete. The developed ANNs used 560 specimens, whereby 70% of the data was used for training and the remaining 30% for validation and testing. The results showed that by utilizing the effective parameters, the ANNs model can be used to estimate the creep behaviour and rut depth of asphalt concrete without the need for costly and time-consuming testing. Table 1 summarizes the ANNs models that were used to predict the performance of asphalt mixtures.
Moreover, the ANNs model was used to predict the rheological and performance of asphalt binder modified with rubber [32,33], SBS [34,35], geopolymer [36], filler [37], and waste engine oil [38]. The ANNs model was also utilised to predict fatigue and rutting performance of asphalt binder [32,35,36,39]. Venudharan and Biligiri [32] used the ANNs model to predict the rutting performance of asphalt binder using the gradation of crumb rubber, mechanical test parameters, and the properties of binder. The dynamic shear rheometer (DSR) test was used to characterise 18 different asphalt binders. The ANNs architecture used a back-propagation learning algorithm with scaled conjugate gradient (SCG) as the training technique, with two hidden layers of seven and three neurons, respectively. The results indicated that the ANNs model is a significant method to predict the performance of asphalt binder with R value of 0.997, 0.994, and 0.977 for G*/sin, , and tan, respectively. Ziari et al. [39] employed ANNs and regression models to predict the rutting performance of a carbon nanotube-modified asphalt binder. A multilayer feed-forward back-propagation method with 480 experimental data points was used to predict the rutting parameter, whereby 60% of the data was used for training, while 40% was used for validation and testing the model. The results showed that the ANNs method outperformed multiple regression and linear regression in predicting rutting performance, with R values of 0.997, 0.819, and 0.420, respectively.
Alas and Ali [36] utilised the ANNs method to predict the shear complex modulus, phase angle, storage modulus, and loss modulus using temperature, frequency, and polymer contents as input parameters. A total of 252 data sets were randomly divided into two groups, with 70% of the empirically observed data being used to train the model and 30% of the data being used to test the model. The results showed that the developed model for the shear complex modulus is excellent with high R values for training and testing data, 0.996 and 0.971, respectively. While the testing data for phase angle and storage modulus achieved the least R with values less than 0.9. The model’s poor prediction performance for the testing data suggested that it was unable to learn the complexity of the data. Uwanuakwa et al. [35] conducted the ANNs to predict the rutting and fatigue performance of unaged and aged asphalt binders. A frequency sweep test using the DSR was performed on the 8 mixes of asphalt binders to measure the complex shear modulus and phase angle at various temperatures. According to the results, the model performed better in estimating the rutting parameter than the fatigue parameter. Furthermore, unaged input variables have a higher level of predictability when it comes to the fatigue parameter. Table 2 summarizes the ANNs models used to predict the rheological and performance of asphalt binder. It was noted that the ANNs model effectively predicts the rheological and performance of modified asphalt binder with high accuracy.
The literature on the use of ANNs in pavement engineering demonstrates that ANNs could be used to determine and understand the performance of asphalt binders and mixtures based on material characteristics and mechanical test data, as demonstrated in Table 1 and Table 2. Also, Many studies have also noticed the effects of additives, temperatures, and frequencies on viscoelastic characteristics. On the other hand, the ANNs model is an effective tool for accurately predicting the rheological and performance of asphalt binder as discussed in the literature review (see Table 2). Therefore, predicting the creep recovery behavior of the asphalt binder using these effects and their changes in viscoelastic characteristics as inputs to the ANNs model could be effective for developing an accurate model that could have a significant effect on saving time and money during laboratory work. This study aimed to predict the recovery (R) and non-recoverable creep compliance (J) behaviour of asphalt binder using the ANNs model, considering the effects of temperatures, frequencies, and additives on the viscoelastic properties of asphalt binders.

Table 1.
Predicting the rheological and performance properties of asphalt mixtures using ANNs model.
Table 1.
Predicting the rheological and performance properties of asphalt mixtures using ANNs model.
| Reference | Predicted Parameter | ANNs Model | Training Algorithm | Main Comments |
|---|---|---|---|---|
| [22] | Fracture Temperature and Strength | Four inputs, one hidden layer with four neurons, and 73 data points. | LM | The asphalt mixture’s Fracture temperature and strength may be predicted using the ANNs model. |
| [40] | Permanent deformation | Five inputs, one hidden layer with ten neurons, and 270 data points. | LM | The use of Nano additives in asphalt mixtures can be decided upon primarily using the ANN model. |
| [13] | Creep compliance | Five inputs, one hidden layer with seven neurons, and 861 data points. | The ANN model achieves the minimum error and increases the accuracy of predictions of creep compliance. | |
| [21] | Dynamic modulus (E*) | Nine inputs, two hidden layers with 15-15 neurons, and 1701 data points. | BPNN | The ANNs model is an effective tool to predict the E* of the asphalt mixture. |
| [23] | Temperature Sensitivity | Five inputs, one hidden layer with four neurons, and 48 data points. | LM | A more accurate model is provided by the ANNs model. |
| [41] | skid resistance | Five inputs, one hidden layer with ten neurons, and 124 data points. | GA-BP | The developed GA-BP model can provide precise and effective long-term skid resistance predictions. |
| [24] | Stiffness modulus and Marshall stability and quotient | 6 inputs, 1 and 3 hidden layers with 8 neurons in each layer. 129 data points. | - | Using the ANNs model during the design phase of asphalt mixtures can be extremely beneficial. |
| [42] | Field permeability | Seven inputs, one hidden layer with 10 neurons | LM | It is advised that ANNs be considered for routine use in predicting field permeability. |
| [26] | Flow and stability | Seven inputs, two hidden layers with 20 and 15 neurons. | LM | The ANNs model can be used to predict the stability and flow of asphalt mixtures. |
| [25] | Marshall stability | Five inputs, one hidden layer with six neurons, and 128 data points. | BPNN | The ANNs model can accurately predict the MS of asphalt concrete reinforced with glass fibre. |
| [43] | Dynamic modulus (E*) | Five inputs, various hidden layers, and 4022 data points. | LM | The proposed model can be utilised successfully and accurately to estimate E*. |
| [44] | Theoretical maximum specific gravity (G) | Three inputs, two hidden layers with 8 and 10 neurons, and 4158 data points. | LM | The suggested model could reduce the amount of time, effort, and material resources required for the mix-design of asphalt mixture. |
Note: BPNN: back-propagation neural network, FT: Fracture Temperature, FS: Fracture Strength, TS: Temperature Sensitivity, ITSM: Stiffness modulus, MS: Marshall stability, MQ: Marshall quotient, GA: Genetic algorithm.

Table 2.
Predicting the rheological and performance properties of asphalt binder using ANNs model.
Table 2.
Predicting the rheological and performance properties of asphalt binder using ANNs model.
| Reference | Predicted Parameter | ANNs Model | Training Algorithm | Main Comments |
|---|---|---|---|---|
| Current study | Recovery and Nonrecoverable Compliance | Five inputs, one hidden layer with five neurons, 880 data points. | LM | The ANNs model is an effective tool to predict the Recovery and Nonrecoverable Compliance using unaged and aged asphalt binders. |
| [45] | Viscosity | Four inputs, three hidden neurons, 216 data points. | LM | The ability of the developed ANN to accurately predict the viscosity values using the viscosity values from other research projects has been demonstrated. |
| [46] | Fraass breaking point, creep stiffness and creep rate | Three models with architecture 19–6–8–1, 19–4–6–1 and 19–5–7–1. | LM | ANN models to predict physical–mechanical properties of modified bitumen were suggested. |
| [37] | G* | Three inputs, two hidden layers with five or four neurons and 201 data points. | LM, CPG, SCG | The ANNs model is a powerful tool for accurately predicting G*. |
| [47] | G* | Six inputs, three hidden layer with six neurons, and 105 data points. | GD | The ANN model is a useful tool for predicting the G*. |
| [32] | , G*/, and | Eight inputs, two hidden layers with seven and three neurons, and 2200 data points. | SCG | The ANNs model could be well used in predicting asphalt binder performance. |
| [48] | adhesion/cohesion force | Eleven inputs, two hidden layers with 25 neurons in each layer, and 1497 data points. | LM | The complicated link between adhesion and test factors used in atomic force microscopy testing can be addressed by neural networks. |
| [39] | G*, and G*/ | Two models with architecture 3–25–1 and 3–10–1, and 480 data points. | LM | Compared to regression models, the ANN method was more accurate in predicting rutting performance. |
| [36] | G*, G, G, and | Three inputs, one hidden layer with eight or five neurons, and 252 data points. | LM, CPG, SCG | The highest performing model was the G* model using the LM algorithm and 1-5-1 network structure. |
| [35] | G*/ and G*· | 16 inputs, one hidden layer with twelve neurons, 1980 and 1668 data points for rutting and fatigue parameters. | - | ANNs model can be used to predict rutting and fatigue parameters with R> 0.95. |
| [38] | G* and | Three inputs, one hidden layer with twelve neurons. | LM | The ANNs model can predict the rheological characteristics of asphalt binders with high accuracy. |
| [33] | Viscosity | Eight inputs, three hidden neurons, 90 data points. | - | The training data for an ANN network model should involve a variety of indicators and be as practical as possible. |
| [49] | Phase angle () | two hidden layer with 8-3 neurons, 1376 data points. | QN | Compared to MLR and PCA, the ANN model is the most effective method for predicting the phase angle. |
Note: SCG: Scaled Conjugate Gradient, LM: Levenberg-Marquardt, CPG: Polak-Ribiere conjugate gradient, GD: gradient-descent, QN: Quasi-Newton, MLR: Multiple Linear Regression, and PCA: Principle Component Analysis.
2. Methodology
2.1. Materials and Methods
In this investigation, 11 mixes of fly ash, SBS polymer, fly ash-based geopolymer, fly ash and glass powder-based geopolymer modified asphalt binder (PG58-28) were utilised to build the database. Table 3 presents the chemical composition of fly ash (Class F) satisfies SiO + AlO + FeO≥ 70% according to ASTM C618-17a [50]. Many scholars advocate that low calcium fly ash (Class F) be utilised because it includes more silica and alumina than high calcium fly ash (Class C) [51,52].

Table 3.
Fly ash chemical composition.
The geopolymer is formed when the aluminosilicate source, such as fly ash, reacts with the alkaline solution. Equations (1) and (2) describe the chemical reactions during the geopolymerisation process [53].
In this study, the geopolymer is prepared using alkali activators and aluminosilicate source, such as fly ash and glass powder. Alkali activators included NaSiO and NaOH at a concentration of 8 molar. The NaOH solution was prepared one day before mixing with the aluminosilicate source to make the geopolymer. Fly ash and geopolymer additives were blended with asphalt binder in various contents at 140 C ± 5 for 60 min using a mechanical shear mixer at a speed of 2000 r/min. While the SBS was mixed with asphalt binder using the high shear mixer at a speed of 2000 r/min and a temperature of 170 C ± 5 for 60 min. Figure 1 presents the preparation of modifiers, asphalt binder mixing, and testing. Following the mixing procedure, all asphalt binders were exposed to short-term aging using a rolling thin-film oven (RTFO) for 85 min at 163 C, as depicted in Figure 1.

Figure 1.
Additive’s preparation and testing.
The DSR was used to investigate the rheological behaviour, according to AASHTO T 315 [54], and recovery and non-recovery properties of asphalt binder, according to AASHTO T350 [55], at high temperatures from 46 to 70 C, with 6 C increments. A frequency sweep test was conducted to investigate the effect of temperatures, frequencies, and additives on the viscosity and storage and loss modulus using a 25 mm diameter plate and a 1 mm gap. The tests were performed at sixteen frequencies ranging from 0.159 Hz to 15 Hz. Two samples were tested, and the average was identified as the test result for each temperature. While Multiple Stress Creep Recovery (MSCR) was performed to evaluate the influence of temperatures, stresses, and additives on the recovery and non-recovery properties of asphalt binders using a 25 mm diameter plate and a 1 mm gap. Two samples were tested, and the average was identified as the test result for each temperature. The test was conducted using (1 s) for creep and (9 s) for recovery, as shown in Figure 2. While the average percent recovery (R), and non-recoverable creep compliance () were calculated using Equations (3) and (4), respectively.
where is accumulated strain after 1 s, is residual strain after 10 s.
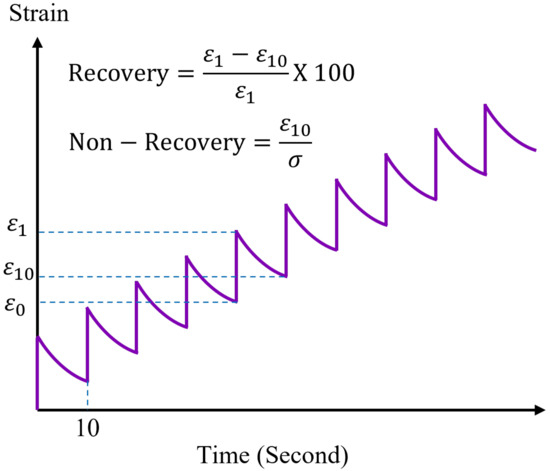
Figure 2.
Typical MSCR test results.
R is the recovery percentage and is non-recoverable creep compliance.
2.2. Artificial Neural Networks Modelling
The Artificial Neural Network (ANN) is a mathematical model formed of elements called neurons. This model consists of three groups of rules: multiplication, summation, and activation. In the multiplication stage, the inputs are weighted by multiplying each input value with its individual weight. After that, all weights and biases are summed in the summation stage. Finally, the sum of previously weighted inputs and bias is passing through the transfer function, acting as the activation function. In this study, the models developed for recovery and non-recovery behaviour of asphalt binder, as shown in Figure 3, involved of three layers: an input layer, a hidden layer, and an output layer. The dataset for these layers was based on experimental observations from the frequency sweep test and MSCR test. The developed ANNs used 880 experimental data points, whereby 70% of the data was used for training and the remaining 30% for validation and testing.
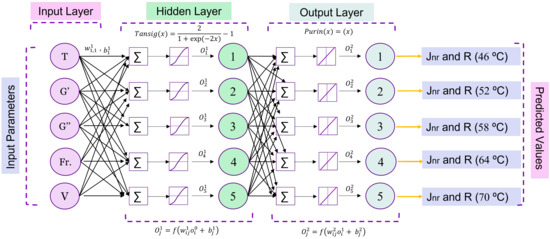
Figure 3.
ANN model for predicting recovery and non-recovery performance of asphalt binder.
The feedforward neural networks were considered in this study. The learning of the network in this form of ANN is supervised, which means that the associated output (target) for each input vector is known. The learning phase entails adjusting the ANN’s connections such that, for each input, the network returns a computed value that is as close to the target as possible. The developed ANNs model considered the effects of external factors (Temperature and frequency) on the rheological properties (storage modulus, loss modulus, and shear viscosity) of neat and modified asphalt binder. These factors and properties were considered as input parameters in the ANNs model to predict each target (J and R). The developed model has one hidden layer with five neurons, whereby the input to each neuron is a summation of all weighted connections between the input and the neuron in the hidden layer [56]. The weighted sum is denoted as (a) and represented in Equation (5).
N represents the number of neurons in the input layer, is the weight factor, is the input vector, and b is the bias term.
Then, the transfer or activation function was used to transfer the neuron to the new output. In this study, the sigmoid function is used as an activation function. The final output of the neuron is given in Equation (6).
In this study, the sigmoidal function is used as a transfer function which has the following expression, Equation (7):
For the multiple neurons, jth in the layer lth the output of the neuron is described in the Equations (8) and (9).
Equation (10) can be used to describe the output of the network at the last layer.
Back-Propagation Calculations
The most common approach for training a supervised neural network is backpropagation. The purpose of this method is to iteratively modify the weights in the network to minimise output error and provide the desired result [56]. Backpropagation is a gradient-descent method that finds an optimal solution by minimising first-order derivatives. The delta rule is used to adjust the weights in the network, whereby the output error can be computed using Equation (11).
where E is the error, t is the target output, y is the predicted output. The sum of the errors in the feedforward network is expressed in Equation (12).
The error is minimized by taking the partial derivative of the total error with respect to the weights in the network using Equation (13).
Using the chain rule, the partial derivative is divided into two parts as expressed in Equation (14).
Then,
At each iteration, the gradient can be evaluated, and the weight values can be optimised in this manner. In this study, the Levenberg-Marquardt (LM) algorithm was used to train the ANNs model. The LM algorithm approximates the Hessian matrix (H) using Jacobian matrix (J) which contains the first derivative of error (E) with respect to the weight, as expressed in Equation (20). The weight update is given in Equation (21).
where I is the identity matrix. At each iteration, the weight is changed using the following equation:
2.3. Data Analysis
The data from the DSR and MSCR tests on the eleven asphalt binders were modelled using MATLAB, whereby the data was divided into three main parts, training, validation, and testing. The training set often contains the majority of the data, while the validation and test sets typically contain smaller quantities of data. 70% of the total data was used to train the neural network, 15% was used to validate the neural network, and 15% was utilised for testing the capability of the network to predict the output. To train neural networks, Scaled Conjugate Gradient (SCG), Levenberg-Marquardt (LM), and Bayesian Regularization (BR) were performed to implement a backpropagation learning process in a feed-forward neural network with one hidden layer and five neurons. After selecting the parameters and calculating the magnitudes of the weights and biases, the neural network was trained using the software’s training data. The weights and biases of the training phase were evaluated after the training session based on the difference between measured and predicted values. Consistently, the test data set was used by the software to understand the neural network’s performance once it had been validated.
3. Results and Discussion
3.1. Temperatures and Frequencies Effects on the Viscosity
Figure 4 demonstrate the effects of different temperatures (46 C, 52 C, 58 C, 64 C, and 70 C) and frequencies (0.1 Hz and 10 Hz) on the shear viscosity of neat and modified asphalt binder. When comparing the modified asphalt binders to the neat asphalt binder, the results showed that the modified asphalt binders had the highest viscosities. Larger molecules present in a fluid can induce increased viscosity, which can be produced by the formation of chain networks in the asphalt binder mixture [57]. At high frequency (10 rad/s), the hybrid binders achieved the highest viscosity at 46 C, 52 C, and 58 C, while 4%SBS binder has the highest viscosity at 64 C, and 70 C. At low frequency (0.1 rad/s), the 4%SBS binder has the highest viscosity compared with the other modifiers at different temperatures. In conclusion, it was observed that the viscosity of asphalt binder is significantly dependent on the effect of additives on asphalt binder characteristics, temperature, and frequency.
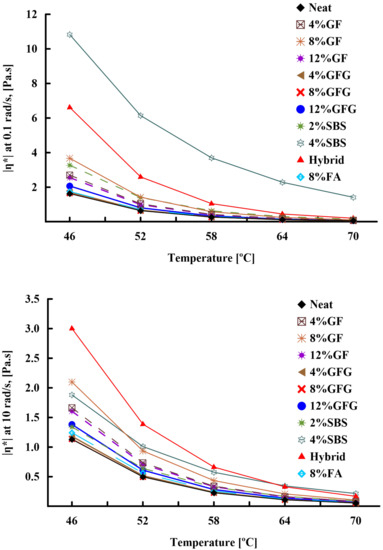
Figure 4.
Effects of temperatures and frequencies on the shear viscosity.
3.2. Temperatures and Frequencies Effects on the Storage and Loss Modulus
The 3D plot in Figure 5 presents the effect of external factors (temperature and frequency) on the storage and loss modules of the unaged neat and GF-modified asphalt binders. G and G values increased geometrically when frequency increased, however both G and G values dropped as temperature increases. The 8%GF binder achieved the highest values of G and G compared to the neat and other modifiers. It is evident that adding geopolymer increases both G and G significantly, enhancing the asphalt binder’s ability to recover and resist deformation. Figure 6 shows the impact of temperatures, and frequencies on the G and G of glass powder/fly ash-based geopolymer (GFG) modified asphalt binder. The results indicated that the GFG modifier with different percentages (4%, 8%, and 12%) has a slight effect on the G and G of the neat binder compared with GF modifier, as demonstrated in Figure 5.
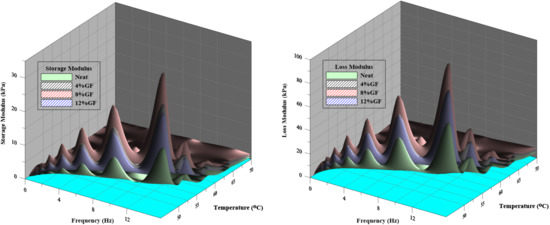
Figure 5.
Temperatures and frequencies effects on the G and G of GF.
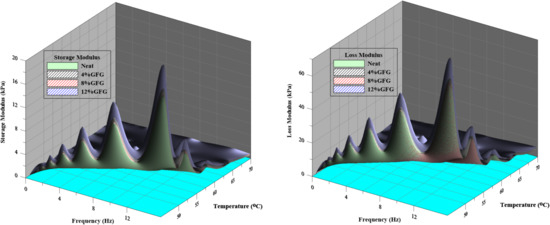
Figure 6.
Temperatures and frequencies effects on the G and G of GFG.
Figure 7 demonstrates the influence of temperatures and frequencies on the G and G of the 8%FA, 2%SBS, 4%SBS, and hybrid asphalt binders. The hybrid binder achieved the highest values of G and G compared with the other modifiers at different temperatures and frequencies. This indicated that the hybrid binder has the highest recovery resistance for deformations. While the 4%SBS binder exhibited more elasticity than neat, 8%FA, 2%SBS binders at low and high frequencies, with the highest value of G. Besides, the 8%FA binders are more viscous than the neat and 2%SBS, with the highest value of the G. Figure 5, Figure 6 and Figure 7 show that the neat and modified asphalt binders have a higher G than G. It’s possible that this is due to the lack of strong interactions between individual molecules [57].
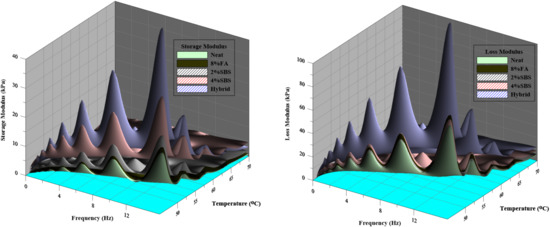
Figure 7.
Temperatures and frequencies effects on the G and G of SBS and FA binders.
3.3. MSCR Test Results
Table 4 presents the MSCR test result of neat and modified asphalt binders at different temperatures. The influence of additives and temperatures on the non-recovery and recovery properties of asphalt binders was investigated. Also, the effect of additives on the traffic level was also evaluated. According to the J values under high stress (3.2 kPa), the traffic loading was classified into four groups: S is standard traffic (≤10 million ESALs), H is heavy traffic (10–30 million ESALs), V is very heavy traffic (≤30 million ESALs), and E is extremely heavy traffic (≥30 million ESALs) with standing traffic [58]. Apart from the neat asphalt binder properties, the modifiers enhance the asphalt binder’s resistance to traffic loading. It was observed that the hybrid and 4%SBS binders achieved the highest ability to resist extremely heavy traffic compared with the other modified asphalt binders. Furthermore, among the other geopolymer modifier percentages, the geopolymer-modified asphalt binders with 8%GF and 8%GFG have the highest creep recovery at 46 C, with 39.5% and 39.8%, respectively. While the hybrid and 4%SBS binders have the highest ability to recover the deformation with 60.1% and 85.5% at 46 C, respectively. In summary, additives and temperatures have significant effects on the non-recovery and recovery properties of asphalt binder.

Table 4.
Temperature effect on the J and R of asphalt binders.
3.4. ANNs Model Results
The results of the frequency sweep and MSCR test indicated that various parameters have significant effects on the neat and modified asphalt binders. So, five input parameters were considered, temperature (T), frequency (f), storage modulus (G), loss modulus (G), and viscosity (V). A total of 880 data points were used for ANNs models to predict the two outputs, percent recovery at 3.2 kPa (R) and non-recoverable creep compliance at 3.2 kPa (J) of unaged and RTFO asphalt binders at different temperatures. To establish the optimal backpropagation learning algorithm for the study, the LM, BR, and SCG training algorithms were used in a feed-forward, single-hidden-layer neural network of 5 neurons. The best neural network was built using the training techniques. Figure 8 shows the statistical fit the model measurements R-value for the outputs using three different training procedures. The LM and BR training methods, with R values more than 0.90, did higher R values than the SCG algorithm. The LM training technique is the better ANN for the study data, according to the results.
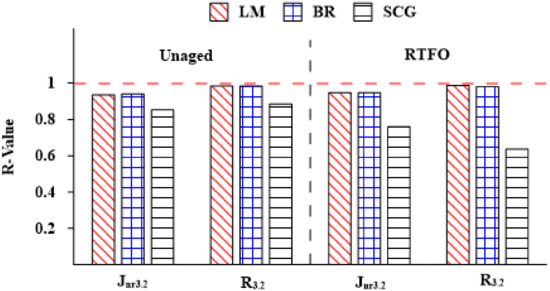
Figure 8.
R-values for different training algorithms.
Figure 9 and Figure 10 describe the relationships between mean squared errors (MSEs) and the number of epochs (Epoch is the number of times all the training data are applied to update the weights at the same time [56].) for J and R, respectively, of unaged and aged asphalt binders. As the number of epochs increased, the MSE value declined. In addition, for unaged and aged J and R, every phase of training, validation, and testing results in a simultaneous MSE magnitude reduction. This reduction approach validates that the training operation was correctly completed with no overfitting in the training, validation, and test sections.
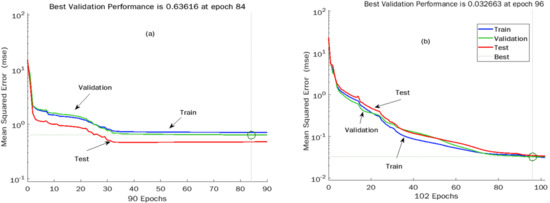
Figure 9.
MSE versus Epoch plot for J of (a) Unaged and (b) RTFO binders.
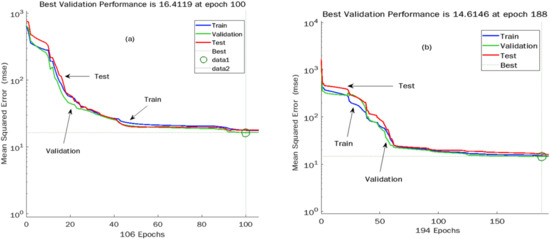
Figure 10.
MSE versus Epoch plot for R of (a) Unaged and (b) RTFO binders.
Figure 11, Figure 12, Figure 13 and Figure 14 present the relationship between the measured and predicted values for J of unaged binder, J of aged binder, R of unaged binder, and R of aged binder, respectively. The figures include graphs for training, validation, test, and total data, which indicate excellent R-values for the total data set of 0.997, 0.985, and 0.987 for J of aged binder, R of unaged binder, and R of aged binder, respectively. While J of unaged binder achieved an R-value of 0.937. R-values for J and R of aged binder and unaged binder demonstrated a very good correlation between measured and predicted output values with high accuracy.
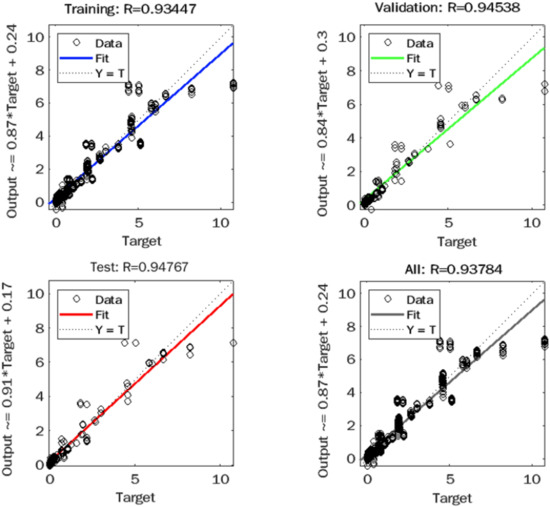
Figure 11.
Observed versus predicted plot for J of unaged binders.
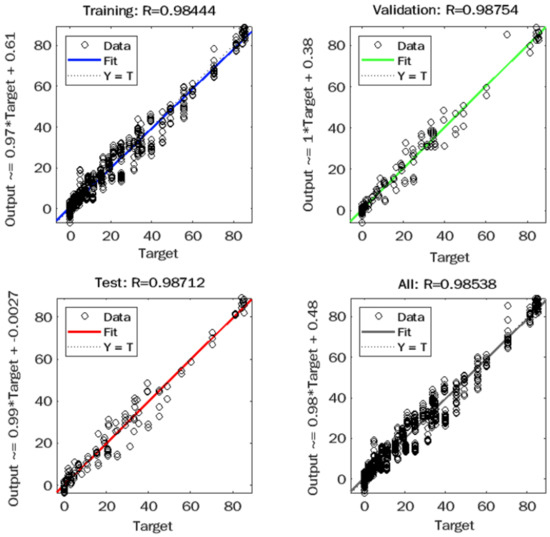
Figure 12.
Observed versus predicted plot for R of unaged binders.
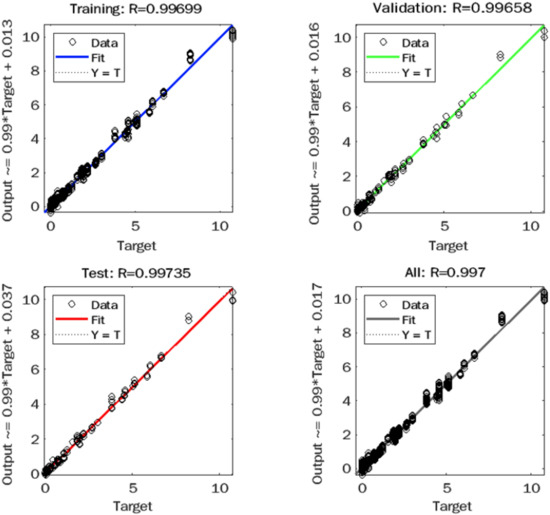
Figure 13.
Observed versus predicted plot for J of RTFO binders.
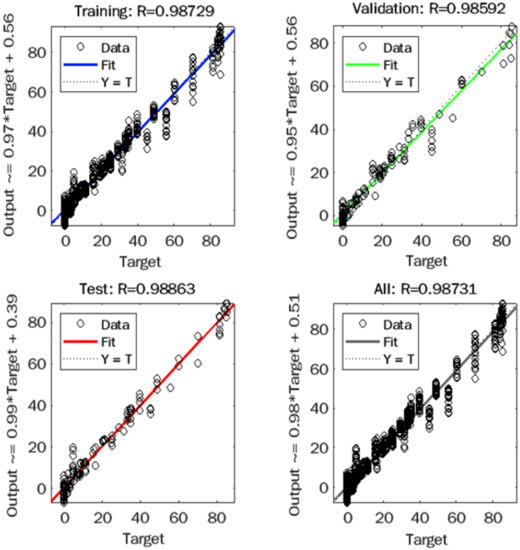
Figure 14.
Observed versus predicted plot for R of RTFO binders.
Table 5, Table 6, Table 7 and Table 8 show the weights and biases for J and R of unaged binders, as well as J and R of RTFO binders, respectively. Once the values of the five-input data are available, the ANNs model’s weights and biases can be used to predict a certain output. The weight and bias matrix of the hidden layer in the optimal network design, which estimates the magnitudes of J and R of unaged binders and J and R of RTFO binders, were 5 by 5 and 5 by 1, respectively. The output layer was 1 by 5. Overall, the non-recovery and recovery properties of asphalt binder are influenced by test temperature and frequency, storage modulus, loss modulus, and viscosity, according to ANN modelling. Figure 15 illustrates the use of the ANNs model to predict J at various temperatures for four binders, PG 58-28, PG 64-28, PG 70-28, and PG 76-28. It was noted that the ANNs model can predict the J of asphalt binders at different temperatures with high accuracy.

Table 5.
Weights and Biases for J model of unaged binders.

Table 6.
Weights and biases for R model of unaged binders.

Table 7.
Weights and biases for R model of RTFO binders.

Table 8.
Weights and biases for J model of RTFO binders.
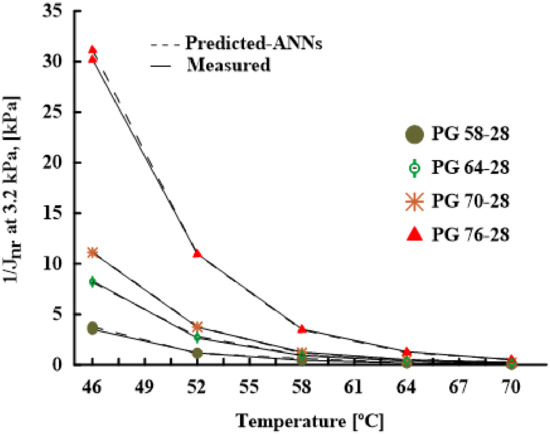
Figure 15.
Observed versus predicted plot for R of RTFO binders.
4. Conclusions
This research aimed to investigate the possibility of using the ANNs model to predict the nonrecoverable compliance and recovery properties of modified asphalt binders using mechanical test parameters and asphalt binder properties. Over 880 data points were covered using eleven mixed asphalt binders, one neat asphalt binder, and four modifiers at various percentages. Frequency sweep and MSCR tests were conducted on all eleven binders at different temperatures. J and R of unaged and aged asphalt binders were predicted using an ANNs model which was developed using five inputs: test temperature and frequency, storage modulus, loss modulus, and viscosity.
The optimal ANN architecture was chosen, and the LM algorithm was used to train the ANN model, a one-hidden-layer neural network with five neurons. For J and R of unaged asphalt binders and J and R of aged asphalt binders, respectively. The statistical goodness of fit values (R) between measured and predicted values were 0.938, 0.985, 0.997 and 0.987, respectively. Thus, the magnitudes of biases and weights specified in this study could be useful in predicting the nonrecoverable compliance and recovery properties of asphalt binders at various temperatures.
The use of the ANN algorithm to determine mathematical weights and biases of the input parameters and examine the influence of different types of modifiers on the nonrecoverable compliance and recovery properties of asphalt binder was a noteworthy contribution of this study. The ANNs model can predict the J and R with high accuracy using the viscoelastic properties of aged and unaged asphalt binders. The MSCR grade is determined using nonrecoverable compliance under high stress. Therefore, the developed ANNs model could be used to predict nonrecoverable compliance at high stress, and then the MSCR grade could be determined using aged or unaged asphalt binder.
The results showed that additive content has a significant influence on increasing resistance to heavy traffic loads and improving strain recovery under high stress and temperatures. The hybrid and 4%SBS binders attained the highest ability to resist extremely heavy traffic compared with the other modified asphalt binders. While the geopolymer-modified asphalt binders with 8%GF and 8%GFG have the highest creep recovery at 46 C, with 39.5% and 39.8%, respectively, compared to the other geopolymer modifier percentages. Also, the hybrid and 4%SBS binders have the highest ability to recover the deformation with 60.1% and 85.5% at 46 C, respectively. Additives and temperatures have been proven to have significant effects on the nonrecoverable compliance and recovery properties of asphalt binder. On the other hand, it was noted that there is a good relationship between MSCR test results and asphalt mixture rutting, as concluded by different studies. Therefore, it would be more interesting if there is a model to predict the asphalt concrete rutting depth using the MSCR test results as well as the effect of temperatures and additive type and amount on the performance of the asphalt binder and mixture.
Author Contributions
Conceptualization, A.H., H.B. and M.E.-H.; methodology, A.H.; software, A.H. and M.E.-H.; validation, A.H. and M.E.-H.; formal analysis, A.H. and M.E.-H.; investigation, A.H.; resources, A.H., H.B. and M.E.-H.; data curation, A.H.; writing—original draft preparation, A.H.; writing—review and editing, A.H., H.B. and M.E.-H.; visualization, A.H.; supervision, H.B. and M.E.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used during the study appear in the submitted article.
Acknowledgments
The authors would like to acknowledge Yellowline Asphalt Products Ltd., Steed and Evans, and the Centre for Pavement and Transportation Technology (CPATT) for providing materials and testing equipment.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Asphalt Institute. Asphalt Handbook, 7th ed.; Asphalt Institute: Lexington, KY, USA, 2007. [Google Scholar]
- D’Angelo, J.A. The Relationship of the MSCR Test to Rutting. Road Mater. Pavement Des. 2009, 10, 61–80. [Google Scholar] [CrossRef]
- Zoorob, S.E.; Castro-Gomes, J.P.; Pereira Oliveira, L.A.; O’Connell, J. Investigating the Multiple Stress Creep Recovery bitumen characterisation test. Constr. Build. Mater. 2012, 30, 734–745. [Google Scholar] [CrossRef]
- White, G. Grading Highly Modified Binders by Multiple Stress Creep Recovery. Road Mater. Pavement Des. 2017, 18, 1322–1337. [Google Scholar] [CrossRef]
- Aurilio, M.; Mikhailenko, P.; Baaj, H.; Poulikakos, D. Properties of Asphalt Binders with Increasing SBS Polymer Modification. In Proceedings of the 5th International Symposium on Asphalt Pavements & Environment (APE); Lecture Notes in Civil Engineering. Springer: Cham, Switzerland, 2019; Volume 48, pp. 55–66. [Google Scholar]
- Dalhat, M.A.; Al-Adham, K.; Al-Abdul Wahhab, H.I. Multiple Stress–Creep–Recovery Behavior and High-Temperature Performance of Styrene Butadiene Styrene and Polyacrylonitrile Fiber–Modified Asphalt Binders. J. Mater. Civ. ASCE 2019, 31, 04019087. [Google Scholar] [CrossRef]
- Harman, T.; Youtcheff, J.; Bukowski, J. The Multiple Stress Creep Recovery (MSCR) Procedure; Federal Highway Administration: Washington, DC, USA, 2011. [Google Scholar]
- Liu, H.; Zeiada, W.; Al-Khateeb, G.G.; Shanableh, A.; Samarai, M. Use of the multiple stress creep recovery (MSCR) test to characterize the rutting potential of asphalt binders: A literature review. Constr. Build. Mater. 2021, 269, 121320. [Google Scholar] [CrossRef]
- Zhang, J.; Walubita, L.F.; Faruk, A.N.M.; Karki, P.; Simate, G.S. Use of the MSCR Test to Characterize the Asphalt Binder Properties Relative to HMA Rutting Performance—A Laboratory Study. Constr. Build. Mater. 2015, 94, 218–227. [Google Scholar] [CrossRef]
- Tabatabaee, N.; Tabatabaee, H.A. Multiple stress creep and recovery and time sweep fatigue tests: Crumb rubber modified binder and mixture performance. Transp. Res. Rec. J. Transp. Res. Board 2010, 2180, 67–74. [Google Scholar] [CrossRef]
- Dreessen, S.; Gallet, T. MSCRT: Performance related test method for rutting prediction of asphalt mixtures from binder rheological characteristics. In Proceedings of the 5th Eurasphalt & Eurobitume Congress, Istanbul, Turkey, 13–15 June 2012. [Google Scholar]
- Cuesta Cordoba, G.A.; Tuhovčák, L.; Tauš, M. Using Artificial Neural Network Models to Assess Water Quality in Water Distribution Networks. Procedia Eng. 2014, 70, 399–408. [Google Scholar] [CrossRef]
- Esfandiarpour, S.; Shalaby, A. Local Calibration of Creep Compliance Models of Asphalt Concrete. Constr. Build. Mater. 2017, 132, 313–322. [Google Scholar] [CrossRef]
- El-Badawy, S.; Abd El-Hakim, R.; Awed, A. Comparing Artificial Neural Networks with Regression Models for Hot-Mix Asphalt Dynamic Modulus Prediction. J. Mater. Civ. Eng. 2018, 30, 04018128. [Google Scholar] [CrossRef]
- Plati, C.; Georgiou, P.; Papavasiliou, V. Simulating Pavement Structural Condition Using Artificial Neural Networks. Struct. Infrastruct. Eng. Maint. Manag. Life-Cycle Des. Perform. 2016, 12, 1127–1136. [Google Scholar] [CrossRef]
- Ceylan, H.; Tutumluer, E.; Barenberg, E.J. Artificial neural networks as design tools in concrete airfield pavement design. In Airport Facilities: Innovations for the Next Century, Proceedings of the 25th International Air Transportation Conference; American Society of Civil Engineers: Reston, VA, USA, 1998. [Google Scholar]
- Rezaei-Tarahomi, A.; Kaya, O.; Ceylan, H.; Gopalakrishnan, K.; Kim, S.; Brill, D.R. Neural networks based prediction of critical responses related to top-down and bottom-up cracking in airfield concrete pavements. In Proceedings of the Tenth International Conference on the Bearing Capacity of Roads, Railways and Airfields, Athens, Greece, 28–30 June 2017. [Google Scholar]
- Kaya, O.; Rezaei-Tarahomi, A.; Ceylan, H.; Gopalakrishnan, K.; Kim, S.; Brill, D.R. Neural network-based multiple-slab response models for top-down cracking mode in airfield pavement design. J. Transp. Eng. Part B Pavements 2018, 144, 04018009. [Google Scholar] [CrossRef]
- Deng, Y.; Shi, X. An accurate, reproducible and robust model to predict the rutting of asphalt pavement: Neural networks coupled with particle swarm optimization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22063–22072. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, S.J.; Moon, K.H.; Jeong, J.H. Prediction of Indirect Tensile Strength of Intermediate Layer of Asphalt Pavements Using Artificial Neural Network Model. Arab. J. Sci. Eng. 2021, 46, 4911–4922. [Google Scholar] [CrossRef]
- Liu, J.; Yan, K.; Liu, J.; Zhao, X. Using artificial neural networks to predict the dynamic modulus of asphalt mixtures containing recycled asphalt shingles. J. Mater. Civ. Eng. 2018, 30, 04018051. [Google Scholar] [CrossRef]
- Tasdemir, Y. Artificial neural networks for predicting low temperature performances of modified asphalt mixtures. Indian J. Eng. Mater. Sci. 2009, 16, 237–244. [Google Scholar]
- Firouzinia, M.; Shafabakhsh, G.H. Investigation of the effect of nano-silica on thermal sensitivity of HMA using artificial neural network. Constr. Build. Mater. 2018, 170, 527–536. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Miani, M. Stiffness modulus and marshall parameters of hot mix asphalts: Laboratory data modeling by artificial neural networks characterized by cross-validation. Appl. Sci. 2019, 9, 3502. [Google Scholar] [CrossRef]
- Upadhya, A.; Thakur, M.S.; Sharma, N.; Sihag, P. Assessment of soft computing-based techniques for the prediction of marshall stability of asphalt concrete reinforced with glass fiber. Int. J. Pavement Res. Technol. 2021, 15, 1366–1385. [Google Scholar] [CrossRef]
- Keskin, M.; Karacasu, M. Artificial Neural Network Modelling for Asphalt Concrete Samples with Boron Waste Modification. J. Eng. Res. 2021, 10, 26–45. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Pasetto, M. Analysis of the Mechanical Behaviour of Asphalt Concretes Using Artificial Neural Networks. Adv. Civ. Eng. 2018, 2018, 1650945. [Google Scholar] [CrossRef]
- Hafeez, I.; Kamal, M.A.; Mirza, M.W.; Barkatullah; Bilal, S. Laboratory Fatigue Performance Evaluation of Different Field Laid Asphalt Mixtures. Constr. Build. Mater. 2013, 44, 792–797. [Google Scholar] [CrossRef]
- Xiao, F.; Amirkhanian, S.; Juang, C.H. Prediction of Fatigue Life of Rubberized Asphalt Concrete Mixtures Containing Reclaimed Asphalt Pavement Using Artificial Neural Networks. J. Mater. Civ. Eng. 2009, 21, 253–261. [Google Scholar] [CrossRef]
- Tapkin, S. Estimation of Fatigue Lives of Fly Ash Modified Dense Bituminous Mixtures Based on Artificial Neural Networks. Mater. Res. 2014, 17, 316–325. [Google Scholar] [CrossRef]
- Kamboozia, N.; Ziari, H.; Behbahani, H. Artificial Neural Networks Approach to Predicting Rut Depth of Asphalt Concrete by Using of Visco-Elastic Parameters. Constr. Build. Mater. 2018, 158, 873–882. [Google Scholar] [CrossRef]
- Venudharan, V.; Biligiri, K.P. Heuristic Principles to Predict the Effect of Crumb Rubber Gradation on Asphalt Binder Rutting Performance. J. Mater. Civ. Eng. 2017, 29, 04017050. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Hou, X.; Xiang, Q.; Xiao, F. Viscosity Prediction of Rubberized Asphalt–Rejuvenated Recycled Asphalt Pavement Binders Using Artificial Neural Network Approach. J. Mater. Civ. Eng. 2021, 33, 04021071. [Google Scholar] [CrossRef]
- Kok, B.V.; Yilmaz, M.; Sengoz, B.; Sengur, A.; Avci, E. Investigation of complex modulus of base and SBS modified bitumen with artificial neural networks. Expert Syst. Appl. 2010, 37, 7775–7780. [Google Scholar] [CrossRef]
- Uwanuakwa, I.D.; Ali, S.I.A.; Hasan, M.R.M.; Akpinar, P.; Sani, A.; Shari, K.A. Artificial Intelligence Prediction of Rutting and Fatigue Parameters in Modified Asphalt Binders. Appl. Sci. 2020, 10, 7764. [Google Scholar] [CrossRef]
- Alas, M.; Ali, S.I.A. Prediction of the High-Temperature Performance of a Geopolymer Modified Asphalt Binder using Artificial Neural Networks. Int. J. Technol. 2019, 10, 417. [Google Scholar] [CrossRef]
- Yan, K.; You, L. Investigation of complex modulus of asphalt mastic by artificial neural networks. Indian J. Eng. Mater. Sci. 2014, 21, 445–450. [Google Scholar]
- Yalccin, E.; Ozdemir, A.M.; Yilmaz, M. Prediction of Rheological Parameters of Asphalt Binders with Artificial Neural Networks. Eurasia Proc. Sci. Technol. Eng. Math. 2021, 12, 7–16. [Google Scholar]
- Ziari, H.; Amini, A.; Goli, A.; Mirzaiyan, D. Predicting Rutting Performance of Carbon Nano Tube (CNT) Asphalt Binders Using Regression Models and Neural Networks. Constr. Build. Mater. 2018, 160, 415–426. [Google Scholar] [CrossRef]
- Shafabakhsh, G.H.; Jafari Ani, O.; Talebsafa, M. Artificial neural network modeling (ANN) for predicting rutting performance of nano-modified hot-mix asphalt mixtures containing steel slag aggregates. Constr. Build. Mater. 2015, 85, 136–143. [Google Scholar] [CrossRef]
- Zheng, D.; Qian, Z.D.; Liu, Y.; Liu, C.B. Prediction and sensitivity analysis of long-term skid resistance of epoxy asphalt mixture based on GA-BP neural network. Constr. Build. Mater. 2018, 158, 614–623. [Google Scholar] [CrossRef]
- Nivedya, M.K.; Mallick, R.B. Artificial neural network-based prediction of field permeability of hot mix asphalt pavement layers. Int. J. Pavement Eng. 2020, 21, 1057–1068. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Karimi, M.M. Predicting the dynamic modulus of asphalt mixture using hybridized artificial neural network and grey wolf optimizer. Int. J. Pavement Eng. 2021. [Google Scholar] [CrossRef]
- Dalhat, M.A.; Osman, S.A. Artifcial Neural Network Modeling of Theoretical Maximum Specifc Gravity for Asphalt Concrete Mix. Int. J. Pavement Res. Technol. 2022. [Google Scholar] [CrossRef]
- Xiao, F.; Putman, B.J.; Amirkhanian, S.N. Viscosity prediction of CRM binders using artificial neural network approach. Int. J. Pavement Eng. 2011, 12, 485–495. [Google Scholar] [CrossRef]
- Golzar, K.; Jalali-Arani, A.; Nematollahi, M. Statistical investigation on physical–mechanical properties of base and polymer modified bitumen using Artificial Neural Network. Constr. Build. Mater. 2012, 37, 822–831. [Google Scholar] [CrossRef]
- Abedali, A.H. Predicting complex shear modulus using artificial neural networks. J. Civ. Eng. Constr. Technol. 2015, 6, 15–26. [Google Scholar]
- Tarefder, R.A.; Ahsan, S.; Arifuzzaman, M. Using a Neural Network Model to Assess the Effect of Antistripping Agents on the Performance of Moisture-Conditioned Asphalt. J. Mater. Civ. Eng. 2017, 29, 04016250. [Google Scholar] [CrossRef]
- Khasawneh, M.A.; Al-Oqaily, D.M. Development of Analytical Models to Predict the Dynamic Shear Rheometer Outcome—Phase Angle. Int. J. Pavement Res. Technol. 2021. [Google Scholar] [CrossRef]
- ASTM C618-17a; Standard Specification for Coal Fly Ash and Raw or Calcined Natural Pozzolan for Use in Concrete. American Society for Testing and Materials (ASTM): West Conshohocke, PA, USA, 2018.
- Hardjito, A.B. Studies on Fly Ash-Based Geopolymer Concrete. Ph.D. Thesis, Curtin University of Technology, Perth, Australia, 2005. [Google Scholar]
- Garcia-Lodeiro, I.; Palomo, A.; Ernandez-Jimenez, A. An overview of the chemistry of alkali-activated cement-based binders. In Handbook of Alkali-Activated Cements, Mortars and Concretes; Elsevier Science, Instituto Eduardo Torroja (IETcc-CSIC): Madrid, Spain, 2015; pp. 19–47. [Google Scholar]
- Hua, X.; Van Deventer, J. The geopolymerisation of alumino-silicate minerals. Int. J. Miner. Process. 2000, 59, 247–266. [Google Scholar]
- AASHTO T 315; Standard Method of Test for Determining the Rheological Properties of Asphalt Binder Using a Dynamic Shear Rheometer (DSR). American Association of State and Highway Transportation Officials (AASHTO): Washington, DC, USA, 2018.
- AASHTO T 350; Standard Method of Test for Multiple Stress Creep Recovery (MSCR) Test of Asphalt Binder Using a Dynamic Shear Rheometer (DSR). American Association of State and Highway Transportation Officials (AASHTO): Washington, DC, USA, 2018.
- Priddy, K.L.; Keller, P.E. Artificial Neural Networks: An Introduction; SPIE—The International Society for Optical Engineering: Bellingham, WA, USA, 2005. [Google Scholar]
- Mezger, T.G. Applied Rheology: With Joe Flow on Rheology Road, 8th ed.; Anton Paar: Graz, Austria, 2021. [Google Scholar]
- AASHTO M 332; Standard Specification for Performance-Graded Asphalt Binder Using Multiple Stress Creep Recovery (MSCR) Test. American Association of State and Highway Transportation Officials (AASHTO): Washington, DC, USA, 2021.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).