A Modified Particle Swarm Optimization Algorithm for Optimizing Artificial Neural Network in Classification Tasks

Abstract

Artificial neural networks (ANNs) have achieved great success in performing machine learning tasks, including classification, regression, prediction, image processing, image recognition, etc., due to their outstanding training, learning, and organizing of data. Conventionally, a gradient-based algorithm known as backpropagation (BP) is frequently used to train the parameters’ value of ANN. However, this method has inherent drawbacks of slow convergence speed, sensitivity to initial solutions, and high tendency to be trapped into local optima. This paper proposes a modified particle swarm optimization (PSO) variant with two-level learning phases to train ANN for image classification. A multi-swarm approach and a social learning scheme are designed into the primary learning phase to enhance the population diversity and the solution quality, respectively. Two modified search operators with different search characteristics are incorporated into the secondary learning phase to improve the algorithm’s robustness in handling various optimization problems. Finally, the proposed algorithm is formulated as a training algorithm of ANN to optimize its neuron weights, biases, and selection of activation function based on the given classification dataset. The ANN model trained by the proposed algorithm is reported to outperform those trained by existing PSO variants in terms of classification accuracy when solving the majority of selected datasets, suggesting its potential applications in challenging real-world problems, such as intelligent condition monitoring of complex industrial systems.

1. Introduction

The human nervous system inspires an artificial neural network (ANN), and many artificial neurons act as interconnected processing elements in ANN to emulate the cerebral cortex of brain structure. In contrast to other conventional machine learning methods, ANNs demonstrate outstanding capabilities in generalizing, organizing, and learning the nonlinear data that are commonly observed in real-world scenarios [1]. Due to these appealing features, ANNs have been widely implemented to solve various real-world application, including intelligent condition monitoring [2], speech recognition [3], fault diagnosis [4], pothole classification [5], etc. Generally, ANN structure can be separated into three parts: the input layer, the hidden layer, and the output layer. Information flows in a single direction within an ANN model, i.e., from the input layer to the hidden layer, followed by the output layer [6]. Each neuron of the layers is incorporated with an activation function to convert the summed weighted input received by each neuron into the nonlinear output. This nonlinear characteristic serves as the cornerstone for ANN to have competitive performance in tackling various challenging machine learning tasks, such as the learning of complex data, functions approximation, and predictions [7].

Before deploying an ANN model to solve machine learning tasks, a training process is performed to determine the optimal combinations of weight and bias values for all neurons that can achieve minimum error. A gradient-based algorithm known as the backpropagation (BP) method is conventionally used to train ANN models [7]. At the beginning stage of ANN training, the initial weight and bias values of neurons are randomly generated, and the actual output values of the network are determined. The error signals between the desired and actual outputs are then calculated and backpropagated to the network to adjust the weight and bias values of each neuron. Despite its popularity, some drawbacks were reported when using the classical BP method to train ANN models, especially when solving complex nonlinear problems. For instance, the BP method has a high tendency to be trapped in local optima and fail to reach global optimum when dealing with solution regions with complex characteristics. The performance of the ANN model when solving complex problems can be significantly degraded due to suboptimal weight and bias values assigned to all neurons [7]. The convergence characteristic of the classical BP method in ANN training is also sensitive to the initial values of weight, bias, and network parameters (e.g., activation function). There might be scenarios where the classical BP method produces poor initial weight and bias values for ANN during the training process, leading to compromised network performances [7]. These limitations of classical BP methods have motivated researchers to seek robust alternatives that can address ANN training problems more efficiently and effectively.

In recent years, metaheuristic search algorithms (MSAs) have emerged as promising solutions to tackle complex optimization problems, such as those reported in [8,9,10,11,12,13]. The excellent global search ability and stochastic characteristic of these MSAs can also be harnessed for training ANN models to solve classification or regression problems. Particle swarm optimization (PSO) is one of the most popular MSAs, and it is motivated by the collective behavior of bird flocks in locating food sources [14]. Each PSO particle can memorize its previous best searching experiences, and this unique feature distinguishes PSO from other MSAs [15]. The search trajectory of each PSO particle is adjusted based on its previous best experience and the best experience achieved by the entire population during the optimization process. Since the inception of the original PSO in 1995, many new variants have been proposed to solve various real-world optimization problems. Despite its appealing features, such as simplicity in implementation and fast convergence speed, the capability of original PSO to solve complex optimization problems such as ANN training remain questionable due to its high tendency to suffer from premature convergence issues when solving complex problems with high-dimensional search space. Therefore, more robust search mechanisms must be incorporated into the original PSO to balance the algorithm’s exploration and exploitation searches.

1.1. Research Motivations

A PSO variant known as particle swarm optimization without velocity (PSOWV) was proposed in [16] by discarding the velocity component of each particle during the search process. PSOWV has demonstrated more competitive performance than the conventional PSO by solving simple benchmark problems with better accuracy in fewer iteration numbers. Despite its promising performance, PSOWV still suffers from some inherent drawbacks that might restrict its feasibility to solve more challenging optimization problems, such as the training of ANN models for classification or regression tasks.

Similar to most MSAs, PSOWV employs a conventional initialization scheme to randomly generate the initial population of particles during the search process. This conventional initialization scheme produces the initial position of each particle using uniform distribution without considering the characteristics or fitness landscapes of given optimization problems [17]. When particles are mistakenly initialized in local optima, it may lead to premature convergence issues and poor solution accuracy. In contrary, the convergence speed of the algorithm can be significantly deteriorated if particles are initialized at solution regions far away from the global optimum. It is more desirable to have a robust initialization scheme that can generate the initial position of each particle more systematically to ensure the initial population has a better solution quality.

When carefully inspecting the search operator of PSOWV, the new position of each particle is directly affected by the directional information of historical best positions, i.e., the personal best position of the particle itself and the global best position of the population. While these historical best positions are beneficial to accelerate the convergence speed of PSOWV at the early stage of optimization, they are less frequently updated at the latter stages [18]. When both personal and global best positions are overemphasized during the search process of PSOWV, the entrapment of these historical best positions into local optima at the early stage of the search process could misguide the remaining particles converging towards the inferior solution regions and lead to premature convergence. To prevent these undesirable scenarios, it is necessary for PSOWV to be incorporated with a more robust diversity preservation scheme when dealing with complex problems. The directional information offered by other non-historical best positions should be leveraged during the search process to prevent the potential negative impacts brought by personal and global best positions.

Finally, it is observed that PSOWV has limited ability to achieve proper trade-off between exploration and exploitation searches because only one search operator is used to perform the search process. Hence, PSOWV can only perform well in certain types of optimization problems (i.e., unimodal problem), and it exhibits poor optimization performance in other problem categories. When solving optimization problems with different complexity levels as governed by the characteristics of fitness landscapes, it is crucial for an algorithm to intelligently regulate its exploration and exploitation strength to locate the global optima [19]. The incorporation of multiple search operators with different levels of exploration and exploitation strengths can be envisioned as an alternative to enhance the robustness of the algorithm to solve different complex optimization problems competitively.

1.2. Research Contributions

To address the shortcomings of PSOWV in solving complex optimization problems such as the ANN model training, an enhanced variant known as multi-swarm-based particle swarm optimization with two-level learning phases (MSPSOTLP) is proposed. Apart from optimizing the weight and bias values of ANN models during the training process, the proposed MSPSOTLP can also determine the optimal activation function of an ANN model to solve the given classification problem. The main modifications introduced into MSPSOTLP to highlight its research contributions are summarized as follows:

• A modified initialization scheme is incorporated into MSPSOTLP to generate an initial population with better robustness and diversity by leveraging the benefits of the chaotic system (CS) and oppositional-based learning (OBL).
• In the primary learning phase of MSPSOTLP, both the multi-swarm concept and social learning concept are incorporated to promote rapid convergence of the population towards the optimal regions by enabling particles to learn from other superior population members while preserving the diversity level of population.
• In the secondary learning phase of MSPSOTLP, two modified search operators with different characteristics are designed for each particle to perform searching with different levels of exploration and exploitation strengths, hence enabling the proposed algorithm to solve different types of optimization problems more competitively.
• The performance of MSPSOTLP in solving global optimization problems is investigated using CEC 2014 benchmark functions. The classification performances of ANN models trained using MSPSOTLP are also evaluated with 16 datasets selected from UCI Machine Learning Repository. The proposed MSPSOTLP is proven more competitive than its peer algorithms at solving the benchmark functions and ANN training.

The remaining sections of this article are organized as follows. Related works of this study are explained in Section 2. The detailed search mechanisms of MSPSOTLP are described in Section 3. Extensive simulation studies performed to investigate the performance of MSPSOTLP in solving global optimization problems and its capability to train ANN models in solving classification problems are presented in Section 4. Finally, Section 5 concludes the research findings and future works.

2. Related Works

2.1. Particle Swarm Optimization (PSO)

PSO is inspired by the collective behavior of bird flocking or fish schooling to search for food sources [14]. Suppose that N is the population size and D is the dimensional size of an optimization problem. Each PSO particle is a potential solution to solve an optimization problem represented with a velocity vector of $V_n=\left[V_{n,1},\dots ,V_{n,d},\dots ,V_{n,D}\right]$ and a position vector of $X_n=\left[X_{n,1},\dots ,X_{n,d},\dots ,X_{n,D}\right]$, where $n=1,\dots ,N$ and $d=1,\dots ,D$ refer to the population index and dimension index, respectively. Unlike other MSAs, each PSO particle can memorize its previous best experience and the best experience achieved by the population, denoted as personal best position of $X_n^{Pbest}=\left[X_{n,1}^{Pbest},\dots ,X_{n,d}^{Pbest},\dots ,X_{n,D}^{Pbest}\right]$ and global best position of $G^{best}=\left[G_1^{best},\dots ,G_d^{best},\dots ,G_D^{best}\right]$, respectively. During the t-th iteration of the search process, the new velocity $V_{n,d}^{t+1}$ of each n-th particle in any d-th dimension is adjusted based on the corresponding dimensional components of the personal best position $X_{n,d}^{Pbest,t}$ (i.e., self-cognitive component) and global best position $G_d^{best,t}$ (i.e., social component) as follows:

$$V_{n,d}^{t+1}=\omega V_{n,d}^t+c_1{r}_1\left(X_{n,d}^{Pbest,t}-X_{n,d}^t\right)+c_2{r}_2\left(G_d^{best,t}-X_{n,d}^t\right)$$

(1)

where $\omega$ is an inertia weight;$c_1$ and $c_2$ are acceleration coefficients;$r_1,r_2\in \left[0,1\right]$ are two random numbers generated from a uniform distribution. Referring to $V_{n,d}^{t+1}$, the new position of each n-th particle in every d-th dimension is updated as:

$$X_{n,d}^{t+1}=V_{n,d}^{t+1}+X_{n,d}^t$$

(2)

The fitness of every n-th particle with updated position is evaluated as $f\left(X_n^{t+1}\right)$ and compared with those of the personal best position and global best position denoted as $f\left(X_n^{Pbest,t}\right)$ and $f\left(G^{best,t}\right)$, respectively. Both of $X_n^{Pbest,t}$ and $G^{best,t}$ will be updated as $X_n^{t+1}$ if the latter solution is superior. The search process of PSO using Equations (1) and (2) is iterated until the predefined termination criteria are satisfied.

2.2. Particle Swarm Optimization without Velocity (PSOWV)

PSOWV is a velocity-discarded version of PSO proposed in [16], aiming to enhance the ability of PSO to locate the global optimum of a given problem with a lesser iteration number. During the search process, the d-th dimension of position for every n-th PSOWV particle (i.e., $X_{n,d}^{t+1}$) can be updated based on the random linear combination between its personal best position (i.e., $X_{n,d}^{Pbest,t}$) and the global best position (i.e., $G_d^{best,t}$) of the population in the same dimensional component as follows:

$$X_{n,d}^{t+1}=c_1{r}_1{X}_{n,d}^{Pbest,t}+c_2{r}_2{G}_d^{best,t}$$

(3)

The fitness evaluation and procedure to update historically best positions (i.e., $X_n^{Pbest,t}$ and $G^{best,t}$) of PSOWV are similar to those of the original PSO. Although PSOWV can solve the simple benchmark functions with a faster convergence speed than the original PSO, its feasibility to solve more challenging real-world optimization problems, such as training ANN models, remains unexplored. Furthermore, preliminary studies also revealed the high tendency of PSOWV to suffer premature convergence issues because its search behavior is governed by a single search operator that highly relies on the directional information provided by historically best positions.

2.3. PSO Variants

Despite appealing characteristics, such as rapid convergence speed and simplistic implementation, the original PSO tends to suffer from rapid loss of population diversity and premature convergence issues when solving more complex optimization problems. Proper balancing of exploration and exploitation searches is considered a fundamental cornerstone for MSAs such as PSO to solve different optimization problems competitively. Therefore, various modification schemes were proposed by researchers over the years to address the demerits of the original PSO.

Parameter adaptation is a popular enhancement strategy of PSO by determining the proper combination of control parameters that can govern its search trajectories. The control parameters to be adjusted include inertia weight, constriction factor, acceleration coefficients, and a variety of these parameters. Some notable PSO variants that were proposed with parameter adaptation approaches are reported in [20,21,22,23]. Neighborhood structure modification is another promising technique of PSO because it governs the broadcast rate of information between population members. Particularly, the fully connected population topology tends to be more exploitative, whereas the partially connected one has stronger exploitation strengths. PSO variants reported in [19,24,25,26,27,28] can achieve proper tradeoffs between the exploration and exploitation searches by varying their population topology with time or based on current search environments. Apart from modifying the neighborhood structure, it is also feasible to introduce single or multiple modified learning strategies into PSO for achieving performance enhancements such as those proposed in [29,30,31,32,33,34,35,36]. To alleviate potential negative impacts brought by the historically best solution (e.g., personal and global best positions), novel exemplars might be constructed by these modified learning strategies from the non-fittest solutions to guide the search process of particles more effectively while preserving the population diversity. Finally, the PSO’s robustness in solving high-complexity real-world problems can be enhanced using the hybridization approach, such as those reported in [37,38,39,40]. Different hybridization frameworks [41] can be designed to leverage the strengths of search operators incorporated in other MSAs for compensating the drawbacks of PSO in solving certain problem classes. The strengths and limitations of selected PSO variants are analyzed and summarized in Table 1.

Table 1. Strengths and limitations of selected PSO variants.

Reference	Year	Strengths	Limitations
[20]	2019	Acceleration coefficients and inertia weight of each particle were adjusted adaptively based on current search environment.	High computation costs incurred by the novel method used to estimate the search environment in each iteration.
[21]	2019	Inertia weights of particles were adjusted based on their personal best fitness. Mutation scheme was performed on stagnated particles to preserve swarm diversity.	Both adaptive inertia weight and mutation scheme were highly relying on the directional information of global best position.
[22]	2019	Periodic trigonometric functions were used to adjust the inertia weight and acceleration coefficient of particle.	Limited ability to adjust exploration and exploitation searches with single search operator. Search process only relied on personal and global best positions.
[23]	2021	Gaussian white noise with different intensity was used to adjust the acceleration coefficients of particles adaptively. Wider exploration search.	Limited ability to adjust exploration and exploitation searches with single search operator. Search process only relied on personal and global best positions.
[24]	2022	Neighborhood structure of each particle was gradually increased from ring topology to fully connected topology.	Limited flexibility to regulate exploration and exploitation searches of algorithm because the swarm diversity level is increased monotonically.
[19]	2018	Neighborhood structure of each particle can be adaptively maintained, decreased, increased or shuffled by referring to the search track record of population.	Expensive computation cost used to adaptively adjust the neighborhood structure of each particle. Laborious works to fine tune the newly introduced parameters.
[25]	2018	Flexible neighborhood structure concept was introduced to achieve proper tradeoff between exploration and exploitation searches.	Expensive computation cost used to adaptively adjust the neighborhood structure of each particle. Relatively poor performances when dealing with unimodal problems.
[26]	2020	A reinforcement learning concept (i.e., Q-learning) was used to select the optimal topology of particle.	Expensive computation cost due to the involvement of Q-learning and computation of swarm diversity. Search process only relied on personal and global best positions.
[27]	2020	Multiple good quality subswarms were constructed based on correlations between group sequences. A dynamic regrouping strategy was introduced to promote information sharing between different subswarms and accelerate their convergence speed.	Overemphasized on the influences of historically best positions to guide the search process of subswarms. Complex population division scheme. Laborious works to fine tune the newly introduced parameters.
[28]	2020	Benefits of holonic organization in multiagent system were leveraged to achieve proper tradeoff between exploration and exploitation searches.	Relatively slow convergence speed when locating the global optima of unimodal problems.
[29]	2017	Multiple subswarms were constructed based on the fitness levels of particles. Directional information of non-fittest particles was used to guide the search process.	Relatively poor performances when dealing with low and medium scale optimization problems.
[30]	2020	Exemplar used to guide the general swarm was derived from the mean positions of elitist swarm. ∙	Limited enhancement of swarm diversity because mean position used to guide the population search was shared by all particles.
[31]	2020	Positions of other particles were updated using mainstream and stochastic learning strategies. Global worst position was handled using terminal replacement mechanism.	Limited enhancement of swarm diversity because mean position used to guide the population search was shared by all particles.
[32]	2020	Forgetting ability was introduced to maintain the population diversity of algorithm.	Neglected the potential benefits brought by non-fittest particles to guide the search process.
[33]	2019	Dimensional learning strategy and comprehensive learning strategy were introduced to achieve proper tradeoff between exploration and exploitation searches.	High fitness evaluation numbers were consumed by dimensional learning strategy when generating the exemplar.
[34]	2019	Oppositional-based learning and convex combination concepts were used to generate exemplar for the fittest particle.	Strong dependency on historically best positions used to guide the non-fittest particles.
[35]	2020	Optimal guide creation module was designed to generate a global exemplar based on two nearest neighbors of global best position.	Expensive computation cost due to the construction of global exemplar in every iteration.
[36]	2021	Construction of main swarm and hover swarm as diversity maintenance scheme. Construction of unique exemplar for main swarm and hover swarm,	Expensive computation cost due to the binary population division scheme and construction of unique exemplar in every iteration.
[37]	2019	Crossover and mutation of genetic algorithm were used to enhance the exploitation and exploration searches of PSO, respectively.	Huge memory consumption to store the individual solutions that offered significant performance gains.
[38]	2019	Grey wolf optimizer was used to update the positions of some particles to enhance exploration.	Increasing execution time due to sequential cascading of grey wolf optimizer and PSO.
[39]	2020	Butterfly optimization algorithm was hybridized with PSO to improve the exploration ability.	Neglected the potential benefits brought by non-fittest particles to guide the search process.
[40]	2022	Differential evolution was hybridized with PSO to achieve better balancing of exploration and exploitation searches of algorithm	Increasing execution time due to sequential cascading of differential evolution and PSO.

2.4. Application of MSAs in Training ANN Models

Given the drawbacks of the conventional BP method, numerous MSAs were designed as promising alternatives to train ANN models with more robust network performances [42]. A two-layer PSO (PSO-PSO) algorithm was proposed in [43] to train a multilayer perceptron (MLP) neural network by interleaving two PSO algorithms. The first layer of PSO was used to optimize the number of perceptrons in the network architecture, whereas the second layer of PSO optimized the weight and bias values based on the network architecture obtained by the first layer. Nevertheless, simulation studies revealed that the ANN models optimized by PSO-PSO did not significantly outperform their peers when solving the classification benchmark datasets. A hybridized PSO and gravitational search algorithm (PSOGSA) was proposed [44] to optimize the weights and biases of the ANN model by leveraging the unique searching behaviors of PSO and GSA. When training the ANN model, PSO was incorporated to alleviate the inherent drawbacks of GSA, i.e., low convergence rate and high tendency to be trapped in local optima. A hybrid improved opposition-based PSO with a backpropagation algorithm (IOPSO-BPA) [45] was introduced to optimize the weight values of ANNs. Both oppositional-based learning and mutation schemes were incorporated as diversity preservation schemes of IOPSO-BPA.

Furthermore, the concepts of time-varying parameters were introduced to improve the convergence characteristic of the algorithm in optimizing the weights of ANN models. Kandasamy and Rajendran [46] proposed a hybrid algorithm to overcome the drawbacks of the conventional BP methods overfitting and entrapment in local optima when training ANN models. PSO was firstly employed to search for the optimal combination of trainable weights of the ANN model by minimizing the classification error function. Subsequently, the steepest descent method was applied to fine tune the near-optimal weight values encoded in the global best position to further improve classification accuracy. In [47], a self-adaptive and strategy-based PSO (SPS-PSO) was designed to solve the large-scale feature selection and ANN training problems for large-scale datasets. Five search operators with different characteristics were introduced in SPS-PSO, and an adaptive mechanism was used to assign a suitable operator for each particle to ensure it can perform searching with balanced exploration and exploitation strengths. A comprehensive adaptive PSO (ACPSO) was designed in [48] to tackle the denoising issue of ultrasound images by optimizing the functional-link neural network (FLNN). The velocity of the ACPSO was only dependent on the global best position, and its controlling parameters were adaptively adjusted based on the personal and global best positions. To mitigate the flooding issue, an ANN model was trained using PSO in [49] to formulate river flow modelling based on the weather and meteorological data. It was revealed that the river flow strongly correlates with selected variables, such as temperature, evaporation, and rainfall. In [50], hybrid intelligent modeling was developed using PSO and ANN (PSO-ANN) to predict the soil matric sanction, i.e., a useful metric to indicate the soil shear strength in addressing sudden landslides issue, with improved prediction accuracy.

The genetic algorithm (GA) [51] is another popular MSA used to train ANN models. A hybrid model of ANN and GA (ANN-GA) was proposed in [52] to optimize the weights and biases of the ANN model used for modeling the slump of ready-mix concrete. The initial weights and biases of ANN-GA were determined using GA and fine-tuned with the BP algorithm. ANN-GA was reported to outperform its peers by leveraging the benefits of GA and BP to promote its global and local search abilities, respectively. In [53], GABPNN was proposed by integrating GA into a BP-trained ANN to optimize the thickness of blow-molded polypropylene bellows. In GABPNN, the BP algorithm was first applied to train the weights of the ANN model using lesser learning samples, and these weights were further evolved in the feasible solution regions using GA. Contrary to ANN-GA, GA promoted the local search behavior of GABPNN by adopting an elitist strategy and a simulated annealing algorithm. GABPNN demonstrated its effectiveness and competitive performance in solving blow molding problems. A hybrid MLP ANN and GA approach (MLPANN-GA) was introduced in [54] to predict sludge bulking for water treatment plants. GA was incorporated to train the weights, activation functions, and thresholds of the MLPANN model. Simulation studies reported that the incorporation of GA to train MLPANN can increase the accuracy of the ANN model in estimating the sludge volume index.

In addition to GA, teaching-learning-based optimization (TLBO) [55] is another popular MSA widely used for ANN optimization. A TLBO-based ANN (TLBOANN) was proposed in [56] to estimate the energy consumption in Turkey. TLBO was applied to search for the optimal weights and biases of the ANN model by minimizing the error function based on the input data provided, i.e., gross domestic product, population, and import and export data in Turkey. An improved hybrid TLBO and ANN (iTLBO-ANN) was proposed in [57] to solve real-world building energy consumption forecasting problems. Three modifications, known as feedback stage, accuracy factor, and worst solution elimination, were introduced to improve the performance of TLBO in optimizing the weights and thresholds of the ANN model within a shorter time. The iTLBO-ANN outperformed other ANN models trained by GA and PSO by predicting building energy consumption with better accuracy and computational speed. Another TLBO-optimized ANN [58] was proposed to improve the performance in predicting the axial capacity of pile foundations. TLBO was used to train the weights of the ANN model by minimizing the mean square error produced when predicting the ultimate capacity of both driven and drilled shaft piles embedded in uncemented soils. The ANN model trained by TLBO outperformed that trained by BP by producing better variance accounted for and determination coefficient. A new TLBO variant known as TLBO-MLPs was used to train ANN model for data classification [59]. Additional mechanisms were introduced in both the teacher and learner phases of TLBO-MLPs to achieve realistic emulation of classroom teaching and learning that can lead to performance gain in solving complex optimization problems [60].

3. Proposed Methodology

3.1. Formulation of ANN Training as an Optimization Problem

An ANN model to be optimized in this study consists of a three-layer structure with P input neurons, Q hidden neurons, and R output neurons in input, hidden, and output layers, respectively, as illustrated in Figure 1. The neurons in each layer are considered a set of processing elements that are connected by weights with other layers. Suppose that $I_p$ refers to the value of $p$-th neuron at the input layer, $H_q$ represents the value of $q$-th neuron at the hidden layer, and $O_r$ is the r-th neuron at the output layer, where $p=1,\dots ,P$,$q=1,\dots ,Q$, and $r=1,\dots ,R$. Denote $W_{p,q}^H$ as the connection weight between $I_p$ and $H_q$; $W_{q,r}^O$ as the connection weight between $H_q$ and $O_r$; $B_q^H$ and $B_r^O$ as the biases of $H_q$ and $O_r$, respectively. The values of each q-th hidden neuron $H_q$ and r-th output neuron $O_r$ can be produced by computing the sum of input weight with the presence of biases, followed by the non-linearization process of this weighted summation with an activation function of $\Phi (·)$ expressed as follows:

$$H_q=\Phi \left({\displaystyle \sum }_{p=1}^P{W}_{p,q}^H{I}_p+B_q^H\right)$$

(4)

$$O_r=\Phi \left({\displaystyle \sum }_{q=1}^Q{W}_{q,r}^O{I}_q+B_r^O\right)$$

(5)

Figure 1. The network architecture of an ANN model with three-layer structure.

Contrary to the majority of existing ANN training algorithms that only focus on searching optimal weights and biases, this study also considers the optimal selection of the activation function used to solve a given classification task. The decision variables to be optimized by the proposed MSPSOTLP when training the ANN model include: (a) weights $W_{p,q}^H,W_{q,r}^O\in \left[-1,1\right]$, (b) biases $B_q^H,B_r^O\in \left[-1,1\right]$, and (c) index $K=\left\{1,2,3,4,5\right\}$ that refer to the candidate activation functions, where Binary Step, Sigmoid [7], Hyperbolic Tangent (Tanh) [7], Inverse Tangent (ATan), and Rectified Linear Unit (ReLU) [61] functions are assigned with indices of 1, 2, 3, 4, and 5, respectively. The mathematical formulation of the candidate activation functions considered in this study is presented in Table 2.

Table 2. The mathematical formulation of the considered activation functions.

Activation Functions	Mathematical Formulation
Binary Step	$\Phi \left(X\right)=\{\begin{array}{c}0, \mathrm{for} X<0\\ 1, \mathrm{for} X\ge 0\end{array}$
Sigmoid	$\Phi \left(X\right)=\frac{X}{1+e^{-X}}$
Hyperbolic Tangent (Tanh)	$\Phi \left(X\right)=\left(\frac{e^X-e^{-X}}{e^{X+e^{-X}}}\right)$
Inverse Tangent (ATan)	$\Phi \left(X\right)={\tan }^{-1}\left(X\right)$
Rectified Linear Unit (ReLU)	$\Phi \left(X\right)=\{\begin{array}{c}X, \mathrm{for} X\ge 0\\ 0, \mathrm{for} X<0\end{array}$

The decision variables to be optimized by the proposed MSPSOTLP in ANN training are encoded into the position vector X of each particle as follows:

$$\begin{array}{c}X\\ =\left[W_{1,1}^H,\dots ,W_{p,q}^H,\dots ,W_{P,Q}^H,W_{1,1}^O,\dots ,W_{q,r}^O,\dots ,W_{Q,R}^O,B_1^H,\dots ,B_q^H,\dots ,B_Q^H,B_1^O,\dots ,B_r^O,\dots ,B_R^O,K\right]\end{array}$$

(6)

Referring to Equation (6), the ANN training considered in the current study can be formulated as an optimization problem with a dimensional size of D, where

$$D=PQ+QR+Q+R+1$$

(7)

In this study, the fitness of each MSPSOTLP particle when it is used to train the ANN model can be evaluated by measuring the mean square error between the predicted and expected output values. Given a dataset with a total of $G$ data samples, the predicted output of g-th data sample produced by an ANN model trained by MSPSOTLP and its corresponding expected outcome stored in the dataset are indicated as ${\Im }_g^{pred}$ and ${\Im }_g^{exp}$, respectively, where $g=1,\dots ,G$. The mean square error $\epsilon \left(X\right)$ produced by an ANN model constructed using the decision variables stored in the position vector X of the particle is calculated as the fitness value $f\left(X\right)$ as follows:

$$f\left(X\right)=\epsilon \left(X\right)=\frac{1}{G}{\displaystyle \sum }_{g=1}^G{\left[{\Im }_g^{pred}\left(X\right)-{\Im }_g^{exp}\right]}^2$$

(8)

Based on Equation (8), the ANN training is considered a minimization problem because it is more desirable to produce an ANN model with a minor error, implying its high classification accuracy in solving a given dataset.

3.2. Proposed MSPSOTLP Algorithm

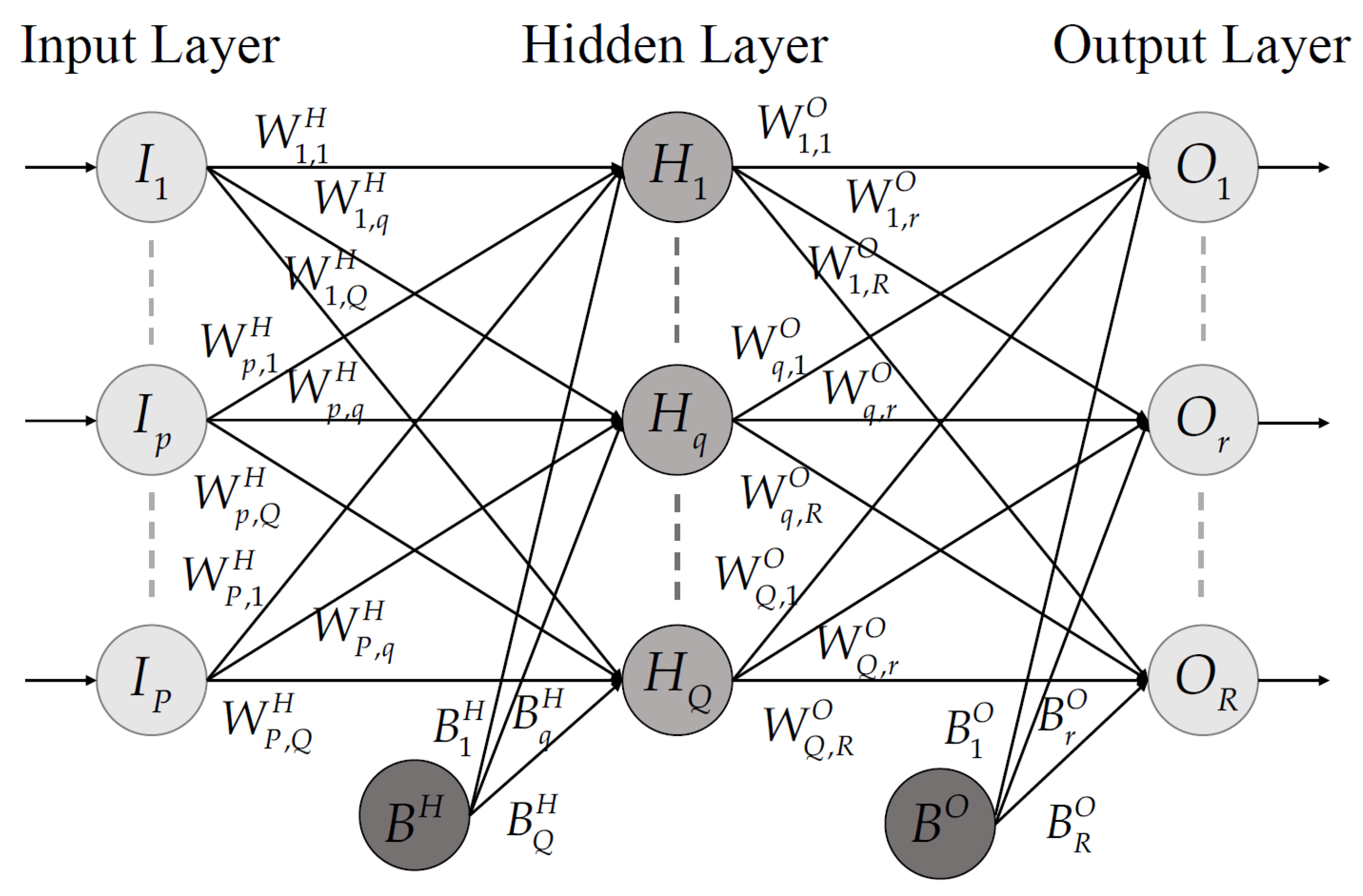
In this study, a new PSO variant known as MSPSOTLP is proposed to solve challenging optimization problems, including the ANN training problem formulated in Equation (8), with improved performances. For the latter problem, the proposed MSPSOTLP is used to optimize the weights, biases, and selection of activation functions of the ANN model when solving the given datasets. The essential modifications introduced to enhance the search performance of MSPSOTLP are described in the following subsections.

3.2.1. Modified Initialization Scheme of MSPSOTLP

Population initialization is considered a crucial process to develop robust MSAs because the quality of initial candidate solutions can influence the algorithm’s convergence rate and searching accuracy [17]. Most PSO variants employed random initialization to generate the initial population without considering any meaningful information about the search environment [17]. The stochastic behavior of the random initialization scheme might produce particles at inferior solution regions at the beginning stage of optimization. This undesirable scenario can prevent the algorithm’s convergence towards the global optimum, thus compromising the algorithm’s overall performance.

In this study, a modified initialization scheme incorporated with the chaotic system (CS) and oppositional-based learning (OBL), namely the CSOBL initialization scheme, is designed for the proposed MSPSOTLP to overcome the drawbacks of the conventional initialization scheme. Unlike a random system that demonstrates completely unpredictable behaviors, CS is considered a more powerful initialization scheme that can produce an initial swarm with better diversity by leveraging its ergodicity and non-repetition natures. Denote ${\vartheta }_0$ as the initial condition of a chaotic variable that is randomly generated in each independent run. ${\vartheta }_z$ refers to the value of the chaotic variable in z-th iteration with $z=1,\dots ,Z$, where $Z$ represents the maximum sequence number. Given the bifurcation coefficient of $\mu =\pi$, the chaotic sequence is updated using a chaotic sine map [62] as:

$${\vartheta }_{z+1}=\sin \left(\mu {\vartheta }_z\right), \mathrm{where} z=1,\dots ,Z$$

(9)

Let $X_d^U$ and $X_d^L$ be the upper and lower limits of the decision variable in each d-th dimension, respectively, where $1=1,\dots ,D$. Given the chaotic variable ${\vartheta }_Z$ produced in the final iteration of Z, the d-th dimension of each n-th chaotic swarm member $X_{n,d}^{CS}$ can be initialized as:

$$X_{n,d}^{CS}=X_d^L+{\vartheta }_Z\left(X_d^U-X_d^L \right)$$

(10)

Referring to Equation (10), a chaotic population with a swarm size of N can be produced and represented as a population set of $P^{CS}=\left[X_1^{CS},\dots ,X_n^{CS},\dots ,X_N^{CS}\right]$.

Despite the benefits of the chaotic map in enhancing population diversity, these chaotic swarm members can be initialized in solution regions far away from the global optimum, leading to the low convergence rate of the algorithm. To overcome this drawback, a solution set opposite with $P^{CS}$ is generated by leveraging the OBL concept [63]. For every d-th dimension of n-th chaotic swarm member represented as $X_{n,d}^{CS}$, the corresponding opposite swarm member $X_{n,d}^{OL}$ is calculated using OBL strategy [17,64] as follows:

$$X_{n,d}^{OL}=X_d^L+X_d^U-X_{n,d}^{CS}$$

(11)

Similarly, an opposite population with a swarm size of N can be generated using Equation (11) and represented as another population set of $P^{OL}=\left[X_1^{OL},\dots ,X_n^{OL},\dots ,X_N^{OL}\right]$.

To produce an initial population with better fitness and wider coverage in the solution space, both of $P^{CS}$ and $P^{OL}$ are merged as a combined population set of $P^{MRG}$ with a swarm size of 2N as follows:

$$P^{MRG}=P^{CS}\cup P^{OL}$$

(12)

Subsequently, the fitness of all solution members in $P^{MRG}$ are evaluated, and a sorting operator of $\mathsf{\Psi }(·)$ is then applied to rearrange these solution members from the best to worst based on their fitness to produce a sorted population set of $P^{Sort}$, where

$$P^{Sort}=\mathsf{\Psi }\left(P^{MRG}\right)$$

(13)

Finally, a truncation operator $\Gamma (·)$ is applied to select the top N solution members of on $P^{Sort}$ to construct the initial population of MSPSOTLP, i.e., $P=\left[X_1,\dots ,X_n,\dots ,X_N\right]$, where

$$P=\Gamma \left(P^{Sort}\right)$$

(14)

The pseudocode used to describe the CSOBL initialization scheme of MSPSOTLP is presented in Algorithm 1.

Algorithm 1. Pseudocode of CSOBL initialization scheme for MSPSOTLP
Input: $N$, $D$, $X^{\mathit{U}}$, $X^{\mathit{L}}$, $Z$
01:	Initialize $P^{CS}\leftarrow \varnothing$ and $P^{OL}\leftarrow \varnothing$;
02:	for each n-th particle do
03:		for each d-th dimension do
04:			Randomly generate initial chaotic variable ${\vartheta }_0\in \left[0,1\right]$;
05:			Initialize the chaotic sequence as $z=1$;
06:			while $z$ is smaller than $Z$ do
07:				Update chaotic variable ${\vartheta }_{z+1}$ using Equation (9);
08:			end while
09:			Compute $X_{n,d}^{CS}$ using Equation (10);
10:			Compute $X_{n,d}^{OL}$ using Equation (11);
11:		end for
12:		$P^{CS}\leftarrow P^{CS}\cup X_n^{CS}$;/* Store new chaotic swarm member */
13:		$P^{OL}\leftarrow P^{OL}\cup X_n^{OL}$;/* Store new opposite swarm member */
14:	end for
15:	Construct $P^{MRG}$ using Equation (12);
16:	Evaluate the fitness of all solution members in $P^{MRG}$;
17:	Sort all solution members of $P^{MRG}$ from the best to worst using Equation (13);
18:	Produce the initial population $P$ using Equation (14);
Output: $P=\left[X_1,\dots ,X_n,\dots ,X_N\right]$

3.2.2. Primary Learning Phase of MSPSOTLP

Most PSO variants, including PSOWV, rely on the global best position to adjust the search trajectories of particles during the optimization process without considering the useful information of other non-fittest particles in the population. Although the directional information of the global best position might be useful to solve simple unimodal problems, it might not necessarily be the best option to handle complex problems with multiple numbers of local optima due to the possibility of the global best position being trapped at the local optima in an earlier stage of optimization. Without a proper diversity preservation scheme, other population members tend to be attracted by misleading information about the global best position and converge towards the inferior region, leading to premature convergence and poor optimization results.

To address the aforementioned issues, several modifications are incorporated into the primary learning phase of MSPSOTLP to achieve a proper balancing of exploration and exploitation searches. The multiswarm concept is first introduced as a diversity preservation scheme at the beginning stage of the primary learning phase by randomly dividing the main population of $P=\left[X_{\mathbf{1}},\dots ,X_{\mathit{n}},\dots ,X_{\mathit{N}}\right]$ into S subswarms. Each s-th subswarm is denoted by $P_s^{sub}=\left[X_1^{sub},\dots ,X_n^{sub},\dots ,X_{N^{sub}}^{sub}\right]$ consists of $N^{sub}=N/S$ particles, where $s=1,\dots ,S$. To produce each s-th subswarm $P_s^{sub}$ from the main population $P$, a reference point of ${\mathbf{ℬ}}_s=\left[X_{s,1}^{ref},\dots ,X_{s,d}^{ref},\dots ,X_{s,D}^{ref}\right]$ is randomly generated in search space. The normalized Euclidean distance between the reference point ${\mathbf{ℛ}}_s$ and personal best position of each n-th particle, i.e., $X_n^{Pbest}=\left[X_{n,1}^{Pbest},\dots ,X_{n,d}^{Pbest},\dots ,X_{n,D}^{Pbest}\right]$ are measured as $\Xi \left(s,n\right)$, i.e.,

$$\Xi \left(s,n\right)=\sqrt{{\displaystyle \sum }_{d=1}^D{\left(\frac{X_{s,d}^{ref}-X_{n,d}^{Pbest}}{X_d^U-X_d^L}\right)}^2}$$

(15)

Referring to the $\Xi \left(s,n\right)$ values computed for all N particles, the $N^{sub}$ particles with the nearest $\Xi \left(s,n\right)$ distances from ${ℛ}_s$ are identified as the members of s-th subswarm and stored in $P_s^{sub}$ before they are discarded from the main population $P$. From Algorithm 2, the reference-point-based population division scheme used to generate the multiswarm for the primary learning phase of MSPSOTLP is repeated until all $S$ subswarms are generated.

Algorithm 2. Pseudocode of reference-point-based population division scheme used to generate the multiswarm for the primary learning phase of MSPSOTLP
Input: $P$, $N$, $S$, $D$, $N^{sub}$, $X^U$, $X^L$
01:	Initialize $s\leftarrow 1$;
02:	while main population $P$ is not empty do
03:		Randomly generate ${ℛ}_s=\left[X_{s,1}^{ref},\dots ,X_{s,d}^{ref},\dots ,X_{s,D}^{ref}\right]$ in search space;
04:		for each n-th particle do
05:			Calculate $\Xi \left(s,n\right)$ using Equation (15);
06:		end for
07:		Select $N^{sub}$ particles with the nearest $\Xi \left(s,n\right)$ from ${ℛ}_s$ to construct $P_s^{sub}$;
08:		Eliminate the members of $P_s^{sub}$ from $P$;
09:		$s\leftarrow s+1$; /* Update the index of subswarm*/
10:	end while
Output: $P_s^{sub}=\left[X_1^{sub},\dots ,X_n^{sub},\dots ,X_{N^{sub}}^{sub}\right]$ where $s=1,\dots ,S$

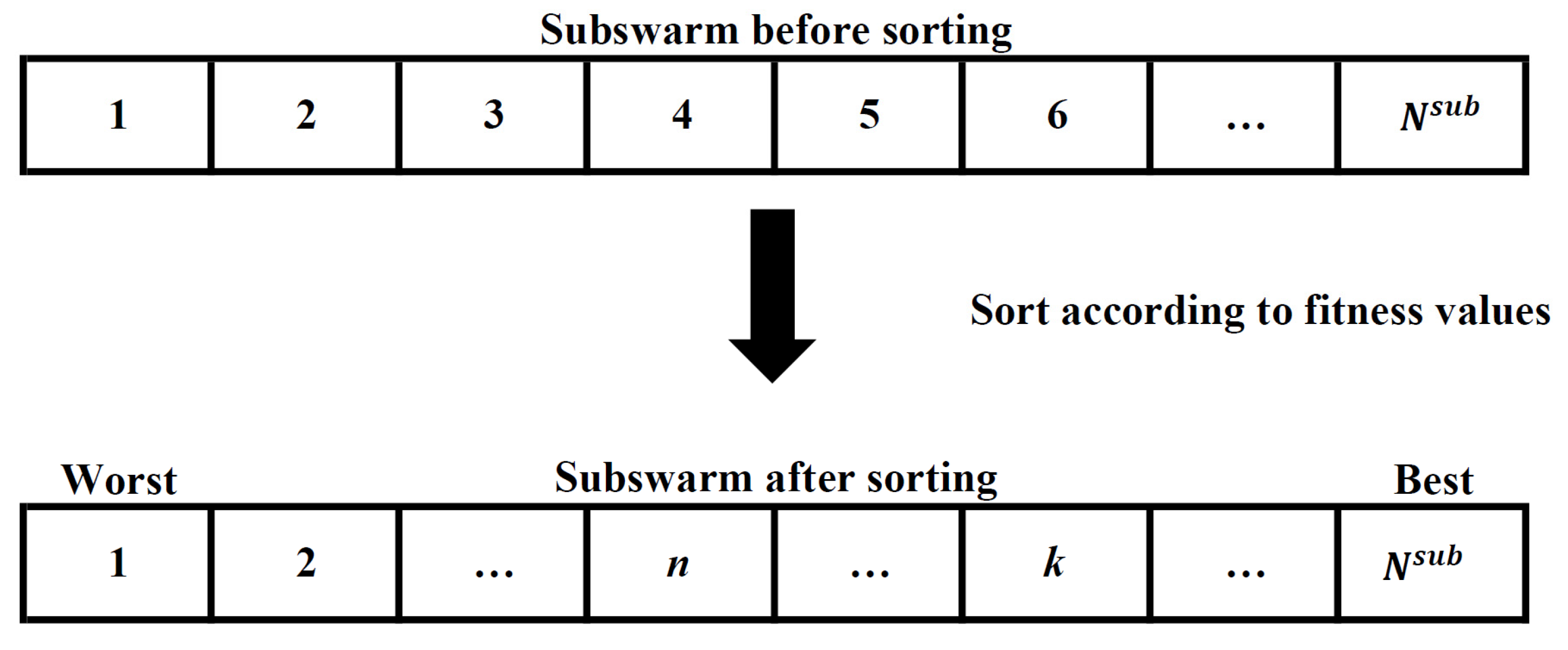
Define $f\left(X_n^{Pbest,s}\right)$ as the personal best fitness of each n-th particle stored in the s-th subswarm $P_s^{sub}$, where $n=1,\dots ,N^{sub}$ and $s=1,\dots ,S$. All $N^{sub}$ particles stored in each s-th subswarm $P_s^{sub}$ are then sorted from the worst to best based on their personal best fitness values, as shown in Figure 2. Accordingly, any k-th particle stored in the sorted $P_s^{sub}$ is considered to have better or equally good personal best fitness than that of n-th particle if the condition of $n\le k\le N^{sub}$ is satisfied. Referring to Figure 2, it is notable that the first particle stored in $P_s^{sub}$ has the worst personal best fitness, whereas the final particle stored in $P_s^{sub}$ has the most competitive personal best fitness after the sorting process. Therefore, the personal best position of the final particle is also considered as the subswarm best position of $P_s^{sub}$ represented as $X_s^{Sbest}=X_{N^{sub}}^{Pbest,s}$ for $s=1,\dots ,S$.

Figure 2. Graphical illustration of sorting all particles stored in each subswarm based on their personal best fitness values.

For each s-th sorted subswarm, define ${\Omega }_n^s=\left\{X_k^{Pbest,s}|k\in \left[n,N^{sub}\right]\right\}$ as a set variable used to store the personal best position of all solution members that are superior to that of n-th solution member for $n=1,\dots ,N^{sub}-1$. Notably, the set variable ${\Omega }_{N^{sub}}^s$ is not constructed for the final solution member because none of the solution members stored in $P_s^{sub}$ has better personal best fitness than $X_{N^{sub}}^{Pbest,s}$ or $X_s^{Sbest}$. Referring to the solution members stored in each ${\Omega }_n^s$, a unique mean position denoted as $X_n^{mean,s}$ is then specifically constructed to guide the search process of every n-th solution member in the s-th subswarm, where:

$$X_n^{mean,s}=\frac{1}{N^{sub}-n+1}\left({\displaystyle \sum }_{k=n}^{N^{sub}}{X}_k^{Pbest,s}\right)$$

(16)

Apart from $X_n^{mean,s}$, a social exemplar $X_n^{SOC,s}=\left[X_{n,1}^{SOC,s},\dots ,X_{n,d}^{SOC,s},\dots ,X_{n,D}^{SOC,s}\right]$ that plays crucial roles to adjust the search trajectory of each n-th particle stored in $P_s^{sub}$ is also formulated. In contrary to global best position, the social exemplar constructed for each n-th particle is unique and it can guide the search process with better diversity by fully utilizing the promising directional information of other particles stored in ${\Omega }_n^s$ with better personal best fitness values. Specifically, each d-th dimension of n-th social learning exemplar for s-th subswarm, i.e., $X_{n,d}^{SOC,s}$, can be contributed by the same dimensional component of any randomly selected solution members of ${\Omega }_n^s$. The procedures used to construct the social exemplar $X_n^{SOC,s}$ for each n-th particle stored in $P_s^{sub}$ are described in Algorithm 3, where $\alpha$ refers to a random integer generated between the indices of $n$ and $N^{sub}$.

Algorithm 3. Pseudocode used to generate the social exemplar for each non-fittest solution member in each subswarm
Input: $D$, $N^{sub}$, $n$, ${\Omega }_n^s$
01:	for each d-th dimension do
02:		Randomly generate an integer $\alpha$ between indices of $n$ and $N^{sub}$;
03:		Extract the associated component of $X_{\alpha ,d}^{Pbest,s}$ from ${\Omega }_n^s$;
04:		$X_{n,d}^{SOC,s}\leftarrow X_{\alpha ,d}^{Pbest,s}$;
05:	end for
Output: $X_n^{SOC,s}$

Given the subswarm best position $X_s^{Sbest}$, mean position $X_n^{mean,s}$ and social exemplar $X_n^{SOC,s}$, the new position $X_n^s$ of each n-th non-fittest solution member stored in the s-th subswarm, where $n=1,\dots ,N^{sub}-1$ and $s=1,\dots ,S$, is updated as follows:

$$X_n^s=X_n^s+c_1{r}_1\left(X_n^{SOC,s}-X_n^s\right)+c_2{r}_2\left(X_s^{Sbest}-X_n^s\right)+c_3{r}_3\left(X_n^{mean,s}-X_n^s\right)$$

(17)

where $c_1$, $c_2$ and $c_3$ represent the acceleration coefficients;$r_1,r_2,r_3\in \left[0,1\right]$ are random numbers generated from uniform distributions. Referring to Equation (17), the directional information contributed by $X_n^{SOC,s}$ and $X_n^{mean,s}$ are unique for each n-th non-fittest solution member of $P_s^{sub}$ because the better solution members are stored in every set variable ${\Omega }_n^s$ are different for $n=1,\dots ,N^{sub}-1$. The social learning concept incorporated in Equation (17) also ensures that only the useful information brought by better-performing solutions is used to guide the search process of each n-th particle to accelerate the algorithm’s convergence rate. Furthermore, this learning strategy does not consider the global best position in updating the new position of each n-th particle; therefore, it has better robustness against premature convergence issues.

On the other hand, different approaches are proposed to generate the mean position and social exemplar used for guiding the search process of the final particle stored in every n-th subswarm because none of the solution members of $P_s^{sub}$ can have better personal best fitness than that of $X_{N^{sub}}^{Pbest,s}$. Define ${\Omega }_{N^{sub}}^s$ as a set variable used to store the subswarm best position of any b-th subswarm $P_b^{sub}$ if $f\left(X_b^{Sbest}\right)$ is better than $f\left(X_s^{Sbest}\right)$, i.e.,

$${\Omega }_{N^{sub}}^s=\left\{X_b^{Sbest}|f\left(X_b^{Sbest}\right) \mathrm{is} \mathrm{better} \mathrm{than} \left(X_s^{Sbest}\right), b\in B^s\right\}$$

(18)

where $B^s$ is a set containing the indices of all subswarms that have better subswarm best fitness than that of s-th subswarm; $\left|B^s \right|$ refers to the size of set $B^s$ in the range of 0 to $S-1$. Obviously,$\left|B^s \right|=0$ is the subswarm best position of s-th subswarm is the same as the global best position $G^{best}$ of population, therefore the empty sets of $B^s={\Omega }_{N^{sub}}^s=\varnothing$ are obtained under this circumstance.

The subswarm consists of $G^{best}$, the unique mean position $X_{N^{sub}}^{mean,s}$ used to guide the search process of the final particle $X_{N^{sub}}^s$ stored in each s-th subswarm based on ${\Omega }_{N^{sub}}^s$ are calculated as follows:

$$X_{N^{sub}}^{mean,s}=\frac{1}{\left|B^s \right|}\left({\displaystyle \sum }_{ b\in B^s,\left|B^s \right|\ne 0}{X}_b^{Sbest}\right)$$

(19)

Similarly, a social exemplar of $X_{N^{sub}}^{SOC,s}=\left[X_{N^{sub},1}^{SOC,s},\dots ,X_{N^{sub},d}^{SOC,s},\dots ,X_{N^{sub},D}^{SOC,s}\right]$ is also derived from adjusting the search trajectory of the final particle $X_{N^{sub}}^s$ stored in each s-th subswarm except for the one consisting of $G^{best}$. As shown in Algorithm 4, each d-th dimension of the social exemplar is assigned to the final particle of s-th subswarm $P_s^{sub}$, i.e., $X_{N^{sub},d}^{SOC,s}$, is contributed by the same dimensional component of any subswarm best position $X_b^{Sbest}$ randomly selected from ${\Omega }_{N^{sub}}^s$, where b refers to a subswarm index randomly selected from $B^s$.

Algorithm 4. Social Exemplar Scheme for the Best Particle in Each Subswarm
Input: $D$, ${\Omega }_{N^{sub}}^s$, $B^s$, $N^{sub}$
01:	for each d-th dimension do
02:		Randomly generated a subswarm index of $b\in B^s$;
03:		Extract the corresponding component of $X_{b,d}^{Sbest}$ from ${\Omega }_{N^{sub}}^s$;
04:		$X_{N^{sub},d}^{SOC,s}\leftarrow X_{b,d}^{Sbest}$;
05:	end for
Output: $X_{N^{sub}}^{SOC,s}=\left[X_{N^{sub},1}^{SOC,s},\dots ,X_{N^{sub},d}^{SOC,s},\dots ,X_{N^{sub},D}^{SOC,s}\right]$

Except for the subswarm consisting of $G^{best}$ with $B^s={\Omega }_{N^{sub}}^s=\varnothing$, the position $X_{N^{sub}}^s$ of final particle stored in each s-th subswarm can be updated as follows:

$$\begin{array}{c}{X}_{N^{sub}}^s=X_{N^{sub}}^s+c_1{r}_4\left(X_{N^{sub}}^{SOC,s}-X_{N^{sub}}^s\right)+c_2{r}_5\left(G^{best}-X_{N^{sub}}^s\right)\\ +c_3{r}_6\left(X_{N^{sub}}^{mean,s}-X_{N^{sub}}^s\right)\end{array}$$

(20)

where $r_4,r_5,r_6\in \left[0,1\right]$ are random numbers generated from a uniform distribution. Similarly, the directional information provided by $X_{N^{sub}}^{SOC,s}$ and $X_{N^{sub}}^{mean,s}$ are unique for each final particle $X_{N^{sub}}^s$ in each s-th subswarm $P_s^{sub}$ because the solution members stored in each ${\Omega }_{N^{sub}}^s$ set are different. Contrary to Equation (17), the social learning concept introduced in Equation (20) allows each subswarm to converge towards the promising solution regions without experiencing rapid loss of population diversity by facilitating the information exchanges between different subswarms. In addition, the employment of $G^{best}$ in Equation (20) is expected to improve the convergence rate of MSPSOTLP.

The overall procedures of the primary learning phase proposed for MSPSOTLP is described in Algorithm 5. For each new position $X_n^s$ obtained from Equations (17) or (20), boundary checking is first performed to ensure all decision variables’ upper and lower limits are not violated. The fitness value corresponding to the updated $X_n^s$ for each particle in s-th subswarm is then evaluated as $f\left(X_n^s\right)$ and compared with those of its personal best position and global best position denoted as $f\left(X_n^{Pbest,s}\right)$ and $f\left(G^{best}\right)$, respectively. Both $X_n^{Pbest,s}$ and $G^{best}$ are replaced by the updated $X_n^s$ if the latter solution is proven to be superior to the latter two solutions.

Algorithm 5. Pseudocode of primary learning phase for MSPSOTLP
Input: $P$, $N$, $S$, $D$, $N^{sub}$, $X^U$, $X^L$,$G^{best}$
01:	Divide main population into multiple subswarm using Algorithm 2;
02:	Sort the solution members of $P_s^{sub}$ from the worst to best based on their personal best fitness values and create ${\Omega }_n^s$ for each s-th subswarm;
03:	Identify the subswarm best position $X_s^{Sbest}$ of each s-th subswarm and create ${\Omega }_{N^{sub}}^s$ for the final particle in all S subswarms using Equation (18);
04:	Determine $B^s$ and $\left|B^s \right|$ for the final particle of all S subswarms based on ${\Omega }_{N^{sub}}^s$;
05:	for each s-th subswarm do
06:		for each n-th particle do
07:			if $n\ne N^{sub}$ then
08:				Calculate $X_n^{mean,s}$ based on ${\Omega }_n^s$ using Equation (16);
09:				Generate $X_n^{SOC,s}$ based on ${\Omega }_n^s$ using Algorithm 3;
10:				Update $X_n^s$ using Equation (17);
11:			else if $n=N^{sub}$ then
12:				if $B^s\ne \varnothing$$\mathrm{and} {\Omega }_{N^{sub}}^s\ne \varnothing$ then
13:					Calculate $X_{N^{sub}}^{mean,s}$ based on ${\Omega }_{N^{sub}}^s$ using Equation (19);
14:					Generate $X_{N^{sub}}^{SOC,s}$ based on ${\Omega }_{N^{sub}}^s$ using Algorithm 4;
15:					Update $X_{N^{sub}}^s$ using Equation (20);
16:				end if
17:			end if
18:			Evaluate $f\left(X_n^s\right)$ of the updated $X_n^s$;
19:			if $f\left(X_n^s\right)$ is better than $f\left(X_n^{Pbest,s}\right)$ then
20:				$X_n^{Pbest,s}\leftarrow X_n^s$$, f\left(X_n^{Pbest,s}\right)\leftarrow f\left(X_n^s\right)$;
21:				if $f\left(X_n^s\right)$ is better than $f\left(G^{best}\right)$ then
22:					$G^{best}\leftarrow X_n^s$$, f\left(G^{best}\right)\leftarrow f\left(X_n^s\right)$;
23:				end if
24:			end if
25:		end for
26:	end for
Output: $X_n^s$$, f\left(X_n^s\right)$$, X_n^{Pbest,s}$$, f\left(X_n^{Pbest,s}\right)$$, G^{best}$$\mathrm{and} f\left(G^{best}\right)$

3.2.3. Secondary Learning Phase of MSPSOTLP

Substantial studies [19,65] reported that most PSO variants employed single search operators that can only solve specific optimization problems with good results, but fail to perform well in the remaining problems due to the limited variations of exploration and exploitation strengths. For some challenging optimization problems, the fitness landscapes contained in different subregions of search space can be significantly different. Therefore, the particles need to adjust their exploration and exploitation strengths dynamically when searching in different regions of the solution space to locate global optimum and deliver good optimization results.

Motivated by these findings, a secondary phase is designed as an alternative framework of MSPSOTLP, where two search operators with different search characteristics are incorporated to guide the search process of particles with varying levels of exploration and exploitation strengths. Unlike the primary learning phase, both search operators assigned in the secondary learning phase aim to further refine those already found promising regions by searching around the personal best positions of all MSPSOTLP particles. Before initiating the secondary learning phase, all S subswarms constructed during the primary learning phase, i.e., $P_s^{sub}$ for $s=1,\dots ,S$, are merged to form the main population $P$ with N particles as shown below:

$$P=P_1^{sub}\cup \dots \cup P_s^{sub}\cup \dots \cup P_S^{sub}$$

(21)

To assign a search operator for each n-th particle during the secondary learning phase of MSPSOTLP, a randomly selected particle with a population index of e is randomly generated, where $e\in \left[1,N\right]$ and $e\ne n$. Define $X_e^{Pbest}$ as the personal best position of this randomly selected e-th particle and its personal best fitness is evaluated as $f\left(X_e^{Pbest}\right)$. If the e-th particle has better personal best fitness than that of $X_n^{Pbest}$, the new personal best position of latter particle can be updated as $X_n^{Pbest,new}$, where

$$X_n^{Pbest,new}=X_n^{Pbest}+r_7\left(X_e^{Pbest}-X_n^{Pbest}\right), \mathrm{if} f\left(X_e^{Pbest}\right) \mathrm{is} \mathrm{better} \mathrm{than} f\left(X_n^{Pbest}\right)$$

(22)

where $r_7\in \left[0,1\right]$ are random numbers generated from a uniform distribution. The search operator of Equation (22) can attract of n-th particle towards the promising solution regions covered by the e-th peer particle, hence it behaves more exploratively.

For the case, if e-th particle has more inferior personal best fitness than that of n-th particle, the former solution is discarded. Another four distinct particles with population indices of w, x, y and z are randomly selected instead, where $w,x,y,z\in \left[1,N\right]$ and $w\ne x\ne y\ne z$. Denote $X_{w,d}^{Pbest}$, $X_{x,d}^{Pbest}$, $X_{y,d}^{Pbest}$ and $X_{z,d}^{Pbest}$ as the d-th dimension of the personal best position for the w-th, x-th, y-th and z-th particles, respectively. Let $G_d^{best}$ be the same d-th dimension of the global best position. For every n-th particle, each of the d-th dimension of its new personal best position can be calculated as:

$$X_{n,d}^{Pbest,new}=\{\begin{array}{c}{G}_d^{best}+{\tau }_1\left(X_{w,d}^{Pbest}-X_{x,d}^{Pbest}\right)+{\tau }_2\left(X_{y,d}^{Pbest}-X_{z,d}^{Pbest}\right), \mathrm{if} r_8>0.5 \\ X_{n,d}^{Pbest} , \mathrm{otherwise}\end{array}$$

(23)

where ${\tau }_1,{\tau }_2,r_8\in \left[0,1\right]$ are random numbers generated from a uniform distribution. From Equation (23), there is a probability for each $X_{n,d}^{Pbest,new}$ to inherit its original information from $X_{n,d}^{Pbest}$ or to perform searching around the nearby region of $G_d^{best}$ with small perturbations based on the information of $X_{w,d}^{Pbest}$, $X_{x,d}^{Pbest}$, $X_{y,d}^{Pbest}$ and $X_{z,d}^{Pbest}$. Hence, the search operator of Equation (23) is considered more exploitative than that of Equation (22). The procedures used to implement the secondary learning phase of MSPSOTLP is shown in Algorithm 6. For each new $X_n^{Pbest,new}$ obtained from Equations (22) or (23), boundary checking is performed. For each n-th particle, the fitness value of its updated $X_n^{Pbest,new}$ is obtained as $f\left(X_n^{Pbest,new}\right)$ and compared with $f\left(X_n^{Pbest}\right)$ and $f\left(G^{best}\right)$. If $X_n^{Pbest,new}$ is better than $X_n^{Pbest}$ and $G^{best}$, the latter two solutions are replaced by the former one.

Algorithm 6. Pseudocode of secondary learning phase for MSPSOTLP
Input: $P_s^{sub}$ for $s=1,\dots ,S$, $G_d^{best}$$, f\left(G^{best}\right)$
01:	Reconstruct main population $P$ using Equation (21);
02:	for each n-th particle do
03:		Randomly select e-th particle from $P$ with $X_e^{Pbest}$ and $f\left(X_e^{Pbest}\right)$;
04:		if $f\left(X_e^{Pbest}\right)$ is better than $f\left(X_n^{Pbest}\right)$ then
05:			Calculate $X_n^{Pbest,new}$ using Equation (22);
06:		else if$f\left(X_e^{Pbest}\right)$ is not better than $f\left(X_n^{Pbest}\right)$ then
07:			for each d-th dimension do
09:				Calculate $X_{n,d}^{Pbest,new}$ using Equation (23);
10:			end for
11:		end if
12:		Evaluate $f\left(X_n^{Pbest,new}\right)$;
13:		if $f\left(X_n^{Pbest,new}\right)$ is better than $f\left(X_n^{Pbest}\right)$ then
14:			$X_n^{Pbest}\leftarrow X_n^{Pbest,new}$$, f\left(X_n^{Pbest}\right)\leftarrow f\left(X_n^{Pbest,new}\right)$;
15:			if $f\left(X_n^{Pbest,new}\right)$ is better than $f\left(G^{best}\right)$ then
16:				$G^{best}\leftarrow X_n^{Pbest}$$, f\left(G^{best}\right)\leftarrow f\left(X_n^{Pbest}\right)$;
17:			end if
18:		end if
19:	end for
Output: $X_n^{Pbest}$, $f\left(X_n^{Pbest}\right)$, $G^{best}$, $f\left(G^{best}\right)$

3.2.4. Overall Framework of MSPSOTLP

The overall framework of MSPSOTLP is described in Algorithm 7. The initial population of MSPSOTLP is first generated using the CSOBL initialization scheme, where the chaotic map and oppositional-based learning concepts are incorporated to enhance the quality and coverage of the initial solutions in the search space, respectively. The primary learning phase is performed to update the positions of particles by leveraging the benefits of the multiswarm and social learning concepts. The secondary learning phase is then executed to fine-tune the personal best position of each particle based on two newly proposed search operators with different search characteristics. These iterative search processes are repeated until the termination criterion of $\gamma >{\Gamma }^{max}$ is satisfied, where $\gamma$ is a counter used to record the fitness evaluation number consumed by MSPSOTLP and ${\Gamma }^{max}$ is a predefined maximum fitness evaluation number. At the end of the optimization process, $G^{best}$ is returned as the best-optimized result found by the proposed algorithm. If MSPSOTLP is used to train the ANN model, then $G^{best}$ can be decoded as the optimal combination of weights, biases, and activation functions used by an ANN model to solve a given dataset.

Algorithm 7 (Main Algorithm). MSPSOTLP
Input: $N$, $D$, $, X^U$, $X^L$, ${\Gamma }^{max}$
01:	Initialize $G^{best}$ as an empty vector and $f\left(G^{best}\right)\leftarrow \infty$;
02:	Initialize $\gamma \leftarrow 0$;
03:	Generate the initial population $P$ using Algorithm 1;
04:	$\gamma \leftarrow \gamma +2N$;
05:	for each n-th particle do
06:		$X_n^{Pbest}\leftarrow X_n$$, f\left(X_n^{Pbest}\right)\leftarrow f\left(X_n\right)$;
07:		If $f\left(X_n\right)$ is better than $f\left(G^{best}\right)$ then
08:			$G^{best} \leftarrow X_n$$, f\left(G^{best}\right)\leftarrow f\left(X_n\right)$;
09:		end if
10:	end for
11:	while $\gamma \le {\Gamma }^{max}$ do
12:		Perform the primary learning phase using Algorithm 5;
13:		$\gamma \leftarrow \gamma +N$;
14:		Perform the secondary learning phase using Algorithm 6;
15:		$\gamma \leftarrow \gamma +N$;
16:	end while
Output: $G^{best}$, $f\left(G^{best}\right)$

4. Performance Analysis of MSPSOTLP

The performance of the proposed MSPSOTLP in solving various types of challenging optimization problems is investigated and compared with well-established PSO variants. This includes the performance of MSPSOTLP in solving CEC 2014 benchmark functions, followed by its performance in optimizing the weights, biases, and activation functions of ANN models for solving classification problems.

4.1. Performance Evaluation of MSPSOTLP in Solving Global Optimization Problems

4.1.1. CEC 2014 Benchmark Functions

The optimization performance of the proposed MSPSOTLP is evaluated using 30 benchmark functions of CEC 2014 [66]. As described in Table 3, the benchmark functions with different fitness landscape characteristics can be classified into four categories, known as (i) unimodal functions (F1–F3), (ii) simple multimodal functions (F4–F16), (iii) hybrid functions (F17–F22) and (iv) composition functions (F23–F30). For all benchmark functions in CEC 2014 with D dimensions, the search range X of each decision variable is constrained between −100 to 100. Furthermore, the fitness value of theoretical global optimum $f\left(X^{*}\right)$ of each function is presented in Table 3.

Table 3. CEC 2014 benchmark functions and its fitness value of theoretical global optimum.

Categories	No.	Function Name	$\mathit{f}\left({\mathit{X}}^{*}\right)$
Unimodal	F1	Rotated High Conditioned Elliptic Function	100
	F2	Rotated Bent Cigar Function	200
	F3	Rotated Discus Function	300
Simple Multimodal	F4	Shifted and Rotated Rosenbrock’s Function	400
	F5	Shifted and Rotated Ackley’s Function	500
	F6	Shifted and Rotated Weierstrass Function	600
	F7	Shifted and Rotated Griewank’s Function	700
	F8	Shifted Rastrigin’s Function	800
	F9	Shifted and Rotated Rastrigin’s Function	900
	F10	Shifted Schewefel’s Function	1000
	F11	Shifted and Rotated Schwefel’s Function	1100
	F12	Shifted and Rotated Katsuura Function	1200
	F13	Shifted and Rotated HappyCat Function	1300
	F14	Shifted and Rotated HGBat Function	1400
	F15	Shifted and Rotated Expanded Griewank’s plus Rosenbrock’s Function	1500
	F16	Shifted and Rotated Expanded Schaffer’s F6 Function	1600
Hybrid	F17	Hybrid Function1	1700
	F18	Hybrid Function 2	1800
	F19	Hybrid Function 3	1900
	F20	Hybrid Function 4	2000
	F21	Hybrid Function 5	2100
	F22	Hybrid Function 6	2200
Composition	F23	Composition Function 1	2300
	F24	Composition Function 2	2400
	F25	Composition Function 3	2500
	F26	Composition Function 4	2600
	F27	Composition Function 5	2700
	F28	Composition Function 6	2800
	F29	Composition Function 7	2900
	F30	Composition Function 8	3000

4.1.2. Performance Metrics for Solving Benchmark Functions

Performances of all compared algorithms are measured using the mean fitness $F_{mean}$ and standard deviation SD. Specifically, $F_{mean}$ is the mean error between the fitness of the best solution produced by an algorithm and the actual global optimum of a benchmark function in multiple runs. At the same time, the SD value measures the consistency of an algorithm in solving a given problem. Smaller F_mean and SD imply the capability of an algorithm to solve a function with better accuracy and consistency, respectively.

A set of non-parametric statistical analysis procedures [67,68] are applied to analyze the performance of the proposed MSPSOTLP and its competitors from a statistical point of view. The Wilcoxon signed rank test [68] is applied to conduct a pairwise comparison between the proposed MSPSOTLP and each competitor at a significance level of $\alpha =0.05$. The results generated by the Wilcoxon signed rank test are presented in terms of $R^{+}$, $R^{-}$, p, and h values. $R^{+}$ and $R^{-}$ summarize the sum of ranks where MSPSOTLP outperforms or underperforms its peer algorithm, respectively. The p-value indicates the minimum significance level required to identify the performance deviations between the two algorithms. If the p-value is smaller than $\alpha =0.05$, the better result achieved by an algorithm is considered statistically significant. Based on the obtained p-value and predefined $\alpha$, the corresponding h value is concluded to be significantly better (i.e., h = “+”), statistically insignificant (i.e., h = “=”), or significantly worse (i.e., h = “-”).

Multiple comparisons among the proposed MSPSOTLP and its competitors is also conducted using the Friedman test [67]. The Friedman test first produces the average ranking of each algorithm. The p-value obtained from the Friedman test measures the global differences among all compared algorithms at a significance level of $\alpha =0.05$. If significant global differences are observed, three post-hoc analyses [67], known as Bonferroni-Dunn, Holm, and Hochberg, are performed to analyze the substantial differences among all compared algorithms based on the adjusted p-values (APVs).

4.1.3. Parameter Settings for Solving Benchmark Functions

The performance of the proposed MSPSOTLP in solving CEC 2014 benchmark functions is compared with seven well-established PSO variants. The selected PSO variants include the conventional PSO (PSO) [14], PSO without velocity (PSOWV) [16], unconstrained version of multi-swarm PSO without velocity (MPSOWV) [15], competitive swarm optimizer (CSO) [69], social learning PSO (SLPSO) [18], hybridized PSO with gravitational search algorithm (PSOGSA) [44], and accelerated PSO (APSO) [70].

The parameter settings of all of the compared algorithms are set with the recommended values in their respective literature and presented in Table 4. All compared algorithms are configured with a population size of $N=100$ to solve each benchmark function at $D=30$ for 30 independent times. The maximum fitness evaluation numbers of all algorithms are set as ${\Gamma }^{max}=10,000\times D$. All compared algorithms are simulated using Matlab 2019b on a personal computer with Intel ^® Core i7-7500 CPU @ 2.70 GHz.

Table 4. Parameter settings of all compared algorithms.

Algorithms	Parameter Settings
PSO	Inertia weight $\mathsf{\omega }:0.9\to 0.2$, acceleration coefficients $c_1=c_2=2.05$
PSOWV	$c_1=1.00$$, c_2=1.70$
MPSOWV	Subpopulation size $N_s^{sub}=10$, where $s=1,\dots ,10$, acceleration coefficients $c_1=c_2=c_2=4.1/3$
CSO	Parameter control the influence of mean position $\phi \in \left[0,0.3\right]$
SLPSO	Exponential component to adjust learning probability $\tilde{\alpha }=0.5$, parameter to control social influence factor $\tilde{\beta }=0.01$
PSOGSA	Initial gravitational constant $G_0=1$, descending coefficient of gravitational constant $\widehat{\alpha }=20$
APSO	Additional acceleration coefficient $A=0.3$$, \mathsf{\omega }=1$$, c_1=c_2=2.05$
MSPSOTLP	$N_s^{sub}=10$, where $s=1,\dots ,10$$, c_1=c_2=c_2=4.1/3$

4.1.4. Performance Comparison in Solving CEC 2014 Benchmark Functions

The simulation results of F_mean and SD produced by the proposed MSPSOTLP and other selected PSO variants in solving the CEC 2014 benchmark functions are presented in Table 5. The algorithms’ best and second-best Fmean obtained are indicated in boldface and underlined, respectively. Moreover, the performance comparison between the proposed MSPSOTLP and selected PSO variants is summarized in #BMF and w/t/l. Specifically, #BMF indicates the number of best F_mean obtained by an algorithm in solving all function, while w/t/l reports that the proposed MSPSOTLP has better performance in w function, similar performance in t function, and worse performance in l function as compared to the particular compared algorithm.

Table 5. F_mean and SD values produced by the proposed MSPSOTLP and other PSO variants in solving CEC 2014 benchmark functions.

Func.	Criteria	MSPSOTLP	PSO	PSOWV	CSO	MPSOWV	SLPSO	PSOGSA	APSO
F1	Fmean	5.61 × 103	6.69 × 106	4.70 × 108	3.12 × 105	1.61 × 108	4.88 × 105	2.47 × 105	1.25 × 108
	SD	2.57 × 103	8.99 × 106	3.79 × 108	1.32 × 105	7.38 × 107	2.86 × 105	7.24 × 104	2.02 × 107
F2	Fmean	0.00 × 100	7.27 × 101	6.94 × 1010	6.84 × 103	2.12 × 1010	1.57 × 104	1.25 × 104	3.01 × 107
	SD	0.00 × 100	2.90 × 102	1.56 × 1010	5.63 × 103	2.74 × 109	1.10 × 104	6.97 × 103	5.81 × 107
F3	Fmean	2.18 × 1011	4.87 × 101	3.18 × 105	7.85 × 103	8.20 × 104	7.26 × 103	6.93 × 103	1.97 × 105
	SD	2.52 × 10−11	6.61 × 101	5.70 × 104	5.62 × 103	2.44 × 104	5.50 × 103	1.33 × 103	3.56 × 104
F4	Fmean	1.44 × 10−2	1.79 × 102	8.66 × 103	5.71 × 101	1.39 × 103	2.56 × 101	4.49 × 101	2.71 × 102
	SD	1.23 × 10−2	5.12 × 101	3.26 × 103	2.31 × 101	3.56 × 102	3.04 × 101	2.91 × 101	3.29 × 101
F5	Fmean	2.01 × 101	2.09 × 101	2.09 × 101	2.10 × 101	2.09 × 101	2.09 × 101	2.00 × 101	2.00 × 101
	SD	5.32 × 10−2	8.52 × 10−2	9.48 × 10−2	3.65 × 10−2	3.01 × 10−2	6.49 × 10−2	2.99 × 10−4	3.26 × 10−2
F6	Fmean	3.25 × 100	2.12 × 101	3.83 × 101	4.08 × 10−1	3.38 × 101	5.43 × 10−1	1.80 × 101	2.45 × 101
	SD	1.02 × 100	5.40 × 100	2.41 × 100	6.73 × 10−1	9.46 × 10−1	6.38 × 10−1	5.22 × 100	3.50 × 100
F7	Fmean	0.00 × 100	2.62 × 10−2	5.61 × 102	1.48 × 10−3	1.62 × 102	1.97 × 10−3	1.23 × 10−2	1.25 × 100
	SD	0.00 × 100	2.21 × 10−2	2.05 × 102	3.12 × 10−3	1.44 × 101	4.41 × 10−3	7.38 × 10−3	6.16 × 10−1
F8	Fmean	1.15 × 101	1.15 × 102	3.87 × 102	8.66 × 100	2.68 × 102	1.37 × 101	1.70 × 102	1.37 × 102
	SD	1.57 × 100	2.51 × 101	3.23 × 101	1.88 × 100	2.21 × 101	3.25 × 100	9.24 × 100	2.75 × 101
F9	Fmean	1.20 × 101	1.39 × 102	4.85 × 102	9.65 × 100	3.29 × 102	1.65 × 101	1.91 × 102	1.98 × 102
	SD	3.16 × 100	1.42 × 101	3.67 × 101	3.78 × 100	1.25 × 101	5.52 × 100	7.06 × 100	2.18 × 101
F10	Fmean	1.52 × 102	2.63 × 103	7.66 × 103	1.78 × 102	6.22 × 103	5.47 × 102	3.89 × 103	3.71 × 103
	SD	7.91 × 101	4.52 × 102	4.67 × 102	1.36 × 102	2.45 × 102	2.60 × 102	3.20 × 102	5.04 × 102
F11	Fmean	2.42 × 103	3.76 × 103	7.56 × 103	2.85 × 102	7.24 × 103	7.21 × 102	4.36 × 103	4.16 × 103
	SD	3.73 × 102	6.08 × 102	4.57 × 102	2.28 × 102	4.44 × 102	2.29 × 102	1.82 × 102	8.01 × 102
F12	Fmean	1.62 × 100	1.74 × 100	2.70 × 100	2.39 × 100	2.65 × 100	2.50 × 100	2.07 × 10−1	5.61 × 10−1
	SD	2.07 × 10−1	3.84 × 10−1	1.22 × 10−1	3.10 × 10−1	1.63 × 10−1	3.68 × 10−1	1.66 × 10−1	2.68 × 10−1
F13	Fmean	1.29 × 10−1	4.82 × 10−1	6.12 × 100	1.34 × 10−1	3.09 × 100	1.97 × 10−1	5.62 × 10−1	5.92 × 10−1
	SD	7.49 × 10−3	1.19 × 10−1	5.58 × 10−1	1.61 × 10−2	2.33 × 10−1	2.41 × 10−2	7.52 × 10−2	1.17 × 10−1
F14	Fmean	1.93 × 10−1	2.90 × 10−1	1.46 × 102	3.94 × 10−1	4.48 × 101	4.42 × 10−1	2.82 × 10−1	2.57 × 10−1
	SD	8.61 × 10−3	9.55 × 10−2	6.54 × 101	4.61 × 10−2	7.08 × 100	7.32 × 10−2	2.23 × 10−2	5.35 × 10−2
F15	Fmean	2.30 × 100	1.10 × 100	3.58 × 106	3.14 × 100	9.90 × 104	5.07 × 100	8.15 × 100	3.16 × 101
	SD	2.08 × 10−1	3.82 × 100	7.86 × 105	4.29 × 10−1	2.26 × 104	4.93 × 100	4.94 × 100	2.06 × 101
F16	Fmean	7.60 × 100	1.16 × 101	1.34 × 101	1.08 × 101	1.30 × 101	1.21 × 101	1.25 × 101	1.28 × 101
	SD	3.86 × 10−1	5.88 × 10−1	2.05 × 10−1	4.73 × 10−1	1.38 × 10−1	1.79 × 10−1	2.12 × 10−1	6.66 × 10−1
F17	Fmean	2.10 × 103	2.86 × 105	1.77 × 107	1.49 × 105	6.01 × 106	1.05 × 105	1.86 × 104	2.05 × 106
	SD	5.36 × 102	3.25 × 105	1.08 × 107	6.66 × 104	1.12 × 106	5.42 × 104	5.76 × 103	2.37 × 106
F18	Fmean	1.22 × 102	3.79 × 103	5.88 × 108	2.17 × 103	2.58 × 108	8.42 × 102	3.84 × 102	1.41 × 105
	SD	6.67 × 101	4.62 × 103	2.87 × 108	3.17 × 103	8.05 × 107	4.97 × 102	1.85 × 102	3.12 × 105
F19	Fmean	4.08 × 100	1.24 × 101	3.64 × 102	5.30 × 100	1.41 × 102	6.13 × 100	1.59 × 101	2.93 × 101
	SD	2.68 × 10−1	3.21 × 100	1.51 × 102	6.33 × 10−1	2.38 × 101	5.50 × 10−1	2.89 × 100	2.74 × 101
F20	Fmean	7.96 × 101	3.74 × 102	2.78 × 105	1.26 × 104	2.90 × 104	2.48 × 104	2.84 × 103	1.02 × 105
	SD	8.58 × 100	2.38 × 102	1.88 × 105	9.04 × 103	9.09 × 103	1.36 × 104	2.73 × 102	4.65 × 104
F21	Fmean	8.02 × 102	6.12 × 104	6.03 × 106	6.92 × 104	1.56 × 106	8.18 × 104	1.18 × 104	1.16 × 106
	SD	2.07 × 102	6.19 × 104	6.96 × 106	3.80 × 104	5.59 × 105	3.84 × 104	1.29 × 103	9.69 × 105
F22	Fmean	3.52 × 101	6.77 × 102	1.08 × 103	1.28 × 102	9.76 × 102	1.51 × 102	7.94 × 102	6.23 × 102
	SD	1.30 × 101	2.68 × 102	2.42 × 102	5.43 × 101	1.96 × 102	1.32 × 101	1.59 × 102	173 × 102
F23	Fmean	3.15 × 102	3.16 × 102	3.15 × 102	3.15 × 102	4.17 × 102	3.15 × 102	2.00 × 102	3.62 × 102
	SD	3.20 × 10−13	3.52 × 10−1	8.04 × 101	9.16 × 10−12	1.26 × 101	4.99 × 10−13	1.06 × 10−7	1.51 × 101
F24	Fmean	2.24 × 102	2.30 × 102	4.66 × 102	2.26 × 102	3.20 × 102	2.33 × 102	2.01 × 102	2.50 × 102
	SD	1.50 × 10−1	6.64 × 100	3.90 × 101	4.74 × 100	1.13 × 101	7.32 × 100	1.09 × 10−1	2.84 × 100
F25	Fmean	2.00 × 102	2.13 × 102	2.59 × 102	2.06 × 102	2.25 × 102	2.06 × 102	2.00 × 102	2.22 × 102
	SD	0.00 × 100	4.81 × 100	2.21 × 101	1.55 × 100	5.87 × 100	2.72 × 100	8.94 × 10−10	2.99 × 100
F26	Fmean	1.00 × 102	1.70 × 102	1.06 × 102	1.00 × 102	1.03 × 102	1.40 × 102	1.00 × 102	1.83 × 102
	SD	2.32 × 10−2	4.81 × 101	1.57 × 100	1.83 × 10−2	5.44 × 10−1	5.47 × 101	1.35 × 10−1	4.59 × 101
F27	Fmean	3.94 × 102	8.49 × 102	1.28 × 103	3.55 × 102	1.14 × 103	3.69 × 102	2.00 × 102	8.02 × 102
	SD	2.91 × 101	3.58 × 102	3.92 × 101	5.77 × 101	6.81 × 101	2.77 × 101	5.10 × 10−9	2.03 × 102
F28	Fmean	8.55 × 102	4.04 × 103	1.82 × 103	8.57 × 102	1.36 × 103	9.77 × 102	2.00 × 102	2.50 × 103
	SD	1.80 × 101	9.59 × 102	5.12 × 102	4.42 × 101	3.69 × 102	1.07 × 102	2.07 × 10−8	5.80 × 102
F29	Fmean	8.60 × 102	1.43 × 103	1.04 × 107	1.63 × 103	2.15 × 106	1.55 × 103	2.02 × 102	1.23 × 107
	SD	5.36 × 101	7.53 × 102	9.14 × 106	4.77 × 102	4.02 × 106	4.57 × 102	2.00 × 10−1	1.88 × 107
F30	Fmean	1.72 × 103	3.56 × 103	3.79 × 105	2.69 × 103	4.04 × 104	3.17 × 103	2.00 × 102	9.88 × 104
	SD	5.39 × 102	1.93 × 103	339 × 105	1.06 × 103	8.14 × 103	3,17 × 103	3.62 × 10−3	3.25 × 104
#BMF		18	0	0	5	0	0	10	1
w/t/l		-	29/1/0	30/0/0	22/3/5	30/0/0	26/1/3	19/2/9	28/0/2

For unimodal functions (i.e., F1–F3), the proposed MSPSOTLP has the most dominating search performance by producing the best F_mean values to solve these three functions. MSPSOTLP is also the only PSO variant to locate the global and near-global optimum solutions of F2 and F3, respectively. Apart from MSPSOTLP, both PSO and PSOGSA are considered to have relatively better search performance than the rest of the algorithms in solving unimodal functions by producing one second-best F_mean. Meanwhile, PSOWV, MPSOWV and APSO have inferior search performance by producing F_mean values that are generally larger than those of the other algorithms.

For simple multimodal functions (i.e., F4-F16), the proposed MSPSOTLP has the most competitive performance in solving these 13 functions with the seven best F_mean (i.e., F4, F7, F10, F13, and F14) and three second-best F_mean (i.e., F5, F8, and F9). MSPSOTLP is also the only algorithm that successfully locates the global optimum of function F7. Contrary to unimodal functions, CSO and SLPSO have exhibited relatively better performance in solving several simple multimodal functions, such as F6, F8, F9, and F11. Although PSO and PSOGSA have good performance in solving unimodal functions, their performances in solving F4, F6, F7, F8, F9, F10, F11, F13, F15, and F16 are relatively inferior. The performance degradations of PSO and PSOGSA reflect the limitation of both algorithms in tackling optimization problems with multiple local optima. Meanwhile, APSO shows relatively better search performance at solving F5, F12, and F14 than PSOWV and MPSOWV.

The excellent optimization performance of the proposed MSPSOTLP is also demonstrated in the hybrid function category (i.e., F17–F22) by solving all six functions with the best F_mean values. PSOGSA follows this, producing three second-best F_mean values for F17, F18, and F21. However, the performance of PSOGSA in solving hybrid functions is not consistent, as shown by its relatively inferior results in F19 and F22. A similar scenario is observed from PSO, CSO, and SLPSO, producing mediocre performance in solving most hybrid functions. Specifically, PSO can solve F20 and F21 with relatively good performance, but it performs poorly in F17, F18, F19, and F22. Meanwhile, CSO is reported to solve F19 and F22 with competitive performance, but delivers poor results for F17, F18, F20, and F21. On the other hand, APSO, PSOWV, and MPSOWV are reported to have inferior search performance in solving all hybrid functions with higher complexity levels.

In the category of composition function (i.e., F23–F30), PSOGSA shows its competitive performance in dealing with these more complex functions, followed by the proposed MSPSOTLP. PSAGSA can solve all eight composite functions with the best F_mean values, while MSPSOTLP produces two best F_mean (i.e., F25 and F26) and five second-best F_mean (i.e., F23, F24, F28, F29, and F30). Although PSOGSA performs better than MSPSOTLP when solving composite functions, PSOGSA performs more inferiorly than MSPSOTLP in three other problem categories. CSO produces one best F_mean (i.e., F26) and three second-best F_mean (i.e., F23, F25, and F27), implying its competitive performance in solving composite functions. Meanwhile, SLPSO is observed to have relatively good performance in solving F23 and F25, but mediocre performance in the remaining composite functions.

Overall, the proposed MSPSOTLP has demonstrated the best search accuracy among all compared PSO variants by producing 18 best F_mean values in solving 30 functions, implying that the search mechanisms incorporated are sufficiently robust to handle optimization problems with different levels of complexity as compared to most of its peer algorithms. This is followed by PSOGSA and CSO, which are reported to have 10 and 5 best F_mean values, respectively. On the other hand, PSOWV is identified as the worst algorithm by producing 26 worst F_mean values in solving 30 CEC 2014, implying its limitations in solving the benchmark functions with simple fitness landscapes.

4.1.5. Non-Parametric Statistical Analyses

Based on the reported F_mean values, Wilcoxon signed rank test [68] is applied to perform a pairwise comparison between the proposed MSPSOTLP and the selected PSO variants. The results in terms of $R^{+}$, $R^{-}$, p, and h values, are presented in Table 6. Accordingly, MSPSOTLP performs significantly better than all other PSO variants at a significance level of $\alpha =0.05$ as indicated by the h value of “+”. Notably, the proposed MSPSOTLP completely dominates PSO, PSOWV, and PSOWV to solve CEC 2014 benchmark functions based on the promising $R^{+}$, $R^{-}$, p and h values reported.

Table 6. Pairwise comparisons by Wilcoxon signed rank test between MSPSOTLP and each peer algorithm.

MSPSOTLP vs.	R+	R−	p Value	h Value
PSO	465.0	0.0	2.00 × 10−6	+
PSOWV	465.0	0.0	2.00 × 10−6	+
CSO	382.5	82.5	1.91 × 10−3	+
MPSOWV	465.0	0.0	2.00 × 10−6	+
SLPSO	390.0	45.0	1.76 × 10−4	+
PSOGSA	347.5	117.5	1.75 × 10−2	+
APSO	459.0	6.0	3.00 × 10−6	+

The Friedman test [67] is further conducted for multiple comparisons between the proposed MSPSOTLP and selected PSO variants based on their F_mean values. The results, in terms of average ranking, chi-square statistics, and p-value, are reported in Table 7. The Friedman test reports that MSPSOTLP has the best performance by scoring an average rank of 1.6833, followed by CSPSO, PSOGSA, SLPSO, PSO, APSO, MPSOWV, and PSOWV with average ranks of 3.0500, 3.0667, 3.7667, 4.4167, 5.6500, 6.6500, and 7.7167, respectively. The p-value determined by the Friedman test through chi-square statistics is smaller than the predefined significance level of $\alpha =0.05$. Therefore, significant global performance deviations among all compared algorithms are observed.

Table 7. Average ranking and p-value produced by Friedman test.

Algorithm	Ranking	Chi-Square Statistics	p value
MSPSOTLP	1.6833	144.636111	0.00 × 100
PSOGSA	3.0667
CSO	3.0500
PSO	4.4167
SLPSO	3.7667
APSO	5.6500
MPSOWV	6.6500
PSOWV	7.7167

Given the global performance difference observed from the Friedman test, three post-hoc statistical analyses [67], known as Bonferroni-Dunn, Holm, and Hochberg, are utilized to identify other concrete performance differences between the proposed MSPSOTLP and different PSO variants. The results, in terms of z values, unadjusted p values, and adjusted p values (APVs), produced by three procedures are reported in Table 8. All post-hoc procedures confirm the significant performance enhancement of MSPSOTLP against PSOWV, MPSOWV, APSO, SLPSO, and PSO at $\alpha =0.05$. The Hochberg procedure has higher sensitivity to detect the significant performance difference between MSPSOTLP, CSO, and PSAGSA. Notably, the Holm procedure can detect the significant performance improvement of MSPSOTLP against CSO and PSOGSA if the threshold level is adjusted to $\alpha =0.10$.

Table 8. Adjusted p values produced by each algorithm through three post-hoc analysis procedures.

MSPSOTLP vs.	z	Unadjusted p	Bonferroni-Dunn p	Holm p	Hochberg p
PSOWV	9.54 × 100	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100
MPSOWV	7.85 × 100	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100
APSO	6.27 × 100	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100
SLPSO	4.32 × 100	1.50 × 10−5	1.08 × 10−4	6.20 × 10−3	6.20 × 10−5
PSO	3.29 × 100	9.88 × 10−4	6.91 × 10−3	2.96 × 10−3	2.96 × 10−3
CSO	2.19 × 100	2.87 × 10−2	2.01 × 10−1	5.75 × 10−2	3.07 × 10−2
PSOGSA	2.16 × 100	3.07 × 10−2	2.15 × 10−1	5.75 × 10−2	3.07 × 10−2

4.1.6. Performance Analysis of Proposed Improvement Strategies

A further performance analysis is conducted in this subsection to investigate the contribution brought by each improvement strategy introduced into MSPSOTLP, i.e., modified initialization scheme (i.e., chaotic map and oppositional based learning), primary learning phase (i.e., multiswarm concept and construction of social exemplar), and secondary learning phase (i.e., two search operators with different search characteristic). The original PSOWV is chosen as the baseline method to be compared in this subsection. Another three variants of MSPSOTLP, i.e., MSPSOTLP-1, MSPSOTLP-2 and MSPSOTLP-3, are also introduced to analyze the performance gains brought by the modified initialization scheme, primary learning phase, and secondary learning phase, respectively. Particularly, MSPSOTLP-1 refers to the PSOWV enhanced with the CSOBL initialization scheme. Meanwhile, MSPSOTLP-2 refers to PSOWV enhanced with the CSOBL initialization scheme and primary learning phase. Finally, MSPSOTLP-3 refers to PSOWV enhanced with the CSOBL initialization scheme and secondary learning phase, where its primary phase is replaced with the original search operator of PSOWV. The performance gain achieved by each MSPSOTLP variants against the original PSOWV when solving every benchmark function is measured as $\Delta G$ as follow:

$$\Delta G=\frac{F_{mean}\left(MSPSOTLP variant\right)-F_{mean}\left(PSOWV\right)}{\left|F_{mean}\left(PSOWV\right)\right|}\times 100\%$$

(24)

Referring to Equation (24), it is evident that a positive value of $\Delta G$ can be obtained if a particular MSPSOTLP variant can solve the benchmark functions with better F_mean value than that of PSOWV and vice versa.

The simulation results in terms of F_mean and $\Delta G$ obtained by PSOWV and all MSPSOTLP variants when solving all CEC 2014 benchmark functions are presented in Table 9. Accordingly, all MSPSOTLP variants have successfully solved the majority of CEC 2014 benchmark functions with different degrees of performance gains. MPSOTLP-1 is observed to outperform PSOWV in the majority of CEC 2014 benchmark functions except for F1, F5, F6, F11, F12, F16, F17, F21, F29, and F30. Although the CSOBL can produce an initial population with better solution quality in terms of fitness and diversity that can lead to performance gain of algorithm, it is not sufficient to solve the complex problem because CSOBL is only executed once during the search process. Some interesting findings can be observed when both variants of MSPSOTLP-2 and MSPSOTLP-3 are used to solve CEC 2014 benchmark functions. Particularly, MSPSOTLP-2 can perform better than MSPSOTLP-3 when solving the unimodal (i.e., F1 to F3), simple multimodal (i.e., F4 to F16) and hybrid (i.e., F17 to F22) functions. Meanwhile, MSPSOTLP-3 is revealed to be more competitive than MSPSOTLP-2 in dealing with the most complex composition function. The performance differences between MSPSOTLP-2 and MSPSOTLP03 can be justified based on their inherent search mechanisms. For MSPSOTLP-2, the primary learning phase is incorporated with multiswarm and social learning concepts used to accelerate the convergence characteristic of the algorithm without compromising its population diversity. When dealing with optimization functions with less complex fitness landscapes (i.e., unimodal, simple multimodal, and hybrid functions), the benefits brought by both the multiswarm and social learning concepts can still suppress the potential negative drawbacks of the historically best position (i.e., global best position in this case). When the fitness landscapes of the optimization problems are increased further, such as those in composition functions, the numbers of local optima in the solution space have increased exponentially. Under this circumstance, the diversity maintenance scheme introduced in the primary learning phase of MSPSOTLP-2 is not sufficient to curb the high tendency of historically best positions to be trapped in these local optima. On the other hand, the secondary learning phase of MSPSOTLP-3 can leverage the useful directional information of other non-fittest solutions to perform searching with greater exploration strengths; thus, it has a higher chance to escape from the inferior regions of the solution space. Finally, the complete MSPSOTLP has exhibited the best performance when solving all CEC 2014 benchmark functions with 26 best and 4 s-best F_mean values. The simulation results reported in Table 9 have verified that each improvement strategy incorporated into MSPSOTLP indeed has different contributions to enhancing the search performance of the proposed algorithm.

Table 9. Simulation results of F_mean and $\Delta P$ obtained by PSOWV and all MSPSOTLP variants when solving CEC 2014 benchmark functions.

Func	Fmean (ΔG)
	PSOWV	MSPSOTLP-1	MSPSOTLP-2	MSPSOTLP-3	MSPSOTLP
F1	$4.70\times {10}^8$(−)	$8.08\times {10}^8$(−71.93%)	$8.42\times {10}^6$(98.21%)	$1.37\times {10}^8$(70.83%)	$\mathbf{5.61}\times {\mathbf{10}}^{\mathbf{3}}$(100.00%)
F2	$6.94\times {10}^{10}$(−)	$1.47\times {10}^{10}$(78.79%)	$2.70\times {10}^7$(99.96%)	$4.95\times {10}^9$(92.87%)	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$(100.00%)
F3	$3.18\times {10}^5$(−)	$8.56\times {10}^4$(73.09%)	$1.10\times {10}^4$(96.53%)	$4.09\times {10}^4$(87.13%)	$\mathbf{2.18}\times {\mathbf{10}}^{-\mathbf{11}}$(100.00%)
F4	$8.66\times {10}^3$(−)	$6.80\times {10}^3$(21.52%)	$1.48\times {10}^2$(98.29%)	$2.43\times {10}^2$(97.20%)	$\mathbf{1.44}\times {\mathbf{10}}^{-\mathbf{2}}$(100.00%)
F5	$2.09\times {10}^1$(−)	$2.10\times {10}^1$(−0.60%)	$2.09\times {10}^1$(0.04%)	$2.08\times {10}^1$(0.43%)	$\mathbf{2.01}\times {\mathbf{10}}^{\mathbf{1}}$(3.83%)
F6	$3.83\times {10}^1$(−)	$4.34\times {10}^1$(−13.26%)	$2.45\times {10}^1$(35.92%)	$2.78\times {10}^1$(27.39%)	$\mathbf{3.25}\times {\mathbf{10}}^{\mathbf{0}}$(91.51%)
F7	$5.61\times {10}^2$(−)	$2.23\times {10}^2$(60.17%)	$1.19\times {10}^0$(99.79%)	$3.68\times {10}^0$(99.34%)	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$(100.00%)
F8	$3.87\times {10}^2$(−)	$2.49\times {10}^2$(35.67%)	$4.13\times {10}^1$(89.34%)	$1.53\times {10}^2$(60.36%)	$\mathbf{1.15}\times {\mathbf{10}}^{\mathbf{1}}$(97.03%)
F9	$4.85\times {10}^2$(−)	$3.16\times {10}^2$(34.90%)	$9.96\times {10}^1$(79.47%)	$1.67\times {10}^2$(65.50%)	$\mathbf{1.20}\times {\mathbf{10}}^{\mathbf{1}}$(97.53%)
F10	$7.66\times {10}^3$(−)	$6.85\times {10}^3$(10.55%)	$2.12\times {10}^3$(72.36%)	$4.47\times {10}^3$(41.70%)	$\mathbf{1.52}\times {\mathbf{10}}^{\mathbf{2}}$(98.02%)
F11	$7.56\times {10}^3$(−)	$8.54\times {10}^3$(−12.92%)	$3.60\times {10}^3$(52.35%)	$4.82\times {10}^3$(36.24%)	$\mathbf{2.42}\times {\mathbf{10}}^{\mathbf{3}}$(67.99%)
F12	$2.70\times {10}^0$(−)	$3.61\times {10}^0$(−33.67%)	$2.15\times {10}^0$(20.26%)	$2.15\times {10}^0$(20.48%)	$\mathbf{1.62}\times {\mathbf{10}}^{\mathbf{0}}$(40.00%)
F13	$6.12\times {10}^0$(−)	5$.14\times {10}^0$(16.06%)	$2.64\times {10}^{-1}$(95.68%)	$7.40\times {10}^{-1}$(87.91%)	$\mathbf{1.29}\times {\mathbf{10}}^{-\mathbf{1}}$(97.89%)
F14	$1.46\times {10}^2$(−)	$1.40\times {10}^2$(3.96%)	$9.63\times {10}^{-1}$(99.34%)	$2.98\times {10}^{-1}$(99.80%)	$\mathbf{1.93}\times {\mathbf{10}}^{-\mathbf{1}}$(99.87%)
F15	$3.58\times {10}^6$(−)	$3.64\times {10}^4$(98.98%)	$1.89\times {10}^1$(100.00%)	$9.12\times {10}^1$(100.00%)	$\mathbf{2.30}\times {\mathbf{10}}^{\mathbf{0}}$(100.00%)
F16	$1.34\times {10}^1$(−)	$1.37\times {10}^1$(−2.00%)	$1.31\times {10}^1$(2.56%)	$1.36\times {10}^1$(−1.63%)	$\mathbf{7.60}\times {\mathbf{10}}^{\mathbf{0}}$(43.28%)
F17	$1.77\times {10}^7$(−)	$5.56\times {10}^7$(−100.00%)	$8.27\times {10}^5$(95.33%)	$6.08\times {10}^5$(95.56%)	$\mathbf{2.10}\times {\mathbf{10}}^{\mathrm{3}}$(99.99%)
F18	$5.88\times {10}^8$(−)	$4.07\times {10}^8$(30.77%)	$2.59\times {10}^4$(100.00%)	$7.51\times {10}^5$(99.87%)	$\mathbf{1.22}\times {\mathbf{10}}^{\mathbf{2}}$(100.00%)
F19	$3.64\times {10}^2$(−)	$1.44\times {10}^2$(60.49%)	$1.06\times {10}^1$(97.09%)	$2.26\times {10}^1$(93.80%)	$\mathbf{4.08}\times {\mathbf{10}}^{\mathbf{0}}$(98.88%)
F20	$2.78\times {10}^5$(−)	$2.54\times {10}^5$(8.77%)	$1.98\times {10}^4$(92.88%)	$5.06\times {10}^3$(98.18%)	$\mathbf{7.96}\times {\mathbf{10}}^{\mathbf{1}}$(99.97%)
F21	$6.03\times {10}^6$(−)	$1.22\times {10}^7$(−100.00%)	$1.21\times {10}^5$(97.99%)	$7.86\times {10}^5$(86.97%)	$\mathbf{8.02}\times {\mathbf{10}}^{\mathbf{2}}$(99.99%)
F22	$1.08\times {10}^3$(−)	$8.96\times {10}^2$(17.07%)	$3.15\times {10}^2$(70.81%)	$4.25\times {10}^2$(60.65%)	$\mathbf{3.52}\times {\mathbf{10}}^{\mathbf{1}}$(96.74%)
F23	$6.74\times {10}^2$(−)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(70.33%)	$3.15\times {10}^2$(53.21%)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(70.33%)	$3.15\times {10}^2$(53.26%)
F24	$4.66\times {10}^2$(−)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(57.08%)	$2.12\times {10}^2$(54.45%)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(57.08%)	$2.24\times {10}^2$(51.93%)
F25	$2.59\times {10}^2$(−)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(22.78%)	$2.07\times {10}^2$(19.92%)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(22.78%)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(22.78%)
F26	$1.06\times {10}^2$(−)	$1.04\times {10}^2$(1.80%)	$1.01\times {10}^2$(5.19%)	$1.01\times {10}^2$(5.13%)	$\mathbf{1.00}\times {\mathbf{10}}^{\mathbf{2}}$(5.66%)
F27	$1.28\times {10}^3$(−)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(84.38%)	$7.58\times {10}^2$(40.76%)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(84.38%)	$3.94\times {10}^2$(69.22%)
F28	$1.82\times {10}^3$(−)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(89.01%)	$8.98\times {10}^2$(50.65%)	$\mathbf{2.00}\times {\mathbf{10}}^{\mathbf{2}}$(89.01%)	$8.55\times {10}^2$(53.02%)
F29	$1.04\times {10}^7$(−)	$3.21\times {10}^7$(−100.00%)	$1.47\times {10}^3$(99.99%)	$5.95\times {10}^4$(99.43%)	$\mathbf{8.60}\times {\mathbf{10}}^{\mathbf{2}}$(99.99%)
F30	$3.79\times {10}^5$(−)	$8.38\times {10}^5$(−100.00%)	$2.54\times {10}^3$(99.33%)	$9.93\times {10}^4$(73.80%)	$\mathbf{1.72}\times {\mathbf{10}}^{\mathbf{3}}$(99.55%)

4.2. Performance Evaluation of MSPSOTLP in Training ANN Models

4.2.1. Classification Datasets for Training ANN Models

Apart from general optimization performance, the capability of the proposed MSPSOTLP in training ANN models for data classification tasks is also evaluated using sixteen standard datasets extracted from the University of California Irvine (UCI) machine learning repository [71]. The sixteen datasets selected for performance evaluation include Iris, Liver Disorder, Blood Transfusion, Statlog Heart, Hepatitis, Wine, Breast Cancer, Seeds, Australian Credit Approval, Haberman’s Survival, New Thyroid, Glass, Balance Scale, Dermatology, Landsat and Bank Note. The properties of each dataset are summarized in Table 10. Each selected dataset is separated into two parts, known as 70% of training samples and 30% of testing samples. Specifically, the training samples are used by MSPSOTLP and other PSO variants to optimize the parameters of ANN models (i.e., weights, biases, and activation function). In contrast, the testing samples are used to evaluate the generalization performance of ANN models trained by all compared algorithms.

Table 10. Properties of datasets selected for ANN model training.

No.	Dataset	# Attributes	# Classes	# Samples
DS1	Iris	4	3	150
DS2	Liver Disorder	6	2	345
DS3	Blood Transfusion	4	2	748
DS4	Statlog Heart	13	2	270
DS5	Hepatitis	19	2	80
DS6	Wine	13	3	178
DS7	Breast Cancer	9	2	277
DS8	Seeds	7	3	210
DS9	Australian Credit Approval	14	2	690
DS10	Haberman’s Survival	3	2	306
DS11	New Thyroid	5	3	215
DS12	Glass	9	6	214
DS13	Balance Scale	4	3	625
DS14	Dermatology	34	6	338
DS15	Landsat	36	6	4435
DS16	Bank Note	4	2	1372

4.2.2. Performance Metrics for ANN Training

Classification accuracy ${ℝ}^C$ is a popular performance metric used to measure the classification performance of an ANN model. Suppose that $\tilde{R}$ refers to the number of correctly classified data samples by the ANN model, while $R$ represents the total number of data samples in each dataset. The ${ℝ}^C$ value is calculated as follow:

$${ℝ}^C=\frac{\tilde{R}}{R}\times 100\%$$

(25)

An ANN model with a larger value of ${ℝ}^C$ is more desirable because it can produce better results in terms of classification accuracy. In addition, the ANN model produces a larger ${ℝ}^C$ value when solving the testing samples s also considered to have better generalization performance due to its excellent capability to accurately classify unseen data in different classes with its understanding of the existing data. Furthermore, the standard deviation SD values are also recorded to observe the consistency of ANN models trained by compared PSO variants in solving classification datasets.

4.2.3. Parameter Settings for ANN Training

Similar to the global optimization, the performance of the ANN model trained by the proposed MSPSOTLP in solving sixteen datasets extracted from the UCI machine learning repository is compared with the seven PSO variants reported in Section 4.1.3. The parameters of all compared algorithms are configured as reported in Table 3 as recommended in their original literature. The same values of $N=100$ and ${\Gamma }^{max}=10,000\times D$ are also configured for all compared PSO variants in solving ANN training problems, where the value of D is calculated based on Equation (7). The ANN model to be trained in this study is constructed by an input layer, a hidden layer, and an output layer. The number of input and output neurons of each ANN model are configured based on the number of attributes and classes of a given dataset, respectively, as presented in Table 8. Meanwhile, the number of neurons in the hidden layer is 15. Similarly, all compared algorithms in training ANN model are simulated using Matlab 2019b on a personal computer with Intel ^® Core i7-7500 CPU @ 2.70GHz.

4.2.4. Performance Comparison in Training ANN Models

The ${ℝ}^C$ and SD values produced by the ANN models optimized by all compared PSO variants when classifying the training and testing samples are presented in Table 11 and Table 12, respectively. Similarly, the best and second best ${ℝ}^C$ values produced by the compared methods in each dataset are indicated in boldface and underlined, respectively. The comparative studies between the ANN models trained by MSPSOTLP and other PSO variants are summarized in $\#B{ℝ}^C$ and w/t/l as similar to those in Table 5. Specifically, $\#B{ℝ}^C$ records the number of best ${ℝ}^C$ values produced by each algorithm in training the ANN models for 16 datasets extracted from UCI machine learning repository.

Table 11. The ${ℝ}^C$ and SD values produced by ANN models trained by the proposed MSPSOTLP and other PSO variants when solving the training samples.

Dataset	Criteria	MSPSOTLP	PSO	PSOWV	CSO	MPSOWV	SLPSO	PSOGSA	APSO
DS1	${ℝ}^C$	99.58	94.58	67.42	79.08	98.67	77.00	90.92	19.83
	SD	4.39 × 10−1	2.25 × 100	1.11 × 101	6.30 × 100	3.73 × 10−1	2.20 × 100	9.84 × 100	4.01 × 101
DS2	${ℝ}^C$	72.72	73.44	52.68	58.55	69.60	57.03	73.26	58.59
	SD	2.45 × 10−1	5.37 × 10−1	5.30 × 100	1.05 × 100	9.12 × 10−1	2.67 × 100	2.09 × 10−1	2.43 × 100
DS3	${ℝ}^C$	80.59	80.55	78.63	78.93	79.45	78.93	81.29	78.90
	SD	5.29 × 10−2	4.83 × 10−1	2.70 × 100	0.00 × 100	3.34 × 10−1	0.00 × 100	1.67 × 10−1	0.00 × 100
DS4	${ℝ}^C$	96.20	94.07	69.82	80.56	91.90	77.69	92.18	52.45
	SD	8.11 × 10−1	2.09 × 100	7.87 × 100	2.12 × 100	5.35 × 10−1	2.41 × 100	1.17 × 100	1.86 × 101
DS5	${ℝ}^C$	96.41	94.53	62.19	75.94	95.00	80.31	92.81	60.94
	SD	1.81 × 100	1.80 × 100	9.55 × 100	0.00 × 100	1.80 × 100	3.61 × 100	9.02 × 10−1	1.18 × 101
DS6	${ℝ}^C$	100.00	94.09	59.58	82.32	99.79	66.41	99.51	28.80
	SD	0.00 × 100	1.08 × 100	2.22 × 101	3.33 × 100	4.07 × 10−1	4.30 × 100	4.07 × 10−1	4.64 × 101
DS7	${ℝ}^C$	82.48	83.29	67.34	74.32	79.69	74.73	79.55	69.73
	SD	3.82 × 10−1	6.88 × 10−1	2.31 × 100	9.38 × 10−1	4.50 × 10−1	6.88 × 10−1	2.74 × 100	4.82 × 100
DS8	${ℝ}^C$	97.50	87.62	60.30	75.77	96.37	77.20	93.10	69.05
	SD	1.04 × 100	7.35 × 100	2.03 × 101	2.81 × 100	3.44 × 10−1	4.81 × 100	9.09 × 10−1	4.70 × 101
DS9	${ℝ}^C$	89.67	89.40	73.55	82.63	88.97	83.97	89.10	88.46
	SD	2.96 × 10−1	1.41 × 100	7.60 × 100	1.73 × 100	4.56 × 10−1	2.20 × 100	3.14 × 10−1	1.56 × 101
DS10	${ℝ}^C$	75.14	75.43	70.94	72.33	75.14	72.04	75.71	72.20
	SD	2.32 × 10−1	2.36 × 10−1	3.89 × 100	8.16 × 10−1	2.36 × 10−1	4.08 × 10−1	1.08 × 100	0.00 × 100
DS11	${ℝ}^C$	98.55	93.20	80.35	92.85	95.87	85.23	94.48	71.28
	SD	1.29 × 100	1.01 × 101	5.53 × 100	3.20 × 100	1.34 × 100	6.40 × 100	6.71 × 10−1	1.11 × 101
DS12	${ℝ}^C$	54.39	45.73	13.22	15.97	41.17	13.74	49.06	45.61
	SD	1.04 × 101	1.32 × 101	1.14 × 101	4.39 × 100	2.06 × 101	2.05 × 100	1.88 × 100	1.49 × 101
DS13	${ℝ}^C$	91.18	86.96	65.06	80.78	89.42	81.46	89.82	77.00
	SD	1.50 × 100	2.31 × 100	4.63 × 100	1.93 × 100	1.15 × 10−1	4.05 × 100	7.02 × 10−1	2.70 × 101
DS14	${ℝ}^C$	29.02	28.50	24.34	27.20	29.02	24.86	27.94	21.33
	SD	9.90 × 10−3	3.03 × 100	2.29 × 100	2.13 × 100	4.35 × 10−15	6.06 × 10−1	3.03 × 100	6.06 × 10−1
DS15	${ℝ}^C$	76.63	71.16	33.35	52.30	75.57	35.53	69.50	33.74
	SD	3.67 × 10−1	1.30 × 100	3.48 × 101	2.20 × 100	8.15 × 100	1.10 × 10−1	8.03 × 100	2.55 × 101
DS16	${ℝ}^C$	100.00	98.48	73.96	96.07	99.46	92.71	99.68	63.37
	SD	0.00 × 100	1.90 × 10−1	6.01 × 100	6.59 × 10−1	0.00 × 100	8.71 × 100	1.58 × 10−1	1.46 × 101
$\#B{ℝ}^C$		12	2	0	0	1	0	2	0
w/t/l		-	13/0/3	16/0/0	16/0/0	14/2/0	16/0/0	13/0/3	16/0/0

Table 12. The ${ℝ}^C$ and SD values produced by ANN models trained by the proposed MSPSOTLP and other PSO variants when solving the testing samples.

Dataset	Criteria	MSPSOTLP	PSO	PSOWV	CSO	MPSOWV	SLPSO	PSOGSA	APSO
DS1	${ℝ}^C$	100.00	99.67	56.67	88.33	97.33	92.33	87.67	16.67
	SD	0.00 × 100	1.49 × 100	3.16 × 101	2.23 × 101	0.00 × 100	0.00 × 100	3.35 × 101	4.88 × 101
DS2	${ℝ}^C$	50.00	47.68	35.80	40.73	47.83	37.10	49.28	55.22
	SD	7.64 × 10−1	6.48 × 10−1	1.51 × 101	7.67 × 100	1.45 × 100	1.35 × 101	5.23 × 100	3.89 × 100
DS3	${ℝ}^C$	58.53	58.53	60.67	63.80	65.33	65.47	49.73	63.13
	SD	2.81 × 10−1	1.19 × 101	1.27 × 101	2.40 × 100	4.37 × 100	7.70 × 10−1	4.23 × 100	2.31 × 100
DS4	${ℝ}^C$	80.37	75.93	61.30	75.00	77.22	72.78	73.15	42.04
	SD	1.56 × 100	3.85 × 100	2.38 × 101	2.14 × 100	1.07 × 100	3.21 × 100	3.85 × 100	1.57 × 101
DS5	${ℝ}^C$	72.50	60.00	51.88	55.63	60.63	60.63	53.13	46.88
	SD	3.23 × 100	3.61 × 100	7.22 × 100	1.30 × 101	9.55 × 100	1.08 × 101	0.00 × 100	1.44 × 101
DS6	${ℝ}^C$	90.28	76.94	34.44	61.11	82.50	42.78	83.06	16.11
	SD	1.46 × 100	3.21 × 100	1.58 × 101	8.93 × 100	2.78 × 100	1.79 × 101	6.99 × 100	4.01 × 101
DS7	${ℝ}^C$	73.82	72.55	59.46	65.09	70.73	66.36	66.91	69.27
	SD	9.39 × 10−1	1.05 × 100	7.57 × 100	3.15 × 100	1.05 × 100	4.81 × 100	2.78 × 100	4.58 × 100
DS8	${ℝ}^C$	100.00	78.33	30.24	32.86	96.19	40.24	74.29	54.76
	SD	7.53 × 10−1	5.22 × 101	3.23 × 101	5.23 × 101	3.71 × 101	2.75 × 100	4.76 × 100	4.81 × 101
DS9	${ℝ}^C$	84.57	82.39	67.75	76.38	82.54	87.31	87.05	86.86
	SD	6.87 × 10−1	2.54 × 100	0.00 × 100	3.16 × 100	2.09× 100	2.09 × 100	3.83 × 100	1.51 × 101
DS10	${ℝ}^C$	78.69	78.03	68.85	73.12	78.53	76.39	67.38	78.53
	SD	0.00 × 100	0.00 × 100	4.41 × 101	1.64 × 100	0.00 × 100	5.91 × 100	1.46 × 101	1.89 × 100
DS11	${ℝ}^C$	84.19	67.21	38.84	48.37	54.19	42.79	47.67	40.47
	SD	1.05 × 101	4.65 × 100	3.55 × 100	4.65 × 100	1.28 × 101	8.70 × 10−15	8.06 × 100	4.03 × 100
DS12	${ℝ}^C$	46.51	44.19	8.14	14.19	29.07	15.58	29.07	25.58
	SD	6.39 × 100	5.85 × 100	2.01 × 101	5.37 × 100	6.15 × 100	7.48 × 100	9.30 × 100	7.48 × 100
DS13	${ℝ}^C$	88.72	85.84	54.80	82.08	87.36	80.24	86.88	80.80
	SD	1.22 × 100	2.01 × 100	8.09 × 100	3.23 × 100	1.67 × 100	7.26 × 100	4.62 × 10−1	3.80 × 101
DS14	${ℝ}^C$	65.83	65.97	57.78	62.64	65.14	59.17	62.78	54.17
	SD	9.71 × 10−1	4.88 × 100	7.13 × 100	6.56 × 100	1.39 × 100	4.01 × 100	2.41 × 100	0.00 × 100
DS15	${ℝ}^C$	80.47	72.66	12.22	25.78	78.19	10.67	63.84	21.76
	SD	1.49 × 100	1.14 × 101	9.85 × 100	2.22 × 100	3.03 × 101	7.81 × 100	3.06 × 101	3.41 × 101
DS16	${ℝ}^C$	92.15	90.18	33.98	4.9	81.35	55.99	86.28	31.68
	SD	3.30 × 100	2.64 × 100	0 × 100	3.39 × 100	1.48 × 101	3.45 × 100	1.16 × 101	3.16 × 101
$\#B{ℝ}^C$		12	1	0	0	1	1	0	1
w/t/l		-	14/1/1	15/0/1	15/0/1	15/0/1	14/0/2	15/0/1	13/0/3

According to Table 11, ANN models trained by the proposed MSPSOTLP are reported to have the best performance for being able to solve 12 out of 16 sets of training samples with the best ${ℝ}^C$ values. Specifically, MSPSOTLP emerges as the best training algorithm for ANN models in dealing with datasets of Iris, Statlog Hearts, Hepatitis, Wine, Seeds, Australian Credit Approval, New Thyroid, Glass, Balance Scale, Dermatology, Landsat, and Bank Note. It is also noteworthy that the proposed MSPSOTLP is the only algorithm that has successfully trained ANN models with 100% of ${ℝ}^C$ values to classify the training sets of Wine and Bank Note. The ANN models trained by PSO and PSAGSA can occasionally deliver good performances by producing two best ${ℝ}^C$ values in solving training samples. Although the ${ℝ}^C$ values produced by ANN models trained by the proposed MSPSOSLP in classifying training samples of Liver Disorder, Blood Transfusion, Breast Cancer, and Haberman’s Survival are slightly lower than PSO and PSOGSA, the performance differences between these algorithms are marginal and not more than 1%. On the other hand, the ANN models trained by MSPSOTLP are reported to have more notable performance differences than PSO and PSOGSA in terms of ${ℝ}^C$ values when classifying the training samples of Iris, Statlog Heart, Hepatitis, Seeds, New Thyroid, Glass, and Landsat. The ANN models trained by PSOWV are reported to have the most inferior performance by producing eight worst and seven second-worst ${ℝ}^C$ values when solving all 16 classification datasets except for Landsat.

In addition to training samples, 30% of datasets are extracted as testing samples to evaluate the generalization performances of ANN models optimized by all compared PSO variants. According to Table 12, ANN models trained by the proposed MSPSOTLP are reported to have the best generalization performance for being able to produce 12 best and 2 s-best ${ℝ}^C$ values when classifying the testing samples of 16 selected datasets. Specifically, ANN models trained by MSPSOTLP successfully produce the best ${ℝ}^C$ in solving the testing samples of Iris, Statlog Heart, Hepatitis, Wine, Breast Cancer, Seeds, Haberman’s Survival, New Thyroid, Glass, Balance Scale, Landsat, and Bank Note. Moreover, MSPSOTLP is also reported to be the only algorithm that can train ANN models to solve the testing samples of Iris and Seeds with 100% of ${ℝ}^C$. On the other hand, the ANN models trained by PSO, MPSOWV, SLPSO, and APSO are reported to produce the best ${ℝ}^C$ values when classifying the testing samples of Dermatology, Blood Transfusion, Australian Credit Approval, and Liver Disorder, respectively. Although ANN models trained by MSPSOTLP are observed to produce relatively inferior ${ℝ}^C$ values in solving the testing samples of these four datasets, some performance differences are insignificant. On the contrary, ANN models trained by MSPSOTLP produce much better ${ℝ}^C$ values than PSO, MPSOWV, SLPSO, and APSO in solving the testing samples of certain datasets, such as Hepatitis, Wine, Seeds, New Thyroid, etc. The ANN models trained by PSOWV perform the worst by producing seven lowest ${ℝ}^C$ values (i.e., testing samples of Liver Disorder, Breast Cancer, Seeds, Australian Credit Approval, New Thyroid, Glass, and Balance Scale) and eight second-worst ${ℝ}^C$ values (i.e., testing samples of Iris, Statlog Heart, Hepatitis, Wine, Haberman’s Survival, Dermatology, Landsat, and Bank Note).

4.2.5. Non-Parametric Statistical Analyses

Similar to those reported in Section 4.1.5, the Wilcoxon signed rank test [68] is applied to perform a pairwise comparison between the proposed MSPSOTLP and the selected PSO variants based on the reported ${ℝ}^C$ values. The $R^{+}$, $R^{-}$, p, and h values produced by ANN models trained by the compared algorithms in classifying the training and testing samples are presented in Table 13 and Table 14, respectively. From Table 13, ANN models trained by the proposed MSPSOTLP have significantly better performance than those of other PSO variants at a significance level of $\alpha =0.05$, as indicated by the h value of “+”. Notably, the ANN model optimized by the proposed MSPSOTLP can completely dominate those of PSOWV, CSO, SLPSO, and APSO when solving the training samples of selected datasets. Similarly, ANN models trained by MSPSOTLP are observed to perform significantly better than other PSO variants in solving all testing samples of datasets chosen, as indicated by the h values of “+” in Table 14. These pairwise comparison results imply the excellent generalization ability of ANN model trained by MSPSOTLP due to its ability to handle unseen data of testing samples effectively.

Table 13. Wilcoxon signed rank test as a pairwise comparison between the ANN models optimized by MSPSOTLP and each PSO variant when classifying the training samples.

MSPSOTLP vs.	R+	R−	p Value	h Value
PSO	122.0	14.0	3.36 × 10−3	+
PSOWV	136.0	0.0	3.05 × 10−5	+
CSO	136.0	0.0	3.05 × 10−5	+
MPSOWV	119.0	1.0	1.22 × 10−4	+
SLPSO	136.0	0.0	3.05 × 10−5	+
PSOGSA	122.0	14.0	3.36 × 10−3	+
APSO	136.0	0.0	3.05 × 10−5	+

Table 14. Wilcoxon signed rank test as pairwise comparison between the ANN models optimized by MSPSOTLP and each PSO variant when classifying the testing samples.

MSPSOTLP vs.	R+	R−	p Value	h Value
PSO	134.0	2.0	9.16 × 10−5	+
PSOWV	135.0	1.0	6.10 × 10−5	+
CSO	134.0	2.0	9.16 × 10−5	+
MPSOWV	125.0	11.0	1.68 × 10−3	+
SLPSO	130.0	6.0	4.27 × 10−4	+
PSOGSA	133.0	3.0	1.53 × 10−4	+
APSO	125.0	11.0	1.68 × 10−3	+

Apart from pairwise comparison, multiple comparisons among the ANN models trained by all compared algorithms are also conducted by Friedman Test [67]. The average ranking values produced by the ANN models trained by all compared algorithms in solving training and testing samples are reported in Table 15 and Table 16, respectively. Table 15 shows that the ANN models trained by MSPSOTLP score the best average ranking when classifying the training datasets, followed by PSOGSA, PSO, MPSOWV, CSO, SLPSO, APSO, and PSOWV. Although Table 7 reports that MPSOWV has a relatively poor ranking in solving CEC 2014 benchmark functions, it performs relatively well in training ANN models in solving training samples. Conversely, CSO does not perform well in training the ANN model despite producing relatively competitive performance in solving CEC 2014 benchmark functions. Table 16 reveals that the ANN model trained by MSPSOTLP has the best average ranking value in classifying the testing samples, followed by MPSOWV, PSO, PSOGSA, SLPSO, CSO, APSO, and PSOWV. Similarly, MPSOWV shows its competitive performance in training the ANN model, despite having inferior performance in solving CEC 2014 benchmark functions. Although the ANN model trained by PSOGSA has the second-best average ranking in solving training samples, as reported in Table 15, it does not perform well in solving testing samples, as reported in Table 16, implying the tendency of PSAGSA to produce the ANN models that suffer with overfitting issues and have poor generalization performance to handle unseen data.

Table 15. The average ranking values of ANN models are trained by all compared algorithms in solving training samples.

Algorithm	Ranking	Chi-Square Statistics	p Value
MSPSOTLP	1.4688	94.875000	0.00 × 100
PSOGSA	2.8125
PSO	2.8750
MPSOWV	2.9062
CPSO	5.5312
SLPSO	5.9062
APSO	6.9375
PSOWV	7.5625

Table 16. The average ranking values of ANN models are trained by all compared algorithms in solving testing samples.

Algorithm	Ranking	Chi-Square Statistics	p value
MSPSOTLP	1.6250	59.864583	0.00 × 100
MPSOWV	2.9688
PSO	3.3750
PSOGSA	4.4688
SLPSO	5.2188
CSO	5.3125
APSO	5.7188
PSOWV	7.3125

Referring to the p values reported in Table 15 and Table 16, significant global performance differences among the ANN models trained by all compared algorithms to solve training and testing samples are observed at a significance level of $\alpha =0.05$. The concrete differences between the ANN models trained by MSPSOTLP and other PSO variants in classifying the training and testing samples are further analyzed using the Bonferroni-Dunn, Holm, and Hochberg procedures, as shown in Table 17 and Table 18, respectively. According to the APVs for solving training samples, as reported in Table 17, all post-hoc procedures confirm the significant performance improvement of ANN models trained by MSPSOTLP against those of PSOWV, APSO, SLPSO, and CPSO at $\alpha =0.05$. On the other hand, all post-hoc procedures can detect the significant performance improvement of ANN models trained by MSPSOTLP against those of PSOWV, APSO, CSO, SLPSO, and PSOGSA in solving testing samples, as indicated by the APVs values in Table 18.

Table 17. Adjusted p values produced by trained ANN models in solving training samples through three post-hoc analysis procedures.

MSPSOTLP vs.	z	Unadjusted p	Bonferroni-Dunn p	Holm p	Hochberg p
PSOWV	7.04 × 100	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100
APSO	6.31 × 100	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100
SLPSO	5.12 × 100	0.00 × 100	2.00 × 10−6	1.00 × 10−5	1.00 × 10−5
CSO	4.69 × 100	3.00 × 10−6	1.70 × 10−5	1.10 × 10−5	1.10 × 10−5
MPSOWV	1.66 × 100	9.69 × 10−2	6.79 × 10−1	2.91 × 10−1	1.21 × 10−1
PSO	1.62 × 100	1.04 × 10−1	7.31 × 10−1	2.91 × 10−1	1.21 × 10−1
PSOGSA	1.55 × 100	1.21 × 10−1	8.45 × 10−1	2.91 × 10−1	1.21 × 10−1

Table 18. Adjusted p values produced by trained ANN models in solving testing samples through three post-hoc analysis procedures.

MSPSOTLP vs.	z	Unadjusted p	Bonferroni-Dunn p	Holm p	Hochberg p
PSOWV	6.57 × 100	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100
APSO	4.73 × 100	0.00 × 100	1.60 × 10−5	1.40 × 10−5	1.40 × 10−5
CSO	4.26 × 100	2.10 × 10−5	1.44 × 10−4	1.03 × 10−4	1.03 × 10−4
SLPSO	4.15 × 100	3.30 × 10−5	2.33 × 10−4	1.33 × 10−4	1.33 × 10−4
PSOGSA	3.28 × 100	1.03 × 10−3	7.17 × 10−3	3.07 × 10−3	3.07 × 10−3
PSO	2.02 × 100	4.33 × 10−2	3.03 × 10−1	8.66 × 10−1	8.66 × 10−1
MPSOWV	1.55 × 100	1.21 × 10−1	8.45 × 10−1	1.21 × 10−1	1.21 × 10−1

5. Conclusions

This study proposes a new PSO variant known as multi-swarm-based particle swarm optimization with two-level learning phases (MSPSOTLP) to address the potential drawbacks of PSOWV. Three significant modifications are introduced into the proposed MSPSOTLP to ensure that proper balancing of the exploration and exploitation searches of the algorithm can be achieved in handling more challenging optimization problems, including the training process of the ANN model. A new population initialization scheme, the CSOBL initialization scheme, is incorporated to replace the conventional random initialization scheme in generating initial solutions with better diversity and broader coverage in the solution space. Both multiswarm and social learning concepts are incorporated into the primary learning phase of MSPSOTLP to guide the search process of particles more effectively without losing population diversity by leveraging the directional information contributed by other non-fittest particles in the population. Additionally, a secondary learning phase is introduced with the adoption of two search operators with different levels of exploration and exploitation strengths, aiming to address the limitations of a single search operator adopted by many existing PSO variants. Extensive simulation studies report that the proposed MSPSOTLP outperforms the selected seven PSO variants in solving benchmark problems from CEC 2014 by producing 18 best mean fitness values out of 30 functions. Moreover, the training process of the ANN model is also formulated as an optimization problem, where the objective is to produce the optimal values of weights and biases and the selection of activation functions. The proposed MSPSOTLP is reported to have the best overall performance in training ANN models to solve classification datasets extracted from the UCI machine learning repository.

While MSPSOTLP has demonstrated competitive performances to solve the CEC 2014 benchmark functions and train ANN model for classifying UCI machine learning datasets, the proposed work still has room for improvement in terms of its search mechanisms and potential real-world applications. First, the main population of MSPSOTLP is divided by the reference-point-based population division scheme into a predefined number of subswarms during the primary learning phase. It is nontrivial to determine the optimal subswarm numbers for optimization problems with different types of fitness landscapes. Second, the solution update process of MSPSOTLP is performed by comparing the fitness values of current and new particles. It is noteworthy that such a greedy selection scheme tends to suppress the survival of novel particles that might have temporary poor performances at the earlier stage of search process, but can contribute for long-term success if given sufficient iteration numbers. Third, the performance of the ANN optimized by MSPSOTLP is currently evaluated using the datasets obtained from a public database. Despite exhibiting promising classification accuracy in most selected datasets, the feasibility of the proposed method to solve more challenging real-world classification and regression problems remains unexplored. Some potential future works are then suggested to address these aforementioned limitations. First, the population division scheme of MSPSOTLBP can be further enhanced such that the optimal subswarm numbers can be determined adaptively based on the types of fitness landscapes encountered by the population. Second, other criteria, such as the fitness improvement rate and population diversity, should be considered by MSPSOTLP during the solution update process to preserve the novel particles that can bring long-term success for the algorithm. Finally, it is worth it to investigate the feasibility of ANN optimized by MSPSOTLP to address challenging issues encountered in the intelligent condition monitoring of complex industrial systems [2], such as the remaining useful life prediction of gear pumps [72], the time series prognosis of fuel cells [73], and predictive maintenance of renewable energy systems [74].