Fault Diagnosis Using Dynamic Principal Component Analysis and GA Feature Selection Modeling for Industrial Processes
Abstract
1. Introduction
- (1)
- First, the feature selection based on genetic algorithm is adopted, which can quickly find the optimal feature subset, which not only refines the original data, but also loses the integrity of the data as little as possible.
- (2)
- The data matrix after feature selection is extended with time delay and the residual space of feature selection is added, which effectively considers the autocorrelation and integrity of the data.
- (3)
- Sliding window filtering technology is adopted to remove the noise existing in the data itself.
- (4)
- An experimental comparative study of the proposed method and existing methods is carried out using the Tennessee Eastman process and the actual coking process.
2. PCA and DPCA
3. GA-DPCA
3.1. Sliding Window Removal Noise
3.2. Feature Selection Based on GA
3.2.1. Initializing the Population
3.2.2. Calculating Fitness
- After decoding the individual code string, the individual phenotype can be obtained.
- The objective function value of the corresponding individual can be calculated from the individual’s phenotype.
- According to the type of optimization problem, the fitness of individuals can be calculated from the objective function value according to certain transformation rules.
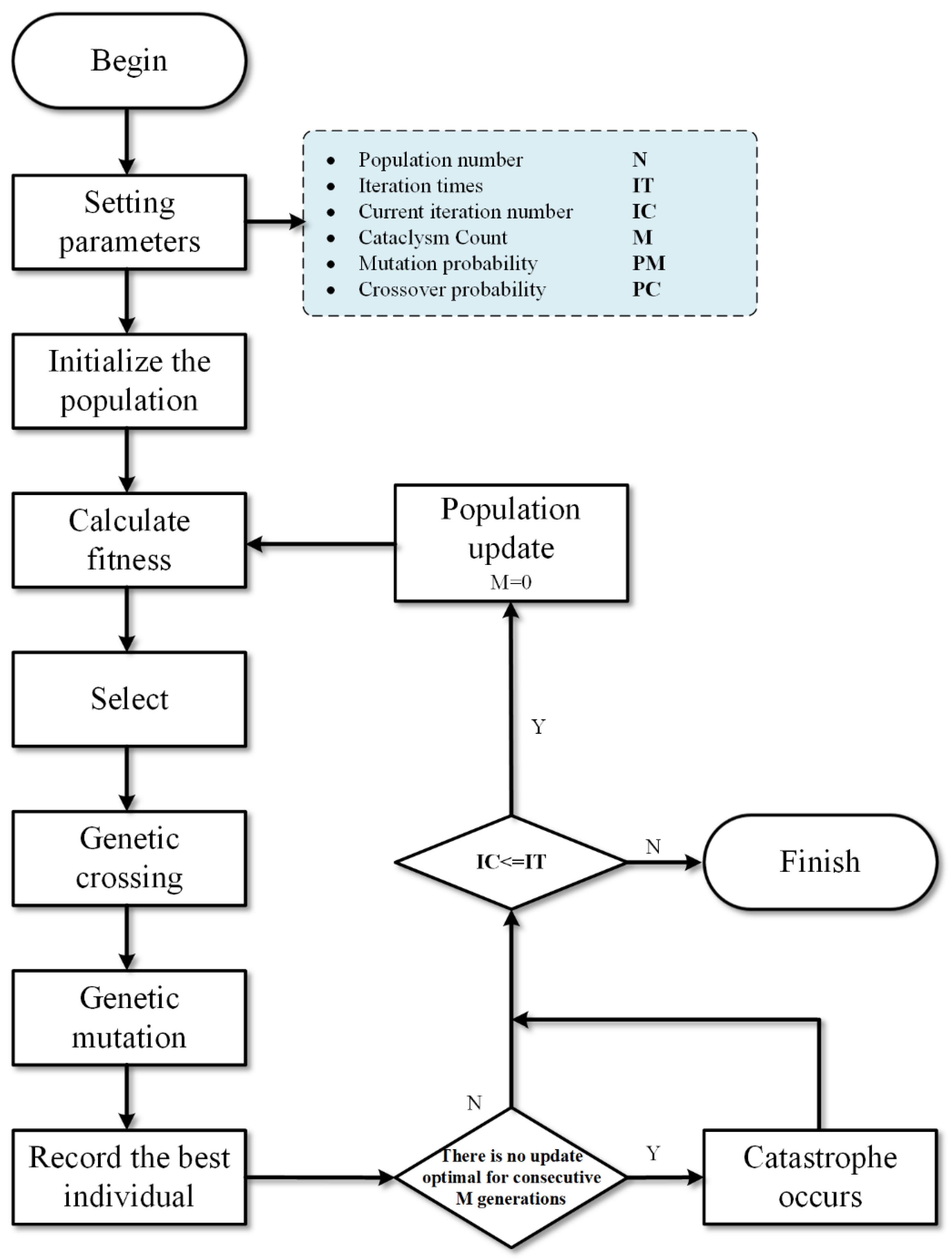
3.2.3. Setting up Genetic Strategies
- (1)
- Elite selection strategy
- (2)
- Gene crossover strategy
- (3)
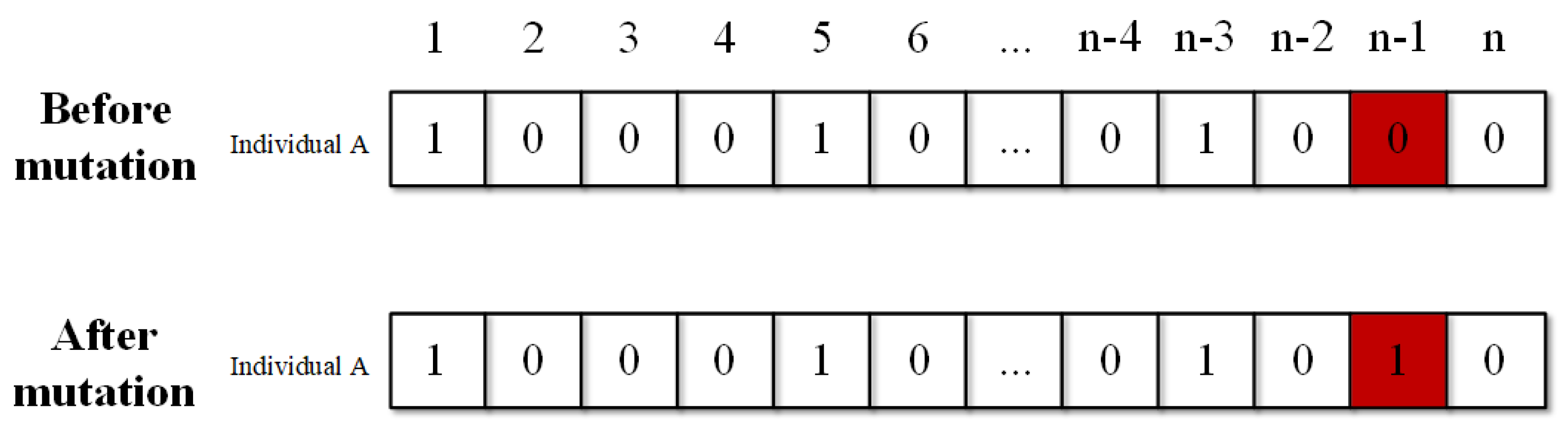
- Gene mutation strategy
- (4)
- Catastrophe Strategy
3.2.4. Update Iteration
3.3. Offline Modeling
- (1)
- Collect the data of normal operation of the chemical process and conduct sliding window denoising on the data to obtain . Then, due to the inconsistency of different variable units of process data, the data needs to be standardized. The standardization process is as follows:where represents the mean matrix established by the mean of each variable in the data and represents the normalized process data matrix.
- (2)
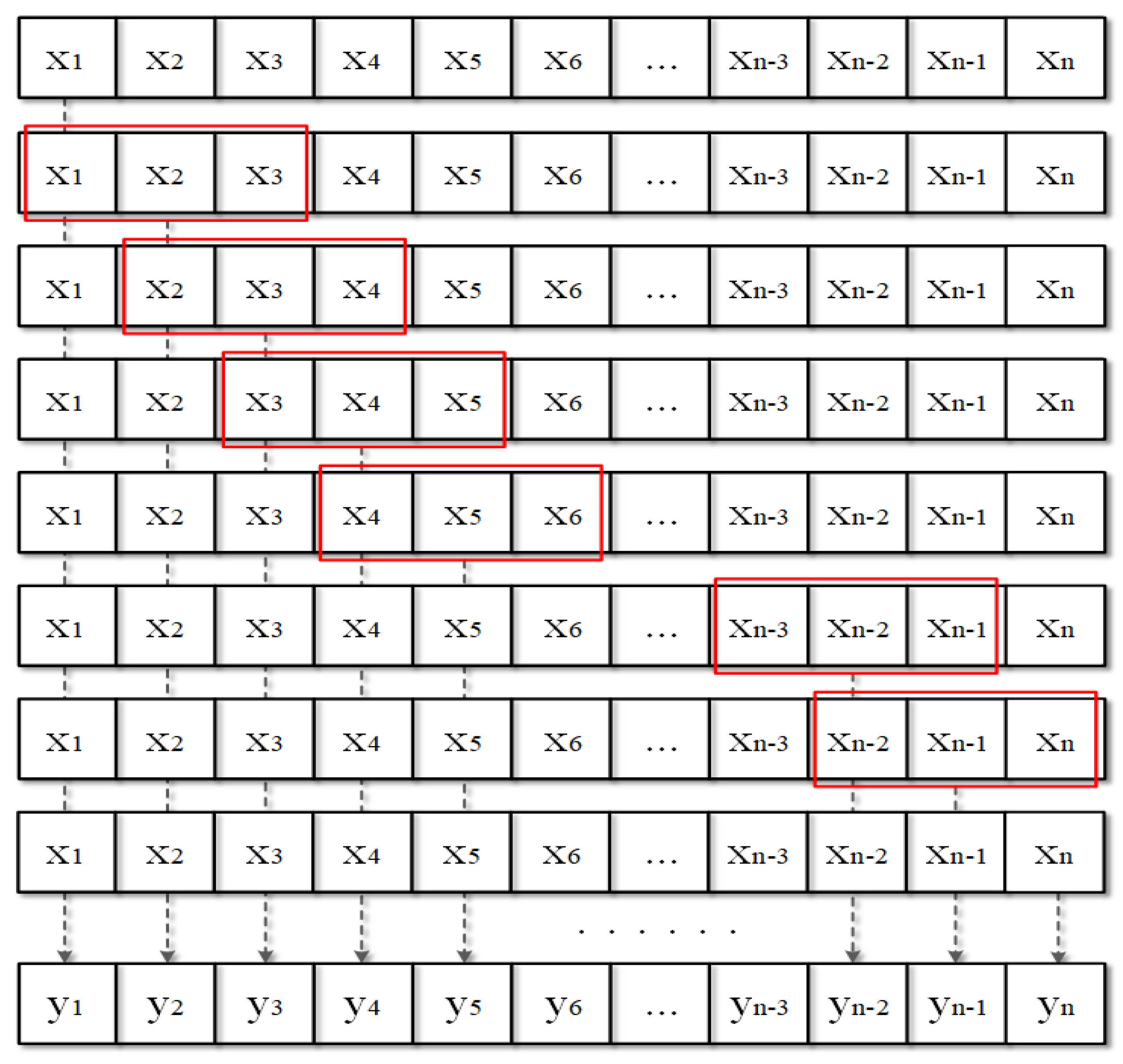
- Overlay the standardized data with observations from previous L moments to construct a new data matrix, , for DGLPP. L is the delay parameter, which is generally 1 or 2 depending on the actual situation. represents data delayed to L steps and selected for features. represents residual data for feature selection.
- (3)
- Establish a monitoring model based on DPCA according to Formulas (1)–(4).
- (4)
- Calculate T2 and Q statistics according to Formulas (5) and (6).
3.4. Determining Control Limits
3.5. Online Monitoring
- (1)
- Collect abnormal data in the process of chemical industry and obtain by sliding window denoising, then standardize the data by using Formula (12). Finally, the new data sample required for DGLPP is constructed as .
- (2)
- Using the projection matrix A obtained from the offline process and the newly acquired data, an online monitoring model based on DPCA is established:where is the vector after projection, is the residual vector, and A is the projection matrix.
- (3)
- Calculate T2 and Q statistics according to Formulas (5) and (6).
- (4)
- Compare with the control limit established in offline modeling to determine whether there is a fault.
3.6. Fault Diagnosis
4. Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Zhou, D.-H.; Si, X.; Chen, M.-Y.; Xu, C.-H. Review of incipient fault diagnosis methods. Kongzhi Lilun Yu Yingyong/Control Theory Appl. 2012, 29, 1517–1529. [Google Scholar]
- Zhang, R.; Peng, Z.; Wu, L.; Yao, B.; Guan, Y. Fault Diagnosis from Raw Sensor Data Using Deep Neural Networks Considering Temporal Coherence. Sensors 2017, 17, 549. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Cui, Y.; Wu, F.; Zhang, R. Fault Monitoring of Chemical Process Based on Sliding Window Wavelet DenoisingGLPP. Processes 2021, 9, 86. [Google Scholar] [CrossRef]
- Liu, K.; Lu, N.; Wu, F.; Zhang, R.; Gao, F. Model Fusion and Multiscale Feature Learning for Fault Diagnosis of Industrial Processes. IEEE Trans. Cybern. 2022, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Yang, F.; Zhang, R.; Gao, F. Intelligent Fault Diagnosis for Chemical Processes Using Deep Learning Multimodel Fusion. IEEE Trans. Cybern. 2022, 52, 7121–7135. [Google Scholar] [CrossRef]
- Lei, Y.; Jiang, W.; Jiang, A.; Zhu, Y.; Niu, H.; Zhang, S. Fault Diagnosis Method for Hydraulic Directional Valves Integrating PCA and XGBoost. Processes 2019, 7, 589. [Google Scholar] [CrossRef]
- Kim, J.; Lee, T.; Lee, S.; Lee, J.; Lee, W.; Kim, Y.; Park, J. A Study on Deep Learning-Based Fault Diagnosis and Classification for Marine Engine System Auxiliary Equipment. Processes 2022, 10, 1345. [Google Scholar] [CrossRef]
- Xu, X.; Feng, J.; Wang, H.; Zhang, N.; Wang, X. Dynamics Analysis of Misalignment and Stator Short-Circuit Coupling Fault in Electric Vehicle Range Extender. Processes 2020, 8, 1037. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, Z.; Xie, Y. Automatic multi-fault recognition in TFDS based on convolutional neural network. Neurocomputing 2017, 222, 127–136. [Google Scholar] [CrossRef]
- Pilario, K.E.; Shafiee, M.; Cao, Y.; Lao, L.; Yang, S.-H. A Review of Kernel Methods for Feature Extraction in Nonlinear Process Monitoring. Processes 2020, 8, 24. [Google Scholar] [CrossRef]
- Chang, Y.W.; Wang, Y.C.; Tao, L.; Wang, Z.J. Fault diagnosis of a mine hoist using PCA and SVM techniques. J. China Univ. Min. Technol. 2008, 18, 327–331. [Google Scholar] [CrossRef]
- Li, C.-H.; Kuo, B.-C.; Lin, C.-T. LDA-Based Clustering Algorithm and Its Application to an Unsupervised Feature Extraction. IEEE Trans. Fuzzy Syst. 2011, 19, 152–163. [Google Scholar] [CrossRef]
- Liu, C.; Wechsler, H. Independent component analysis of Gabor features for face recognition. IEEE Trans. Neural. Netw. 2003, 14, 919–928. [Google Scholar]
- Nomikos, P.; MacGregor, J.F. Monitoring batch processes using multiway principal component analysis. AIChE J. 1994, 40, 1361–1375. [Google Scholar] [CrossRef]
- Nomikos, P.; MacGregor, J.F. Multi-way partial least squares in monitoring batch processes. Chemom. Intell. Lab. Syst. 1995, 30, 97–108. [Google Scholar] [CrossRef]
- Ku, W.; Storer, R.H.; Georgakis, C. Disturbance detection and isolation by dynamic principal component analysis. Chemom. Intell. Lab. Syst. 1995, 30, 179–196. [Google Scholar] [CrossRef]
- Choi, S.W.; Lee, C.; Lee, J.-M.; Park, J.H.; Lee, I.-B. Fault detection and identification of nonlinear processes based on kernel PCA. Chemom. Intell. Lab. Syst. 2005, 75, 55–67. [Google Scholar] [CrossRef]
- Cao, L.J.; Chua, K.S.; Chong, W.K.; Lee, H.P.; Gu, Q.M. A comparison of PCA, KPCA and ICA for dimensionality reduction in support vector machine. Neurocomputing 2003, 55, 321–336. [Google Scholar] [CrossRef]
- Joe Qin, S.; Dunia, R. Determining the Number of Principal Components for Best Reconstruction. IFAC Proc. Vol. 1998, 31, 357–362. [Google Scholar] [CrossRef]
- MacGregor, J. Multivariate Statistical Approaches to Fault Detection and Isolation. IFAC Proc. Vol. 2003, 36, 549–554. [Google Scholar] [CrossRef]
- Lee, J.-M.; Yoo, C.; Lee, I.-B. Statistical process monitoring with independent component analysis. J. Process Control. 2004, 14, 467–485. [Google Scholar] [CrossRef]
- Chen, Y.; Zi, Y.; Cao, H.; He, Z.; Sun, H. A data-driven threshold for wavelet sliding window denoising in mechanical fault detection. Sci. China Technol. Sci. 2014, 57, 589–597. [Google Scholar] [CrossRef]
- Yongguo, L. Feature Subset Selection Based on Genetic Algorithm. Comput. Eng. 2003, 29, 19–20. [Google Scholar]
- ElAlami, M.E. A filter model for feature subset selection based on genetic algorithm. Knowl. Based Syst. 2009, 22, 356–362. [Google Scholar] [CrossRef]
- Iba, K. Reactive power optimization by genetic algorithm. IEEE Trans. Power Syst. 1994, 9, 685–692. [Google Scholar] [CrossRef]
- Lingaraj, H. A Study on Genetic Algorithm and its Applications. Int. J. Comput. Sci. Eng. 2016, 4, 139–143. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Xiaohang, C.; Huifeng, X. Design of Elitist Adaptive Genetic Algorithm in Arrival Aircrafts Scheduling. Comput. Commun. 2006, 24, 91–94. [Google Scholar]
- Liao, M. Study on the Effect of Cataclysm Operator on Genetic Algorithm. Comput. Eng. Appl. 2005, 41, 54–57. [Google Scholar]
- Peng, Z. A Partheno-genetic Algorithm Based on Cataclysm. J. Hubei Automot. Ind. Inst. 2007, 2, 19–21. [Google Scholar]
- Crammer, K.; Singer, Y. On the Learnability and Design of Output Codes for Multiclass Problems. Mach. Learn. 2002, 47, 201–233. [Google Scholar] [CrossRef]
- Lyman, P.R.; Georgakis, C. Plant-wide control of the Tennessee Eastman problem. Comput. Chem. Eng. 1995, 19, 321–331. [Google Scholar] [CrossRef]
- Wang, H.; Song, Z.; Hui, W. Statistical process monitoring using improved PCA with optimized sensor locations. J. Process Control. 2002, 12, 735–744. [Google Scholar] [CrossRef]
- Wang, H.; Song, Z.; Ping, L.I. Improved PCA with application to process monitoring and fault diagnosis. J. Chem. Ind. Eng. 2001, 52, 471–475. [Google Scholar]
- Wang, K.; Chen, J.; Song, Z. Performance Analysis of Dynamic PCA for Closed-Loop Process Monitoring and Its Improvement by Output Oversampling Scheme. IEEE Trans. Control. Syst. Technol. 2019, 27, 378–385. [Google Scholar] [CrossRef]



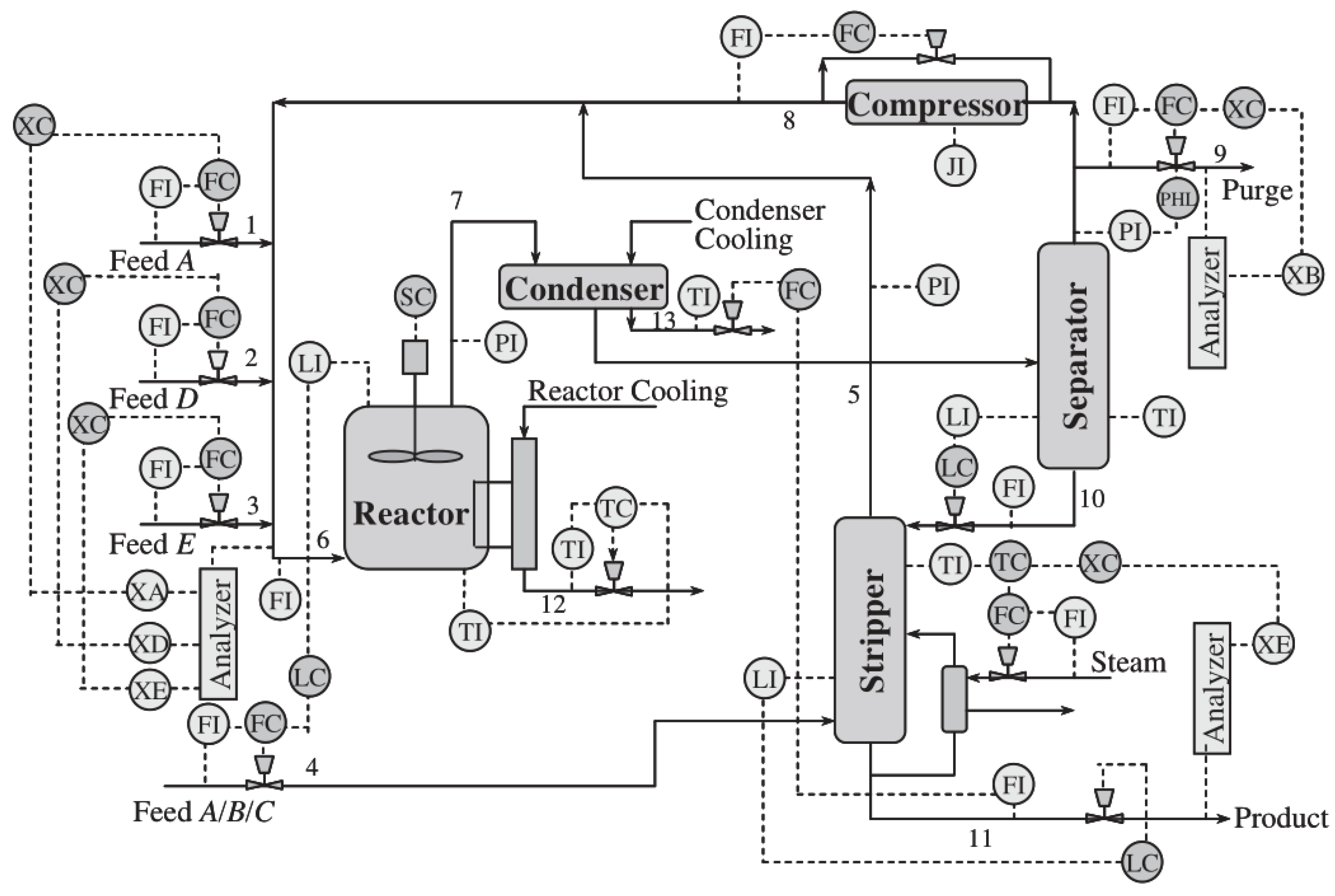
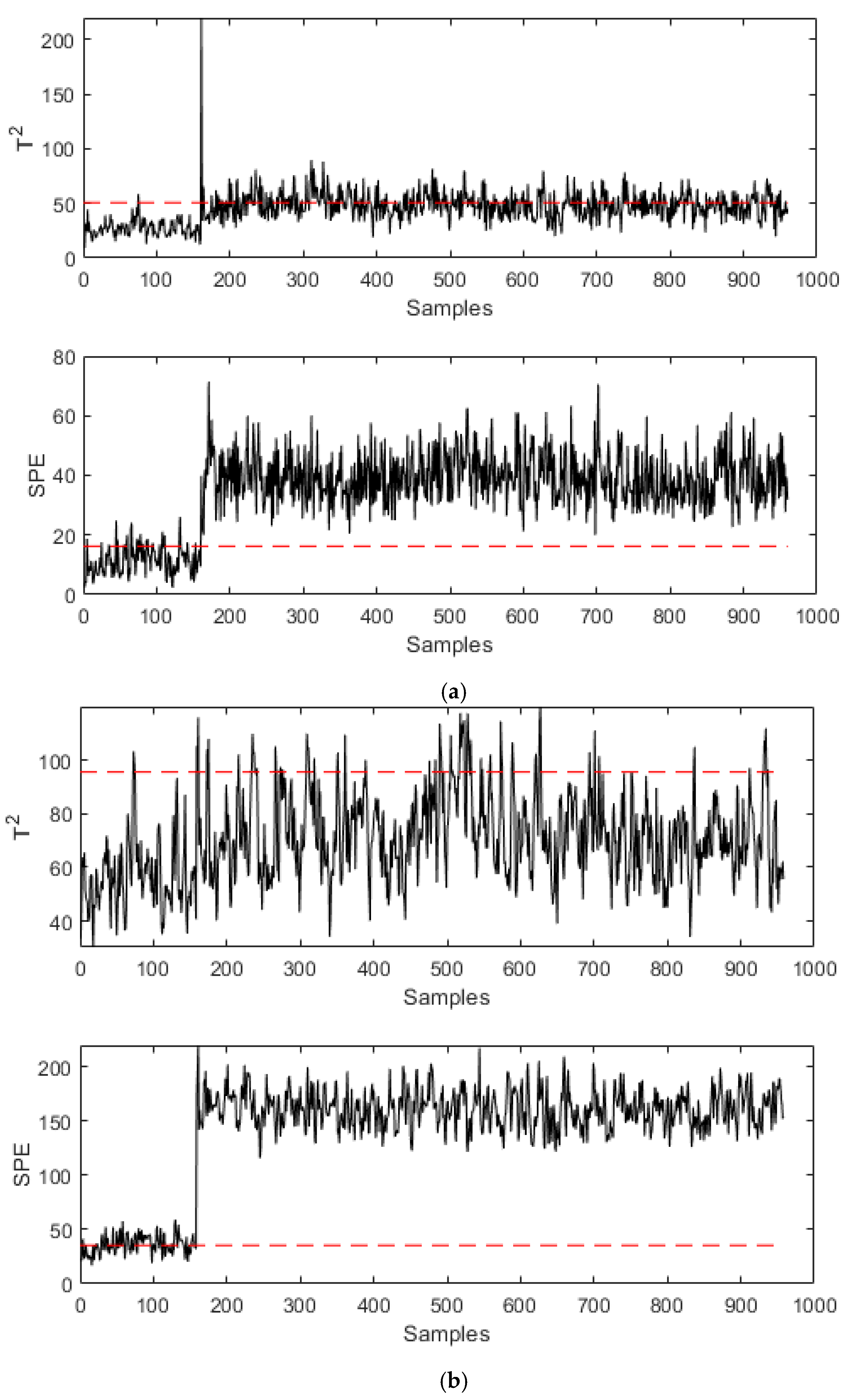
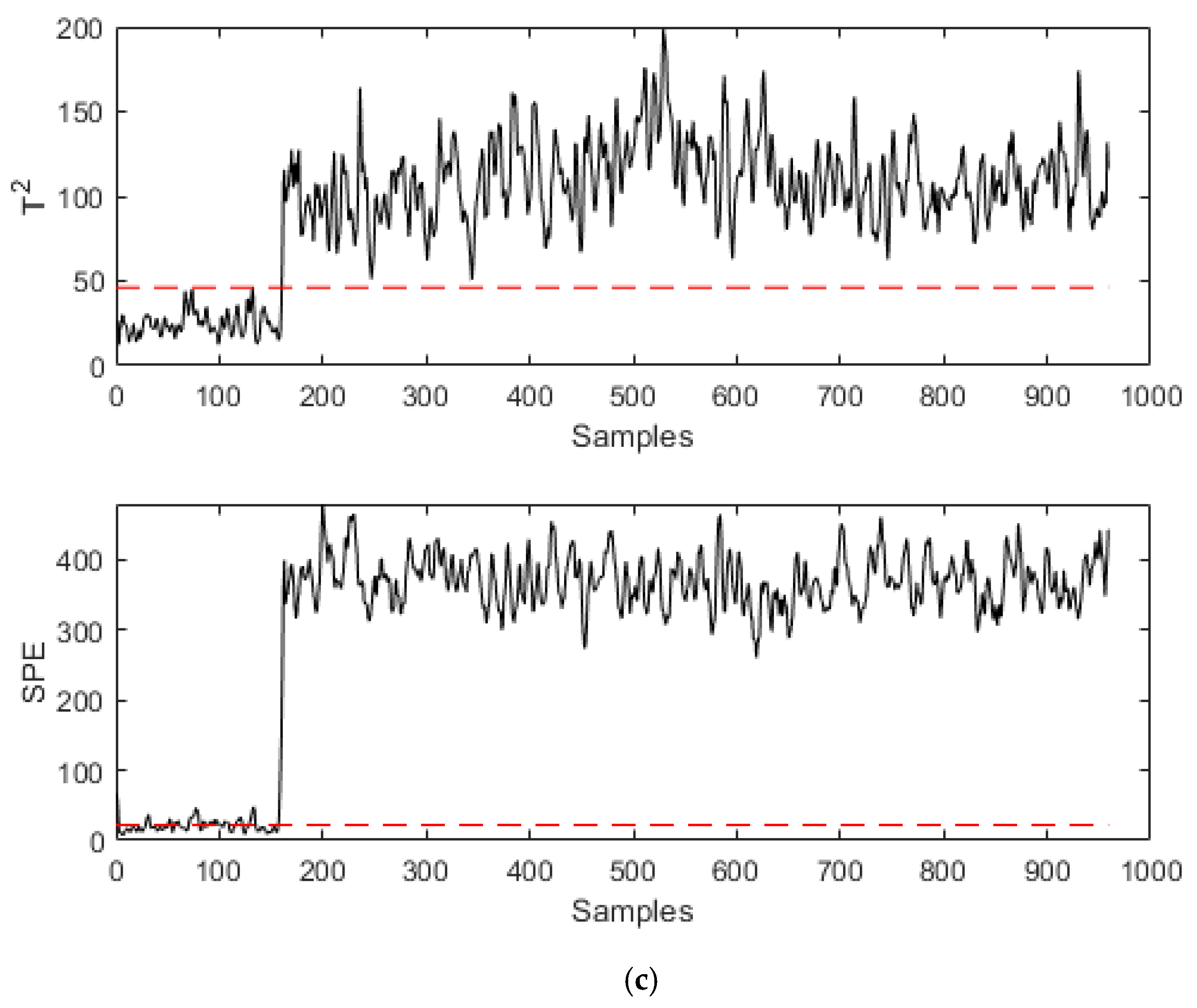


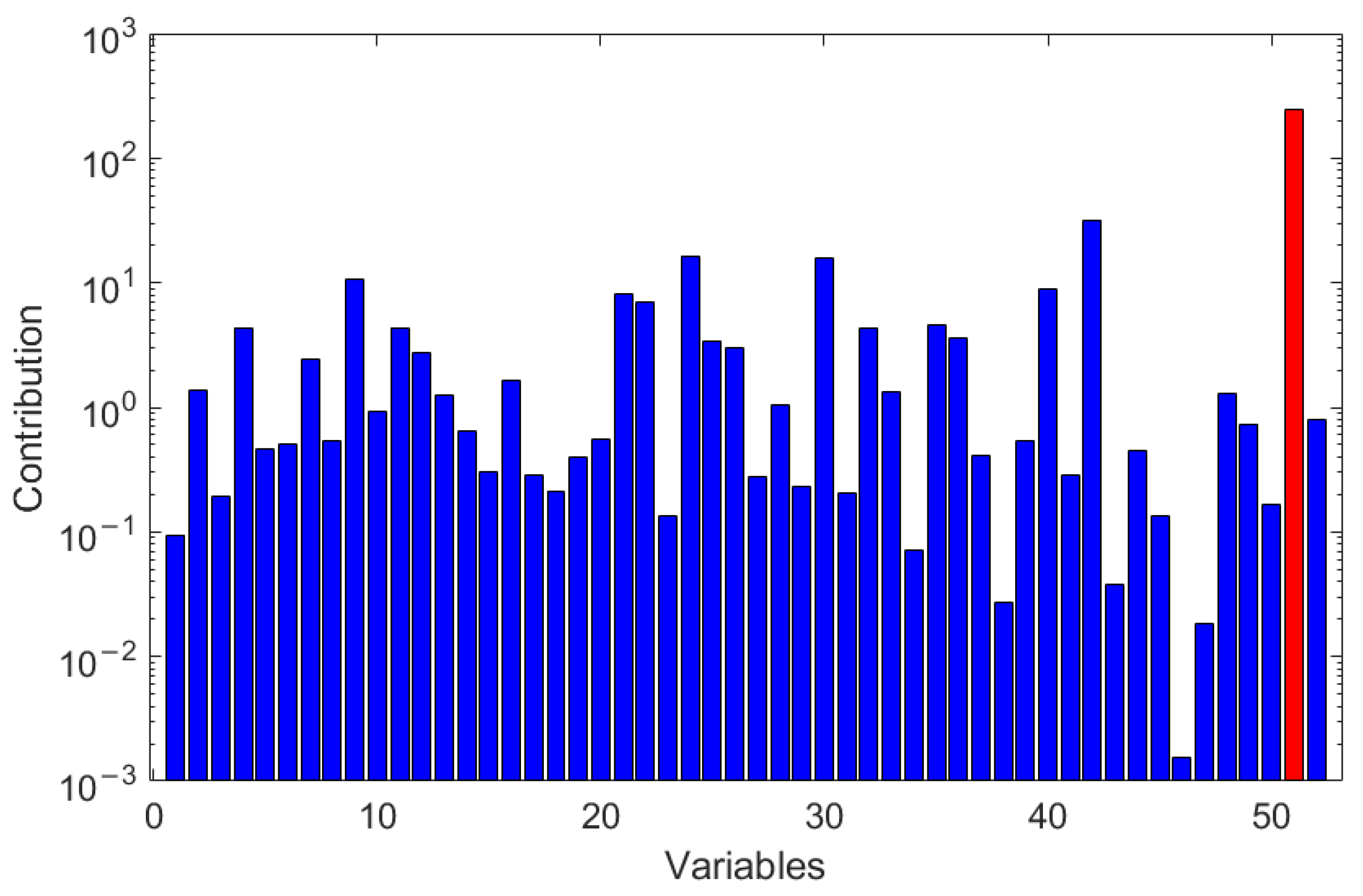

| No. | Variables | No. | Variables |
|---|---|---|---|
| 1 | A feed (stream 1) | 27 | Ingredient E (stream 6) |
| 2 | D feed (stream 2) | 28 | Ingredient F (stream 6) |
| 3 | E feed (stream 3) | 29 | Ingredient A (stream 9) |
| 4 | Total feed (stream 4) | 30 | Ingredient B (stream 9) |
| 5 | Recycle flow (stream 8) | 31 | Ingredient C (stream 9) |
| 6 | Reactor feed rate (stream 6) | 32 | Ingredient D (stream 9) |
| 7 | Reactor pressure | 33 | Ingredient E (stream 9) |
| 8 | Reactor level | 34 | Ingredient F (stream 9) |
| 9 | Reactor temperature | 35 | Ingredient G (stream 9) |
| 10 | Purge rate (stream 9) | 36 | Ingredient H (stream 9) |
| 11 | Product separator temperature | 37 | Ingredient D (stream 11) |
| 12 | Product separator level | 38 | Ingredient E (stream 11) |
| 13 | Product separator pressure | 39 | Ingredient F (stream 11) |
| 14 | Product separator underflow (stream 10) | 40 | Ingredient G (stream 11) |
| 15 | Stripper level | 41 | Ingredient H (stream 11) |
| 16 | Stripper pressure | 42 | D feed flow valve (stream 2) |
| 17 | Stripper underflow (stream 11) | 43 | E feed flow valve (stream 3) |
| 18 | Stripper temperature | 44 | A feed flow valve (stream 1) |
| 19 | Stripper steam Flow | 45 | Total feed flow valve (stream4) |
| 20 | Compressor work | 46 | Compressor recycle valve |
| 21 | Reactor cooling water outlet temperature | 47 | Purge valve (stream 9) |
| 22 | Separator cooling water outlet temperature | 48 | Separator pot liquid flow valve (stream 10) |
| 23 | Ingredient A (stream 6) | 49 | Stripper liquid product flow valve (stream 11) |
| 24 | Ingredient B (stream 6) | 50 | Stripper steam valve |
| 25 | Ingredient C (stream 6) | 51 | Reactor cooling water flow |
| 26 | Ingredient D (stream 6) | 52 | Condenser cooling water flow |
| Fault Number | Process Variable | Type |
|---|---|---|
| 1 | A/C feed ratio, B composition constant (stream 4) | Step |
| 2 | B composition, A/C ratio constant (stream 4) | Step |
| 3 | D feed temperature (stream 2) | Step |
| 4 | Reactor cooling water inlet temperature | Step |
| 5 | Condenser cooling water inlet temperature | Step |
| 6 | A feed loss (stream 1) | Step |
| 7 | C header pressure loss-reduced availability (stream 4) | Step |
| 8 | A, B, C feed composition (stream 4) | Random variation |
| 9 | D feed temperature (stream 2) | Random variation |
| 10 | C feed temperature (stream 4) | Random variation |
| 11 | Reactor cooling water inlet temperature | Random variation |
| 12 | Condenser cooling water inlet temperature | Random variation |
| 13 | Reaction kinetics | Slow drift |
| 14 | Reactor cooling water valve | Sticking |
| 15 | Condenser cooling water valve | Sticking |
| 16 | Unknown | Unknown |
| 17 | Unknown | Unknown |
| 18 | Unknown | Unknown |
| 19 | Unknown | Unknown |
| 20 | Unknown | Unknown |
| 21 | Valve position constant (stream 4) | Constant position |
| Fault Number | PCA | DPCA | GA-DPCA | |||
|---|---|---|---|---|---|---|
| T2 | Q | T2 | Q | T2 | Q | |
| 1 | 99.58% | 98.02% | 99.58% | 91.14% | 99.27% | 92.91% |
| 2 | 98.44% | 96.88% | 98.75% | 91.46% | 98.85% | 94.79% |
| 3 | 18.54% | 28.75% | 17.19% | 55.92% | 21.79% | 46.56% |
| 4 | 50.73% | 97.19% | 23.85% | 91.77% | 93.53% | 93.12% |
| 5 | 38.44% | 49.80% | 37.29% | 77.29% | 51.30% | 91.97% |
| 6 | 99.17% | 98.54% | 99.38% | 93.57% | 99.79% | 95.20% |
| 7 | 100.00% | 98.13% | 100.00% | 94.20% | 99.79% | 94.16% |
| 8 | 97.81% | 96.88% | 97.71% | 92.10% | 97.39% | 93.01% |
| 9 | 18.85% | 28.33% | 16.87% | 54.89% | 21.48% | 50.42% |
| 10 | 51.36% | 74.06% | 52.71% | 83.57% | 64.03% | 84.37% |
| 11 | 60.00% | 76.05% | 42.39% | 91.37% | 83.94% | 92.60% |
| 12 | 98.85% | 95.84% | 99.27% | 93.46% | 99.06% | 94.06% |
| 13 | 95.94% | 95.21% | 95.83% | 92.32% | 96.14% | 92.70% |
| 14 | 99.80% | 96.67% | 99.90% | 90.82% | 34.20% | 90.83% |
| 15 | 20.73% | 32.08% | 19.48% | 52.71% | 30.03% | 46.67% |
| 16 | 34.90% | 68.54% | 32.29% | 82.51% | 45.15% | 81.14% |
| 17 | 83.23% | 94.90% | 81.67% | 90.74% | 91.76% | 90.20% |
| 18 | 90.94% | 91.98% | 91.04% | 87.49% | 92.18% | 88.85% |
| 19 | 22.29% | 56.35% | 21.25% | 89.60% | 26.28% | 67.40% |
| 20 | 47.81% | 73.02% | 48.75% | 84.60% | 56.73% | 87.29% |
| 21 | 47.92% | 65.21% | 51.46% | 75.20% | 67.47% | 71.97% |
| Average | 65.49% | 76.78% | 63.17% | 83.65% | 70.01% | 82.87% |
| Method | T2 | Q |
|---|---|---|
| PCA | 4.52% | 6.09% |
| DPCA | 6.84% | −0.78% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Bai, J.; Wu, F. Fault Diagnosis Using Dynamic Principal Component Analysis and GA Feature Selection Modeling for Industrial Processes. Processes 2022, 10, 2570. https://doi.org/10.3390/pr10122570
Liu C, Bai J, Wu F. Fault Diagnosis Using Dynamic Principal Component Analysis and GA Feature Selection Modeling for Industrial Processes. Processes. 2022; 10(12):2570. https://doi.org/10.3390/pr10122570
Chicago/Turabian StyleLiu, Chenpeng, Jianjun Bai, and Feng Wu. 2022. "Fault Diagnosis Using Dynamic Principal Component Analysis and GA Feature Selection Modeling for Industrial Processes" Processes 10, no. 12: 2570. https://doi.org/10.3390/pr10122570
APA StyleLiu, C., Bai, J., & Wu, F. (2022). Fault Diagnosis Using Dynamic Principal Component Analysis and GA Feature Selection Modeling for Industrial Processes. Processes, 10(12), 2570. https://doi.org/10.3390/pr10122570





