Abstract
In this work, the principle of metamorphic mechanism is optimized for the product design based on variable topological structures. One metamorphic element consisting of kinematic pair and kinematic size is proposed firstly and a configuration synthesis strategy for feed mechanism is performed in term of the translocation, inversion and duplication variation methods. Metamorphic elements are obtained by decomposing the source metamorphic mechanism. A novelty configuration scheme based on constraint variation features is established by the solution of the constraint relationship of metamorphic elements, and three kinds of configurations are synthesized. Comparisons with kinematic performances between source mechanism and developed mechanism configurations are modelled by the kinematic simulation. Results demonstrate that the multiple types of metamorphic mechanisms can be successfully synthesized, and the demands of functional targets are satisfied completely.
1. Introduction
The metamorphic mechanism initially originated from the concept of metamorphosis in view of the evolutionary sense. Its variable topology characteristics contribute to the acceptance of series changes in configurations, self-reorganizations, and reconstructions varying from environments, working conditions and task requirements [1,2,3]. Based on the metamorphic mechanism principle, a new mechanism is proposed by using changeable shapes, topologies and configurations to meet the demands of the different functional tasks. Tian et al. [4] established a configuration synthesis of metamorphic mechanisms on the basis of the five metamorphic modes, including the geometry, motion, force, driving joint, and combined metamorphic modes. Carbonari et al. [5] presented a reconfigurable modular parallel robot stemming from the 3-CPS (cylindrical pair, prismatic pair and spherical pair) under-actuated topology, demonstrating that the robot can perform different types of motions, especially for pure translation and rotation. Aimedee et al. [6] analyzed the metamorphic and reconfigurable mechanism-based morphing types, and categorized the morphing types into topological, geometrical and furcating morphing. Wang et al. [7] introduced a novel plane-space polyhedral metamorphic mechanism that was governed by the edge forming principle. Moreover, evolution principles and movement conditions of the isomorphic mechanism were analyzed. Li et al. [8] proposed the structure formulation and composition methodology of planar metamorphic mechanisms using AAGs (augmented Assur groups), where basic problems, including mobility and the synthesis of a constrained metamorphic working mobility-configuration, were investigated. Yan et al. [9,10] performed the mobility analysis on configuration singularity of the mechanism with variable topologies. In addition, a design methodology for the configuration synthesis was obtained. Goel et al. [11] reported the design, development and deployment of a knowledge-based computer aided design system for supporting biologically inspired design. Chen et al. [12] set up a special line and plane symmetric Bricard linkage to derive closure equations of the linkage and provide the possibility in reconfigurable structures design. Kong et al. [13] established a synthesis method of variable-DOF (degree of freedom) single-loop mechanisms by inserting two joints to a multi-DOF single-loop over-constrained mechanism, and reconfigured a variable-DOF single-loop 7R (revolute pair) mechanism. López-Custodi et al. [14] designed a method of metamorphic mechanism based on the intersection curve of two toroids, where a set of special Bricard linkage mechanisms with various reconstructed branches for the plane-symmetric case were accomplished. Zhang et al. [15,16] developed a methodology for the synthesis and configuration design of metamorphic mechanisms, as well as the genetic evolution with biological building blocks and the subphase working mechanisms. Gan et al. [17] established a new metamorphic parallel mechanism with a reconfigurable revolute joint for the investigation of the reconfiguration principle of a reconfigurable revolute joint. Galletti et al. [18] presented the four kinds of kinemetatropic single loop linkages and a method for synthesizing them. Padey et al. [19] deduced the extreme value distributions of robot positional errors by using the maximum entropy principle, and the reliability of a robotic manipulator was discussed details. Yin et al. [20] developed a gradient-based topology optimization method to synthesize mechanisms consisting of both linkages and gears. Ye et al. [21] presented a method of constructing reconfigurable limbs by integrating the metamorphic linkages as subchains, and provided the reconfigurable parallel mechanism for different configurations with the metamorphic linkages in different phases. Nokleby et al. [22] developed a Grashof five-bar mechanism synthesis routine based on a quasi-Newton optimization routine and Grashof criteria. Ruggiu et al. [23] analyzed the mobility of the moving platform of the parallel manipulator in the CPS and planar operational modes via screw theory. Balli et al. [24,25] built up the analytical methods of synthesis in a planar linkage mechanism with variable topology among the two dead-center and the two finite-separated positions. Zhang et al. [26] proposed a unified elementary matrix operation for revealing the topological variation and topological status, and the geometry of the metamorphic mechanism in an evolutionary process was analyzed. Plitea et al. [27] presented the structural design in relation to kinematics and the workspace of a parallel reconfigurable robot, as well as the structural design of an innovative parallel robot configuration with six degrees of freedom. Kang et al. [28] presented a constraint equation based on third- and fourth-order kinematics, and two linearly independent relationships between joint angular accelerations at the same singular configuration were obtained. Nurahmi et al. [29] decomposed the 4-RUP (revolute universal pair) parallel manipulator into two 2-RUP parallel manipulators, in which three operation modes were utilized to change the manipulator operation mode. Kang et al. [30] proposed a metamorphic mechanism by adding a link to the parallelogram mechanism and changing the properties of some kinematic joints, obtaining some novel metamorphic mechanisms with variable sizes and different configurations.
To date, most studies have mainly been focused on the metamorphic mechanism of the parallel mechanism, such as 6 Revolute linkage, 5 Revolute linkage and other spatial parallel mechanisms. However, analysis of planar mechanisms based on the mechanism composition principle and reports on the mechanism configuration are inadequate. According to the mechanism composition principle and certain rules, the basic groups are synthesized to quickly obtain the various types of mechanisms, which are very meaningful for the topology design of mechanisms. Regarding the globally metamorphic mechanism, its configuration synthesis needs to be combined with its own unique working and constraint variation characteristics. A configuration synthesis strategy for the metamorphic mechanism based on constraint variation characteristics is proposed in this work. The correlation-coupling among the metamorphic mechanism, the metamorphic element, the kinematic pair and size, and the variation modes of metamorphic elements are improved. By analyzing the constraint relationship and configuration scheme of metamorphic elements of the feed mechanism in the sewing equipment, the configuration of the metamorphic mechanism is established. Using kinematic simulation, comparisons between the source and new metamorphic mechanisms are conducted by the parameters of displacement, velocity and acceleration, and it is confirmed that the performances of the new mechanisms are better.
2. Algorithm of Metamorphic Mechanism
2.1. Compositions of Metamorphic Elements
The metamorphic mechanism can be considered as a series of kinematic chains accompanied with continuous changes. The essence of the evolution of the metamorphic mechanism is to understand how to change the relationship of metamorphic elements. Metamorphic element defined by kinematic link and its kinematic pair constitutes the simplest combination, in which the degree of freedom is set to zero. Metamorphic element is composed of the kinematic pair and size.
Kinematic pair Pa in planar mechanism is divided into the higher and the lower pairs, and their characteristics can be expressed as Table 1.

Table 1.
Characteristics of kinematic pair.
Kinematic size D can affect mechanism movement characteristics to some extent, which is determined by the relative position of kinematic pairs, such as the position of revolute pair center and the orientation of the prismatic pair and guide path. Kinematic size D is represented as
where 0 means that kinematic size is zero, 1~d represents the length relationship of the kinematic size, and 1 < 2 < 3 < … < d.
2.2. Variation Modes of Metamorphic Elements
When the input motion remains constant, the variation of metamorphic elements can be detected by using kinematic pair or kinematic size. There are three modes of variation, i.e., the changing type of the kinematic pair, the position of the kinematic pair, and the kinematic size.
- (1)
- Translocation operation
Translocation operation is used to change the type of kinematic pair and identify the evolution of the metamorphic elements. The operation is recorded as
where and are the characteristics of the kinematic pair n before and after the translocation operation, respectively.
A schematic diagram of the translocation operation is shown in Figure 1. The octagon represents the serial number of the kinematic pair, and numbers on the bar show the kinematic size. The translocation operation represents that kinematic pair 2 is changed from 1 to 0, and varies from prismatic pair to revolute pair.
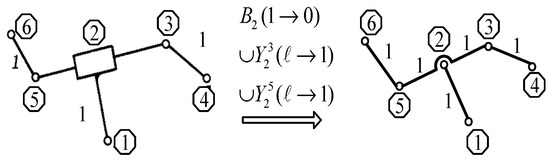
Figure 1.
Translocation operation.
- (2)
- Inversion operation
The inversion operation is used to rearrange the position of the kinematic pair n, and identify the evolution of the metamorphic elements. It is only utilized to rearrange of kinematic pair rather than changing quantities of kinematic pairs of metamorphic elements. The operation is recorded as
where and are the serial number of the kinematic pair connected with kinematic pair n before and after the inversion operation, respectively; is the kinematic size from kinematic pair n to the next kinematic pair i along the motion transmission direction; is the kinematic size from n to after the inversion operation.
In Figure 2, inversion operation represents that kinematic pair 6 is being rearranged and replaced kinematic pair 5, as well as kinematic pair 6 is being with kinematic pair 4. The corresponding kinematic size maintains its stable status.
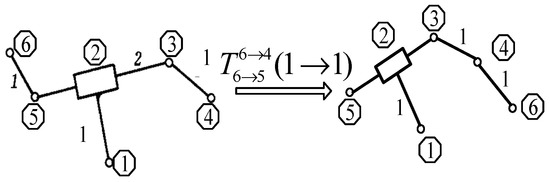
Figure 2.
Inversion operation.
- (3)
- Duplication operation
The duplication operation is used to increase or decrease the kinematic size , and to form a new metamorphic element. The operation is recorded as
In Figure 3, duplication operation represents that kinematic size between kinematic pair 3 and kinematic pair 4 is varied from 1 to 2.
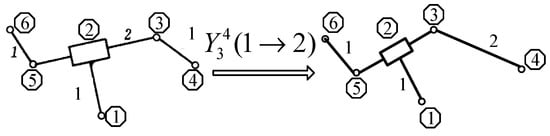
Figure 3.
Duplication operation.
3. Configuration Synthesis Method of the Metamorphic Mechanism
The basic idea of configuration synthesis of the metamorphic mechanism is illustrated as follows: (1) the acquirement of the division scheme of each metamorphic element based on the disintegrating source metamorphic mechanism; (2) the establishment of constraint functions of metamorphic elements; (3) the establishment of the configuration scheme of metamorphic elements based on the constraint variation; (4) the synthetization of configuration of the metamorphic mechanism. Detailed steps are given as follows.
3.1. Source Metamorphic Mechanism Disintegration
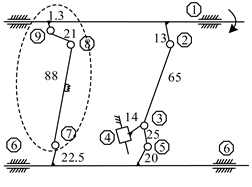
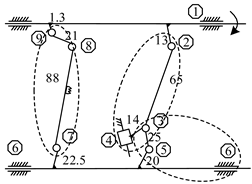
A lockstitch sewing machine is mainly composed of the feed mechanism, upper shaft mechanism, needle bar rocking mechanism, and rotary hook mechanism, where the most complicated mechanism can be attributed to the structure of the feed mechanism. Its function is to make the feed dog complete the periodic feeding when passing through the motion track of the closed wire ring, depicting the realization of forward and backward movement and upward and downward movement of the feed dog during a working cycle. Figure 4 is the source metamorphic mechanism of the feed mechanism, which is divided into three metamorphic elements (see Figure 5). The unit of kinematic size in the figure is mm, and will remain in mm.
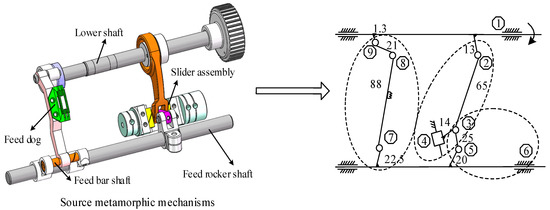
Figure 4.
Source metamorphic mechanism of the feed mechanism.
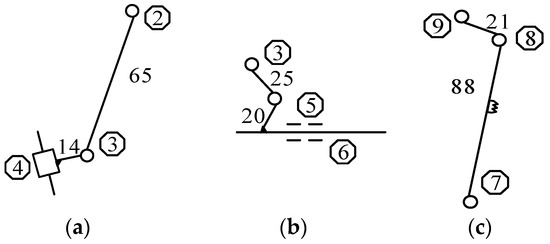
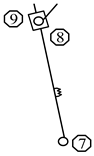
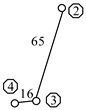
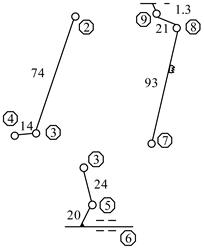
Figure 5.
Source metamorphic elements of the feed mechanism. (a) Metamorphic element 1. (b) Metamorphic element 2. (c) Metamorphic element 3.
3.2. Constraint Functions of Metamorphic Elements
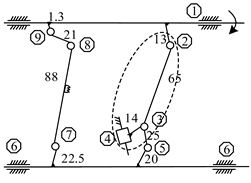
As seen from Figure 6, the constraint relationship with the feed mechanism belongs to the closed vector polygons in different views. Using the matrix method, the sum of vectors in closed vector polygons is equal to zero, and the following constraint relationships of the metamorphic elements are acquired.
where di is the kinematic size between kinematic pairs, Δd is the displacement of kinematic pair 4, θ1 is the rotation angle of the lower shaft, θ3 is the rotation angle of the feed rocker shaft.
where and are the rotation angles of the feed rocker shaft under the limit displacement state of kinematic pair 4, α is the relative rotation angle of the feed rocker shaft, x is the displacement of forward and backward movement of the feed dog.
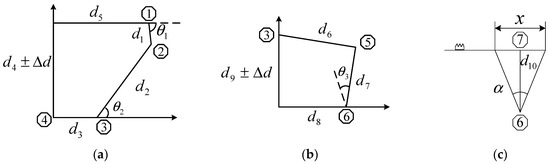
Figure 6.
Constraint relationship diagrams of the feed mechanism. (a) Constraint relationship diagram 1. (b) Constraint relationship diagram 2. (c) Constraint relationship diagram 3.
The common needle pitch of a high-speed lockstitch sewing machine is set between −5 and 5 mm, implying that the displacement of forward and backward movement of the feed dog x = 0~10 mm. Setting it to the target value, and taking d2, d3 and d6 that affect the target value to some extent as the variables, the relationship between the target value and the variable is calculated by Equations (4)–(10).
The kinematic sizes are set to d1 = 13 mm, d4 = 64 mm, d5 = 29 mm, d7 = 20 mm, d8 = 20 mm, d9 = 25 mm and d10 = 22 mm, respectively. When setting d3 as 14 mm and d6 as 25 mm, the influence of kinematic size d2 on the displacement x is studied, as shown in Figure 7. The displacement x is directly proportional to d2. When d2 < 64 mm, the displacement x is relatively smaller than 1 mm. If the displacement x is large enough, d2 should not be too small. However, when d2 ≥ 74 mm, the solution of the constraint relationship is invalid, so the variation range of d2 should range from 65 to 73 mm.
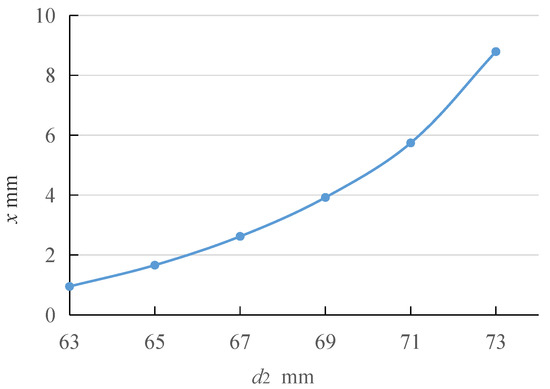
Figure 7.
Relationship between d2 and x.
Setting d2 as 65 mm and d6 as 25 mm, the influence of kinematic size d3 on the displacement x is revealed, as shown in Figure 8, where kinematic size d3 is a function of displacement x. When the kinematic size d3 increases from 13 mm to 23 mm, the distribution of displacement x generally presents a ladder shape. When d3 increases from 13 mm to 17 mm, the displacement x increases by 5%. Even when d3 increases continuously, the displacement x essentially remains unchanged. When d3 ≥ 21 mm, the displacement x shows a downward trend, x decreases by less than 4%. Therefore, the increase of d3 results in the change of displacement x within a smaller range, implying that the change of variable d3 is not sensitive to the displacement x. In order to control the size of the feed mechanism, the variation range of d3 ranges from 13 to 17 mm.
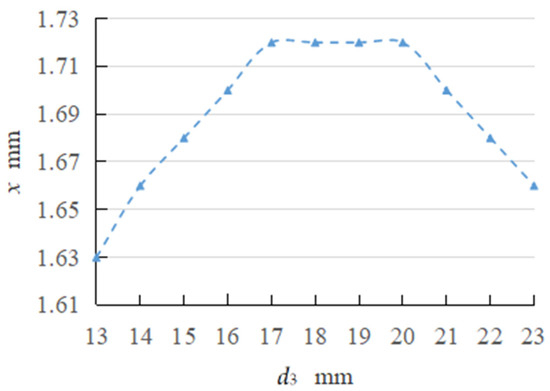
Figure 8.
Relationship between d3 and x.
Setting d2 as 65 mm and d3 as 14 mm, Figure 9 shows the relationship between the kinematic size d6 and the displacement x. When the kinematic size d6 increases from 23 mm to 38 mm, the relationship curve is parabolic with a minimum value. With the increase of d6, the displacement x gradually decreases. When d6 continues to increase, the displacement x gradually increases in excess of the minimum value, but the increasing trend becomes slower. When d6 increases from 29 to 39 mm, the increment x is less than 1 mm as a result of the excessive increase in the size of the feed mechanism. Therefore, the variation range of d6 is from 23 mm to 25 mm.
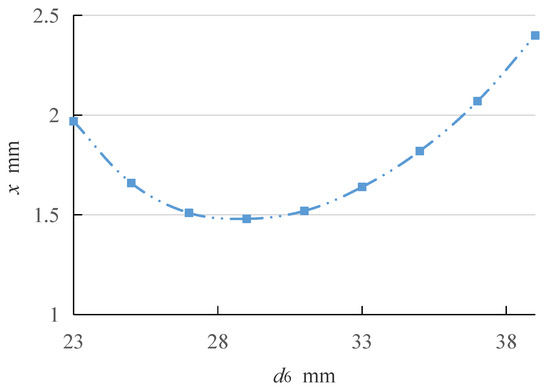
Figure 9.
Relationship between d6 and x.
3.3. Metamorphic Element Configuration Scheme
It can be seen from Figure 5 that the feed mechanism is decomposed into three kinds of source metamorphic elements belonging to Assur group II (Assur group: the simplest component group with zero degrees of freedom) [31]. According to the principle of similarity, the configuration design of metamorphic elements is also primarily determined by Assur group II. Figure 10 shows the configuration scheme set of Assur group II and the corresponding variation modes.
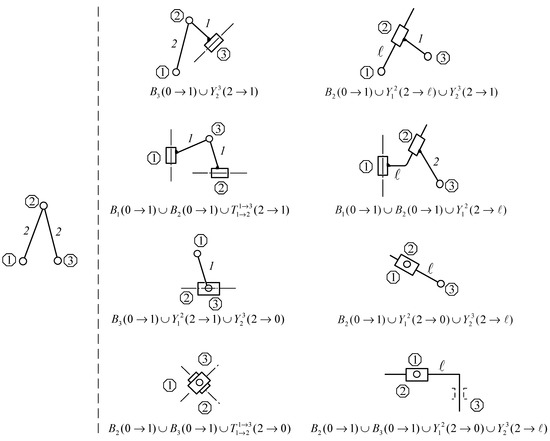
Figure 10.
Configuration scheme set of Assur group II.
According to the motion requirements of the feed mechanism, configuration design of each metamorphic element is conducted: (1) kinematic sizes of the metamorphic element are determined accordingly by the constraint relationship from the variable value range; (2) configuration schemes of each metamorphic element should have similar structures, functions and features. The configuration sets of each metamorphic element are shown as Figure 11.
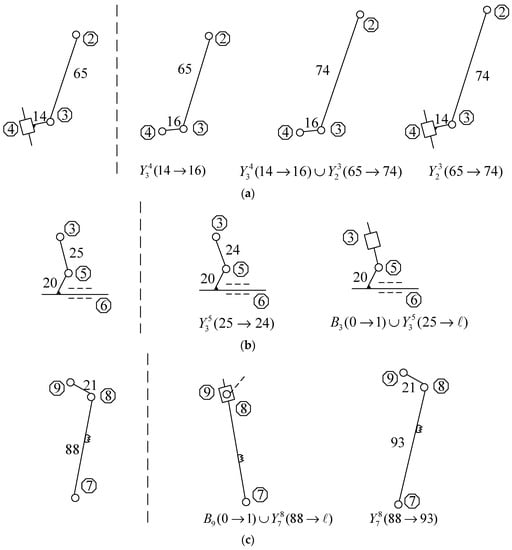
Figure 11.
Configuration scheme sets of each metamorphic element of the feed mechanism. Configuration set of metamorphic (a) element 1, (b) element 2, and (c) element 3.
3.4. Configuration Synthesis of Metamorphic Mechanism
The configuration synthesis of the metamorphic mechanism is obtained by aggregating the kinematic pairs in connection with multiple metamorphic elements, as well as driving the link and frame in turn. The following rules are responsible for the aggregation process:
- (1)
- The aggregated two metamorphic elements have the same motion directions.
- (2)
- The characteristics of aggregated kinematic pairs are consistent.
- (3)
- When the metamorphic elements are aggregated, the kinematic pairs of a metamorphic element fail to connect to the same metamorphic element.
- (4)
- The relative position of other kinematic pairs remains constant.
Selecting the appropriate configuration from the configuration scheme sets, the corresponding variation mode is shown in Table 2. The mechanism configuration schemes of the feed mechanism are designed in light of the aggregation of metamorphic elements, and the corresponding 3D digital models are constructed (see Figure 12).

Table 2.
Variation modes of metamorphic elements.
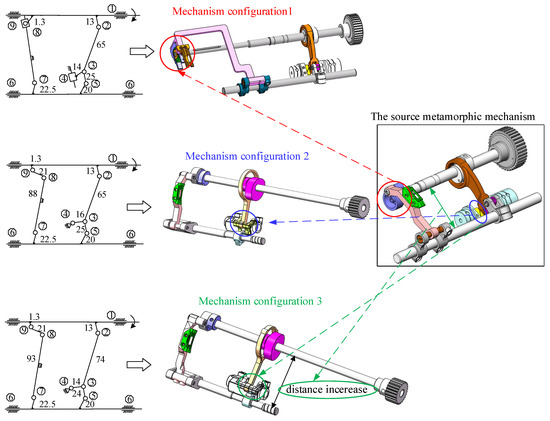
Figure 12.
Mechanism configurations of the feed mechanism.
4. Comparison of the Mechanism Configurations
Feed dog is a kind of end-effector of a lockstitch sewing machine, in which motion parameters can be used to represent the performance indexes for evaluating the lockstitch sewing machine. The kinematics simulation is performed by software ADAMS, with the lower shaft speed set to 18,000 d/s and the corresponding motion pairs for each motion joint, including revolute pairs, prismatic pairs, fixed pairs, etc., are also valued. The material parameters of each part are a density of 7.801 × 10−6 kg/mm3, a Young’s modulus of 2.07 × 105 N/mm2, and a Poisson’s ratio of 0.29. The curves of displacement, velocity and acceleration of the feed dog are acquired.
Figure 13 and Figure 14 show the forward and backward, upward and downward movement curves of the feed dog. The profiles of velocity and acceleration are continuously changed, without suddenly changing, denoting that there is no impact during the movement of the feed dog.
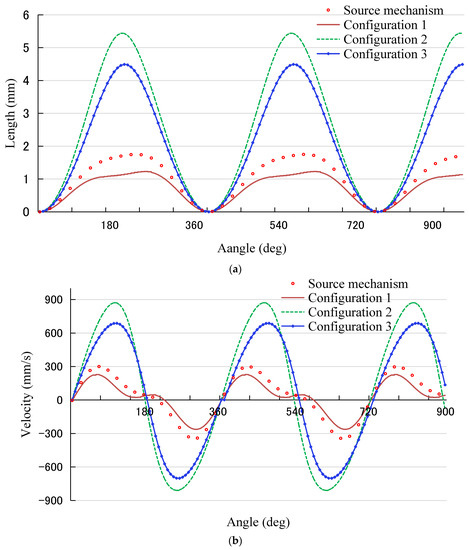
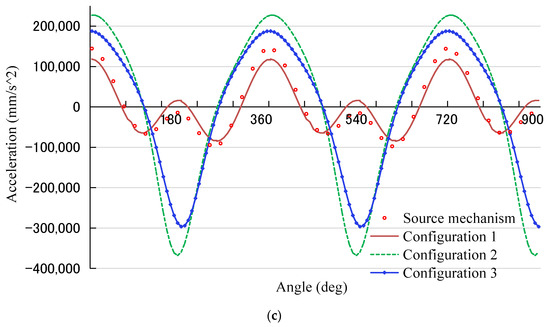
Figure 13.
Forward and backward movement curves of the feed dog. Forward and backward (a) movement displacement, (b) movement velocity, and (c) movement acceleration of the feed dog.
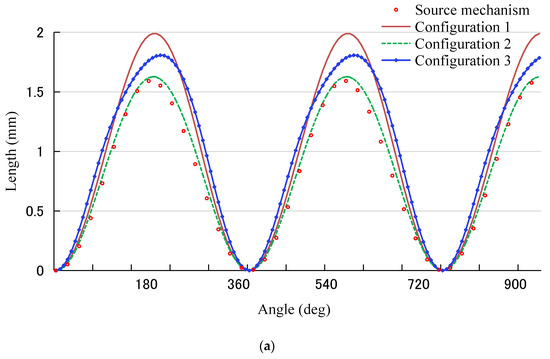
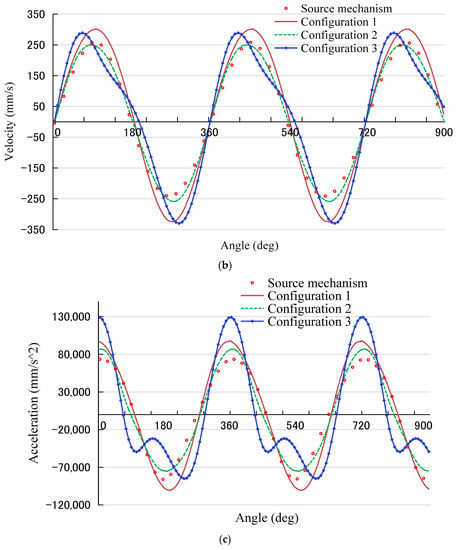
Figure 14.
Upward and downward movement curves of the feed dog. Upward and downward (a) movement displacement, (b) movement velocity, and (c) movement acceleration of the feed dog.
The amount of forward and backward movement of the feed dog is proportional to the sewing needle distances. For a lockstitch sewing machine, the increasing needle distance leads to a decreasing in the rising slope and the pressure of the presser foot, resulting in the effective sewing efficiency. In Figure 13a, the forward and backward displacement of mechanism configuration 1 is the smallest, approximately 1.23 mm, indicating that the sewing needle distance is the smallest. The displacements of mechanism configurations 2 and 3 are relatively larger; configuration 2 has the largest displacement of 5.33 mm, and configuration 3 has a displacement of 4.45 mm. The forward and backward displacement of configuration 2 is 67.4% higher than that of the source mechanism. This can be explained by slider assembly being used for the source mechanism and mechanism configuration 1, and link assembly being used for the mechanism configurations 2 and 3. The slider drives the feed rocker shaft to rotate at a smaller angle, leading to a relatively small forward and backward displacement of configuration 1.
In Figure 13b, the velocity curves of the source mechanism and mechanism configuration 1 are similar, where their fluctuations are approximately 180° and 540°. The velocity curves of mechanism configurations 2 and 3 approach the function of a sine wave, and the velocity changes are relatively stable. In Figure 13c, the acceleration curves of the source mechanism and the mechanism configuration 1 fluctuate approximately 180° and 540°, resulting in the additional pressure in the motion pair during the operation of the lockstitch sewing machine, and an increase in the vibration and noise of the lockstitch sewing machine. Due to the reciprocating motion of the slider in the source mechanism and mechanism configuration 1, fluctuations of velocity and acceleration are promoted. Those curves of mechanism configurations 2 and 3 are similar to the function of cosine waves, and acceleration changes remain to be stable, which is beneficial for keeping the lockstitch sewing machine functioning well.
The amount of upward and downward movement of the feed dog can be interpreted by the lifting height. The larger the lifting height, the greater the feed force, which is suitable for thick material sewing. In Figure 14a, the displacement of mechanism configuration 1 has the largest value of 1.99 mm, which is 20% higher than that of the source mechanism, as a result of the common influence of both the eccentric wheel on the lower shaft and the feed bar slide block assembly at the same time. The displacement of mechanism configuration 2 is almost equal to the source mechanism. The displacement of mechanism configuration 3 is about 1.81 mm, which is about 1% larger than that of mechanism configuration 2 due to the slight difference between them.
In Figure 14b, the velocity curve of each mechanism exhibits the sine wave, and velocity fluctuations of mechanism configuration 3 are slight. In Figure 14c, the acceleration curve of the source mechanism, mechanism configurations 1 and 2 are similar to cosine waves. In spite of the acceleration curve of mechanism configuration 3 being similar to a cosine wave, fluctuations are approximately180°, 540°, etc. The reason is that there is a larger distance between the lower shaft and the feed rocker shaft compared to those of the rest of the mechanism configurations, which changes the initial angle of the feed bar shaft against the lower shaft, with an angle offset by 10.15° as well, incurring the variation of the mechanism movement. Thus, the more the acceleration motion fluctuates, the greater the change in motion inertia force. The displacement, velocity and acceleration motion curves of mechanism configurations 2 and 3 are quite different, reflecting that the kinematic sizes will also have a sufficient impact on the performance of the working machine. This demonstrates that the lifting height of the feed dog in mechanism configuration 1 is relatively larger, but a smaller needle distance is suitable for sewing thick material. Larger needle distances of mechanism configurations 2 and 3 are appropriate for the highly efficient working conditions. The comprehensive movement of mechanism configuration 2 is significantly stable for the higher speed parts.
5. Conclusions
In this paper, the feed mechanism of a lockstitch sewing machine is considered as a source metamorphic mechanism, and an improved mechanism configuration synthesis method is proposed based on the principle of metamorphic mechanism. Under standardized mass production conditions, an exclusive design to meet the different functional requirements is realized, as follows.
- (1)
- Metamorphic element mode consisting of kinematic pair and kinematic size, and a three-layer coupling relationship of the metamorphic mechanism, metamorphic element, kinematic pair and kinematic size are established. An optimization of the variation modes of the metamorphic element, such as translocation, inversion and duplication, are performed successfully.
- (2)
- Feed mechanism is decomposed into three kinds of metamorphic elements of Assur group II. The constraint equations of metamorphic elements and their influence relationships among three kinematic sizes and the displacement of the feed dog are revealed. An interesting finding is that the displacement x is proportional to the kinematic size d2, trapezoidal to the kinematic size d3, and parabolic to the kinematic size d6. The value ranges of the three kinematic sizes are obtained, with d2 = (5, 73) mm, d3 = (13, 17) mm, and d6 = (23, 25) mm, respectively.
- (3)
- Configuration schemes of three metamorphic elements and three mechanism configurations of the feed mechanism are synthesized successfully.
- (4)
- The upward and downward displacement of mechanism configuration 1 is suitable for sewing thick material with the largest value of 1.99 mm, which is one-fifth higher than that of the source mechanism. Forward and backward displacement of mechanism configuration 2 is 1.7 times higher than the source mechanism counterpart, as well as relatively larger that configuration 3. Regarding global movements, mechanism configuration 2 exhibits better stability behavior, which is more suitable for efficient and high-speed places, verifying that the proposed mechanism is better than the source mechanism.
- (5)
- This work provides guidance for the design of the lockstitch sewing machine with differently functional requirements. In our future studies, the dynamic behavior of the three proposed configurations and the source mechanism will be further investigated by manufacturing verification machines, and applying the method to the design of more types of sewing equipment.
Author Contributions
Conception and design of study: L.Z., Y.L. and Y.Z. Acquisition of data: Y.L. Analysis and interpretation of data: L.Z. and Y.Z. Drafting the manuscript: L.Z. and Y.L. Revising the manuscript for important intellectual content: L.Z. and Y.L. Approval of the version of the manuscript to be published: L.Z., Y.L. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful for the financial support from the Zhejiang Province Key Research and Development Projects, China (No. 2020C01064, No. 2021C01054).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dai, J.S.; Jones, J.R. Matrix Representation of Topological Changes in Metamorphic Mechanisms. J. Mech. Des. 2005, 127, 837–840. [Google Scholar] [CrossRef]
- Valsamos, C.; Moulianitis, V.; Aspragathos, N. Index based optimal anatomy of a metamorphic manipulator for a given task. Robot. Comput. Integr. Manuf. 2012, 28, 517–529. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, T.; Ding, X. An optimization method for metamorphic mechanisms based on multidisciplinary design optimization. Chin. J. Aeronaut. 2014, 27, 1612–1618. [Google Scholar] [CrossRef][Green Version]
- Tian, H.-B.; Ma, H.-W.; Ma, K. Method for configuration synthesis of metamorphic mechanisms based on functional analyses. Mech. Mach. Theory 2018, 123, 27–39. [Google Scholar] [CrossRef]
- Carbonari, L.; Callegari, M.; Palmieri, G.; Palpacelli, M.C. A new class of reconfigurable parallel kinematic machines. Mech. Mach. Theory. 2014, 74, 173–183. [Google Scholar] [CrossRef]
- Aimedee, F.; Gogu, G.; Dai, J.; Bouzgarrou, C.; Bouton, N. Systematization of morphing in reconfigurable mechanisms. Mech. Mach. Theory 2016, 96, 215–224. [Google Scholar] [CrossRef]
- Wang, R.; Liao, Y.; Dai, J.S.; Chen, H.; Cai, G. The isomorphic design and analysis of a novel plane-space polyhedral metamorphic mechanism. Mech. Mach. Theory 2019, 131, 152–171. [Google Scholar] [CrossRef]
- Li, S.; Dai, J.S. Structure Synthesis of Single-Driven Metamorphic Mechanisms Based on the Augmented Assur Groups. J. Mech. Robot. 2012, 4, 031004. [Google Scholar] [CrossRef]
- Kuo, C.-H.; Yan, H.-S.; Kuo, C.H. On the Mobility and Configuration Singularity of Mechanisms with Variable Topologies. J. Mech. Des. 2007, 129, 617–624. [Google Scholar] [CrossRef]
- Yan, H.-S.; Kang, C.-H. Configuration synthesis of mechanisms with variable topologies. Mech. Mach. Theory 2009, 44, 896–911. [Google Scholar] [CrossRef]
- Goel, A.K.; Vattam, S.; Wiltgen, B.; Helms, M. Cognitive, collaborative, conceptual and creative-four characteristics of the next generation of knowledge-based CAD systems: A study in biologically inspired design. Comput. Aided Design. 2012, 44, 879–900. [Google Scholar] [CrossRef]
- Chen, Y.; Chai, W.H. Bifurcation of a special line and plane symmetric Bricard linkage. Mech. Mach. Theory 2011, 46, 515–533. [Google Scholar] [CrossRef]
- Kong, X.; Pfurner, M. Type synthesis and reconfiguration analysis of a class of variable-DOF single-loop mechanisms. Mech. Mach. Theory 2015, 85, 116–128. [Google Scholar] [CrossRef]
- Lopez-Custodio, P.C.; Dai, J.S.; Rico, J.M. Branch Reconfiguration of Bricard Linkages Based on Toroids Intersections: Line-Symmetric Case. J. Mech. Robot. 2018, 10, 031003. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, D.; Dai, J.S. Biological Modeling and Evolution Based Synthesis of Metamorphic Mechanisms. J. Mech. Des. 2008, 130, 072303. [Google Scholar] [CrossRef]
- Zhang, L.; Dai, J.S. Reconfiguration of Spatial Metamorphic Mechanisms. J. Mech. Robot. 2009, 1, 011012. [Google Scholar] [CrossRef]
- Gan, D.; Dai, J.S.; Dias, J.; Seneviratne, L. Reconfiguration and Static Joint Force Variation of a 3rRPS Metamorphic Parallel Mechanism with 3R and 1T2R Motion. Mech. Mach. Theory 2016, 36, 213–222. [Google Scholar] [CrossRef]
- Galletti, C.; Fanghella, P. Single-loop kinematotropic mechanisms. Mech. Mach. Theory 2001, 36, 743–761. [Google Scholar] [CrossRef]
- Padey, M.D.; Zhang, X.F. System reliability analysis of the robotic manipulator with random joint clearances. Mech. Mach. Theory 2012, 58, 137–152. [Google Scholar]
- Yim, N.H.; Kang, S.W.; Kim, Y.Y. Topology Optimization of Planar Gear-Linkage Mechanisms. J. Mech. Des. 2019, 141, 032301. [Google Scholar] [CrossRef]
- Ye, W.; Fang, Y.; Guo, S. Reconfigurable parallel mechanisms with planar five-bar metamorphic linkages. Sci. China Technol. Sci. 2017, 57, 210–218. [Google Scholar] [CrossRef]
- Nokleby, S.B.; Podhorodeski, R.P. Optimization-Based Synthesis of Grashof Geared Five-Bar Mechanisms. J. Mech. Des. 2001, 123, 529–534. [Google Scholar] [CrossRef]
- Ruggiu, M.; Kong, X. Mobility and kinematic analysis of a parallel mechanism with both PPR and planar operation modes. Mech. Mach. Theory 2012, 55, 77–90. [Google Scholar] [CrossRef]
- Balli, S.S.; Chand, S. Synthesis of a five-bar mechanism with variable topology for motion between extreme positions (SYNFBVTM). Mech. Mach. Theory 2001, 36, 1147–1156. [Google Scholar] [CrossRef]
- Balli, S.S.; Chand, S. Synthesis of a planar seven-link mechanism with variable topology for motion between two dead-center positions. Mech. Mach. Theory 2003, 38, 1271–1287. [Google Scholar] [CrossRef]
- Zhang, K.; Dai, J.S.; Fang, Y. Topology and Constraint Analysis of Phase Change in the Metamorphic Chain and Its Evolved Mechanism. J. Mech. Des. 2010, 132, 121001. [Google Scholar] [CrossRef]
- Plitea, N.; Lese, D.; Pisla, D.; Vaida, C. Structural design and kinematics of a new parallel reconfigurable robot. J. Robot. Comput. Integr. Manuf. 2013, 23, 219–235. [Google Scholar] [CrossRef]
- Kang, X.; Feng, H.; Dai, J.S.; Yu, H. High-order based revelation of bifurcation of novel Schatz-inspired metamorphic mechanisms using screw theory. Mech. Mach. Theory 2020, 152, 103931. [Google Scholar] [CrossRef]
- Nurahmi, L.; Caro, S.; Wenger, P.; Schadlbauer, J.; Husty, M. Reconfiguration analysis of a 4-RUU parallel manipulator. Mech. Mach. Theory 2016, 96, 269–289. [Google Scholar] [CrossRef]
- Kang, X.; Lei, H.; Li, B. Multiple bifurcated reconfiguration of double-loop metamorphic mechanisms with prismatic joints. Mech. Mach. Theory 2022, 178, 105081. [Google Scholar] [CrossRef]
- Sun, H.; Ge, W.J. Theory of Machines and Mechanisms; Higher Education Press: Beijing, China, 2021; ISBN 9787040555899. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).