Abstract
In this paper, we study the Parisian time of a reflected Brownian motion with drift on a finite collection of rays. We derive the Laplace transform of the Parisian time using a recursive method, and provide an exact simulation algorithm to sample from the distribution of the Parisian time. The paper was motivated by the settlement delay in the real-time gross settlement (RTGS) system. Both the central bank and the participating banks in the system are concerned about the liquidity risk, and are interested in the first time that the duration of settlement delay exceeds a predefined limit. We reduce this problem to the calculation of the Parisian time. The Parisian time is also crucial in the pricing of Parisian type options; to this end, we will compare our results to the existing literature.
1. Introduction
Suppose we have a system of rays emanating from a common origin and a particle moving on this system. On each ray, the particle behaves as a reflected Brownian motion with drift; and once at the origin, it instantaneously chooses a ray for its next excursion randomly according to a given distribution. We are interested in the time length the particle spends on each ray, and the first time that the excursion time length on a ray exceeds a predefined threshold. We call this first exceeding time of threshold a Parisian time, as it generalizes the concept of Parisian time of standard Brownian motion in literature.
The study of excursion time length of Brownian motion goes back to Chung (1976). Other aspects of Brownian excursion have also been considered. Durrett et al. (1977) developed the relationships between the Brownian excursions, meanders and bridges using the limit processes of conditional functionals of Brownian motion. Imhof (1984) derived the joint density concerning the maximum of Brownian motion and 3-dimensional Bessel process. Kennedy (1976) derived the distribution of the maximum of excursion via the limiting processes and relates it to the standard Brownian motion. Getoor and Sharpe (1979) obtained a limiting result on the distribution of additive functionals over Brownian excursions. A literature review can be found in Zhang (2014).
More recently, Chesney et al. (1997) studied the Parisian time of Brownian motion, and used the result to price the Parisian type options. They are path-dependent options whose payoff depends not only on the final value of the underlying asset, but also on the path trajectory of the underlying above or below a predetermined barrier for a length of time. The two-sided Parisian option was considered in Dassios and Wu (2010), its pricing depends on the Parisian time of a drifted Brownian motion with a two-sided excursion time threshold. It turns out that the Parisian times derived in Chesney et al. (1997) and Dassios and Wu (2010) can be viewed as the special cases of our result. Moreover, the results in the current paper can be used to price more complicated Parisian type options. For more details about Parisian options, see Schröder (2003); Anderluh and van der Weide (2009) and Labart and Lelong (2009).
This paper is motivated by the real-time gross settlement system (RTGS, and known as CHAPS in
the UK, see McDonough 1997; Padoa-Schioppa 2005). The participating banks in the RTGS system are concerned about liquidity risk and wish to prevent the excessive liquidity exposure between two banks. There is evidence suggesting that in CHAPS, banks usually set bilateral or multilateral limits on the exposed position with others (see Becher et al. 2008), this mechanism was studied by Che and Dassios (2013) using a Markov model. For a single bank, namely bank A, let a reflected Brownian motion be the net balance between bank A and bank i, and let be the bilateral limit set up by bank A for bank i, Che and Dassios (2013) calculated the probability that the limit is exceeded in a finite time.
We consider another source of liquidity risk, the time-lag between the execution of the transaction and its final completion. As it is explained in McDonough (1997) and Padoa-Schioppa (2005), if a counterparty does not settle an obligation for the full value when due but at some unspecified time thereafter, the expected liquidity position of the payee could be affected. The settlement delay may force the payee to cover its cash-flow shortage by funding at short notice from other sources, which may result in a financial loss due to higher financing costs or to damage to its reputation. In more extreme cases, it may be unable to cover its cash-flow shortage at any price, in which case it may be unable to meet its obligation to others. As the settlement delay is the major source of liquidity risk in the RTGS system, both the central bank and the participating banks are interested in the length of the delay. Previous research in Che and Dassios (2013) has shown that the Markov-type models are adequate for CHAPS, we will extend this model here to study the settlement delay. For bank A and bank i in CHAPS, we view the net balance between them as a reflected Brownian motion with drift. Assume that bank A has set a time limit on the duration of settlement delay for bank i, and they are interested in the first time that the limit is exceeded. In practice, an individual bank could set multiple limits or even remove the limit on different types of counterparties. We reduce this problem to the calculation of the Parisian time of a reflected Brownian motion with drift on rays. For more details about the CHAPS, see Che (2011) and Soramäki et al. (2007).
We construct the reflected Brownian motion with drift on rays in Section 2, then calculate the Laplace transform of the Parisian time in Section 3. An exact simulation algorithm to sample from the distribution of the Parisian time is provided in Section 4. We discuss the application of these results in Section 5.
2. Construction of the Underlying Process and the Parisian Time
In this section, we construct the reflected Brownian motion with drift on a finite collection of rays, and define the Parisian time we are interested in. Let n be a finite positive integer, we denote by S a system containing n rays emanating from the common origin, i.e., , and fix a distribution , so that . We also define the functions and for , where and are constants (see Figure 1).
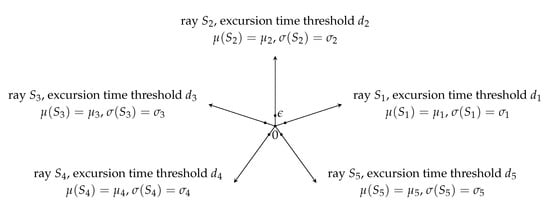
Figure 1.
A system of 5 rays emanating from a common origin.
Consider a planar process on the system of rays S. We represent the position of by , where denotes the distance between and the origin, and indicates the current ray of the process. Let be the “driving process”, and be the Skorokhod reflection of , i.e.,
Then, has the same distribution as a reflected Brownian motion with drift and dispersion . A proof of this can be seen in Jeanblanc et al. (2009) Section 4.1, Peskir (2006) and Graversen and Shiryaev (2000).
We expect to be constant during each excursion of away from the origin and has the same distribution as P when returns to the origin. To this end, we initialize with , , and let remain constant whenever . Once , is randomized according to P, i.e.,
This means the coefficients of remain constant whenever , and the Skorokhod reflection of has the same distribution as a reflected Brownian motion with drift and dispersion on each ray .
Therefore, we summarize the behaviour of as follows. The initial state of is distributed as , . Then it behaves as a Brownian motion with drift and dispersion on ray , as long as it does not return to the origin. Once at the origin, it instantaneously chooses a new ray according to P, independently of the past behaviour; that is,
There are some special cases of . When and for , becomes a Walsh Brownian motion. When , , and , recovers the skew Brownian motion. We also obtain a Brownian motion with drift and dispersion by setting , , , and ; and a reflected Brownian motion by setting , , and .
Next, we define the last zero time and excursion time length of as and . Then represents the time length has spent in the current ray since last time at the origin. On each ray , there is a threshold for the excursion time length, our target is to find the first time that the threshold is exceeded by . Thus, we are interested in the Parisian time defined as
Note that may make an excursion with infinite time length on a ray if the drift on this ray is positive. Since our target is to study the Parisian time , we are only interested in the excursion time length up to , even if the total length is infinite.
We need to calculate the excursion time length of , but the problem is there is no first excursion from zero; before any , the process has made an infinite number of small excursions away from the origin. To approximate the dynamic of a Brownian motion, Dassios and Wu (2010) introduced the “perturbed Brownian motion”, we will extend this idea here.
For every , we define a perturbed process on the system of rays S. On each ray , behaves as a reflected Brownian motion with drift , dispersion and starting from , as long as it does not return to the origin. Once at the origin, not only chooses a new ray according to P, but also jumps to on the new ray. In other words, has a perturbation of size at the origin which can be described as
Hence, we describe the behaviour of as follows. The initial state of is distributed as , . Then it behaves as a Brownian motion with drift , dispersion and starting from on ray , as long as it does not return to the origin. Once at the origin, it instantaneously chooses a new ray according to P and jumps to on the new ray.
We define the Parisian time of similarly as before. Let and . We are interested in the Parisian time defined as
As , the perturbation at origin vanishes, and in a pathwise sense, then in distribution. Hence, we will first derive the Laplace transform of , then take the limit to calculate the Laplace transform of the Parisian time .
3. Laplace Transform of
We present the main result of the paper in this section. For simplicity, we denote the symmetric function
where is the cumulative distribution function of standard normal distribution, and the constant
where , , and are defined in Section 2. For , , and , we deduce from the definition that .
Theorem 1.
Let be a reflected Brownian motion with drift on a system of rays S, where , , and are the drift, dispersion, entering probability and excursion time threshold of ray , . For , the Laplace transform of the Parisian time τ is
and the expectation of τ is
Proof.
We prepare some preliminary formulas for the proof. From Section 2, we know starts from on ray , and behaves as a Brownian motion with drift and dispersion as long as it does not return to the origin. Let be the density of the first hitting time at 0 of such a Brownian motion, then
We define the following functions in ,
and call them and for convenience. In their Laplace transforms respectively, represents the excursion time length of on ray if it is shorter than the threshold , and represents the excursion time length if it is longer than . In the latter case, we set the excursion time length to be because we are only interested in the excursion up to the threshold.
These functions have the limits
Moreover, we calculate the limits of their derivatives to be
the last equation can be checked using , which is obtained by a direct calculation from the definition of .
Now we study the Parisian time . Define the sequence of random times
recursively, and the mutually exclusive events
Then, denotes the event that the exceeding of threshold occurs during the -th excursion of away from the origin. Next, we set for an arbitrary but fixed i, and calculate the Laplace transforms for .
For , we interpret as follows. Starting from on ray , spends more than time before hitting the origin, hence the exceeding occurs during the first excursion. This is equivalent to the event that a Brownian motion with drift and dispersion spends more than time to travel from to 0, which has probability . Thus , and
Next, we consider the event . In this case, the duration of the first excursion of is shorter than , and the Laplace transform of the duration is . After the first excursion, returns to the origin and jumps to with probability , then exceeds the excursion time threshold before returning to the origin. The behaviour of during the second excursion is similar to what we described for , with the index i replaced by k. Thus, we have
In the same way, we consider the event . In this case, the duration of the first excursion of is shorter than , with the Laplace transform . After the first excursion, returns to the origin and jumps to with probability . Restarting from , will exceed the excursion time threshold exactly during the second excursion (hence the third in total). The behaviour of during the second and third excursions is similar to what we described for , with the index i replaced by k. Hence,
The same explanation applies to for any positive integer m, i.e., the duration of the first excursion of is shorter than , after that restarts from and exceeds the threshold exactly during the m-th excursion. Hence, we deduce that
This implies a recursive structure between the Laplace transforms of conditioned on and , we solve for
Since the exceeding of threshold may occur during any excursion of , we need to sum the result over , this gives
the last equation holds because for each k, is a probability density function on , so for any ,
Equation (6) boils down the Laplace transform of to the initial state of , which is distributed as . Then we calculate the Laplace transform of to be
As in Section 2, can be reduced to a Brownian motion with drift or a standard Brownian motion by choosing the parameters accordingly, then we can compare Theorem 1 with the results in the existing literature.
Remark 1.
When , , , , and , , Equation (2) becomes the Laplace transform of the two-sided Parisian time of a Brownian motion with drift
this is the main result of Dassios and Wu (2010). Moreover, for , , , , we set and let , then Equation (2) gives the Laplace transform of the one-sided Parisian time of a standard Brownian motion
this was derived in Section 8.4.1 of Chesney et al. (1997).
4. Exact Simulation Algorithm of the Parisian Time
In this section, we provide an exact simulation algorithm to sample from the distribution of the Parisian time . Our algorithm is based on the exact simulation schemes of the truncated Lévy subordinator developed in Dassios et al. (2020). We refer to Algorithms 4.3 and 4.4 of Dassios et al. (2020) as AlgorithmI(.) and AlgorithmII(. , .),their full steps are attached in Appendix A.
Theorem 2.
Exact simulation algorithm of the Parisian time τ.
- 1.
- Initialize , , , and calculate for . Set .
- 2.
- Generate a multinomial random variable I whose probability function isvia the following steps:
- (a)
- Generate an uniform random variable .
- (b)
- Set . For , find the unique i such thatthen return .
- 3.
- Generate a random variable via the following steps:
- (a)
- Generate an exponential random variable by setting , then return .
- (b)
- For each , generate the following subordinator:
- If , generate a subordinator by setting and
- If , generate a subordinator by setting and
- (c)
- Set .
- 4.
- Output .
Proof.
For simplicity, we denote by and , then the Laplace transform (2) can be written as
Since for , we know , and the denominator of is positive. This enables us to rewrite the Laplace transform in an integration format using the exponential function
Equation (8) can be understood as a product of the Laplace transforms of two independent random variables, hence we can generate them separately, and view the Parisian time as their summation.
Denote by I a multinomial random variable with the probability function
then we can generate I using the strip method, this becomes Step 2. Note that the random variable has the Laplace transform
Next, we denote by the random variable whose Laplace transform is
For each i, we interpret the expression
as the Laplace transform of the random variable , where is a subordinator with truncated Lévy measure
at time . Comparing (10) with (A1), we know can be generated via Algorithms 4.3 and 4.4 in Appendix A.
Moreover, (9) implies that , where is an exponential random variable. Hence, we generate T in Step 3(a), sample from in Step 3(b) and calculate via Step 3(c).
Finally, since , we have the representation , where and are independent, then can be generated via Step 4. □
Next, we illustrate the accuracy and performance of the exact simulation algorithm with a numerical example. We set , and
Using the exact simulation algorithm, we generate samples from the Parisian time and calculate their average. On the other hand, we use Equation (3) to calculate the true expectation of to be . Then we consider the following two standard measures for the associated error of the algorithm,
- difference = sample average − true expectation
- standard error
Table 1 reports the results, we see that the algorithm can achieve a high accuracy, and one has to generate more samples to decrease the standard error.

Table 1.
Sample average and accuracy of the exact simulation algorithm.
In addition, we estimate the distribution function of the Parisian time. Using the exact simulation algorithm and the smoothing techniques (see Bowman and Azzalini 1997), we get the estimated curve for the distribution function. On the other hand, we apply the Gaver–Stehfest method (see Cohen 2007) to invert the Laplace transform numerically and obtain the inverted curve for the distribution function. These curves are provided in Figure 2, they show that the exact simulation algorithm provides a good approximation for the distribution of the Parisian time.
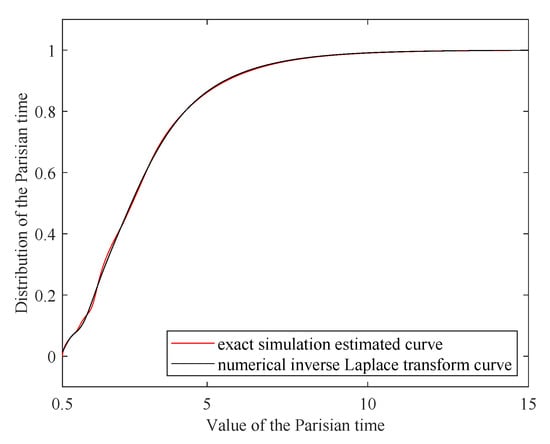
Figure 2.
Inverted and numerical estimated curves of the distribution function.
We also illustrate the performance of the algorithm by recording the CPU time needed to generate these samples from the Parisian time. The experiment is implemented on an Intel Core i5-5200U CPU@2.20GHz processor, 8.00GB RAM, Windows 10, 64-bit Operating System and performed in Matlab R2019b. No parallel computing is used. Table 2 reports the results.

Table 2.
CPU time of the exact simulation algorithm.
5. Discussion
We can apply this model to study the settlement delay in CHAPS. For an individual bank A, we assume that there are n counterparties in the system, namely bank 1, bank 2, ..., bank n. We also assume that bank A uses an internal queue to manage its outgoing payments, and once the current payment is settled, it has probability to make another payment to bank i, . Let a reflected Brownian motion with drift and dispersion be the net balance between bank A and bank i. To avoid the excessive exposure to liquidity risk, a time limit has been set for the duration of settlement delay between bank A and bank i. Both the central bank and the participating banks are interested in the first time that the limit is exceeded.
We model the net balance between bank A and the counterparties by the planar process , and view the first exceeding time as the Parisian time of . Using the results in the current paper, we can sample from this first exceeding time and estimate its distribution function numerically. We remark that this approach can be adopted by both the policymaker in the central bank and the credit control departments of the participating banks to lay down decisive actions. For example, the central bank may use time-dependent transaction fees to provide incentives to earlier settlements. Alternatively, the participating banks may also learn to coordinate their payments over time, creating non-binding behavioural conventions or implicit contracts.
In particular, an empirical method has been developed in Denbee and Zimmerman (2012) to detect the apparent `free-riding’ in the RTGS system, referring to the behaviour that the banks wait for incoming payments to fund subsequent outgoing payments and not supply an amount of liquidity to the system commensurate with the share of payments they are responsible for. Suppose the banks are required to hold buffers of liquid assets in order that they can make payments in a stress scenario, and the buffers are continuously calculated based on past activity. Banks may have an incentive to delay their payments so that the regulatory buffer will be reduced at subsequent recalibrations. The method in Denbee and Zimmerman (2012) could help to detect this behaviour and calibrate buffers independent of strategic actions. The study in the current paper provides another point of view towards this method. We can estimate the distribution of the settlement delay and take this into consideration when calculating the buffers.
It is also possible to extend the model in the current paper to the settlement systems other than CHAPS. For example, the structure of settlement delay in Interbank Electronic Payment System (SPEI operated by Banco de México) has been specified in Alexandrova-Kabadjova and Solis (2012) with real transactions data from 7 April to 7 May 2010. We may assume that the Markov model is adequate for SPEI, and use these data to calibrate the parameters of the model. Moreover, the observations in Alexandrova-Kabadjova and Solis (2012) suggest that low value payments do not increase the settlement delay in the system. This is reasonable under the assumption that the net balance between two banks follows a reflected Brownian motion with drift, because the process will make an infinite number of small excursions at the origin.
This paper has focused on the model with one central bank (or agent) and several domestic participants, which is classified as a `within border payment system’ (see Bech et al. 2020). For a cross-border payment system, however, we need to consider a model containing two or more central banks, each with their own domestic participants. Assume that the system offers payment versus payment (PvP, see Bech et al. 2020) services, then the settlement delay may originate in any local system, and the first exceeding time of settlement delay of the whole system can be viewed as the joint distribution of the Parisian times of the local systems. With the technique developed in this paper, we are able to simulate the marginal distributions of the local exceeding time, but not the joint distribution. This is a topic for future research, and the result would be beneficial on a global scale.
In addition, our Brownian-type model reflects the random fluctuations of payments and delays, but the external events that can influence these are not taken into account. For example, the operational risks related to computer and telecommunication system breakdown may increase the settlement delay, see Rochet and Tirole (1996) for the impact of computer problem of the Bank of New York in 1985 and the San Francisco earthquake in 1989. More recently, many reports have suggested the impact of global pandemic in 2020 on the settlement systems. These might be interesting for a further study.
Author Contributions
Methodology, A.D. and J.Z.; software, J.Z.; formal analysis, A.D. and J.Z.; writing—original draft preparation, J.Z.; writing—review and editing, A.D.; supervision, A.D.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to the editor for handling this manuscript and both reviewers for giving us very helpful and inspiring comments, especially during the difficult time of pandemic.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Exact Simulation of Truncated Subordinator
In this appendix, we attach Algorithms 4.3 and 4.4 of Dassios et al. (2020). These algorithms exactly generate samples from the truncated subordinator with Laplace transform
We first present two ancillary algorithms, namely Algorithms 4.1 and 4.2 of Dassios et al. (2020).
Lemma A1
(Algorithm 4.1 of Dassios et al. 2020). Exact simulation of .
- 1.
- Set ; .
- 2.
- minimise .
- 3.
- record critical value ; set .
- 4.
- repeat {
- 5.
- sample ; ,
- 6.
- set ; ,
- 7.
- sample ; .
- 8.
- if , break.
- 9.
- }
- 10.
- sample ,
- 11.
- set ; .
- 12.
- return .
Lemma A2
(Algorithm 4.2 of Dassios et al. 2020). Exact simulation of .
- 1.
- sample ; set .
- 2.
- repeat {
- 3.
- sample ; set .
- 4.
- if , break.
- 5.
- }
- 6.
- return Z.
Next we provide the Algorithm 4.3 and 4.4 of Dassios et al. (2020).
Theorem A1
(Algorithm 4.3 of Dassios et al. 2020). Exact simulation of the subordinator when . The input is t.
- 1.
- set ; .
- 2.
- repeat {
- 3.
- sample via Algorithm 4.1; set , .
- 4.
- if , break.
- 5.
- }
- 6.
- set ; sample via Algorithm 4.2.
- 7.
- return .
Theorem A2
(Algorithm 4.4 of Dassios et al. 2020). Exact simulation of the subordinator when . The inputs are .
- 1.
- repeat {
- 2.
- sample via Algorithm 4.3; .
- 3.
- if , break.
- 4.
- }
- 5.
- return .
Proof.
For the proof as well as the motivation of the algorithms above, see Dassios et al. (2020). □
References
- Alexandrova-Kabadjova, Biliana, and Francisco Solis. 2012. The mexican experience in how the settlement of large payments is performed in the presence of a high volume of small payments. Diagnostics for the Financial Markets–Computational Studies of Payment System. Available online: https://ssrn.com/abstract=2191794 (accessed on 21 November 2020).
- Anderluh, Jasper H. M., and Jan A. M. van der Weide. 2009. Double-sided Parisian option pricing. Finance and Stochastics 13: 205–38. [Google Scholar] [CrossRef]
- Bech, Morten L., Umar Faruqui, and Takeshi Shirakami. 2020. Payments without borders. BIS Quarterly Review. March 1. Available online: https://ssrn.com/abstract=3561190 (accessed on 21 November 2020).
- Becher, Christopher, Marco Galbiati, and Merxe Tudela. 2008. The timing and funding of CHAPS Sterling payments. Economic Policy Review 14: 113–33. [Google Scholar] [CrossRef]
- Bowman, Adrian W., and Adelchi Azzalini. 1997. Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations. Oxford: OUP, vol. 18. [Google Scholar]
- Che, Xiaonan. 2011. Markov Type Models for Large-Valued Interbank Payment Systems. Ph. D. dissertation, The London School of Economics and Political Science (LSE), London, UK. [Google Scholar]
- Che, Xiaonan, and Angelos Dassios. 2013. Stochastic boundary crossing probabilities for the Brownian motion. Journal of Applied Probability 50: 419–29. [Google Scholar] [CrossRef]
- Chesney, Marc, Monique Jeanblanc-Picqué, and Marc Yor. 1997. Brownian excursions and Parisian barrier options. Advances in Applied Probability 29: 165–84. [Google Scholar] [CrossRef]
- Chung, Kai Lai. 1976. Excursions in Brownian motion. Arkiv för Matematik 14: 155–77. [Google Scholar] [CrossRef]
- Cohen, Alan M. 2007. Numerical Methods for Laplace Transform Inversion. New York: Springer, vol. 5. [Google Scholar]
- Dassios, Angelos, Jia Wei Lim, and Yan Qu. 2020. Exact simulation of a truncated Lévy subordinator. ACM Transactions on Modeling and Computer Simulation 30: 26. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Shanle Wu. 2010. Perturbed Brownian motion and its application to Parisian option pricing. Finance and Stochastics 14: 473–94. [Google Scholar] [CrossRef]
- Denbee, Edward, and Rodney Garratt-Peter Zimmerman. 2012. Methods for evaluating liquidity provision in real-time gross settlement payment systems. Diagnostics for the Financial Markets–Computational Studies of Payment System. Available online: https://www.econstor.eu/bitstream/10419/212978/1/e45-bof-sci-monographs.pdf#page=55 (accessed on 21 November 2020).
- Durrett, Richard T., Donald L. Iglehart, and Douglas R. Miller. 1977. Weak convergence to Brownian meander and Brownian excursion. The Annals of Probability 5: 117–29. [Google Scholar] [CrossRef]
- Getoor, Ronald K., and Michael J. Sharpe. 1979. Excursions of Brownian motion and Bessel processes. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 47: 83–106. [Google Scholar] [CrossRef]
- Graversen, Svend Erik, and Albert N. Shiryaev. 2000. An extension of P. Lévy’s distributional properties to the case of a Brownian motion with drift. Bernoulli 6: 615–20. [Google Scholar] [CrossRef]
- Imhof, Jan-Pierre. 1984. Density factorizations for Brownian motion, meander and the three-dimensional Bessel process, and applications. Journal of Applied Probability 21: 500–10. [Google Scholar] [CrossRef]
- Jeanblanc, Monique, Marc Yor, and Marc Chesney. 2009. Mathematical Methods for Financial Markets. Springer Finance. London: Springer. [Google Scholar]
- Kennedy, Douglas P. 1976. The distribution of the maximum Brownian excursion. Journal of Applied Probability 13: 371–76. [Google Scholar] [CrossRef]
- Labart, Céline, and Jérôme Lelong. 2009. Pricing double barrier Parisian options using Laplace transforms. International Journal of Theoretical and Applied Finance 12: 19–44. [Google Scholar] [CrossRef]
- McDonough, William J. 1997. Real-Time Gross Settlement Systems. Basel: Committee on Payment and Settlement Systems, Bank for International Settlements. [Google Scholar]
- Padoa-Schioppa, Tommaso. 2005. New Developments in Large-Value Payment Systems. Basel: Committee on Payment and Settlement Systems, Bank for International Settlements. [Google Scholar]
- Peskir, Goran. 2006. On reflecting Brownian motion with drift. Paper presented at 37th ISCIE International Symposium on Stochastic Systems Theory and Its Applications, Kyoto, Japan; pp. 1–5. [Google Scholar]
- Rochet, Jean-Charles, and Jean Tirole. 1996. Controlling risk in payment systems. Journal of Money, Credit and Banking 28: 832–62. [Google Scholar] [CrossRef]
- Schröder, Michael. 2003. Brownian excursions and Parisian barrier options: A note. Journal of Applied Probability 40: 855–64. [Google Scholar] [CrossRef]
- Soramäki, Kimmo, Morten L. Bech, Jeffrey Arnold, Robert J. Glass, and Walter E. Beyeler. 2007. The topology of interbank payment flows. Physica A: Statistical Mechanics and Its Applications 379: 317–33. [Google Scholar] [CrossRef]
- Zhang, Youyou. 2014. Brownian Excursions in Mathematical Finance. Ph. D. dissertation, The London School of Economics and Political Science, London, UK. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).