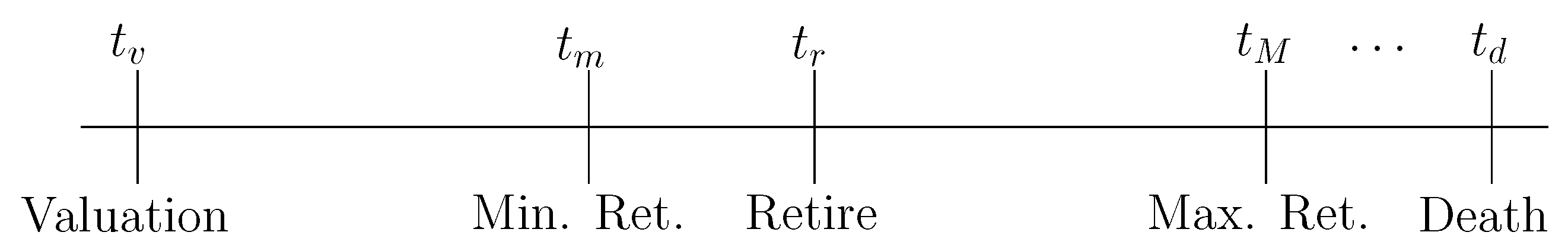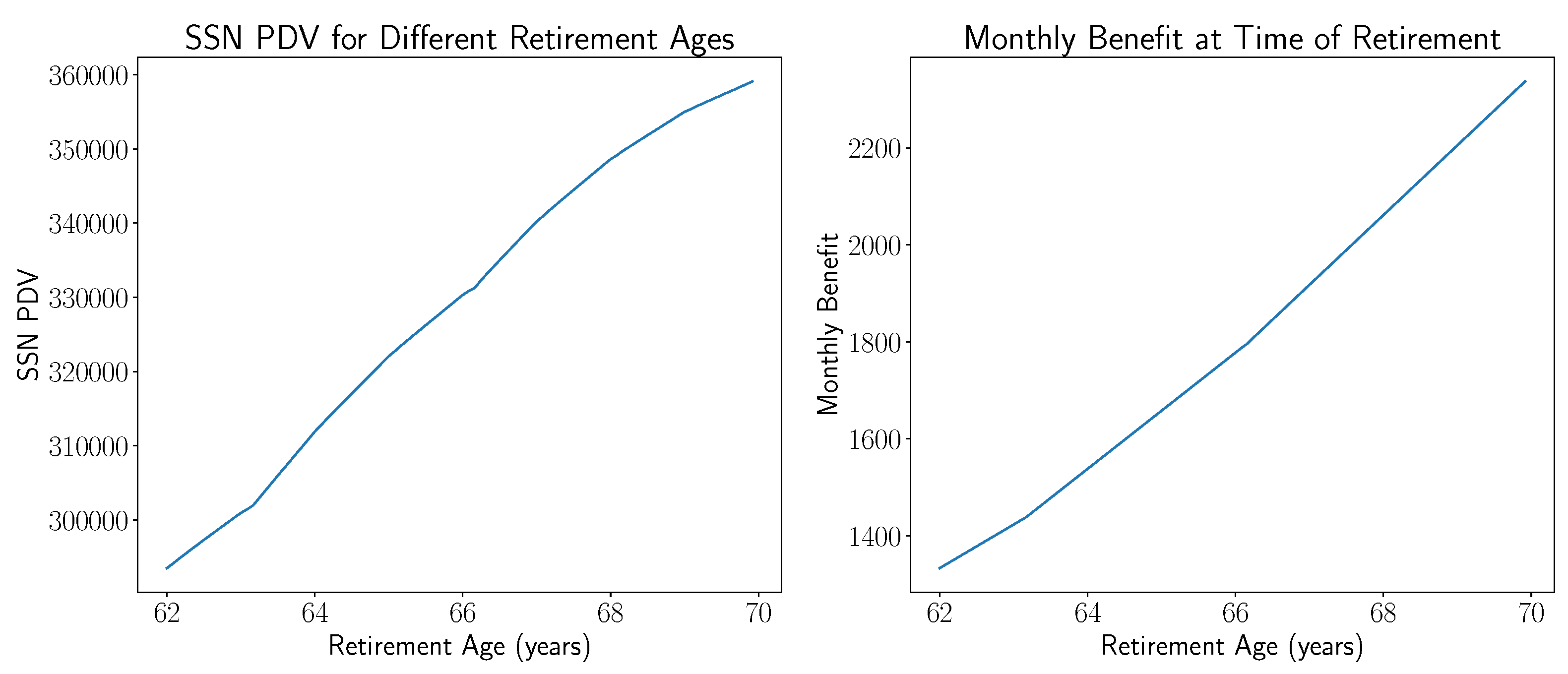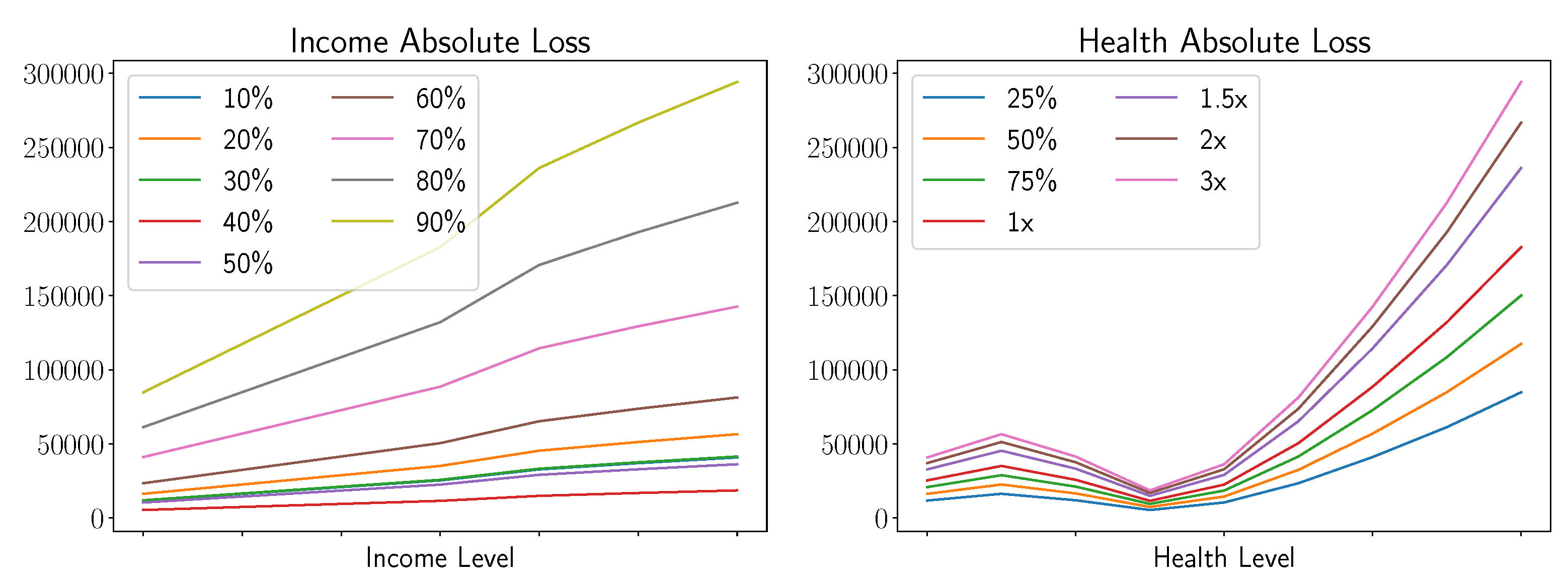Social Security Benefit Valuation, Risk, and Optimal Retirement

Abstract

We develop valuation and risk techniques for the future benefits of a retiree who participates in the American Social Security program based on their chosen date of retirement, the term structure of interest rates, and forecasted life expectancy. These valuation methods are then used to determine the optimal retirement time of a beneficiary given a specific wage history and health profile in the sense of maximizing the present value of cash flows received during retirement years. We then examine how a number of risk factors including interest rates, disease diagnosis, and mortality risks impact benefit value. Specifically, we utilize principal component analysis in order to assess both interest rate and mortality risk. We then conduct numerical studies to examine how such risks range over distinct income and demographic groups and finally summarize future research directions.

1. Introduction and Overview

Labor force participants typically rely on accumulated wealth during their working years to finance retirement through voluntary or mandatory means. For example, regular deductions are taken from American employees’ wages to fund a variety of retirement oriented investment vehicles including mandatory programs such as Social Security and state administered 401(a) plans. In addition, employees may also supplement retirement savings through voluntary programs, the most prominent being employer sponsored 401(k) plans. Finally, excess savings may be self-managed or be invested at the discretion of a financial advisor in annuities, real estate, brokerage accounts, or money market instruments, among other assets, cf. (Kwak 2013; Merton 2014) for a more detailed discussion and comparison of retirement planning options. Among these options, Social Security benefits comprise a major source of retirement funding (Feldstein 1974). In particular, as of 2019, Social Security benefits account for approximately one third of the retirement income of the elderly population in the United States (Social Security Administration 2019).

When planning for retirement and allocating capital between different investment options, it is crucial to estimate the present value of each option under consideration. In fact, the work in Gustman and Steinmeier (1998) found that approximately half of all individuals surveyed in their study were not knowledgeable about the present value of their Social Security or pension benefits. In addition, the work in Luchak and Gunderson (2000) found that employees have a limited understanding of the benefit structure of private pension plans. In a similar vein, Americans hold misconceptions related to their Social Security benefits (Dominitz et al. 2003) in terms of both benefit levels and long term program solvency. In actuality, Social Security benefits often comprise a substantial, and often majority, portion of the fixed income component of a beneficiary’s retirement portfolio. This should be considered in tandem with alternative investment options when designing a retirement portfolio from a holistic perspective. However, the valuation of Social Security benefits involves additional complexities that are not present in traditional fixed income securities. The most notable such feature is that the date of death of the beneficiary is unknown as of the valuation date. It must be carefully modeled, as incorrect estimation will significantly influence the number of future cash flows received.

We focus on the valuation of the future benefits received from the American Social Security program from a pensioner’s perspective. A number of approaches have been considered for pension valuation. In (Sundaresan and Zapatero 1997), the authors developed stochastic process based techniques to model the relationship between a worker’s wage history, the risk free interest rate, and pension benefit value. Public pension future liabilities for distinct age groups were considered in (Novy-Marx and Rauh 2011) under different accrual methods, which were aggregated to determine program level liabilities. Program cost differences between pensioners initiating benefits at early and late ages were considered in (Nalebuff and Zeckhauser 1984). In (Stock and Wise 1990), the authors examined pension valuation in the setting of studying the opportunity cost of continued work versus when to retire and receive payouts from a single firm’s pension plan. Longevity risk was considered in (Fong et al. 2010), where the authors used annuity valuation techniques to argue that state level mandates to annuitize retirement assets can be beneficial for both adverse asset selection and the longevity risk of an individual. In (Brown 2003), similar annuity valuation questions were considered in the context of longevity insurance varying over different cohorts with differing mortality rates.

We proceed in a similar manner, valuing Social Security benefits from the point of view of the beneficiary receiving a future stream of cash flows from their date of retirement until death. In particular, as a motivating application, we identify the optimal retirement date and value of future Social Security benefits based on their wage history and life expectancy in addition to external factors such as the term structure of interest rates. We note however that the valuation and risk techniques developed below are not only limited to Social Security benefit valuation, but have applicability to a variety of fixed income securities. In addition, we will incorporate granular life table information into the forecasting model developed in (Mitchell et al. 2013) in order to project the future life expectancy of the beneficiary on an annual basis, which substantively impacts benefit present value. Finally, we develop a PCA based model to understand the impact of interest rate risk on benefit value and also develop a health risk modeling framework to enable a retiree to gauge the change in present value of future Social Security cash flows after contracting a disease. We note that this is distinct from stochastic process based yield curve models (cf. (Brigo and Mercurio 2007) for a review) and hope to compare these in subsequent work.

Although we focus on optimizing the present value of future Social Security benefits, we note that circumstances may arise where a beneficiary may have a different financial goal in mind. For example, in (Choi et al. 2008), the authors considered optimal portfolio construction, while taking into account the retirement consumption and leisure utility of the beneficiary. In (Huang et al. 2012), the interplay between the consumption rate of the retirement savings of a beneficiary and simultaneous health status was modeled as a stochastic process. Within this framework, the authors considered the optimal retirement consumption problem. A similar life-cycle model was studied in (Bloom et al. 2004), where the authors optimized the lifetime expected utility of an individual which roughly represented the tradeoff between their felicity, life expectancy, and the dis-utility of labor. Each of these works provided a means of modeling the individual preferences of a beneficiary through a utility function. We limit the scope of this initial work only to present value maximization of future benefit cash flows; however, we seek to broaden the framework below to incorporate beneficiary utility in future work.

The life expectancy of the beneficiary is the primary determinant of Social Security benefit value. Mortality rate forecasting is a widely studied topic, cf. (Booth and Tickle 2008) for a survey. The Lee–Carter model (Lee and Carter 1992) is utilized for life table forecasting, by the Social Security Administration for their internal program solvency studies, as well as by the Census Bureau for population forecasting (Hollmann et al. 2000). Since the publication of this seminal work, a number of extensions have been developed, which involve restricting to specific cohorts as in (Renshaw and Haberman 2006) or extending to more complex predictive models with the aim of achieving stronger predictive performance (Richman and Wüthrich 2018). In addition, related stochastic mortality models that extend the Lee–Carter model are surveyed and compared in (Cairns et al. 2009). We consider one such minimal extension developed by (Mitchell et al. 2013) where the authors remained within the Lee–Carter framework; however, they demonstrated that if one estimates the model using mortality rate changes as opposed to absolute rates as originally specified, significant performance improvements may be realized while retaining the complexity of the original model. This motivates our application of this refined model to mortality rate forecasting.

In addition, we consider the two central risk factors associated with Social Security benefit valuation, which include interest rate and health risk. Principal component analysis (PCA) is a widely utilized technique to decompose the time variation of interest rate and commodity curves (Cortazar and Schwartz 1994; Litterman and Scheinkman 1991) into their maximal directions of variation, thereby defining risk factors. We first perform a PCA on the discount curve used to present the value of future cash flows in order to understand the most significant interest rate risks. Then, we consider scenario analyses by perturbing the current discount curve in this direction in proportion to the factors’ observed standard deviation and estimate associated changes in benefit value for several risk scenarios. Secondly, we examine health related risks including the event that a beneficiary contracts a mortal disease. In particular, given a survival curve conditional on the retiree’s age and severity of diagnosis, we estimate an associated updated life expectancy distribution and compare the new Social Security value to the prior value. We consider three diseases including, heart failure, pancreatic cancer, and Alzheimer’s disease. We do not consider program solvency risks in the form of benefit reductions, increased retirement age, or other plan parameter changes and leave these issues for subsequent studies.

Finally, we carry out a number of numerical studies that utilize these valuation and risk techniques. In particular, we first demonstrate the differences in future Social Security payment present value as a function of the date of death of the beneficiary. This in turn is used with life expectancy forecast data for the entire American population to determine the present value for each possible retirement date of the beneficiary, which allows one to determine the optimal retirement date. Next, we compare differences in Social Security value depending on when the beneficiary makes the best and worst possible retirement date decisions as a function of income. We next examine how such optimal retirement decisions vary for beneficiaries who have different health profiles. Then, we consider similar studies for distinct demographic cohorts in order to understand which groups are most impacted by sub-optimal retirement decisions. In addition, we develop a number of risk scenarios based on PCA techniques for both yield curve and life table mortality rates.

This article contains several new contributions, which include:

• An application of present value pricing methods that incorporate life table forecasting techniques, which are fit on current yearly frequency mortality rate data, to the problem of valuing future Social Security cash flows.
• The development of principal component analysis based risk scenarios designed to measure the sensitivity of Social Security benefit value to future yield curve changes. Specifically, we estimate the first two principal components of the United States swap curve and then perturb the discount curve in the directions of these principal components and revalue future cash flows to understand the risk inherent in such scenarios.
• We offer a number of new health and demographic studies that examine how the value of future Social Security cash flows varies by gender and demographic group. These studies incorporate the life table forecasting models described above and current mortality rate data for each such group.
• In addition, we provide a number of new numerical studies that examine how Social Security present value and optimal retirement age vary by cohort, income level, and health profile of the beneficiary. We also examine how contracting a disease impacts the present value of future benefits and the optimal retirement date for a retiree.

This paper is organized as follows: In Section 2, we fix notation and describe how to value future Social Security benefit cash flows. In Section 3, we review the construction, estimation, and forecasting of mortality rates and their incorporation into Social Security valuation. Then, in Section 4, we summarize the Social Security valuation algorithm and associated methodology that will be utilized in the numerical studies below. Next in Section 5, we turn from valuation methods to the development of risk techniques. Specifically, we quantify interest rate and life expectancy risks that impact the value of future Social Security cash flows. We utilize principal component analysis to construct the most likely risk scenarios, which are run to examine how the present benefit value is adjusted in such situations. Then, in Section 6, we provide a description of a number of data sources that were required to carry out several valuation and risk numerical studies considered throughout this section. Finally, in Section 7, we summarize our main findings, as well as discuss a number of future research directions.

2. Social Security Benefit Valuation

Payroll taxes are regularly deducted from American employee wages during the course of their career with the intent of providing the employee with an income stream during their retirement years. They are received in the form of a monthly benefit, which terminates upon the death of the beneficiary. The monthly benefit amount is determined in large part by the employee’s salary and work history length.

In the case of the Social Security program, the beneficiary is able to select the date when they receive their first payment, which we refer to as the retirement date. There are constraints on the retirement date; specifically, one may only start receiving Social Security payments after reaching age 62 and must initiate these payments prior to reaching age 70. If the beneficiary chooses to delay receipt of their initial payment, then the amount received for their monthly benefit will increase; however, they will receive fewer payments over their lifetime. We will investigate the tradeoff between these two factors while also taking into account the health profile of the beneficiary when considering the optimal retirement date studies below.

To fix notation, we let $t_v$ denote the date on which we will value future Social Security benefits and let $t_r\ge t_v$ represent the time until the retiree’s retirement date, on which the first benefit payment is received. We let $t_m$ and $t_M$ denote the minimum and maximum times that the beneficiary may initiate payments, which in the case of Social Security corresponds to the time when the beneficiary reaches age 62 and age 70, respectively.

After retirement benefit initiation, the retiree will receive monthly cash flows at times $t_1,\dots ,t_{n-1},t_n,t_{n+1}=t_d$ after his/her retirement date $t_0=t_r$ until the month prior to the death date $t_d$. We denote the cash flows associated with $t_i$ by $c_i$ for $i=1,\dots ,n$. Regarding notation, we note that $t_r$ and $t_d$ denote specific dates and not time indices, whereas $t_i$ indexes the n distinct cash flows previously described. All times may be summarized graphically on the timeline of Figure 1.

Note that the entirety of Social Security benefits may be thought of as a coupon only bearing bond with variable maturity date $t_d$. In addition, $t_d$ typically ranges between twenty and thirty years. As a result, long term interest rate changes have a significant effect on benefit value as is the case with zero-coupon or long maturity bonds.

Given a fixed date $t_d$, one can compute the present value of all future benefit payments assuming continuous compounding in the usual fashion. Here, we take t and x to range over discrete groups of annual times and age groups with a single year spacing, e.g., 2010 and the 55 to 56 age range, respectively.

In particular, let $r\left(t\right)$ denote the spot discount curve on the valuation date $t_v$. Then, the present value of the future cash flows is given by:

$$P\left(t_v\right)=\sum _{i=1}^n{e}^{-r\left(t_i\right)t_i}{c}_i,$$

(1)

where we note that $t_i$ typically occur at monthly intervals, $t_1$ occurs one month after the retiree initiates benefits upon retiring at time $t_r$, and $t_n$ occurs one month prior to the date of death of the retiree. We note that n depends on the date of death of the retiree, is modeled as a stochastic input below via the future month of death distribution of the beneficiary, and is unknown at the valuation time $t_v$. In addition, the value of the $c_i$ payments is determined by the Social Security Administration predominately as a function of the wage history and time of retirement of the retiree; they are independent of interest rates and the death date of the retiree.

Note that Equation (1) contains all the essential risk factors associated with Social Security benefits that will be further examined below. First, the date of death $t_d$ impacts the total number of payments received corresponding to the number of terms in the sum. Second, increases in the discount curve $r\left(t\right)$ will reduce the value of future cash flows. Finally, the size of the cash flows $c_i$ depends on the retirement date, and the constraints $t_r\in [t_m,t_M]$ may be altered by the program administrator in the case of program solvency issues. Our aim will be to investigate how these variables influence the price and risk of the present value of future benefits.

3. Life Expectancy Forecasting

The life expectancy of the beneficiary is the predominant factor associated with the present value of future benefit payments. For example, all other variables being comparable, the present value of the benefits of a retiree with a long life expectancy is typically several times greater than that of an individual with a short life expectancy. Mortality rate data, which contain this life expectancy information, are typically presented in the form of life tables, which contain the probability of survival over a given time window (usually one or five years), conditional on survival to the first age in this interval.

We first derive an expression for the conditional probability of a beneficiary living to a given age assuming death rates $p_i$ for a fixed calendar year, which denote the probability of death prior to age $i+1$ conditional on living to age i. A life table contains a collection of these $p_i$ values for a specific demographic group. Given that these occur at yearly frequencies, one may determine the distribution of the year of death of the beneficiary from the $p_i$ values. In particular, conditioned on living to age i, there is a $1-p_i$ chance of surviving between ages i and $i+1$. Similarly, the probability of death between ages i and $i+2$ is then $(1-p_i)p_{i+1}$ where the first factor accounts for the necessary survival from ages i to $i+1$. Continuing, the probability of death between years j and $j+1$ is $w_j=p_j{\prod }_{i=1}^{j-1}(1-p_i)$, which vanishes every year after the first year that $p_i=1$. Given a life table for an individual, we may construct a distribution for their death date given their current age from this process. 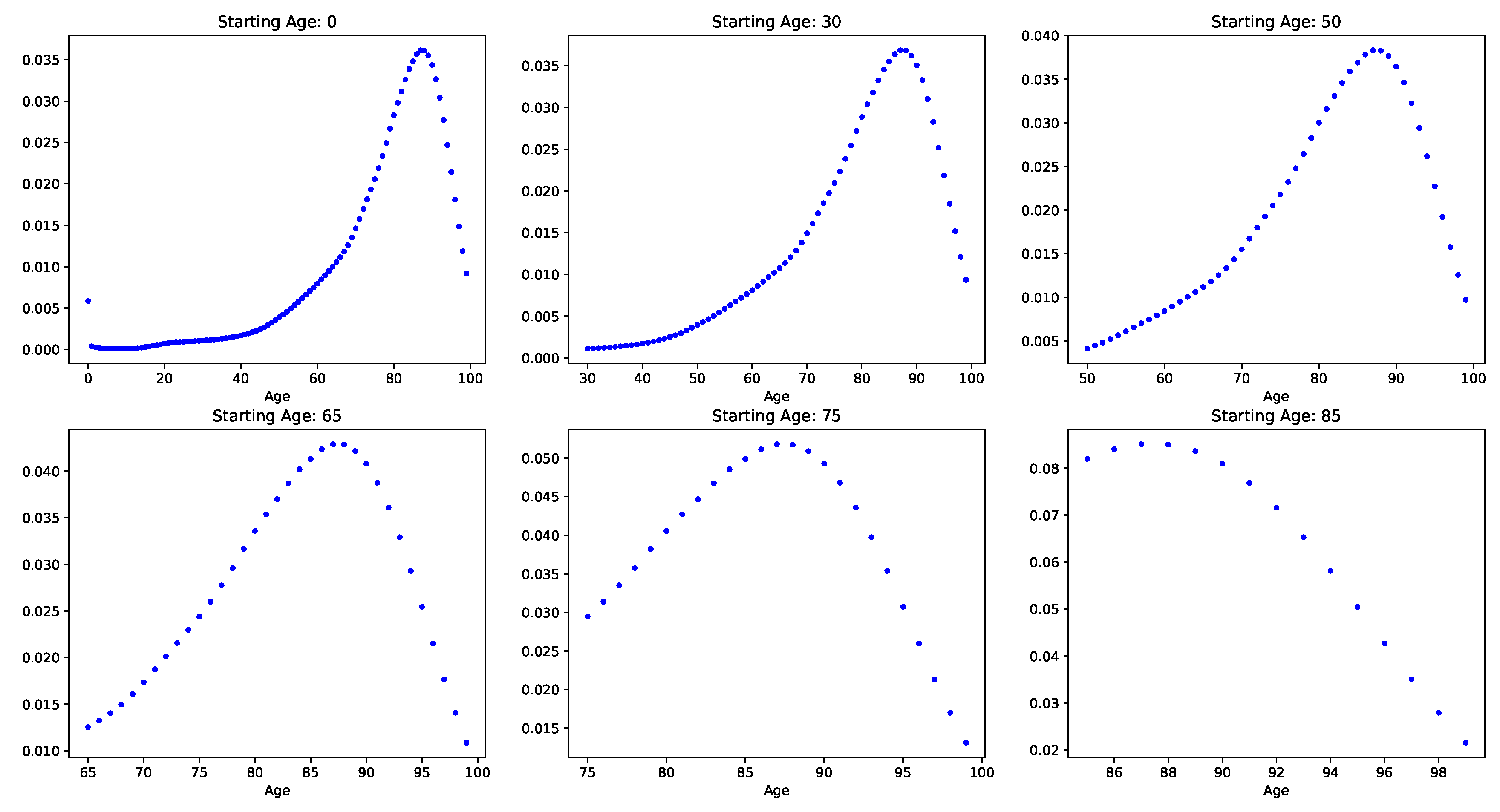We plot several example dates of death distributions in Figure 2 conditioned upon surviving to various ages.

Next, we note that for a given cohort, the $p_i$ vary over time and, in particular, generally decline over long time frames. We denote time varying life table probabilities by $p_i^t$, which represents the probability in calendar year t of living from age i to $i+1$. Then, as before, the probability of living to age j is $w_j=p_j^{t+j}{\prod }_{i=1}^{j-1}(1-p_i^{t+i})$. The process of estimating future $p_j^t$ values is referred to as life table forecasting; we review a few techniques designed to handle this task below.

Life Table Forecasting

Life expectancies evolve over time, and estimates for how they will most likely change in the future for different cohorts and age groups need to be incorporated into a Social Security valuation framework. In particular, death rates generally decrease since life expectancies tend to increase over time; however, there are situations where death rates for certain age groups increase, as we demonstrate in a numerical study below, typically over a few years of time. Since benefit payments tend to occur over several decades, incorporating forecasts of future life expectancy is essential to estimate accurately the future value of benefits one will potentially receive.

It is not uncommon for benefit payments to persist to the beneficiary for several decades beyond initiation during which time life expectancies may significantly increase. Accounting for this increased longevity is important when estimating the date of death distribution of the beneficiary. There is an extensive literature on life table forecasting; cf. (Ramirez 2015) for a survey. We now briefly review areas of this literature that will be relevant to the forecasting techniques, which we will incorporate into the Social Security pricing and risk techniques outlined in further detail below. The seminal Lee–Carter forecasting model (Girosi and King 2007; Lee and Carter 1992) has gained widespread adoption for both its relative simplicity and strong forecasting accuracy. A number of extensions have been developed to further improve the predictive performance of the Lee–Carter model, which vary in complexity from simple single factor cohort additions (Renshaw and Haberman 2006) to neural network based generalizations (Richman and Wüthrich 2018). We consider one such extension which focuses on model simplicity while simultaneously gaining significant performance improvements initially developed in (Mitchell et al. 2013). We provide detailed descriptions of both of these models in Appendix A.

4. Social Security Valuation Methodology

We now turn to combining the topics discussed in the prior sections to develop a methodology to value future Social Security payments. First, we summarize the process set by the Social Security Administration (SSA) to determine the monthly benefit payment for a beneficiary. We then forecast the date of death distribution as previously described and determine the present date value of future cash flows for each date of death of the beneficiary. Finally, we take an expectation over these values with respect to the date of the death distribution of the beneficiary. Each step of this procedure is now described in further detail.

The procedure utilized by the Social Security Administration to determine the monthly benefit amount a retiree will receive largely depends on career earnings and the age upon benefit initiation. More specifically, the main variables that influence the monthly benefit payment are the salary history during the top thirty-five working years of the retiree and the year and month of life during which when one retires.

We follow the benefits calculation form specified in Appendix D of SSA’s Annual Statistical Supplement (Social Security Administration 2018) to estimate the monthly benefit payment for a retiree. There are subtle differences between the actual Social Security benefit calculation and the output of this form; however, for practical purposes and in particular the applications considered below, such differences are marginal. We now provide a brief description of the content of this procedure.

The initial step involves the specification of the number of computation years for which the retiree’s payroll taxes will be considered in the benefit calculation. Then, the top thirty-five years of employment of the retiree are obtained, and one takes the minimum between these values and the maximum taxable amount of wages per year for which Social Security was collected. Next, we compute the average indexed monthly earnings (AIME) of the beneficiary by dividing the sum of these contributions by 420 and rounding down to the nearest dollar.

Next in the fourth step, the first and second bend points are defined; they are determined by the year that the retiree reaches age sixty-two. Using this information, the primary insurance amount (PIA) is calculated based on the values of these tie points and the process outlined in Step 4. Finally, in Step 5, the monthly benefit is determined by adjusting the PIA based on early or delayed retirement of the beneficiary.

This resulting estimated monthly benefit is one of the central inputs into the subsequent numerical studies below. It constitutes a baseline monthly payment upon retirement that the beneficiary will receive until their month of death. A premature or prolonged date of death will significantly influence the value of these payments.

Valuation Algorithm Outline

We now provide a detailed description of how the preceding ideas of benefit valuation, life table forecasting, and the monthly benefit calculation may be combined to develop a procedure to estimate the present value of future Social Security payments. The sequential descriptions below provide an outline for this valuation process, which will be utilized in the below numerical studies.

• First, we assume that the retiree has reached the age of 62 at time $t_v$ and would like to determine which month $t_r$ to start receiving Social Security benefits over the subsequent eight years until reaching age 70, i.e., $t_r>t_v$, with $t_r-t_v<8$. We note that when restricting to this age range, monthly benefit calculations are completely specified in Appendix D of (Social Security Administration 2018), whereas one would need to include additional assumptions in order to consider $t_v<62$ for retirement planning purposes. Since the minimum retirement age $t_m=62$, this condition is not exceedingly restrictive.
• We next consider life table data reported by the Center for Disease Control (CDC) for distinct cohorts (Arias and Xu 2018); specifically, all combinations of gender and three races: African American, Asian, Caucasian, and Hispanic. We note that the CDC life tables do not extend beyond age 100; this is accounted for in CDC life table data by assigning a probability of one for death over the subsequent year of life to any person that survives to age 100. For example, in 2015, according to the CDC, if the average American lives to age 98, the probability of death prior to reaching age 99 is 31.1%; however, the probability of dying prior to age 101 conditional on living to age 100 is one. Although effects on present value estimation associated with this assumption are minor during years prior to 2015, when one forecasts out life expectancies to later years, e.g., 2065, then the probability of living to 100 is no longer negligible. In addition, the jump in death probability from approximately 30% to one biases dependent present value calculations. With this in mind, we linearly extrapolated death rates based on the 98–99 and 99–100 rates with a maximum value of one to compensate for this issue. Finally, we note that there are a number of authors who have developed more accurate means of extrapolating death rates; cf. (Ediev 2018) and the included references. However, since the probability of the beneficiary living to such ages is low, we found that final present value results were not significantly impacted by the choice of extrapolation procedure, and as a result, we utilized a simple linear extrapolation method.
• Now, the life table forecasting model in Equation (A3) is used to estimate death rate evolution for the subsequent fifty years (until 2065) for the cohort under consideration using the method described in Section 3; this results in a death rate forecast for the survival probability of each future one year interval of life for the beneficiary. We finally construct a two-dimensional linear interpolation of these forecasted death rates to ensure we can sample them on a monthly frequency, which is used for the evaluation of the continuous expectation below in Equation (6).
• Now, we denote the forecasted death rate by $p_j^t$, which represents the probability at time t conditioned on living to age $x_j$ of dying prior to age $x_{j+1}$. From this, we construct weights:

  $$w_j=p_j^{t+j}\prod _{i=1}^{j-1}(1-p_i^{t+i}),$$

  (2)

  which we note may be done recursively through:

  $$\frac{w_{j+1}}{w_j}=\frac{p_{j+1}^{t+j+1}}{p_j^{t+j}}(1-p_j^{t+j}).$$

  (3)
  We assume that $p_j^t=1$ beyond a sufficiently large j for all t so that there is an m where $w_j=0$ for all $j\ge m$. From these weights, we are able to construct the date of death distribution $\varphi (y;x_t)$ of the beneficiary conditional on living to a given age.
• Let $f(t,T,S)$ denote the forward rate curve at time t, which represents the rate of return of a risk free loan from time T to time $S>T$. We will use the forward rate curve $f(t,t_r,s)$ to discount future cash flows back to the retirement date $t_r$ to determine the future value on the retirement date of Social Security benefits. Then, we present the value of these cash flows back to the valuation date $t_v$. Specifically, we estimate the future cash flows that the beneficiary will receive based on their date of death distribution. For each month between $t_r$ and the month prior to death, the beneficiary will receive a cash flow $c_j=c\left(t_j\right)$, which is constant for any given year and increases annually by a cost of living factor given by the average cost of living increase. Since 1998, the cost of living annual increases range from a minimum of 0.0% in 2010, 2011, and 2016 to a 5.8% increase in 2009. Given the wide variation in cost of living increases, we utilized the mean cost of living increase over the past twenty years in the subsequent model. A twenty year window was selected, due to the atypical increases from 2009 to 2011, which were 5.8%, 0.0%, and 0.0%, respectively, which make the consideration of say a shorter ten year lookback period prohibitive. We estimated the cost of living increase factor averaging the Social Security cost of living increases over the twenty years prior to 2018 to be $\gamma =0.02195$. Thus, we recursively defined monthly cash flows by $c_{i+12}=(1+\gamma )c_i$ taking $c_0$ to be the monthly benefit estimate as determined by the process described above. We then computed the value of these cash flows at time $t_v$ for one month prior to the death date, denoted $t_k$, by:

  $$P_k\left(t_v\right)=e^{-r\left(\tau \right)\tau }\sum _j^{t_k}c\left(t_j\right)exp(-f(t,t_a,t_j)(t_j-t_r)),$$

  (4)

  where here, $\tau =t_r-t_v$ and the forward curve is constructed from the current discount curve $r\left(t\right)$ through:

  $$f(t,T,S)=\frac{lnq(t,T)-lnq(t,S)}{S-T},q(t,T)=e^{-r\left(t\right)T}.$$

  (5)

  for times $S>T\ge t_v$ where we assume continuous compounding in all the above, and here, $q(t,T)$ may be viewed as the price of a zero-coupon bond at time t with maturity T.
• We finally estimated the present value of future Social Security payments through linearly interpolating the date of death distribution, denoted $\varphi \left(t\right)$, and present value functions in order to align disparate frequencies between these two datasets and estimate the present value of future cash flows at the valuation date:

  $$PV\left(t_v\right)=\mathbb{E}\left(P\left(t\right)\right)=\int P_k\left(T\right)\varphi \left(T\right)dT,$$

  (6)

  through an adaptive numerical quadrature method.

This process will form the basis for valuing Social Security benefits in different applications below. For example, when estimating the optimal age to initiate Social Security benefits, we will replicate this computation for each retirement month possible for the beneficiary between ages 62 and 70 to determine which date results in the greatest present value. In another study, we will incorporate life table forecasts for different cohorts and repeat the above. In summary, the preceding Social Security valuation technique integrates the SSA’s monthly benefit calculation and life table forecasting methods to estimate the expected value of future Social Security benefits.

We finally note that a number of authors have investigated how retirement decisions vary by demographic group; we now compare the above results to this work when applicable, as well as motivate further studies that would be of interest to investigate in future work. In (Venti and Wise 2015), the authors considered, among other related issues, how education level and current health influence the decision to initiate Social Security benefits early. The found that the proportion of persons who initiated social security early between the ages of 62 and 64 decreased as their level of education increased independent of current health condition. In addition, they noted that for less than high school level education, that on average, 71% of women and 66% of men initiated social security benefits early. For those with at least a colleague degree, 44% of women and 40% of men did the same. A central aim of this study was to demonstrate that such decisions can be highly detrimental from a present day value perspective in addition to providing methods to compute the expected percentage loss from making a sub-optimal decision. Such methods are especially helpful to the low education low health group considered in (Venti and Wise 2015) where approximately 80% of the sample initiated Social security benefits early.

Next, in (Munnell et al. 2016), the authors considered how socioeconomic status can lead to individuals underestimating their cost of living during retirement and make poor decisions to retire too early. In addition, they estimated a target retirement age depending on socioeconomic status of the retiree conditioned on maintaining a similar pre-retirement standard of living. They concluded that approximately 70% of retirees that retired early at age 62 were unprepared for retirement, whereas only 22% of those who retired at age 70 would have obtained sufficient assets to maintain the same standard of living during retirement. In (Sanzenbacher et al. 2015), the authors further investigated this topic and considered the question of how many years beyond age 65 retirees must work depending on their socioeconomic status. In (Jijie et al. 2019), the authors demonstrated that pay-as-you-go defined benefit plans put low social economic classes at a disadvantage and proposed additional pension schemes that resolve this issue. We hope that the techniques developed in this work will enable one to consider this problem at a more granular level by valuing the future social security benefits of a retiree, which typically comprises a substantial portion of an individual’s retirement portfolio. In addition, it would be interesting to consider the analogue of these methods applied to the new pension schemes developed in (Jijie et al. 2019) and compare how present values change versus the current Social Security system.

5. Interest Rate and Life Expectancy Risk

Next, we consider the two most prominent risk factors that influence the present value of Social Security benefits. First, we examine the impact of changes in the discount curve to the value of future benefit payments. Given that the collection of Social Security payments may be viewed as a long dated coupon only bearing bond with variable maturity, it exhibits similar interest rate risk to long duration fixed income securities. In particular, the value is inversely related to interest rates. We quantify this relationship through a principal component analysis (PCA) study of the historical movements of a discount curve composed of swap rates; for a further description of why we utilized interest rate swap rates for long dated discount rates, please see Section 6.1. After identifying the directions in which the rate curve varied most significantly, we designed related yield curve scenario analyses from the principal components to examine the impact of such changes on Social Security benefit values. Stated another way, principal component analysis was utilized to determine the most likely interest rate curve movement risk scenarios.

Next, we considered the question of how disease diagnosis impacts the present value of future Social Security payments. In particular, when life expectancy considerably shortens due to the contraction of a disease, we addressed how one can incorporate the survival curve associated with the disease into a modified present value calculation. The numerical examples below provide a further demonstration of how such considerations affect the optimal date to initiate Social Security payments.

5.1. Yield Curve PCA Risk

Interest rate risk is a primary concern in fixed income portfolio management. When interest rates rise, the value of future cash flows declines and vice versa. The degree of change depends on the reference time for the rate, for example, three month, two year, and thirty year rates will have distinct percentage changes over any given day; although, as we will see below, they will be highly correlated. PCA provides a means of determining how the interest rate curve in its entirety based on historical changes. In particular, one may view PCA as a technique to decompose yield curve movements into a basis of the most likely future interest rate movements. One can use this in turn to design risk scenarios. This information may be used to determine the associated price risk of future Social Security benefit cash flows. We provide a review of the method of principal component analysis in Appendix B.

In order to incorporate the yield curve principal components into an interest rate risk framework, we recall that the first principal component can be interpreted as the direction of maximal variation of data being considered. The second principal component depicts the direction of maximal variation on the $n-1$ dimensional subspace, which is the orthogonal complement of the first. In addition, all principal components are independent in this covariance matrix setting. With this interpretation in mind, we define a perturbed yield curve,

$$r_c(t;c,m)=r\left(t\right)+c\sum _{i=1}^m\sqrt{{\lambda }_i}{e}_i,$$

(7)

in the direction of the first m principal components with the magnitude given by the square root of the eigenvalues that are scaled by a factor of $c>0$. In subsequent interest rate risk applications, we will revalue future benefit payments using the perturbed yield curve and examine the impact on the total value of all such payments when compared with the current market yield curve.

5.2. Life Expectancy Risk

The most significant variable impacting the present day value of future Social Security payments is the life expectancy of the beneficiary. Typically, a retiree expects to receive monthly benefit payments for two to three decades after initiating retirement. However, if the beneficiary contracts a disease that significantly shortens his/her life expectancy, one may only receive a fraction of the expected payments.

If a beneficiary who was otherwise healthy is diagnosed with a disease, we account for this in the preceding benefit valuation model by updating his/her date of death distribution to the survival function of the illness, which is largely a function of the age of the beneficiary at the time of diagnosis and the severity of diagnosis. In the numerical studies below, we will examine to what extent Social Security valuation is impacted by contracting three common mortal diseases.

Secondarily, a retiree is subject to longevity risks related to the entire population. In a similar manner to the yield curve risk model we described above, we consider a PCA based life table risk measure. In particular, as noted in (Bell and Monsell 1991; Bozik and Bell 1987; Girosi and King 2007), the Lee–Carter model can be viewed as a single factor principal component model. We wish to examine higher order risks associated with life table changes from a principal component study.

More specifically, denote a life table function $l(t,x)$, where here, x represents the age group variable, which can be viewed as an interpolated version of life table data previously considered $(t_i,p_i)$, where here, $p_i$ denote the conditional probabilities of death over the subsequent period for $i=1,\dots ,n$. We are interested in understanding the relative change of Social Security payment values due to a change in the life expectancy. Let $({\delta }_i,P_i)$ denote the eigenvalues and associated eigenvectors of a time series of historical life tables. Given a base expected life table $l\left(t\right)$, we can then perturb in the direction of the principal components through:

$$l_c(t;c,m)=l\left(t\right)+ϵ\sum _i^m\sqrt{{\delta }_i}{P}_i,$$

(8)

where here, we denote the scale constant by $ϵ$ and eigenvectors by $P_i$ in order to prevent confusion with the interest rate example. Then, we compute the Social Security benefit present value change through:

$${\mathsf{\Delta }}_{l_c}PV=\frac{PV\left(l_c\right)-PV\left(l\right)}{PV\left(l\right)}.$$

(9)

These relative changes in value are calculated in a number of numerical studies below. Finally, we note that one may perform this life table PCA on different time frequencies, i.e., instead of just one year intervals, one may consider five or ten year intervals to ascertain long term trends in life table changes.

6. Numerical Studies

We now turn to several numerical studies to provide demonstrations of the above Social Security valuation and risk techniques. The studies rely on data gathered from a variety of sources, which we summarize in the first subsection below. Next, we identify how one may determine the optimal year and month to initiate Social Security benefits based on the wage history and health profile of the beneficiary. Building on this study, we then investigate the difference in present value of future Social Security payments between the worst and best times to initiate benefits. This is considered for a range of health and income profiles. Next, we examine how these minimum and maximum present value bounds vary over different cohorts including Caucasian, African, and Hispanic males and females, as well as provide explanations for the qualitative differences between these values.

Then, we develop a number of risk scenarios based on the PCA techniques described above. First, we develop interest rate swap curve simulations by first computing and depicting the principal components of a discount curve composed of swap rates on daily, monthly, quarterly, and semi-annual frequencies. We then revalue future Social Security cash flows based on perturbations of the discount curve in the direction of the principal components and determine the percentage change in the present value of these future payments. We finally turn to health risk considerations by first incorporating the survival curves of pancreatic cancer, heart failure, and Alzheimer’s disease into the valuation procedure. We demonstrate a dramatic decrease in value if one contracts any of these diseases. Finally, we examine population level life table risk by computing the principal components of mortality rates for the full American population and developing associated risk scenarios as in the case of the swap rate example.

6.1. Data and Implementation Description

We first summarize the content, aggregation, and cleaning process for all datasets required in the subsequent numerical studies. In particular, we utilized five main data sources including information related to the specification of the SSA’s monthly benefit calculation, historical mean American annualized wages, life table data for multiple age group frequencies for the cohorts under consideration, swap rate time series for discounting and rate risk studies, and finally, survival curve information related to the diseases under consideration for health risk studies.

The calculation of the amount of one’s Social Security monthly benefit as specified according to the form in Appendix D of (Social Security Administration 2018) relies on multiple tables provided in this reference. This includes two worksheets to compute the indexed earnings and primary insurance amount of the beneficiary. In addition, it involves the use of tables that provide indexed earning factors, a type of inflation adjustment, cumulative cost of living adjustments, and maximum reduction limits given that the beneficiary takes early retirement.

Next, in order to carry out income related studies, we obtain data representing the average American’s annual wages that are subject to federal income and Social Security taxes. This information is contained in (Social Security Administration 2018), as well, and updated annually by the SSA. We note that it differs from mean income data gathered by other governmental organizations, e.g., the Census Bureau or Department of Labor, in that it only represents the portion of income that is subject to federal payroll taxes.

The most involved data gathering task consisted of obtaining historical life table data for varying cohorts. This information is available in the annually compiled United States life tables, which are part of the National Vital Statistics Reports Series published by the Center for Disease Control; cf. (Arias and Xu 2018). Specifically, these life tables contain the probability of survival over the following year for an individual who has lived to a fixed age; this information is available for various ages, genders, and races, as well as geographically distinct groups. The availability of data depends on the group being considered, as well as the desired age group frequency. For example, we were only able to obtain life expectancy data for yearly age groups for the Hispanic population from 2007 to 2015, whereas the same data are available from 1996 to 2015 for the Caucasian and African American male and female cohorts.

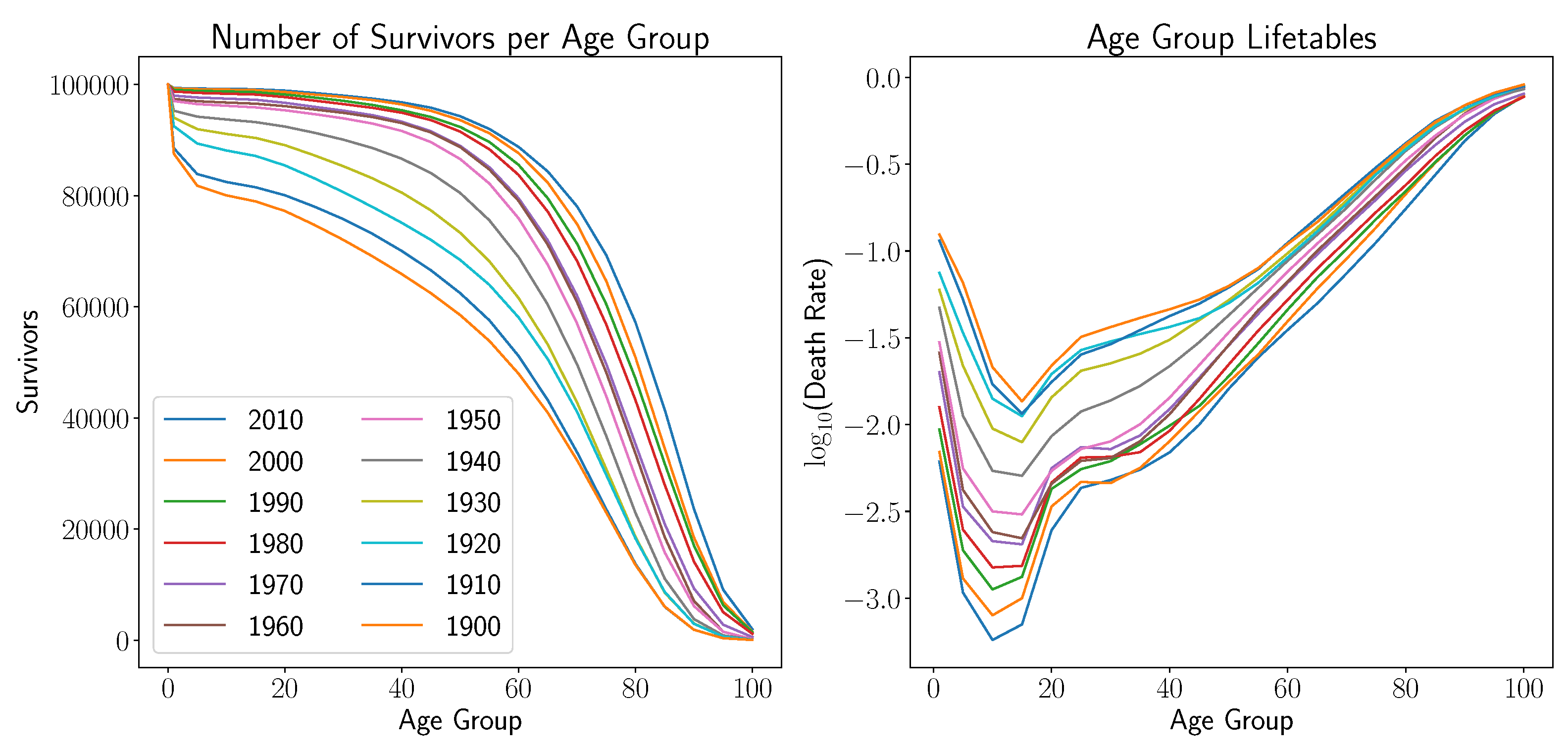
In addition, we gathered life table data for the entire population collected during the decennial census surveys from 1900 to 2010. The associated survivor and log death rate curves are displayed in Figure 3.

Note here that younger age groups, in particular infants, have seen dramatic increases in life expectancy, whereas such gains are less pronounced for older age groups. The varying changes per age group displayed in these graphs are precisely what the life table forecasting models previously discussed try to capture.

Next, we constructed a dataset of interest rate time series for the principal component and interest rate risk studies considered below. In American markets, liquidity of securities directly tied to interest rates can roughly be segmented into three groups based on maturity. In particular, for short term rates not exceeding one year, money market instruments such as treasury bills are the most liquid. On one to five year time frames, Eurodollar futures tend to be the most actively traded interest rate products. On longer time scales from five to fifty years, the interest rate swap market consists of the most liquid rates market. Specifically, since one expects to receive Social Security payments over multiple decades, we downloaded historical interest rate swap data for the following tenors consisting of 1 through 10, 12, 15, 20, 25, 30, 40, and 50 years from 2005 through the end of 2015. We downloaded these time series using Bloomberg’s Python API along with the Python packages tia and pandas. We then restricted to dates for which data were available for all rates under consideration.

Lastly, for the health risk studies discussed below, we sourced survival curve data for the three example diseases from the medical literature. Such information ranges from only a few data points to involved hazard rate models, which fit the parametric functional form to actual survival data. We considered pancreatic cancer survival data from Kaplan–Meier survival curves fit in (Wahutu et al. 2016), on data consisting of one, five, and ten year survival rates for patients encountering heart failure in (Taylor et al. 2017), and piecewise constant survival curves for Alzheimer’s diagnosis from (Brookmeyer et al. 2002).

Finally, we note that all numerical studies were implemented in the Python programming language. Data were first read, formatted, cleaned, and merged with the pandas package. Then, we utilized numpy and scipy’s optimization package for model estimation. Finally, graphical results are displayed using the matplotlib plotting package.

6.2. Optimal Benefit Initiation Time

We first consider an experiment designed to determine the optimal retirement age of an American with an average health profile and historical annual wage in the sense of maximizing the present value of his/her future Social Security benefits. Specifically, we assumed that the beneficiary had the average American population life table as of 2015 given in Table 1 of (Arias and Xu 2018). These data were used to fit the life table forecasting model (Mitchell et al. 2013) from which the date of death distribution for the average American from a health perspective was estimated. In addition, we assumed that they had earned the average American wage over the past thirty-five years using wage data from the national average wage index.

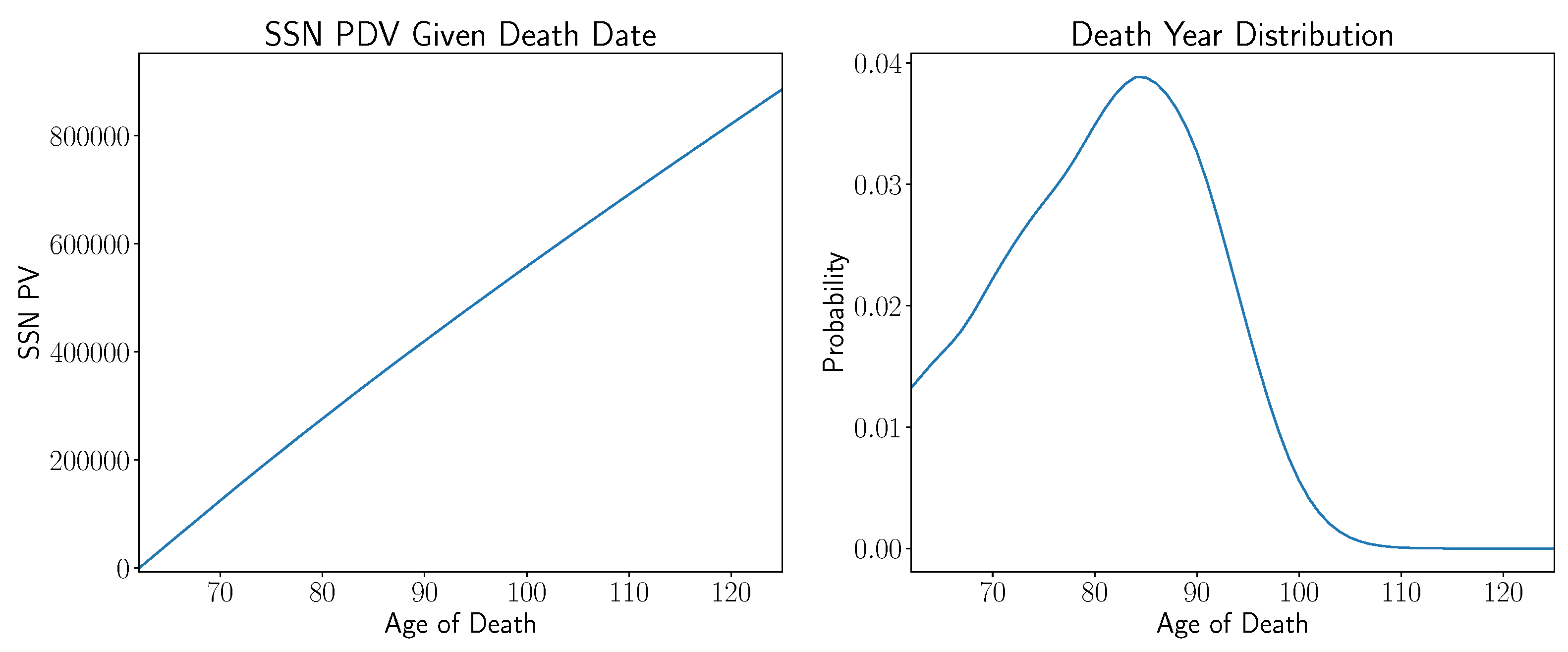
Moreover, we assumed that the beneficiary was presently age 62 and was seeking to understand which month within the next eight years to initiate Social Security benefits. First, in Figure 4, in the left subplot, we display the present value of future Social Security cash flows given that the beneficiary had a deterministic death date indicated by values on the x-axis, assuming Social Security payments were initiated at age 62. For example, if the beneficiary died just after reaching age 62, then he/she would receive a $0 benefit. However, if the beneficiary lived to age 80, the benefits were worth approximately $200,000, whereas at age 100, they were worth approximately $400,000. In addition, we note that the present value graph given a death date was slightly concave. More specifically, this curve had negative second order finite differences for all death dates. Moreover, these asymptoted to zero for longer death dates so that the original present value curve asymptoted to a line.

We note that this behavior may be seen in a simpler example of a constant rate annuity with a constant discount rate whose valuation formula consists of a sum of exponential functions with an increasingly reduced argument for longer maturities. The present value curve in this situation qualitatively exhibited the same asymptotic and concavity features.

The right subplot of Figure 4 is the corresponding date of death distribution of the beneficiary conditioned on living to age 62; assuming death rates according to the average American life table. In order to determine the expected present value of the beneficiary, we integrated the product of these two functions. The associated value was approximately $293,000, which was the present value of future Social Security payments given that the beneficiary chooses to retire at the age of 62; this is displayed in the left subplot of Figure 5. In other words, the values in the left subplot of Figure 5 can be thought of as the market value of all future Social Security payments given a date of retirement between age 62 and 70. The main reason for the large increase in value was due to the monthly benefit increase for delayed retirement depicted in the left subplot of Figure 5.

If a beneficiary waits until reaching age 70, the present value of future Social Security payments will be approximately $357,000, e.g., a $64,000 difference compared with initiating retirement at the earliest date possible. Notice that one can see the influence of the two tie points in the Social Security monthly benefit calculator in this graph between retirement ages 63 and 64, as well as near age 66. In the left present value graph of Figure 6, we note that the derivative of the plotted curve increases only at both tie points and decreases as a function of age everywhere else. In addition, in the monthly benefits subplot to the right, we display the values of the original monthly benefit dependent on which month the beneficiary decided to initiate retirement. Note that one can see the influence of both tie points there, as well as the rate of increase of the value of the monthly benefit increases after each tie point.

6.3. Optimal vs. Worst Retirement Decision

One of the most striking conclusions from the prior study was that there was approximately a 23% difference between making the best and worst retirement date initiation decisions. Our next aim is to explore how such percentages vary as a function of the historical income and health profile of the beneficiary.

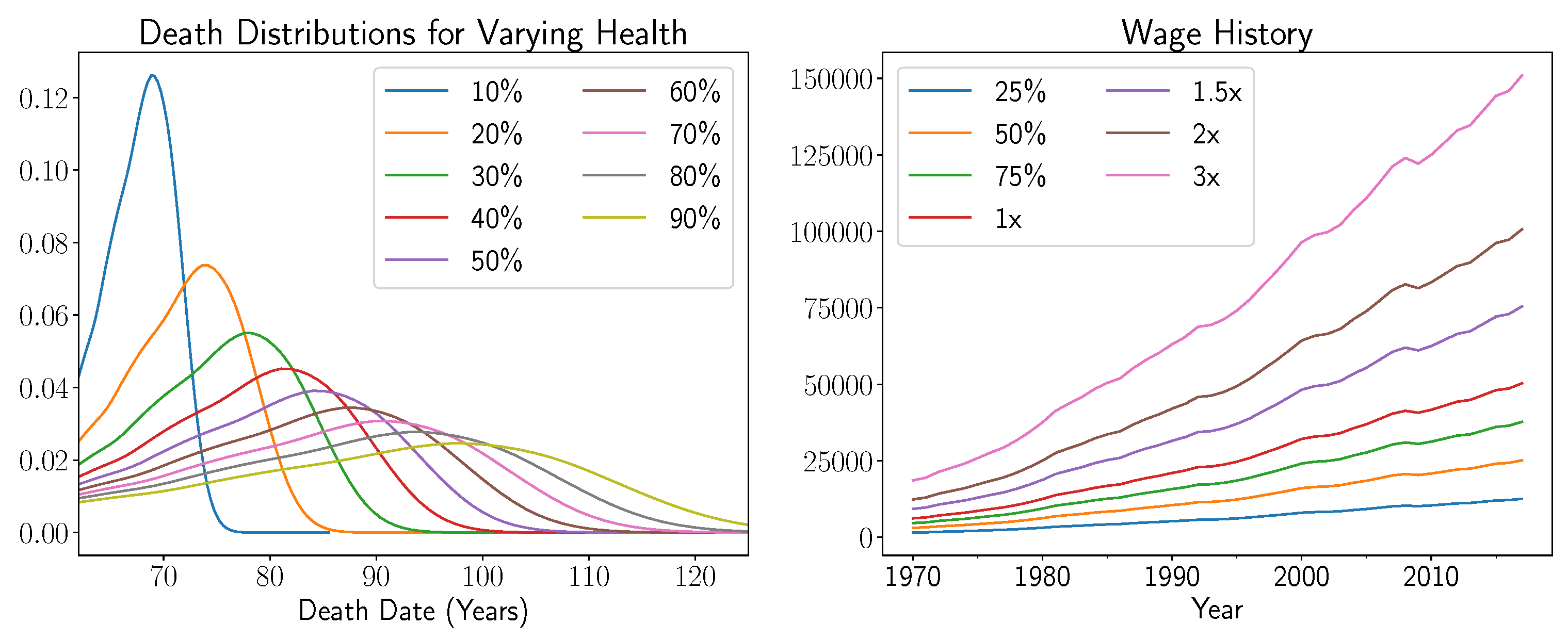
We first parametrized beneficiary income and health levels. We considered the national average American wage index as a baseline income measure. This index is intended to represent the average annual wages per worker that are subject to federal payroll taxes and is also used as an inflation index when the SSA considers cost of living adjustments on a yearly basis (Clingman and Kunkel 1992). In this study, we consider seven possible historical income scenarios for a beneficiary who is presently aged 62 who first started working in 1970 and earned 25%, 50%, 75%, 1, 1.5, 2, and 3 times the national wage index. Time series of the non-inflation adjusted wages for each case are displayed in the right subplot of Figure 6.

Next, we constructed eight possible health scenarios for the beneficiary based on the forecasted average American date of death distribution conditioned on living to age 62 constructed in Section 6.2. Specifically, we first estimated the deciles of this distribution and secondly rescaled its domain and the corresponding functional form for the distribution so that the resulting median value matched the associated deciles. The result was a collection of nine distributions whose median values were the quantiles of the average American date of death distribution. In addition, the general shape of the average distribution was retained through the rescaling procedure, and we plot the probability density functions of each such distribution in the left subplot of Figure 6. Here, the blue distribution represents the lowest life expectancy situation with the dark yellow representing the longest living scenario.

The distinct combinations of historical wage and future death distribution scenarios will comprise the main data content of this study. We first computed the expected present value of future benefits assuming the average American forecasted life table and associated monthly benefits based on the selected age of retirement and display the results in

Table 1. Present day value of future Social Security benefits based on age of retirement and income level as a multiple of the national average wage index.

Age/Income	25%	50%	75%	$1\times$	$1.5\times$	$2\times$	$3\times$
62	136.2	188.6	241.1	293.5	379.3	428.5	472.7
63	139.6	193.4	247.2	300.9	389.0	439.4	484.7
64	144.7	200.5	256.2	311.9	403.2	455.4	502.3
65	149.5	207.0	264.6	322.1	416.3	470.2	518.7
66	153.3	212.3	271.4	330.3	427.0	482.3	532.0
67	157.9	218.7	279.4	340.2	439.8	496.7	547.9
68	161.8	224.1	286.4	348.6	450.6	509.0	561.5
69	164.7	228.2	291.6	355.0	458.9	518.3	571.7
70	166.8	231.1	295.3	359.5	464.6	524.8	578.9

and

Table 2. Monthly benefit amounts according to SSA’s benefit estimator for varying age of retirement and historical income scenarios. The column headers indicate the multiple of the national average wage index considered in each scenario.

Age/Income	25%	50%	75%	$1\times$	$1.5\times$	$2\times$	$3\times$
62	619	857	1095	1333	1723	1947	2147
63	660	915	1169	1423	1840	2078	2292
64	714	989	1263	1538	1988	2246	2477
65	769	1066	1362	1657	2143	2420	2670
66	825	1143	1460	1778	2298	2596	2863
67	890	1233	1575	1918	2479	2800	3088
68	957	1325	1693	2061	2665	3010	3319
69	1023	1417	1812	2205	2850	3220	3551
70	1090	1510	1930	2349	3036	3429	3782

, respectively.

Note that the relative difference between the greatest and least present value corresponding to initiating benefits at age 70 rather than age 62 was nearly constant across varying incomes. In particular, there was a 18.4% difference in value between retiring at the age that maximized present value vs. that which minimized this amount.

We display corresponding monthly benefit amounts for each income and retirement age combination in Table 2, which also had a constant difference across income level between age 62 and 70 given by 43.2%. Stated another way, the penalty one pays for taking early retirement is equivalent on a relative basis across income, although it increases from the perspective of an absolute dollar amount.

Now, we examined the joint effects of health and income on the present value of future Social Security cash flows. We wished to understand how the percentage difference between the best and worst retirement times from a present value point of view varied as a function of these two variables. We first note that it did not depend on income level, just as we saw in the specific case above. With this in mind, in

Table 3. Best and worst age to initiate Social Security benefits and associated percentage difference in the present value of future Social Security payments based on these days.

Health Percentile	10	20	30	40	50	60	70	80	90
Best Age	62	62	62	65.2	68.2	69.3	70	70	70
Worst Age	70	70	70	70	62	62	62	62	62
Rel.Diff	692%	71.3%	20.7%	5.4%	7.7%	13.4%	19.0%	23.5%	27.4%

, we display the best and worst retirement ages for each health level, as well as the associated relative difference in Social Security present value.

Note that in the case of very poor 10th percentile health that it was optimal to take Social Security as quickly as possible at age 62 due to short life expectancy. Moreover the difference between the worst and best months to initiate benefits was quite substantial, being nearly a factor of seven. This was due to the fact that one is unlikely to live to age seventy, and if one delays benefit initiation to this date, he/she is likely to have zero value. Next, for near median health levels, note that the percentages were much lower, which may provide justification for a beneficiary to initiate benefits earlier at a smaller penalty. For healthy individuals with longer life expectancies, it is in their best interest to prolong retirement until the maximum age in order to realize the increased monthly benefit over several decades to come.

Next, we graphically depict the absolute dollar difference between the best and worst decisions as a function of health and income levels in Figure 7. Here, in the left subplot, the domain represents the seven income scenarios considered in increasing order, and the line plots depict the absolute dollar difference between making the best and worst retirement date decisions for varying health profiles. The left subplot contains the same information, but now varies over nine health scenarios and displays one line plot per income level.

Note that as a function of income, level losses rise with increased slope. In addition, one can see the influence of the two tie points in the Social Security benefits estimators in each such plot. When viewed as a function of health level, the plots show that for very low or high income, there was significant variance among losses between the best and worst decisions. However, for near median health levels, in particular between the 30th percentile and 50th percentile, the differences were minor.

6.4. Cohort Studies

We now turn to considering how the Social Security present value varies over different demographic cohorts. Specifically, we consider African American, Caucasian, and Hispanic male and female groups. We omit Asian Americans as we were unable to obtain sufficient data in order to estimate the life table forecasting model accurately. Data for the Hispanic population was available going back to 2007 and to 2016 for African Americans and Caucasians.

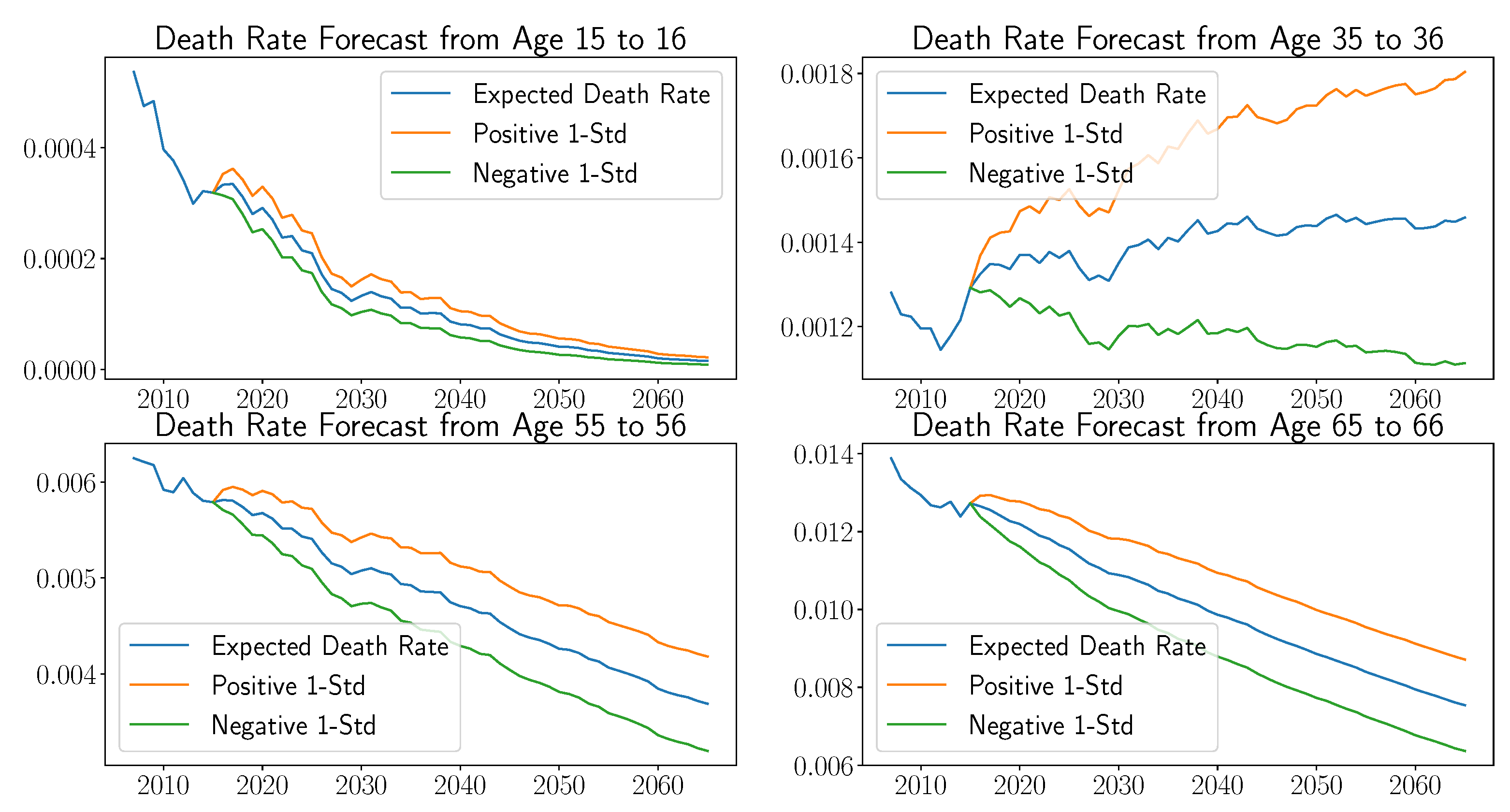
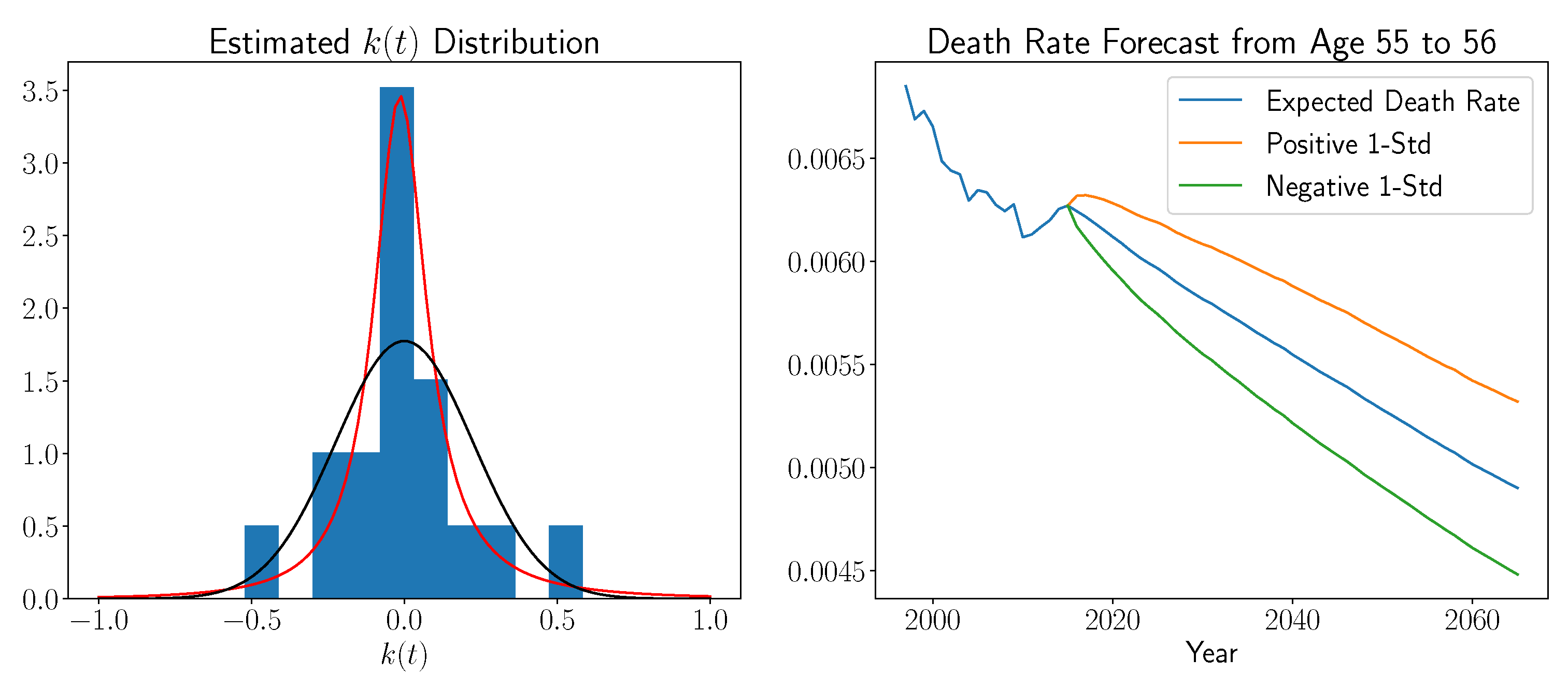
Although life expectancies generally increased for the majority of age groups for each cohort over this time period, we found a few interesting exceptions. For example, in Figure 8 below, we display actual and forecasted life table rates for the 15–16, 35–36, 55–56, and 65–66 age groups for Hispanic males. Prior to 2015, we plot actual death probabilities, and after this date, we plot forecasted probabilities along with associated standard deviation bounds.

Three of the age groups exhibited typical forecasting behavior; namely, a steady decline of death probabilities over time. Note that in these three examples, the standard deviation of the forecast was largely determined by the variance of the actual mortality rate data. Now, the 35–36 age group demonstrated non-standard behavior. In particular, the death rate for this age group starting at 2007 decreased until 2012 and then increased beyond the 2007 level in 2015. As a result, the associated forecasting curves slightly increased with large variation. We found similar effects for older ages in our sample, specifically, the mid-nineties age groups. However, overall, they had marginal contributions to the present value calculations as the probability of living to such ages is quite low.

Next, we examined how the minimum and maximum possible present value of future Social Security payments varied for the different demographic groups we were considering. In particular, for each of the three races, we computed the present value for the female and male sub-populations, as well as the entire population over all possible retirement dates. We then report the minimum and maximum present value along with the associated absolute and relative differences in

Table 4. Display of the present value (in units of $1000) of future Social Security payments for nine cohorts determined by gender and race. We assume that each group earned the national average wage index so that the below study examines average health differences between cohorts. In all cases, the minimum value was at 62 and the maximum at age 70.

Model	Min PV	Max PV	Abs.Diff	Pct.Diff.
Caucasian Male	267.3	320.6	53.3	16.6%
Female	319.0	391.5	72.5	18.5%
All	295.4	360.8	65.4	18.1%
African Male	234.4	287.6	53.2	18.5%
Female	289.2	358.4	69.2	19.3%
All	265.3	329.3	64.1	19.4%
Hispanic Male	316.9	393.9	77.1	19.6%
Female	359.5	450.1	90.6	20.1%
All	341.4	427.9	86.5	20.2%

. Here, we assumed that all groups earned the national average wage index over the past 35 years, so that only health effects were under consideration.

We first note that there was rather considerable variation between values between the different groups. Female present values exceeded those of males for each group due to longer expected female life expectancies. Interestingly, the Hispanic population had a considerably longer life expectancy over the time frame we were considering than either the Caucasian or African American groups. There have been a number of studies that examined this issue; for example, in (Diaz et al. 2016), the authors partially attributed this increased longevity to the fact that a large portion of the United States’ Hispanic population is migratory and that it is more likely those in good health would endure the stresses of migration than those who are in poor health. We finally note that the percentage differences between making the best and worst retirement decisions were roughly uniform across the different groups with Caucasians having the least loss at 18.1% and the Hispanic population having the largest losses at 20.2%.

6.5. Interest Rate Risk

Next, we examine how risk associated with yield curve changes impacts the value of future benefit payments. Since these payments often are received over several decades, it is important to understand how the full term structure of rates may evolve. Our aim is to develop a scenario analysis based on plausible future changes of the yield curve. In particular, we pursued a PCA based framework for identifying the directions in which the yield curve moved that corresponded to the most severe rate risks. In more detail, after we identified the most likely directions in which the interest rate curve may move, we then perturbed the yield curve in this direction and revalued future social security cash flows using the valuation techniques previously considered. Then, we finally compared the original benefit value to that post-perturbation; the associated percentage loss or gain in value allows one to assess the impact of such a scenario.

First, we studied how interest rate risk impacts the present value of future Social Security payments. Benefit payments may be viewed as a coupon only bearing bond, the interest rate risk profile exhibiting similarities to traditional bonds. Specifically, as interest rates rise, the present value of future cash flows decreases and vice versa.

We sought to design realistic risk scenarios by understanding the historical evolution of the discount curve used to present value future cash flows. We considered a subset of rates from Bloomberg’s US23 swap curve for this example. Specifically, we considered the swap rates at annual intervals from Years 1 to 10, as well as the 12, 15, 20, 25, 30, 40, and 50 year swap rates on a daily basis from the beginning of 2005 to the end of 2015. In addition, we considered rate curve changes on different frequencies; daily, monthly, quarterly, and annually. As described in Section 5, denote spot rates by $r_i^j$, where here, $j=1,\dots ,m$ ranges over tenors and $i=1,\dots ,n$ ranges over the frequency rates being considered, e.g., daily, monthly, etc. The covariance matrix and principal components were constructed for each rate dataset, which will be used to define the perturbed yield curve $l_1(t;ϵ,m)$ in Equation (8). Here, we will take $m=3$ as this accounts for nearly all the variability of the swap curve we are considering.

We considered changes in the yield curve on four different frequencies. First, we computed absolute rate changes based on end of day, month, quarter, and semi-annual intervals. In each case, this was done on a rolling daily basis from 2005 to 2015. The principal components were then calculated from the covariance matrix of absolute rate changes and its corresponding eigenvalues and eigenvectors. 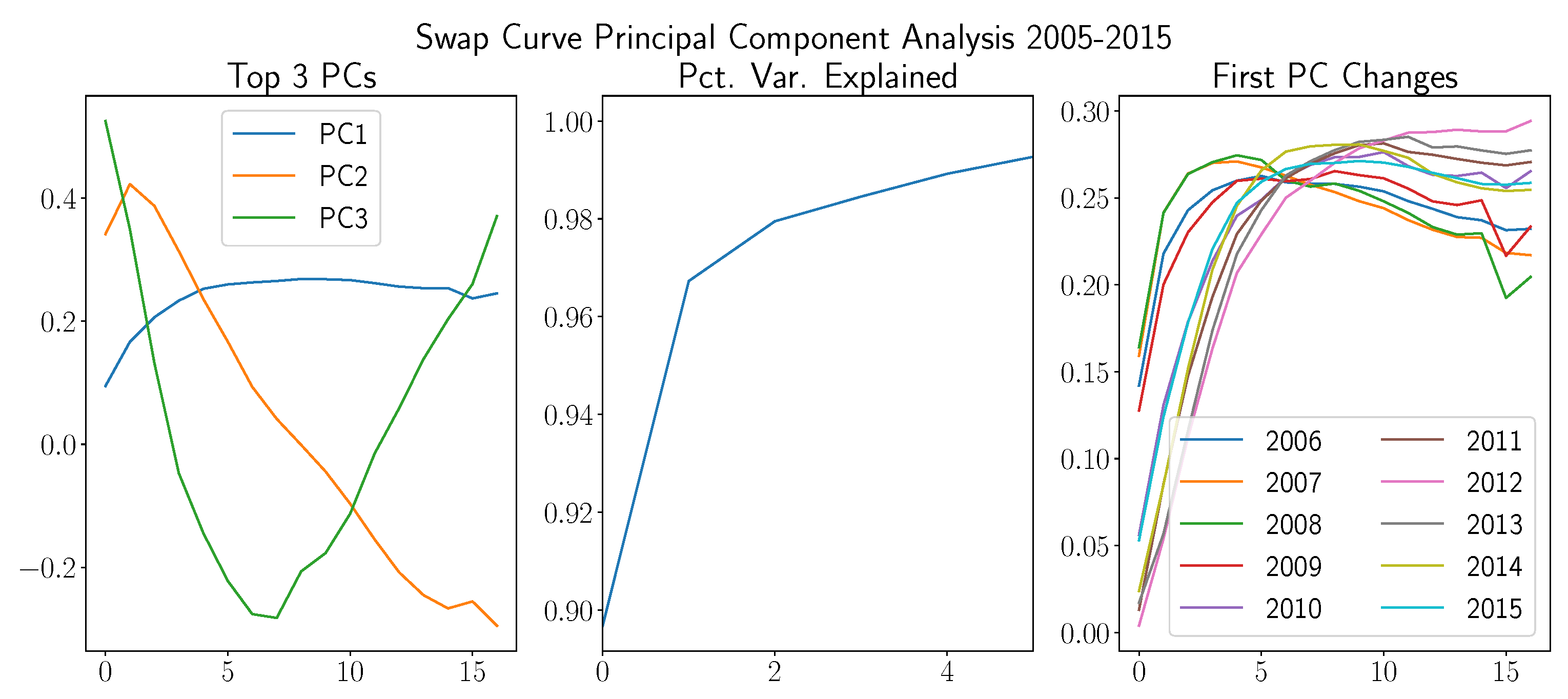We plot these principal components in the case of daily changes in Figure 9 along side an associated percentage variance explained graph. In addition, we considered how the first principal component changes over time in order to assess its stability qualitatively.

Note that the greatest three principal components estimated over the full ten year dataset had associated interpretations. In particular, the first principal component was nearly a constant function with the exception of slight variations for shorter term rates. The second principal component was a decreasing line (similarly, it may be represented as an increasing line since the principal components were only defined up to a sign), and lastly, the third principal component represented a bowing effect with high positive weight on short and long term rates with the opposite negative weight on mid-maturity rates. Next, in the middle subplot, we display the cumulative percentage variance explained by the first five principal components. Note that the bulk of the variation of the yield curve occurred in the direction of the first principal component, which explained approximately 90% of the variance. The first two principal components explained 97%, and the first three combined explained approximately 98% with marginal subsequent increases. This indicated that although many rates went into the construction of the yield curve term structure, the majority of its variation occurred in two directions. In the third subplot, we changed the estimation procedure to only consider one year of prior rate data when computing the covariance matrix. We then stored the first principal component, moved forward one year, and repeated this process. Note that these curves exhibited reasonable stability over time. However, there was a significant decrease in the values of the first principal component for short rates starting in 2010. This corresponded to the time when interest rates were lowered to near zero values after the 2008 financial crisis. Since rates were held at these values for several subsequent years, there was very little variation that occurred in short term rates, as is reflected in this plot. However, overall, these curves were reasonably stable over time, which provided motivation for their utilization in benefit value interest rate scenario analyses.

We now considered the change in present value for a Social Security beneficiary with the average population health profile who earned the national average wage index for the past 35 years in the below yield curve risk scenarios. We considered two types of scenarios based on the first and greatest three principal components. Specifically, we shifted the yield curve in the direction of the first principal component with the magnitude given by the square root of the associated eigenvalue in the former case and shifted by the sum of the top three principal components in the latter. We shifted the yield curve down for each scenario and scaled the shifts by factors that ranged from minor shift of 0.25 to a major one represented by a factor of three. The intent of these studies is to enable retirees to better understand the impact on the present value of their Social Security determined by plausible yield curve movement scenarios.

In

Table 5. Basis point decreases in swap curve risk scenarios for one and three principal components cases for the 5, 10, 20, 30, and 50 year swap rates. Here, PC1 scenarios only utilize the first principal component, whereas the full scenarios are constructed from sums of the first three principal components. Here, principal components are estimated from daily, monthly, quarterly, and semi-annual changes in interest rates.

Scen./BPShift	5 y	10 y	20 y	30 y	50 y
Daily PC1	5.92	6.29	6.01	5.95	5.75
Monthly PC1	27.8	28.6	25.6	24.6	25.5
Quarterly PC1	39.1	40.4	38.7	38.8	39.3
Semi Ann.PC1	62.8	64.0	59.3	57.8	56.9
Full Daily	7.87	6.48	4.48	3.64	2.80
Full Monthly	31.5	25.3	19.9	18.9	19.6
Full Quarterly	23.0	41.6	53.4	56.8	58.0
Full Semi Ann.	41.2	65.2	81.3	84.8	83.5

, we display the downward shift in basis points of the yield curve in each of the eight scenarios considered for the 5, 10, 20, 30, and 50 year rates. We performed the PCA and revaluation considering different frequencies of yield curve data. In particular, we examined daily, monthly, quarterly, and semi-annual interest rate changes. In the PC1 scenarios, we only adjusted the current swap curve by shifting by the first principal component of the absolute rate changes in the downward direction. In the Full PCA scenarios considered in the bottom portion of Table 5, we perturbed in the direction of a sum of the first three principal components. Since these components were only defined up to a sign, we considered both positive and negative shifts of the second principal component, which can be identified by the values of the rates described in the scenarios below. Specifically, note that the full PCA daily and monthly scenarios had decreasing rates as maturity increased, whereas the quarterly and semi-annual rates increased. This is reflective of the fact that we perturbed by a decreasing second principal component in the first two cases and an increasing one in the later two.

Note that scenarios that only considered the first principal component were nearly uniform across the different rates considered, whereas the full three principal component scenarios exhibited more variation due to the influence of the second principal component. We display results of relative changes to the present value of future Social Security payments in

Table 6. Percentage change in the value of future Social Security payments for each scenario where the perturbation by the principal components is scaled by the value in the column header.

Scen./$\mathit{ϵ}$	25%	50%	$1\times$	$2\times$	$3\times$
PC1 Daily	0.26	0.53	1.06	2.13	3.21
PC1 Monthly	1.16	2.33	4.73	9.70	14.94
PC1 Quarterly	1.69	3.42	6.97	14.5	22.62
PC1 Semi Ann.	2.65	5.38	11.09	23.58	37.64
Full Daily	0.23	0.45	0.91	1.83	2.75
Full Monthly	0.92	1.86	3.75	7.65	11.71
Full Quarterly	2.12	4.30	8.83	18.67	29.64
Full Semi Ann.	3.27	6.68	13.94	30.37	49.84

for each scenario. Here, we scaled the yield curve changes by a factor $ϵ$ described in the column header of the table to consider yield curve movements of increasing severity. For example, if $ϵ=2$, then the thirty year rate would be shifted by 11.9 basis points in the daily PC1 example.

Note that since Social Security payments are expected to be long dated, even relatively short rate changes can have a significant impact of the present value of future Social Security payments. Relatively small single digit basis point changes in the yield curve result in approximately a one percent change in future payment present value. Only in the more extreme scenarios over quarterly or semiannual time periods do we find large changes in benefit value.

6.6. Life Expectancy Risk

We finally turn to the examination of the sensitivity of Social Security payment value to changes in the life expectancy of the beneficiary. There were two distinct varieties of life table related risk that we examined. First, we wished to understand the impact of a major change in the health status of the beneficiary on the optimal retirement date, as well as the value of future expected payments. We incorporated this change in health into our framework through the survival curve of the beneficiary that resulted from a contracted disease. In particular, we considered three specific examples for diseases with high mortality rates, including pancreatic cancer, heart failure, and Alzheimer’s disease.

Next, we studied how changes in broader population scale death rates impacted the present value of future payments of the beneficiary. Recall that in (Bell and Monsell 1991; Bozik and Bell 1987; Girosi and King 2007), the authors mentioned that the Lee–Carter method could be viewed as a single factor principal component analysis. With this in mind, we computed higher order principal components and designed an associated scenario analysis as in the case of the yield curve.

6.6.1. Individual Health Risk

When a beneficiary is diagnosed with a disease with a high mortality rate, the present value of their future Social Security benefits is significantly reduced. The amount of decline depends largely on the type and severity of the disease, which is quantified through a survival curve, in addition to the age of the beneficiary. We considered three examples of diseases with available survival curve data including pancreatic cancer, heart failure, and Alzheimer’s disease.

In order to understand the impact of being diagnosed with one of these diseases on Social Security value, we replaced the life distribution with the associated survival curve of the disease and then revalued future benefit payments. Our central aim was to understand the expected decline in benefit value due to such a change.

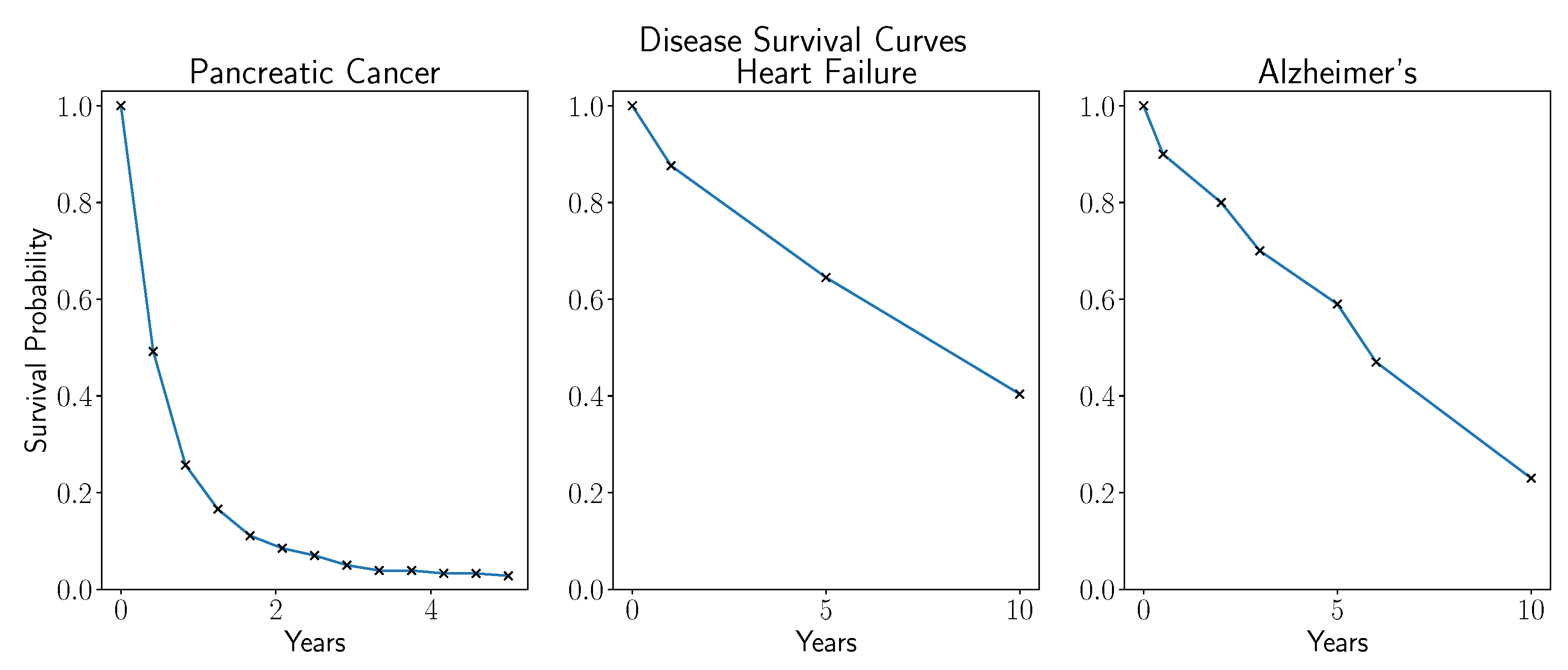
We sourced survival curve data for the three diseases under consideration from the medical literature. This information ranged from only a few data points per curve to involving hazard rate model function fits to actual survival data. We considered pancreatic cancer survival data from the Kaplan–Meier survival curves fit in (Wahutu et al. 2016), one, five, and ten year survival rates for patients encountering heart failure in (Taylor et al. 2017), and piecewise constant survival curves for Alzheimer’s diagnosis from (Brookmeyer et al. 2002). We display the survival curves considered in Figure 10, where here, we use piecewise linear interpolation to define rates between data points.

We finally extrapolated future survival probabilities in each case using linear extrapolation based on the final two survival data points of each disease. We note that there is a variety of techniques that examine the problem of survival probability extrapolation in further detail (cf. Day et al. 2015; Jackson et al. 2016); however, since the aim of this example was to demonstrate how survival curve data can be incorporated into the above benefit valuation and risk framework, we sought to keep the extrapolation method simple and leave higher fidelity survival curve modeling for future work. These three diseases were considered to examine the impact of differences between a high mortality disease like pancreatic cancer with a moderate disease such as Alzheimer’s and a relatively high survival probability example like heart failure. However, losses are quite significant in each case where we estimated a loss of 87.7% in the case of Alzheimer’s, 83.5% for heart failure, and 96.6% in the case of pancreatic cancer. Note that the median survival times for each of these diseases were approximately five years, six years, and four months, respectively. By contrast, a healthy individual had a median life expectancy of approximately 27 years conditioned on living to age sixty-two. This large decline in life expectancy was the main contributing factor for the associated very large losses in Social Security present value.

6.6.2. Population Life Table Risk

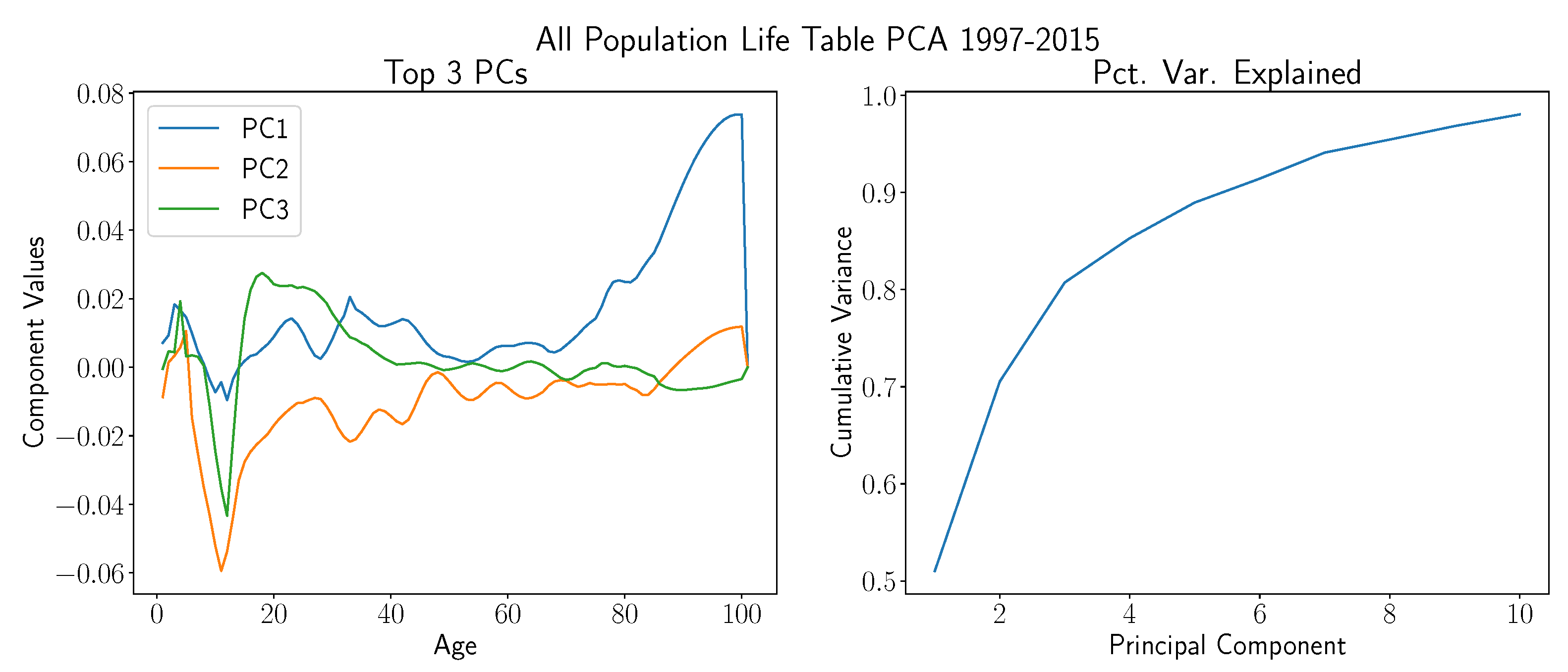
Lastly, we examined how broader mortality rate changes may influence Social Security present value by applying PCA techniques to historical life tables for the entire American population. We note that similar methods have been applied to life table modeling; cf. (Yang et al. 2010). For this study, we computed relative changes for each age group from all the population life tables from 1997 to 2015. We then computed the principal components of this dataset and plot them alongside the associated percentage variance explained in Figure 11.

First note that the cumulative percentage variance explained right subplot qualitatively differs from that of the prior swap curve example that we considered. In particular, it increases more gradually, and there is not a clear distinction between signal and noise components. However, approximately 80% of the variance is explained by the first three principal components, which will be utilized for the life table risk scenario design below. The values of the principal components are displayed in the left subplot.

The most notable features of these plots are the spikes on the second and third principal components near the ten year age, as well as the large increase in variance for older ages. For Social Security present value estimation purposes, we assumed that the beneficiary lived to age 62, so the artifacts for younger ages would not impact the associated risk scenarios. Beyond this age, the second and third principal components were relatively stagnant, whereas the first had a sizeable slope.

We consider two types of risk scenarios associated with these principal components in

Table 7. Percentage return estimates for varying population life table PCA based risk scenarios. We add positive and negative perturbations to forecasted life tables based on different standard deviation multiples of the first principal component and the sum of first three principal components.

Scen./Std. Mult.	$-3$	$-2$	$-1$	1	2	3
PC1	5.3	3.4	1.6	−1.5	−2.9	−4.2
Full PC	6.9	4.4	2.1	−1.9	−3.6	−5.2

below. Here, we add on the first principal component scaled by a factor represented in the associated column header onto each life table in order to simulate an increase or decline of the average population life expectancies. Here, we used the six positive and negative combinations of one, two, and three as multiples to design the scenarios. After the life tables were shifted, we revalued future cash flows in order to estimate the percentage change in the benefit value associated with the optimal retirement decision when compared with those estimated in Table 1.

We note that these changes were relatively minor when compared with the disease risk scenarios considered above. In addition, note that this table is not symmetric as, for example, one realizes a large 6.9% increase for the three full principal component multiples in the event of increased life expectancies vs. a 5.2% decrease in present day value when we decrease life expectancies by three times the full principal component sum.

7. Conclusions and Future Extensions

We presented a collection of techniques for the valuation and risk assessment of the present value of future Social Security benefits that incorporate the retirement age and health profile of the beneficiary, life table forecasting models, and the SSA’s monthly benefit specifications. The associated risk metrics are based on the principal components of both the discount curve and historical life tables for the cohort under consideration.

In addition, we considered a number of numerical studies that included the determination of the optimal retirement age of a beneficiary based on their current health profile and prior wage history. For further work, we would like to develop a public calculator and dashboard visualization to make these techniques accessible to wealth managers and those who need to estimate the value of their future Social Security benefits for asset allocation purposes. We also seek to incorporate survival curves for major diseases with associated high mortality rates in order to better advise individuals on when to start receiving Social Security benefits, as well as estimating expected losses associated with sub-optimal initiation decisions.

Furthermore, we seek to refine the manner in which disease survival curves are incorporated into the Social Security present valuation framework. Specifically, if the beneficiary had a greater than average life expectancy prior to contracting a treatable disease, then it is likely that he/she will also have an above average life expectancy while treating the disease. We seek to apply Bayesian techniques to incorporate the current health profile of the beneficiary as prior information into the estimation of the survival curve of the diseases specific to the beneficiary. This in turn would be incorporated into the present value framework.

We seek to extend the methods developed in this article to investigate solvency issues related to the Social Security program. In particular, we seek to forecast the future American workforce demographic distribution and utilize the present valuation methods developed in this article to determine upper and lower bounds on future program liabilities based on the best and worst times that beneficiaries from each cohort can retire from a present value perspective. This will be compared alongside future revenue expectations to estimate program solvency duration. Finally, we would like to incorporate the utility of the retiree into the optimal retirement framework in order to compare results in the maximum present value case to situations where beneficiaries place more emphasis on utilizing early Social Security cash flows to fund investment opportunities, consumption, or leisure activities.

Next, we note that in (Fellows et al. 2019), the authors found that for greater than sixty percent of the American population, it is optimal to delay retirement until age 70. Yet, they also found that approximately 65% of Americans took early retirement at age 62 to their financial detriment. We wish to better understand what influences these decisions in addition to developing valuation tools and associated visualizations that the enable retirees to make more informed decisions regarding when to initiate Social Security benefits.

Lastly, we note that Social Security income is typically one of many means that an individual utilizes to fund his/her retirement. For example, one may have accumulated savings in the form of real estate investments, equity, and fixed income positions in a brokerage account or money market savings. During retirement, an individual may drawdown simultaneously from each of these investment vehicles. Optimizing Social Security cash flow present value alone may potentially be detrimental to funding alternative investments that have stronger risk adjusted returns. In addition, when allocating capital to equity, real estate, and other non-pension related investments, one should take into account the value of future Social Security payments, which often consist of a sizable fixed income portion of their retirement portfolio. This initial study was focused on maximizing Social Security present value independent of other investments. In subsequent work, we hope to integrate the Social Security valuation and risk techniques developed in this article into a holistic retirement portfolio asset allocation technique with the goal of providing individual recommendations on how to allocate capital across the previously mentioned investment vehicles. In particular, we hope to compare social security benefits from a return on investment perspective to fixed income securities including sovereign bonds, corporate bonds, and TIPS. In addition, to extend the life expectancy and interest rate risk measures considered in this work, we aim to study the sensitivity of future Social Security cash flows to inflation in subsequent research.