Abstract
This article is concerned with the study of the tail correlation among equity indices by means of dynamic copula functions. The main idea is to consider the impact of the use of copula functions in the accuracy of the model’s parameters and in the computation of Value-at-Risk (VaR). Results show that copulas provide more sophisticated results in terms of the accuracy of the forecasted VaR, in particular, if they are compared with the results obtained from Dynamic Conditional Correlation (DCC) model.
1. Introduction
One common mistake in portfolio theory is to assume that multivariate financial returns are normally distributed. In practice, this assumption does not hold given that financial returns are usually found to be leptokurtic and asymmetric: they exhibit greater dependence during market downturns or upturns.
For this reason, we will assume that the joint distribution of log-returns on the FTSE (Financial Times Stock Exchange) MIB (Milano Indice di Borsa) pairwise with the DAX 30 (German Exchange Index) and the IBEX 35 (Spanish Exchange Index), respectively, is described by a copula function, defined as
where u and v are the uniform transforms of the marginals.1
The use of copulas is straightforward because of the theorem by Sklar (1959): It assesses that given F, joint distribution function, and given the marginal distributions , , then there exists a copula function such that, for all in
meaning that any multivariate cumulative distribution function can be written in terms of a copula C, which describes the joint structure of the risk factors, and in terms of the cumulative distribution functions of the single risk factors.
The parameters characterizing the copula are assumed to be time-varying. An interesting approach in the context of copula theory is the one proposed by Patton (2006); he extended Sklar’s theorem, allowing the dependence parameter to be conditional and time varying.
In a further work, Oh and Patton (2018) improved the time-varying equation for copulas via the so-called generalized autoregressive score (GAS) model.
Another interesting methodology combines regime Markov switching models and copulas. It has been introduced by Hamilton (1989) and assumes that a time series’ evolution is influenced by two different states of the economy, i.e., by a Markov chain with two states. Jondeau and Rockinger (2006) suggest that the time-varying parameter, i.e., the copula parameter, is driven by the following equation:
where is the value assumed by the dependence parameter during a low-dependence regime, the value assumed during high-dependence regime, and is the unobserved regime at time t. In this study, we will consider only the dynamics proposed by Patton (2006) and Oh and Patton (2018).
We want to introduce an approach to modeling dependence between financial returns allowing for two time-varying structures: we keep fixed one copula function across the two regimes characterizing equity markets, choosing between two copula forms.
An alternative to this approach is the one proposed by Rodriguez (2007), which assumes time variation in the functional form of the copula. We do not consider this possibility here.
The significance tests for the copula parameters are mainly settled on the Cramér–von Mises test statistic (t.s.). As in (Genest et al. 2009), we simulate from the hypothesized copula structure to get a distribution of fitted parameter from which we will obtain the desired error measure. Simulated pairs of observations from a given copula function are easy to obtain once the analytical form of the copula is known. As suggested by McNeil et al. (2015), we just need to rely on the inverse function of the copula density.
We are interested in comparing different dynamic copula models in terms of their ability to:
- Describe the evolution of the dependence in the tails via the computation of tail indices2.
- Forecast capital losses, computing and then forecasting one popular risk measure, like Value-at-Risk (VaR).
Given the importance of extreme events for risk management purposes, we select the best model according to VaR forecasts tests proposed by Kupiec (1995) and Christoffersen (1998), for equally-weighted portfolios composed by the returns of the DAX 30 and IBEX 35 indices in pair with the FTSE MIB returns.
As will be seen later, given that the distribution of the portfolio is unknown, being that the portfolio itself a sum of Generalized Autoregressive Conditional Heteroscedasticity (GARCH)-distributed risk factors, we rely on Monte Carlo simulation technique to obtain such risk measures (Christoffersen 2011).
Once several simulated statuses of the portfolio for each time step t are computed, we test the goodness of the VaR forecasts considering the two aforementioned tests: the Unconditional Coverage Test introduced by Kupiec (1995) and the Conditional Coverage Test by Christoffersen (1998).
We want to prove that dynamic copula models are a better specification in covering capital losses with respect to “traditional” models, like the Dynamic Conditional Correlation (DCC), which takes into account only the linear correlation coefficient as the dependence measure describing the joint behaviour of the single risk factors.
2. Model
2.1. Data Description
We consider daily log-returns of the stock indices IBEX 35, DAX 30, and FTSE MIB from 1 March 2006 to 8 June 2017. The data were downloaded from the Yahoo Finance website. The total number of observations is 2850: The first 2300 are used to fit the in-sample model, and the residual 550 are used for forecasting purposes. The daily returns we consider are those observed for simultaneous trading days occurring in all the Italian, German, and Spanish stock markets. For this reason, we dropped from the original data set all Italian, German, and Spanish closing days of the corresponding National Stock Exchange markets.
The period covered by our data sample comprises some main stock market crashes: first, the subprime crisis, during the period 2008–2009; and second, the explosion of the European debt crisis, from middle 2011 up to 2012, which was mainly driven by the Italian economic and political instability. For this reason, the period January–March 2013 will also be of particular interest, given the occurrence of the Italian Parliamentary election.
A few descriptive statistics of the returns are provided in Table 1.

Table 1.
Descriptive statistics of the three stock indexes, FTSE (Financial Times Stock Exchange) MIB (Milano Indice di Borsa), IBEX 35 (Spanish Exchange Index), and DAX 30 (German Exchange Index).
2.2. Estimation
The copula estimation method adopted will be the Inference For Margins (IFM) method. As suggested in Joe (1997), we first make an assumption on the marginal distributions of the single risk factors. Once the marginal distributions’ set of parameters is fitted, we assume a particular analytic form for the copula describing their joint behaviour. This straightforward procedure is possible because of the particular structure of the copula likelihood
where is the marginal density of x, the marginal density of y, and c is the copula density defined as
In Equation (1), the first sum refers to the joint distribution, whereas the second sum depends only on the marginals, meaning that IFM method consists of a two-steps optimization: first, two separate optimizations of the univariate likelihoods and then a maximization of the multivariate likelihood as a function of the dependence parameter vector. This procedure is computationally simpler than estimating all parameters simultaneously.
2.3. Marginal Distributions
In Table 1, there is evidence of sign of excess kurtosis. For this reason, we assume that the errors have a Student-t distribution. To capture the leverage effect, we also consider asymmetric GARCH specifications, such as the eGARCH model.
We selected an autoregressive moving average model (ARMA)(2,3)—eGARCH(1,1) with Student-t errors for FTSE MIB returns and an ARMA(2,2)—eGARCH(1,1) with Student-t errors for DAX 30 and IBEX 35 returns.
where is the log-return at time t, the residual at time t, and is a Student-t random variable with degrees of freedom.
2.4. Joint Distribution
We consider two particular copula forms from the class of parametric copulas. These copula functions have the willing property of being completely described by a vector of parameters and by a generator function, like
with called the generator function and the vector of the parameters.
The two functional forms for the copula are: a BB1 copula, as defined in Joe (1997), like
with and and a Symmetrized Joe-Clayton (SJC) copula,
with and . is the BB7 Joe-Clayton copula defined as
The interesting feature of copula functions is the possibility to calculate upper and lower tail indices through closed formulas. In particular, the expressions for the upper and lower tail indices, for the BB1 copula, are given by
and in the case of the SJC copula, by
The parameters are assumed to be time-varying. The first dynamic we consider is the one proposed by Patton (2006):
where is the parameter of the copula under analysis and is a given transformation. To keep the parameters in the right domain, we consider the following transformations:
- If , then we will set .
- If , we will set .
Equation (6) contains an autoregressive term, , and a forcing variable with coefficient . The identification of a forcing variable for a time-varying copula parameter is somewhat difficult: Patton (2006) suggests the use of the mean absolute difference between and over the previous 10 observations.
An alternative definition for the dynamic equation of the copula parameters is the GAS model, proposed by Oh and Patton (2018).
The evolution equation for the copula parameter is given by
where
with
being the score of the log-copula density function and a scaling factor, i.e.,
with as the Hessian matrix and . For simplicity, we will consider .
As stated in Creal et al. (2013), the reason for using the score as a forcing variable is that it depends on the complete density, and not only on the first- or second-order moments of the observations , so it may provide a more complete information about the improvement of the model’s local fit in terms of the likelihood.
2.5. Value-at-Risk
The computation of VaR will be performed on an equally weighted portfolio, like
with and the returns on the assets under analysis; in our case, is the return on FTSE MIB, and the return on DAX 30 and IBEX 35, respectively.
For the computation of portfolio VaR from copula models, we need to rely on Monte Carlo simulation techniques, given that the distribution of is hard to obtain, being itself a sum of GARCH-distributed risk factors. As suggested by Christoffersen (2011), Monte Carlo simulation essentially reverses the steps taken in model building:
- First, generate a random sample from the selected copula .
- Second, create shocks from the copula probabilities using the marginal inverse cumulative distribution functions on each asset.
- Third, create returns , from shocks using the dynamic volatility models.
Random samples in copula theory can be obtained considering the conditional probability distribution, defined as
The simulation algorithm goes through the following steps:
- Generate two independent uniform rvs u and s.
- Set , where is the inverse of .
- The desired pair is .
Once we have simulated N vectors of returns from the model, it is easy to compute the simulated portfolio returns using a given portfolio allocation. We consider a “rolling window” approach to compute one-step ahead forecasted VaR for the period February 2015–June 2017, just taking the -quantile on each vector of simulated states of the portfolio for each time step t. In particular, we will consider .
3. Results
The results of the estimation procedure are reported in Table 2.

Table 2.
Fitted coefficients and standard errors.
The choice of an eGARCH model with Student-t distribution for the marginals is justified by the results of Kolmogorov-Smirnov (KS) test, which are reported in Table 3.

Table 3.
Kolmogorov-Smirnov (KS) test results.
We tested for the null of uniform distribution for the probability transforms
where are standardized residuals and is the cumulative distribution function (cdf) of a Student-t distribution with degrees of freedom.
We do not reject the null of uniform distribution for the probability transforms of standardized residuals at all common significance levels.
The significance test adopted for the copulas is based on the Cramér–von Mises t.s., defined as:
with n being the sample size, , uniform transform of log-returns, and the estimated vector of parameters of the copula to be tested. The Cramér–von Mises t.s. is a measure of the mean squared difference between the empirical copula, defined as
and the hypothesized copula; one criterion is to select the copula that minimizes this quadratic distance between , the estimated copula, and .
A significance test suggested by Genest et al. (2009), and based on the Cramér–von Mises statistic, is then performed. We want to test the null
with being the family of parametric copula under analysis.
The structure of the test is summarized in the following algorithm.
- Compute , the empirical copula, from the uniform transforms and estimate the vector of copula parameters θ, say θn, via maximum likelihood.
- Compute the t.s. Sn.
- For some large N, repeat the following steps, .
- (a)
- Generate a random sample from copula , then compute their associated rank vectors , .
- (b)
- Compute and letbe the empirical copula. Compute an estimate of from via maximum likelihood.
- (c)
- Compute an approximate realization of by
- An approximation for the p-value of the test is given byKojadinovic et al. (2010) suggest using the following formula for the computation of p-values:in order to ensure that they are in the open interval .

Table 4.
Fitted coefficients, Cramér–von Mises test statistic (t.s.), and log-likelihood for the BB1, and for the Symmetrized Joe-Clayton (SJC) copulas with dynamic as in Equation (6).

Table 5.
Fitted coefficients, Cramér–von Mises t.s., and log-likelihood for the BB1, and for the SJC copulas with generalized autoregressive score model (GAS) dynamic as in Equation (7).
Small p-values can be observed in the case of a BB1 specification of the copula for both FTSE–IBEX and FTSE–DAX indices, whereas the null of an SJC copula distribution is accepted at all significance levels, provided that p-values in this case are equal to 0.67 for FTSE–IBEX indices (0.24 for FTSE–DAX, respectively). A similar result is obtained if a GAS dynamic is assumed for the copula parameters: the SJC–GAS copula specification is significant at level in the case of the FTSE–IBEX and only at level in the case of the FTSE–DAX. The null hypothesis of a BB1–GAS copula is rejected at all significance levels for both FTSE–DAX and FTSE-IBEX indices.
Value in brackets in Table 4 and Table 5 refer to an error measure of the fitted coefficients obtained via Monte Carlo simulation technique; once we fitted the coefficients via maximum likelihood, we have simulated from the selected copula 1000 times with parameters equal to the fitted ones, and then we re-fitted the coefficients from the simulated pairs of observations. We collected all the “simulated parameters” to get the desired confidence intervals. In particular, the values in brackets represent the mean of all the 1000 simulated parameters. A schematic representation of this procedure is given in the following algorithm:
- Estimate the vector of parameters , say , via maximum likelihood.
- For some large N, say , repeat the following three steps, .
- Generate a random sample from copula .
- Estimate of from via maximum likelihood.
- Collect .
The mean values of simulated parameters are close to the fitted values in the case of SJC copula, whereas in the case of BB1 copula, this happens only for few parameters. In the case of the SJC–GAS copula, a significant distance between fitted and mean value is observed only in the case of for the FTSE–IBEX pair of indices. For the BB1–GAS parameters, only fitted values for , , , and are close to the mean values of simulated parameters, for both pairs of indices.
The time evolution patterns of upper and lower correlations are provided in Figure 1, Figure 2, Figure 3 and Figure 4, where the blue line refers to the tail indices computed considering a static copula approach (i.e., only a particular copula structure is selected without allowing for the parameters to be time-varying). We recall that the computation of tail indices uses formulas in Equations (4) and (5).
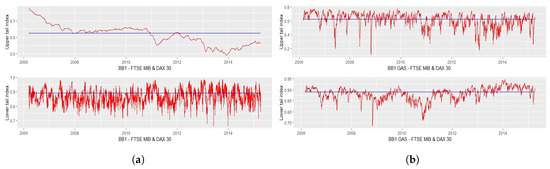
Figure 1.
Upper and lower tail indices of FTSE MIB–DAX 30. (a) BB1 with dynamic Equation (6); (b) BB1 copula with dynamic Equation (7).
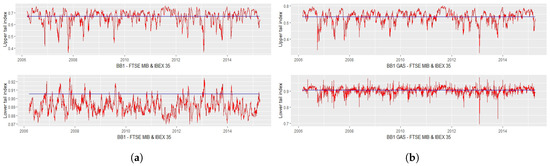
Figure 2.
Upper and lower tail indices of FTSE MIB–IBEX 35; (a) BB1 copula with dynamic Equation (6); (b) BB1 copula with dynamic Equation (7).
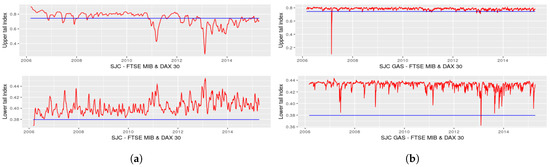
Figure 3.
Upper and lower tail indices of FTSE MIB–DAX 30; (a) SJC copula with dynamic Equation (6); (b) SJC copula with dynamic Equation (7).
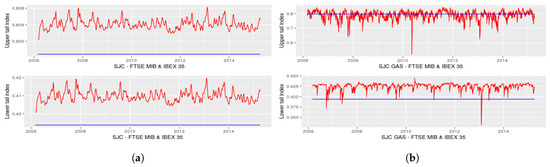
Figure 4.
Upper and lower tail indices of FTSE MIB–IBEX 35; (a) SJC copula with dynamic Equation (6); (b) SJC copula with dynamic Equation (7).
The symmetric behaviour between upper and lower tail indices is evident in the case of a BB1 copula specification with dynamic Equation (6) for the Italian-Spanish pair of indices, as shown in Figure 2a; there are peaks in the lower tail index—and, consequently, drops in the upper tail index—in the last part of 2007 and from middle 2009 up to the beginning of 2011. The upward trend in the lower tail index starts again in the middle of 2011, just before the explosion of the European debt crisis, and continues until 2013, where it reaches another maximum level.
In the case of tail indices obtained from SJC copula, it can be observed, as shown in Figure 3a and Figure 4a, that the values for the lower and for the upper tail indices are, in the case of the FTSE–IBEX pair, systematically above the values obtained from static SJC copula, meaning that the static approach seems to be more “conservative” with respect to the dynamic structure of Equation (6). Lower weight is given to lower tail indices in the case of SJC copula, with average values of 0.37 for the FTSE–IBEX pair and 0.38 for the FTSE–DAX pair.
Relevant peaks can be observed during periods of political instability in Italy: in particular, the period December 2011–January 2012, due to the beginning of president Monti’s technical government and during February 2013, on the occasion of the Italian Parliamentary election.
It is interesting to underline the joint behaviour of the two tail indices: in the case of the FTSE–IBEX pair, we get the same pattern in the upper and in the lower tail indices, meaning that the correlation between Italian and Spanish equity markets moves in the same way in both the right and the left tail. Instead, from Figure 3a, it can be observed that an increase in the lower tail index corresponds to a decrease in the upper tail index for the FTSE–DAX pair, and vice versa. In this case, we would say that Italian and German tail correlation behave in a symmetric way during shock periods.
We now analyse the time evolution patterns of the tail indices, considering a BB1 copula and an SJC copula with dynamic equation as in (7).
The SJC–GAS model tends to provide more stable results: in particular, in Figure 3b it can be observed that the upper tail index for FTSE–DAX is flat around 0.8 with one only exception at the beginning of 2007, where the index reaches the minimum value of 0.15. Greater variability is provided by the BB1–GAS model, as shown in Figure 1b and Figure 2a; the minimum value for lower tail index for the FTSE–DAX is reached in the second half of 2008, with a subsequent sudden jump. Another shock is observed just before the beginning of 2011, with a persistent trend around the static value of 0.89. At some points in time, particularly during the second half of 2008, the upper tail index reaches values close to 0 for the FTSE–DAX pair, meaning that asymptotic independence in the right tail is observed during severe economic crashes, as in September 2008. The trend is more stable in the case of the FTSE–IBEX pair, considering always a BB1–GAS specification, with values always greater than 0.7 for the lower tail index and 0.3 for the upper t.i.
Fluctuations of the upper and lower tail indices are observed in the case of the BB1–GAS copula: as shown in Figure 1b, during the fall of 2008 for the FTSE–DAX and, particularly, at the beginning of 2013 for both FTSE–DAX and FTSE–IBEX pairs, there is a considerable shock in the upper and lower tail correlations.
The results for the p-values shown in Table 4 and Table 5 suggest that the best copula specification is an SJC copula instead of a BB1 copula. For this reason, the SJC copula with dynamics given by Equations (6) and (7) will be taken into account for the computation of VaR.
In Figure 5, a graphical representation of the one-step-ahead forecasted VaR is provided.
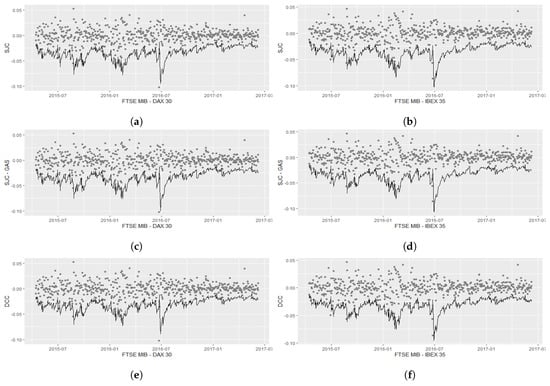
Figure 5.
Value-at-Risk (VaR) forecasts time patterns considering an SJC copula with dynamic Equation (6) (a,b), an SJC–GAS copula (c,d), and a DCC model (e,f). (a,c,e) refer to the FTSE MIB–DAX 30 portfolio VaR, while (b,d,f) to the FTSE MIB–IBEX 35 portofolio.
To evaluate the VaR forecasts, we use the Unconditional Coverage test proposed by Kupiec (1995) and the Conditional Coverage test by Christoffersen (1998). It is possible to construct an indicator sequence , , defined as
with being the return of the portfolio at time t; this is a straightforward way to count the number of violations.
The Unconditional Coverage test is a test for the null that the fraction of violations is significantly different from the assumed fraction . The t.s. is a likelihood ratio statistic given by
where , is the observed number of violations, and is the number of returns with indicator 0.
We can easily estimate from . is a chi-square distribution with one degree of freedom.
We do not want the VaR violations to come in clusters; if the VaR violations are clustered, then we can predict that if today is a violation, then tomorrow is more than · 100% likely to be a violation. Christoffersen (1998) proposed a combined test for both unconditional coverage and independence in the sequence , with being the null hypothesis of serial independence and a violation rate of of the violations . The test statistic in this case is given by
where is the number of returns with indicator i followed by returns with indicator j, with and . In this case, the chi-square distribution has two degrees of freedom.
Under , , meaning that, if the exceedances are independent, the probability of observing a new violation of the VaR at t is the same, independent of what happened in the earlier instant.
The two tests were performed on three multivariate models: an SJC copula with dynamic equation as in (6), an SJC copula with GAS dynamic, and a DCC model. Results are provided in Table 6. P-values are always equal to 0 if we consider a DCC model describing the joint behaviour of FTSE MIB and DAX 30, IBEX 35, respectively.

Table 6.
Test statistic (t.s.) and, in brackets, p-values for Kupiec test and Christoffersen test, considering –VaR on an equally weighted portfolio.
4. Concluding Remarks
In Table 4 and Table 5, small p-values can be observed in the case of a BB1 specification of the copula for both FTSE–IBEX and FTSE–DAX indices, whereas the null of an SJC copula distribution with the same dynamic is accepted at all significance levels, provided that p-values in this case are equal to 0.67 for FTSE–IBEX indices (0.24 for FTSE–DAX, respectively), considering the dynamic as in Equation (6). p-values for the SJC–GAS copula are significant at level in the case of the FTSE–IBEX and only at level in the case of the FTSE–DAX. The null hypothesis of a BB1–GAS copula is rejected at all significance levels for both FTSE–DAX and FTSE–IBEX indices.
SJC copula always provides higher p-values, meaning that it should be considered as the best specification in terms of the goodness of the fitted parameters.
The results of the Kupiec test and of the Christoffersen test are provided in Table 6: for the –VaR the null of the expected number of violations close to is not rejected at all common significance levels for the FTSE–IBEX portfolio and at level for the FTSE–DAX, considering both dynamic copulas under analysis. The null hypothesis of the Kupiec test is rejected at all common significance levels for –VaR if it is computed considering a DCC dynamic.
P-values for the conditional coverage test are always equal to 0 considering a DCC dynamic, whereas they are greater than for the FTSE–IBEX portfolio with both the SJC–GAS copula and SJC copula with dynamic as in (6). In the case of the FTSE–DAX portfolio, we get a p-value for the SJC–GAS copula, greater than and a p-value greater than for the SJC copula with dynamic as in (6).
The DCC joint structure should be rejected if the –VaR is considered, whereas both the SJC copula with dynamic as in (6) and the SJC–GAS copula perform well in the VaR forecasts tests considered.
We conclude saying that dynamic copulas, in comparison with the DCC model, not only provide a more sophisticated measure of the correlation (providing a specific measure for the dependence in the left and in the right tail), but they are also preferable in covering capital losses.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| rv | random variable |
| SJC | Symmetrized Joe-Clayton |
| GAS | Generalized Autoregressive Score |
| t.i. | tail index |
| cdf | cumulative distribution function |
| t.s. | test statistic |
| DCC | Dynamic Conditional Correlation |
References
- Christoffersen, Peter F. 1998. Evaluating interval forecasts. International Economic Review 39: 841–62. [Google Scholar] [CrossRef]
- Christoffersen, Peter. 2011. Elements of Financial Risk Management. Cambridge: Academic Press. [Google Scholar]
- Creal, Drew, Siem Jan Koopman, and André Lucas. 2013. Generalized autoregressive score models with applications. Journal of Applied Econometrics 28: 777–95. [Google Scholar] [CrossRef]
- Furman, Edward, Alexey Kuznetsov, Jianxi Su, and Ričardas Zitikis. 2016. Tail dependence of the gaussian copula revisited. Insurance: Mathematics and Economics 69: 97–103. [Google Scholar]
- Genest, Christian, Bruno Rémillard, and David Beaudoin. 2009. Goodness-of-fit tests for copulas: A review and a power study. Insurance: Mathematics and Economics 44: 199–213. [Google Scholar] [CrossRef]
- Hamilton, James D. 1989. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica: Journal of the Econometric Society 57: 357–84. [Google Scholar] [CrossRef]
- Joe, Harry. 1997. Multivariate Models and Multivariate Dependence Concepts. Boca Raton: CRC Press. [Google Scholar]
- Jondeau, Eric, and Michael Rockinger. 2006. The copula-garch model of conditional dependencies: An international stock market application. Journal of International Money and Finance 25: 827–53. [Google Scholar] [CrossRef]
- Kojadinovic, Ivan, and Jun Yan. 2010. Modeling multivariate distributions with continuous margins using the copula r package. Journal of Statistical Software 34: 1–20. [Google Scholar] [CrossRef]
- Kupiec, Paul. 1995. Techniques for verifying the accuracy of risk measurement models. The Journal of Derivatives 3: 2. [Google Scholar] [CrossRef]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2015. Quantitative Risk Management: Concepts, Techniques and Tools-Revised Edition. Princeton: Princeton University Press. [Google Scholar]
- Oh, Dong Hwan, and Andrew J Patton. 2018. Time-varying systemic risk: Evidence from a dynamic copula model of cds spreads. Journal of Business & Economic Statistics 36: 181–95. [Google Scholar]
- Patton, Andrew J. 2006. Modelling asymmetric exchange rate dependence. International Economic Review 47: 527–56. [Google Scholar] [CrossRef]
- Rodriguez, Juan Carlos. 2007. Measuring financial contagion: A copula approach. Journal of Empirical Finance 14: 401–23. [Google Scholar] [CrossRef]
- Sklar, A. 1959. Fonctions dé repartition à n dimension et leurs marges. Université Paris 8: 1–3. [Google Scholar]
| 1 | Uniform transforms can be defined in the following way: if x has cumulative distribution function and y has cumulative distribution function , then and are standard uniform distributed. |
| 2 | We make use of the classical tail dependence indices for simplicity; as will be seen later, they can be easily obtained using a closed form formula, once a particular copula function is settled, but the reader should be aware of the shortcomings in the use of classical tail indices when moving apart from the "Gaussian world". For details, see Furman et al. (2016), where the authors urge that the classical measures of tail dependence may underestimate the level of tail dependence in copulas. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).